Dynamics of multibody chains in circular orbit: non-integrability of equations of motion

Abstract

This paper discusses the dynamics of systems of point masses joined by massless rigid rods in the field of a potential force. The general form of equations of motion for such systems is obtained. The dynamics of a linear chain of mass points moving around a central body in an orbit is analysed. The non-integrability of the chain of three masses moving in a circular Kepler orbit around a central body is proven. This was achieved thanks to an analysis of variational equations along two particular solutions and an investigation of their differential Galois groups.

1 Introduction

Investigations of multibody systems dynamics are relevant for space missions such as space robots, tethered systems, and space stations. In the simplest models, systems of points connected with joints having specific properties are considered. For example, in the perfect dumb-bell model, two point masses are joined by a massless rigid rod. An example of investigations of motion of a dumb-bell in an orbit can be found in Celletti and Sidorenko (2008). This model is in fact a simplification of a system describing the motion of a symmetric rigid body in an orbit. One can also consider a spring dumb-bell in an orbit; see, e.g., papers (Burov and Kosenko 2013; Burov 2011; Sidorenko and Celletti 2010) and references therein. These kinds of systems can serve as models with a deformable body.

Other models of deformable extended bodies consist of point masses joined by massless rigid rods with spherical hinges. The simplest of them are just open chains. A system of $(n+1)$ points can be joined one after another to form an open chain with n links. It is called n-chain. The most general description of this type of systems in an orbital environment was done by Guerman (2003, (2006). Among other things, for such systems certain families of equilibria were found.

A peculiar dynamical property of linear chains is that if $n>2$, then equations of their free motion are not integrable; see, e.g., (Szumiński 2014). Moreover, an n-chain with one fixed end is just a multiple pendulum. Amazingly, even in the absence of the gravity field, the system is not integrable for $n>2$; see Salnikov (2013). Free systems of coupled planar rigid bodies were investigated also by Sreenath et al. (1988) and by Oh et al. (1989).

In this paper we derive equations of motion for an open chain in an arbitrary potential field. Next, we obtain equations of motion for a chain whose centre of mass moves in a circular orbit. We show that equations for 2-chains are not integrable. To obtain this result we investigate variational equations along two families of particular solutions. Thanks to this, we were able to prove the non-integrability for all allowable values of the system parameters.

2 Equations of motion and main result

We consider a system of $(n+1)$ points $P_0$, ..., $P_n$. Point $P_i$ is connected with point $P_{i+1}$ by a massless perfectly rigid rod and the junction is a spherical hinge. Thus, the points form an open chain with n links. Example of three points with two links forming 2-chain is given in Fig. 1.

Let $m_i$ and $\varvec{q}_i$ denote the mass and the radius vector of point $P_i$, respectively. The rigid rods put n holonomic constraints

$$\begin{aligned} ||\varvec{q}_i-\varvec{q}_{i-1} ||=l_i>0, \quad \text {for}\quad i =1,\ldots , n, \end{aligned}$$

(2.1)

on the system. We can set

$$\begin{aligned} \varvec{q}_{i} = \varvec{q}_{i-1} + l_i \varvec{e}_i=\varvec{q}_0+\sum _{k=1}^{i} l_k \varvec{e}_k = \varvec{q}_0+\sum _{k=1}^{n} \theta _{i,k} l_k \varvec{e}_k , \end{aligned}$$

(2.2)

where

$$\begin{aligned} \varvec{e}_i = \frac{1}{l_i}\left( \varvec{q}_i-\varvec{q}_{i-1} \right) , \quad \text {for}\quad i=1, \ldots , n. \end{aligned}$$

(2.3)

Fig. 1

Geometry of the linear 2-chain

and

$$\begin{aligned} \theta _{i,j}:= {\left\{ \begin{array}{ll} 1 &{} \quad \text {for}\quad j\le i,\\ 0 &{} \quad \text {otherwise.}\quad \end{array}\right. } \end{aligned}$$

(2.4)

Clearly, $(\varvec{q}_0, \varvec{e}_1, \ldots , \varvec{e}_n)$ specify the configuration of the system. Hence, its configuration space is $M^{2n+3}=\mathbb {R}^3\times \left( {\mathbb {S}}^2 \right) ^n$, or, in the planar case $M^{2+n}=\mathbb {R}^2\times \left( {\mathbb {S}}^1 \right) ^{n}=\mathbb {R}^2\times \mathbb {T}^n$. Notice that instead of $\varvec{q}_0$ we can take an arbitrary point $\varvec{q}_i$ with $0\le i \le n$. However, it is natural to specify a configuration by $(\varvec{r}, \varvec{e}_1, \ldots , \varvec{e}_n)$, where $\varvec{r}$ is the radius vector of the centre of the mass

$$\begin{aligned} \varvec{r}=\frac{1}{m}\sum _{i=0}^n m_i \varvec{q}_i, \quad \text {where}\quad m=\sum _{i=0}^nm_i. \end{aligned}$$

(2.5)

Then, from (2.2) we obtain

$$\begin{aligned} \varvec{r}= \varvec{q}_0 + \frac{1}{m}\sum _{j=1}^n \sigma _jl_j \varvec{e}_j, \quad \text {with}\quad \sigma _j=\sum _{k=j}^n m_k, \end{aligned}$$

(2.6)

Hence, we can write

$$\begin{aligned} \varvec{q}_i = \varvec{r}+ \varvec{r}_i, \quad \text {where}\quad \varvec{r}_i= \sum _{j=1}^n \left( \theta _{i,j}-\frac{\sigma _j}{m} \right) l_j \varvec{e}_j, \end{aligned}$$

(2.7)

for $i=0, \ldots , n$. Obviously, we have

$$\begin{aligned} \sum _{i=0}^nm_i\varvec{r}_i = \varvec{0}. \end{aligned}$$

(2.8)

Application of this equality gives

$$\begin{aligned} \sum _{i=0}^nm_i \varvec{q}_i\cdot \varvec{q}_i= \sum _{i=0}^nm_i \left( \varvec{r}+\varvec{r}_i \right) \cdot \left( \varvec{r}+\varvec{r}_i \right) = m \varvec{r}\cdot \varvec{r}+ \sum _{i=0}^n m_i \varvec{r}_i\cdot \varvec{r}_i, \end{aligned}$$

(2.9)

and similarly, we have

$$\begin{aligned} \sum _{i=0}^nm_i ||\dot{\varvec{q}}_i ||^2= m ||\dot{\varvec{r}} ||^2 + \sum _{i=0}^n m_i \dot{\varvec{r}}_i\cdot \dot{\varvec{r}}_i. \end{aligned}$$

(2.10)

Next, we introduce a symmetric $n\times n$ matrix $I=[I_{\alpha ,\beta }]$ defined by

$$\begin{aligned} \sum _{i=0}^n m_i\, \varvec{r}_i\cdot \varvec{r}_i = \sum _{\alpha ,\beta =1}^n I_{\alpha ,\beta }\, \varvec{e}_\alpha \cdot \varvec{e}_\beta . \end{aligned}$$

(2.11)

Using the definition of $\varvec{r}_i$, see (2.7), we find that

$$\begin{aligned} I_{\alpha ,\beta }= \sum _{i=0}^n m_i \left( \theta _{i,\alpha }-\frac{\sigma _\alpha }{m} \right) l_\alpha \left( \theta _{i,\beta }-\frac{\sigma _\beta }{m} \right) l_\beta . \end{aligned}$$

(2.12)

Here, we notice that

$$\begin{aligned} \sum _{i=0}^n m_i\theta _{i,\alpha }=\sigma _{\alpha }, \quad \theta _{i,\alpha }\theta _{i,\beta }=\theta _{i,\gamma }, \quad \text {with}\quad \gamma =\max (\alpha ,\beta ). \end{aligned}$$

(2.13)

Using the above relations, one can find

$$\begin{aligned} I_{\alpha ,\beta } = l_{\alpha } l_{\beta } \left( \sigma _{\gamma } - \frac{\sigma _{\alpha }\sigma _{\beta }}{m} \right) \quad \text {with}\quad \gamma =\max (\alpha ,\beta ). \end{aligned}$$

(2.14)

The kinetic energy has the form

$$\begin{aligned} T = \frac{1}{2}m ||\dot{\varvec{r}} ||^2 + \frac{1}{2}\sum _{\alpha , \beta =1}^{n} I_{\alpha ,\beta }\,\dot{\varvec{e}}_{\alpha }\cdot \dot{\varvec{e}}_{\beta }. \end{aligned}$$

(2.15)

Let $V(\varvec{r},\varvec{e}_1, \ldots , \varvec{e}_n)$ be the potential of an external forces. Then the Lagrange function is

$$\begin{aligned} L = T - V, \end{aligned}$$

(2.16)

and the equations of motion have the form

$$\begin{aligned} \begin{aligned} m \ddot{\varvec{r}} + \dfrac{\partial V }{\partial \varvec{r}} =&\, \varvec{0}, \\ \sum _{\beta =1}^n I_{\alpha ,\beta }\ddot{\varvec{e}}_{\beta } + \dfrac{\partial V }{\partial \varvec{e}_{\alpha }} =&\, \lambda _{\alpha } \varvec{e}_{\alpha }, \quad \alpha =1, \ldots , n, \end{aligned} \end{aligned}$$

(2.17)

where $\lambda _{\alpha }$ are the Lagrange multipliers. Their dependence on dynamical variables $\varvec{r}$, $\varvec{e}_1$, ..., $\varvec{e}_n$ and velocities $\dot{\varvec{r}}$, $\dot{\varvec{e}}_1$, ..., $\dot{\varvec{e}}_n$ can be deduced from constraints

$$\begin{aligned} \varvec{e}_{\alpha }\cdot \varvec{e}_{\alpha }=1, \quad \varvec{e}_{\alpha }\cdot \dot{\varvec{e}}_{\alpha }=0, \quad \alpha =1, \ldots , n. \end{aligned}$$

(2.18)

Example 2.1

Let us assume that the chain moves in a constant gravity field. The potential energy of a point mass m is given by $V= -m\,\varvec{n}\cdot \varvec{q}$, where $\varvec{n}$ is a constant vector of a gravity field intensity. Thus, the potential energy of the chain is

$$\begin{aligned} V = - \sum _{i=0}^n m_i\, \varvec{n}\cdot \varvec{q}_i= -\sum _{i=0}^n m_i\, \varvec{n}\cdot \left( \varvec{r}+ \varvec{r}_i\right) =-m\, \varvec{n}\cdot \varvec{r}. \end{aligned}$$

(2.19)

It implies that the motion of the centre of the mass of the chain moves like a point in a constant gravity field. Nevertheless, the motion of the chain is highly complicated. If $n>2$, the system is not integrable.

Remark 2.1

If in the above example we fix one end of the chain, then we obtain just a multiple pendulum. This modification changes the dynamics of the system. In fact, even for $n=2$ the system is not integrable. This problem was investigated by many authors; see, e.g., (Burov and Nechaev 2002; Moauro and Negrini 1998; Paul and Richter 1994).

Now, let us assume that the chain moves around a central body with mass M along an orbit. The potential energy of the chain is

$$\begin{aligned} V = -\sum _{i=0}^n \frac{GMm_i}{||\varvec{r}+ \varvec{r}_i ||}. \end{aligned}$$

(2.20)

Let us assume that lengths of the chain links are small in comparison to the dimension of the orbit of its mass centre. It means that the following quantity

$$\begin{aligned} \varepsilon :=\max _{0\le i \le n} \frac{||\varvec{r}_i ||}{||\varvec{r} ||}, \end{aligned}$$

(2.21)

is small. It is customary to approximate the potential by its truncated form. We take expansion

$$\begin{aligned} \frac{1}{||\varvec{r}+\varvec{r}_i ||}= \frac{1}{||\varvec{r} ||} -\frac{\varvec{r}\cdot \varvec{r}_i}{||\varvec{r} ||^3} +\frac{3 \left( \varvec{r}\cdot \varvec{r}_i \right) ^2 -||\varvec{r} ||^2||\varvec{r}_i ||^2}{2||\varvec{r} ||^5}+\cdots , \end{aligned}$$

(2.22)

where dots denote terms of order higher than $\varepsilon ^2$, which we neglect. Then using formula (2.13) we obtain

$$\begin{aligned} V= -\frac{GMm}{||\varvec{r} ||}- \frac{GMm}{2||\varvec{r} ||^3} \sum _{\alpha ,\beta =1}^n I_{\alpha ,\beta } \left[ 3 (\varvec{e}_{\varvec{r}}\cdot \varvec{e}_{\alpha } ) ( \varvec{e}_{\varvec{r}}\cdot \varvec{e}_{\beta }) - \varvec{e}_{\alpha }\cdot \varvec{e}_{\beta }\right] , \end{aligned}$$

(2.23)

where $\varvec{e}_{\varvec{r}}=\varvec{r}/||\varvec{r} ||$.

Now we fix the orbit. More precisely, we assume that the centre of mass of the chain moves in a circular Keplerian orbit of radius a. The motion of the chain is conveniently investigated in its orbital frame. The first axis of this frame is directed along the radius vector, and the third axis is normal to the plane of the orbit and has the direction of the orbital angular momentum. The orbital frame rotates around the origin with constant angular velocity $\omega$ defined by

$$\begin{aligned} \omega := \sqrt{\frac{G M m}{a^3}}. \end{aligned}$$

(2.24)

In our notation, $\varvec{e}_i=(x_i,y_i,z_i)^T$ denotes the coordinates of unit vector

$$\begin{aligned} \overline{e}_i:=\frac{\overline{P_{i-1}P_i}}{ | \overline{P_{i-1}P_{i} }|} \end{aligned}$$

(2.25)

in the chosen inertial frame. Coordinates of this vector in the orbital frame are denoted by $\varvec{s}_i=(X_i, Y_i, Z_i)^T$. The relation between these two sets of coordinates is given by $\varvec{e}_i=\varvec{A}(t) \varvec{s}_i$, where $\varvec{A}(t)$ is the rotation matrix. We can assume with no loss of generality that the orbit plane coincides with the (x, y)-plane of the inertial frame and then

$$\begin{aligned} \varvec{A}(t) = \begin{bmatrix} \cos \omega t&\quad -\sin \omega t&\quad 0 \\ \sin \omega t&\quad \cos \omega t&\quad 0\\ 0&\quad 0&\quad 1 \end{bmatrix}. \end{aligned}$$

(2.26)

The time derivative of $\varvec{e}_i$ is given by

$$\begin{aligned} \dot{\varvec{e}}_i = \varvec{A}(t) \left( \dot{\varvec{s}}_i + \varvec{\omega }\times \varvec{s}_i \right) , \end{aligned}$$

(2.27)

where

$$\begin{aligned} \varvec{\omega }= \omega \left( 0,0,1 \right) ^T \end{aligned}$$

(2.28)

is the vector of the orbital angular velocity. Using the above identities, we can rewrite the Lagrange function in the form

$$\begin{aligned} L = \frac{1}{2} \sum _{\alpha ,\beta =1}^n I_{\alpha ,\beta } \left( \dot{\varvec{s}}_{\alpha } +\varvec{\omega }\times \varvec{s}_{\alpha } \right) \cdot \left( \dot{\varvec{s}}_{\beta } +\varvec{\omega }\times \varvec{s}_{\beta } \right) -V, \end{aligned}$$

(2.29)

where

$$\begin{aligned} V = - \frac{1}{2} \omega ^{2} \sum _{\alpha ,\beta =1}^n I_{\alpha ,\beta } \left[ 3 (\varvec{s}\cdot \varvec{s}_{\alpha } ) ( \varvec{s}\cdot \varvec{s}_{\beta }) - \varvec{s}_{\alpha }\cdot \varvec{s}_{\beta }\right] , \end{aligned}$$

(2.30)

and $\varvec{s}=(1,0,0)^T$. Let us notice that we neglected terms describing the motion of the mass centre. By a proper choice of the unit of time, we can achieve that $\omega =1$.

2.1 Planar 2-chain problem

In the rest of this paper, we investigate the motion of a 2-chain, which moves in the plane of the orbit, see in Fig. 1. As coordinates we take two angles $(\varphi _1, \varphi _2)$ such that

$$\begin{aligned} \varvec{s}_1=(\cos \varphi _1, \sin \varphi _1,0)^T, \quad \varvec{s}_2=(\cos \varphi _2 , \sin \varphi _2,0)^T. \end{aligned}$$

(2.31)

In these coordinates, the Lagrange function reads

$$\begin{aligned} L= & {} \frac{1}{2} \left[ I_{1,1} \left( \dot{\varphi }_1 +1 \right) ^2 + I_{2,2} \left( \dot{\varphi }_2 +1 \right) ^2 \right] \nonumber \\&+\, I_{1,2}\cos (\varphi _1-\varphi _2) \left( \dot{\varphi }_1 +1 \right) \left( \dot{\varphi }_2 +1 \right) - V(\varphi _1,\varphi _2), \end{aligned}$$

(2.32)

where

$$\begin{aligned} V(\varphi _1,\varphi _2) =- \frac{1}{2} \sum _{\alpha ,\beta =1}^2 I_{\alpha ,\beta } \left[ 3 \cos \varphi _{\alpha } \cos \varphi _{\beta } - \cos (\varphi _{\alpha }-\varphi _{\beta } ) \right] . \end{aligned}$$

(2.33)

Explicit forms of entries of the tensor of inertia for a 2-chain are as follows

$$\begin{aligned} I_{11}=\dfrac{m_0(m_1+m_2)l_1^2}{m_0+m_1+m_2},\quad I_{22}=\dfrac{m_2(m_0+m_1)l_2^2}{m_0+m_1+m_2},\quad I_{12}=I_{21}=\dfrac{m_0m_2l_1l_2}{m_0+m_1+m_2}, \end{aligned}$$

where $l_1$ and $l_2$ are lengths of arms between masses $m_0$ and $m_1$, and $m_1$ and $m_2$, respectively.

For further considerations, it is convenient to introduce relative coordinates $x_1 = \varphi _1$ and $x_2=\varphi _2-\varphi _1$. Using these coordinates, we rewrite Lagrange equations in a form of the following system of first-order differential equations

$$\begin{aligned} \begin{aligned} \dot{x}_1 =&\, y_1, \\ \dot{y}_1 =&\, \frac{1}{D} \left\{ \lambda _2 \sin x_2 \left[ 3+ 2(y_1+y_2)(y_1+y_2+2) +3\cos (2(x_1+x_2))\right] \right. \\&\left. +\, y_1\left( 2+ y_1 \right) \sin 2x_2 + 3\sin (x_1+2x_2)\cos x_1 + \frac{3}{2} \left[ 1-2\lambda _1\lambda _2\right] \sin 2x_1 \right\} , \\ \dot{x}_2 =&\, y_2, \\ \dot{y}_2 =&\,- \frac{\sin x_2}{D}\left\{ \lambda \left[ 3 + 2(y_1+y_2)(y_1+y_2+2) \right] - 2 \lambda _1 y_2 \left( 2y_1 + y_2 + 2\right) \right. \\&\left. +\, 2\left[ 3 + 2y_1 (y_1+2) + y_2( 2y_1+y_2+2) \right] \cos x_2 \right. \\&\left. +\, 3\lambda _1\cos 2x_1+ 3\lambda _2 \left[ \cos (2(x_1+x_2)) +2\lambda _1\cos (2x_1+x_2) \right] \right\} , \end{aligned} \end{aligned}$$

(2.34)

where

$$\begin{aligned} \lambda _1= & {} \frac{I_{1,1}}{I_{1,2}}, \quad \lambda _2 = \frac{I_{2,2}}{I_{1,2}},\quad \lambda = \lambda _1+\lambda _2, \end{aligned}$$

(2.35)

$$\begin{aligned} D= & {} 2 \left( \lambda _1\lambda _2 -\cos ^2x_2\right) . \end{aligned}$$

(2.36)

The above system is a Hamiltonian; however, coordinates $(x_1,y_1,x_2, y_2)$ are not canonical. The Hamiltonian function in these variables reads

$$\begin{aligned} H= & {} \frac{1}{2}\left[ (\lambda + 2\cos x_2) y_1^2 + 2 y_1y_2 (\lambda _2 + \cos x_2) + \lambda _2 y_2^2 \right] \nonumber \\&-\, \frac{3}{4} \left[ \lambda + \lambda _1 \cos (2 x_1) +\lambda _2 \cos (2(x_1+x_2)) +2\cos x_2 + 2 \cos (2x_1+x_2) \right] .\nonumber \\ \end{aligned}$$

(2.37)

Parameters $\lambda _1$ and $\lambda _2$ are positive, and moreover,

$$\begin{aligned} \lambda _1\lambda _2 -1 = \frac{m_1}{m_0m_2}\left( m_0 +m_1+m_2 \right) >0, \end{aligned}$$

(2.38)

so the set of physically admissible values of $(\lambda _1,\lambda _2)$ is given by

$$\begin{aligned} \Lambda :=\{(\lambda _1,\lambda _2)\in \mathbb {R}^2\ |\ \lambda _1>0,\lambda _2>0,\lambda _1\lambda _2 -1 >0\}. \end{aligned}$$

2.2 Main theorem

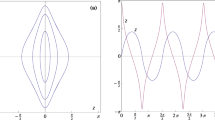
Numerical tests (see Fig. 2) show that, in general, the system (2.34) is not integrable. However, such tests do not exclude the possibility that the system is integrable for certain values of $(\lambda _1,\lambda _2)\in \Lambda$. Our aim is to prove that no such values exist.

Fig. 2

Poincaré cross section for system (2.34) with parameters $(\lambda _1,\lambda _2)=(2,2)$ in the level $H=-3.5$ of the first integral (2.37). The surface of the cross section is $x_1=0$ and the local coordinates on it are $(x_2, y_2)$

For the considered system, the configuration space is a two-dimensional torus $\mathbb {T}^2$ with coordinates $(x_1, x_2) \mod 2\pi$. The phase space is $T^{\star } \mathbb {T}^{2}\simeq \mathbb {T}^2 \times \mathbb {R}^2$, and $(x_1, x_2, y_1,y_2)$ are coordinates on it.

Functions $f(x_1, x_2, y_1,y_2)$ defined on the phase space are periodic with respect to the first two arguments. We extend our system to the complex phase space, so considered functions are complex functions of complex variables $(x_1, x_2, y_1,y_2)\in \mathbb {C}^4$.

The main result of this paper is the following theorem.

Theorem 2.1

The complex system (2.34) does not have a first integral which is meromorphic and functionally independent of H.

3 Proof

In this section, we prove our main theorem by analysing properties of the differential Galois group of variational equations for certain particular solutions of the system. Our considerations are based on the general theorem of Morales Ruiz (1999), Morales-Ruiz and Ramis (2001) that formulates necessary integrability conditions using properties of the differential Galois group of variational equations.

Theorem 3.1

(Morales–Ramis). Assume that a Hamiltonian system is meromorphically integrable in the Liouville sense in a neighbourhood of a phase curve $\Gamma$. Then the identity component of the differential Galois group of the variational equations along $\Gamma$ is Abelian.

The main steps of the proof are as follows. At first we find two families of particular solutions of our system. They describe oscillations (and rotations) of the chain. These solutions describe the motion of the chain when its two parts are either parallel or anti-parallel. Then we derive the variational equations and transform their normal subsystems into the form of second-order equations with rational coefficients. These equations are Fuchsian, and their differential Galois groups are subgroups of $\mathrm {SL}(2,\mathbb {C})$.

Local analysis of variational equations shows that solutions of normal variational equations have logarithmic terms. Hence, it is impossible that all their solutions are algebraic. This fact simplifies further consideration. To complete the proof of non-integrability, it is enough to show that the equations do not have exponential solutions. At this point, we apply a part of the Kovacic algorithm.

3.1 Particular solutions and variational equations

System (2.34) has two invariant manifolds

$$\begin{aligned} {{\mathscr {N}}}_k=\left\{ {(x_1,x_2,y_1,y_2)\in \mathbb {C}^4}\;\vert \;\; { x_2=(k-1) \pi ,\quad y_2=0} \,\right\} ,\quad \text {where}\quad k=1, 2, \end{aligned}$$

and its restriction to ${{\mathscr {N}}}_k$ reads

$$\begin{aligned} \dot{x}=y,\quad \dot{y}=-\dfrac{3}{2}\sin (2 x), \quad (x,y)=(x_1,y_1). \end{aligned}$$

(3.1)

These equations have the energy integral

$$\begin{aligned} h=\dfrac{y^2}{2}-\dfrac{3}{4}\cos (2 x). \end{aligned}$$

(3.2)

Let $\Gamma (\eta )\in \mathbb {C}^2$ denote a phase curve of system (3.1) lying on the level $h(x,y)=\eta$, and $\Gamma _k(\eta )\subset {{\mathscr {N}}}_k$ with $k=1,2$ are the respective phase curves of system (2.34).

If we denote by $[X_1,Y_1,X_2,Y_2]^T$ variations of phase variables $[x_1,y_1,x_2,y_2]^T$, then the variational equations along $\Gamma _k(\eta )$ have the form

$$\begin{aligned} \begin{bmatrix} \dot{X}_1 \\ \dot{Y}_1 \\ \dot{X}_2\\ \dot{Y}_2 \end{bmatrix} = \begin{bmatrix} 0&\quad 1&\quad 0&\quad 0\\ -3\cos (2x)&\quad 0&\quad a_k(x,y)&\quad 0\\ 0&\quad 0&\quad 0&\quad 1\\ 0&\quad 0&\quad b_k(x,y)&\quad 0 \end{bmatrix} \begin{bmatrix} X_1 \\ Y_1 \\ X_2 \\ Y_2 \end{bmatrix}, \end{aligned}$$

(3.3)

where $(x,y)\in \Gamma (\eta )$ and

$$\begin{aligned} \begin{aligned} a_k(x,y)=&\,\frac{1-\varepsilon _k\lambda _2}{2(\lambda _1\lambda _2 -1)} \left[ 3 + 2y(2+y)+ 3\cos (2x) \right] ,\\ b_k(x,y)=&\, c_{k} \left( 3 + 2y(2+y) \right) + 3 (c_k-1)\cos (2 x), \end{aligned} \end{aligned}$$

and

$$\begin{aligned} c_k = \frac{\varepsilon _k \lambda - 2 }{2(\lambda _1\lambda _2 -1)}, \quad \varepsilon _k =(-1)^k, \end{aligned}$$

for $k=1, 2$.

The last two equations in (3.3) form a closed subsystem, which is called the normal variational equations. The equivalent second-order differential equation reads

$$\begin{aligned} \ddot{X} -b_k(x,y)X=0, \quad (x,y)\in \Gamma _k(\eta ), \quad k=1,2. \end{aligned}$$

(3.4)

For both phase curves $\Gamma _1(\eta )$ and $\Gamma _2(\eta )$, we fix the same level of integral h, so

$$\begin{aligned} \eta = \frac{2}{3}y^2 -\cos (2x) \quad \text {for}\quad (x,y)\in \Gamma (\eta ). \end{aligned}$$

(3.5)

For further considerations, it is convenient to make the following change of independent variable

$$\begin{aligned} t\longmapsto z=\frac{1}{\sqrt{3}}y(t). \end{aligned}$$

(3.6)

Then from (3.5), we obtain

$$\begin{aligned} \cos (2x)=2 z^2 -\eta , \end{aligned}$$

and

$$\begin{aligned} (\dot{z})^2= - \frac{3}{4}\left[ \left( \eta - 2 z^2 \right) ^2-1\right] ,\quad \ddot{z}= 3z \left( \eta - 2 z^2 \right) . \end{aligned}$$

Using the above formulae, we transform equations (3.4) to the following form

$$\begin{aligned} X''+P(z)X'+Q_k(z)X=0, \end{aligned}$$

(3.7)

where prime denotes the derivative with respect to z, and rational coefficients of these equations are as follows

$$\begin{aligned} \begin{aligned} P(z)=&\,\dfrac{\ddot{z}}{(\dot{z})^2}= \frac{2z}{2z^2 -\eta +1} + \frac{2z}{2z^2 -\eta -1} ,\\ Q_k(z)=&-\dfrac{b_k}{(\dot{z})^2}=\frac{4\left[ -6 z^2 + c_k (3 + 4 z (\sqrt{3} + 3 z) - 3 \eta ) + 3 \eta \right] }{3\left[ \left( \eta - 2 z^2 \right) ^2-1\right] }. \end{aligned} \end{aligned}$$

(3.8)

Next, we make the following change of dependent variable

$$\begin{aligned} X=w\exp \left[ -\frac{1}{2}\int ^zP(v)dv\right] , \end{aligned}$$

(3.9)

which convert equations (3.7) into its reduced form

$$\begin{aligned} w''=r_k(z)w,\quad r_k(z)=\frac{1}{2}P'(z)+\frac{1}{4}P(z)^2-Q_k(z). \end{aligned}$$

(3.10)

Moreover, we fix the energy $\eta =1$ for both particular solutions. It is clear that for this value of $\eta$ two singular points of equation (3.10) collapse into one at $z=0$. Then, the coefficient $r_k$ is given by

$$\begin{aligned} r_k(z)=\frac{3/4}{z^2}-\frac{3/16}{(z-1)^2}-\frac{3/16}{(z+1)^2} + \frac{4c_k}{\sqrt{3}z} + \frac{39 -32 c_k(3+\sqrt{3}z)}{24(z^2-1)}. \end{aligned}$$

(3.11)

It is worth to notice here that $r_k$ is a symmetric function of $\lambda _1$ and $\lambda _2$. In fact, we have

$$\begin{aligned} c_k = \frac{\varepsilon _k \lambda -2}{2\sigma }, \quad \text {where}\quad \sigma := \lambda _1\lambda _2-1, \quad \lambda :=\lambda _1+\lambda _2. \end{aligned}$$

(3.12)

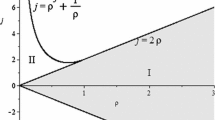
The admissible values of parameters $(\lambda ,\sigma )$ are distinguished by the following inequalities

$$\begin{aligned} \lambda>0, \quad \sigma >0 \quad \text {and}\quad \lambda ^2 -4(\sigma +1)\ge 0, \end{aligned}$$

(3.13)

see Fig. 3.

Fig. 3

Range of parameters satisfying physical restrictions

Equation (3.10) with the above coefficient $r_k$ is a Fuchsian equation with four regular singular points $z_0=0$, $z_{\pm 1}=\pm 1$ and $z_\infty =\infty$. The respective differences of exponents at these points are as follows

$$\begin{aligned} \Delta _0=2,\quad \Delta _{\pm 1}=\frac{1}{2},\quad \Delta _{\infty }=\delta _{k}, \end{aligned}$$

(3.14)

where

$$\begin{aligned} \delta _k=\sqrt{1+8\frac{( \lambda _1-\varepsilon _k) (\lambda _2-\varepsilon _k)}{(\lambda _1 \lambda _2-1)}}, \quad \text {for}\quad k=1,2, \end{aligned}$$

(3.15)

respectively. In terms of $\sigma$ and $\lambda$, these quantities read

$$\begin{aligned} \delta _1 = \sqrt{9 +8 \frac{2+\lambda }{\sigma }}, \quad \delta _2 = \sqrt{9 +8 \frac{2-\lambda }{\sigma }}. \end{aligned}$$

(3.16)

Moreover, rational functions $r_k(z)$, see (3.11), can be rewritten in the following form

$$\begin{aligned} r_k(z) = \frac{9 -42z^2+24 z^4 + (\delta _k^2-9) z(\sqrt{3}+3z)(z^2-1)}{12 z^2(z^2-1)^2}. \end{aligned}$$

(3.17)

3.2 Logarithmic terms

Since the difference of exponents $\Delta _0=2$ is an integer, local solutions near $z=0$ can have logarithmic terms; see, e.g., (Whittaker and Watson 1935, Chap. 10) and (Maciejewski et al. 2013, App. B). More precisely, two linearly independent local solutions $w_1$ and $w_2$ of (3.10) in a neighbourhood of $z=0$ have the following form

$$\begin{aligned} w_1(z) =z^{3/2} f(z), \quad w_2(z)= g w_1(z)\ln z+z^{-1/2} h(z), \end{aligned}$$

(3.18)

where f(z) and h(z) are holomorphic at $z=0$ and $f(0)\ne 0$. Coefficient g multiplying the logarithmic term is

$$\begin{aligned} g = \frac{1}{6} \left( 8 c_k^2-6c_k +3 \right) . \end{aligned}$$

(3.19)

Since $g>0$ for arbitrary $c_k\in \mathbb {R}$, the logarithmic term appears in local solutions of the variational equation for all values of the parameters.

A continuation of the matrix of fundamental solutions along a small loop $\gamma$ encircling the origin $z=0$ counterclockwise gives rise to a triangular monodromy matrix

$$\begin{aligned} \begin{bmatrix} w_1(z)&\; w_2(z) \\ w_1'(z)&\; w_2'(z) \end{bmatrix} \xrightarrow [\gamma ]{\quad } \begin{bmatrix} w_1(z)&\; w_2(z) \\ w_1'(z)&\; w_2'(z) \end{bmatrix} \begin{bmatrix} -1&\; -2\pi i \\ 0&\; -1 \end{bmatrix}. \end{aligned}$$

(3.20)

Hence, the monodromy group of equation (3.10) contains matrix

$$\begin{aligned} M_0:= \begin{bmatrix} -1&-2\pi i \\ 0&-1 \end{bmatrix}. \end{aligned}$$

(3.21)

which is not diagonalisable.

3.3 Differential Galois group of the variational equation

The variational equation (3.10) is a parameterised family of second-order differential equations of the following form

$$\begin{aligned} y''=r(z) y, \quad r(z)\in \mathbb {C}(z) . \end{aligned}$$

(3.22)

For such equations, their differential Galois group ${{\mathcal {G}}}$ is an algebraic subgroup of $\mathrm {SL}(2,\mathbb {C})$. The following lemma describes all possible types of ${{\mathcal {G}}}$ and relates these types to forms of solution of (3.22); see (Kovacic 1986; Morales Ruiz 1999).

Lemma 3.1

Let ${{\mathcal {G}}}$ be the differential Galois group of equation (3.22). Then one of four cases can occur.

• 1. ${{\mathcal {G}}}$ is reducible (it is conjugated to a subgroup of a triangular group); in this case equation (3.22) has an exponential solution of the form $y=\exp \int \omega$, where $\omega \in \mathbb {C}(z)$,

• 2. ${{\mathcal {G}}}$ is conjugated with a subgroup of

  $$\begin{aligned} D^\dag = \left\{ \begin{bmatrix} c&0\\ 0&c^{-1} \end{bmatrix} \; \biggl | \; c\in \mathbb {C}^*\right\} \cup \left\{ \begin{bmatrix} 0&c\\ c^{-1}&0 \end{bmatrix} \; \biggl | \; c\in \mathbb {C}^*\right\} . \end{aligned}$$

  in this case equation (3.22) has a solution of the form $y=\exp \int \omega$, where $\omega$ is algebraic over $\mathbb {C}(z)$ of degree 2,

• 3. ${{\mathcal {G}}}$ is primitive and finite; in this case all solutions of equation (3.22) are algebraic,

• 4. ${{\mathcal {G}}}= \mathrm {SL}(2,\mathbb {C})$ and equation (3.22) has no Liouvillian solution.

For the notion of Liouvillian solutions, see, e.g., Kovacic (1986) and references therein. Now, let us return to our variational equation (3.10). Let ${{\mathscr {M}}}_{k}$ and ${{\mathscr {G}}}_k$ denote its monodromy and differential Galois group, respectively. It is known that ${{\mathscr {M}}}_{k} \subset {{\mathscr {G}}}_{k}$. We showed that its monodromy group contains non-diagonalisable matrix $M_0$. Thus, ${{\mathscr {G}}}_k$ is not a finite subgroup of $\mathrm {SL}(2,\mathbb {C})$. In this way, we exclude the third case of Lemma 3.1.

By the same reason, ${{\mathscr {G}}}_k$ cannot be also a subgroup of the dihedral group $D^\dag$ because it cannot contain a non-diagonalisable triangular matrix. Thus, the differential Galois group ${{\mathscr {G}}}_k$ of the variational equation is either a triangular subgroup of $\mathrm {SL}(2,\mathbb {C})$ or $\mathrm {SL}(2,\mathbb {C})$.

3.4 Elimination of the first case of Lemma 3.1

Let us assume that for our variational equation (3.10) the first case of Lemma 3.1 occurs. Then this equation has a nonzero solution of the form

$$\begin{aligned} w=P(z)\exp \left[ \int ^z \omega (s) \mathrm {d}s \right] , \quad P\in \mathbb {C}[z], \quad \omega (z)\in \mathbb {C}(z). \end{aligned}$$

(3.23)

see Kovacic (1986). If such a solution exists, then polynomial P(z) of degree d and rational function $\omega (z)$ can be found by application of Case 1 of the Kovacic algorithm, see Kovacic (1986). In order to construct this solution, first we calculate for each singularity auxiliary sets

$$\begin{aligned} {{\mathscr {E}}}_i=\left\{ \frac{1}{2}\left( 1\pm \Delta _i\right) \right\} ,\quad \text {for}\quad i\in \{-1,0,1,\infty \}. \end{aligned}$$

Next, we select from the Cartesian product

$$\begin{aligned} {{\mathscr {E}}}={{\mathscr {E}}}_{-1} \times {{\mathscr {E}}}_0\times {{\mathscr {E}}}_{1}\times {{\mathscr {E}}}_{\infty }, \end{aligned}$$

these elements $\varvec{\rho }=(\rho _{-1},\rho _0,\rho _1,\rho _\infty )\in {{\mathscr {E}}}$ for which

$$\begin{aligned} d(\varvec{\rho }):=\rho _\infty -\sum _{i=-1}^1 \rho _i \end{aligned}$$

(3.24)

is a non-negative integer. The integer $d(\varvec{\rho })$ is the degree of polynomial P(z) entering into solution (3.23). For each selected element $\varvec{\rho }\in {{\mathscr {E}}}$, we define the corresponding rational function

$$\begin{aligned} \omega =\sum _{i=-1}^{1}\frac{\rho _i}{z-z_i}. \end{aligned}$$

(3.25)

Moreover, polynomial P must satisfy equation

$$\begin{aligned} P''+2\omega P'+(\omega '+\omega ^2-r_k)P=0. \end{aligned}$$

(3.26)

For our normal variational equations, the auxiliary sets are the following

$$\begin{aligned} {{\mathscr {E}}}_0=\left\{ -\frac{1}{2},\frac{3}{2}\right\} ,\quad {{\mathscr {E}}}_1={{\mathscr {E}}}_{-1}=\left\{ \frac{1}{4},\frac{3}{4}\right\} ,\quad {{\mathscr {E}}}_{\infty }=\left\{ \frac{1}{2}(1-\delta _k),\frac{1}{2}(1+\delta _k)\right\} . \end{aligned}$$

For possible choices of $\varvec{\rho }$, we have that

$$\begin{aligned} d(\varvec{\rho })=\frac{1}{2}(1-\delta _k),\quad \text {or}\quad d(\varvec{\rho })=\frac{1}{2}(\delta _k-m), \end{aligned}$$

with $m\in \{-1,0,1,3,4,5\}$. We require that $d(\varvec{\rho })$ is a non-negative integer for $k=1$ and $k=2$. This implies that $\delta _1$ and $\delta _2$ are integers, which we denote by $n_k = \delta _k$. Using equation (3.16), one can express parameters $(\lambda _1,\lambda _2)$ in terms of $(n_1,n_2)$ and symmetric functions $\lambda$ and $\sigma$ defined in Eq. (3.12) take the forms

$$\begin{aligned} \lambda =\dfrac{2(n_1^2-n_2^2)}{n_1^2+n_2^2-18},\quad \sigma = \dfrac{32}{n_1^2+n_2^2-18}. \end{aligned}$$

(3.27)

Now the last inequality in (3.13) expressed in terms of $(n_1,n_2)$ reads

$$\begin{aligned} 16 \frac{63 + n_1^2 +n_2^2 -n_1^2n_2^2 }{(n_1^2+n_2^2-18)^2}\ge 0. \end{aligned}$$

(3.28)

Hence, $n_1$ and $n_2$ are non-negative integers, which satisfy three inequalities

$$\begin{aligned} 63+n_1^2+n_2^2-n_1^2n_2^2\ge 0, \quad n_1^2>n_2^2, \quad n_1^2+n_2^2>18. \end{aligned}$$

(3.29)

From the last two conditions, it follows that $n_1^2>9$. Putting $n_1^2 = 9 + a$, with a certain $a>0$, from the first condition (3.29) we obtain

$$\begin{aligned} 9>\frac{72+a}{8+a}>n_2^2 \quad \text {for}\quad a\in (0,\infty ). \end{aligned}$$

(3.30)

Thus, we conclude that there is only a finite number of admissible values of $n_2$, namely $n_2\in \{0,1,2\}$. We investigate these three cases using the variational equation corresponding to the second particular solution, i.e., we fix $k=2$.

If $n_2 =\delta _2=0$, then ${{\mathscr {E}}}_\infty =\{1/2\}$. There are two possible choices of $\varvec{\rho }\in {{\mathscr {E}}}$ for which $d(\varvec{\rho })$ is a non-negative integer, namely

$$\begin{aligned} \begin{aligned} \text {for} \quad \varvec{\rho }_1=\left( \frac{1}{4}, -\frac{1}{2},\frac{3}{4},\frac{1}{2}\right) ,&\quad d(\varvec{\rho }_1)=0,\\ \text {for}\quad \varvec{\rho }_2=\left( \frac{3}{4}, -\frac{1}{2},\frac{1}{4},\frac{1}{2}\right) ,&\quad d(\varvec{\rho }_2)=0.\\ \end{aligned} \end{aligned}$$

So, the polynomial P(z) is a nonzero constant polynomial, and we can assume that $P(z)=1$. Then equation (3.26) reduces to the following one

$$\begin{aligned} \omega '+\omega ^2-r_2(z) = 0, \end{aligned}$$

(3.31)

with $\omega =\omega (z)$ given by (3.25). In the considered case, this function reads

$$\begin{aligned} \omega =\frac{z^2 \pm z + 1}{2z(z^2-1)}, \end{aligned}$$

(3.32)

with an upper sign for $\varvec{\rho }_1$. Moreover, as $\delta _2=0$, coefficient $r_2$ in (3.17) simplifies to

$$\begin{aligned} r_2 = \frac{3 -14z^2+8 z^4 -3 z(\sqrt{3}+3z)(z^2-1)}{4 z^2(z^2-1)^2}. \end{aligned}$$

Hence,

$$\begin{aligned} \omega '+\omega ^2-r_2(z) = \frac{3\sqrt{3}\mp 2}{4z(z^2-1)} \ne 0. \end{aligned}$$

(3.33)

In other words, this case is excluded.

If $\delta _2=1$, then ${{\mathscr {E}}}_4=\{1,0\}$, and

$$\begin{aligned} r_2(z) = \frac{9 -42z^2+24 z^4 - 8z(\sqrt{3}+3z)(z^2-1)}{12 z^2(z^2-1)^2}. \end{aligned}$$

One can find that there are three admissible vectors $\varvec{\rho }\in {{\mathscr {E}}}$, namely

$$\begin{aligned} \begin{aligned} \text {for}\quad \varvec{\rho }_1=\left( \frac{3}{4}, -\frac{1}{2},\frac{3}{4},1\right) ,&\quad d(\varvec{\rho }_1)=0,\\ \text {for}\quad \varvec{\rho }_2=\left( \frac{1}{4}, -\frac{1}{2},\frac{1}{4},0\right) ,&\quad d(\varvec{\rho }_2)=0,\\ \text {for}\quad \varvec{\rho }_3=\left( \frac{1}{4}, -\frac{1}{2},\frac{1}{4},1\right) ,&\quad d(\varvec{\rho }_3)=1. \end{aligned} \end{aligned}$$

For these vectors, the respective rational functions $\omega$ are as follows

$$\begin{aligned} \begin{aligned} \text {for}\quad \varvec{\rho }_1,&\quad \omega = \frac{1+2z}{2z(z^2-1)}, \\ \text {for} \quad \varvec{\rho }_2 \quad \text {and}\quad \varvec{\rho }_3,&\quad \omega = \frac{1}{2z(z^2-1)}. \end{aligned} \end{aligned}$$

For $\varvec{\rho }_1$ and $\varvec{\rho }_2$, we can set $P(z)=1$, and we have to check if equation (3.31) is satisfied. But for both vectors, we obtain

$$\begin{aligned} \omega '+\omega ^2-r_2(z) = \frac{2}{\sqrt{3}z(z^2-1)} \ne 0. \end{aligned}$$

For $\varvec{\rho }_3$, we can set $P(z)=z + a$ with a certain $a\in \mathbb {C}$. This polynomial must fulfill equation (3.26), which reduces to

$$\begin{aligned} \frac{3+2\sqrt{3}(z+a)}{3z(z^2-1)}\ne 0, \end{aligned}$$

for an arbitrary $a\in \mathbb {C}$. Thus, this case is also excluded.

If $\delta _2=2$, then ${{\mathscr {E}}}_4=\{-1/2,3/2\}$, and

$$\begin{aligned} r_2(z) = \frac{9 -42z^2+24 z^4 - 5z(\sqrt{3}+3z)(z^2-1)}{12 z^2(z^2-1)^2}. \end{aligned}$$

Now, we have two possible choices for $\varvec{\rho }$. Namely,

$$\begin{aligned} \begin{aligned} \text {for}\quad \varvec{\rho }_1=\left( \frac{1}{4}, -\frac{1}{2},\frac{3}{4},\frac{3}{2}\right) ,&\quad d(\varvec{\rho }_1)=1,\\ \text {for}\quad \varvec{\rho }_2=\left( \frac{3}{4}, -\frac{1}{2},\frac{1}{4},\frac{3}{2}\right) ,&\quad d(\varvec{\rho }_2)=1.\\ \end{aligned} \end{aligned}$$

The respective functions $\omega$ are given by (3.32), and we can put $P=z+a$. Then equation (3.26) reduces to equality

$$\begin{aligned} \frac{12 + a ( \mp 6 +5 \sqrt{3})+(\pm 6 +5 \sqrt{3} -12a)z }{12z(z^2-1)}=0, \end{aligned}$$

which cannot be fulfilled for any $a\in \mathbb {C}$. Thus, this case is also excluded.

In summary, it is impossible that for both variational equations their differential Galois groups are triangular subgroups of $\mathrm {SL}(2,\mathbb {C})$. At the same time, this shows also that at least for one particular solution the identity component of the differential Galois group of the respective normal variational equation is not Abelian. Thus, by Theorem 3.1, the system is non-integrable.