Periodic orbits and bifurcations in the Sitnikov four-body problem

Abstract

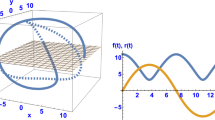
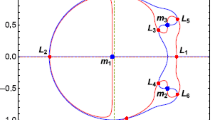
We study the existence, linear stability and bifurcations of what we call the Sitnikov family of straight line periodic orbits in the case of the restricted four-body problem, where the three equal mass primary bodies are rotating on a circle and the fourth (small body) is moving in the direction vertical to the center mass of the other three. In contrast to the restricted three-body Sitnikov problem, where the Sitnikov family has infinitely many stability intervals (hence infinitely many Sitnikov critical orbits), as the “family parameter” ż₀ varies within a finite interval (while z ₀ tends to infinity), in the four-body problem this family has only one stability interval and only twelve 3-dimensional (3D) families of symmetric periodic orbits exist which bifurcate from twelve corresponding critical Sitnikov periodic orbits. We also calculate the evolution of the characteristic curves of these 3D branch-families and determine their stability. More importantly, we study the phase space dynamics in the vicinity of these orbits in two ways: First, we use the SALI index to investigate the extent of bounded motion of the small particle off the z-axis along its interval of stable Sitnikov orbits, and secondly, through suitably chosen Poincaré maps, we chart the motion near one of the 3D families of plane-symmetric periodic orbits. Our study reveals in both cases a fascinating structure of ordered motion surrounded by “sticky” and chaotic orbits as well as orbits which rapidly escape to infinity.