1 Introduction

Single atom catalysis is widely studied to minimize the amount of catalyst material while simultaneously maximizing performance. Consider that the expense and scarcity of platinum group metal (PGM) catalysts represents a major economic and manufacturing roadblock to the adoption of fuel cell electric vehicles [1,2,3]. The PGM loading for a hydrogen fuel cell is typically 10 times higher than the amount present in a catalytic converter. Pt single atom catalysts (SAC) have exhibited increased catalytic mass activity by approximately 37 times when compared to state-of-the-art Pt/C catalysts for the hydrogen evolution reaction [4]. As only surface atoms significantly contribute to performance, SAC is the most efficient possible use of chemically active material [5, 6] and hence of enormous economic relevance to a wide range of industrial applications.

Yet the term single atom catalysis may be misleading, because the molecular coordination of a SAC is of crucial consequence to stability and chemical activity [7,8,9]. Both the presence of coordinating ligands and the support material have been shown to strongly influence catalytic activation energy barriers [10,11,12,13]. Many investigations have focused on the role of the relationship between electronic charge transfer and catalytic energy barriers [12, 14,15,16,17,18]. Recent work has shown that magnetic moment also plays a role in the catalytic reactivity of O2, which is unusually stable with a triplet ground state [19]. Distinguishing the effects of spin state from more traditionally investigated mechanisms such as charge transfer requires understanding the spin polarized density of states of SAC environments, which is most readily accessible with a first principles approach. While advances in electron microscopy imaging and spectroscopy through techniques such as monochromated scanning transmission electron microscopy coupled with electron energy loss spectroscopy (STEM-EELS) [20] and electron magnetic circular dichroism (EMCD) [21, 22] may enable the correlation of not only local electronic but also magnetic structure with atomic structure, the huge range of stabilizing surface defects and transition metal SAC candidates presents a challenge in terms of throughput. Hence, we present a computational materials discovery approach to identify especially promising SAC candidates. Specifically, we investigate SAC composed of transition metals on two structurally similar graphene defect moieties. The single vacancy has a significant localized magnetic moment, while the pyridinic N defect moiety does not. Our ability to produce high surface area, porous 3-dimensional bicontinuous turbostratic graphene scaffolds, with morphology that facilitates efficient mass transfer as well as simultaneous high electrical conductivity that is important for a catalytic support [23,24,25,26] further motivates identification of earth abundant transition metals and fundamental mechanisms in order to inform the design of molecular dopants and adatoms on graphene that optimize catalytic activity.

Chemical reactions undergoing spin inversion have been considered to be spin forbidden or too slow to be practical [27]. Recently, first principles calculations on O2 dissociation facilitated by gold and silver clusters demonstrated that spin-crossing is more likely when spin states are close in energy. Specifically, clusters with odd and hence, unpaired electrons, exhibited energy barriers that were lower than systems with even number of electrons and this was attributed to spin-crossed pathways [28]. The effect of spin-dependent chemical pathways for transition metal SAC supported on graphene defects has been examined only recently. Orellana examined spin-constrained, non-equilibrium chemical pathways of O2 dissociation on transition metal SAC supported on a double vacancy N doped graphene defect and found small energy differences (below 0.1 eV) at points along these pathways increase the probability of spin-crossing during the reaction, enabling lower reaction barriers over spin-conserved reactions [29]. Our work expands this perspective to examine the magnetic moment of the surface defect and the TM and how this affects bonding energy. We then investigate the chemical activity during CO oxidation of four earth abundant TM atoms (V, Fe, Mo, Ta) coordinated with two graphene defect moieties using density functional theory (DFT). Single vacancy and pyridinic N-doped single vacancy defects are two structurally similar graphene defect moieties that have similar charge transfer to metal adatoms but differing magnetic moments. CO oxidation is examined as it has many relevant industrial uses, including catalytic converters in vehicles, smoke stack emission control, and respiration filters [30].

Climbing image-nudged elastic band (CI-NEB) calculations of activation energy barriers of CO oxidation on all transition metal SAC in relaxed geometries on both defect moieties show all barrier energies on N-doped single vacancy defects were 0.8 eV or less. There were significant decreases in activation barrier energies for V and Ta, no difference in the case of Fe, and a slight increase for Mo when the N dopant was present. Hence, the common understanding of pyridinic N dopants improving catalytic behavior is simplistic. Due to the similar charge transfer calculated for both defect moieties, changes in activation barrier energy values were correlated with differences in bonding arrangements and local magnetic moment. A closer inspection of the density of states of the chemical pathways calculated via CI-NEB shows that lower activation energy barriers are associated with larger spin state asymmetry near the Fermi level in all cases, and in several cases the change in electronic charge transfer and bonding geometry was similar. Thus, spin state asymmetry provides new avenues for tailoring the molecular environment of promising support structures for SAC and guides choices for further experimental analysis, opening up additional lower energy chemical pathways for catalysis.

1.1 Calculation Details

Spin-polarized density functional theory calculations were implemented with the Vienna Ab initio Simulation Package (VASP) [31, 32] using the projector augmented wave (PAW) pseudopotentials [33, 34] and the generalized gradient approximation of the Perdew, Burke, and Ernzerhof (PBE) exchange–correlation functional [35], PBE incorporating a Hubbard correction term [36] to account for d electron self-interaction effects (PBE + U), as well as the strongly constrained and appropriately normed (SCAN) meta-generalized gradient approximation (meta-GGA) functional [37]. A Hubbard U of 2.0 eV and an on-site exchange constant of J of 0 eV were applied to the single Ta atom [38]. As the first meta-GGA, SCAN includes the gradient of the kinetic energy density, which satisfies 17 known possible exact constraints and can accurately capture intermediate range weak interactions in non-bonded systems and rare-gas atoms due to appropriate norming [37]. SCAN can often meet or even exceed the performance of more expensive hybrid calculations such as HSE06 (which were computationally intractable for the size of this system, with over 70 atoms) for many material properties [37, 39].

Binding energies, bond lengths, charge transfer, and magnetic moments were calculated for a Ta adatom bound to either a bare single vacancy (N0) or pyridinic N doped single vacancy (N1) graphene substrate with PBE, PBE + U, and SCAN, results listed in Table S1. All three functionals capture similar shifts in the Ta binding energy, charge transfer, and magnetic moments across the N0 and N1 defect moieties. However, the binding energies calculated by PBE are significantly closer in value to those calculated by SCAN than PBE + U. Additionally, the magnetic moments calculated by PBE are overall closer to the SCAN values than those calculated with PBE + U. To further verify the choice of the PBE functional, the total density of states (DOS) for Ta/N0 was calculated with PBE, PBE + U, and SCAN and plotted in Figure S1. The PBE and SCAN DOS plots both show a single spin down peak near the Fermi energy, while the PBE + U DOS shows two small spin down peaks. The DOS calculated with PBE is a closer match to the SCAN DOS than PBE + U. Overall, comparison of the functionals demonstrate that PBE most accurately captured structural, electronic, and magnetic properties of interest for a single Ta atom secured to both graphene surface defect moieties investigated in this work.

The pseudopotential of each transition metal was chosen to represent the largest number of valence electrons for increased accuracy, while still utilizing the frozen core electron approximation for increased computational efficiency. In all calculations, the electron wave functions were expanded with a plane wave cut-off of 400 eV. The graphene substrates consist of a 6 × 6 repeating graphene unit cell with a vacuum spacing of 25 Å between repeating images in the z direction. The large unit cell size and vacuum spacing were chosen to minimize spurious interactions between adsorbed adatoms due to the periodic boundary conditions.

For structural relaxations, reciprocal space was sampled with a 5 × 5 × 1 gamma centered Monkhorst–Pack grid [40] and a Gaussian smearing of 0.01 eV. Standard convergence testing was performed with the reported cut-off and k point values chosen based on total energy values changing by less than 1 meV. The entire substrate was allowed to relax until the Hellmann–Feynman forces fell beneath 0.025 eV/ Å. The cohesive binding energies (EB) for each transition metal adatom were calculated via

$${\text{E}}_{{\text{B}}} = {\text{ E}}_{{\text{G - TM}}} - {\text{ E}}_{{\text{G}}} {-}{\text{ E}}_{{{\text{TM}}}}$$
(1)

EG represents the energy of the bare graphene substrate, ETM the energy of the isolated transition metal atom, and EG-TM the total energy of the transition metal adatom adsorbed to the graphene substrate, each of which have been allowed to relax in identical hexagonal unit cells (14.7 × 14.7 × 25 Å). Charge density difference plots are defined by the following equation

$$\Delta {\text{n}}\left( {\text{r}} \right) \, = {\text{ n}}_{{\text{G - TM}}} - {\text{ n}}_{{\text{G}}} {-}{\text{ n}}_{{{\text{TM}}}}$$
(2)

where nG represents the charge density of the optimized bare graphene substrate, nTM the charge density of the optimized transition metal adatom, and nG-TM the charge density of the optimized total system of the transition metal adsorbed adatom to the graphene substrate.

Density of states calculations were performed with 9 × 9 × 1 k points and a broader Gaussian smearing of 0.1 eV for visualization. Charge transfer and transition state analysis were carried out with tools from the VASP Transition State Theory (VTST) package. Specifically, charge transfer was calculated with the Bader charge analysis method [41], as implemented by Henkelman et al. [42] Initial transition states along the minimum energy pathway were identified with the climbing image nudged elastic band method [43] and then further refined with the dimer method [44]. These two methods were also used to investigate spin-constrained reaction pathways of CO oxidation with the spin state specified using the NUPDOWN tag.

2 Results and Discussion

2.1 Magnetic Properties of Graphene Defects

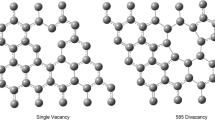
The two common defect moieties in graphene that are investigated in this work have similar charge transfer to TM and differing magnetic moment [45, 46], as well as reported differences in activity of supported single atom catalysts such as Pt [44] and Fe [16]. These surfaces allow us to examine correlations between magnetic moment and reaction energy barriers. The first defect moiety is the single vacancy (N0) defect; the absence of the single carbon atom in the graphene lattice gives rise to a significant magnetic moment, with a calculated total value of 1.36 μB, in agreement with previous reports [47, 48]. The magnetization is mostly localized to a neighboring C atom from the vacancy (Fig. 1a). The second defect also consists of a single C vacancy with a neighboring N-dopant in a pyridinic configuration (N1). Pyridinic N is a p-type doping site on graphene [49, 50] characterized as having two C bonds and known to contribute one electron to the delocalized graphene π orbitals. The additional electron contributed by the pyridinic N-dopant extinguishes the magnetic moment of the N1 defect moiety (Fig. 1b). Additionally, the distance between the two remaining C nearest neighbor atoms shortens from 1.98 to 1.79 Å, forming a shorter bond with no magnetic moment.

Fig. 1
figure 1

Optimized geometry and magnetization density of a undoped single C vacancy (N0) and b single C vacancy with pyridinic N dopant (N1) on graphene surfaces. Grey atoms represent C while the purple atom is N. Isosurfaces drawn at a value of 0.01 e/Å3 to facilitate comparison with the literature [47, 51]. N0 defect moiety has a total magnetic moment of 1.36 µB while N1 defect moiety has no magnetic moment

Full size image

Binding energies for all four transition metal (TM) atoms (V, Fe, Mo, Ta) on both defects in relaxed geometries are calculated and the electronic and magnetic properties are compared; binding energies, bond lengths, Bader charge transfer, and magnetic moments are summarized in Table S2. Pristine graphene is not analyzed, as both our previous work [17] and many examples in the literature have demonstrated that pristine graphene has unsuitably low adsorption and diffusion barrier energies to support single molecules or atoms [45, 52, 53]. Previous work on N defect moieties supported on graphene surfaces has associated enhanced catalytic activity due to the N dopants altering O2 binding energies with values approaching that of O2 on Pt surfaces [29, 54, 55]. However, the underlying mechanisms of this shift in binding energy is not completely understood. Here, the addition of the pyridinic N dopant in the N1 defect moiety consistently decreases the binding energy of the TM adatoms by an average value of 1.98 eV. The binding energy is plotted as a function of the charge transfer between the TM adatom and the surrounding defect, as calculated with Bader charge analysis, and is shown in Fig. 2a. There is remarkably little difference in the charge transferred between each TM atom when comparing N0 to N1. For example, in charge density difference plots of Ta/N0 and Ta/N1, shown, in Fig. 2b and c, respectively, electronic charge is transferred from the adsorbed metal adatom to the surrounding graphene substrate and the two surfaces exhibit only minor differences in isosurface symmetry. All metal adatoms investigated become cationic independent of defect moiety. In contrast to the charge transfer, the binding energy and local magnetic moment of the TM adatom both vary on the two defects as observed in Fig. 2d. Plots of the total magnetic moment illustrate the strong localization of the magnetic moment while also illustrating the increase in magnetization from the N0 to the N1 defect moiety, and is shown for the case of Ta in Fig. 2e and f, respectively. (Charge density difference and magnetization plots for all TM atoms can be found in Figure S2 of the Supplementary Information.) With the adsorption of a TM atom, the total magnetization of the N1 system increases by an average of 0.92 µB, approaching the value of one additional unpaired electron. Thus, these graphene defect moieties allow one to assess the effect of magnetic moment nearly independent from charge transfer. Furthermore, the bonding geometry of metal adatoms on both defect moieties does not significantly change as shown in Table S2. The trend of defects with higher magnetic moments inducing stronger binding energies was also identified for Fe and other TM on similar N-doped graphene defects [29, 46]. Kattel et al. found that when the final coordinated TM SAC exhibited a magnetic moment, the binding energy became weaker [56], similar to our results for TM/N1, which have higher magnetic moments in the final state geometry and weaker binding energies. Considering that previous work has correlated the binding energy of O2 with enhanced catalytic activity, this suggests that tuning the magnetic moment of an impurity on a defect site provides an additional knob to optimize catalytic performance.

Fig. 2
figure 2

The local a charge transfer and d magnetic moment plotted against the binding energy of the TM to N0 (circles) and N1 (triangles) defect moieties. Dashed lines are provided as guides for the eye. Charge density difference Δn(r) of b Ta/N0 and c Ta/N1. All isosurfaces are drawn at levels of 0.01 e/Å3. Yellow (blue) isosurfaces correspond to an increase (decrease) in charge density. Magnetization density isosurfaces of e Ta/N0 and f Ta/N1. Yellow isosurfaces correspond to spin up electron density. Grey and purple spheres correspond to carbon and nitrogen atoms, respectively

Full size image

2.2 Effect of Magnetic Moment on Gas Adsorption and CO Oxidation

The binding energies of CO, CO2, and O2 molecules, involved in CO oxidation, were calculated for both N0 and N1 SAC systems to assess resistance to CO poisoning and elucidate chemical pathways. The binding energy of CO2 is weak and in some cases positive; the values are shown in Table S3 of Supporting Information. O2 is always adsorbed more strongly than CO, which is favorable to mitigate CO poisoning of the catalyst [57] on all metal adatoms investigated on both defect moieties. Figure 3a plots the binding energy trends for O2 and CO and illustrates that gas molecules generally adsorb more strongly to TM SAC coordinated to N1, all of which were shown to have higher magnetic moments compared to N0 (Table S2). All gas molecule magnetic moment values are tabulated in Table S3 of the Supporting Information. This is consistent with data shown in Fig. 2d where bare N0 has a higher magnetic moment and consequently higher EB to SAC than bare N1. One notable exception is O2–V, where the magnetic moment on the O2–V system is calculated as zero on both defect types. The total density of states (DOS) for each TM SAC was also calculated and shown in Figure S4. Correlation between gas molecule binding energy with proximity of d-orbitals to the Fermi level was not observed by comparing DOS in Figure S4 and calculated binding energies of gas molecules. For example, the DOS of Fe/N0 and V/N1 would predict higher gas binding energies than Fe/N1 and V/N0, respectively, by this criterion. However, both O2 and CO have higher binding energies on Fe/N1 versus Fe/N0 as shown in Fig. 3. Similarly, the CO binding energy increases on V/N1 with respect to V/N0, while on the other hand, the O2 binding energy is much weaker on V/N1. Interestingly, a shift from side-on (Fig. 3b) for the N0 defect to end-on (Fig. 3c) for the N1 defect bonding geometry is observed. Here we postulate that the additional unpaired electron contributed by the N1 defect favors the end-on configuration for O2–V to obtain a ground state with no magnetic moment and lower system energy. Bonding geometry changes have been associated with minimizing magnetic moment to lower system energy in a few other studies [29, 58]. This result would explain the weaker binding energy for O2–V on N1, as the end-on geometry appears to minimize the additional magnetic moment imparted by the N dopant. In line with previous work that correlates the binding energy of O2 to catalytic performance [54, 59, 60], we are motivated to examine more closely the effect of binding energy and magnetic moment on CO oxidation barrier energy.

Fig. 3
figure 3

a The binding energy of CO and O2 adsorbed to each TM on N0 (circles) and N1 (triangles) defect moieties for Fe (purple), V (red), Mo (blue), and Ta (black). Relaxed bonding geometry of O2 adsorbed to b V/N0, note the side-on configuration of the linear O2 molecule, c V/N1 where the O2 molecule adsorbs in an end-on configuration. Grey, purple, red, and green spheres correspond to carbon, nitrogen, oxygen, and vanadium atoms, respectively

Full size image

The relatively weaker binding energy of CO versus O2 in Fig. 3a suggest that the modified Eley–Rideal reaction [18, 61] pathway (wherein CO reacts with adsorbed O2 to form CO2 and O) is most appropriate for this system, rather than the Langmuir–Hinshelwood reaction mechanism. Fe/N0 has previously been found to proceed via the modified Eley–Rideal pathway as well [62]. The climbing image nudged elastic band (CI-NEB) method was used to model the modified Eley–Rideal reaction path and calculate the barrier energies without constraining the spin state, typically done in prior studies, for each combination of a TM-SAC and the graphene defect moieties investigated. Previous work investigating spin-constrained reaction pathways revealed that these pathways are close in energy for TM SACs on graphene defects, increasing the likelihood of spin inversion events between reaction steps that benefit catalytic activity [29, 63], making spin unrestricted calculations more appropriate for these systems.

The calculated barrier energies between the initial state (IS) and transition state (TS), listed in Table 1, were under 1 eV and impressively, all barrier energies for N1 were less than 0.8 eV. Generally, reactions below 0.8 eV are considered feasible at room temperature [64]. All relaxed geometries and energy levels of IS, TS, and final states (FS) for each TM are provided in the Supplementary Information in Figure S3, S4, and Table S4. The energy barrier calculated for Fe/N0 is in agreement with previous reports [62, 63]. For all TM SAC on N1, the addition of a pyridinic N dopant appears to favor the formation of a COOO intermediate [65,66,67] at the transition state, with the exception of Ta (see Figure S6). On N0, Fe SAC also forms a similar intermediate and all others do not (see Figure S5). Interestingly, as observed in Table 1, the Fe SAC barrier energies are the same on both defect moieties despite N doped defects often being attributed to increasing catalytic activity for both Fe [54] and Pt [68] SAC. Overall, for all SAC on N1 and N0 defect moieties, there is no clear trend of the relationship with defect moiety and energy barrier. V and Ta both demonstrated significant decreases in activation barrier energies, Fe had no change, and Mo showed a slight increase in value on N1 with respect to N0. Insight of physical mechanisms behind these trends can be obtained by examining the spin polarized projected density of states (PDOS) of the transition states, shown in Figs. 4, 5 and 6. We find that the magnetic state of atomic and molecular orbitals near the Fermi level exhibits common features, i.e., asymmetry of spin states, for systems with lowest activation energy barriers. Each TM SAC will be discussed in the following section in turn.

Table 1 Activation barrier energies of CO oxidation on different defect moieties
Full size table

The relaxed geometries and energy levels for CO oxidation on Mo on the two defect types are illustrated in Fig. 4a. The barrier energy is approximately 9% higher on N1 with respect to N0, where values are shown in Table 1. We systematically examine physical mechanisms, starting with geometry, charge transfer and induced magnetic moment as past studies clearly indicate geometry and charge transfer play a role and we seek to find cases where only magnetic moment changes. The geometry of O2 is the same, side-on, for both moieties, illustrated by the insets of Fig. 4a. Additionally, charge transfer and even magnetic moment of O2 on Mo/N0 and Mo/N1 TS are very similar, values are shown in Table S4. The main observable difference is the PDOS. In Fig. 4c, Mo/N1 shows spin state asymmetry in the O2 peaks near the Fermi level, however the spin state splitting of these peaks is more pronounced for Mo/N0 (Fig. 4b). Additionally, near the Fermi level (within 1 eV), Mo/N1 shows greater overlap between CO, O2, and Mo 4d orbital peaks, however Mo/N0 retains a slightly lower energy barrier, emphasizing the unique effect of spin split orbitals on reactivity. Spin state splitting of the orbital peaks with the greatest proximity to the Fermi level was also present in the DOS of the best performing Au SAC analyzed in a previous theoretical work [69]. Furthermore, the PDOS of O2–Fe on both defect moieties, shown in Figure S5, has the same CO oxidation energy barrier for both Fe/N0 and Fe/N1. This can be understood by considering the similar level of spin state asymmetry near the Fermi level on both defects. Even though there is greater charge transfer to O2 adsorbed to Fe/N1, and a greater local magnetic moment for O2 adsorbed to Fe/N0, the energy barrier values most closely correlate to the behavior of the spin split orbitals near the Fermi level in the PDOS.

Fig. 4
figure 4

a Energy levels of the initial state (IS), transition state (TS), and final state (FS) for N0 (solid black) and N1 (hollow bar). Insets show relaxed geometry for TS of O2–Mo/N0 and O2–Mo/N1. Grey, purple, red, and light purple spheres correspond to C, N, O, and Mo atoms, respectively. Spin polarized projected density of states (PDOS) for TS of b O2–Mo/N0 and c O2–Mo/N1 with Fermi energy highlighted with a vertical dashed line. Blue dashed curve shows local PDOS of adsorbed TM adatom d orbitals. Red dotted and black solid curves show local PDOS for CO and O2 molecules, respectively. All positive values correspond to spin up and all negative values are spin down

Full size image

The chemical activity of Ta SAC for CO oxidation showed a significant improvement on N1 in terms of lower barrier energy compared to Ta/N0, with an activation energy barrier of 0.66 eV compared to 0.91 eV as shown in Fig. 5a. The electronic charge transfer to O2, shown in Table S4, for Ta/N0 and Ta/N1 was remarkably similar. Furthermore, the geometric structures of O2 on the Ta/N0 and Ta/N1 TS, observed in the insets of Fig. 5a, both exhibit a side-on bonding configuration (see also Table S2). In contrast to the similar charge transfer and geometry between Ta defect moieties, there is a clear difference in the PDOS of Ta/N0 compared to Ta/N1. The symmetry of the PDOS of Ta/N0, in Fig. 5b, has no discernable magnetic moment and shows a higher number of states very close to the Fermi level (within 1 eV). Additionally, both the PDOS of Ta/N0 and Ta/N1 have similar densities of Ta 5d orbitals near the Fermi level. However, the PDOS for the Ta/N1 TS (Fig. 5c) shows a large spin state asymmetry near the Fermi level for the adsorbed O2 molecule. Thus, spin state asymmetry appears to destabilize the O2 bond, increasing reactivity and lowering the barrier energy for CO oxidation on Ta/N1 by 27%.

Fig. 5
figure 5

a Energy levels of the initial state (IS), transition state (TS), and final state (FS) for N0 (solid black) and N1 (hollow bar). Insets show relaxed geometry for TS of O2–Ta/N0 and O2–Ta/N1. Grey, purple, red, and yellow spheres correspond to C, N, O, and Ta atoms, respectively. Spin polarized density of states for TS of b O2–Ta/N0 and c O2–Ta/N1. Blue dashed curve shows local PDOS of adsorbed TM adatom d orbitals. Red dotted and black solid curves show local PDOS for CO and O2 molecules, respectively. The Fermi levels have been set to 0 eV, indicated with a vertical dashed black line. All positive values correspond to spin up and all negative values are spin down

Full size image

The initial, transition, and final states of CO oxidation on Ta/N0 produced with NEB calculations had zero magnetic moment. This motivated additional NEB calculations to compare the activation barrier energies of spin-constrained reaction pathways having differing spin states. By constraining the magnetic moment of the CO oxidation reaction facilitated by Ta/N0 to be either 1 (doublet) or 3 (quartet) states, we found significantly lower energy barriers compared to the non-magnetic spin state, shown in Table 2. The energy barriers of the doublet and quartet spin states were found to be quite similar with less than 0.05 eV of difference. Since mainly the frontier orbital affects bonding, magnetic moment alone does not explain differences in chemical activity. Higher spin states may consist of unpaired electrons in both the frontier as well as orbitals further away from the Fermi energy, thus they are expected to have similar energy barriers when the spin asymmetry near the Fermi energy is similar.

Table 2 Activation barrier energies of spin-constrained CO oxidation on Ta/N0
Full size table

Lastly, we consider the impressive improvement between V/N0 and V/N1, a decrease in activation energy barrier of 44%, comparable to CO oxidation on a Pt surface [70]. The adsorbing O2 molecule undergoes a shift in geometry, from side-on to end-on absorption for the N0 and N1 molecular environments, respectively, as discussed previously and which can be seen in the insets of Fig. 6a. This shift is not thought to result in a beneficial steric advantage. Despite the the increased proximity of the end-on O2 molecule to the reacting physisorbed CO molecule, previous work has found that a similar end-on O2 adsorbed on Au SAC displayed significantly higher activation energy barriers for CO oxidation than side-on [69]. The increased magnetic moment conferred by the N1 defect moiety could also be responsible for the change in O2 adsorption geometry from side-on to end-on, which agrees with a finding demonstrated by Orellana for a similar system [29]. Rather than steric advantage explaining the lower energy barrier for V/N1, there is a strong spin state asymmetry in the V peaks near the Fermi level, larger in energy separation and magnitude as compared to the TS for V/N0 (Fig. 6b). This effect could explain why the activation energy barrier for V/N1 is 44% lower than V/N0, despite V/N0 having more charge transfer to O2 shown in Table S4. Thus spin state asymmetry appears to lower the barrier energies for CO oxidation for all systems.

Fig. 6
figure 6

a Energy levels of the initial state (IS), transition state (TS), and final state (FS) for N0 (solid black) and N1 (hollow bar). Insets show relaxed geometry for TS of O2–V/N0 and O2–V/N1. Grey, purple, red, and green spheres correspond to C, N, O, and V atoms, respectively. Spin polarized density of states for TS of b O2–V/N0 and c O2–V/N1. Blue dashed curve shows local PDOS of adsorbed TM adatom d orbitals. Red dotted and black solid curves show local PDOS for CO and O2 molecules, respectively. The Fermi levels have been set to 0 eV, indicated with a vertical dashed black line. All positive values correspond to spin up and all negative values are spin down

Full size image

3 Conclusion

Through first principles calculations, the performance of a wide range of earth-abundant transition metals (V, Fe, Mo, and Ta) as SAC for CO oxidation on two types of graphene surface defects (N0, N1) has been evaluated. Further, by calculating the activation energy barriers of CO oxidation reactions facilitated by these stabilized SAC through a modified Eley–Rideal pathway, we found that all four metals have energy barriers < 1 eV on both defect types and significantly the pyridinic N dopant accesses energy barriers below 0.8 eV for all metals. Compared to our previous work modelling the same reaction with single atom Pt for a Langmuir–Hinshelwood pathway, V on N1 is comparable to the performance of a Pt surface [70] and is the most competitive with SAC Pt catalysts [17, 71] with an activation energy of 0.55 eV. The spin polarized projected density of states shows that greater spin state asymmetry in atomic and molecular orbital peaks near the Fermi level is associated with lower activation energy barriers, where associated decreases in activation barrier energies of CO oxidation of 44% and 27% were observed for V and Ta, respectively. Our work both extends the range of earth-abundant choices for SAC and reveals the importance of molecular coordination affecting the magnetic moment and in turn binding energies and activation energy barriers. This provides further means for improving the chemical activity of earth-abundant transition metals. Parsing the large parameter space composed of TM elements and surface defects will aid in the design of earth abundant and sustainable catalysts. These results can guide selection of materials for investigations using techniques such as high-angle annular dark-field-scanning transmission electron microscopy (HAADF-STEM) and spin-resolved electron energy loss spectroscopy (EELS) to probe chemical bonding and local electronic structure alongside with in situ catalytic reactions. Relationships between molecular coordination, local magnetic moment, and catalytic activity gleaned from experiments can further elucidate how spin state can provide an additional knob for tuning chemical activity. A promising future avenue is to explore the effect of spin on other molecular coordinations of TM SAC on graphene in order to identify systems that may meet or exceed the performance of PGM.