Skip to main content
SpringerLink
Log in

Boundary-Value Problems for Space-Time Fractional Differential Filtration Dynamics in Fractured-Porous Media

  • Published:
Cybernetics and Systems Analysis Aims and scope

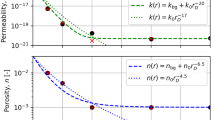
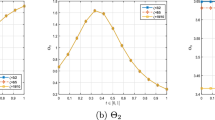
Abstract

Closed-form solutions are obtained for some non-stationary boundary-value problems of filtration dynamics in fractured-porous formations, posed within the framework of fractional-differential mathematical models, taking into account the space-time nonlocality of the process. The mathematical models of anomalous filtration dynamics are formulated using the Hilfer or Caputo derivatives with respect to the time variable and the Riemann–Liouville derivative with respect to the geometric variable. Along with direct filtration problems, the authors also consider the inverse boundary-value problem of determining the unknown source function that depends only on the geometric variable. Conditions of the existence of regular solutions to the considered problems are given.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. P. Ya. Polubarinova-Kochina, V. G. Pryazhinskaya, and V. N. Emikh, Mathematical Methods in Irrigation [in Russian], Nauka, Moscow (1969).

    Google Scholar 

  2. I. I. Lyashko, L. I. Demchenko, and G. E. Mistetskii, Numerical Solution of the Problems of Heat and Mass Transfer in Porous Media [in Russian], Naukova Dumka, Kyiv (1991).

    Google Scholar 

  3. S. I. Lyashko, D. A. Klyushin, A. A. Timoshenko, N. I. Lyashko, and E. S. Bondar, “Optimal control of intensity of water point sources in unsaturated porous medium,” J. Autom. Inform. Sci., Vol. 51, No. 7, 24–33 (2019).

    Article  Google Scholar 

  4. V.V. Uchaikin, Method of Fractional Derivatives [in Russian], Artishok, Ul’yanovsk (2008).

    Google Scholar 

  5. F. Mainardi, Fractional Calculus and Waves in Linear Viscoelasticity, Imperial College Press, London (2010).

    Book  Google Scholar 

  6. V. M. Bulavatsky, Iu. G. Kryvonos, and V. V. Skopetsky, Nonclassical Mathematical Models of Heat and Mass Transfer Processes [in Russian], Naukova Dumka, Kyiv (2005).

  7. M. M. Khasanov and G. T. Bulgakova, Nonlinear and Non-Equilibrium Effects in Rheologically Complex Media [in Russian], Moscow–Izhevsk, Inst. Komp. Issled. (2003).

  8. T. Sandev and Z. Tomovsky, Fractional Equations and Models. Theory and Applications, Springer Nature Switzerland AG, Cham (2019).

  9. T. M. Atanackovic, S. Pilipovic, B. Stankovic, and D. Zorica, Fractional Calculus with Applications in Mechanics, John Willey & Sons Inc, Hoboken (2014).

    Book  Google Scholar 

  10. A. Allwright and A. Atangana, “Fractal advection-dispersion equation for groundwater transport in fractured aquifers with self-similarities,” The Europ. Phys. J. Plus., Vol. 133, No. 2, 1–14 (2018).

    Article  Google Scholar 

  11. A. N. Kochubei, “Distributed order calculus and equations of ultraslow diffusion,” J. Math. Anal. Appl., Vol. 340, 252–281 (2008).

    Article  MathSciNet  Google Scholar 

  12. A. V. Chechkin, R. Gorenflo, I. M. Sokolov, and V. Y. Gonchar, “Distributed order time fractional diffusion equation,” Fract. Calc. Appl. Anal., No. 6, 259–281 (2003).

    MathSciNet  MATH  Google Scholar 

  13. V. Bogaenko and V. Bulavatsky, “Fractional-fractal modeling of filtration-consolidation processes in saline saturated soils,” Fractal and Fractional, Vol. 59, No. 4, 2–12 (2020).

    Google Scholar 

  14. V. M. Bulavatsky, “Mathematical modeling of fractional differential filtration dynamics based on models with Hilfer–Prabhakar derivative,” Cybern. Syst. Analysis, Vol. 53, No. 2, 204–216 (2017). https://doi.org/10.1007/s10559-017-9920-z.

  15. V. M. Bulavatsky and V. A. Bogaenko, “Mathematical modeling of the dynamics of nonequilibrium in time convection–diffusion processes in domains with free boundaries,” Cybern. Syst. Analysis, Vol. 52, No. 3, 427–440 (2016). https://doi.org/10.1007/s10559-016-9843-0.

    Article  MathSciNet  MATH  Google Scholar 

  16. G. I. Barenblatt and Yu. P. Zheltov, “On the basic equations of filtration of homogeneous fluids in fractured rocks,” Dokl. AN SSSR, Vol. 132, No. 3, 545–548 (1960).

    Google Scholar 

  17. G. I. Barenblatt, Yu. P. Zheltov, and I. N. Kochina, “On the basic representations of the theory of filtration of homogeneous fluids in fractured rocks,” Prikl. Mat. Mekh., Vol. 24, No. 3, 852–864 (1960).

    Google Scholar 

  18. G. I. Barenblatt, V. N. Entov, and V. M. Ryzhik, Motions of Liquids and Gases in Natural Layers [in Russian], Nedra, Moscow (1984).

    Google Scholar 

  19. V. N. Nikolaevskii, K. S. Basniev, A. T. Gorbunov, and G. A. Zotov, Mechanics of Saturated Porous Media [in Russian], Nedra, Moscow (1970).

    Google Scholar 

  20. R. Hilfer, “Fractional time evolution,” in: R. Hilfer (ed.), Applications of Fractional Calculus in Physics, World Scientific, Singapore (2000), pp. 87–130.

    Chapter  Google Scholar 

  21. A. A. Kilbas, H. M. Srivastava, and J. J. Trujillo, Theory and Applications of Fractional Differential Equations, Elsevier, Amsterdam (2006).

    MATH  Google Scholar 

  22. R. Gorenflo, A. A. Kilbas, F. Mainardi, and S. V. Rogosin, Mittag-Leffler Functions, Related Topics and Applications, Springer Verlag, Berlin (2014).

    MATH  Google Scholar 

  23. S. G. Samko, A. A. Kilbas, and O. I. Marichev, Fractional Integrals and Derivatives and Some of their Applications [in Russian], Nauka i Tekhnika, Minsk (1987).

    MATH  Google Scholar 

  24. A. M. Nakhushev, Fractional Calculus and its Application [in Russian], Fizmatlit, Moscow (2003).

    MATH  Google Scholar 

  25. T. S. Aleroev, M. Kirane, and Y.-F. Tang, “Boundary-value problems for differential equations of fractional order,” J. Math. Sci., Vol. 194, No. 5, 499–512 (2013).

    Article  MathSciNet  Google Scholar 

  26. M. V. Khasambiev and T. S. Aleroev, “Boundary-value problem for one-dimensional fractional differential advection-diffusion equation,” Vestn. Mos. Gos. Stroit. Univ., No. 6, 71–76 (2014).

    Google Scholar 

  27. T. S. Aleroev, M. Kirane, and S. A. Malik, “Determination of source term for a time fractional diffusion equation with an integral type over-determining condition,” Electronic J. of Diff. Eq., Vol. 270, 1–16 (2013).

    MathSciNet  MATH  Google Scholar 

  28. L. Plociniczak, “Eigenvalue asymptotics for a fractional boundary-value problem,” Appl. Math. and Comp., Vol. 241, 125–128 (2014).

    Article  MathSciNet  Google Scholar 

  29. Y. Lin and C. Xu, “Finite difference/spectral approximations for the time-fractional diffusion equation,” J. Comput. Phys., Vol. 225, No. 2, 1533–1552 (2007).

    Article  MathSciNet  Google Scholar 

  30. C. Tadjeran, H. M. Meerschaert, and H. P. Scheffler, “A second-order accurate numerical approximation for the fractional diffusion equation,” J. Comput. Phys., Vol. 213, No. 1, 205–213 (2006).

    Article  MathSciNet  Google Scholar 

  31. Z. Q. Deng, V. P. Singh, and L. Bengtsson, “Numerical solution of fractional advection-dispersion equation,” J. Hydraul. Eng. (ASCE), Vol. 130, No. 5, 422–431 (2004).

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. V. M. Glushkov Institute of Cybernetics, National Academy of Sciences of Ukraine, Kyiv, Ukraine

    V. M. Bulavatsky & V. O. Bohaienko

Authors
  1. V. M. Bulavatsky
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. V. O. Bohaienko
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to V. M. Bulavatsky.

Additional information

Translated from Kibernetyka ta Systemnyi Analiz, No. 3, May–June, 2022, pp. 47–60.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bulavatsky, V.M., Bohaienko, V.O. Boundary-Value Problems for Space-Time Fractional Differential Filtration Dynamics in Fractured-Porous Media. Cybern Syst Anal 58, 358–371 (2022). https://doi.org/10.1007/s10559-022-00468-9

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10559-022-00468-9

Keywords

Search

Navigation