Abstract
For about two decades now, the localization of the brain regions involved in reasoning processes is being investigated through fMRI studies, and it is known that for a transitive form of reasoning the frontal and parietal regions are most active. In contrast, less is known about the information exchange during the performance of such complex tasks. In this study, the propagation of brain activity during a transitive reasoning task was investigated and compared to the propagation during a simple memory task. We studied EEG transmission patterns obtained for physiological indicators of brain activity and determined whether there are frequency bands specifically related to this type of cognitive operations. The analysis was performed by means of the directed transfer function. The transmission patterns were determined in the theta, alpha and gamma bands. The results show stronger transmissions in theta and alpha bands from frontal to parietal as well as within frontal regions in reasoning trials comparing to memory trials. The increase in theta and alpha transmissions was accompanied by flows in gamma band from right posterior to left posterior and anterior sites. These results are consistent with previous neuroimaging (fMRI) data concerning fronto-parietal regions involvement in reasoning and working memory processes and also provide new evidence for the executive role of frontal theta waves in organizing the cognition.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Deductive reasoning is one of the fundamental human abilities. Many inferences, not only formal, but also those present in daily life, depend on intact reasoning processes. One of the most studied forms of deductive reasoning is linear order reasoning, which is based on the logic of transitivity (for a review, see Halford et al. 1998; Leth-Steensen and Marley 2000), i.e., for any A, B and C, if A > B and B > C then logically A > C. The “>” denotes a transitive relation that might be either physical (taller than), psychological (smarter than), or abstract. Linear order reasoning is a basic and crucial component of our reasoning ability and because such ability facilitates adaptive predictions (which tree is the tallest? who is the most dominant?), it is available in the simplest concrete form not only to humans since early childhood, but also to animals (Halford et al. 1998).
Deductive reasoning has been the subject of psychological inquiry for a long time and very specific cognitive models of reasoning mechanisms have been proposed (see for example Evans 2006; Johnson-Laird et al. 1992; Rips 1983). The same is true for linear order (or transitive) reasoning, which has been the topic of considerable interest in cognitive and developmental psychology (e.g., Rabinowitz et al. 1994; Sedek and von Hecker 2004; Sternberg 1980). One of the major findings in this area refers to the generative processes of rearranging incoming piecemeal information into a comprehensive mental model (mental array). Neuroimaging experiments have shown the involvement of frontal and parietal regions in reasoning-related tasks. The right prefrontal and the bilateral parietal cortex have been found to be active in tasks with nonspecific stimuli (lacking conceptual content, like letters in our study) or when not enough information is available to determine the relationship between the presented elements (which is also true for our reasoning task) (Fangmeier et al. 2006; Goel et al. 2009).
Although transitive reasoning tasks have not been studied through EEG experiments, the important role of frontal and fronto-parietal theta waves in cognitive tasks has been shown during mental calculation, maze navigation, concentration, short-term and working memory loads and heightened attention (Gevins et al. 1997; Kahana et al. 1999; Onton et al. 2005; Scheeringa et al. 2009). Moreover, an increase in the magnitude of frontal theta oscillations and increased frontal-posterior theta coherence are thought to reflect the executive functions of the working memory system (Sauseng et al. 2005) or top-down processes which help to maintain long-term memory (LTM) representations in the face of interference (Sarnthein et al. 1998; Sauseng et al. 2007).
Gamma oscillatory activity has been also related to cognitive functions such as attention, associative learning, memory or mental rotation (Miltner et al. 1999; Bhattacharya et al. 2001), as well as to gestalt perception (Kaiser and Lutzenberger 2003; Singer et al. 1997). Kawasaki and Watanabe (2007) showed in a very elegant way that the gamma-band increase in the frontal and parietal regions is associated with manipulation of visual mental representations, particularly successive ones, thus the increase in gamma-band may reflect higher demands on the frontal and parietal regions upon manipulation (Kawasaki and Watanabe 2007). Synchronous gamma activity between widely distributed cell groups is treated as an indicator that there are neural mechanisms for integrating information processed in distributed cortical areas into a coherent cognitive percept or process (Kaiser and Lutzenberger 2003).
In order to examine the direction of information transmission between regions known from previous studies to be involved in transitive reasoning, we compared the transitive reasoning task to a very similar memory task, which served as the control condition. We applied the direct transfer function (DTF) method to investigate the direction of information flow between different (mainly prefrontal and parietal) brain areas during reasoning tasks. As theta and gamma rhythms are important for complex tasks solving, we hypothesized that changes in these frequency bands will be visible, when comparing reasoning tasks to the memory task.
Materials and Methods
Participants
Seven right-handed adults (3 men, 4 women) participated in the study, all without history of neurological disorders or chronic diseases, and aged 23–25 years (mean = 24, SD = 0.66). All subjects were volunteers. Participants were compensated for their participation. All participants gave informed consent in accordance with the Ethical Review Board at the Medical University of Warsaw.
Procedure
Stimuli
In all tasks, we used capital letters as stimuli instead of whole sentences in order to avoid linguistic connotations. In the task requiring reasoning, the symbol indicating the order relation between elements (“>”) was additionally presented. The arrangement of the letters was randomized in order to minimize the possible interference induced by implied the alphabetical ordering of letters. All stimuli were projected on a computer screen with the software package ‘‘Presentation’’ (Presentation 11.0, www.neurobs.com).
Task Conditions
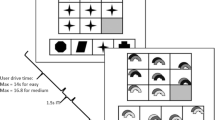
There were two conditions in this study—reasoning and memory (control) tasks; each of them consisted of 21 trials (repetitions). The design of the experiment and time course of the reasoning and memory conditions are shown in Fig. 1. Each task started with the presentation of an instruction that indicated whether what followed was a reasoning or a memory task.
There were two phases of each task—learning and testing. In the learning phase of the reasoning condition, participants had to integrate the presented information from three premises, where the first two were not related until the third premise appeared (A > B was followed by C > D and in the end by B > C). In the test phase, subjects had to answer questions about relations between the presented elements as well as about relations between elements which were not directly presented (e.g., A > C or A > D). The queries shown were either deductible (true in the given order relation) (e.g., A > C, A > D) or untrue (e.g., D > B, B > A). Note, that in the above, example premises, consecutive letters from the alphabet were used in order to explain the idea of the paradigm, in the actual task exactly random letters were used as stimuli, to make sure participants would only deduct from the given premises, and not from their knowledge of the alphabet.
There was a possibility that using letters as stimuli could evoke a Stroop effect, namely, the trials with letters presented in a non-alphabetical order could produce bigger interference and longer reaction times than trials with letters presented in the well-known alphabetical order relation. To examine this possibility, we divided the questions we asked our participants into two groups: “non-interfering” trials (e.g., C > H?) and “interfering” trials (e.g., K > D?) and checked whether these two types of question caused different reactions. The comparison showed no difference in reaction times (RT) between “interfering” (2,455 ms) and “non interfering” (2,575 ms) trials (Wilcoxon test: Z = −1.5; NS), so we could assume that the potential difference between two tasks used in our study would be due to integration requirements present in the reasoning condition and not due to the presumed interference effect.
The memory condition required the memorization of three pairs of unrelated elements, e.g., after the presentation of three pairs of objects: G T, U R, and W S, every subject was asked whether the presented pair of letters was shown before or not. The structure of the reasoning and the memory conditions was very similar, but in the memory task there was no need to integrate the presented information at any moment. The memory task served as a control condition for the reasoning condition.
Before presenting the premises (in the reasoning condition) or the pairs of elements (in the memory condition) to be remembered, a short instruction appeared, and also before the answering part of the experiment a short instruction was presented, each instruction lasted 5 s. Every premise or pair of elements, respectively, was presented for 5 s, the fixation point (inter-stimulus interval) between them was shown randomly for 3.5, 4 or 4.5 s (see Fig. 1). The electrical brain activity was analyzed during the learning phases of each trial, in which subjects were required to create a mental representation of stimuli by integrating incoming information (in the reasoning condition) or just to maintain the information (in the memory condition).
EEG Acquisition and Signal Analysis
The EEG was recorded from 64 Ag/AgCl electrodes arranged according to the 10-5 system in a WaveGuard EEG Cap (Advanced Neuro Technology, ANT). Additionally, an EOG-channel was recorded (electrodes placed in the outer corners of the eyes) and used to improve ocular artifacts rejection. A linked mastoid reference was used. Impedance was kept below 10 kΩ. The bioelectrical signals were recorded and digitalized by an ANT 64-channel amplifier (ANT Company) with a sampling rate of 512 Hz and then were offline downsampled to 128 Hz. The EEG recordings were visually inspected for any artifacts, and the epochs with artifacts were rejected from further processing. For the purposes of DTF analysis, 20 electrodes were chosen: Fp1, Fpz, Fp2, F3, F4, F7, F8, Fz, C3, C4, Cz, Cp5, Cp6, P7, P8, P3, P4, Pz, O1 and O2. The reduction of the number of electrodes to 20 was connected with the fact that the number of parameters of MVAR has to be much smaller than the number of data points. The number of data points is proportional to the number of channels, but the number of parameters is proportional to its square. The choice of derivations for analysis was preceded by a study involving different combinations of electrodes, after which the derivations which did not bring much information, were discarded.
Epochs of the first 2,000 ms (1,024 samples) after the stimulus were extracted for analysis. We chose not to take a longer interval, because, as is well-known, information processing is performed mainly right after the stimulus, and, moreover, later epochs were, in our case, more contaminated with artifacts. From 21 trials for each condition, after the elimination of artifacts, from 9 to 21 trials for memory tasks (mean for all subjects = 15.43, SD = 4.39) and from 12 to 18 trials for reasoning tasks (mean for all subjects = 14.14, SD = 1.95) were left for analysis.
Transmission Estimation
Transmission was estimated by means of the Directed Transfer Function (DTF) (Kaminski and Blinowska 1991). DTF is based on a multivariate autoregressive model (MVAR) and its concept may be derived from the Granger causality principle (Granger 1969). The Granger causality principle states that, if some series Y(t) contains information in past terms that helps in the prediction of series X(t), then Y(t) is said to cause X(t). The formulation of Granger causality is compatible with a two channel autoregressive model. The Granger causality principle was originally formulated for two time series, however, in a later publication Granger (1980) pointed out that the causality principle holds only if there are no other channels influencing the process. To account for the whole multivariate structure of a process of k channels, a multichannel autoregressive model has to be considered.For a multivariate k-channel process X(t):
The model takes the form:
where E(t) are vectors of size k and the coefficients A are k × k-sized matrices. Equation 1 can be easily transformed to describe relations in the frequency domain. By changing the sign of A, Eq. 1 can be rewritten in the form:
the application of Z transform yields
From the form of the above equations we see that the model can be considered as a linear filter with white noises E(f) on its input and the signals X(f) on its output. The matrix of filter coefficients H(f) is called the transfer matrix of the system. It contains information about all relations between data channels in the given set including the phase relations between signals.
Based on the properties of the transfer function of MVAR, the Directed Transfer Function (DTF) for an arbitrary number of channels may be defined:
DTF describes the causal influence of channel j on channel i at frequency f. The above equation defines a normalized version of DTF, which takes values from 0 to 1 producing a ratio between the inflow from channel j to channel i and all the inflows to channel i. In order to get a correct pattern of transmissions between channels, the model has to be fitted to all interdependent channels simultaneously, not pair-wise. The bivariate estimators of transmission may give totally misleading results as was demonstrated in Blinowska et al. (2004) and Kus et al. (2004).
The estimation of propagation by means of DTF is based on a phase difference between channels, therefore signals of the same phase do not influence the DTF values. The volume conduction is practically instantaneous, so it did not produce a phase difference between EEG derivations, therefore its influence in case of DTF is quite minor. In virtue of its property of extracting only phase differences, the DTF method is able to detect propagations even in case of very noisy signals.
When multiple repetitions of an experiment are available, the ensemble averaging over realization (repetitions) may be applied in the procedure of the model fitting (Ding et al. 2000, Kaminski et al. 2001). The determination of the model coefficients is based on the estimation of the correlation matrix R ij . This matrix was calculated by averaging over N T realizations (approximately 100–200, depending on the case):
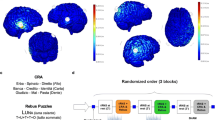
The epoch length N S was 256 points (2 s). The averaging concerns correlation matrices—the data are not averaged in the process. In this way, the information from all the repetitions of the experiment is incorporated into one model enhancing the common features of the signals, which results in an increase of statistical significance of the results. An example of DTF functions obtained by means of the above procedure for one subject is presented in Fig. 2.
A typical example of the DTF functions for one subject during memory (a) and reasoning condition (b). In each small panel, DTF (or power spectrum) is a function of frequency (from 1 to 40 Hz). Power spectra are marked on the diagonal. Off-diagonal flows are from the electrode marked below to the electrode marked at the left of the picture
Our aim was to find changes of propagation for different EEG rhythms between reasoning and memory tasks. We integrated the DTF function in the chosen frequency ranges: theta (4–8 Hz), alpha (8–12 Hz) and gamma (35–60 Hz). The resulting values were compared by means of a non-parametric paired-sample Wilcoxon signed rank test. The significant changes of transmission values between different types of tasks were plotted in the form of arrows, with an orange-red color scale for increases and a blue color scale for decreases of transmissions in the reasoning task in comparison to the memory task (Fig. 3).
The information flows in theta (a), alpha (b) and gamma (c) bands in reasoning tasks compared to memory. Figures show only significant differences between conditions computed by Wilcoxon test (α < 0.05). Colors from yellow to red indicate higher information transmission in reasoning tasks than in memory tasks, whereas blue arrows indicate lower transmission in reasoning tasks compared to memory tasks
Results
Normalized DTF estimates the amount of activity that is emitted from the given channel in respect to all inflows to that channel, so it shows the proper activity of a given channel. Non-normalized DTF shows the total outflow of activity from the given channel including also inflows. It was shown, by means of modeling of the neural populations, that non-normalized DTF is directly proportional to the strength of coupling between the channels (Kaminski et al. 2001). In this work we have used the normalized version of DTF, since it shows the intrinsic activity emitted from the given channel (we have estimated also non-normalized DTF, however, the results were less selective).
Normalized DTF is not linearly proportional to the coupling between channels, however, it contains information about the coupling strengths. Taking advantage from the fact that DTF contains meaningful frequency information, we have estimated the propagation in the frequency bands of interest.
The Theta Band (4–8 Hz)
The comparison of information flow (propagation) between reasoning and memory conditions in the theta (4–8 Hz) band showed significant increase of information flow in the reasoning condition within frontal and from frontal to parietal regions. The strongest increases were observed from Fz site to several frontal and parietal sites: Fp1, Fpz, Fp2, F4, F8, Cp5, P3, Pz, P4, P8. There was no significant decrease of information flow in the theta band at any electrode in the reasoning condition compared to the memory condition. A detailed illustration of results in the theta band is presented in Fig. 3a.
The Alpha Band (8–12 Hz)
The comparison between reasoning and memory tasks in the alpha (8–12 Hz) band, revealed enhanced transmission of information in the reasoning task, similar to results obtained for theta band. Transmissions from Fz site to F8 and to O1 and from F3 to Fz were the most pronounced ones. Additionally, we observed a significantly stronger transmission from Fpz to O1. There were also decreases in flows, from electrode F4 to C4 and Fz, which differentiated these results from the ones for transmissions in the theta band as described above. Significant changes in the information flow between reasoning and memory tasks are illustrated in Fig. 3b.
The Gamma Band (35–60 Hz)
The last comparison concerned the differences between reasoning and memory tasks in information flows within the gamma (35–60 Hz) band. It revealed several significant short-range increases and decreases of information transmission in the reasoning condition compared to the memory condition. The strongest increases of flows were observed from Cp6 and P4, also from P8. It seems that these electrodes were engaged in mutual transmissions connected with information processing. From the right posterior sites connected with Cp6, P4 and P8, propagation toward more frontal sites was observed. The propagation activity from the left hemisphere was much less pronounced. A detailed illustration of results in the gamma band is presented in Fig. 3c.
Results Summary
We compared information transfers in reasoning and memory tasks, according to three EEG bands (theta, alpha and gamma). They revealed strong, long-distance, fronto-parietal information flows in the theta and alpha bands during transitive reasoning tasks. Theta band transmissions had a focused site—the frontal (Fz) electrode—whereas for information transfers in the alpha band such a clear characteristic was not present. In gamma band, the pattern of changes in information transmissions was more complex—they were mainly short distance and dispersed around the right parietal region.
Discussion
In this study, we consider the propagation in the sensor space. Although the volume conduction does not affect the results obtained by means of DTF, the orientation of the source dipoles can influence the results and the dispersion of electromagnetic signals from the cortex to the sensors deteriorates the resolution. Therefore, the localization of possible sources of activity is not very accurate. We can talk about some sites connected with the position of a given electrode.
In this study, we have observed an increase of information flow from prefrontal to parietal cortex during transitive reasoning trials when compared to the memory condition. This transmission is mostly expressed within the theta band (4–8 Hz), but is also present in the alpha band (8–12 Hz). In addition to this long-range connection, frontal short-range (from Fz to neighboring electrodes) transfers in theta and alpha were increased during the reasoning condition. Furthermore, comparison of reasoning versus memory showed enhanced information transfer in the gamma band during reasoning. In this case the right posterior sites acted as a transmitter and the transfers were mostly short-ranged and dispersed.
In order to examine the reasoning processes, we used linear syllogism (linear order) tasks, which are classified as a “nonmatch” order type (Foos et al. 1976). It means that there are no common elements presented in consecutive pairs and all information has to be kept separately in memory, until the last premise is presented. In the moment of the last premise presentation, integration of information occurred. Performing such mental operations—simultaneous maintenance and manipulation of information—is described as working memory (e.g., Miyake and Shah 1999). What is more important in the context of our results, is that the reasoning ability is often related to the working memory system (Unsworth et al. 2009). Some authors have pronounced strong statements on this, such as: “reasoning ability is (little more than) working-memory capacity?!” (Kyllonen and Christal 1990). There are also studies showing that reasoning ability could be predicted by ‘‘storage in the context of processing’’ and ‘‘coordination’’, which both are defined as working memory functions (Buehner et al. 2005).
Baddeley’s model of working memory, the best-known model, distinguishes between central executive (attentional) functions and storage functions. The latter are related to the two “slave” systems: the phonological loop for maintaining verbal information, and a visuospatial sketch pad, which is responsible for the storage of visuospatial information (Baddeley 1992). The executive processes are most often related to frontal lobe functioning (for a review see Collette and Van der Linden 2002), although there is some evidence that they could rely on a more distributed, fronto-parietal network (Babiloni et al. 2004; Collette et al. 1999). Results of many studies also showed that tasks involving the phonological loop primarily activate areas in the left hemisphere, whereas the visuospatial sketch pad is mainly related to activations within the right hemisphere (e.g., Clark et al. 2001; Smith et al. 1996). Taking this information into account we can relate the enhanced long-range transmission in the theta band obtained in our experiment to the fronto-parietal executive network, whereas short-range transfers from posterior sites in the gamma band could reflect the visuospatial sketchpad activity.
Support for such considerations comes also from a study conducted by Sauseng and colleagues (Sauseng et al. 2005), who assumed that coherent activity of frontal and parietal regions in theta and alpha oscillations reflects the central executive component of the working memory system. They tested this hypothesis in an experiment with two working memory conditions, with and without the necessity of manipulation of objects. The results of their study clearly pinpointed that theta enhancement in long-range connectivity was associated with increased central executive demands.
Moreover, the accompanying, mainly short-range, elevated information flows in alpha band within the frontal region probably reflects another mechanism involved in task performance—the active inhibition, which previously has been related to increased alpha (Klimesch et al. 2007). Solving transitive reasoning tasks not only requires the active manipulation and integration of information, but also involves inhibiting of irrelevant information (in this case the mental models which are not appropriate in the light of the information delivered with the third premise).
Some authors use the term theta band for oscillation activity up to 10–12 Hz (e.g., Young and McNaughton 2009), so these two oscillations (theta and alpha) could in fact reflect the same mechanism, but further research is necessary in order to decide which interpretation of increased transmission in alpha band is correct.
On the other hand, support for our understanding of gamma band transmissions as reflecting the visuospatial sketchpad activity comes from a study by Kawasaki and Watanabe (2007), who showed increased parietal and frontal gamma activity accompanying enhanced fronto-parietal theta during visuospatial working memory task. Taking into account the involvement of the right parietal region connected with enhanced transmissions in the gamma band from that region, in the context of results reported by Kawasaki and Watanabe (2007), we can conclude that increase of information flows in gamma band reflects the larger visuospatial demands of the reasoning task used in our study.
To summarize, our results suggest that the transfer of information in theta band reflects the functioning of the central executive mechanism located in frontal lobes, and the transfer in gamma band activity reflects visuospatial manipulation. The results concerning theta activity shed some light on many other experiments showing fronto-parietal theta enhanced activity during working memory tasks (Kawasaki and Watanabe 2007; Onton et al. 2005). It appears that the fronto-parietal pattern of theta activity is driven mainly by the frontal sites. In the case of theta band transmissions, we observed a focused source of information flow, whereas in gamma band this pattern is more complex. There are mainly short distance information flows which are congruent with previous studies of coherence (Sauseng et al. 2005), and the main origin of information transfer in gamma band in the reasoning task is located in the right parietal site.
These findings, especially concerning fronto-parietal network involvement, have a solid ground in the existing literature on neural (fMRI) correlates of relational reasoning. They also fit very well into a wide scope of evidence concerning the role of theta and gamma oscillations in working memory tasks, but they shed new light on the nature of information transfer between the engaged areas.
References
Babiloni C, Babiloni F, Carducci F, Cappa SF, Cincotti F, Del Percio C, Miniussi C, Moretti DV, Rossi S, Sosta K, Rossini PM (2004) Human cortical responses during one-bit short-term memory. A high-resolution EEG study on delayed choice reaction time tasks. Clin Neurophysiol 115:161–170
Baddeley A (1992) Working memory. Science 255(5044):556–559
Bhattacharya J, Petsche H, Feldmann U, Rescher B (2001) EEG gamma-band synchronization between posterior and frontal cortex during mental rotation in humans. Neurosci Lett 311(1):29–32
Blinowska KJ, Kuś R, Kamiński M (2004) Granger causality and information flow in multivariate processes. Phys Rev E, 70:050902; Virt J Biol Phys Res 8(11)
Buehner M, Krumm S, Pick M (2005) Reasoning is working memory and not attention. Intelligence 33(3):251–272
Clark CR, Moores KA, Lewis A, Weber DL, Fitzgibbon S, Greenblatt R, Brown G, Taylor J (2001) Cortical network dynamics during verbal working memory functions. Int J Psychophysiol 42(2):161–176
Collette F, Van der Linden M (2002) Brain imaging of the central executive component of working memory. Neurosci Biobehav Rev 26(2):105–125
Collette F, Salmon E, Van der Linden M, Chicherio C, Belleville S, Degueldre C, Delfiore G, Franck G (1999) Regional brain activity during tasks devoted to the central executive of working memory. Cogn Brain Res 7:411–417
Ding M, Bressler SL, Yang W, Liang H (2000) Short-window spectral analysis of cortical event-related potentials by adaptive multivariate autoregressive modeling: data preprocessing, model validation, and variability assessment. Biol Cybern 83:35–45
Evans JStBT (2006) The heuristic-analytic theory of reasoning: Extension and evaluation. Psychon Bull Rev 13(3):378–395
Fangmeier T, Knauff M, Ruff CC, Sloutsky V (2006) fMRI evidence for a three-stage model of deductive reasoning. J Cogn Neurosci 18(3):320–334
Foos PW, Smith KH, Sabol MA, Mynatt BT (1976) Constructive processes in simple linear order problems. J Exp Psychol Hum Learn Mem 2:759–766
Gevins A, Smith ME, McEvoy L, Yu D (1997) High-resolution EEG mapping of cortical activation related to working memory: effects of task difficulty, type of processing, and practice. Cereb Cortex 7(4):374–385
Goel V, Stollstorff M, Nakic M, Knutson K, Grafman J (2009) A role for right ventral lateral prefrontal cortex in reasoning about indeterminate relations. Neuropsychologia 47(13):2790–2797
Granger CWJ (1969) Investigating causal relations in by econometric models and cross-spectral methods. Econometrica 37:424–438
Granger CWJ (1980) Testing for causality: a personal viewpoint. J Econ Dyn Control 2:329–352
Halford GS, Wilson WH, Phillips S (1998) Processing capacity defined by relational complexity: implications for comparative, developmental, and cognitive psychology. Behav Brain Sci 21(6):803–864
Johnson-Laird PN, Byrne RMJ, Schaeken WS (1992) Propositional reasoning by model. Psychol Rev 99(3):418–439
Kahana MJ, Sekuler R, Caplan JB, Kirschen M, Madsen JR (1999) Human theta oscillations exhibit task dependence during virtual maze navigation. Nature 399:781–784
Kaiser J, Lutzenberger W (2003) Induced gamma-band activity and human brain function. Neuroscientist 9(6):475–484
Kamiński M, Blinowska KJ (1991) A new method of the description of the information flow in brain structures. Biol Cybern 65:203–210
Kamiński M, Ding M, Truccolo W, Bressler S (2001) Evaluating causal relations in neural systems: granger causality, directed transfer function and statistical assessment of significance. Biol Cybern 85:145–157
Kawasaki M, Watanabe M (2007) Oscillatory gamma and theta activity during repeated mental manipulations of a visual image. Neurosci Lett 422(2):141–145
Klimesch W, Sauseng P, Hanslmayr S (2007) EEG alpha oscillations: the inhibition-timing hypothesis. Brain Res Rev 53(1):63–88
Kuś R, Kamiński M, Blinowska KJ (2004) Determination of EEG activity propagation: pair-wise versus multichannel estimate. IEEE Trans Biomed Eng 51:1501–1510
Kyllonen PC, Christal RE (1990) Reasoning ability is (little more than) working-memory capacity?!. Intelligence 14:389–433
Leth-Steensen C, Marley AAJ (2000) A model of response time effect in symbolic comparison. Psychol Rev 107(1):62–100
Miltner WH, Braun C, Arnold M, Witte H, Taub E (1999) Coherence of gamma-band EEG activity as a basis for associative learning. Nature 397(6718):434–436
Miyake A, Shah P (eds) (1999) Models of working memory: mechanisms of active maintenance and executive control. Cambridge University Press, New York
Onton J, Delorme A, Makeig S (2005) Frontal midline EEG dynamics during working memory. Neuroimage 27(2):341–356
Rabinowitz FM, Grant MJ, Howe ML, Walsh C (1994) Reasoning in middle childhood: a dynamic model of performance on transitive tasks. J Exp Child Psychol 58(2):252–288
Rips LJ (1983) Cognitive processes in propositional reasoning. Psychol Rev 90:38–71
Sarnthein J, Petsche H, Rappelsberger P, Shaw GL, von Stein A (1998) Synchronization between prefrontal and posterior association cortex during human working memory. Proc Natl Acad Sci 95(12):7092–7096
Sauseng P, Klimesch W, Schabus M, Doppelmayr M (2005) Fronto-parietal coherence in theta and upper alpha reflect central executive functions of working memory. Int J Psychophysiol 57(2):97–103
Sauseng P, Hoppe J, Klimesch W, Gerloff C, Hummel F (2007) Dissociation of sustained attention from central executive functions: local activity and interregional connectivity in the theta range. Eur J Neurosci 25(2):587–593
Scheeringa R, Petersson KM, Oostenveld R, Norris DG, Hagoort P, Bastiaansen MC (2009) Trial-by-trial coupling between EEG and BOLD identifies networks related to alpha and theta EEG power increases during working memory maintenance. Neuroimage 44(3):1224–1238
Sedek G, von Hecker U (2004) Effects of subclinical depression and aging on generative reasoning about linear orders: same or different processing limitations? J Exp Psychol Gen 133:237–260
Singer W, Engel AK, Kreiter A, Munk MHJ, Neuenschwander S, Roelfsema PR (1997) Neuronal assemblies: necessity, signature and detectability. Trends Cogn Sci 1(7):252–261
Smith EE, Jonides J, Koeppe RA (1996) Dissociating verbal and spatial working memory using PET. Cereb Cortex 6(1):11–20
Sternberg RJ (1980) Representation and process in linear syllogistic reasoning. J Exp Psychol Gen 109(2):119–159
Unsworth N, Spillers GJ, Brewer GA (2009) Examining the relations among working memory capacity, attention control, and fluid intelligence from a dual-component framework. Psychol Sci Q 51(4):388–402
Young CK, McNaughton N (2009) Coupling of theta oscillations between anterior and posterior midline cortex and with the hippocampus in freely behaving rats. Cereb Cortex 19(1):24–40
Acknowledgments
The authors acknowledge the support for the herein reported research from the grant of the Polish Ministry of Science and Higher Education (N106 017 31/1344) and NEUROMATH Action. The authors are also grateful to Prof. W. Szelenberger for the courteous invitation to use his EEG laboratory.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Brzezicka, A., Kamiński, M., Kamiński, J. et al. Information Transfer During a Transitive Reasoning Task. Brain Topogr 24, 1–8 (2011). https://doi.org/10.1007/s10548-010-0158-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10548-010-0158-6