Formulation, Implementation and Validation of a 1D Boundary Layer Inflow Scheme for the QUIC Modeling System

Abstract

Recent studies have highlighted the importance of accurate meteorological conditions for urban transport and dispersion calculations. In this work, we present a novel scheme to compute the meteorological input in the Quick Urban & Industrial Complex (QUIC) diagnostic urban wind solver to improve the characterization of upstream wind veer and shear in the Atmospheric Boundary Layer (ABL). The new formulation is based on a coupled set of Ordinary Differential Equations (ODEs) derived from the Reynolds Averaged Navier–Stokes (RANS) equations, and is fast to compute. Building upon recent progress in modeling the idealized ABL, we include effects from surface roughness, turbulent stress, Coriolis force, buoyancy and baroclinicity. We verify the performance of the new scheme with canonical Large Eddy Simulation (LES) tests with the GPU-accelerated FastEddy solver in neutral, stable, unstable and baroclinic conditions with different surface roughness. Furthermore, we evaluate QUIC calculations with and without the new inflow scheme with real data from the Urban Threat Dispersion (UTD) field experiment, which includes Lidar-based wind measurements as well as concentration observations from multiple outdoor releases of a non-reactive tracer in downtown New York City. Compared to previous inflow capabilities that were limited to a constant wind direction with height, we show that the new scheme can model wind veer in the ABL and enhance the prediction of the surface cross-isobaric angle, improving evaluation statistics of simulated concentrations paired in time and space with UTD measurements.

1 Introduction

Reliable estimates of hazardous airborne contaminants levels in urban areas are necessary for several decision-makers, including environmental regulators (Kadaverugu et al. 2019), emergency responders (Donnelly et al. 2009), and national security, defense and military agencies (Warner et al. 2008). However, the problem of urban transport and dispersion of contaminants is challenging as several scales of atmospheric motions influence the contaminants concentrations at any space-time point (Wiersema et al. 2020). For instance, mesoscale and synoptic circulations determine the prevailing wind characteristics, which can be locally altered by the small-scale interactions of the flow with urban built-up areas, such as street canyons (Zajic et al. 2011; Nelson et al. 2007), channeling (Britter and Hanna 2003), building-induced updrafts and downdrafts (Belcher 2005; Lamer et al. 2022a), recirculation zones and wake areas (Fernando et al. 2010), among others.

Early attempts to calculate transport and dispersion of contaminants relied on the Gaussian plume approximation (Venkatram 1996), which has the advantage of being semi-analytical and relatively simple to implement. Nonetheless, several key assumptions of the Gaussian plume theory—such as constant inflow wind and homogeneous and flat terrain—limited its applicability in urban areas, where the complex three-dimensional (3D) wind field is far from homogeneous (Singh et al. 2008). Recent advances in computational resources have enabled the transition from these early efforts to Computational Fluid Dynamics (CFD) solvers, which can calculate 3D wind fields around buildings as well as model turbulence characteristics and the dispersion of tracers (Gowardhan et al. 2021). Although CFD solvers are physically based and numerically integrate the governing equations of motion, several assumptions and modeling choices are required to calculate subgrid turbulence and to specify the inflow boundary conditions (Hanna et al. 2006). In addition, CFD solvers are computationally demanding and may not be sufficient for many applications related to the release of harmful contaminants in cities and/or industrial facilities, where fast response is necessary (Gowardhan et al. 2011).

An intermediate approach between CFD solvers and semi-analytical models is the Quick Urban & Industrial Complex (QUIC) modeling system developed at Los Alamos National Laboratory, which is based on Röckle (1990) methodology (Robinson et al. 2023). The modeling system includes a 3D fast-running and building-aware wind solver (QUIC-URB) and a Lagrangian particle-tracking code for transport and dispersion calculations (QUIC-PLUME). QUIC has been used for fast turn around national security problems related to the dispersion of chemical, biological and radiological (CBR) agents, including vulnerability assessments, accidental releases at industrial facilities, dust transport studies, and back calculations of ultrafine emissions from downwind measurements (Brown et al. 2013; Musolino et al. 2013). The QUIC-URB formulation consists of several empirical parameterizations to specify an initial 3D wind field that accounts for the physics of the flow around buildings (e.g., street canyons, wake and cavity zones), and of a correction step, where the initially specified wind field is forced to satisfy mass consistency for incompressible flow (i.e., zero divergence in the 3D wind field). More information about QUIC-URB formulation can be found in Singh et al. (2008) and Gowardhan et al. (2010). The QUIC modeling system has been validated against wind tunnel measurements (Singh et al. 2008; Pol et al. 2006; Gowardhan et al. 2010), and it was found to perform comparably to other CFD models based on Reynolds-Averaged Navier Stokes (RANS) and Large Eddy Simulation (LES) turbulence closures during the Oklahoma City Joint Urban 2003 (JU03) Experiment (Neophytou et al. 2011).

The accuracy of QUIC solutions (and other urban dispersion models) is strongly dependent upon the input meteorological conditions, which result from the unresolved larger-scale dynamics within and above the Atmospheric Boundary Layer (ABL). By validating different transport models to calculate dispersion of chemical and biological warfare agents, Chang et al. (2003) showed that the dosage predictions are highly dependent on the input meteorology and the diagnostic wind solvers. Brown et al. (2008) and Rodriguez et al. (2013) studied the sensitivity of QUIC to the uncertainty in the wind direction and concluded that even a few degrees shift ($\sim 10^{\circ }$) can make a large difference in the dosage predictions, for specific urban configurations (e.g., blockage by large buildings close to the source location). Note that the sensitivity to the input meteorology is a common problem in CFD models as well, where large-scale dynamics is typically not resolved and is introduced in the model as the inflow boundary conditions. During the Urban Dispersion International Evaluation Exercise (UDINEE) project, several studies also stressed the importance of inflow conditions to have accurate concentration predictions with different urban dispersion models (Tinarelli and Trini Castelli 2019; Hernández-Ceballos et al. 2019). Recent studies focused on the offline coupling between mesoscale models and microscale models (including QUIC and CFD codes), to specify inflow profiles derived from mesoscale models such as the widely used Weather Research and Forecasting (WRF) code (Wyszogrodzki et al. 2012; Kochanski et al. 2015; Chen et al. 2011). While promising results were achieved with the mesoscale-microscale offline coupling technique, computational cost increased substantially because of the expensive WRF simulations.

In this work, we address the challenge of input meteorology in QUIC and propose a new 1D scheme to calculate the time-averaged inflow conditions. The new scheme is fast to compute, physically based and adds more flexibility compared to existing QUIC capabilities. Specifically, we include different effects that influence the inflow profile, including buoyancy (atmospheric stratification), surface roughness, height-varying pressure gradient (baroclinicity), Coriolis force, and turbulence stresses. The new scheme can model 2D and 3D effects such as wind rotation and baroclinicity with 1D Ordinary Differential Equations (ODE). We validate the new scheme with idealized LES data and we show the importance of input meteorology by comparing sensitivity simulations with field data from the Urban Threat Dispersion (UTD) field experiment (Lamer et al. 2022b; Chavez 2022). The UTD experiment includes wind measurements as well as concentration/dosage gas samples from different tracer releases in downtown New York City (NYC).

The remainder of the article is organized as follows. Section 2 reviews existing QUIC capabilities to calculate inflow boundary conditions as well as their challenges. Section 3 presents the new model formulation and numerical implementation. The verification and evaluation with LES data and UTD field data is documented in Sects. 4 and 5, respectively. We summarize the main findings in Sect. 6.

2 Overview and Challenges of QUIC Meteorological Input

For 3D CFD simulations of the ABL, the large-scale meteorological forcing is prescribed with initial and/or boundary conditions (e.g., initial soundings, specified inflow conditions, Dirichlet lateral boundaries). Similarly, the meteorological forcing in QUIC is prescribed with the undisturbed time-averaged 3D wind field ($U_m$), i.e. the velocity field before the QUIC solver applies the buildings parameterizations and the divergence correction. Several options are available in QUIC to specify the time-averaged undisturbed field, from spatially homogeneous 1D analytical profiles ($U_m = U_m(z)$) to spatially heterogeneous 3D solutions derived from mesoscale models like WRF and/or sensors-based interpolations ($U_m = U_m(x,y,z)$). The 1D analytical options include Monin and Obukhov (1954) similarity theory (MOST), an empirical power-law function and a semi-empirical canopy profile, and are described in detail in the Supplementary Material. Here, we describe their two main limitations that motivated the development of a new approach.

First, the QUIC domain top can extend to hundreds of meters to include the effect of tall high-rises in urban areas (that can be >500 m), but MOST applicability is theoretically confined within the Atmospheric Surface Layer (ASL), which only covers $\sim$50 m above ground level. In the ASL, the constant flux layer assumption is invoked to derive the log scaling either from dimensional arguments or from a first-order turbulence closure with eddy viscosity set to $\kappa u_* z$, where $u_*$ is the friction velocity and $\kappa$ is the von Kármán constant. However, turbulent stresses are not constant above the ASL and the constant flux assumption is even questionable within the ASL itself (Constantin and Johnson 2019). The power-law formulation is empirical and reliable for extrapolating surface winds to wind turbine hub heights, typically in the order of 100 m a.g.l, but its applicability beyond that is not guaranteed (Crippa et al. 2021). In addition, it requires specifying the arbitrary $\alpha$ exponent, which is site-, time- and problem-specific.

The second set of challenges is related to the constant wind direction assumption, which may not be valid above and within the ABL because of Coriolis effects. In addition to the constant flux layer, MOST assumes an infinite surface Rossby number ($Ro_0$) to neglect Coriolis effects and justify a constant wind direction, although measurements show non-zero cross-isobaric angles ($\vartheta _0$), which are related to finite $Ro_0$ effects (Peña and Floors 2014). For strongly stratified conditions, the Coriolis force also has a large influence in the formation of low-level jets and the velocity magnitude profile in the outer layer (Optis et al. 2014). Different studies proposed novel analytical (Ghannam and Bou-Zeid 2021) and numerical (Van Der Laan et al. 2021) formulations to include finite $Ro_0$ effects and to model the wind veer close to the surface, and they showed that realistic cross-isobaric angles are typically within the infinite Rossby number limit (0$^{\circ }$) and the Ekman (1905) constant eddy viscosity limit (45$^{\circ }$). In the context of QUIC, modeling the wind veer at the surface correctly is important to get the right wind direction at the release level, which was shown to be a key parameter to determine the final accuracy of QUIC predictions (Rodriguez et al. 2013). Finally, neither MOST nor other empirical formulations account for other traditionally neglected processes in the ABL that influence the ABL vertical structure, such as the effect of non-constant pressure gradients in a baroclinic atmosphere where large-scale temperature gradients exist (as typical at mid-latitudes). Shear in the geostrophic winds (or equivalently in the pressure gradients) can significantly influence both the velocity magnitude and the wind rotation close to the surface (Momen et al. 2018).

With the goal of addressing these challenges, in the following subsection we present a comprehensive formulation that is appropriate for both the ASL and the outer layer above the ASL. The new formulation builds on previous efforts (Blackadar 1962; Noh et al. 2003; Optis et al. 2014; van der Laan et al. 2020) and is based on the 1D RANS horizontal momentum equations.

3 A New Formulation for the QUIC Undisturbed Flow Field

3.1 Governing Equations

A Cartesian coordinate system (x, y, z) is used to write the governing equations, and the velocity vector is represented by the three components u, v and w in the x-, y- and z-direction, respectively. The steady-state horizontal velocity field in the idealized ABL over flat terrain can be described by the incompressible horizontal momentum RANS equations, where horizontal homogeneity ($\partial / \partial x = 0$, $\partial / \partial y = 0$) and no subsidence ($\langle \overline{w} \rangle =0$) are assumed:

$$\begin{aligned} \begin{aligned} \frac{d}{dz}\langle \overline{u'w'} \rangle&= \, f \langle \bar{v} \rangle + \frac{dp}{dx}, \\ \frac{d}{dz} \langle \overline{v'w'} \rangle&= -f \langle \bar{u} \rangle + \frac{dp}{dy}, \end{aligned} \end{aligned}$$

(1)

where $\langle \bar{u} \rangle = \langle \bar{u} \rangle (z)$ and $\langle \bar{v} \rangle = \langle \bar{v} \rangle (z)$ are the time ($\bar{\cdot }$) and space ($\langle \cdot \rangle$) averaged zonal and meridional velocity components, respectively, the prime symbol denotes fluctuations from the time average, $dp/dx = \left[ dp/dx\right] (z)$ and $dp/dy = \left[ dp/dy\right] (z)$ are the height-dependent pressure gradients in the x- and y-direction, $f = 2\Omega \sin (\varphi )$ is the Coriolis parameter, $\varphi$ is the latitude and $\Omega$ is the rotation rate of the Earth. $\langle \overline{u'w'} \rangle$ and $\langle \overline{v'w'} \rangle$ are the u-momentum and v-momentum turbulent fluxes that arise from fluctuations with respect to the time average, which are equivalent to the fluxes that would arise from fluctuations with respect to both space and time averages, with the assumption that dispersive fluxes are zero (Calaf et al. 2010). Note that $\langle \bar{u} \rangle$ and $\langle \bar{v} \rangle$ are only a function of z because of the time average operator (no dependence on t) and the horizontal homogeneity assumption (no dependence on x and y). The assumption of horizontal homogeneity seems appropriate for the undisturbed flow over a limited urban area typical of QUIC domains, and it simplifies the solution of the equations by (i) reducing the problem dimensions from 3D to 1D (i.e., $U = U(z)$) and (ii) making advection negligible (if we also assume zero subsidence). The steady-state assumption is consistent with QUIC formulation, which solves for the steady-state flow field around arbitrary obstacles. Unsteadiness in QUIC can be approximated by multiple steady-state time instances.

Equation 1 represents a balance of forces normalized by mass (i.e., accelerations) in the x- and y-direction. At steady-state, the horizontal pressure gradient is balanced by the turbulent stress (momentum sink due to surface friction) and the Coriolis force. Above the boundary layer, where turbulent stresses become negligible, the geostrophic balance between the pressure gradient force and Coriolis force is established:

$$\begin{aligned} V_g= & {} -\frac{1}{f}\frac{dp}{dx}, \end{aligned}$$

(2)

$$\begin{aligned} U_g= & {} \,\frac{1}{f}\frac{dp}{dy}, \end{aligned}$$

(3)

where we denoted $U_g = U_g(z)$ and $V_g = V_g(z)$ the geostrophic winds in the x- and y-directions. Note that we retained the dependence on z of the geostrophic winds (and the pressure gradients), whereas most analytical and numerical studies of the idealized ABL make the barotropic assumption (i.e., $U_g$ and $V_g$ are constant with height), as discussed in Momen (2022); Ghannam and Bou-Zeid (2021). We will revisit the geostrophic dependence on z when we discuss the effect of baroclinicity.

If we prescribe the geostrophic forcing $U_g(z)$ and $V_g(z)$, Eq. 1 can be solved for $\langle \bar{u} \rangle (z)$ and $\langle \bar{v} \rangle (z)$ given some appropriate boundary conditions and a proper turbulence closure for the l.h.s. terms in Eq. 1, which will be discussed in the next subsection. Once the solution for $\langle \bar{u} \rangle (z)$ and $\langle \bar{v} \rangle (z)$ is reached, the undisturbed velocity magnitude and direction for QUIC can be calculated from the following vector relationships:

$$\begin{aligned} U_m(z)= & {} \sqrt{\langle \bar{u} \rangle (z)^2+\langle \bar{v} \rangle (z)^2}, \end{aligned}$$

(4)

$$\begin{aligned} \vartheta (z)= & {} \tan ^{-1}\left( \frac{\langle \bar{v} \rangle (z)}{\langle \bar{u} \rangle (z)} \right) . \end{aligned}$$

(5)

3.2 Blackadar’s Turbulence Closure

Within the ABL, the solutions for $\langle \bar{u} \rangle$ and $\langle \bar{v} \rangle$ are strongly influenced by the turbulence closure of the $\langle \overline{u'w'} \rangle$ and $\langle \overline{v'w'} \rangle$ terms. A common choice is the linear stress–strain relationship (Kosović 1997), where the turbulent fluxes (stress) are proportional to the shear in the velocity components (strain) through the eddy viscosity $K_V$:

$$\begin{aligned} \langle \overline{u'w'} \rangle= & {} -K_V \frac{d\langle \bar{u} \rangle }{dz}, \end{aligned}$$

(6)

$$\begin{aligned} \langle \overline{v'w'} \rangle= & {} -K_V \frac{d\langle \bar{v} \rangle }{dz}. \end{aligned}$$

(7)

Specifying the function that describes the $K_V = K_V(z)$ vertical profile is where most of the existing RANS formulations differ. If we assume a constant value for $K_V$, Eq. 1 can be solved analytically and the Ekman spiral solution is obtained (Ekman 1905). A characteristic feature of the Ekman solution is the 45$^{\circ }$ cross-isobaric angle at the surface, which is independent from the specific value of $K_V$. However, observations of $\vartheta _0$ show significant departures from the 45$^{\circ }$ prediction of Ekman’s theory, which motivated extensive research to formulate more flexible methodologies to model $K_V$. Constantin and Johnson (2019) and Van Der Laan et al. (2021) provide a comprehensive overview of such approaches, which range from linearly increasing values ($K_V = u_*\kappa z$, Ellison (1956)) to empirical functions that limit the eddy viscosity ($K_V = u_*\kappa z \exp \left( -z/h\right)$, where h is the height of maximum eddy viscosity) and numerical models based on Prandtl’s mixing-length theory ($K_V = \ell ^2\,S$, where $\ell$ is the characteristic length scale of turbulent fluctuations and S is the magnitude of the strain rate tensor). In this work, we follow Prandtl’s theory and specify the length scale based on the early work of Blackadar (1962), which we refer to as B62 hereafter:

$$\begin{aligned} K_V = \ell ^2 S, \quad \ell = \frac{\kappa z}{1 + \frac{\kappa z}{\ell _{\max }}}, \quad S = \sqrt{\left( \frac{d\langle \bar{u} \rangle }{dz} \right) ^2 + \left( \frac{d\langle \bar{v} \rangle }{dz} \right) ^2}, \end{aligned}$$

(8)

where $\ell _{\max }$ is a maximum turbulence length scale in the outer layer. The relative complexity of B62 compared to other simplified models that allow analytical solutions (e.g., Ekman’s, Ellison’s) is justified by having more realistic $K_V$ profiles for the entire boundary layer, as the characteristic length and velocity scales of turbulence extend beyond the surface layer. For instance, in Ellison’s model the length scale $\kappa z$ is adequate in the surface layer but assumed to grow indefinitely. In contrast, B62 is a limited mixing-length model, where the turbulence length scale is limited by $\ell _{\max }$. An alternative valid choice for the turbulence closure is the $k-\epsilon$ model, which is commonly used in commercial CFD software for engineering applications (Shirzadi et al. 2017; van der Laan et al. 2017). For 1D ABL simulations, van der Laan et al. (2020) showed that there are limited differences between the B62 mixing-length model and the $k-\epsilon$ one; therefore, we will focus our discussion only on the B62 formulation.

Compared to the original B62 model, we make three different extensions to (i) account for buoyancy in the ASL and the outer layer, (ii) include baroclinicity, and (iii) recast the problem in terms of boundary layer height rather than the outer layer turbulence scale $\ell _{\max }$. The three extensions are described in the next subsections.

3.3 Extensions to B62: Buoyancy in the ASL and the outer layer

The inverse length scale in B62 is the sum of two reciprocal length scales, one appropriate for the ASL ($\kappa z)$ and one for the outer layer ($\ell _{\max }$). As van der Laan et al. (2020) recently showed, a more adequate length scale that accounts for non-neutral conditions in the ASL is $\kappa z/\phi _m$, where $\phi _m$ is the dimensionless wind gradient in MOST that is a function of z/L, where L is the Obukhov length scale (Monin and Obukhov 1954) defined by:

$$\begin{aligned} L = -\frac{u_*^3 \theta _0}{\kappa g \left( \overline{w'\theta '}_s\right) }. \end{aligned}$$

(9)

In Eq. 9, g is the gravitational acceleration, $\theta _0$ is the reference potential temperature and $\overline{w'\theta '}_s$ is the surface flux of potential temperature. Using the latter length scale for the ASL, the combined length scale in the eddy viscosity formulation becomes:

$$\begin{aligned} \ell= & {} \frac{\kappa z}{\phi _m + \kappa z/{\ell _{\max }} }. \end{aligned}$$

(10)

Because of the nature of Businger et al. (1971) function for stable stratification ($\phi _m = 1 + \beta z/L$), the functional form of the length scale remains the same, with a different effective maximum length scale ($\ell _{\max ,\text {eff}}$):

$$\begin{aligned} \ell= & {} \frac{\kappa z}{1 + \beta z/L + \kappa z/{\ell _{\max }} } = \frac{\kappa z}{1+\kappa z/\ell _{\max ,\text {eff}}}, \quad \ell _{\max ,\text {eff}} = \left( \frac{\beta }{\kappa L} + \frac{1}{\ell _{\max }}\right) ^{-1}, \end{aligned}$$

(11)

where $\beta =4.7$ is the coefficient derived by Businger et al. (1971) from the Kansas experiment. From a practical perspective, Eq. 11 implies that for stable stratification we can use the original B62 length scale formulation with a reduced value of the length scale in the outer layer ($\ell _{\max ,\text {eff}} < \ell _{\max }$) that depends on the inverse Obukhov length.

For unstable conditions, we use the full algebraic form of Eq. 10 because $\phi _m = \left( 1 - \gamma _1 z/L \right) ^{-1/4}$ is not linearly dependent with z ($\gamma _1 = 15$ from the Kansas experiment). However, we found that the van der Laan et al. (2020) extension in the ASL may not be enough to properly represent the outer layer of the canonical neutral boundary layer (NBL) and the convective boundary layer (CBL), especially when the boundary layer is capped by a strong inversion layer. The reason is the formulation of the eddy viscosity velocity scale based on the velocity shear, that cannot properly account for the vanishing u gradient in the well-mixed CBL. For such cases, we propose an alternative formulation for the eddy viscosity that is only valid when $L^{-1} \le 0$:

$$\begin{aligned} K_V= & {} \kappa w_s z \left( 1 - \frac{z}{h} \right) ^p, \end{aligned}$$

(12)

$$\begin{aligned} w_s= & {} (u_*^3 + \phi _m\left( 0.1z/L\right) \kappa w_*^3 z/h ) ^{1/3}, \end{aligned}$$

(13)

where $w_s$ is a height-dependent velocity scale, h is the boundary layer height, $w_* = (-u_*^3 h /\kappa L)^{1/3}$ is the Deardorff velocity scale (Deardorff 1970) and p ranges from 2 to 3. The theoretical foundations of Eq. 12 are described in Hong and Pan (1996); Noh et al. (2003); Hong et al. (2006) and underlie the 1D Yonsei University Scheme (YSU) implemented in different mesoscale 3D models. Note that the eddy viscosity in Eq. 12 does not depend on the velocity shear, but only on the velocity scale in the mixed layer and the boundary layer height. In addition, we explicitly add a non-local countergradient term ($\gamma _u$ and $\gamma _v$) to properly account for turbulence in the zero-gradient mixed layer, for the convective boundary layer:

$$\begin{aligned} \langle \overline{u'w'} \rangle = -K_V \left( \frac{d\langle \bar{u} \rangle }{dz} - \gamma _u \right) , \end{aligned}$$

(14)

$$\begin{aligned} \langle \overline{v'w'} \rangle = -K_V \left( \frac{d\langle \bar{v} \rangle }{dz} - \gamma _v \right) . \end{aligned}$$

(15)

The countergradient terms $\gamma _u$ and $\gamma _v$ are calculated with a non-local approach (i.e., based on the surface flux rather than local gradients):

$$\begin{aligned} \gamma _u = b\frac{\langle \overline{u'w'} \rangle _0}{( w_{s0} h )}, \qquad \gamma _v = b\frac{\langle \overline{v'w'} \rangle _0}{( w_{s0} h )}, \end{aligned}$$

(16)

where $\langle \overline{u'w'} \rangle _0$ and $\langle \overline{v'w'} \rangle _0$ are the surface fluxes of u- and v-momentum, $w_{s0}$ is the $w_s$ velocity scale evaluated at the top of the surface layer (defined as 0.1h) and $b=6.5$ is a constant derived in Noh et al. (2003).

3.4 Extensions to B62: Length Scale in the Outer Layer

With the B62 formulation extended to include buoyancy in the ASL and the alternative formulation for $K_V$ for the NBL and CBL, the entire input space includes five parameters $[G, f, z_0, L, \ell _{\max }]$, where we assume to have a coordinate system oriented with the geostrophic wind with magnitude G, without loss of generality. Buckingham $\pi$ theorem suggests that there should be three dimensionless numbers that completely define the solution. We can write the similarity relationship in terms of three different Rossby numbers for the boundary layer height:

$$\begin{aligned} \tilde{h} = \frac{|f|h}{G} = \Lambda \left( Ro_0, Ro_L, Ro_{\ell }\right) , \end{aligned}$$

(17)

where the Rossby numbers are defined as follows:

$$\begin{aligned} Ro_0 = \frac{G}{|f|z_0}, \quad Ro_L = \frac{-G}{|f|L}, \quad Ro_{\ell } = \frac{G}{|f|\ell _{\max }}. \end{aligned}$$

(18)

Eq. 17 implies that there exists a relationship between h and the other parameters through the unknown $\Lambda$ function. As specifying $\ell _{\max }$ as an input parameter might require fine tuning and expert information, we use Eq. 17 to recast the problem in terms of h rather than $\ell _{\max }$ and eliminate the issue of specifying $\ell _{\max }$ in the input parameters. In other words, once h is specified $\ell _{\max }$ can be calculated by inverting the $\Lambda$ function in Eq. 17. We use the Geostrophic Drag Law (GDL) and empirical data to determine the functional form of $\Lambda$, as detailed in the Appendix.

3.5 Extensions to B62: Baroclinicity

Traditional textbook representations of the vertical structure of the 1D ABL, including B62, YSU and many others (Ekman 1905; Hess and Garratt 2002a, b; Shah and Bou-Zeid 2014; van der Laan et al. 2020), assume a steady and barotropic atmosphere, which implies that the pressure gradients in both x- and y-directions do not vary with time nor height (or alternatively, that the geostrophic wind shear is zero). However, that is rarely the case at mid-latitudes and in active mesoscale systems such as sea breezes and atmospheric fronts (Arya and Wyngaard 1975; Zilitinkevich and Esau (2005)), where horizontal temperature gradients create non-zero vertical geostrophic wind shear, that can be on the order of 5 m s$^{-1}$ per 1000 m of depth (Zilitinkevich and Esau 2003). The barotropic idealization has proven valuable in shaping our understanding of the basic behaviour of the ABL, but recent studies have highlighted that including baroclinicity is perhaps the most important next step in furthering our knowledge of ABL processes (Momen et al. 2018; Ghannam and Bou-Zeid 2021). A baroclinic environment can strongly modulate the wind speed profile, low-level jets formation, the cross-isobaric angle, turbulence structures, and mixing.

As an extension to B62 and YSU, we propose to relax the assumption of the barotropic atmosphere and impose non-zero geostrophic wind shear. As in Momen et al. (2018); Sorbjan (2004); Brown (1996), we assume that the second derivative of both components of the geostrophic winds is zero—i.e., this is equivalent to assuming that the underlying horizontal temperature gradient is constant within the domain height. Such assumption implies a linear vertical profile for $U_g(z)$ and $V_g(z)$, where the slopes of the linear functions are $b_u = dU_g/dz$ and $b_v = dV_g/dz$ and the velocities at the domain top are $U_{g0}$ and $V_{g0}$. The parameters $b_u$ and $b_v$ are related to horizontal temperature gradients with the thermal wind equations (Floors et al. 2015; Momen et al. 2018):

$$\begin{aligned} b_u= & {} \frac{dU_g}{dz} = -\frac{g}{f\theta _r}\frac{\partial \overline{\theta }}{\partial y}, \end{aligned}$$

(19)

$$\begin{aligned} b_v= & {} \frac{dV_g}{dz} = \frac{g}{f\theta _r}\frac{\partial \overline{\theta }}{\partial x}, \end{aligned}$$

(20)

where $\theta _r$ is the Boussinesq reference potential temperature and $\overline{\theta }$ is the Reynolds-Averaged potential temperature. Equations 19 and 20 can be derived by differentiating the definition of $U_g$ and $V_g$ (Eqs. 2 and 3) with respect to z and using the ideal gas law and the hydrostatic approximation (see Momen et al. (2018)).

3.6 Boundary Conditions and Numerical Implementation

Equation 1 is a boundary value problem (BVP) of two second order ODEs that describe the vertical structure of $\langle \bar{u} \rangle (z)$ and $\langle \bar{v} \rangle (z)$ in the ABL. The second-order coupled BVP can be recast into a set of four first-order ODEs where the unknowns are $[\langle \bar{u} \rangle , \langle \bar{v} \rangle , \langle \overline{u'w'} \rangle , \langle \overline{v'w'} \rangle ]$:

$$\begin{aligned} \begin{aligned}&\frac{d}{dz}\langle \overline{u'w'} \rangle&= \, f \langle \bar{v} \rangle + \frac{dp}{dx} \\&\frac{d}{dz}\langle \overline{v'w'} \rangle&= -f \langle \bar{u} \rangle + \frac{dp}{dy} \\&\frac{d}{dz}\langle \bar{u} \rangle&= \gamma _u - \frac{\langle \overline{u'w'} \rangle }{K_V} \\&\frac{d}{dz}\langle \bar{v} \rangle&= \gamma _v - \frac{\langle \overline{v'w'} \rangle }{K_V}, \end{aligned} \end{aligned}$$

(21)

The solution of Eq. 21 requires four boundary conditions. We specify Dirichlet boundary conditions at the domain top $u(z_{\text {top}}) = U_{g0}$ and $v(z_{\text {top}}) = V_{g0}$, and Neumann boundary conditions (rough wall) at the bottom to model the momentum sink due to friction:

$$\begin{aligned} \frac{d\langle \bar{u} \rangle }{dz}\bigg |_{z_{1}}= & {} -\frac{\langle \overline{u'w'} \rangle (z_1)}{u_* \kappa z_{1}} \phi _m \left( \frac{z_1}{L} \right) , \end{aligned}$$

(22)

$$\begin{aligned} \frac{d\langle \bar{v} \rangle }{dz}\bigg |_{z_{1}}= & {} -\frac{\langle \overline{v'w'} \rangle (z_1)}{u_* \kappa z_{1}} \phi _m \left( \frac{z_1}{L} \right) . \end{aligned}$$

(23)

Equations 22 and 23 require information for the surface fluxes of u- and v-momentum and the velocity scale in the ASL $u_*$. Let $z_1$ denote the nearest grid point to the surface in the discretized domain. The friction velocity and the surface momentum fluxes can be computed as follows:

$$\begin{aligned} u_*= & {} \kappa \sqrt{\langle \bar{u} \rangle (z_1)^2 + \langle \bar{v} \rangle (z_1)^2} \left[ \int _{z_0}^{z_1} \frac{\phi _{m}(z/L)dz}{z} \right] ^{-1}, \end{aligned}$$

(24)

$$\begin{aligned} \langle \overline{u'w'} \rangle (z_1)= & {} \kappa u(z_1)u_* \left[ \int _{z_0}^{z_1} \frac{\phi _{m}(z/L)dz}{z} \right] ^{-1}, \end{aligned}$$

(25)

$$\begin{aligned} \langle \overline{v'w'} \rangle (z_1)= & {} \kappa v(z_1)u_* \left[ \int _{z_0}^{z_1} \frac{\phi _{m}(z/L)dz}{z} \right] ^{-1}. \end{aligned}$$

(26)

The solution of Eq. 21 is relatively stiff, especially with the extended B62 turbulence closure. The collocation-based bvp4c solver is used to obtain a fourth-order accurate solution on an adaptive mesh. The full description of the general solver can be found in Kierzenka and Shampine (2001). The solver is finally integrated with the QUIC Graphical User Interface (GUI) and the QUIC-URB software to be used as an additional option to provide inflow conditions for the undisturbed flow field.

4 Verification with LES Data

4.1 Overview of Benchmark LES Simulations

The implementation of the 1D RANS code based on the Sect. 3 formulation is verified with LES data. Specifically, we run seven highly idealized and horizontally homogeneous LES canonical tests to evaluate the agreement between the 1D RANS scheme and spatially- and temporally-averaged LES results. In other words, we aim to assess if the turbulence closure that we proposed in Sect. 3 can represent the averaged mean vertical profiles derived from 3D LES simulations, where most of the energy-containing turbulent eddies are explicitly resolved.

Table 1 List of domain setups, forcing conditions and mean boundary layer features for the canonical LES tests. The latitude in all the LES cases is set to 40.7128N. $\Delta x, \Delta y, \Delta z, N_x, N_y, N_z$, are the LES grid spacings and total number of grid points in x-, y- and z-directions, respectively. $\overline{w'\theta '}_s$ is the surface flux of potential temperature ($\theta$)

Table 1 reports the main features of the seven canonical experiments presented in this work, and Table S1 provides the associated Rossby numbers. We use the dry dynamical core of FastEddy (Sauer and Muñoz-Esparza 2020) to solve the compressible and filtered Navier–Stokes Equations with the different configurations presented in Table 1. FastEddy is a LES model that uses Graphics Processing Units (GPUs) to accelerate computations, and the full description of the dynamical core can be found in Sauer and Muñoz-Esparza (2020); Muñoz-Esparza et al. (2022). The domain of the reference NBL simulation is a 1.92 x 1.92 x 1.15 km³ cuboid with vertical stretching in the z direction, with a capping inversion of strength $\partial \theta / \partial z = 0.08$ K m ^-1 located at $z=500$m, and a second inversion of strength $\partial \theta / \partial z = 0.003$ K m^-1 starting at $z = 650$m. The initial potential temperature in the zero-gradient region is 300K. No surface heat flux is prescribed at the bottom. The surface momentum sink due to surface friction is modeled with MOST boundary conditions. Other input parameters are the roughness length ($z_0 = 0.01$m) and the Coriolis parameter ($f=9.49 \times 10^{-5}$ s$^{-1}$), which is set to match the latitude of New York City (approximately 40.7128N). The flow is driven by a constant (in time and height) pressure gradient in the y-direction ($U_{g0} = 10$ m s$^{-1}$ and $V_{g0} = 0$ m s$^{-1}$). Subgrid turbulence stresses are computed with the Lilly (1967) closure, where the eddy viscosities and eddy diffusivities are calculated based on the prognostically evolving turbulent kinetic energy (TKE). To initiate turbulent motions, stochastic potential temperature perturbations are applied near the inflow boundaries according to the cell perturbation method (Muñoz-Esparza et al. 2014; Muñoz-Esparza and Kosovic 2018). Rayleigh damping is also applied in the top 200 m of the domain, to minimize unphysical reflection of propagating wave energy back into the model domain (Klemp et al. 2008). Note that this is a rather standard benchmark NBL case and is often referred to as the Conventionally Neutral Boundary Layer (CNBL) due to the capping inversion (Liu et al. 2021; Abkar and Porté-Agel (2013); Taylor and Sarkar 2008).

We perturb the benchmark NBL configuration to test different roughness at the surface, stabilities and baroclinic cases. Specifically, we perform two additional tests with different roughness lengths ($z_0 = 0.001$m and $z_0 = 0.1$m), denoted as low and high roughness, respectively. Two additional simulations with prescribed non-zero surface fluxes of potential temperature ($\theta$) are performed to test the RANS code in unstable ($\overline{w'\theta '}_s =$ 0.10 K m s$^{-1}$) and stable ($\overline{w'\theta '}_s =$ $-$0.015 K m s$^{-1}$) conditions. Similarly to Sauer and Muñoz-Esparza (2020), in the stable boundary layer (SBL) case the potential temperature profile is initialized with zero $\theta$ gradient for $z < 100$m (where potential temperature is set to 265K) and an inversion layer ($\partial \theta / \partial z = 0.01$ K m^-1) for z $\ge 100$m. In the unstable case (CBL), the initial potential temperature sounding has a zero $\theta$ gradient across the boundary layer, with an initial potential temperature value of 309K. Note that the grid spacing, time step and domain size of the SBL case are lower than the NBL reference, to resolve small-scale turbulence from Kelvin-Helmholtz instabilities. Finally, we include two canonical tests for a baroclinic boundary layer, which are similar to the ones presented in Momen et al. (2018); Momen (2022). In the positive geostrophic shear case (NBL-SHEAR), we directly impose a height-varying pressure gradient in the y-direction, with the value of $U_g$ doubling within the boundary layer. Note that this case does not imply any geostrophic directional shear. On the other hand, in the cold advection case (NBL-ADV) the pressure gradient in the y-direction is kept constant, whereas we prescribe an increase in $V_g$ with height (from zero at the surface to 10 m s$^{-1}$ at the boundary layer height). The cold advection case features geostrophic directional shear. Increasing $V_g$ with height implies that (i) there exists a positive temperature gradient in the x-direction and (ii) heat is advected because of the misalignment between the geostrophic wind vector and the temperature gradient (hence, the name cold advection).

In the next subsections, we compare results from the 1D RANS scheme against the benchmark LES data in terms of velocity calculations, turbulent fluxes, eddy viscosities and the balance between Coriolis force, pressure gradient force and turbulent stress. Note that, for the eddy viscosity comparison, we infer the LES eddy viscosities from LES data directly, i.e.:

$$\begin{aligned} K_{V,\text {LES}} = \frac{\sqrt{\langle \overline{u'w'} \rangle ^2 + \langle \overline{v'w'} \rangle ^2}}{\sqrt{\left( \frac{d\langle \bar{u}\rangle }{dz} - \gamma _u\right) ^2 + \left( \frac{d\langle \bar{v}\rangle }{dz} - \gamma _v\right) ^2} }, \end{aligned}$$

(27)

where all the terms on the right hand side in Eq. 27 are evaluated with LES data.

4.2 Canonical NBL Test and Dependence on $z_0$

In this subsection, we compare results from the 1D RANS scheme with horizontally and temporally averaged LES data for the NBL test cases with different values of $z_0$. We integrate the NBL reference test case for 1.5 inertial time scales ($\tau _{ABL} = 2\pi /f \approx 18.5h$) with a time step $\Delta t = 0.04$s. We take temporal averages over the last 4 h of simulation, although the simulation appears to be converged well before one inertial time scale (not shown). We calculate spatial averages across computational x-y planes.

Figure 1 shows the comparison between LES data and the 1D RANS scheme. Overall, we achieve a good agreement between LES data and the implemented 1D solver. For the 1D RANS simulations, we use the YSU-type eddy viscosity, p=3 (O’Brien 1970) and different values of h for the three cases in Fig. 1 (550, 575 and 600 m from lowest to largest roughness). LES data show that larger roughness at the surface produces slightly deeper boundary layers, because of the larger turbulent stress and related entrainment of high momentum air at the boundary layer top. This is an expected result from Eq. 17, where we underline that there is a dependence between the nondimensional boundary layer height and the surface Rossby number. The largest discrepancies between LES and 1D RANS are found in the entrainment zone, where the supergeostrophic wind magnitude calculate by the set of ODEs exceeds the LES supergeostrophic wind. However, the overall trend of the vertical profile in the entrainment zone is satisfactory, as supergeostrophic winds are correctly produced (despite having larger magnitude) before returning to the geostrophic value, which is the top boundary condition. The average discrepancy between the 1D RANS and 3D LES calculations, quantified as the Root Mean Square Error (RMSE), is about 0.3 m s$^{-1}$ and is similar across different roughness values. For the wind direction, the average discrepancy is approximately 1 degree.

Fig. 1

Comparison between horizontally and temporally averaged LES data and 1D RANS scheme calculations for the NBL canonical tests with different roughness: a wind speed and b wind direction

One metric of particular interest for QUIC simulations is the cross-isobaric angle at the surface $\vartheta _0$, which has a large influence on contaminants dispersion close to the surface. As expected, $\vartheta _0$ is highly dependent on the terrain roughness, with smoother surfaces showing lower wind veer at the ground ($\vartheta _0 \approx 20^\circ$ in the reference case as opposed to $\vartheta _0 \approx 28^\circ$ and $\vartheta _0 \approx 15^\circ$ in the rough and smooth cases, respectively). The agreement on the value of $\vartheta _0$ between the 1D RANS scheme and the LES data is within ±2 degrees.

Figure 2 shows the balance of forces as calculated by the 1D RANS code. Equation 1 is the steady-state conservation of momentum, which means that the pressure gradient force needs to be balanced by turbulent stress and Coriolis force. This provides an interesting diagnostic to further understand where the calculated wind veer originates. In the y-direction, there is a constant non-zero pressure gradient force that is balanced entirely by Coriolis above the boundary layer. Within the boundary layer—which by definition is the atmospheric layer where surface effects are important—the turbulent stress induces a non-zero shear in $\langle \bar{u} \rangle$ (see y-direction Equation in Eq. 1), which needs to be balanced by a non-zero $\langle \bar{v} \rangle$ (from the first Equation). In our NBL test case with zero $V_g$, generation of v is what determines the wind veer. As roughness increases, the turbulence stress and the generation of $\langle \bar{v} \rangle$ by this mechanism becomes larger, which explains the physical intuition (and numerical results) that larger roughness corresponds to larger wind veer. Finally, we report additional diagnostics in Figure S1 and Figure S2, which show the comparison of turbulent fluxes and eddy viscosities, respectively, between LES data and the 1D RANS scheme.

Fig. 2

1D RANS scheme calculations of Pressure Gradient Force, Coriolis Force and Turbulent Stress across the boundary layer for the NBL test cases with different roughness: a x-direction forces and b y-direction forces

4.3 Stable and Unstable Tests

Buoyancy has a considerable impact on the vertical structure of the boundary layer. We consider the two canonical test cases to evaluate the 1D RANS code flexibility under stable and unstable scenarios (CBL-REF and SBL-REF). For the CBL-REF case, the configuration is similar to the LES simulation presented in Brown (1996), with a stress-free rigid lid to form the boundary-layer top rather than a capping inversion. This allows the simulation to be run for a sufficiently long time without problems associated with the rise of the inversion layer. As in Brown (1996), we integrate the Equations for 100,000 s to reach approximate inertial equilibrium, and temporally average over the last 10,000 s. A discussion of the difference between inversion-capped and stress-free rigid lid CBL simulations can be found in Brown (1996). For the SBL case, the equations are integrated for 12 h and averaged over the last hour, where good convergence is observed (not shown).

Figure 3 shows the comparison between the 1D RANS scheme and the full 3D calculations with FastEddy for the mean boundary layer structure. The equivalent comparisons for turbulent fluxes and eddy viscosities are shown in Figure S3 and Figure S4, respectively. Overall, the strong stratification with large wind speed shear in SBL-REF and the almost uniform mixed layer velocity in CBL-REF are well-captured by the 1D RANS scheme. Cross-isobaric angles are also reproduced reasonably well, within $\pm 5$ degrees. The unstable case shows much more mixing and less wind veer compared to the strongly sheared SBL, resulting in much lower cross-isobaric angles compared to SBL-REF. The strong low-level jet in SBL-REF is underestimated by the B62 closure, although the height and the overall profile shape is well reproduced. Discrepancies between the 1D RANS scheme and LES data are slightly larger than the neutral cases, with a maximum RMSE of about 0.7 m s$^{-1}$ and of approximately 4 degrees for SBL-REF.

Fig. 3

Comparison between horizontally and temporally averaged LES data and 1D RANS scheme calculations for NBL-REF, SBL-REF and CBL-REF test cases: a wind speed and b wind direction

The forces diagram is presented in Fig. 4. The largest turbulent stresses (balanced by Coriolis) are found in the SBL-REF case, which explain the largest wind direction veer observed in Fig. 3. The rather uniform turbulent stress in the mixed layer in CBL-REF creates the quasi-constant mixed layer velocity. Note that the CBL closure uses the countergradient non-local fluxes as described in Eqs. 14 and 15, which lead to a more homogeneous boundary layer. The 1D scheme for matching SBL-REF uses the B62 closure instead, with the modified $\ell _{\max }$ ($\ell _{\max ,\text {eff}}$) that accounts for the positive value of $L^{-1}$ that is imposed from the LES constant surface flux.

Fig. 4

1D RANS scheme calculations of Pressure Gradient Force, Coriolis Force and Turbulent Stress across the boundary layer for the NBL-REF, SBL-REF and CBL-REF test cases: a x-direction forces and b y-direction forces

4.4 Baroclinic Tests

Baroclinicity is expected to have a significant influence on wind shear and veer within the boundary layer. For the two cases considered in this work (NBL-ADV and NBL-SHEAR), we integrate the equations for 1.5 inertial time scales with $\Delta t = 0.04$s, and temporally average over the last 4 h of simulation, similarly to the reference simulation. For the turbulence closure in the RANS calculations, the two NBL baroclinic cases use the same parameters as the reference NBL test case. Turbulent fluxes and eddy viscosities calculated in all the baroclinic cases are shown in Figure S5 and Figure S6.

Figure 5 compares wind speed and direction from LES data and 1D RANS simulations for the two baroclinic test cases. The RANS ODEs compute a similar vertical structure of the boundary layer in both cases, compared to LES data. With the baroclinic cases, we show how our RANS methodology is quite flexible and can even predict a negative cross-isobaric angle ($\theta _0 \approx -2^\circ )$ in the cold advection case due to the shear in $V_g$. A negative cross-isobaric angle can only be the result of baroclinic shear because the Coriolis force can only achieve positive cross-isobaric angles in the Northern Hemisphere (veer to the right). Similarly to the cases analyzed in previous sections, the largest differences are found close to the boundary layer top. The maximum average RMSE discrepancy for wind speed and direction is about 0.8 m s$^{-1}$ and 2 degrees for NBL-SHEAR and NBL-ADV, respectively. However, for QUIC applications we are more concerned to accurately predict surface properties such as the cross-isobaric angle, which is correctly reproduced in both baroclinic cases. Note that in our 1D RANS code there is no calibration or parameters estimation based on LES data. Despite the same initialization for the temperature profile, the LES data show a marginally deeper boundary layer in NBL-SHEAR ($h=625$m) compared to the NBL-ADV ($h=600$m) and NBL-REF ($h=575$m). This is related to the larger shear in NBL-ADV created by baroclinicity, which results in stronger shear-generated turbulence that entrains air from above the boundary layer more efficiently.

Fig. 5

Comparison between horizontally and temporally averaged LES data and 1D RANS scheme calculations for the NBL baroclinic tests: a wind speed and b wind direction

The force diagrams (Fig. 6) from the ODEs become more complex in the presence of baroclinicity. To balance the additional shear in $U_g$ in the NBL-SHEAR case, the turbulent stress and the Coriolis force increase in the entire boundary layer in the x-direction. In the NBL-ADV case, negative cross-isobaric angles are generated as the pressure gradient decreases from the boundary layer top to approximately zero at the surface. The increase in pressure gradient in the x-direction in the NBL-ADV case corresponds to a temperature gradient of $4.5 \times 10^{-5}$ K m$^{-1}$ in the x-direction, whereas the increase in the y-direction pressure gradient in NBL-SHEAR corresponds to a gradient of $-4.5 \times 10^{-5}$ K m$^{-1}$ in the y-direction, from the thermal wind equations. Both temperature gradients are quite large but not unrealistic for coastal locations at midlatitudes, where strong synoptic gradients can exist given the North-South energy imbalance and the different heat capacity among land and ocean.

Fig. 6

1D RANS scheme calculations of Pressure Gradient Force, Coriolis Force and Turbulent Stress across the boundary layer for the NBL baroclinic test cases: a x-direction forces and b y-direction forces

5 Sensitivity and Evaluation of the New 1D RANS Scheme with UTD Field Experiment Data

5.1 Overview of the UTD Field Experiment and Model Setup

In the previous section, we have verified the implementation of the 1D RANS scheme with idealized LES data. In this section, we present the implementation of the 1D RANS scheme into QUIC and illustrate the sensitivity of QUIC to the new scheme compared to previous capabilities, with a real case application.

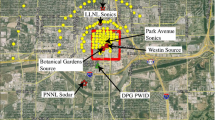
We use data from the Urban Threat Dispersion (UTD) field experiment, which was a large scale tracer sampling study in downtown NYC during October 2021, funded by the Department of Homeland Security Science and Technology Directorate (Chavez 2022; Lamer et al. 2022b). Although multiple inert gas tracers were released at three different outdoor locations over a five day period during the UTD experiment, this work will only focus on the three outdoor releases of perfluoromethylcyclopentane (PMCP) in Lower Manhattan near the Oculus Center that occurred on October 18 (IOP1), 20 (IOP3) and 21 (IOP4), 2021. For each of the considered IOPs, the total release mass of PMCP is known and consequent PMCP concentrations and dosages after the release were measured via gas samplers in different locations across the city. We use six observations sites that were within 200 to 1000 m of the release location to the east, north, northeast, south, and southeast to evaluate the transport and dispersion calculations with the QUIC model and show the sensitivity of these calculations with and without the new 1D RANS scheme.

To characterize the inflow winds, as well as boundary layer height and clouds, we use data from Brookhaven National Laboratory Center for Multiscale Applied Sensing (CMAS) mobile observatory (Lamer et al. 2022b). Data collection and preprocessing procedures are described in the Supplementary Material. For a few selected times, complementary 3 m height wind data were also collected by a weather station onboard the CMAS mobile observatory. Both wind datasets were averaged in 15 min time windows for comparison with the $\langle \bar{u} \rangle$ and $\langle \bar{v} \rangle$ vertical profiles from 1D RANS simulations. In the next subsections, we discuss the performance of the 1D RANS scheme to characterize the undisturbed $\langle \bar{u} \rangle$ and $\langle \bar{v} \rangle$ vertical profiles compared to Lidar and surface measurements and we use the 1D RANS scheme as the QUIC undisturbed flow field to drive QUIC simulations of the tracers releases for IOP1, IOP3 and IOP4 in Lower Manhattan. We also run additional sensitivity QUIC simulations by fitting a MOST log profile to the Lidar data, which is the typical procedure in QUIC (as done for instance in Brown et al. (2013) and many other QUIC studies). Note that the MOST option implies a constant wind direction with height, which we take as the average of the Lidar measurements.

The QUIC computational domain (Fig. 7) covers most of Lower Manhattan and is 2.40km $\times$ 2.25km $\times$ 0.70km in size, with the horizontal grid spacing set to 5 m and the vertical grid spacing set to 2 m with vertical stretching in the z-direction (total of 480 $\times$ 450 $\times$ 50 $= 10.8$ million grid points). Building characteristics in downtown Manhattan (shapes, heights, widths) are obtained from the ONEGEO 3D Buildings data source (accessed May 2022). We set the roughness length to 0.52m. which is a typical value for urban areas (Holland et al. 2008). The tallest building (World Trade Center) in the domain extends to about 541 m, which is the reason why we use a rather deep (700 m) computational domain. The parameterizations used in QUIC-URB and QUIC-PLUME are similar to Brown et al. (2013), and meteorological input for QUIC-PLUME—potential temperature profiles, moisture profiles, atmospheric pressure, precipitation—are derived from ERA5 reanalysis data (Hersbach et al. 2020) (0.25 degrees resolution). We release approximately five million particles per simulation for the dispersion calculations in QUIC-PLUME. Calculations are performed on a single Intel quad-core CPU with OpenMP. The total running time of QUIC-URB is approximately 10 min, whereas QUIC-PLUME calculations are more expensive given the large amount of particles and approximately take 60 min.

Fig. 7

Three-dimensional rendering of the building geometry and the computational domain used for the QUIC simulations presented in this work

5.2 QUIC Undisturbed Flow Field for IOP4

We begin our discussion by analyzing the comparison between the 1D RANS scheme and Lidar and surface wind measurements during IOP4. The reason why we choose IOP4 for an in-depth analysis is that we have complete surface measurements of winds available only during IOP4. We use the surface wind speed and wind direction measurements to evaluate predictions from the 1D RANS scheme, especially in terms of cross-isobaric angle.

Observations suggest that IOP4 was a cloud-free day and a rather stratified boundary layer at the release time was observed (11 LT). Using observations from the ceilometer lidar (preprocessing information in the Supplementary Material), we estimate that the boundary layer is about 377 m deep at 11LT (Fig. 8).

Fig. 8

Time-height contours of ceilometer lidar normalized range corrected signal. Overlaid is the 15-s PBL height (dashed black line) as well as the median PBL height (colorful lines) and its interquartile range (shading) for four time windows corresponding to the time and colors used in Fig. 9

ERA5 data at 11 LT during IOP4 show $h=330$m, which is in fair agreement with our local measurements in NYC. By 12 LT, the boundary layer has grown to about 662 m according to the ceilometer data (Fig. 8), with ERA5 data also showing a similar boundary layer growth (up to $\sim$800 m).

We model 15 min averages of $\langle \bar{u} \rangle$ and $\langle \bar{v} \rangle$ vertical profiles with multiple solutions of the 1D RANS scheme using the extended B62 closure. The vertical profiles are calculated at four different time points, representing 15 min averages from 11 LT to 12 LT. Time labels in the remainder of the manuscript refer to the starting time of the 15 min interval, e.g. 11 LT refers to the 15 min average between 1100 and 1115 LT. After 12 LT most of the plume exited the domain (the average time to traverse the domain diagonally with 5 m s$^{-1}$ winds is about 11 min), and so there is no need to have inflow information after 12 LT. The entire input parameter space in the 1D RANS scheme is $[U_{g0}, V_{g0}, f, z_0, L, h, b_u, b_v]$. We constrain three of these input parameters directly from Lidar observations. Specifically, $U_{g0}$ and $V_{g0}$ are set to the time-varying observed velocities at the boundary layer height, whereas h is set from backscatter Lidar measurements as described above (and compared to ERA5 data to check for significant discrepancies). The Coriolis parameter is $f = 9.49 \times 10^{-5}$ to match NYC latitude and the roughness length is $z_0=0.52$m (as for the QUIC simulation) for all time points. Finally, the three remaining parameters (L, $b_u$ and $b_v$) are estimated to fit the Lidar vertical profiles through a nonlinear optimization algorithm, similarly to how we typically fit L and $u_*$ for the MOST logarithmic profile (e.g., in Brown et al. (2013)).

The four RANS solutions compared to the corresponding Lidar measurements are shown in Fig. 9. On the optimization routine, note that (i) surface measurements are not included to estimate L, $b_u$ and $b_v$, but are only used as an evaluation metric and (ii) wind speed and wind direction are estimated simultaneously from the 1D RANS scheme predictions of $\langle \bar{u} \rangle$ and $\langle \bar{v} \rangle$, and are not fitted separately with different models. There is generally a good agreement between the 1D RANS scheme and the measurements, especially for the cross-isobaric angles that are within $\pm 10$ degrees of the weather station measurements.

From Lidar measurements, it appears that the boundary layer grows and becomes more mixed with less wind veer and shear during the four time points. Accordingly, the maximum length scale $\ell _{\text {max}}$ increases as a result of boundary layer growth and the estimated $L^{-1}$ from the optimization routine decreases from 0.011 m$^{-1}$ at 11 LT to 0.002 m$^{-1}$ at 12 LT. Checking the optimization results in terms of $L^{-1}$ serves as a reliable way of verifying that the optimization process is producing results that are physically meaningful. Some tuning is needed in the optimization routine to avoid obtaining unphysical results (e.g., setting the upper and lower bounds of the search space to be within a physically acceptable range).

Fig. 9

Comparison between 1D RANS scheme vertical profiles of a wind speed and b direction (following meteorological convention) with Lidar and Surface measurements during IOP4. The entire evolution of the boundary layer from 11 LT to 1145 LT is shown

Moreover, we find that the boundary layer during IOP4 is baroclinic at 11 LT, with estimates of $b_u = 0.0098$ s$^{-1}$ and $b_v = 0.00063$ s$^{-1}$. To gauge the physical meaning of such estimates, we convert the geostrophic shear into horizontal temperature gradients with the thermal wind equation (Eqs. 19 and 20) and we find that the values of $b_u$ and $b_v$ correspond to $\partial \overline{\theta }/\partial x = 1.84 \times 10^{-6}$ K m$^{-1}$ and $\partial \overline{\theta }/\partial y = -2.86\times 10^{-5}$ K m$^{-1}$. A sixth-order finite difference calculation of the temperature gradients at the boundary layer height from ERA5 data in the proximity of NYC gives $\partial \overline{\theta /}\partial x = 7.30 \times 10^{-6}$ K m$^{-1}$ and $\partial \overline{\theta /}\partial y = -1.64\times 10^{-5}$ K m$^{-1}$, which share the same sign and order of magnitude as the estimates obtained from the 1D RANS scheme fit to the Lidar data. The ERA5 potential temperature contours at a constant height level (440 m above sea level) is presented in Figure S7, where the gradients that explain the values of $b_u$ of $b_v$ are illustrated (note especially the strong negative gradient in the y direction) along with the general synoptic behavior during IOP4. The purpose of comparing ERA5 large-scale potential temperature gradients with the optimization routine results is to ensure the consistency of the numerical estimates of the parameters with physical arguments.

5.3 Dispersion of PMCP during IOP1, IOP3 and IOP4

The vertical profiles shown in Fig. 9 represent the undisturbed flow field for the QUIC simulation during IOP4. In this section, we also consider IOP1 and IOP3 to increase the amount of data points and meteorological conditions for comparison (Fig. 10).

Fig. 10

Comparison between 1D RANS scheme vertical profiles of a wind speed and b direction (following meteorological convention) with Lidar and Surface measurements during IOP1 and IOP3 at 1115 LT (the only time point where we have surface measurements during IOP3)

Figure 11 shows the evolution of the plumes during IOP1, IOP3 and IOP4. Specifically, we consider the total integrated dosage D(x, y) over the entire simulation time, defined as $D(x,y) = M^{-1}\int _0^{T} C(x,y,t)dt$, where C(x, y, t) is the predicted concentration at the first vertical model level, $T=1$h is the total simulation time and M is the release mass.

Fig. 11

Comparison between release-normalized QUIC-calculated dosage D(x, y) in min m$^{-3}$ with 1D RANS Inflow a, c, e and MOST inflow b, d, f during IOP1 (a, b), IOP3 (c, d) and IOP4 (e, f)

In the simulations with MOST inflow conditions and a constant average wind direction, the plume is transported in significantly different directions during IOP3 and IOP4 compared to the 1D RANS inflow, whereas the plume evolution is qualitatively similar during IOP1. The differences in the plume transport and dispersion are related to the amount of shear and veer in the inflow profiles. IOP1 is a cloud-topped day and shows strong mixing at 11 LT, with low wind veer and shear. Although IOP3 has a similar wind direction aloft compared to IOP1, it exhibits a significant amount of shear and veer, which is more similar to the cloud-free stratified characteristics of IOP4 at 11 LT described in the previous Section. As in IOP4, the boundary layer grows and becomes more mixed towards 12 LT during IOP3 (not shown). The differences between the dosages in the two sensitivity simulations are shown in Figure S8, where nonlinear interactions of the flow with the urban environment (e.g., channeling, dispersion in open areas) are illustrated. For example, there are large differences near the release location even during IOP1, because of the blockage of the buildings near to the release location. A few degrees of wind direction shift during IOP1 produces dosages differences of approximately 2.5 mg min m$^{-3}$, which is about 16% of the maximum dosage calculated during IOP1 (15.5 mg min m$^{-3}$). Similarly, the alignment of the 1D RANS wind direction with Fulton Street produces larger dosages on the entire channel. Similar phenomena occur on IOP4, when the wind direction becomes aligned with Church Street and channels the plume along that transect, whereas the MOST inflow spreads the plume in the open area to the right (where no blockage is present). The maximum dosage difference during IOP4 is about 5.3 mg min m$^{-3}$, which is also about 15% of the maximum dosage calculated during IOP4 (35.69 mg min m$^{-3}$) and also occurs near the release location.

Finally, the comparison between concentration measurements and QUIC predictions are shown in Fig. 12. Predictions and observations are paired in time and space during all IOPs considered in this work. Measurements are averaged every 5 min during the first 15 min after the release, every 15 min from 15 min to one hour after the release, and every 30 min from 1 h to 3 h after the release. Overall, the 1D RANS inflow scheme reduces the scatter between predictions and observations, and the majority of the data points are within a factor of 5 of their paired measurements. In addition, the number of unmatched zeros (i.e., number of points when the predictions are non-zero and the measurements are zero, or vice versa) decreases significantly with the 1D RANS inflow, increasing the overall model accuracy. A quantitative comparison of the two sensitivity simulations is presented in Table 2. We use Chang and Hanna (2004) performance measures to evaluate QUIC results. For urban dispersion applications, Hanna and Chang (2012) suggests that a good quality simulation should have arc-maximum concentrations with a fractional bias (FB) lower than 0.67, normalized mean square error (NMSE) lower than 6 and the fraction of points within a factor of 2 (FAC2) greater than 0.3. Note that in our evaluation we consider concentrations paired in both time and space, which is much more stringent than arc-maximum values. The simulation with the 1D RANS inflow achieves FB$=$ $-$0.84, NMSE$=$9.87 and FAC2$=$0.18, which are on the edge of Hanna and Chang (2012) thresholds for arc-maximum concentrations.

Fig. 12

Measurements of PMCP during IOP1, IOP3 and IOP4 paired in time and space with QUIC calculations. Dashed lines indicate 1:2 and 2:1 lines, dash-dotted lines indicate 1:5 and 5:1 lines and dotted lines indicate 1:10 and 10:1 lines

Table 2 Performance metrics for paired in time and space concentrations during UTD. R is the correlation coefficient in log space, MG stands for Geometric Mean Bias and VG stands for Geometric Variance. The formal definitions of all the metrics can be found in Chang and Hanna (2004)

Given the complexity of the problem (dispersion in lower Manhattan) and the stringent evaluation metrics (pairing in time and space), we argue that QUIC simulations with the 1D RANS inflow scheme produce reasonable results and compare favourably with previous validation exercises during the JU03 Field Experiment (Brown et al. 2013). The fraction of points within a factor of 10 (FAC10) is 0.82, which means that the order of magnitude is captured for the majority of the measurements. On the other hand, the MOST inflow simulation obtains FB$=$ $-$1.77, NMSE$=$84.8, FAC10$=$0.67, FAC2$=$0.24, which is somewhat unsatisfactory and remarkably similar to the findings of Hanna et al. (2011), where a constant wind direction derived from Sodar measurements 100 m above ground level is used.

The largest improvement with the 1D RANS scheme occurs during IOP3 (squares in Fig. 12), where the simulated plumes are transported in significantly different directions in the two simulations given the different calculations of the cross-isobaric angles by the 1D RANS scheme and MOST (Fig. 10). By contrast, the 1D RANS scheme and MOST show a closer agreement on the surface wind direction (Figure S9 and Fig. 10) during IOP1 (diamonds in Fig. 12), overall leading to considerably less pronounced differences in accuracy between the two simulations. Moreover, less data points are available for analysis during IOP1 because of a few missed sensors under IOP1 wind direction. IOP4 shows an intermediate behavior between the two (circles in Fig. 12), with more sensitivity compared to IOP1 but less than IOP3. We can draw two interesting conclusions from the differences in IOPs and Fig. 12: (i) we expect the largest sensitivity to the new 1D RANS scheme when meteorological conditions are such to produce significant wind direction changes in the boundary layer, for instance because of stable conditions or a baroclinic environment (as in IOP3) and (ii) QUIC calculations are generally fairly accurate to predict the order of magnitude of PMCP concentrations and dosages in the complex environment of lower Manhattan, although we present a limited amount of field data in this work and more in-depth evaluations (considering more model diagnostics) can improve our understanding of the overall model evaluation for the UTD field experiment.

6 Discussion and Conclusions

As recent studies have underscored the importance of accurate inflow conditions for diagnostic wind solvers and CFD codes (e.g., the UDINEE intercomparison project, see Tinarelli and Trini Castelli (2019); Kopka et al. (2019); Oldrini and Armand (2019)), in this work we propose a new 1D RANS scheme for the undisturbed flow field in QUIC based on a set of two second-order ODEs. The formulation of the proposed scheme integrates recent pioneering work in modeling the 1D vertical structure of the ABL. Specifically, we go beyond the typical ASL MOST formulation in diagnostic wind solvers and CFD codes by including effects of non-constant pressure gradient and baroclinicity within the ABL (discussed recently in Momen et al. (2018); Momen (2022); Ghannam and Bou-Zeid (2021), among others), turbulent stresses within and above the ASL (van der Laan et al. 2020; Van Der Laan et al. 2021) and the effects of the Coriolis force, surface roughness and buoyancy (Noh et al. 2003; Hong et al. 2006). The aim of the proposed scheme is to provide a physically consistent formulation of the ASL and the outer layer above the ASL, that can capture wind veer and shear in realistic conditions. It extends previous capabilities in specifying the undisturbed flow field in QUIC, which were limited to formulations that are only theoretically valid in the ASL and cannot model wind rotation in the ABL. Moreover, the computational time to calculate the numerical solution of the inflow profile is consistent with the QUIC fast computation approach.

To verify the accuracy of the proposed scheme, we compare the ODEs output with horizontally and temporally averaged LES data for a number of different canonical tests that include baroclinic, stable, unstable and different roughness configurations. Overall, the 1D RANS scheme performs favorably against LES data, especially in terms of cross-isobaric angles that are important for QUIC simulations. In addition, we evaluate the implementation of the 1D RANS scheme in QUIC with real tracer dispersion experiments in downtown Manhattan. First, the 1D RANS scheme can reasonably reproduce cross-isobaric angles and the general structure of the baroclinic and non-neutral inflow boundary layer measured with a Doppler Lidar and a weather station in the field. Moreover, we run sensitivity simulation with QUIC to gauge the influence of the new scheme compared to existing capabilities for dispersion calculations. For paired in time and space concentrations of a non-reactive tracer (PMCP), we obtain improved Chang and Hanna (2004) evaluation scores compared to MOST, and we show that the improved scores show similar performance to JU03 and UDINEE metrics with both CFD and QUIC simulations (Kopka et al. 2019; Brown et al. 2013; Hanna et al. 2011).

There are several sources of uncertainty that can affect the calculations of PMCP concentration levels, such as the assumptions related to the QUIC undisturbed flow field (e.g., the absence of time tendency in Eq. 1, parameters estimation, Lidar measurements located approximately 5 km away from the release point) and neglecting potential sinks and sources of PMCP, which may occur due to the infiltration of the outdoor plume into the subway through street vents and entrances, and the subsequent exfiltration of the plume via the same mechanism. Additional and more detailed analysis of the UTD experiment can provide more insights on other aspects of the QUIC simulations and the UTD measurements, but would exceed the scope of the present work focused on the implementation of the 1D RANS scheme. Future studies will present more in-depth comparison and sensitivity analysis of QUIC simulations with UTD data, and will potentially improve the accuracy of QUIC simulations by further tuning the configuration to the UTD setup. Significant efforts are ongoing to include subway effects in the calculations as part of the larger UTD project. An interesting extension of this work could also analyze different urban configurations, to test the sensitivity of the model to different surface wind directions in considerably different domain setups.

Finally, the proposed inflow scheme is also a good candidate for CFD codes and other diagnostic wind solvers, which typically rely on MOST profiles as inflow boundary conditions that do not account for wind veer in the ABL (Amorim et al. 2013; Oldrini and Armand 2019; Tinarelli and Trini Castelli 2019). Note that the new scheme requires extra parameters compared to MOST, i.e. the boundary layer height, the geostrophic components of wind and baroclinicity parameters, which in our study were estimated via dedicated in-situ lidar and ceilometer measurements. If dedicated observations are not available, (re)analysis or model data can be used to derive first-order estimates of these parameters for real case simulations, although in-situ measurements would likely provide more accuracy. Overall, having more realistic inflow conditions shows improvements in the accuracy of transport and dispersion simulations with QUIC and is expected to have similar effects for other wind and plume transport solvers.

Appendix 1: Rossby Number Similarity Functions

Here we derive the GDL equations based on the three Rossby numbers defined in Sect. 3. We start the discussion from the CNBL, and we then extend it to the case when $L^{-1} < 0$. The dimensionless height of the CNBL ($\tilde{h}_E$) depends only on $Ro_{\ell }$ and $Ro_{0}$, and can be estimated rearranging Zilitinkevich et al. (2007) and Liu et al. (2021) formulations:

$$\begin{aligned} \frac{\tilde{h}_EG}{u_*} = C_R(1+\frac{u_*}{G}Ro_{\ell } C_R^2/C_N^2)^{-1/2}, \end{aligned}$$

(28)

where $C_R=0.5$ and $C_N=1.6$ are dimensionless constants (revised by Liu et al. (2021)). The dependence to $Ro_0$ is contained in the geostrophic drag coefficient $u_*/G$. Note that in our notation $Ro_{\ell }u_*/G$ is equivalent to the Zilitinkevich number $\mu _N=N/f$ (as named by Esau (2004)), where N is the Brunt-Väisälä frequency of the capping inversion layer. The relationship between $\mu _N$ and $Ro_{\ell }$ is via the Kitaigordoskii length scale, $\ell _{\max }=u_*/N$ (Kitaigorodskii and Joffre (1988)), which makes $\mu _N$ equivalent to $Ro_{\ell }u_*/G$ in our notation.

The geostrophic drag coefficient $u_{*}/G$ can be determined using the GDL equations:

$$\begin{aligned} A = \ln {\left( \frac{u_*}{|f|z_0} \right) } - \frac{\kappa G}{u_*} \cos {\vartheta _0}, \quad B =\pm \frac{\kappa G}{u_*} \sin {\vartheta _0}. \end{aligned}$$

(29)

Which can be combined into a single implicit equation for $u_*/G$ (van der Laan et al. 2020):

$$\begin{aligned} \frac{u_*}{G} = \kappa \left( {\sqrt{\left[ \ln {Ro_0} + \ln {\left( \frac{u_*}{G}\right) } - A \right] ^2 + B^2 }}\right) ^{-1}. \end{aligned}$$

(30)

In Eq. 30, A and B are universal constants for the Truly Neutral Boundary Layer (TNBL), but functions of $\mu _N$ (or $Ro_{\ell }$) for the CNBL:

$$\begin{aligned} A = -am + \ln \left( {a_0+m}\right) - \ln {\left( \frac{\tilde{h}_EG}{u_*}\right) }, \end{aligned}$$

(31)

$$\begin{aligned} B =\frac{\tilde{h}_EG}{u_*}\left( b_0 + bm^2 \right) , \end{aligned}$$

(32)

where $a=0.65$, $a_0=1.3$, $b=7$, $b_0=8$ are constants revised by Liu et al. (2021) for a large range of $\mu _N$. m is the composite stratification parameter:

$$\begin{aligned} m = \left[ 1 + (C_m Ro_{\ell } u_*/G)^2 \right] ^{1/2}\frac{\tilde{h}_EG}{u_*}, \end{aligned}$$

(33)

where $C_m=0.1$. When $Ro_0$ and $Ro_{\ell }$ are specified, Eqs. 28, 30, 31, 32 and 33 form a set of five equations with five dimensionless unknowns ($\tilde{h}_E$, $u_*/G$, A, B, m). The set of equations represents the $\Lambda$ function in Sect. 3 in the neutral case. We use the same model constants for the stable case, replacing $\ell _{\max }$ with $\ell _{\max ,\text {eff}}$ according to Eq. 11. Note that the model constants in Liu et al. (2021) are derived from the CNBL case, but they match the boundary layer height from mixing length theory (Eq. 11) even for the stable case with low values of $\ell _{\max }$ (Figure S10).

The final Equation that relates the dimensional boundary layer height to $\tilde{h}_E$, including the dependence on $Ro_{L}$, is the following:

$$\begin{aligned} h = \left( C_{wd}\tilde{h}_E + \Delta z_{L}(Ro_L,Ro_{\ell })\right) G/|f|, \end{aligned}$$

(34)

where we introduce two empirical corrections compared to the CNBL GDL estimate ($\tilde{h}_EG/f$). First, we define a dimensionless coefficient $C_{wd} = 2.3$ to account for the different definition of the boundary layer height in this work (second crossing of the wind direction profile with the geostrophic line, as in van der Laan et al. (2020)) and the one used in Zilitinkevich et al. (2007); Liu et al. (2021) (level at which the momentum flux becomes less than 5% of the surface value). We derive $C_{wd}$ from a linear fit between $\tilde{h}$ and h (Figure S10). Second, we define a quantity $\Delta z_{L}$ that represents the height increase due to negative $L^{-1}$ in the CBL, since Zilitinkevich et al. (2007) calculations are only valid for neutral and stable conditions. We assume the following parabolic parametric structures (i.e., second-order polynomials) for $\Delta z_L$:

$$\begin{aligned} \log _{10}\Delta z_{L} = m_1\left( \log _{10}\left( Ro_{\ell }\right) \right) ^2 + m_2\log _{10}\left( Ro_{\ell }\right) + m_3, \end{aligned}$$

(35)

where $m_1$, $m_2$ and $m_3$ are parameters to be estimated that are functions of $Ro_L$. We assume the same second order polynomial for $m_1$, $m_2$ and $m_3$:

$$\begin{aligned} m_1(Ro_L) = n_1 \left( \log _{10}\left( Ro_{L}\right) \right) ^2 + n_2\log _{10}\left( Ro_{L}\right) + n_3, \end{aligned}$$

(36)

$$\begin{aligned} m_2(Ro_L) = n_4 \left( \log _{10}\left( Ro_{L}\right) \right) ^2 + n_5\log _{10}\left( Ro_{L}\right) + n_6, \end{aligned}$$

(37)

$$\begin{aligned} m_3(Ro_L) = n_7 \left( \log _{10}\left( Ro_{L}\right) \right) ^2 + n_8\log _{10}\left( Ro_{L}\right) + n_9, \end{aligned}$$

(38)

where $n_1$ to $n_9$ are constants to be estimated. We work in $\log _{10}$ space because physically meaningful Rossby numbers span several orders of magnitude. The empirical values of $n_1$ through $n_9$, as well as $C_{wd}$, are estimated from a set of 1D RANS simulations that cover reasonable combinations of the Rossby numbers. The choice of the parabolic structure is somewhat arbitrary (any polynomial of arbitrary order would be a valid choice), but we find that second order polynomials provide good fit to the data without an excessive amount of parameters to be estimated. Future work will focus on introducing physical arguments to embed the dependence on $Ro_{L}$ in a more consistent way. Finally, Fig. 13 shows the parametric fit and the dependence of the dimensionless boundary layer height $\tilde{h}=C_{wd}\tilde{h}_E + \Delta z_{L}(Ro_L, Ro_{\ell })$ on the three Rossby numbers. As expected, the largest dependence of the boundary layer height is on $Ro_{\ell }$, with smaller sensitivities to $Ro_L$ and $Ro_0$. Assuming a constant geostrophic wind speed G and a given latitude with Coriolis parameter f, increasing $Ro_{\ell }$ (horizontal axis in Fig. 13) implies decreasing the maximum turbulent length scale $\ell _{\max }$, which corresponds to a decrease in boundary layer height. This can also be interpreted as an increase in N, via $N = u_*/\ell _{\max }$, which yields the same effect of decreasing the boundary layer height. Increasing $Ro_0$ (from red to yellow lines in Fig. 13a) implies a decrease in $z_0$, and a corresponding decrease in the boundary layer height, because of lower friction at the bottom. Conversely, increasing $Ro_L$ (from blue to cyan lines in Fig. 13) implies an increase in $L^{-1}$ (and in the surface heat flux), deepening the boundary layer.

Fig. 13

Dependence of the nondimensional boundary layer height to a $Ro_{\ell }$ and $Ro_{0}$ at $Ro_L = 0$, and b to $Ro_{\ell }$ and $Ro_{L}$ at $Ro_0 = 10^6$ (right). Lines are evaluations of the function in Eq. 34, whereas dots represent measurements from the true 1D ODEs solutions