A Model for Low-Frequency, Anisotropic Wind Fluctuations and Coherences in the Marine Atmosphere

Abstract

To assess dynamic loads, large offshore wind turbines need detailed and reliable statistical information on the inflow turbulence. We present a model that includes low frequencies down to $\sim 1$ hr$^{-1}$ using the observed $S(f) \propto f^{-5/3}$ in that range. The presented model contains a parameter representing the anisotropy of the two-dimensional, incompressible turbulence, and it assumes the low-frequency fluctuations to be homogeneous in the vertical direction. Combined with a three-dimensional model for the smaller scales, the model can predict correlations between different points. We have validated the model against two offshore wind data sets: a nacelle-mounted, forward-looking Doppler lidar with four beams at the Hywind Scotland offshore wind farm and sonic anemometer measurements at the FINO1 research platform in the North Sea. One-point auto spectra and two-point cross spectra were calculated after splitting the data into different atmospheric stability classes. The relative strength of the 2D low-frequency fluctuations to the 3D fluctuations was higher under stable conditions. The combined 2D+3D model was able to fit the measured spectra with good accuracy and could then predict the two-point cross spectra, co-coherences, and phase angles between wind fluctuations at different lateral and vertical separations. Good agreement was found between the measured and predicted values, albeit with exceptions. The model can generate stochastic wind fields for investigating wake meandering in wind farms or dynamic loads on floating wind turbines.

1 Introduction

The growth in the offshore wind energy sector and technology maturity have led to a significant increase in the size of modern wind turbines. The installation of wind turbines having up to 250 m rotor diameter is now state-of-the-art. For such large rotors, the incoming wind field may not be uniform, and it can have large spatial and temporal variations. This can lead to a significant impact on the blade and tower loads and power performance of large wind turbines. Large offshore turbines have lower natural frequencies and can get easily excited by the low-frequency fluctuations in the wind. The response of a floating wind turbine to low-frequency wind fluctuations is even stronger due to the more degrees of freedom of the floater platform and its low eigenfrequencies. In two separate studies, Nybø et al. (2021) and Nybø et al. (2022) analyzed the impact of low-frequency wind fluctuations on a fixed bottom DTU 10 MW reference wind turbine and a floating IEA 15 MW reference wind turbine, respectively. Their studies revealed that wind fluctuations lower than 0.01 Hz have a strong impact on the tower bottom fore-aft and blade flap-wise damage equivalent moments. Doubrawa et al. (2019) and Bachynski and Eliassen (2019) also highlighted the importance of low-frequency wind fluctuations on the floating wind turbine’s global motion and increased excitation of components such as mooring lines.

The load estimation studies of wind turbines generally use turbulence wind field simulation tools to generate stochastic and realistic wind fields. The International Electrotechnical Commission (IEC) standard 61400-1:2019 (IEC 2019) suggests two input wind field models, i.e., the Kaimal spectrum model (Kaimal et al. 1972) with exponential coherence function (Davenport 1977), and the Uniform Shear turbulence model of Mann (1994), see also Mann (1998). These models are initially made for high-frequency wind fluctuations and neutral atmospheric conditions. These two models often differ in predicting the wind turbine response to different design load conditions due to differences in their inherent physics (Bachynski and Eliassen 2019; Nybø et al. 2020, 2021). To analyze the effect of low-frequency fluctuations on wind turbine response, Proper Orthogonal Decomposition (POD) [(see Eliassen and Andersen (2016) and Saranyasoontorn and Manuel (2005)] or low-pass filter techniques are usually employed to filter out the high-frequency fluctuations. These techniques often bring large statistical uncertainty in the loads’ analysis. Thus, there is a need for a model that can reliably predict the low-frequency fluctuations corresponding to that of a marine atmosphere.

Numerous studies have comprehensively examined the energy spectrum across a wide range of frequencies or wavenumbers. Among the most noteworthy are the works of Vinnichenko (1970); Kraichnan (1967), and Gage and Nastrom (1986) where it was established through experimental data that the energy spectrum E(k) in the mesoscale 2D turbulence follows a power-law scaling of $k^{-5/3}$ with k representing the wavenumber. From the structure functions analysis of the wind data recorded through commercial aircraft flights, Lindborg (1999) derived a formulation for one-dimensional energy spectrum i.e. $E_1(k) = d_1k^{-5/3} + d_2k^{-3}$, where $d_1$ and $d_2$ are scaling factors. In this relation, the first and second terms represent the energy distribution in the mesoscales and synoptic scales, respectively. More recent studies (Courtney and Troen 1990; Högström et al. 2002; Larsén et al. 2013) focus on the divide between mesoscale and microscale turbulence and particularly on the presence or absence of a spectral gap. Larsén et al. (2013) presented a wind spectrum relation analogous to that of Lindborg’s energy spectrum relation expressed as $S(f) = a_1f^{-5/3} + a_2f^{-3}$, where f is the frequency, and $a_1$ and $a_2$ act as the scaling factors for the mesoscale and synoptic turbulence terms, respectively. This relation exhibited a very good agreement with the longitudinal wind component spectrum recorded at two offshore sites. Expanding upon this work, Larsén et al. (2016) employed the same relation for modeling synoptic and mesoscale turbulence alongside the Kaimal spectrum model for microscale turbulence to characterize the full-range spectrum of the boundary layer winds at two sites in Denmark. They observed that a spectral gap exists between low-frequency and high-frequency fluctuations, and its width depends on the relative strength of mesoscale and microscale turbulence. Furthermore, Larsén et al. (2021) demonstrated that the lateral wind velocity component could also be effectively represented in the low-frequency range using the same spectral relation. Cheynet et al. (2018) also utilized this model to fit the low- and high-frequency wind fluctuations measured at the FINO1 research platform in the North Sea and found a good agreement between the model and the observed data. Notably, their study highlighted that the spectral gap is not visible under unstable and neutral conditions but becomes distinct in the presence of strong stratification in the atmosphere.

This article presents a model for characterizing low-frequency fluctuations in longitudinal and lateral wind components based on the two-dimensional spectral velocity tensor. The energy spectrum in the mesoscale range follows the $k^{-5/3}$ scaling. In addition, two other parameters are introduced in this formulation: a characteristic length scale corresponding to the peak of mesoscale turbulence and an anisotropy parameter that describes the spectral distortion in the wavenumber domain. In contrast to the previously described one-dimensional low-frequency spectral relationship, the model presented in this article operates in a two-dimensional domain, enabling an investigation of two-point statistics. The low-frequency turbulence model is validated against two distinct sets of offshore measurements. The first dataset comprises line-of-sight (LOS) wind component measurements made by a nacelle-mounted lidar on a 6-MW floating turbine at the Hywind Scotland wind farm. This dataset provides a unique opportunity to model and predict the lateral and vertical co-coherences because of multiple lidar beams measuring at lateral separations ranging up to 206 m and vertical separations ranging up to 72 m. The second dataset is the multiple sonic anemometer measurements at various heights above mean sea level from the FINO1 research platform in the North Sea. The FINO1 measurements are also used to predict the co-coherences at low frequencies, with a particular focus on vertical separations of 20 m and 40 m.

This article is organized into the following sections: First, the anisotropic, low-frequency turbulence model is presented. In the next two sections, the model is validated against two sets of measurements, followed by the Discussion and Conclusion sections.

2 Anisotropic 2D Turbulence Model

The two-dimensional spectral velocity tensor is the Fourier transform of covariance tensor $R_{ij}^{2D}(\varvec{x})=\left< u_i(\varvec{x'})u_j(\varvec{x'}+\varvec{x})\right>$ where $\varvec{x}=(x_1,x_2)$ is a horizontal separation vector and, because of homogeneity, $\varvec{x'}$ is arbitrary. It follows from the Wiener–Khinchin theorem (Batchelor 1953) that:

$$\begin{aligned} \phi _{ij}(k_1,k_2)&= \int _{-\infty }^\infty \int _{-\infty }^\infty R_{ij}^{2D}(x_1,x_2) \text {exp}(-\iota \varvec{k}\cdot \varvec{x}) dx_1 dx_2 \nonumber \\&= \langle {\hat{u}}_i^*(k_1,k_2){\hat{u}}_j(k_1,k_2)\rangle , \end{aligned}$$

(1)

where $^*$ indicates the complex conjugate. Furthermore, according to Batchelor (1953), a two-rank, isotropic, two-dimensional velocity tensor has the form:

$$\begin{aligned} \phi _{ij}(k_1,k_2) = f(k) k_i k_j + g(k) \delta _{ij} ~~~~ \text{( }i,j = 1,2\text{) } ~, \end{aligned}$$

(2)

where f and g are functions of the length of the horizontal wavenumber vector $k=| \varvec{k}| = \sqrt{k_1^2 + k_2^2}$ and $\delta _{ij}$ is the Kronecker delta. Assuming that the two-dimensional flow is incompressible implies $k_i \phi _{ij}=0$. Incompressibility in the horizontal plane is actually not true for atmospheric flows, but for larger scales, it may be a good approximation. Two-dimensional incompressibility suggests that:

$$\begin{aligned} k^2 f(k) = -g(k). \end{aligned}$$

(3)

If we define the two-dimensional energy spectrum E(k) by $g(k) = E(k)/(\pi k)$, then the spectral tensor becomes:

$$\begin{aligned} \phi _{ij}(k_1,k_2) = \frac{E(k)}{\pi k}\left( \delta _{ij} - \frac{k_i k_j}{k^2} \right) ~~. \end{aligned}$$

(4)

Let us now assume that the energy spectrum is given by:

$$\begin{aligned} E(k) = \frac{c k^3}{\left( L_{2D}^{-2} + k^2 \right) ^{7/3}}~~~, \end{aligned}$$

(5)

where c is a constant and a scaling parameter, and $L_{2D}$ is the corresponding length scale of 2D fluctuations. The particular shape of (5) is inspired by von Kármán (1948). The high k range of the spectrum ensures $E(k) \propto k^{-5/3}$ as $k \rightarrow \infty$ while the low k form $E(k) \propto k^3$ guarantees that the integral length scale is non-zero and finite.¹ The isotropic spectral tensor would consequently be:

$$\begin{aligned} \phi _{ij}(\varvec{k}) = f^2(k) \begin{pmatrix} k_2^2&{} -k_1 k_2 \\ -k_1 k_2 &{} k_1^2 \end{pmatrix}~, \end{aligned}$$

(6)

where f is only a function of $k=| \varvec{k}|$ and $f^2(k) = ( E(k)/\pi )\cdot k^{-3}$. The one-dimensional spectra as functions of $k_1$ can be calculated as:

$$\begin{aligned} F_{11}^{2D}(k_1)= & {} \int _{-\infty }^\infty \phi _{11}(k_1,k_2) d k_2\nonumber \\= & {} \int _{-\infty }^\infty \frac{c}{\pi \left( L_{2D}^{-2}+k^2\right) ^{7/3}} k_2^2 dk_2 \nonumber \\= & {} c \frac{9 \varGamma (\frac{5}{6})}{8 \sqrt{\pi }\varGamma (\frac{1}{3})} \left( L_{2D}^{-2}+k_1^2\right) ^{-5/6} ~~, \end{aligned}$$

(7)

$$\begin{aligned} F_{22}^{2D}(k_1)= & {} \int _{-\infty }^\infty \phi _{22}(k_1,k_2) d k_2\nonumber \\= & {} c \frac{15 \varGamma (\frac{5}{6})k_1^2}{8 \sqrt{\pi }\varGamma (\frac{1}{3})} \left( L_{2D}^{-2}+k_1^2\right) ^{-11/6} ~~~, \end{aligned}$$

(8)

where $\varGamma$ is the Gamma function. We can obtain the variance as:

$$\begin{aligned} \sigma ^2=\sigma _{11}^2=\sigma _{22}^2= \frac{9}{8} c L_{2D}^{2/3}~~. \end{aligned}$$

(9)

The energy spectrum in (5) can now be represented as:

$$\begin{aligned} E(k) = \frac{8 \sigma ^2 L_{2D}}{9} \frac{(k L_{2D})^3}{\left( 1 + (k L_{2D})^2 \right) ^{7/3}}~~~, \end{aligned}$$

(10)

where c is substituted with $(8 \sigma ^2 L_{2D}^{-2/3})/9$. The symbol $\sigma ^2$ is the variance of any horizontal velocity component and the integral of $E_h$ from 0 to $\infty$ is exactly $\sigma ^2$ which is also equal to the kinetic energy (ignoring the mass, i.e. half the sum of the two component variances).

We can extend this model to include scale-independent anisotropy, where the incompressible, homogeneous, two-dimensional velocity field can be written as a sum of Fourier modes:

$$\begin{aligned} \hat{\varvec{u}}(\varvec{k}) \exp (\iota \varvec{k\cdot x})~, \end{aligned}$$

(11)

where $\varvec{k}=(k_1,k_2)$ and $\varvec{x}$ are only two-dimensional. The Fourier amplitudes can be written as:

$$\begin{aligned} \hat{\varvec{u}}(\varvec{k})= a \hat{\varvec{k}} f(\varvec{k})~, \end{aligned}$$

(12)

where a is a random, complex, Gaussian variable with zero mean and unit variance ($\left<|a|^2\right>=\left<a^* a\right>=\left<\Re (a)^2\right>+\left<\Im (a)^2\right>=1$), $\hat{\varvec{k}}$ is the vector $(-k_2,k_1)$ perpendicular to $\varvec{k}$, and f is now a real, scalar function of the vector $\varvec{k}$ and not as before in (6) only a function of k. Now we can alter the function f to make the spectral tensor anisotropic in a scale-independent way:

$$\begin{aligned} f(k_1,k_2) = f(\kappa ) \end{aligned}$$

(13)

where:

$$\begin{aligned} \kappa ^2 = 2(k_1^2 \cos ^2 \psi + k_2^2 \sin ^2\psi ) \end{aligned}$$

(14)

with $0<\psi <\pi /2$ is the anisotropy parameter. The anisotropic spectral tensor would be:

$$\begin{aligned} \phi _{ij}(k_1,k_2)=\frac{8 \sigma ^2 L_{2D}^2}{9\pi } \frac{1}{\left( 1 + \kappa ^2 L_{2D}^2 \right) ^{7/3}} L_{2D}^2 \begin{pmatrix} k_2^2&{} -k_1 k_2 \\ -k_1 k_2 &{} k_1^2 \end{pmatrix}. \end{aligned}$$

(15)

When $\psi =\pi /4$, then $\kappa = k$ and we get the isotropic 2D spectra (6). Figure 1 presents the two dimensional spectra $\phi _{11}$ and $\phi _{22}$ for various values of $\psi$. Notice the effect of anisotropy on the 2D spectra, as reducing the magnitude of the anisotropy parameter $\psi$ makes $\phi _{11}$ much more energetic than $\phi _{22}$. The inverse is true for values of $\psi$ greater than $45^\circ$.

Fig. 1

Two dimensional spectra $\varPhi _{11}$ and $\varPhi _{22}$ as a function of a $\psi = 45^{\circ }$, b $\psi = 30^{\circ }$, and c $\psi = 60^{\circ }$ as described in 15. Here the length scale L is set equal to $10^3$ m, and the variance $\sigma ^2$ is 1 m$^2$s$^{-2}$

The anisotropic one-dimensional spectra become:

$$\begin{aligned} F_{11}^{2D}(k_1) = \sigma ^2 L_{2D} \frac{\varGamma \left( \frac{5}{6} \right) }{2^{3/2} \pi ^{1/2} \varGamma \left( \frac{1}{3} \right) \sin ^3\psi } \rho ^{-5/3} ~~, \end{aligned}$$

(16)

and:

$$\begin{aligned} F_{22}^{2D}(k_1) = \sigma ^2 L_{2D} \frac{5\varGamma \left( \frac{5}{6} \right) }{3 \cdot 2^{1/2} \pi ^{1/2} \varGamma \left( \frac{1}{3} \right) \sin \psi } \frac{k_1^2 L_{2D}^2}{\rho ^{11/3}} ~~, \end{aligned}$$

(17)

where:

$$\begin{aligned} \rho ^2 = 1+2 k_1^2 L_{2D}^2 \cos ^2\psi ~~. \end{aligned}$$

(18)

Due to anisotropy the variances of longitudinal and transverse components are different and can be shown to become:

$$\begin{aligned} \sigma _{11}^2= & {} \frac{\sigma ^2}{4 \cos \psi \sin ^3\psi } ~~, \end{aligned}$$

(19)

$$\begin{aligned} \sigma _{22}^2= & {} \frac{\sigma ^2}{4 \cos ^3\psi \sin \psi } ~~, \end{aligned}$$

(20)

and:

$$\begin{aligned} \frac{\sigma _{11}^2}{\sigma _{22}^2} = \cot ^2\psi ~~, \end{aligned}$$

(21)

where $\sigma ^2$ is the variance if the spectra are isotropic (9). Figure 2 illustrates the effect of anisotropy on one-dimensional spectra of longitudinal and transverse components. We can observe the change in variance $\sigma ^2$ with respect to the variation in the anisotropy parameter $\psi$. At $\psi = 30^\circ$, the variance of the longitudinal component is higher. The opposite is true for $\psi = 60^\circ$ where $\sigma _{22}^2$ is many times higher than $\sigma _{11}^2$. At $\psi = 45^\circ$, both variances are equal, and the turbulence is isotropic.

Fig. 2

Model component spectra from Eqs. (16) and (17). The black curves are the isotropic spectra while the red curves have $\sigma ^2_{11} < \sigma ^2_{22}$ and the blue have $\sigma ^2_{11} > \sigma ^2_{22}$, the latter being the model realistic

It should be noted that for the isotropic case:

$$\begin{aligned} F_{11}^{2D}(k_2)=F_{22}^{2D}(k_1) ~, \end{aligned}$$

(22)

and:

$$\begin{aligned} F_{22}^{2D}(k_2)=F_{11}^{2D}(k_1) ~. \end{aligned}$$

(23)

For other values of $\psi$, one-dimensional spectra in terms of $k_2$ can be obtained by integrating the anisotropic spectral tensor in (15). Similarly, the normalized lateral cross spectra can be computed analytically as:

$$\begin{aligned} \begin{aligned} \frac{\chi _{11}(k_1,\varDelta y)}{F_{11}^{2D}(k_1)}&= \frac{\pi \rho \mu ^{5/6}}{6\cdot 2^{1/4}\varGamma \left( \frac{5}{6} \right) \sin ^{11/6}\psi L_{2D}} \Biggl (\frac{2L_{2D}\sin \psi }{\rho } \left\{ 3 I_{-\frac{5}{6}}\left( \frac{\mu }{\sqrt{2}\sin \psi }\right) \right. \\&\qquad \left. - 8 I_\frac{5}{6}\left( \frac{\mu }{\sqrt{2}\sin \psi }\right) \right\} \\&\qquad + 3 \cdot 2^{1/2} \varDelta y\left\{ I_\frac{1}{6}\left( \frac{\mu }{\sqrt{2}\sin \psi }\right) \right. \\&\qquad \left. -I_\frac{11}{6}\left( \frac{\mu }{\sqrt{2}\sin \psi }\right) \right\} \Biggr ), \end{aligned} \end{aligned}$$

(24)

and:

$$\begin{aligned} \frac{\chi _{22}(k_1,\varDelta y)}{F_{22}^{2D}(k_1)} = \frac{3}{5\cdot 2^{3/4} \sin ^{11/6}\psi \varGamma (5/6)} \mu ^{11/6} K_\frac{11}{6}\left( \frac{\mu }{\sqrt{2}\sin \psi }\right) ~~, \end{aligned}$$

(25)

where $\mu = \varDelta y \rho /L_{2D}$, and $\varDelta y$ is the lateral separation distance. $I_n$ is the modified Bessel function of the first kind, and $K_n$ is the modified Bessel function of the second kind.

2.1 2D Turbulence Model with Attenuation at High Frequencies

The low-frequency turbulence model described above can have an unwanted effect on the high-frequency turbulence spectra. If not attenuated at higher frequencies, the 2D turbulence adds to the 3D turbulence and contaminates the classical turbulence ratios at high frequencies. Especially in the inertial sub-range, the turbulence is isotropic and follows a power law (Pope 2000), which is distorted if the 2D turbulence is not attenuated at higher frequencies. The assumption of two-dimensionality hinges on the fact that if an eddy is much larger than the extent of the boundary layer $z_i$, then it can only be horizontal. Therefore it makes sense to attenuate the two-dimensional spectrum for $\kappa >1/z_i$. If we define the attenuation factor as:

$$\begin{aligned} \frac{1}{1+\kappa ^2z_i^2}~~, \end{aligned}$$

(26)

where $z_i$ is the boundary-layer height, the attenuated energy spectrum would become:

$$\begin{aligned} E(\kappa ) = \frac{c \kappa ^3}{\left( L_{2D}^{-2} + \kappa ^2 \right) ^{7/3}} ~ \frac{1}{1+\kappa ^2z_i^2}~~. \end{aligned}$$

(27)

Here the attenuation factor is a special kind of activation function (similar to an inverse sigmoid function) that has an “inverse S" shape. This function ensures that the energy spectrum smoothly drops to zero for wavenumbers greater than $1/z_i$. This drop is accelerated due to an increased negative slope of the spectrum for $\kappa >1/z_i$ i.e., $E(\kappa ) \propto \kappa ^{-11/3}$. Other sigmoid functions like a hyperbolic tangent or a logistic function can also be used as an attenuation factor. The one-dimensional spectra $F_{11}$ and $F_{22}$ can be obtained from the attenuated energy spectrum using a similar method as outlined earlier. The final expressions are described in Appendix 1.

3 Model Validation with Offshore Nacelle Lidar Data

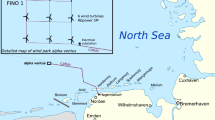
A nacelle-mounted WindIris wind lidar (Vaisala) recorded line-of-sight (LOS) wind speed data on the HS4 wind turbine in the Hywind Scotland offshore wind farm. The location of the HS4 turbine is shown in Fig. 3. The HyWind Scotland turbines have a power rating of 6 MW with a hub height of 98.4 m and a rotor diameter of 154 m. The lidar measured LOS velocities from 4 different beams oriented at different azimuth and tilt angles. The WindIris measures at 10 different range gates at distances from 50 to 400 m for each LOS. The four beams have fixed azimuth and tilt angles, $\phi = 15^{\circ }$ and $\theta = 5^{\circ }$ respectively. A schematic of the wind turbine and the orientation of the four lidar beams is shown in Fig. 4. Due to a high thrust force acting on the wind turbine close to the rated wind speed, the lower two beams (Beams 3 and 4) are mostly horizontal at these wind speeds (Angelou et al. 2023).

Fig. 3

Hywind Scotland Offshore wind farm and the location of HS4 turbine on which the WindIris lidar is mounted

Fig. 4

a Schematic showing the orientation of four lidar beams with respect to the incoming wind flow assuming that the incoming flow is in positive x direction. b and c displays the side and top views, respectively

3.1 Data Processing

The measurements were available for 3 months in total from September 2019 to November 2019. To have good-quality data and long stationary time series, we applied several filters to the data set, which reduced the amount of available data considerably. A brief overview of the filtering criteria is given in Table 1. The time to record LOS values at all 10 range gates for a single beam took 1 s, so the resulting data was measured at a frequency of 1/4 Hz. We selected only those hours where the wind turbine was producing at least 100 kW. To ensure that the flow is undisturbed and wake-free, we selected 1-hour periods where the mean wind direction was southerly (90$^\circ$ $\le$ wind direction $\le$ 270$^\circ$). The LOS speed availability status parameter was analyzed for every hour in the data set and only those hours with mean LOS speed status > 90% at all 10 range gates were selected. Due to the induction effect of the wind turbine, a reduction in upstream horizontal wind speed was observed. An upstream wind induction model described in Simley et al. (2016) was fitted to the measured LOS values at all range gates. The procedure is described in detail in Angelou et al. (2023). To ensure the homogeneity of the incoming flow, only those hours were selected where the error between measurements and fit was less than 0.15 m s$^{-1}$. Since we are trying to model the spectrum at low frequencies (up to 1 hr$^{-1}$), we require a large statistical significance at the lower end of the spectrum. Therefore, we selected only those periods in the data set with at least eight consecutive hours. The number of hours in each period is mentioned in Table 2. Finally, each period was checked for undisturbed wind speed stationarity. The criterion to define stationarity is described as follows: (1) First, a linear fit was applied to the mean hourly speeds for each period, (2) The extreme values of the linear fit were compared with the mean value of the data, (3) If the extreme values lie within 20% deviation from the mean, the period was declared to be stationary or otherwise non-stationary. After applying all the criteria, we are left with 186 h ($\sim$10% of the total available data) divided into 10 periods. The starting and ending time stamps of these periods are described in Table 2 along with the mean undisturbed wind speed $U_{\infty }$ and the mean wind direction obtained from SCADA.

Table 1 The number of hours available after applying each data filtering criterion

Table 2 Details of selected periods after data processing

Table 2 also describes the stability classes observed during each period. We estimated the atmospheric stability using the bulk Richardson number Ri$_{b}$ described as:

$$\begin{aligned} \text {Ri}_b = -\frac{g z \left( \varDelta T-z\varGamma _l \right) }{T_{\text {z}} U_z^2}, \end{aligned}$$

(28)

where g is the Earth’s gravitational acceleration, z is the height at which temperature $T_z$ and wind speed $U_z$ measures are recorded (in this case the hub height), $\varGamma _l=0.0098$ K m$^{-1}$ is the adiabatic lapse rate, and $\varDelta T=T_{\text {sea}}-T_z$, being $T_{\text {sea}}$ the sea surface temperature. The Ri$_{b}$ class from measurements was evaluated using HS4 SCADA and sea surface temperature measurements. For every half-hour interval in each period, a Ri$_{b}$ value was obtained. The overall stability for the whole period is computed by obtaining the mode value of stability classes during each period. The stability classification based on Ri$_{b}$ number is described in Table 3. From Table 2, we can note that the atmospheric conditions during half of the selected periods were stable, and the rest were observed as neutral.

Table 3 Atmospheric stability classification based on Ri$_b$ number

3.2 Spectral Analysis

To fit the model to measured spectra, we computed the mean LOS spectra at all range gates for Beams 3 and 4. The frequency spectra were computed for 1-hr time series chunks. Using Taylor’s frozen turbulence hypothesis, the spectra were converted into a wavenumber $k_1$ domain. The combined 2D+3D modeled spectra have been fitted to the mean spectra of Beams 3 and 4 using the downhill simplex algorithm (available in almost all high-level programming languages). Details on how to combine the 2D and 3D spectra models for nacelle lidar measurements are given in Appendix 2. The anisotropy parameter $\varGamma _{\text {M}}$ of the 3D Mann spectral model was fixed at 2.5, a value in the middle of the range of typically estimated values at the FINO1 platform in the North Sea. The other two parameters $\alpha \epsilon ^{2/3}$, and $L_{3D}$ were evaluated by fitting the spectra given by (A15). The fitting process also evaluates the scaling parameter c in the 2D spectral model. Figure 5 shows the measured LOS spectra for all 10 periods mentioned in Table 2. Since we did not observe any low-frequency fluctuations peak in the measured spectra, we assumed an infinite $L_{2D}$ for fitting purposes. The anisotropy parameter for each fit was evaluated by reconstructing the u and v components from Beams 3 and 4 LOS. Assuming zero tilt due to the thrust force acting on the turbine, the two wind components can be defined as:

$$\begin{aligned} u= \frac{\text {LOS}_{4}+\text {LOS}_{3}}{2 \cos \phi }, \end{aligned}$$

(29)

$$\begin{aligned} v= \frac{\text {LOS}_{4}-\text {LOS}_{3}}{2 \sin \phi }, \end{aligned}$$

(30)

Fig. 5

Measured (solid blue curves) LOS spectra fitted with theoretical 2D + 3D spectra (dashed black curves), and 3D spectra (dotted black curves) for the 10 periods mentioned in Table 2. The fitting parameters are also mentioned in Table 4. The atmospheric stability during each period is also mentioned here: (n) represents neutral conditions, and (s) represents stable conditions

where u and v are the longitudinal and transverse wind components, LOS$_{3}$ and LOS$_{4}$ are the LOS speed measured by beams 3 and 4, respectively, and $\phi$ is the azimuth angle. From the anisotropic extension of the 2D turbulence model and assuming $k_1 > L_{2D}^{-1}$, the anisotropy parameter can be evaluated as:

$$\begin{aligned} \psi = \arctan \left( \sqrt{\frac{3}{5} \frac{F_{22}}{F_{11}}}\right) , \end{aligned}$$

(31)

where $F_{11}$ and $F_{22}$ are the one-dimensional spectrum of the longitudinal and transverse wind components. The v component shows large variance (large magnitude at higher frequencies), which is a result of the product of the ratio between the difference of two slightly noisy LOS values to a small number from the sine of the opening angle (30). Since we are only interested in the spectra at the lower frequencies, we can ignore this large and unrealistic variance in the v component. $\psi$ can be obtained by incorporating the spectral ratio $S_{v}/S_{u}$ at lower frequencies ($< 10^{-3}$ Hz) into (31). A summary of the three parameters obtained by the fitting process (c, $\alpha \epsilon ^{^{2/3}}$, and $L_{3D}$) is given in Table 4. Figure 5 also shows the fitted 2D+3D spectra for each period in dashed lines. The accuracy of the fit is analyzed by computing the Root Mean Square Error (RMSE) between the fitted and measured spectra. No strong correlation was found between RMSE and atmospheric stability. However, having more hours in a certain period can reduce the RMSE and provide a better fit, especially in the low-frequency part of the spectrum. By observing the fitted and measured spectra, it is evident that there is a large energy in the spectrum at lower frequencies relative to higher frequencies during periods with stable stratification. A larger correlation was found between Ri$_{b}$ class and the Mann model length scale $L_{3D}$, where much lower values ($< 25$ m) were found for stable stratification. The parameters c and $\alpha \epsilon ^{^2/3}$ are scaling parameters and do not impact the spectrum’s shape. As a comparison, Fig. 5 also shows the 3D spectra fitted to the measured spectra. It is evident that the 3D turbulence model fails to fit the low-wavenumber part of the spectra in all ten periods shown in Fig. 5.

Table 4 Spectral fitting results for each of the analyzed periods

3.3 Lateral Co-coherences

Co-coherence is a measure of how much the wind turbulence is correlated at a certain frequency or wavenumber between two points separated by a distance. Here we measure and predict the co-coherence between the two WindIris beams pointing in different directions and separated by distances ranging from 26 m to 206 m (see Fig. 6). We can now compare the modeled co-coherence with the measured co-coherence between beams 3 and 4, where $\varvec{m}$ and $\varvec{n}$ are unit vectors of the two beams:

$$\begin{aligned} \text {co-coh}_{\varvec{mn}}(k_{1},\varDelta y)=\frac{\Re (\chi _{\varvec{mn}}(k_{1},\varDelta y))}{{\sqrt{F_{\varvec{m}}(k_{1})F_{\varvec{n}}(k_{1})}}}. \end{aligned}$$

(32)

Fig. 6

On the left: WindIris Beams 3 and 4 configuration and the lateral distances between the two beams at different range gates. On the right: Beams 2 and 4 configuration and the vertical distances between the two beams at different range gates

Fig. 7

Measured and predicted lateral co-coherences as a function of $k_1$ a for Period 6 and b for Period 7

Figure 7 exhibits the measured and modeled co-coherences as a function of $k_{1}$ for Period 6 and Period 7. For Period 6, when the atmosphere was stably stratified, we can observe the effect on predicted co-coherences by including the low-frequency fluctuations (the 2D turbulence) in the co-coherence modeling. Table 5 describes the summary of RMSE obtained from predicted co-coherences for all 10 periods. Here, RMSE represents the mean of RMSE values at all ten separation distances obtained by comparing the predicted and modeled co-coherence at different lateral separations. For Period 6, a 24% reduction in RMSE was observed by including the low-frequency fluctuations in the co-coherence prediction as compared to just high-frequency 3D fluctuations. This can be observed from Fig. 7a, where there is a large difference between the two prediction models, especially at low $k_1$ values. Here, the co-coherence prediction in the 3D case is made by $c \rightarrow 0$ in the combined spectra fit. For Period 7, when the atmosphere was neutral, we did not observe a large difference between the two co-coherence prediction models because the turbulence spectrum here contains mostly 3D high-frequency turbulence. Although at lower $k_1$ values, the spread in co-coherence values at different separations is better simulated by the 2D+3D model. The RMSE, in this case, is around 10% higher by including low-frequency fluctuations in the prediction. We can also observe the comparison in Fig. 7b, where the measured co-coherence seems to have a better match with the prediction model with just 3D turbulence.

Table 5 Summary of errors obtained from lateral co-coherence modeling

Further analyzing Table 5 reveals that the reduction in errors of co-coherence modeling by including both 2D low-frequency fluctuations and 3D high-frequency turbulence is quite significant for stable stratification. For Periods 2, 3, 4, 5, and 6, we observed a large reduction in RMSE of modeled co-coherence by incorporating the 2D fluctuations. This is because the low-frequency part of the turbulence spectrum is much stronger during stable stratification than neutral stratification. For neutral stratification, we even observed an increase in RMSE for the former model, as observed in Periods 1, 7, 8, and 9. For the stable stratification cases, the co-coherence at all separations tends to converge much closer to 1 at very low $k_{1}$ values, meaning the turbulence fluctuations are highly correlated at lower frequencies irrespective of the lateral separation distance. The variation between co-coherences at different separations is also not large at higher $k_{1}$ values in the stable periods. For neutrally stratified cases, we observe a large variation in co-coherence values for different separations at higher $k_{1}$, and the co-coherence values do not tend to converge at lower $k_{1}$ values.

3.4 Vertical Co-coherences

To model co-coherence with vertical separation, we assume that the two lower beams are completely horizontal due to the thrust force acting on the wind turbine. This assumption is valid here because the wind speeds for the ten periods under study are close to the rated wind speed of the turbine at which the positive pitch angle of the turbine compensates for the negative tilt angle of lidar beams (Angelou et al. 2023). The following analysis is done on Beams 2 and 4, which have vertical separations ranging from 9 to 71 m. Beam 2 makes a tilt angle $\theta$ of 10${^\circ }$ with Beam 4, while the azimuth angle $\phi$ of both beams is 15${^\circ }$ (see Fig. 6). We also assume that the low-frequency, 2D part of the flow is homogeneous at all instants in the vertical direction; the 2D cross-spectrum between the two beams does not depend on the vertical separation distance $\varDelta z$ and can be described as:

$$\begin{aligned} \chi _{\varvec{m}\varvec{n}}^{2D} (k_{1})= \cos ^{2}\theta (\cos ^{2}\phi F_{11}^{2D} (k_{1})+\sin ^{2}\phi F_{22}^{2D} (k_{1})), \end{aligned}$$

(33)

which is also equal to the auto-spectrum. Here we will not discuss the fitting of one-point spectra of Beams 2 and 4, since the fitting results in almost the same parameters obtained after the spectra fitting of Beams 3 and 4 (see Table 4). However, we will shed light on the assumption of flow homogeneity at low wavenumbers by analyzing the cross spectra between the two vertical beams at different separations. Figures 8a, b exhibit the measured and predicted cross spectra between Beams 2 and 4 for different vertical separations. As observed from the measured cross-spectra for both periods (Periods 6 and 7), the cross-spectra at low wave numbers strongly depends on the separation distance between two beams. We also investigated the variation in auto-spectra for Beams 2 and 4. If the flow is homogeneous, these would have the same magnitude. Still, we observed a decrease in the auto spectra with height, highlighting the flow in-homogeneity in the vertical direction.

Fig. 8

Measured and predicted vertical cross spectra a for Period 6 and b for Period 7

The vertical co-coherences for Periods 6 and 7 are shown in Fig. 9. The co-coherences are plotted as a function of $k_1$, and as expected, the measured co-coherences do not converge at lower $k_1$ values because of the flow inhomogeneity. This leads to an overestimation of co-coherence at lower wavenumbers when using the 2D+3D model (see Fig. 9a). For neutral conditions during Period 7, the low-frequency fluctuations are relatively weaker, so the measured co-coherence matches more closely with the 3D model prediction. In both cases, the measured co-coherences drop to 0 for all separations in the high-wavenumber region. While in predictions, the co-coherence decay is not as strong for the three smallest separations i.e. 9 m, 14 m, and 21 m. The underestimation of co-coherences in the measured data can be attributed to random errors inherent in the LOS velocities obtained from lidar data. These errors manifest as high-frequency signal noise, detected in the measured auto-spectrum, ultimately resulting in decreased observed coherences (Angelou et al. 2012).

Fig. 9

Measured and predicted vertical co-coherences as a function of $k_1$ (a) for Period 6 and (b) for Period 7

4 Model Validation with FINO1 Meteorological Mast Data

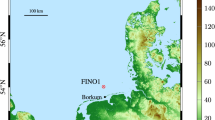
FINO1 is a research platform located in German Bight in the North Sea, approximately 45 km north of the island of Borkum. The platform has multiple instruments recording the meteorological, hydrography, and sea-state parameters. The platform was erected in 2003 and has been recording meteorological parameters at multiple heights ranging from 30 to 100 m above sea level. The platform was deployed to provide offshore resource assessment for wind power projects in the North Sea. Since 2009, many offshore wind farms have been commissioned in the vicinity, and the measurements at FINO1 are highly affected by the wake flow of the neighboring wind farms. For the analysis presented in this article, we selected the 2 years of data before the commissioning of surrounding wind farms i.e. from Jan 2007 to Dec 2008. During that period, three Gill R3-50 sonic anemometers were mounted at 41.5 m, 61.5 m, and 81.5 m above mean sea level. These sonic anemometers recorded three wind components u, v, w, and air temperature T at a sampling frequency of 10 Hz. The location of FINO1 met mast is shown in Fig. 10 with the wind farms commissioned as of 2017. More information about the FINO1 met mast can be found in Riedel et al. (2005); Muñoz-Esparza et al. (2012).

Fig. 10

FINO1 met mast location in the North Sea and the surrounding wind farms in 2017. The surrounding wind farms were not commissioned during the period analyzed in this study i.e. 2007–2008

4.1 Data Processing

The time period analyzed in this study is similar to the study done by Cheynet et al. (2018). Two years of 10 Hz wind and temperature data from Jan 2007 to Dec 2008 was obtained from the mast measured at three different heights i.e. 41.5 m, 61.5 m, and 81.5 m. The number of hours for which the data is available during the 2 years is 16,998 h, which corresponds to about 97% of total hours. Cheynet et al. (2018) processed this data for tilt correction using the Planar Fit method (Wilczak et al. 2001). Only wind speeds between the cut-in and cut-out range of modern wind turbines i.e. 4 and 26 ms$^{-1}$ were of interest in this study. The hours when the mean wind speed at z=81.5 m occurs outside this range were excluded from the analysis. About 76% of the data satisfied this condition. Although the recorded wind components are not disturbed by wind turbine wakes, the mast shadow caused flow distortion in some directions. The sonic anemometer booms are pointing in the North-West direction i.e. 311$^\circ$ for $z=81.5$ m, and 308$^\circ$ for $z=61.5$ m, and $z=41.5$ m. In their study, Cheynet et al. (2018) selected only wind coming from directions between 190$^\circ$ and 360$^\circ$. This seems like a suitable choice, and we also selected the same wind directions in the present study. After this data-processing step, we are left with only $\sim$47% of the total data.

In wind turbine load estimation analyses, we assume stationarity of the first and second-order statistics. There is no standard method to determine the stationarity of a wind time series, as discussed by Nybø et al. (2019). In the present study, we did not want to apply a conservative stationarity test that excludes the low-frequency fluctuations since our main objective is to fit the low-frequency turbulence. Here, we apply a two-step stationarity test where the first step detects a linear trend in time series (Cheynet et al. 2018; Nybø et al. 2019). This is similar to the test applied to nacelle lidar data in the previous section. The second step involves the comparison of the mean and standard deviation of a moving window with the mean and standard deviation of the whole time series. If the maximum of the means and standard deviations of all windows exceeds the threshold values, the time series is considered non-stationary of first-order and second-order, respectively. The choice of threshold and window length can highly affect the results of this test. In the present analysis, we selected a window length of 10 min and the threshold values for mean and standard deviation to be 30% and 90%, respectively. This ensured that extreme cases of non-stationary data were detected and excluded from the analysis. Only 523 hly time series were detected as non-stationary through these two tests. A brief overview of the data processing steps is shown in Fig. 11. About 44.3% of the total data was used in the next analysis.

Fig. 11

FINO1 data processing

Before calculating the spectra, the data is divided into different stability classes based on the Obukhov length L:

$$\begin{aligned} L= -\frac{u_{*}^{3}}{\kappa _{\text {K}} (g/T)\overline{w'\varTheta '_{v}}} ~~, \end{aligned}$$

(34)

where $u_{*}$ is the frictional velocity, $\kappa _{\text {K}}$ is the von Kármán constant, g is the gravitational acceleration, T is the reference temperature, and $\overline{w'\varTheta '_{v}}$ is the virtual kinematic heat flux where $\varTheta _{v}$ is the virtual potential temperature. We used the atmospheric stability classes suggested in Gryning et al. (2007). Table 6 describes seven different stability classes from “Very Unstable” to “Very Stable” based on Obukhov length L. Here, we utilized the wind components and temperature recorded at $z=81.5$ m to calculate L for every hour (Cheynet et al. 2018). The resulting stability classes show a distribution slightly skewed towards unstable conditions as seen in Table 6. The neutral conditions are the most dominant, with 40% of the data representing such conditions. The very-unstable and very-stable extreme conditions have the lowest occurrence, both having less than 10% share in the total analyzed data. The contribution of the rest of the four classes (u, nnu, nns, s) is fairly large, with each class occurring between $\sim$10 and 20% in the total data.

Table 6 Stability classes

4.2 Spectral Analysis

The probability distribution of ${\overline{U}}$ at z = 81.5 m revealed that wind speeds between 6 and 14 ms$^{-1}$ are most commonly occurring. For brevity, the spectral analysis is presented for only three wind speed ranges: 6–8, 8–10, and 10–12 ms$^{-1}$. Most modern wind turbines have rated wind speeds between 10 and 12 ms$^{-1}$, but the maximum loads and bending moments occur at below-rated wind speeds when the thrust force is highest. Hence, the spectral analysis of below-rated wind speeds is of significant importance. Moreover, among the seven stability classes presented in Table 6, results from only three stability classes i.e. “Unstable (u)", “Neutral (n)", and “Stable (s)" will be discussed here for conciseness.

Figure 12 displays the measured and fitted spectra $k_1 F(k_1)$ in terms of wavenumber $k_1$ at z = 81.5 m. The spectra are plotted for three wind speed ranges: 6–8, 8–10, and 10–2 ms$^{-1}$ and three stability classes: u, n, and s. The spectra were calculated for each hour, and mean spectra were obtained for the number of hours in each classification. Figure 12 also displays the hours utilized to get mean spectra for each plot. From the spectra plots, it is evident that the number of hours exhibiting neutral conditions increases significantly when the wind speed is increased from 6–8 to 10–12 ms$^{-1}$. Before calculating the spectra for each hourly time series, a spike detection algorithm was applied to remove any potential spikes in time series data. For the spectra calculation, no linear detrending was applied, no overlapping segments were used, and no window function was employed. Moreover, the random error was minimized by taking the ensemble average of spectra for all hours in a single class. The measured spectra shown here are two-sided spectra, which means $\int _0^\infty F_i(k_1) dk_1 = \sigma _i^2 /2$.

Fig. 12

FINO1 measured and fitted spectra at $z=81.5$ m for three wind speed ranges and three stability classes

The measured u and v spectra have significant low-frequency fluctuations in all three stability conditions. The spectra in each plot can be divided into three distinct regions: (1) a low-frequency region where $k_1\cdot F(k_1) \propto k_1^{-2/3}$ for the u and v components, while the $F(k_1)\rightarrow 0$ for the w component (2) a spectral-gap or plateau region where $d(k_1\cdot F(k_1))/dk_1 \approx 0$, and (3) an inertial sub-range region where $k_1\cdot F(k_1) \propto k_1^{-2/3}$ and the transverse v and vertical w component spectra have more energy than the longitudinal component u spectrum. The spectral gap represents the transition from mesoscale 2D fluctuations to microscale 3D turbulence. The spectral gap is mostly visible in stable cases, where the 3D turbulence has less intensity than the large-scale 2D fluctuations. This is because 3D turbulence in stable conditions has smaller length scales, so the 2D fluctuations are easily spotted, and so is the spectral gap.

The 2D low-frequency and 3D Mann uniform-shear turbulence spectra models are fitted to the measured spectra, and the four fitting parameters are obtained for each case. The 2D turbulence scaling parameter c is obtained from $F_{2D}(k_1)$ fitting, and the parameters $\alpha \epsilon ^{2/3}$, $L_{3D}$, and $\varGamma _{\text {M}}$ represent the high-frequency Mann turbulence spectra $F_{3D}(k_1)$. $\psi$ is obtained from (31) for $f<10^{-3}$ Hz. The boundary-layer height $z_i=500$ m is chosen based on the study by Krogsæter and Reuder (2015). The downhill simplex algorithm (McKinnon 1998) was applied to minimize the error function, which is described as:

$$\begin{aligned}{} & {} \sum _{i=1}^{2} \sum _{j=1}^{N} \left( k_j\cdot F_{i, 2D+3D}(k_j) - k_j\cdot F_{i, \text {meas.}}(k_j)\right) ^2 \nonumber \\{} & {} \quad + \sum _{j=1}^{N} \left( k_j\cdot F_{3, 3D}(k_j) - k_j\cdot F_{3, \text {meas.}}(k_j)\right) ^2 \nonumber \\{} & {} \quad + \sum _{j=1}^{N} \left( k_j\cdot F_{13, 3D}(k_j) - k_j\cdot F_{13, \text {meas.}}(k_j)\right) ^2 ~~, \end{aligned}$$

(35)

where $F_i~~(i = 1,2,3)$ is the auto-spectrum of u, v, and w components, respectively, $F_{13}$ is the co-spectrum between u, and w components, and N is the number of wavenumbers in estimated spectra after logarithmic bin averaging. There is an overall good agreement between the fitted and measured spectra for all wind speed ranges and stability conditions. Although the Mann 3D model was originally developed for neutral stratification, here we also observed a good fit for the stable cases as well, also observed by Peña (2019) and Peña et al. (2010). A slight mismatch between the measured and fitted spectra is observed in the spectral gap of the v component in unstable and neutral conditions. This deviation also translates into the modeled co-coherences discussed in the next section. In unstable and neutral conditions, large energy is also observed in the w spectrum at low k values, which is not well represented by the Mann 3D turbulence model.

4.3 Vertical Co-coherences

The vertical co-coherences between u,  v, and w components are evaluated for two vertical separation distances, $\varDelta z = 20$ m and $\varDelta z = 40$ m. The co-coherences are modeled using both the low-frequency and high-frequency modeled spectra and cross-spectra. Here we also assume that the low-frequency turbulence is homogeneous in the vertical direction, so the 2D cross-spectrum would be the same as the auto-spectrum. For the 3D cross-spectra calculation, the average of the Mann model parameters at two heights was used. The 3D cross-spectrum is obtained through the numerical integration:

$$\begin{aligned} \chi _{ij} (k_1,\varDelta z) = \int _{-\infty }^{\infty } \int _{-\infty }^{\infty } \varPhi _{ij}(k_1,k_2,k_3) \, \text {exp}(-\iota k_3 dz) \, dk_2 \, dk_3, \end{aligned}$$

(36)

where $\varPhi _{ij}(k_1,k_2,k_3)$ is the Mann uniform shear spectral tensor and $k_2$ and $k_3$ are wavenumbers in lateral and vertical directions, respectively. Figures 13 and 14 display the measured and modeled co-coherences at $\varDelta z = 20$ m and $\varDelta z = 40$ m, respectively. The co-coherences are plotted as a function of $k_1 \varDelta z$. The measured and modeled co-coherences show good agreement for u and w at all wind speed ranges and stability conditions. The most obvious mismatch happens in the v co-coherence at the $k_1\varDelta z$ values corresponding to the spectral gap in neutral and stable conditions. In the region where $k_1\varDelta z < 0.5$, representing low-frequency fluctuations, we observed a strong match between the measured and modeled co-coherences of u and v, albeit with a slight tendency toward overprediction with increasing $\varDelta z$. This can be attributed to the model’s assumption of vertical homogeneity in 2D turbulence, a simplification that, in reality, isn’t entirely accurate.

Fig. 13

Co-coherences between u, v, and w components between $z = 81.5$ m, and $z = 61.5$ m ($\varDelta z = 20$ m). Solid lines are measured co-coherences, while dashed lines represent modeled co-coherences

Fig. 14

Co-coherences between u, v, and w components at $z = 81.5$ m, and $z = 41.5$ m ($\varDelta z = 40$ m). Solid lines are measured co-coherences, while dashed lines represent modeled co-coherences

4.4 Phase Angles Analysis

Another important parameter is the phase difference between u, v, and w fluctuations at different heights. The phase difference is a consequence of vertical shear in the surface layer. This implies that the wind fluctuations in a wind turbine rotor plane can get out of sync with respect to distance to the surface. The large difference in phase angle can cause increased fatigue and bending loads on a wind turbine. Previous studies such as Chougule et al. (2012) have shown that for neutral stratification, $\varphi _v> \varphi _u > \varphi _w$ for $k_1\varDelta z < 1$. Here, we have plotted measured and modeled phase angles for two vertical separation distances ($\varDelta z = 20$ m and $\varDelta z = 40$ m), three different stability conditions (u, n, s), and three wind speed ranges (see Figs. 15 and 16).

It is apparent from both figures that $\varphi _v> \varphi _u > \varphi _w$ for $k_1\varDelta z < 1$ for all stability conditions and wind speed ranges. A detailed explanation for this effect can be found in Chougule et al. (2012). For all stability classes and wind speed ranges, we observed higher $\varphi$ values for $\varDelta z = 40$ m compared to $\varDelta z = 20$ m. Furthermore, the large phase angles during stable conditions are observed, possibly because of the smaller size of eddies and increased shear. During unstable conditions, there is less vertical shear, and eddies are relatively larger; hence, the fluctuations at different heights are more in sync. For $k_1\varDelta z < 0.1$, which corresponds to 2D turbulence, we can observe almost close to zero phase angles for both the model and measurements. This agrees with the assumption of vertical homogeneity for the low-frequency wind fluctuations.

Fig. 15

Phase angles between u, v, and w fluctuations at $z = 81.5$ m, and $z = 61.5$ m ($\varDelta z = 20$ m). Solid lines are measured phase angles, while dashed lines represent modeled phase angles

Fig. 16

Phase angles between u, v, and w fluctuations at $z = 81.5$ m, and $z = 41.5$ m ($\varDelta z = 40$ m). Solid lines are measured phase angles, while dashed lines represent modeled phase angles

5 Discussion

5.1 The Effect of Blockage

The Mann Uniform Shear model assumes that one-point cross-spectra of longitudinal and vertical fluctuations is real, so $\Im (\chi _{uw}(k_1,\varDelta z=0))=0$. While this is true for stable and neutral stratification, where the eddies’ sizes are relatively small and do not feel the effect of the surface, the same can not be said for unstable stratification. Even at $z = 81.5$ m, the surface constrains the size of eddies during unstable stratification. This can be observed in the measured $\chi _{uw}(k_1)$ in Fig. 17 where there is a large $\Im (\chi _{uw}(k_1))$ during unstable conditions. This blocking effect can be modeled using the Mann Uniform Shear + Blocking (US+B) model described by Mann (1994). Compare with Mann (1994) Figures 7b and 10b, where the quad-spectrum is very small. Here we evaluate the three parameters obtained by fitting the measured spectra with US and US+B models. Figure 18 illustrates the variation in $L_{3D}$, $\alpha \epsilon ^{2/3}$, and $\varGamma _{\text {M}}$ for seven stability conditions, three wind speed ranges, and three heights above mean sea level. One can observe that there is little effect of wind speed range on the value of $L_{3D}$, but it decreases significantly with increasing stability in the atmosphere. There is little variation between US and US+B $L_{3D}$ values for the stable cases, while during unstable conditions, the variation is quite large. For $\alpha \epsilon ^{2/3}$, the US+B model produced almost the same values as the US model. The $\alpha \epsilon ^{2/3}$ values were observed maximum at 41.5 m among the three heights. Among the stability classes, the highest dissipation was observed in neutral and near-neutral conditions. For the anisotropy parameter $\varGamma _{\text {M}}$, the highest values for all stability classes were observed at 41.5 m. Furthermore, a slight increase in $\varGamma _{\text {M}}$ was observed with increasing stability. The US + B model produces slightly higher values of $\varGamma _{\text {M}}$ than the US model. The US model parameters obtained at FINO1 are consistent with the findings of de Maré and Mann (2014) at Rødsand offshore wind farm, and Peña et al. (2010) at the Høvsøre test site in Denmark.

Fig. 17

Measured u, v, and w spectra, and uw cross spectra at $z = 81.5$ m for wind speed range 10–12 ms$^{-1}$

Fig. 18

Mann uniform shear (US) Model and Mann Uniform Shear + Blocking (US+B) Model parameters obtained through fitting the measured spectra at FINO1

5.2 Limitations of the 2D Turbulence Model

Atmospheric stability is one of the factors in determining large-scale wind flow homogeneity. Large vertical shear and potential temperature gradients during stable conditions inhibit mixing and thus can be a source of inhomogeneity. On the other hand, in neutral and unstable conditions, large mixing length scales are present; thus, the w component exhibits low-frequency energy as observed in some FINO1 spectra (Fig. 12). This implies that low-frequency wind fluctuations may not always be two-dimensional. The model presented here cannot predict the low-frequency w fluctuations because of its two-dimensional nature.

The low-frequency turbulence model presented in this study assumes flow homogeneity in the vertical direction. Analysis based on data from FINO1 reveals that the 2D turbulence model effectively predicts co-coherences and phase angles between fluctuations in the u, v, and w components at two vertical separations of $\varDelta z = 20$ m and $\varDelta z = 40$ m. However, in certain instances, a minor discrepancy between model predictions and measurements was observed at low wavenumbers due to flow inhomogeneity. Additionally, there is a slight mismatch between the model and measurements in the vertical cross spectra measured by nacelle lidar, particularly for low $k_1$ values (as illustrated in Fig. 8). Hence, it’s worth noting that this assumption may not hold under certain conditions.

5.3 Effect of Atmospheric Conditions on the 2D Turbulence Model Parameters

Figure 19 illustrates the variation in the scaling parameters of the 2D and 3D turbulence models, c and $\alpha \epsilon ^{2/3}$, respectively. These parameters are obtained by fitting the measured spectra from FINO1 for three atmospheric stability conditions: neutral (n), stable (s), and unstable (u). The parameters are obtained for 1 ms$^{-1}$ mean wind speed bins ranging from 3 to 25 ms$^{-1}$, given that there are at least 10 h of data available in each bin. There are no data points for stable and unstable conditions for ${\overline{U}}>14$ ms$^{-1}$. From Fig. 19, it can be observed that $\alpha \epsilon ^{2/3}$ increases with the ${\overline{U}}$ and this increase is directly proportional to ${\overline{U}}^2$. The same was not observed for the 2D turbulence scaling parameter c. For the neutral conditions, c increases in a slightly linear trend with ${\overline{U}}$. For the stable and unstable conditions, we do not have enough data points to comment on the trend of c with ${\overline{U}}$. However, we can still observe for the limited data points that there is a slight decrease in c with increasing ${\overline{U}}$ for stable conditions, while for the unstable conditions, c increases sharply with increasing ${\overline{U}}$.

The other 2D turbulence model parameter is $\psi$, which is discussed in detail in the following subsection. Figure 20 shows the change in $\psi$ with the mean wind speed ${\overline{U}}$. The values are obtained with the same criteria as c and $\alpha \epsilon ^{2/3}$. We observed no significant trend in $\psi$ with respect to ${\overline{U}}$ since the values fluctuate around 45$^{\circ }$ mostly. Hence, it can be concluded that the low-frequency fluctuations at FINO1 are close to isotropic. To gain further insight into the 2D turbulence parameters, low-frequency wind spectra from other sites must be analyzed. Some general recommendations regarding the usage of this model will be presented in future studies.

Fig. 19

Comparison of the scaling parameters of the 2D and 3D turbulence models from the measurements obtained at FINO1 at $z=81.5$m. The absence of data points means the absence of the required amount of data to avoid uncertainty

Fig. 20

Anisotropy parameter ($\psi$) of the 2D turbulence model measured from FINO1 measurements at $z=81.5$m. The absence of data points means the absence of the required amount of data to avoid uncertainty

5.4 On the Isotropy in 2D Turbulence

Here, we explore the anisotropy parameter $\psi$ and its influence on 2D turbulence. Figure 20 displays the variation of $\psi$ across different atmospheric stability conditions and wind speeds for the FINO1 data. $\psi$ is evaluated using (31) for frequencies below $10^{-3}$ Hz. The values remain consistently close to 45$^{\circ }$ at all wind speed ranges and stability conditions. Based on the low-frequency wind fluctuations model, $\psi =45^{\circ }$ presents two-dimensional isotropy where $S_v/S_u = 5/3$. When $S_v/S_u = 1$ the corresponding value of $\psi$ is 37.76$^{\circ }$. Data from FINO1 shows that $S_v/S_u > 1$ for $f<10^{-3}$ Hz in all the cases analyzed here.

Larsén et al. (2013) observed that, for wind measurements at Horns Rev and Nysted offshore wind farm sites, the average value of $S_v/S_u$ is around 0.8 within the frequency range of $2\times 10^{-4}~\text {Hz}<f<10^{-3}$ Hz, but exceeds 1 when $f<2\times 10^{-4}$ Hz. A similar analysis was made by Larsén et al. (2016), who noted that, at Horns Rev and Høvsøre test site in Denmark, $S_v/S_u$ averaged around 1.25 within the range of $10^{-5}~ \text {Hz}< f< 2\times 10^{-4} \text {Hz}$. In both of these studies, $S_v/S_u$ exceeds 1 for frequencies below $2\times 10^{-4} \text {Hz}$ suggesting that 2D turbulence at these sites tends to exhibit isotropic behavior as f drops below $2\times 10^{-4}$ Hz. Interestingly, at FINO1, we observed a slightly higher average value of $S_v/S_u$ when $10^{-4}~\text {Hz}<f<10^{-3}$ Hz, averaging around 1.6. This value closely aligns with the isotropic value of 5/3.

Furthermore, in another study, Larsen et al. (1990) analyzed the low-frequency fluctuations for near-neutral and stable conditions recorded in the Lammefjord experiment. It was observed that $S_v/S_u < 1$ within the frequency range of $10^{-4}~\text {Hz}<f<10^{-3}$ Hz. This implies that for the onshore sites or near-shore sites, 2D turbulence may not display isotropic characteristics within the specified frequency range.

The measurements from Hywind Scotland showed a different range of $\psi$: between 25$^{\circ }$ and 35$^{\circ }$ (see Table 4). This indicates that, for all 10 periods analyzed in the data set, $S_v/S_u < 1$ when the frequency is in the range of $10^{-4}~\text {Hz}<f<10^{-3}$ Hz. However, the uncertainty in $\psi$ values obtained at Hywind is quite large and can be attributed to two factors. First, the available data to evaluate $\psi$ values is relatively limited. Second, determining $\psi$ involves the reconstruction of u and v components from the LOS measurements with beams mainly oriented in the x-direction.

The assumption of scale independence of the anisotropy in 2D turbulence can certainly be questioned. However, we are aiming for simplicity of the model. The scale-dependent anisotropy can be observed in the atmosphere at extremely low frequencies irrelevant to wind energy applications. One example is the inverse energy cascade in 2D turbulence in the presence of some forcing element. For instance, due to variation in the Coriolis parameter, the horizontal symmetry breaks down and leads to jet flows in the geostrophic turbulence which exhibits strong anisotropy at different scales (Galperin et al. 2010). Geophysical flows such as Rossby waves also show scale-dependent anisotropy because of the earth’s rotation and can interact with smaller-scale turbulence in a scale-dependent manner (Galperin et al. 2014). An interesting example of scale-dependent anisotropy at large scales can be found in non-Kolmogorov turbulence, such as optical turbulence that often occurs near the Earth’s surface, where it is influenced by factors such as temperature gradients, humidity, and wind shear (Toselli 2014).

A useful tool to visualize the anisotropy in turbulence is the Lumley triangle proposed by Lumley (1979) and Choi and Lumley (2001). The Reynolds stress tensor can be divided into an isotropic part and a deviatoric part as:

$$\begin{aligned} R_{ij} = \frac{1}{3} R_{kk}\delta _{ij} + R_{ij}' ~, \end{aligned}$$

(37)

where the first term is the isotropic part. In the case of isotropy, $R_{ij}'=0$. The normalized anisotropy tensor is given by:

$$\begin{aligned} b_{ij} = \frac{\left<u_i'u_j'\right>}{\text {tr}(R_{ij})}-\frac{\delta _{ij}}{3} ~, \end{aligned}$$

(38)

where $\text {tr}(R_{ij})$ is the trace of the covariance matrix (also equal to twice the turbulence kinetic energy). The normalized anisotropy matrix ${\textbf {b}}$ has zero trace and two invariants. The three eigenvalues are $\lambda _1, \lambda _2, \lambda _3$ where $\lambda _1+\lambda _2+\lambda _3=0$. From Pope (2000), any turbulent flow can be presented on a $\eta -\xi$ plane, where $\eta$ and $\xi$ are the two invariants:

$$\begin{aligned} \eta ^2 = -\frac{1}{3} (\lambda _1\lambda _2 + \lambda _2\lambda _3 + \lambda _1\lambda _3) ~, \end{aligned}$$

(39)

and:

$$\begin{aligned} \xi ^3 = \frac{1}{2} (\lambda _1\lambda _2\lambda _3) ~. \end{aligned}$$

(40)

Fig. 21 illustrates the anisotropy map of the 2D turbulence model. All the possible realizations of pure 2D turbulence exist on the green curve, where the data point $(\xi ,\eta )=(-1/6,1/6)$ represents the isotropic 2D turbulence ($\psi =45^{\circ }$). As the value of $\psi$ deviates from $45^{\circ }$ in either direction, both $\xi$ and $\eta$ start to increase. The anisotropy leads to the deformation of the circle into ellipse-like turbulent eddies. When $\psi \rightarrow 0^{\circ }$ or $90^{\circ }$, $(\xi ,\eta )=(1/3,1/3)$ and the turbulence eddy transforms into a 1D line-like structure. The anisotropy behavior of the Mann uniform shear model (3D turbulence model) is also compared. $(\xi ,\eta )=(0,0)$ presents the point where the statistics of the turbulence eddies is spherical and isotropic. At this point, the value of the anisotropy parameter $\varGamma _{\text {M}}=0$. As $\varGamma _{\text {M}}$ is increased, the sphere-like statistics turns into a pointed or prolate spheroid. The diamond markers in Fig. 21 are from FINO1 measurements at different mean wind speeds (3 to 24 ms$^{-1}$) from 1-hr measurements. These data points are plotted for different stability conditions: n, s, and u. It can be observed that the measured turbulence is a mix between 2D and 3D turbulence. Most of the data points are located close to the green curve and have an oblate spheroid shape, which implies that the 2D turbulence is more prominent than the 3D part. It is important to emphasize that the points will move closer to the green curve (2D turbulence) if we obtain $\xi$ and $\eta$ from time series longer than 1-hr since it will include more 2D turbulence.

Fig. 21

Lumley triangle showing 2D and 3D turbulence anisotropy. On the green curve, data points from the 2D turbulence model are presented (circles). $(\xi ,\eta )=(-1/6,1/6)$ represents isotropic 2D turbulence with $\psi =45^{\circ }$. The triangle markers present data points from the 3D Mann turbulence model where $\varGamma _{\text {M}}$ is the anisotropy parameter. $(\xi ,\eta )=(0,0)$ represent isotropic 3D turbulence where $\varGamma _{\text {M}}=0$. The diamond markers present FINO1 measurements at different wind speeds for different atmospheric conditions (n, s, u)

Stiperski and Calaf (2018) observed that during stable atmospheric conditions over the land, the turbulence becomes closer to one-component structures i.e. $\eta \rightarrow 1/3$, and $\xi \rightarrow 1/3$. They derived these results from sonic anemometer measurements at different height levels up to 55 m as part of the Cooperative Atmosphere-Surface Exchange Study 1999 (CASES-99) field experiment in Kansas, USA. It was noted that one-component turbulence occurs during weak wind conditions when fluxes are close to zero, and vertical velocity variance is significantly lower than horizontal velocity variance. This is also marked by higher buoyancy destruction of turbulence as compared to shear generation in the TKE budget. Additionally, a correlation was observed between the anisotropy states of turbulence and the averaging time during stable stratification. Specifically, more isotropic turbulence structures (three components) were identified when using 1-min averages of data compared to 30-min averaging periods. These distinct averaging periods were selected to mitigate the influence of mesoscale turbulence. It is essential to note that in this study, the data from FINO1 is averaged over a 1-hour period, encompassing both mesoscale turbulence and three-dimensional turbulence. This prolonged averaging time leads to a higher energy concentration in the low-frequency turbulence, resulting in a prevalence of two-component turbulence relative to one-component turbulence. Stiperski et al. (2019) and Stiperski and Calaf (2023) expanded the analysis to 12 land sites with varying degrees of terrain complexity and found a similar pattern of turbulence behavior during stable stratification at other sites. These observations have been instrumental in formulating generalized scaling relationships in the surface layer by incorporating information on turbulence anisotropy.

6 Conclusions

A model for low-frequency wind fluctuations is introduced, which models the large-scale and slow-moving fluctuations for the longitudinal and transverse components of the wind vector. The model contains a length scale corresponding to the peak of mesoscale turbulence. An anisotropy parameter is also incorporated in the model, which does not depend on other atmospheric parameters but rather on the ratio between the spectra of the longitudinal and transverse components. The model can generate stochastic two-dimensional wind fields, which are assumed statistically independent of the more detailed three-dimensional wind fields. These fields could be useful for studying wake meandering in wind farms or dynamic loads on some types of floating wind turbines. The 2D spectra model can be combined with any 3D turbulence spectra model (here, we use the Mann uniform shear spectral model) to produce velocity spectra for a wide frequency range. The one-point spectra and two-point cross-spectra obtained from the model can be effectively utilized to predict lateral and vertical coherences for low-frequency fluctuations. The model is validated against two datasets: forward-looking, nacelle-mounted WindIris lidar data from a wind turbine in Hywind Scotland and point measurements from sonic anemometers at three height levels on the meteorological mast at FINO1 research platform in the North Sea. Following are the main findings and conclusions of this study.

• Low-frequency fluctuations of longitudinal and lateral wind components were found in lidar and point measurements of 1-hr long time series at two offshore sites. These low-frequency fluctuations represent quasi-2D turbulence as these do not contain strong vertical wind component fluctuations. The relative strength of the 2D turbulence is strongest for stably stratified flow. The 2D turbulence is separated from the 3D turbulence by a transition zone called a ’spectral gap’. The width of the spectral gap also depends on atmospheric stability.

• The 2D and 3D turbulence models were fitted to the measured spectra from lidar LOS measurements and point measurements. An excellent agreement was found for low-frequency fluctuations with the model. The model can also fit the spectral gap observed during stable conditions.

• The lateral and vertical co-coherences estimated from the model showed a very good agreement with the measurements. Using both 2D and 3D turbulence models improved the co-coherence prediction for 1-hr long time series, as compared to using just a 3D turbulence model. The improved prediction was more prominent in stable conditions. The model slightly overestimated the vertical coherences against both sets of measurements.

• The phase angles between wind fluctuations at two vertically separated points were also estimated using the combined 2D+3D turbulence model. It was noted that the model successfully predicts the order of wind components with respect to changes in the phase angle. The rate of change in phase angles for the three wind components with the frequency (or wavenumber) was also predicted considerably well.

• The values of the anisotropy parameter $\psi$ obtained through the fitting process of spectra at FINO1 revealed that the low-frequency fluctuations are close to isotropic ($\psi =45^{\circ }$) for the periods analyzed. The $\psi$ values computed at Hywind Scotland showed anisotropy in low-frequency fluctuations.

The main application of this low-frequency turbulence model includes generating stochastic wind fields for wind turbine load estimation analysis. As wind turbines continue to grow in size, we believe this new spectral model would be relevant for predicting large-scale, low-frequency fluctuations and their impact on loads on wind turbine structures and meandering of wakes. Future work involves creating a methodology for generating such wind fields and their impact on wind turbine structural loads and moments.

Appendices

Appendix 1: 2D spectra with attenuation at high frequencies

For the attenuated energy spectrum in (27) the isotropic variance $\sigma ^2$ can be defined as a function of $L_{2D}$ and z as in (A1). This is obtained by integrating (27) from 0 to $\infty$:

$$\begin{aligned} \begin{aligned} \sigma ^2&= \frac{c L_{2D}^{\frac{8}{3}}}{24 d^{\frac{1}{3}} \left( L_{2D}^2 - z_i^2\right) ^2} \biggl \{ -8 \sqrt{3} L_{2D}^2 \pi + 27 L_{2D}^2 d^{\frac{1}{3}} + 9 d^{\frac{1}{3}} z_i^2 \\&\quad - 12 \sqrt{3} L_{2D}^2 {{\,\textrm{arctan2}\,}}\left( -\frac{\sqrt{3}}{2 d^{\frac{1}{3}}}, 1 - \frac{1}{2 d^{\frac{1}{3}}}\right) + 6 L_{2D}^2 \log \left( 1 + \frac{1}{d^{\frac{2}{3}}} - \frac{1}{d^{\frac{1}{3}}}\right) \\&\quad - 12 L_{2D}^2 \log \left( 1 + \frac{1}{d^{\frac{1}{3}}}\right) \biggr \}~, \end{aligned} \end{aligned}$$

(A1)

where:

$$\begin{aligned} d=\frac{L_{2D}^2-z_i^2}{z_i^2}~. \end{aligned}$$

(A2)

Integrating the attenuated anisotropic spectral tensor would yield one-dimensional spectra. The procedure is similar to that described in the Section 2.

$$\begin{aligned} \begin{aligned} F_{11}^{2D}(k_1) = c \Bigg (&\frac{ \varGamma \left( \frac{11}{6}\right) \, L_{2D}^{\frac{11}{3}}\Big \{-p \, _2F_1\left( \frac{5}{6}, 1; \frac{1}{2}; p\right) - 7 \, _2F_1\left( \frac{5}{6}, 1; \frac{1}{2}; p\right) + 2 \, _2F_1\left( -\frac{1}{6}, 1; \frac{1}{2}; p\right) \Big \}}{10\sqrt{2\pi } \varGamma \left( \frac{7}{3}\right) \left( L_{2D}^2 - z_i^2\right) \sin ^3(\psi ) \, a^{\frac{5}{6}}}\\&+ \frac{L_{2D}^{\frac{14}{3}} \, \sqrt{b}}{2 \sqrt{2}\, d^{\frac{7}{3}}\, z_i^3 \,\sin ^3(\psi ) }\Bigg )~, \end{aligned} \end{aligned}$$

(A3)

and

$$\begin{aligned} F_{22}^{2D}(k_1)= & {} c k_1^2 \Bigg ( - \frac{z_i^4 \, a^\frac{1}{6} \, L_{2D}^\frac{11}{3} \, \varGamma \left( \frac{17}{6}\right) }{55\sqrt{2\pi } \, \left( L_{2D}^2 - z_i^2\right) ^2 \, b \, \varGamma \left( \frac{7}{3}\right) \,\sin (\psi )} \left( -9-26\, _2F_1\left( -\frac{1}{6}, 1; \frac{1}{2}; p\right) \right. \nonumber \\{} & {} + p^2 \left\{ 15-30\, _2F_1\left( -\frac{1}{6}, 1; \frac{1}{2}; p\right) -59 \, _2F_1\left( \frac{5}{6}, 1; \frac{1}{2}; p\right) \right\} \nonumber \\{} & {} + 35\, _2F_1\left( \frac{5}{6}, 1; \frac{1}{2}; p\right) +15p^3 \, _2F_1\left( \frac{5}{6}, 1; \frac{1}{2}; p\right) \nonumber \\{} & {} +p \left\{ -54+88 \, _2F_1\left( -\frac{1}{6}, 1; \frac{1}{2}; p\right) +9 \, _2F_1\left( \frac{5}{6}, 1; \frac{1}{2}; p\right) \right\} \Bigg ) \nonumber \\{} & {} - \left. \left. \frac{L_{2D}^\frac{14}{3}}{\sqrt{2b}\,d^\frac{7}{3}\, z_i\,\sin (\psi ) } \right) \right. , \end{aligned}$$

(A4)

where

$$\begin{aligned} a&= 1+2k_1^2 L_{2D}^2 \cos ^2(\psi )~, \end{aligned}$$

(A5)

$$\begin{aligned} b&= 1+2k_1^2 z_i^2 \cos ^2(\psi )~, \end{aligned}$$

(A6)

$$\begin{aligned} p&= \frac{L_{2D}^2\, b}{z_i^2\, a}~, \end{aligned}$$

(A7)

and $_2F_1$ is a hypergeometric function. The two-point cross spectra $\chi _{11}(k_1,\varDelta y)$ and $\chi _{22}(k_1,\varDelta y)$ for the attenuated energy spectrum in (27) to our knowledge do not have any analytical solution but can be obtained through numerical integration techniques.

Appendix 2: Combining low-frequency fluctuations model with a 3D turbulence model for nacelle lidar measurements

For the 3D spectra, we choose the Mann spectral tensor model (Mann 1994), which was originally developed for purely neutral conditions and was applied to point measurements at a certain location. Here we modify the one-dimensional spectrum obtained from the 3D Mann spectral tensor since we do not have point measurements from lidar but rather a weighted average of the LOS components along the beam. Due to a non-zero azimuth angle of the lidar beams, the lidar is not measuring the u-component of the wind vector, rather it measures the LOS component. The LOS obtained from a single beam of lidar can be expressed (Held and Mann 2019) as:

$$\begin{aligned} v_{r}(\varvec{x})=\int ^{\infty }_{-\infty } \varphi (s)\varvec{n\,\cdot \,u}(\varvec{n}(d_{f}+s)+\varvec{x})ds ~~, \end{aligned}$$

(A8)

where $\varvec{n}$ is a unit vector along the direction of the beam, $d_{f}$ is the distance from the instrument to the center of the range gate, s is the distance along the beam from that center, and $\varphi$ is a weighting function that represents the filtering induced due to the probe length. The spectrum of the LOS measurements can be modeled as (see Mann et al. 2008):

$$\begin{aligned} F_{v_{r}}(k_{1})=\iint ^{\infty }_{-\infty } |{\hat{\varphi }}(\varvec{n}\,\cdot \,\varvec{k})|^{2}\,n_{i} \varPhi _{ij} n_{j} dk_{2}dk_{3} ~~. \end{aligned}$$

(A9)

Here ${\hat{\varphi }}$ is the Fourier transform of the weighting function. We choose a Gaussian weighting function given by:

$$\begin{aligned} \varphi (s)= \frac{1}{l_{avg} \sqrt{2\pi }} \,\exp \left( {-\frac{s^{2}}{2\,l_{avg}^{2}}}\right) ~~, \end{aligned}$$

(A10)

where $l_{avg}$ is the averaging length and is related to the probe length or FWHM of the lidar by:

$$\begin{aligned} l_{avg}=\frac{\text {FWHM}}{2\sqrt{2\,\ln 2}} ~~. \end{aligned}$$

(A11)

Here we assume that the FWHM of the WindIris is 30 m, so $l_{avg}$ is about 13 m. Similarly, the cross-spectrum of two LOS measurements by two beams having unit vectors $\varvec{m}$ and $\varvec{n}$ at distance $d_{f}$ is given by:

$$\begin{aligned} \chi _{mn}(k_{1})=\int \int ^{\infty }_{-\infty } {\hat{\varphi }}(\varvec{m}.\,\varvec{k}) {\hat{\varphi }}^{*}(\varvec{n}.\,\varvec{k}) m_{i} \varPhi _{ij}(k) n_{j} \exp (i\varvec{k}.\,(\varvec{m}-\varvec{n})d_{f}) dk_{2}dk_{3} ~~. \end{aligned}$$

(A12)

We can now combine the low-frequency spectral tensor, $\phi _{ij}$ and the high-frequency turbulence Mann spectral tensor $\varPhi _{ij}$ to get:

$$\begin{aligned} \varPsi _{ij}(\varvec{k}) = \varPhi _{ij}(\varvec{k}) + \phi _{ij}(k_1,k_2) ~~, \end{aligned}$$

(A13)

where the last term is zero if either i or j is 3.

The spectra and cross-spectra measured by the WindIris are not quite in the x-direction but the are measured in two directions described by the unit vectors $\varvec{m}$ and $\varvec{n}$. Held and Mann (2019) shows how to use the three-dimensional spectral tensor to calculate spectra and cross-spectra observed by the lidar for any configuration of beams. Here we will see how to combine the analytical expressions for the 2D turbulence model to get spectra. These do not need to consider the effect of averaging because they have almost all energy at the lowest frequencies. The 2D auto-spectrum for a unit vector $\varvec{m}$, where $m_3$ is not necessarily zero, is:

$$\begin{aligned} F^{2D}_{\varvec{m}}(k_1) = m_i F^{2D}_{ij}(k_1) m_j = m_1^2F^{2D}_{11}(k_1) + m_2^2F^{2D}_{22}(k_1) ~~. \end{aligned}$$

(A14)

Now we can combine the 2D and 3D one-point spectra by simply adding the respective terms:

$$\begin{aligned} F_{total}(k_1) = F^{2D}(k_1)+F^{3D}(k_1) ~~, \end{aligned}$$

(A15)

using (A3) and (A4) for the first term, and (A9) for the second term which can be solved by numerical integration (see Held and Mann 2019)).

The cross-spectrum, assuming that the beams are measuring at the same upwind distance is:

$$\begin{aligned} \chi ^{2D}_{\varvec{mn}}(k_1, \varDelta y) = m_i \chi _{ij}(k_1,\varDelta y) n_i ~~, \end{aligned}$$

(A16)

and if $n_2 = -m_2$ then this reduces to:

$$\begin{aligned} \chi ^{2D}_{\varvec{mn}}(k_1, \varDelta y) = m_1^2 \chi _{11}(k_1,\varDelta y) + m_2^2 \chi _{22}(k_1,\varDelta y) ~~. \end{aligned}$$

(A17)

Now the total cross-spectrum can be evaluated by just adding the 2D and 3D terms:

$$\begin{aligned} \chi _{total}(k_1, \varDelta y) = \chi ^\textrm{2D}(k_1, \varDelta y) + \chi ^\textrm{3D}(k_1, \varDelta y) ~~, \end{aligned}$$

(A18)

where both 2D and 3D terms can be obtained using numerical integration.