1 Introduction

Modelling the stably stratified planetary boundary layer (SBL) is of considerable importance for numerical weather prediction, climate studies, and related applications. Model errors associated with the SBL, a regime characterized by relatively weak turbulence and low mixing intensity, are often substantial (Holtslag et al. 2013), and it is still largely unclear how the trouble can be cured. Many SBL features are poorly understood (see, e.g., Mahrt 2014, for discussion). One particularly challenging issue is the strongly stable boundary layer over a thermally heterogeneous surface. In the present study, we use direct numerical simulation (DNS) to gain insight into the effect of surface thermal heterogeneity on the structure and transport properties in a strongly stable boundary layer.

Mironov and Sullivan (2016, hereafter MS16) used large-eddy simulation (LES) to examine turbulence in the atmospheric SBL over thermally homogeneous and thermally heterogeneous surfaces. The LES data were used to perform a comparative analysis of second-moment budgets and mixing intensity in homogeneous and heterogeneous SBLs. A physically plausible explanation of the enhanced mixing in the heterogeneous SBL was found, and possible ways to parameterize the heterogeneity effects in atmospheric models were discussed. It should be emphasized that the results of MS16 are pertinent to weakly-to-moderately stable boundary layers characterized by continuous and rather vigorous turbulence. The structure and mixing intensity in strongly stable boundary layers characterized by weak and often intermittent turbulence are still largely unknown and need to be investigated. The present study attempts to make a step forward in this direction.

Among the many questions to explore, the following outstanding questions should be addressed: (i) If turbulence dies out over a homogeneous surface due to strong stability, does it survive over a heterogeneous surface? (ii) If turbulence survives, how anisotropic is it and does it generate appreciable vertical fluxes of momentum and scalars? (iii) What are the particular features of the second-moment budgets in a strongly stable regime, and what is the role of pressure-scrambling and third-order transport in maintaining the variance and flux budgets? The present contribution addresses issues (i) and (ii). Analysis of the second-moment budgets is left for future work.

The present study is not aimed at simulating a specific real-world geophysical (e.g., atmospheric or oceanic) flow. Instead, we focus on physical processes at work in strongly stratified boundary-layer flows, namely on the effect of surface thermal heterogeneity on the structure and transport properties of turbulence. To this end, we use an idealized plane Couette flow set-up (a physical analog of our numerical configuration is discussed in the next section). The flow is driven by a fixed velocity of the upper surface, while the lower surface is at rest. The stable density stratification is imposed by a fixed temperature difference between the upper and lower boundaries. The temperature at the horizontal upper and lower surfaces is either homogeneous or varies sinusoidally in the streamwise direction, while the horizontal-mean temperature is the same in all cases. The DNS data are used to compute vertical profiles of mean fields, second-order and (some) third-order statistical moments of turbulence, and to analyze the structure and mixing intensity over thermally homogeneous and thermally heterogeneous surfaces.

Clearly, a real-world atmospheric SBL and an idealized Couette flow differ in many respects (e.g., the surface roughness can play an important role). We tend to think, however, that results from the present analysis with respect to the maintenance of turbulence in heterogeneous strongly stable flows are relevant to the real-world flows, at least qualitatively. The relevance of our DNS findings for atmospheric SBL flows is further discussed in Sect. 5.

The plane Couette flow configuration is often used to study various aspects of neutral, convective, and stably stratified turbulence (see, e.g., Lee and Kim 1991; Komminaho et al. 1996; Papavassiliou and Hanratty 1997; Sullivan et al. 2000; Sullivan and McWilliams 2002; García-Villalba et al. 2011; Pirozzoli et al. 2014; Avsarkisov et al. 2014; Richter and Sullivan 2014; Deusebio et al. 2015; Zhou et al. 2017; Lee and Moser 2018; van Hooijdonk et al. 2018; Alcántara-Ávila et al. 2019; Glazunov et al. 2019; Mortikov et al. 2019, and references therein). To the best of the authors’ knowledge, DNS of Couette flows over thermally heterogeneous surfaces has not been performed so far.

A few words are in order to make clear what is referred to as “turbulence” in the context of the present study. By applying averaging over horizontal planes to compute turbulence statistics (see Sect. 3), we basically assume that turbulence incorporates all fluctuations within the DNS model domain. That is, turbulence encompasses both nearly isotropic and nearly homogeneous small-scale fluctuations and quasi-organized coherent structures that are strongly non-isotropic and non-homogeneous (a discussion of coherent structures encountered in our Couette-flow configuration is given in Sect. 4). Different definitions are used by different research communities, however. Quite often, quasi-organized coherent motions would not be classified as turbulence in the atmospheric science literature. Those motions are referred to as “sub-meso-scale motions” to discriminate them from the classical Kolmogorov-type nearly isotropic and nearly homogeneous turbulence.

From the standpoint of a large-scale or meso-scale atmospheric model, for which the entire DNS domain is a single model grid box, the definition adopted in the present study would mean that turbulence comprises all sub-grid scale (SGS) fluctuations. Statistical moments of SGS fluctuating velocity and scalar fields (fluxes and variances) should be described by a turbulence parameterization scheme. Note, however, that atmospheric models with relatively coarse resolution do not apply a single parameterization scheme that describes the effects of various types of SGS fluctuations in a unified framework. A number of parameterization schemes are applied instead, where each scheme serves to describe the effects of a particular process separately, e.g., the effects of internal gravity waves, cumulus convection (shallow and deep), and turbulence. This artificial separation of processes in numerical models of the atmosphere causes many conceptual and practical problems (see, e.g., Arakawa 2004; Mironov 2009, for discussion). It is desirable to achieve a more coherent description of the various types of SGS fluctuations within a unified parameterization framework. The present-day tendency with high-resolution models is to switch off gravity-wave and cumulus-convection parameterization schemes (at least deep convection scheme), or to make those schemes less active, assuming that at high resolution the SGS motions are more isotropic and homogeneous. Then, the relative importance of turbulence parameterization schemes considerably increases. It should be emphasized, however, that even with the finest resolution attainable today (and likely for many years to come) for numerical weather prediction and climate models the SGS fluctuating velocity and scalar fields remain anisotropic and heterogeneous, and this is especially true for stably stratified boundary layers. It is this type of boundary layers that is the focus of the present study.

The present paper is closely related to the legacy of Sergej Zilitinkevich, who had keen interest in the stably stratified boundary layers throughout his scientific career. Sergej’s contributions to the SBL studies include the now classical SBL depth scale (Zilitinkevich 1972), resistance and heat-transfer laws for stably stratified boundary layers (e.g., Zilitinkevich 1989a, b), and turbulence closure models for stably stratified flows (e.g., Zilitinkevich et al. 2013), to mention a few. Sergej showed particular interest in the problem of maintenance of turbulence in strongly stable boundary-layer flows and the role of coherent quasi-organized motions in setting the SBL mean and turbulent structure. In this regard (and in relation to the present paper), the work of Glazunov et al. (2019) should be mentioned, where DNS of plane Couette flow is used to get insight into the SBL structure.

Now we give an outline of the paper. The flow configuration and governing equations are described in Sect. 2. Details of the simulations performed are given in Sect. 3. Simulation results are discussed in Sect. 4. Conclusions are presented in Sect. 5.

2 Flow Configuration and Governing Equations

We consider a three-dimensional, stably stratified, plane Couette flow. The fluid depth is H, the lower boundary is at rest, and the upper boundary moves with a constant velocity \(U_\textrm{u}\). Stable buoyancy stratification is maintained by a temperature difference \(\varDelta \theta =\theta _\textrm{u}-\theta _\textrm{l}\) between the upper and lower boundaries. The physical characteristics of the fluid are the kinematic molecular viscosity \(\nu \), the molecular temperature conductivity \(\kappa \), and the buoyancy parameter \(\beta _i=-g_i\alpha _\textrm{T}\), where \(g_i\) is the acceleration due to gravity and \(\alpha _\textrm{T}\) is the thermal expansion coefficient. Both \(\nu \) and \(\kappa \) are taken to be constant in our simulations. The Boussinesq approximation is used, and the simplest linear equation of state is utilized, \(\rho =\rho _\textrm{r}\left[ 1-\alpha _\textrm{T}\left( \theta -\theta _\textrm{r}\right) \right] \), where \(\rho \) is the fluid density, \(\rho _\textrm{r}\) is the constant reference density, \(\theta \) is the potential temperature (for the sake of brevity, it will also be referred to as simply “temperature”), and \(\theta _\textrm{r}\) is the constant reference potential temperature. Both \(\alpha _\textrm{T}\) and \(\beta _i\) are constant.

The governing equations given below contain three dimensionless parameters. These are the bulk Reynolds number,

$$\begin{aligned} \hbox {Re} = \frac{U_\textrm{u} H}{\nu } , \end{aligned}$$
(1)

the Prandtl number,

$$\begin{aligned} \hbox {Pr} = \frac{\nu }{\kappa } , \end{aligned}$$
(2)

and the Richardson number,

$$\begin{aligned} \hbox {Ri} = \frac{g_3 H \alpha _\textrm{T}\varDelta \theta }{U_\textrm{u}^2} , \end{aligned}$$
(3)

where \(g_3\) is the magnitude of the gravity vector; in the co-ordinate system used here \(g_i=\left( 0,0,-g_3\right) \).

A real-world flow configuration closely analogous to our numerical configuration can hardly be found in geophysical flows. A conceivable physical analog of our numerical set-up is a laboratory tank (a channel-like apparatus of infinite band type) filled with fresh water at room temperature. Using \(H=0.25\) m, \(U_\textrm{u}=0.04\) m s\(^{-1}\), and \(\nu =10^{-6}\) m\(^2\) s\(^{-1}\) (the value for fresh water at \(20\,^{\circ }\)C), we obtain \(\hbox {Re}=10^{4}\). Using a quadratic fresh-water equation of state (Mironov et al. 2010), \(\rho =\rho _\textrm{r}\left[ 1-\displaystyle \frac{1}{2}a_\textrm{T}\left( \theta -\theta _\textrm{r}\right) ^2\right] \), where \(a_\textrm{T}=1.6509\times 10^{-5}\) K\(^{-2}\) is an empirical coefficient and \(\theta _\textrm{r}=277.13\) K is the temperature of maximum density of fresh water, we find that a temperature difference between the upper and lower horizontal boundaries of about 1 K is needed to obtain \(\hbox {Ri}=0.5\). To arrive at this estimate, we recast the Richardson number in terms of the buoyancy difference between the upper and lower horizontal boundaries, \(\hbox {Ri}=H\varDelta b/U_\textrm{u}^2\), where \(b=g_3\left( \rho _\textrm{r}-\rho \right) /\rho _\textrm{r}\), \(g_3=9.81\) m s\(^{-1}\), \(\theta _\textrm{l}=292.65\) K (\(19.5\,^{\circ }\)C), and \(\theta _\textrm{u}=293.65\) K (\(20.5\,^{\circ }\)C). Note that the Prandtl number is about 7 for fresh water (at \(20\,^{\circ }\)C), which is considerably higher than the value of \(\hbox {Pr}=1\) that we adopt for our numerical fluid.

The flow variables are made dimensionless with the length scale H, velocity scale \(U_\textrm{u}\), time scale \(H/U_\textrm{u}\), and temperature scale \(\varDelta \theta \), and dimensionless temperature \(\hat{\theta }=\left( \theta -\theta _\textrm{l}\right) /\left( \theta _\textrm{u}-\theta _\textrm{l}\right) \) is introduced. The governing equations written in dimensionless form are (in order to simplify the notation, we omit hats over dimensionless variables):

$$\begin{aligned}{} & {} \left( \frac{\partial }{\partial {t}} + {u}_k \displaystyle \frac{\partial }{\partial {x}_k} \right) {u}_i = - \frac{\partial {p}}{\partial {x}_i} + \delta _{i3}\hbox {Ri}{\theta } + \frac{1}{\hbox {Re}}\displaystyle \frac{\partial ^2 {u}_i }{\partial {x}_{k}^2}, \end{aligned}$$
(4)
$$\begin{aligned}{} & {} \quad \displaystyle \frac{\partial {u}_i}{\partial {x}_i} = 0, \end{aligned}$$
(5)
$$\begin{aligned}{} & {} \quad \left( \displaystyle \frac{\partial }{\partial {t}} + {u}_i \displaystyle \frac{\partial }{\partial {x}_i} \right) {\theta } = \frac{1}{\hbox {Pr} \hbox {Re}} \displaystyle \frac{\partial ^2 {\theta }}{\partial {x}_{i}^2}. \end{aligned}$$
(6)

Here, t is time, \({x}_{i}\) are the right-hand Cartesian co-ordinates, \({u}_{i}\) are the velocity components, and p is the kinematic pressure (deviation of pressure from the hydrostatically balanced reference pressure divided by the constant reference density). The Einstein summation convention for repeated indices is adopted. The origin of the co-ordinate system is at the lower boundary, the \({x}_3\) axis is aligned with the gravity vector and is positive upward, and the \({x}_1\) axis is in the direction of \(U_\textrm{u}\). Note that, since the vertical-velocity equation in our simulations is solved for the fluctuation of \({u}_3\) about its horizontal mean, \(\theta _\textrm{r}\) can be set equal to \(\theta _\textrm{l}\) so that the dimensionless reference temperature \(\left( \theta _\textrm{r}-\theta _\textrm{l}\right) /\left( \theta _\textrm{u}-\theta _\textrm{l}\right) \) drops out from the buoyancy term on the right-hand side (r.h.s.) of Eq. 4.

Periodic boundary conditions for \({u}_i\) and \({\theta }\) are applied in both \({x}_1\) and \({x}_2\) horizontal directions. At the horizontal boundaries, the following Dirichlet boundary conditions are used:

$$\begin{aligned} \displaystyle \begin{array}{llll} {u}_1=0, \; \; &{} {u}_2={u}_3=0 \; \; \; \; \; \; &{} {\textrm{at}} &{} \; {x}_3=0 , \\ {u}_1=1, \; \; &{} {u}_2={u}_3=0 \; \; \; \; \; \; &{} {\textrm{at}} &{} \; {x}_3=1 , \end{array} \end{aligned}$$
(7)

and:

$$\begin{aligned} \displaystyle \begin{array}{lll} {\theta } = {\delta \theta }\sin \left[ 2\pi n {x}_1/{L}_1 \right] \; \; \; \; \; \; &{} {\textrm{at}} &{} \; {x}_3=0 , \\ {\theta } = 1 + {\delta \theta }\sin \left[ 2\pi n\left( {x}_1-{U}_\textrm{u} {t}\right) /{L}_1 \right] \; \; \; \; \; \; &{} {\textrm{at}} &{} \; {x}_3=1 , \end{array} \end{aligned}$$
(8)

where \({L}_1\) is the domain size in the \({x}_1\) direction, \({\delta \theta }\) is the (dimensionless) amplitude of the temperature variations at the upper and lower surfaces, and n is the number of cold and warm stripes (the number of surface temperature waves). In the homogeneous case, \({\delta \theta }=0\). In the heterogeneous cases, \({\delta \theta }>0\) but the horizontal-mean surface temperature is the same as in the homogeneous case.

Notice the lower and upper boundary conditions (7) and (8) preserve the flow symmetry of a Couette flow configuration. Along the upper boundary the temperature waves propagate in the \(x_1\) direction with boundary speed \(U_\textrm{u}\) which generates a thermally heterogeneous surface matching its counterpart along the lower wall. The Couette set-up although idealized has desirable features for the present application: the average boundary temperatures are constant in time, and with no mean pressure gradient forcing the average total momentum and temperature fluxes are constant with height. As a result, we are able to acquire stationary statistics by long temporal integration even under strongly stable intermittent flow conditions. Couette flow with constant momentum and temperature fluxes is an approximate analog to the assumed constant flux layer in a high Reynolds number boundary layer flow (e.g., Wyngaard 2010, p. 215).

3 Simulations Performed

The DNS code and its parallelization used in the present study are described in detail in Sullivan et al. (2000), Sullivan and McWilliams (2002), and Sullivan and Patton (2011). A description of the code is not repeated here; readers are referred to the above papers.

One simulation with homogeneous lower and upper surfaces (HOM) and three simulations with heterogeneous surfaces (HET) are performed. In all simulated cases, the fixed values of \(\hbox {Pr}=1\), \(\hbox {Re}=10^{4}\), and \(\hbox {Ri}=0.25\) are used. The number of grid points is (512, 512, 256) in the (streamwise \(x_1\), spanwise \(x_2\), vertical \(x_3\)) directions, respectively. The domain size in the vertical direction is 1, and the domain size in both horizontal directions is 8. The number of cold and warm stripes (the number of surface temperature waves) in the heterogeneous cases is 4. Governing parameters of the simulations performed are summarized in Table 1.

Table 1 Governing parameters of simulated cases
Full size table

In Table 1, \(T_\textrm{t}\) is the total length of the simulation in dimensionless time units, \(T_\textrm{s}\) is the length of the sampling period (at the end of the run), \(\hbox {Re}_{\tau }=u_* \hbox {Re}\) is the wall Reynolds number based on the surface friction velocity \(u_*\), \(\hbox {Ri}_{\tau }=u_*^{-2}\hbox {Ri}=\hbox {Re}_{\tau }^{-2}\hbox {Re}^2\hbox {Ri}\) is the Richardson number based on the surface friction velocity \(u_*\) (e.g., Gandía-Barberá et al. 2021), \(Q_*\) is the surface temperature flux, and 1/L is a bulk stability measure where \(L = -u_*^3/\kappa \hbox {Ri} Q_*\) is the Obukhov length (Obukhov 1954), and \(\kappa =0.4\) is the von Kármán constant. Recall that all variables are made dimensionless with the scales H, \(U_\textrm{u}\), \(H/U_\textrm{u}\), and \(\varDelta \theta \) for length, velocity, time, and temperature, respectively.

The homogeneous simulation starts with a fully developed, stationary, neutral Couette flow. The stable buoyancy stratification is established by gradually (linearly in time) increasing the Richardson number over 100 dimensionless time units from \(\hbox {Ri}=0\) to \(\hbox {Ri}=0.25\). The simulations are then continued until turbulence dies out, and a laminar Couette flow regime is achieved. The value of \(\hbox {Ri}=0.25\) proves to be sufficient to fully quench turbulence in the homogeneous case. Based on the stability measures \(\hbox {Ri}_{\tau }\) and 1/L, all of the simulations in Table 1 are in the very stable regime. As a comparison, Nieuwstadt (2005) finds that turbulence is not sustained when \(1/L > 0.5\) in channel flow: we modified the definition of L in Nieuwstadt (2005) to match the present definition.

The heterogeneous flows start with \(\hbox {Ri}=0\), \(\delta \theta =0\), and a linear velocity profile. In order to assist initial turbulence spin-up, velocity and temperature fluctuations taken from the neutral turbulent Couette flow are added in the lower 1/4 and the upper 1/4 of the computational domain. The Richardson number is increased (linearly in time) from \(\hbox {Ri}=0\) to \(\hbox {Ri}=0.25\) over 10 time units, while the temperature difference \(\delta \theta \) is increased from zero to its value given in Table 1 over 100 time units. The simulations over heterogeneous surfaces are carried forward over many time units until a quasi-stationary flow regime is reached; the flow is considered stationarity when the average momentum and scalar flux profiles are constant with height. The number of time samples differs between the cases, but the sampling period in the heterogeneous cases covers more than 150 time units (see Table 1).

The DNS data are averaged over horizontal planes, and the resulting profiles are then averaged over several thousand time steps. These horizontal and time mean quantities are treated as approximations to the ensemble-mean quantities. In what follows, an overbar denotes a horizontal-mean quantity, a prime denotes a fluctuation about a horizontal mean, and the angle brackets denote quantities averaged over time.

Note that, apart from the results from the homogeneous simulation HOM and three heterogeneous simulations HET025, HET050, and HET075 (which are the major focus of the present study), results from the fully turbulent neutral and convective Couette-flow simulations are also shown for comparison in Figs. 3 and 8. The neutral run (used to initialize the stably stratified homogeneous run HOM) and the convective run (used to initialize the neutral run) are similar to HOM, but the Richardson numbers are \(\hbox {Ri}=0\) and \(\hbox {Ri}=-\,0.2\), respectively, and the length of the sampling period is \(T_\textrm{s}=100\).

4 Results

4.1 Mean Fields

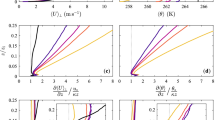
Vertical profiles of the streamwise mean-velocity component \(U=\left<\overline{u}_1\right>\) and mean temperature \(\varTheta =\left<\overline{\theta }\right>\) are shown in Fig. 1. The spanwise mean-velocity component is negligibly small in all simulations and is not shown. In the homogeneous case, the profiles of both U and \(\varTheta \) are linear, corresponding to the laminar solution of the plane Couette problem. Although we provide turbulence a good chance to survive by starting the homogeneous simulation with a vigorously turbulent neutral flow and gradually increase the Richardson number, the buoyancy stratification at \(\hbox {Ri}=0.25\) is strong enough to fully extinguish turbulence.

Fig. 1
figure 1

(Left) streamwise component of mean velocity, and (right) mean temperature from simulations HET025 (blue), HET050 (green), and HET075 (red). Black dotted line shows the laminar solution

Full size image
Fig. 2
figure 2

Vertical profiles of (shear, buoyancy) frequencies \((S^2, N^2)\) denoted by (solid, dotted) lines, respectively (left panel), and gradient Richardson number \(\hbox {Ri}_\textrm{g}\) (right panel) for the heterogeneous simulations HET025 (blue), HET050 (green), and HET075 (red)

Full size image

As seen from Fig. 1, the mean velocity is only slightly affected by the surface thermal heterogeneity, the mean flow gradient in the middle of the domain is only slightly larger than the laminar Couette value, \(\partial U/\partial x_3>1\). The situation is noticeably different for mean temperature. As the amplitude \(\delta \theta \) of the surface temperature variations increases, the flow becomes increasingly mixed with respect to \(\varTheta \) away from the walls. The associated increase of the temperature gradient near the horizontal boundaries is due to the fixed temperature boundary conditions. Note that the effect of temperature heterogeneity on mean temperature is appreciable because of the relatively large values of \(\delta \theta \) in simulations HET050 and HET075. In simulation HET025, \(\delta \theta \) is comparatively smaller, the effect of surface heterogeneity is weak, and the temperature profile is nearly linear. Vertical profiles of the (shear, buoyancy) frequencies \((S^2, N^2)\) and gradient Richardson number \(\hbox {Ri}_\textrm{g}\), shown in Fig. 2, further expose the impact of surface heterogeneity on the mean flow state, especially in the wall region. Here,

$$\begin{aligned} S^2 = \left( \frac{\partial U}{\partial x_3}\right) ^2\ , \; \; \; \; \; \; \; N^2 = g_3\alpha _\textrm{T}\frac{\partial \varTheta }{\partial x_3}\ , \; \; \; \; \; \; \; \hbox {Ri}_\textrm{g} = \frac{N^2}{S^2} \ . \end{aligned}$$
(9)

Inspection of Fig. 2 reveals a surprisingly complex dependence on \(\delta \theta \), not apparent in Fig. 1, especially for the shear frequency. Notice the variation of \(S^2\) at a fixed vertical location near the boundaries below \(x_3 < 0.2\) is not monotonic with increasing \(\delta \theta \), e.g., at \(x_3 = 0.1\) \(S^2 = (1.02, 0.25, 0.51)\) with increasing amplitude of the heterogeneity. At the same height, \(N^2 = (0.25, 0.36, 0.36)\). As a result, the vertical profile of the gradient Richardson number varies in a complex way and simulation HET050 features the largest most stable \(\hbox {Ri}_\textrm{g} \sim 1.4\) at locations \(x_3 = (0.1, 0.9)\) near the walls. The turbulent fluctuations generated near the boundary do impact the mean flow gradients in the middle of the domain, \(\hbox {Ri}_\textrm{g}\) smoothly decreases as the amplitude of the heterogeneity increases.

Figure 3 shows profiles of the streamwise mean-velocity component in wall units \((U^{+}, x_3^+) = (U/u_*, x_3\hbox {Re}_{\tau })\). The flow in the close vicinity of the boundaries is very well resolved in our simulations. The first grid point above the surface is \(x_3^{+}\approx 0.2\). A larger grid spacing may be used in neutral Couette flows, but the resolution cannot be compromised in our simulations because of the need to resolve the large temperature gradients in the near-wall thermal boundary layers. It is these temperature gradients that drive turbulence in the heterogeneous simulations. Test runs with lower resolution in the vertical direction yield results (not shown) that are quantitatively and even qualitatively different from the results of our high-resolution simulations and are not trustworthy. Note the domain size in the horizontal directions cannot be compromised either because of the need to simulate large-scale elongated structures characteristic of plane Couette flows (e.g., Komminaho et al. 1996; Papavassiliou and Hanratty 1997; Pirozzoli et al. 2014; Avsarkisov et al. 2014; Jiménez 2018; Lee and Moser 2018).

Fig. 3
figure 3

Streamwise mean-velocity component plotted in wall units. Solid curves show the profiles from simulations HET025 (blue), HET050 (green), HET075 (red), and from the neutrally stratified Couette flow (black). Black dashed line shows the logarithmic velocity profile, and green dot-dashed line shows the Monin–Obukhov log-linear velocity profile computed with the surface friction velocity and the surface buoyancy flux from the simulation HET050 (see text for details)

Full size image

Black solid and dashed lines in Fig. 3 show, respectively, the streamwise velocity from the neutral Couette-flow simulation and the logarithmic velocity profile:

$$\begin{aligned} U^{+}=\frac{1}{\kappa }\ln \left( x_3^{+}\right) +B_0, \end{aligned}$$
(10)

where \(B_0=5.0\) is a dimensionless constant. The neutral velocity profile closely follows classic log-layer scaling over the height range \(20\le x_3^{+}\le 200\). This is not the case for the flows over thermally heterogeneous surfaces, where the velocity profiles reveal no log-layer scaling. The green dot-dashed curve in Fig. 3 shows the Monin–Obukhov log-linear velocity profile (Obukhov 1954; Monin and Obukhov 1954; Monin and Yaglom 1971):

$$\begin{aligned} U^{+}=\frac{1}{\kappa }\ln \left( x_3^{+}\right) +B_0+ \frac{C_\textrm{u}}{\kappa }\frac{x_3^{+}}{L^{+}}, \end{aligned}$$
(11)

where \(C_\textrm{u}=5\) is a dimensionless constant, and \(L^{+} = LRe_{\tau }\) is the Obukhov length in wall units. The Monin–Obukhov velocity profile in Fig. 3 uses \((u_*, Q_*)\) from simulation HET050 and external parameters (Re, Ri). Inspection of the results in Fig. 3 shows the velocity profile in case HET050 (green solid curve) does not show similarity to (11). This is not surprising however, because the Monin–Obukhov surface-layer flux–profile relationships are only applicable to turbulent layers over homogeneous surfaces. For thermally heterogeneous surfaces, different flux-profile relationships are required.

Fig. 4
figure 4

Turbulence kinetic energy from simulations HET025 (blue), HET050 (green), and HET075 (red)

Full size image
Fig. 5
figure 5

(Left) streamwise velocity variance, and (right) spanwise (dot-dashed curves) and vertical (dashed curves) velocity variances from simulations HET025 (blue), HET050 (green), and HET075 (red)

Full size image

4.2 Second-Order Moments

Vertical profiles of turbulence kinetic energy TKE \(=\frac{1}{2}\left<\overline{u_i'^2}\right>\) are shown in Fig. 4. TKE increases with increasing amplitude of the surface temperature variations. The turbulence level is very low in case HET025, as \(\delta \theta =0.25\) proves to be too small to make the flow vigorously turbulent.

Velocity variances \(uu=\left<\overline{u_1'^2}\right>\) (streamwise), \(vv=\left<\overline{u_2'^2}\right>\) (spanwise), and \(ww=\left<\overline{u_3'^2}\right>\) (vertical) are shown in Fig. 5. In the cases HET050 and HET075, both the spanwise and the vertical velocity variances are considerable; they are roughly a factor of 3 smaller than the streamwise velocity variance. In case HET025, the dominate contribution to the TKE is uu, with only small contributions from vv and ww.

Figure 6 shows the velocity variances in wall units (i.e., \(uu^{+}=uu/u_*^2\), \(vv^{+}=vv/u_*^2\), and \(ww^{+}=ww/u_*^2\) as function of \(x_3^+=x_3\hbox {Re}_{\tau }\)). The streamwise velocity variances do not collapse on the same curve, but the results from simulations HET050 and HET075 (green and red curves in Fig. 6) get somewhat closer to each other if the surface friction velocity is used for normalization. A similar statement can be made about the vertical velocity variances (although with a less confidence), but not about the spanwise velocity variances.

Fig. 6
figure 6

Velocity variances plotted in wall units for the lower part of the model domain. (left) Streamwise velocity variance and (right) spanwise (dot-dashed curves) and vertical (dashed curves) velocity variances from simulations HET025 (blue), HET050 (green), and HET075 (red)

Full size image

In strongly stable flows, Mahrt (2014) finds an abundance of structures with intermittent turbulence mixed with wavelike motions and anisotropic two-dimensional modes. To quantify the turbulence anisotropy in our flows, we use the departure-from-isotropy tensor (see, e.g., Pope 2000):

$$\begin{aligned} b_{ij} = \frac{\left<\overline{u_i'u_j'}\right>}{\left<\overline{u_k'^2}\right>} - \frac{1}{3}\delta _{ij} \, , \end{aligned}$$
(12)

recall that all components of \(b_{ij}\) are zero in isotropic turbulence. In the two-component limit, where velocity fluctuations in one direction (e.g., vertical) are suppressed, the corresponding diagonal component of \(b_{ij}\) is equal to \(-1/3\). As seen from Fig. 7, \(b_{33}\) is negative throughout the flow in simulations HET050 and HET075, indicating that the vertical-velocity fluctuations are strongly damped by buoyancy and the turbulence is mainly confined in a horizontal plane. In simulation HET025, \(b_{33}\) is slightly positive in small regions near the boundaries, but overall turbulence in HET025 is very weak and all three velocity variances and hence the TKE are negligibly small, see Figs. 4 and 5.

Fig. 7
figure 7

The \(b_{33}\) component of the departure-from-isotropy tensor, Eq. 12, from simulations HET025 (blue), HET050 (green), and HET075 (red)

Full size image

An informative diagnostic used to characterize the turbulence anisotropy are the second \(\textrm{II}=b_{ij}b_{ij}\) and third \(\textrm{III}=b_{ij}b_{jk}b_{ik}\) invariants of the departure-from-isotropy tensor (e.g., Lumley and Newman 1977). These invariants are also often defined as: \(\textrm{II}=-\frac{1}{2}b_{ij}b_{ij}\) and \(\textrm{III}=\frac{1}{3}b_{ij}b_{jk}b_{ik}\) (e.g., Lumley 1978; Choi and Lumley 2001). Alternatively, one can use the quantities \(\xi =\left( \frac{1}{6}b_{ij}b_{ij}\right) ^{1/2}\) and \(\eta =\left( \frac{1}{6}b_{ij}b_{jk}b_{ik}\right) ^{1/3}\). An anisotropy map in the \(\xi -\eta \) plane is known as the Lumley triangle (Pope 2000), although one side is not straight. Figure 8 shows results from five Couette-flow simulations in the \(\xi -\eta \) plane, where each circle corresponds to one vertical grid level. Results from the fully turbulent neutral and convective simulations are shown for comparison with the three heterogeneous cases. The non-monotonic variation of the orange circles illustrates the complex structural evolution of convective turbulence with increasing distance from the boundary. Convective turbulence features several anisotropic states: ranging from a nearly two-component (2C) state close to the walls where horizontal velocity fluctuations dominate to an axisymmetric state with a tendency towards a one-component (1C) limit in regions away from the walls where the vertical velocity fluctuations are dominant. The black open circles form a pattern characteristic of a neutral wall-bounded flow (cf. Fig. 11.1 in Pope 2000, showing DNS of channel flow). Blue circles indicate that turbulence in the heterogeneous case HET025 is either in a 1C or 2C state. The two-component state in HET025 is of little interest as the regions of the flow with 2C turbulence have negligibly small TKE. The turbulence in HET050 and HET075 is in a 2C state near the walls but smoothly transitions into an axisymmetric state similar to the neutral case above the boundary. Notice, in all three heterogeneous cases near the mid-plane \(x_3 = 1/2\) 3D turbulence is nearly quenched and the residual motions are 1C \(u_1'\) sloshing motions.

Fig. 8
figure 8

(Left) the Lumley triangle on the \(\xi -\eta \) plane, and (right) a blow-up of the area close to the upper right triangle vertex corresponding to the one-component limit. Circles show data from simulations HET025 (blue), HET050 (green), HET075 (red), and from the convective (orange) and neutrally stratified (black) Couette flows

Full size image

As expected, the temperature variance \(\theta \theta =\left<\overline{\theta '^2}\right>\) increases with increasing amplitude of the surface temperature variations \(\delta \theta \), see Fig. 9. It is significant that the large values of \(\theta \theta \) are confined to the immediate vicinity of the lower and upper boundaries, while the temperature variance is small in the bulk of the flow interior \(0.1\le x_3\le 0.9\).

Fig. 9
figure 9

(Left) temperature variance from simulations HET025 (blue), HET050 (green), and HET075 (red). (right) The same as in the left panel but for the lower part of the domain

Full size image

Vertical profiles of the streamwise momentum-flux component (denoted wu) and vertical temperature flux (denoted \(w\theta \)) are shown in Figs. 10 and 11, respectively. The spanwise momentum-flux component (not shown) is negligibly small in all simulations. In the steady state, the total fluxes, i.e., the sum of turbulent and molecular fluxes, are depth constant. That is,

$$\begin{aligned} \displaystyle \left<\overline{u_3'u_1'}\right> - \frac{1}{\hbox {Re}} \frac{\partial \left<\overline{u_1}\right>}{\partial x_3} = \hbox {const}, \end{aligned}$$
(13)

and:

$$\begin{aligned} \left<\overline{u_3'\theta '}\right> - \frac{1}{\hbox {PrRe}} \frac{\partial \left<\overline{\theta }\right>}{\partial x_3} = \hbox {const}. \end{aligned}$$
(14)

In the laminar Couette flow, the contributions to wu and \(w\theta \) are solely due to molecular diffusion with total fluxes equal to \(\hbox {Re}^{-1}\) and \(\left( {\hbox {Pr}} {\hbox {Re}}\right) ^{-1}\), respectively.

Fig. 10
figure 10

Streamwise momentum-flux component from simulations HET025 (blue), HET050 (green), and HET075 (red). Solid curves show total (turbulent plus molecular) flux, and dot-dashed and dashed curves show contributions due to turbulence and due to molecular diffusion, respectively

Full size image
Fig. 11
figure 11

(Left) vertical component of the temperature flux from simulations HET025 (blue), HET050 (green), and HET075 (red). Solid curves show total (turbulent plus molecular) flux, and dot-dashed and dashed curves show contributions due to turbulence and due to molecular diffusion, respectively. (right) The same as in the left panel but for the lower part of the domain

Full size image

As seen from Fig. 10, the magnitude of the total streamwise momentum-flux component increases with the increasing amplitude of the surface temperature variations. In the simulation HET025, the turbulent momentum flux is very small and the total flux is virtually the same as in the laminar flow. In the simulations HET050 and HET075, both the turbulent and molecular fluxes are negative, contributing to downward momentum transport, only small positive values of \(\left<\overline{u_3'u_1'}\right>\) can be identified in case HET050.

The total vertical temperature flux, see Fig. 11, decreases with the increasing amplitude of the surface temperature variations. This is counter to the total streamwise momentum-flux component. The total temperature flux in simulation HET025 is very close to that in laminar flow. However, the turbulent temperature flux \(\left<\overline{u_3'\theta '}\right>\) is not entirely negligible. A remarkable feature of the heterogeneous simulations is the sign of the vertical turbulent temperature flux. Although the flow is stably stratified in the mean and the total (molecular plus turbulent) vertical temperature flux is negative, the turbulent heat flux proves to be positive. Turbulent motions generated by the surface thermal heterogeneity transfer heat up the gradient of the mean temperature. It somewhat resembles convective boundary-layer flows, where quasi-organized cell-like structures induce counter-gradient heat transport.

4.3 Vertical-Velocity and Temperature Skewness and Flow Structure

Figure 12 presents vertical profiles of vertical-velocity and temperature skewness:

$$\begin{aligned} S_w \ = \ \frac{\langle \overline{u_3'^3}\rangle }{\langle \overline{u_3'^2}\rangle ^{3/2}} ~~~\textrm{and} ~~~ S_{\theta } \ = \ \frac{\langle \overline{\theta '^3}\rangle }{\langle \overline{\theta '^2}\rangle ^{3/2}} \, . \end{aligned}$$
(15)

As seen from the plots, in all three heterogeneous simulations \((S_w, S_{\theta }) > 0\) near the lower boundary, and by symmetry about the mid-plane \(x_3=1/2\), \((S_w, S_{\theta }) < 0\) near the upper boundary. \(S_w > 0\) indicates that positive (upward) vertical velocity has a lower fractional area coverage (more localized) than negative (downward) vertical velocity. Likewise, \(S_{\theta } > 0\) indicates a stronger localization of positive temperature fluctuations (about the horizontal-mean temperature) as compared to negative temperature fluctuations.

Fig. 12
figure 12

(Left) vertical-velocity skewness and (right) temperature skewness from simulations HET025 (blue), HET050 (green), and HET075 (red)

Full size image

The statistics from our stably stratified Couette flow with surface thermal heterogeneity are broadly similar to a dry convective boundary layer (CBL) driven by surface potential-temperature (buoyancy) flux (e.g., Lenschow et al. 2012) or Rayleigh–Bénard convection between plates of fixed temperature (e.g., Moeng and Rotunno 1990). Both \(S_w\) and \(S_{\theta }\) are positive in the major part of the CBL, where highly localized positive potential-temperature anomalies are collocated with positive vertical velocity, forming familiar convective plume structures which account for most of the upward potential-temperature flux.

Flow visualization of the \((u_3, \theta )\) fields in our heterogeneous simulations reveals strongly localized quasi-coherent flow structures characterized by large positive fluctuations in vertical velocity and temperature. As a result, these structures generate positive turbulent temperature flux in the lower part of the flow (Fig. 11), i.e., precisely where both \(S_w\) and \(S_{\theta }\) are positive (Fig. 12). In the upper part of the flow, large negative vertical velocity with \(S_w < 0\) is collocated with large negative potential-temperature fluctuation \(S_{\theta } < 0\), leading to a positive turbulent temperature flux.

The instantaneous snapshots in Figs. 13 and 14 reveal spatially intermittent turbulent flow structures in the wall region. Figure 13 shows fluctuations of vertical velocity, \(u_3'\), and of potential temperature, \(\theta '\), in an \(x_1-x_2\) plane just above the lower surface for simulation HET050; for reference, the streamwise variation of the surface temperature \(\theta _{sfc} = \theta (x_3 =0)\) given by (8) is also shown in the figures. The most vigorous positive and negative vertical velocity fluctuations are concentrated at the same streamwise locations \(x_1 \approx (0.9, 2.9)\) with quiescent nearly laminar motions at intermediate locations \(x_1 \approx (2,4)\). Thus, the vigorous fluctuations in \(u_3'\) occur at a streamwise location roughly 70 degrees forward of the peak surface temperature but behind the location of maximum \(-\,\partial \theta _{sfc}/\partial x_1\) at \(x_1 = (1,3)\). Visualization also shows positive fluctuations in streamwise velocity \(u_1'\) positioned farther downstream than the peak in \(\theta '\). Apparently horizontal advection in the wall region transports high amplitude turbulence forward of the location of the peak surface temperature variation, similar to weakly stratified heterogeneous flows, e.g., Stoll and Porté-Agel (2009) and MS16, and the temperature field responds more rapidly to the surface boundary conditions than streamwise velocity. It is important to mention that the spatially intermittent flow structures in our very stable heterogeneous simulations are noticeably different from the tilted temperature fronts found in weakly stable boundary layers and stratified Couette flows with continuous turbulence (e.g., García-Villalba et al. 2011; Chung and Matheou 2012; Sullivan et al. 2016; Glazunov et al. 2019).

Fig. 13
figure 13

Horizontal cross sections of the fluctuations of vertical velocity (left panel) and potential temperature (right panel) about their horizontal mean values for simulation HET050. The cross sections are taken at \(x_3=0.076\) (\(x_3^+=8.19\)) above the lower surface near the end of the sampling period; to highlight details only 1/4 of numerical domain is shown. Red (blue) colors correspond to positive (negative) values of \(u_3'\) (\(\times 10^2\)) and \(\theta '\) as shown in the color scale bars. For reference the spatial variation of the imposed surface temperature \(\theta _{sfc}\) is shown in the bottom panel of each figure

Full size image
Fig. 14
figure 14

Horizontal cross section of the vertical temperature flux for simulations HET050 (a) and HET075 (b). The cross section is taken at \(x_3=0.076\) (\(x^{+}_{3}=8.19\) in HET050, and \(x^{+}_{3}=8.52\) in HET075) above the lower surface near the end of the sampling period. Red (blue) colors correspond to positive (negative) values of the temperature flux (\(\times 10^3\)) as shown in the color scale bar. Note the range of the color bar is different between (a) and (b). For reference the spatial variation of the imposed surface temperature \(\theta _{sfc}\) is shown in the bottom panel of each figure

Full size image

Coherent patterns of strong positive \(u_3'\) nearly collocated with the patterns of strong positive \(\theta '\) are readily identified, and their spatial correlation results in positive (upward) turbulent temperature flux over a considerable part of the flow as shown in Fig. 14. Although positive values of \(u_3'\theta '\) cover a smaller fractional area (more localized) than negative values of \(u_3'\theta '\), their amplitude is large. The peak positive values of \(u_3'\theta '\) are roughly four times larger in magnitude compared to their peak negative counterparts; the fluctuations \(u_3'\theta '\) are an order of magnitude larger than their horizontal average \(\overline{u_3'\theta '}\) and the horizontal-mean turbulent temperature flux is positive (upward). Importantly, the flow remains stably stratified in a global (horizontal mean) sense, and the total, i.e., turbulent plus molecular, temperature flux remains negative (downward). The flow visualization supports the explanation of positive turbulent temperature flux suggested by the vertical-velocity and temperature skewness. The visualization in panel b) of Fig. 14 shows vertical turbulent temperature flux for simulation HET075. Although the pattern of \(u_3'\theta '\) differs in detail between simulations HET050 and HET075, e.g., in terms of distance between the “arrow-shaped” regions of strong positive \(u_3'\theta '\) and an increased amplitude in HET075, the overall picture of temperature flux remains the same between the two simulations.

4.4 Flux of Temperature Variance

Using LES, MS16 performed a comparative analysis of the second-moment budgets and mixing intensity in weakly (moderately) stable boundary layers over thermally homogeneous and thermally heterogeneous surfaces. Among other things, the study revealed a key role of the temperature variance in turbulent mixing in a horizontally heterogeneous SBL and the importance of the third-order turbulent transport term in maintaining the temperature-variance budget. Due to the surface heterogeneity, the third-order moment, i.e., the vertical flux of temperature variance (denoted by \(w\theta \theta \)), is nonzero at the surface. As a result, the turbulent transport term (divergence of the temperature-variance flux) not only redistributes the temperature variance in the vertical, but is a net gain.

The following expression is used to estimate the vertical flux of temperature variance on the basis of LES data:

$$\begin{aligned} w\theta \theta = \left<{\overline{\tilde{u}_3'\tilde{\theta }'^2}}\right> + \left<\overline{\tilde{u}_3'\widetilde{\theta ^{s2}}'}\right> + 2\left<\overline{\tilde{\theta }'\widetilde{u_3^s\theta ^s}'}\right> + \left<\overline{\widetilde{u_3^s\theta ^{s2}}}\right> , \end{aligned}$$
(16)

where a tilde denotes a resolved-scale (filtered) quantity, and the superscript “s” denotes a sub-grid (sub-filter) scale fluctuation. As in the previous sections, an overbar denotes a horizontal-mean quantity, a prime denotes a fluctuation about a horizontal mean, and angle brackets denote quantities averaged over time. The first two terms on the r.h.s. of Eq. 16 are zero at the surface because \(\tilde{u}_3 = 0\). The last term cannot be estimated from LES but is presumably small (see MS16 and Machulskaya and Mironov 2018, for discussion). The third term is zero in the homogeneous SBL because \(\tilde{\theta }' = 0\) at the surface. In the heterogeneous SBL, surface temperature variations modify local stability conditions and thus modulate the surface temperature flux. The surface temperature \(\tilde{\theta }\) and the surface temperature flux \(\widetilde{u_3^s\theta ^s}\) prove to be positively correlated, leading to a positive flux of temperature variance at the surface.

Within the DNS framework, the expression for the vertical flux of temperature variance reads:

$$\begin{aligned} w\theta \theta = \left<{\overline{u_{3}'\theta '^{2}}}\right> - \frac{1}{\hbox {Pr} \hbox {Re}} \frac{\partial \left<{\overline{\theta '^{2}}}\right>}{\partial x_{3}} . \end{aligned}$$
(17)

It is instructive to establish the correspondence between the LES and DNS estimates of the temperature-variance flux.

The first two terms on the r.h.s. of Eq. 16 describe the transport of resolved (first term) and sub-grid (second term) temperature variance by the resolved vertical velocity \(\tilde{u}_3\). The sum of these terms is in one-to-one correspondence with the first term on the r.h.s. of Eq. 17 that describes the transport of temperature variance by the vertical velocity (there are no sub-grid scale quantities in DNS, hence there is only “total” velocity and “total” temperature variance).

There is no one-to-one matching of the third and the fourth terms on the r.h.s. of Eq. 16 with the second term on the r.h.s. of Eq. 17. It can be readily seen, however, that under certain conditions the LES and DNS terms are closely analogous. If the resolution is sufficiently high, most energy-containing scales of motion are simulated explicitly by LES with nearly isotropic sub-grid scale turbulence. Then, the sub-grid scale temperature flux is of diffusive and down-gradient character, that is, \(\widetilde{u_i^s\theta ^s}=-\tilde{\kappa }_{s}\partial \tilde{\theta }/\partial x_i\), where \(\tilde{\kappa }_{s}\) is the sub-grid scale temperature diffusivity. The third term on the r.h.s. of Eq. 16 becomes:

$$\begin{aligned} 2\left<\overline{\tilde{\theta }'\widetilde{u_3^s\theta ^s}'}\right> = - \left<\overline{\tilde{\kappa }}_{s}\frac{\partial \overline{\tilde{\theta }'^2}}{\partial x_3}\right> - \left<\overline{\tilde{\kappa }_{s}'\frac{\partial \tilde{\theta }'^2}{\partial x_3}}\right> - \left<\overline{\tilde{\kappa }_{s}'\tilde{\theta }'} \frac{\partial \overline{\tilde{\theta }}}{\partial x_3}\right> . \end{aligned}$$
(18)

Applying a diffusive down-gradient approximation to the fourth term on the r.h.s. of Eq. 16, we obtain:

$$\begin{aligned} \left<\overline{\widetilde{u_3^s\theta ^{s2}}}\right> = - \left<\overline{\tilde{\kappa }}_{s}\frac{\partial \overline{\widetilde{\theta ^{s2}}}}{\partial x_3}\right> - \left<\overline{\tilde{\kappa }_{s}'\frac{\partial \widetilde{\theta ^{s2}}'}{\partial x_3}}\right> . \end{aligned}$$
(19)

If the temperature diffusivity \(\tilde{\kappa }_\textrm{s}\) does not change considerably in space (\(\tilde{\kappa }_\textrm{s}'\) is small) the second and the third terms on the r.h.s. of Eq. 18 and the second term on the r.h.s. of Eq. 19 can be neglected. If changes of \(\tilde{\kappa }_\textrm{s}\) in time can also be neglected (\(\overline{\tilde{\kappa }}_\textrm{s}-\left<\overline{\tilde{\kappa }}_\textrm{s}\right>\) is small), then Eqs. 16, 18 and 19 yield the following expression for the LES-based vertical temperature-variance flux:

$$\begin{aligned} w\theta \theta = \left<{\overline{\tilde{u}_3'\left( \tilde{\theta }'^2+\widetilde{\theta ^{s2}}'\right) }}\right> - \frac{1}{{{\hbox {Pr}}_\textrm{s}} {{\hbox {Re}}_\textrm{s}}}\frac{\partial \left< \overline{\tilde{\theta }'^2}+\overline{\widetilde{\theta ^{s2}}}\right>}{\partial x_{3}} . \end{aligned}$$
(20)

Here, \(\hbox {Pr}_\textrm{s}\) and \(\hbox {Re}_\textrm{s}\) are the Prandtl number and the Reynolds number, respectively, defined in terms of (constant) sub-grid scale viscosity and (constant) sub-grid scale temperature diffusivity. Thus, the estimates of the vertical temperature-variance flux based on DNS, Eq. 17, and on LES, Eq. 20, coincide up to definitions of the temperature variance and of the Prandtl and Reynolds numbers.

Fig. 15
figure 15

(Left) third-order vertical velocity-temperature covariance (vertical flux of the temperature variance) from simulations HET025 (blue), HET050 (green), and HET075 (red). Solid curves show total (turbulent plus molecular) covariance, and dot-dashed and dashed curves show contributions due to turbulence and due to molecular diffusion, respectively. (right) The same as in the left panel but for the lower part of the domain for simulations HET050 (green) and HET075 (red)

Full size image

Vertical profiles of \(w\theta \theta \) from our heterogeneous DNS runs are shown in Fig. 15. Both the turbulent and molecular contributions to \(w\theta \theta \) given by the first and second terms on the r.h.s. of Eq. 17, respectively, are positive close to the lower boundary; by symmetry, these contributions are negative close to the upper boundary. Importantly, the molecular temperature-variance flux is nonzero at the surface. Hence, the third-order transport term not only redistributes the temperature variance in the vertical, but is a net gain. The situation is broadly similar to that in weakly (moderately) stable flows, where the surface thermal heterogeneity produces \(w\theta \theta \) that serves to increase the temperature variance in the boundary layer.

5 Conclusions

Direct numerical simulations at bulk Reynolds number \(\hbox {Re}=10^{4}\) and bulk Richardson number \(\hbox {Ri}=0.25\) are performed to analyze the structure and mixing intensity in strongly stable boundary-layer flows over thermally homogeneous and heterogeneous surfaces. An idealized plane Couette flow set-up is used as a proxy for real-world flows. The flow is driven by a fixed velocity at the upper surface, while the lower surface is at rest. The temperature at the horizontal upper and lower surfaces is either homogeneous or varies sinusoidally in the streamwise direction, while the horizontal-mean temperature is the same in the homogeneous and heterogeneous cases.

The stratification is strong enough to quench turbulence over homogeneous surfaces, resulting in linear velocity and temperature profiles. However, turbulence survives over heterogeneous surfaces. Both the molecular diffusion and the turbulence contribute to the downward, i.e., the down-gradient, transfer of horizontal momentum. The total (diffusive plus turbulent) heat flux is directed downward. However, the turbulent contribution to the heat flux appears to be positive, i.e., up the gradient of the mean temperature. An analysis of the second-order velocity and temperature covariances and of the vertical-velocity and temperature skewness suggests that the counter-gradient heat transport is due to quasi-organized cell-like vortex motions generated by the surface thermal heterogeneity. These motions act to transfer heat upwards similar to quasi-organized cell-like structures that transfer heat upwards in convective boundary layers. This finding is corroborated by visualization of the velocity and temperature fields. Thus, the flow over heterogeneous surface features local convective instabilities and upward eddy heat transport, although the overall stratification remains stable and the heat is transported downward in the mean.

Due to the surface thermal heterogeneity, the vertical flux of temperature variance is nonzero at the surface. As a result, the transport term (divergence of the temperature-variance flux) in the temperature-variance budget not only redistributes the temperature variance in the vertical, but is a net gain. The same effect is encountered in weakly (moderately) stable flows over thermally heterogeneous surfaces, where the third-order transport terms serves to increase the temperature variance in the boundary layer.

A few words are in order concerning the relevance of our DNS findings to the real-world atmospheric flows. For instance, the temperature contrast between the warm and cold stripes in our simulations may look unrealistically high at first glance. The following simple example demonstrates, however, that the governing parameters of our idealized flow configurations may be quite similar to the governing parameters of the real-world atmospheric SBL flows. Take the following values that are fairly typical of an atmospheric stably stratified boundary layer during calm clear nights: the SBL depth is 70 m, the wind speed at the SBL top is 4 m s\(^{-1}\), and the temperature difference across the SBL (from top to bottom) is 2 K. With the gravitational acceleration of 9.81 m s\(^{-2}\) and the reference temperature of 280 K, we obtain \(\hbox {Ri}=0.31\), which is close to \(\hbox {Ri}=0.25\) in our simulations. With a 2 K temperature difference across the SBL, a 4 K difference between warm and cold stripes is needed to obtain the flow configuration very similar to that of our simulation HET050. Such a surface temperature difference is clearly possible; furthermore, even larger temperature differences at real-world surfaces are quite likely. In order to make a more definitive quantitative statement, data from targeted field measurements are required. Rough estimates may be obtained using crowdsourced data.

A subject of our future work is a comprehensive analysis of the second-moment budgets, where the emphasis is on the turbulence anisotropy and the role of pressure-scrambling effects in maintaining the budgets. It should also be examined whether major conclusions from the present analysis remain valid at higher values of the Reynolds number and for other flow configurations, e.g., for pressure-gradient driven channel flows over homogeneous and heterogeneous surfaces. Further open issues are the effects of the surface roughness, of the surface heterogeneity orientation (e.g., temperature-wave crests normal vs. parallel to the mean flow), and of the size and form of the surface patches on the flow structure and mixing intensity. Finally, efforts should be made to use the DNS findings to improve parameterizations of strongly stable boundary layers in large-scale atmospheric models.