Interaction Between Waves and Turbulence Within the Nocturnal Boundary Layer

Abstract

The presence of waves is proven to be ubiquitous within nocturnal stable boundary layers over complex terrain, where turbulence is in a continuous, although weak, state of activity. The typical approach based on Reynolds decomposition is unable to disaggregate waves from turbulence contributions, thus hiding any information about the production/destruction of turbulence energy injected/subtracted by the wave motion. We adopt a triple-decomposition approach to disaggregate the mean, wave, and turbulence contributions within near-surface boundary-layer flows, with the aim of unveiling the role of wave motion as a source and/or sink of turbulence kinetic and potential energies in the respective explicit budgets. By exploring the balance between buoyancy (driving waves) and shear (driving turbulence), a simple interpretation paradigm is introduced to distinguish two layers, namely the near-ground and far-ground sublayer, estimating where the turbulence kinetic energy can significantly feed or be fed by the wave. To prove this paradigm, a nocturnal valley flow is used as a case study to detail the role of wave motions on the kinetic and potential energy budgets within the two sublayers. From this dataset, the explicit kinetic and potential energy budgets are calculated, relying on a variance–covariance analysis to further comprehend the balance of energy production/destruction in each sublayer. With this investigation, we propose a simple interpretation scheme to capture and interpret the extent of the complex interaction between waves and turbulence in nocturnal stable boundary layers.

1 Introduction

Nocturnal boundary layers are typically characterized by a stable thermal stratification and by terrain-following flows. The typical shape of the flow streamlines depends on the terrain complexity, i.e., the collection of heterogeneity responsible for the irregularity with respect to flow over flat terrain. Different atmospheric phenomena can be referred to as typical for a stable boundary layer (SBL) regardless of the terrain homogeneity. Among others, it is common to observe non-turbulent submesoscale motions. The submesoscale motions are a class of atmospheric phenomena whose spectral scale range between the micro-$\alpha$ scale (order of hundred metres) and the meso-$\gamma$ scale (order of few thousand metres) of the Orlanski (1975) classification (Mahrt 2009). These motions can display various structures such as steps, ramps, pulses, waves, or complex patterns that cannot be approximated by a single shape (Mahrt 2010; Belušić and Mahrt 2012; Kang et al. 2014). Of particular interest, the wave-like submesoscale motions are ubiquitous in the SBL. Following the classification proposed by Sun et al. (2015b), the wave activity within the SBL can be summarized into two categories according to the restoring force: the vorticity waves (driven by transverse vorticity), and the buoyancy waves (governed by buoyant forces). Vorticity waves are typically associated with Kelvin–Helmholtz instability, shear instability, and inflection points in the wind profile, and their growth is governed by their own instability. Buoyancy waves are driven by vertical displacement of the flow streamlines triggered by the flow interaction with either a physical obstacle (such as topography or a roughness element) or disturbed density interfaces caused by cold pools, density currents, turbulent patches, or convective systems.

In addition to non-turbulent motions, the atmospheric flows over complex terrain are known to be in a weak but continuous state of turbulence due to the breakdown of critical internal waves. This process is less effective over flat terrain, where turbulence remains highly intermittent and patchy (Fernando 2010). The coexistence of turbulence and submesoscale motions in the SBL has been inferred from the bimodal shape of the power spectra of the velocity and temperature variances (Vickers and Mahrt 2006; Hiscox et al. 2010; Liang et al. 2014; Stiperski et al. 2019). In the presence of turbulence and submesoscale motions, the power spectra are typically subdivided into two ranges of frequencies by a spectral gap ranging between 60 s and 450 s depending on the atmospheric stability, the geographical location, and the terrain complexity. Considering an SBL, characteristic spectral-gap times close to 60 s were found over vegetated canopies (Campos et al. 2009) and complex terrains (Stiperski et al. 2019), while reaching 450 s under intense shear over arid deserts (Liang et al. 2014). An estimation of the spectral-gap scale can be obtained from the inverse of the Ozmidov scale, which is physically interpreted as the size of the largest eddy unaffected by buoyancy (Mater et al. 2013); as such, it can be used to separate the buoyancy subrange from the inertial subrange, and thus the submesoscale motions from the turbulence contributions. A more direct method involves the estimation of a cut-off frequency on the observed spectra, as directly evaluated from measurements.

The interaction between buoyancy and inertial subranges is the key to understand how submesoscale motions drive turbulence and how turbulence influences the evolution of the submesoscale motions (Staquet and Sommeria 2002). Laboratory experiments (Dohan and Sutherland 2003) and numerical investigations (Renfrew 2004; Largeron et al. 2013) have detected the formation of submesoscale waves in katabatic flows caused by turbulent jets breaking into it. Sun et al. (2012), and more recently Cava et al. (2015, 2019), observed a degradation of buoyancy waves close to the terrain caused by turbulence mixing due to shear. Conversely, it is undeniable that submesoscale motions can cause sufficient shear for generating local turbulence patches (Baklanov et al. 2011; Mahrt et al. 2012). The vorticity waves can trigger intermittent turbulence driving turbulent events embedded in each transverse vorticity roll (Sun et al. 2015b). The buoyancy waves can generate intermittent turbulence in time and space after their breakdown (Einaudi et al. 1978; Sun et al. 2015a) and by periodically reducing the near-surface Richardson number of very stable flows below its critical value (Finnigan 1999).

Despite the discussion of the relationship between turbulence and waves in the literature, open questions still remain regarding the nature of their interaction and the consequences on flow structure, energy distribution, and mutual exchange. Although the research of an overall mechanism explaining the turbulence–wave interaction is a fascinating topic, we can ask ourselves how is the turbulence–wave interaction involved in the energy cascade? How are the energy budgets modified as a consequence of this interaction? Few studies (e.g., Finnigan and Einaudi 1981; Finnigan et al. 1984) have delved into the topic by adopting a triple-decomposition approach (originally developed by Reynolds and Hussain 1972). Different from the Reynolds decomposition, this approach enables separation of a periodic motion from the small-scale turbulence and evaluation of their interaction. However, the triple-decomposition approach envisages the existence of a single reference oscillator with constant amplitude and frequency; as such, it provides limited application to field experiments, even accounting for more recent improvements (e.g., Finnigan 1988). Nevertheless, this approach still provides a useful conceptual framework of the complex wave–turbulence interaction, thus proving a valid support for its interpretation.

In this paper, we adopt a practical approach based on different averaging time intervals to disaggregate and evaluate the low-frequency wave activity and high-frequency turbulence within a nocturnal SBL flow, proposing an interpretation scheme to capture the extents of the wave–turbulence interaction. The case study is provided by real-world measurements of a valley flow collected at Dugway Proving Ground (north-western Utah) during the Mountain Terrain Atmospheric Modeling and Observations (MATERHORN) Program (Fernando et al. 2015).

Below, Sect. 2 describes the theoretical framework adopted to compute the energy budgets in the presence of waves. Section 3 describes the measurement site, the equipment, the data processing, and the methods used to evaluate the wave activity and turbulence contributions. Section 4 is devoted to the discussion of the potency of the wave contributions in the near-surface budgets. Finally, Sect. 5 draws the conclusions.

2 Energy Budgets in the Presence of Waves

2.1 The Theoretical Frame of the Triple Decomposition

The typical approach for dealing with atmospheric turbulence prescribes the Reynolds decomposition to separate the contribution of turbulence from the mean flow. As known, this decomposition states that a state variable A characterizing a flow in the atmospheric boundary layer can be split into an average value and a fluctuation whose mean is zero. The average value is associated with the mean flow, while the fluctuation accounts for the turbulence, representing all temporal and spatial scales in ranges dependent on the averaging interval. The Reynolds decomposition involves the whole active part of the spectra, and thus it is unable to disaggregate wave from turbulence contributions. In other words, wave motions and turbulence can evolve on different characteristic times that a double decomposition is unable to discern. The use of a triple decomposition would allow the elucidation of the effects of a specific periodic motion and that of turbulence in the budget equations. Specifically, Reynolds and Hussain (1972), Finnigan and Einaudi (1981), and Finnigan et al. (1984) propose and use a triple decomposition to be applied to the velocity, temperature, and pressure fields in order to disaggregate a specific periodic motion from turbulence. The characterization of the state variables uses two different averages: a time average identified by brackets $\langle$ $\rangle$ and a phase average (i.e., the average over a large ensemble of points having the same phase with respect to a reference oscillator) identified by the overline symbol $^{-}$. Therefore, in the presence of a wave, the state variable A becomes $A=\langle A\rangle +{\tilde{a}}+a'$; as a consequence, the fluctuation is $a={\tilde{a}}+a'$ where $a'$ refers to the small-scale turbulence and ${\tilde{a}}$ to the wave. To characterize these new contributions, Reynolds and Hussain (1972) used the phase average to obtain a second average contribution that reads ${\overline{a}}=\langle A\rangle +{\tilde{a}}$. As the fluctuation includes only wave and small-scale turbulence, the phase average rejects this last contribution representing the organized motions from the observation. As defined for the Reynolds decomposition, the triple-decomposed quantities undergo different basic properties, as described by Reynolds and Hussain (1972) and Finnigan et al. (1984). Defining $B=\langle B\rangle +{\tilde{b}}+b'$, the triple-decomposition properties read:

$$\begin{aligned} \begin{array}{lll} i.\,\overline{a'}=0,\qquad &{}ii.\,\langle {\tilde{a}}\rangle =0,\qquad &{}iii.\,\langle a'\rangle =0,\qquad \\ iv.\,\langle \langle A\rangle B\rangle =\langle A\rangle \langle B\rangle ,\qquad &{}v.\,\overline{{\tilde{a}}B}={\tilde{a}}{\overline{B}},\qquad &{}vi.\,\overline{\langle A\rangle B}=\langle A\rangle {\overline{B}},\qquad \\ vii.\,\overline{\langle A\rangle }=\langle A\rangle ,\qquad &{}viii.\,\langle {\overline{A}}\rangle =\langle A\rangle ,\qquad &{}ix.\,\langle {\tilde{a}}b'\rangle =\overline{\langle {\tilde{a}}b'\rangle }=0. \end{array} \end{aligned}$$

Conditions i. and iii. state the complete random nature of the small-scale turbulence, while the wave part has just a zero time average (condition ii.) to maintain as null the time-averaged fluctuation. Conditions iv. to viii. state the invariance of the mean-flow contribution to time and phase averages, as well as for the wave part to the sole phase average. The last condition (ix.) asserts the statistical independence of the wave from the small-scale turbulence (Reynolds and Hussain 1972).

2.2 The Practical Frame of the Double Time Average

The formal theory of the Reynolds decomposition suggests the use of ensemble averages to separate the fluctuations from the mean. Practical application to field measurements often uses a time average due to the limitation of the instrumental apparati, choosing an averaging time interval long enough to include all the possible realizations. For the current investigation, we adopt this last formulation using different averaging time intervals in order to disaggregate the fluctuations and filter the wave from the small-scale turbulence. Using a single averaging interval prevents the separation between wave and small-scale turbulence because conventional averaging times (as 5 or 30 min) include the contribution of the waves (Smedman 1988).

The identification of the averaging intervals is described as follows. We use a conventional 30-min average to define the quantities related to the mean flow $\langle A\rangle$. As suggested by Smedman (1988), the fluctuation resulting from $a=A-\langle A\rangle$ (as resulting from a Reynolds decomposition) are indeed the sum of wave and turbulence contributions. To filter the wave, a second averaging interval is identified from the power spectra. The presence of a spectral gap in the power spectra is a common feature of the equilibrium between wave and small-scale turbulence. The characteristic frequency of the spectral gap is used as the cutting time between wave and small-scale turbulence, leading to the identification of the small-scale turbulence averaging interval as we discuss in Sect. 3.2. Therefore, we apply a 2-min average to the measurements in order to filter the wave from the small-scale turbulence, followed by a second average of the obtained 15 values to get the 30-min average of the small-scale turbulent quantities $\langle a'b'\rangle$. The 2-min average used to filter the waves is in line with the spectral-gap time scales within nocturnal SBLs introduced in Sect. 1. Finally, by taking the difference between the total fluctuations $\langle a\rangle$ obtained from the Reynolds decomposition and the small-scale turbulence $\langle a^\prime \rangle$ from the double time average, we have an estimation of the contribution associated with the wave activity $\langle {\tilde{a}}\rangle$. Although less formal, this practical approach is more suitable for field-experiment applications as it releases the evaluation of the wave activity from the specific wave type, which makes it preferable in this context.

2.3 Kinetic and Potential Energy Budgets in the Presence of Waves

The triple decomposition described in Sect. 2.1 is invoked in the computation of the energy budgets. We start from the governing equations in Eq. 1 (in order, continuity, momentum, and potential temperature equation)

$$\begin{aligned}&\frac{\partial {U}_i}{\partial x_i}=0, \end{aligned}$$

(1a)

$$\begin{aligned}&\frac{\mathrm {D} {U}_i}{\mathrm {D} t}= -\frac{\partial {P}}{\partial x_i}+\beta {{{\Theta }}} \delta _{i3} +\nu \frac{\partial ^2 {U}_i}{\partial x_j \partial x_j}, \end{aligned}$$

(1b)

$$\begin{aligned}&\frac{\mathrm {D} {{\Theta }}}{\mathrm {D} t}= \nu _{\Theta } \frac{\partial ^2 {{\Theta }}}{\partial x_j \partial x_j}, \end{aligned}$$

(1c)

to derive the kinetic energy and potential-temperature variance. Here, $U_i$ is the wind velocity with components in the directions $x_i$, t is time, P the pressure, ${\Theta }$ the potential temperature, $\nu$ and $\nu _{\Theta }$ the kinematic viscosity and thermal diffusivity, $\delta _{i3}$ the Kronecker delta, and $\beta =g/{\Theta }_0$ (with g the acceleration due to gravity and ${\Theta }_0$ the reference potential temperature at the surface). The triple decomposition is applied to the velocity, pressure and potential temperature so that the variables

$$\begin{aligned}&U_i = \langle U_i\rangle +{\tilde{u}}_i+u'_i,\nonumber \\&P = \langle P\rangle +{\tilde{p}}+p', \end{aligned}$$

(2a)

and

$$\begin{aligned} {\Theta } = \langle {{\Theta }}\rangle +\tilde{{\Theta }}+{\Theta }', \end{aligned}$$

(2b)

are then substituted into Eq. 1 to separate the contributions. The equations for the first-order moments of the wind velocity in Eq. 2a and the potential temperature in Eq. 2b are derived for the mean, wave, and small-scale turbulence contributions separately, following the decomposition properties in Sect. 2.1. The equations for the kinetic energies are then obtained by multiplying the resulting first-order moment equations for the mean, wave, and small-scale turbulence contributions respectively by $\langle U_k\rangle$, $\tilde{u_k}$ and $u'_k$, and then taking the phase and the time averages of the second-order moment equation, considering $i=k$. A similar procedure is applied to the equations for the potential temperature to derive that of the potential-temperature variances and ultimately the potential energies (see Appendix 1 for the detailed derivation).

The equation for the wave mean kinetic energy reads

$$\begin{aligned} \underbrace{\frac{1}{2}\frac{\mathrm {D} \langle {\tilde{u}}_i{\tilde{u}}_i \rangle }{\mathrm {D} t}}_{\mathrm {I}}= & {} -\underbrace{\frac{1}{2}\frac{\partial }{\partial x_j}\langle {\tilde{u}}_i {\tilde{u}}_i {\tilde{u}}_j \rangle }_{\mathrm {II}}-\underbrace{\frac{\partial }{\partial x_i}\langle {\tilde{p}}{\tilde{u}}_i \rangle }_{\mathrm {III}} -\underbrace{\langle {\tilde{u}}_j{\tilde{u}}_i\rangle \frac{\partial \langle U_i\rangle }{\partial x_j}}_{\mathrm {IV}} +\underbrace{\beta \langle {\tilde{u}}_i \tilde{{\Theta }} \rangle \delta _{i3}}_{\mathrm {V}} \nonumber \\&-\underbrace{\frac{\partial }{\partial x_j} \left\langle {\tilde{u}}_i\overline{u'_j u'_i}\right\rangle }_{\mathrm {VI}} +\underbrace{\left\langle \overline{u'_j u'_i}\frac{\partial {\tilde{u}}_i}{\partial x_j} \right\rangle }_{\mathrm {VII}}, \end{aligned}$$

(3)

while the equation for the small-scale mean turbulence kinetic energy (TKE) is

$$\begin{aligned} \underbrace{\frac{1}{2}\frac{\mathrm {D} \langle u'_i u'_i \rangle }{\mathrm {D} t}}_{\mathrm {I}}= & {} -\underbrace{\frac{1}{2}\frac{\partial }{\partial x_j}\langle u'_i u'_i u'_j \rangle }_{\mathrm {II}}-\underbrace{\frac{\partial }{\partial x_i}\langle p' u'_i \rangle }_{\mathrm {III}} -\underbrace{\langle u'_j u'_i\rangle \frac{\partial \langle U_i\rangle }{\partial x_j}}_{\mathrm {IV}} +\underbrace{\beta \langle u'_i{\Theta }'\rangle \delta _{i3}}_{\mathrm {V}} \nonumber \\&-\underbrace{\frac{\partial }{\partial x_j}\left\langle {\tilde{u}}_j\overline{u'_i u'_i}\right\rangle }_{\mathrm {VI}} -\underbrace{\left\langle \overline{u'_j u'_i}\frac{\partial {\tilde{u}}_i}{\partial x_j}\right\rangle }_{\mathrm {VII}} -\underbrace{\nu \left\langle \frac{\partial u'_i}{\partial x_j}\frac{\partial u'_i}{\partial x_j} \right\rangle }_{\mathrm {VIII}}. \end{aligned}$$

(4)

Both equations show a total derivative (terms I), transport (terms II), pressure covariance divergence (terms III), shear production (terms IV), and buoyancy (terms V) of kinetic energy associated with the wave (Eq. 3) and the small-scale turbulence (Eq. 4). The viscous term associated with the wave kinetic energy is neglected in Eq. 3, assuming a large Reynolds number, while the TKE dissipation $\epsilon _T$ is directly computed as in term VIII of Eq. 4. Terms VI and VII in both equations couple the wave and small-scale turbulence contributions as mutual interactions between the processes. Specifically, terms VII appear with opposite signs in the wave and small-scale turbulence equations, similarly to the shear production associated to the mean flow. Therefore, terms VII can be interpreted as wave-shear production,

$$\begin{aligned} \varPi =\left\langle \overline{u'_j u'_i}\frac{\partial {\tilde{u}}_i}{\partial x_j}\right\rangle , \end{aligned}$$

(5)

representing the production of small-scale turbulence energy in phase with the wave. Following Finnigan and Einaudi (1981), $\varPi <0$ away from the surface, meaning that the wave is feeding the small-scale turbulence. Therefore, we may expect $\varPi \approx 0$ at the surface with negligible wave–turbulence interaction.

Term VI in Eq. 3,

$$\begin{aligned} \varPi _W=-\frac{\partial }{\partial x_j} \left\langle {\tilde{u}}_i \overline{u'_j u'_i}\right\rangle , \end{aligned}$$

(6)

represents the transport of small-scale turbulence energy in phase with the wave. Conversely, term VI in Eq. 4

$$\begin{aligned} \varPi _T=\frac{\partial }{\partial x_j}\left\langle {\tilde{u}}_j\overline{u'_i u'_i}\right\rangle \end{aligned}$$

(7)

can be interpreted as the advection of the wave-like part of the small-scale TKE in phase with the wave (Finnigan and Einaudi 1981). While the value of $\varPi _T$ is typically close to zero, the single-layer local value of $\varPi _W<0$ (Finnigan and Einaudi 1981). It is worth mentioning that both terms $\varPi _T$ and $\varPi _W$ are divergences of third-order moments accounting for the interaction between wave and small-scale turbulence. Their local effects can not be neglected in principle, and we will retain both in the following analysis. Recalling that the total fluctuation part $E_K$ of the kinetic energy is the sum of the wave $E_W$ and the small-scale turbulence $E_T$, the fluctuation energy can be written as $E_K=E_W+E_T$ or $\frac{1}{2}u_iu_i=\frac{1}{2}{\tilde{u}}_i{\tilde{u}}_i+\frac{1}{2}u'_iu'_i$. Thus, the equation for the kinetic energy of the total fluctuation is obtained summing Eqs. 3 and 4 as

$$\begin{aligned}&\underbrace{\frac{1}{2}\frac{\mathrm {D} \langle u_i u_i \rangle }{\mathrm {D} t}}_{\mathrm {I}}+ \underbrace{\frac{\partial }{\partial x_j}\left[ \left\langle {\tilde{u}}_j \left( \frac{{\tilde{u}}_i {\tilde{u}}_i}{2}+{\tilde{p}}\right) \right\rangle + \left\langle u'_j \left( \frac{u'_i u'_i}{2}+p'\right) \right\rangle \right] }_{\mathrm {II}} \nonumber \\&\quad =-\underbrace{\langle u_j u_i\rangle \frac{\partial U_i}{\partial x_j}}_{\mathrm {III}}+ \underbrace{\beta \langle {\Theta } u_i\rangle \delta _{i3}}_{\mathrm {VI}} -\underbrace{\epsilon _{T}}_{\mathrm {V}}+\underbrace{\varPi _W-\varPi _T}_{\chi _K}, \end{aligned}$$

(8)

where $\chi _K$ describes the mutual interactions between wave and small-scale turbulence. The fluctuation budget in Eq. 8 is the counterpart, accounting for waves and turbulence, of the one obtained from the Reynolds decomposition, with the single terms expressing the same meaning (I is the total derivative, II the transport and pressure divergence, III production, IV buoyancy, V dissipation) with the addition of the term describing the wave–turbulence interactions. Quantities between square brackets in term II are the third-order moments of the wave and small-scale turbulence fluctuations, taken independently of each other. The TKE dissipation $\epsilon _T$ is associated with the smaller scales of motion and thus with the inertial subrange (Grachev et al. 2016); the $\chi _K$ term accounts for the spectral flux of energy due to the exchanges among scales. Following the Reynolds-decomposition approach, there is a continuous production of turbulence transferred from the mean shear (and buoyancy) that is dissipated into internal energy (Monin and Yaglom 1971). In the presence of a wave, the oscillatory motion distorts the turbulent field while subtracting energy from the mean flow, altering the energy budgets of the small-scale turbulence.

Similar to the kinetic energy computation, the equations for the mean potential-temperature variance associated with the wave reads

$$\begin{aligned}&\underbrace{\frac{1}{2}\frac{\mathrm {D} \langle \tilde{{\Theta }}^2\rangle }{\mathrm {D} t}}_{\mathrm {I}} +\underbrace{\frac{1}{2}\frac{\partial \langle {\tilde{u}}_j \tilde{{\Theta }}^2\rangle }{\partial x_j}}_{\mathrm {II}}= -\underbrace{\langle \tilde{{\Theta }}{\tilde{u}}_j\rangle \frac{\partial \langle {\Theta }\rangle }{\partial x_j}}_{\mathrm {III}} -\underbrace{\frac{\partial }{\partial x_j} \left\langle \tilde{{\Theta }}\overline{u'_j {\Theta }'}\right\rangle }_{\mathrm {IV}} +\underbrace{\left\langle \overline{u'_j {\Theta }'} \frac{\partial }{\partial x_j} \tilde{{\Theta }}\right\rangle }_{\mathrm {V}}, \end{aligned}$$

(9)

while the small-scale turbulence mean potential-temperature variance equation reads

$$\begin{aligned} \underbrace{\frac{1}{2}\frac{\mathrm {D} \langle {\Theta }^{\prime 2}\rangle }{\mathrm {D} t}}_{\mathrm {I}} +\underbrace{\frac{1}{2}\frac{\partial }{\partial x_j}\langle u'_j{\Theta }^{\prime 2}\rangle }_{\mathrm {II}}= & {} -\underbrace{\langle {\Theta }' u'_j\rangle \frac{\partial \langle {\Theta }\rangle }{\partial x_j}}_{\mathrm {III}} -\underbrace{\frac{\partial }{\partial x_j} \left\langle {\tilde{u}}_j\overline{{\Theta }^{\prime 2}}\right\rangle }_{\mathrm {IV}} \nonumber \\&-\underbrace{\left\langle \overline{{\Theta }' u'_j}\frac{\partial \tilde{{\Theta }} }{\partial x_j}\right\rangle }_{\mathrm {V}} -\underbrace{\nu _{\Theta }\left\langle \frac{\partial {\Theta }'}{\partial x_k}\frac{\partial {\Theta }'}{\partial x_k} \right\rangle }_{\mathrm {VI}}. \end{aligned}$$

(10)

It appears evident that even in the absence of the small-scale turbulence heat flux, the waves can feed the temperature variance of the small-scale turbulence. Again, both equations depend on the total derivative (terms I), transport (terms II), and transfer from the mean flow (terms III) of the potential-temperature variance associated with the wave (Eq. 9) and the small-scale turbulence (Eq. 10), respectively. The viscosity associated with the wave is neglected, while the turbulent potential-temperature dissipation $\epsilon _{\Theta }$ is directly computed as term VI of Eq. 10. Once again, terms IV and V in both equations couple the wave with the small-scale turbulence, describing exchange processes between them. Terms V appear with an opposite sign in the equations, representing the small-scale turbulence potential-temperature productions subtracted from the wave. Defining these terms as

$$\begin{aligned} \varPi _{\Theta }=\left\langle \overline{u'_j {\Theta }'}\frac{\partial \tilde{{\Theta }}}{\partial x_j}\right\rangle , \end{aligned}$$

(11)

they represent an exchange of small-scale turbulence energy in phase with the wave. Term IV in Eq. 9 can be defined as

$$\begin{aligned} \varPi _{{\Theta } W}=-\frac{\partial }{\partial x_j} \left\langle \tilde{{\Theta }} \overline{u'_j {\Theta }'}\right\rangle , \end{aligned}$$

(12)

representing the transport of small-scale turbulence potential-temperature variance in phase with the wave. Term IV in Eq. 10,

$$\begin{aligned} \varPi _{{\Theta } T}=\frac{\partial }{\partial x_j} \left\langle {\tilde{u}}_j\overline{{\Theta }^{\prime 2}}\right\rangle , \end{aligned}$$

(13)

can be interpreted as advection of the wave-like potential-temperature variance in phase with the wave (Finnigan and Einaudi 1981). The total fluctuation of the potential-temperature variance results from the sum of the wave and the small-scale turbulence contributions, so that ${\Theta }^2 = \tilde{{\Theta }^2} + {\Theta }'^2$. As such, the equation for the total variance of potential temperature is obtained summing Eqs. 9 and 10 as

$$\begin{aligned} \underbrace{\frac{1}{2}\frac{\mathrm {D} \langle {\Theta }^2\rangle }{\mathrm {D} t}}_{\mathrm {I}}+ \underbrace{\frac{1}{2}\frac{\partial }{\partial x_j}\left[ \langle {\tilde{u}}_j \tilde{{\Theta }}^2\rangle +\langle u'_j{\Theta }^{\prime 2}\rangle \right] }_{\mathrm {II}} =-\underbrace{\langle {\Theta } u_j\rangle \frac{\partial \langle {\Theta }\rangle }{\partial x_j}}_{\mathrm {III}}- \underbrace{\epsilon _{{\Theta }}}_{\mathrm {IV}}+\underbrace{\varPi _{{\Theta } W}-\varPi _{{\Theta } T}}_{\chi _{{\Theta }}}. \end{aligned}$$

(14)

The interpretation of the various terms of Eq. 14 is analogous to the one given for the kinetic energy budget Eq. 8: again, the interaction between wave and small-scale turbulence is described by $\chi _{\Theta }$, which represents the potential-temperature variance spectral flux.

The simplified Eq. 14 can easily compute the potential energy of the total fluctuations by multiplying each term by $\beta (d\langle {\Theta }\rangle /dz)^{-1}$. The result envisages the energy given in potential to the fluid particle, which is vertically displaced by means of a potential-temperature variation (Bolgiano 1962; Tampieri 2017). Defining the potential energy of fluctuations $E_{PK}$ and the potential-energy dissipation $\epsilon _p$ as

$$\begin{aligned} E_{PK} = \frac{1}{2}\beta \left( \frac{d\langle {\Theta }\rangle }{dz}\right) ^{-1}\langle {\Theta }^2\rangle \qquad \text{ and } \qquad \epsilon _p=\beta \left( \frac{d\langle {\Theta }\rangle }{dz}\right) ^{-1}\epsilon _{{\Theta }}, \end{aligned}$$

(15)

respectively (Zilitinkevich et al. 2013), Eq. 14 can be rewritten as

$$\begin{aligned}&\frac{\mathrm {D} E_{PK}}{\mathrm {D} t}+ \frac{1}{2}\beta \frac{d }{dz}\left[ \langle {\tilde{u}}_j \tilde{{\Theta }}^2\rangle +\langle u'_j{\Theta }^{\prime 2}\rangle \right] \left( \frac{d\langle {\Theta }\rangle }{dz}\right) ^{-1}=-\beta \langle u_j{\Theta }\rangle \nonumber \\&\quad -\epsilon _{p}+\beta \left( \frac{d\langle {\Theta }\rangle }{dz}\right) ^{-1}\chi _{{\Theta }}. \end{aligned}$$

(16)

Note again that the potential energy of fluctuations can be rewritten as the sum of wave $E_{PW}$ and small-scale turbulence $E_{PT}$, so that $E_{PK}=E_{PW}+E_{PT}$.

In conclusion, the triple decomposition has allowed us to address the explicit contributions and interactions between waves and small-scale turbulence within the energy budgets.

2.4 The Energy Budgets at the Surface: A Paradigm of the Stable Layer

The theoretical framework introduced so far has potential application in atmospheric turbulent flows in the presence of waves. A typical environment is represented by the nocturnal SBL, where waves have been often observed. A typical approach to study turbulence and waves in real environments is the measurement of the fundamental variables through ground-based instrumentation, mostly fast-sampling sensors mounted on tens-of-metres high towers. This approach formally details the boundary layer and the effect of the terrain on the atmospheric processes. The interaction with the terrain has a well-known impact on the flow caused by the increasing friction. Given that stability is a typical factor regulating the wave intensity (Monti et al. 2002), the approaching terrain is observed to reduce the wave intensity as well (Cava et al. 2019). Moreover, as shear increases approaching the ground, we can expect a smaller influence of the wave compared to the small-scale turbulence. A simplified evaluation based on order of magnitudes may help to visualize this concept.

Let us assume that the kinetic energy of the small-scale turbulence $E_T$ is mainly produced by the shear and modulated by buoyancy, while neglecting the turbulent transport under the assumption that turbulence and non-turbulent motions are close to local equilibrium (see Sect. 3.4). In very simplified form, the budget equation can be written as a balance between shear production, buoyancy and dissipation $\epsilon$ as

$$\begin{aligned} \tau \frac{dU}{dz}\left( 1+\frac{\beta \langle w{\Theta }\rangle }{\tau dU/dz}\right) -\epsilon =0, \end{aligned}$$

(17)

where $\tau =(\langle wu\rangle ^2+\langle wv\rangle ^2)^{1/2}$ is the vertical stress, $\langle w{\Theta }\rangle$ is the kinematic heat flux, and U is the wind speed. Under weakly or moderately stable conditions, dissipation can be rewritten according to Basu et al. (2021) as

$$\begin{aligned} \epsilon =\alpha _BE_T\frac{dU}{dz}, \end{aligned}$$

(18)

with $\alpha _B$ $=$ 0.23. Note that the absolute value of dU/dz represents the inverse of the turbulence relaxation time (dU/dz $\propto$ $E_K/\epsilon$, see for example Zilitinkevich et al. 2013) and, in the framework of this parametrization must be considered positive by definition. This ensures we avoid having a non-physical negative dissipation. Assuming a flux–gradient relationship for $\tau =K_MdU/dz$ and $\langle w{\Theta }\rangle =-P_R^{-1}K_Md{\Theta }/dz$ ($K_M$ is the eddy viscosity and $P_R$ the Prandtl number), introducing the gradient Richardson number

$$\begin{aligned} Ri=\frac{\beta d{\Theta }/dz}{\left( dU/dz\right) ^2} \end{aligned}$$

(19)

and using Eqs. 17 and 18 can be used to make explicit the small-scale TKE as

$$\begin{aligned} E_T=\frac{\tau }{\alpha _B}\left( 1-P_R^{-1}Ri\right) . \end{aligned}$$

(20)

Note that Eq. 20 denotes a local relationship which holds even if $\tau$ and Ri are z-dependent. Under weakly stable conditions, the Prandtl number is a constant (Zilitinkevich et al. 2013), and the ratio $E_T/\tau =1/\alpha _B\left( 1-P_R^{-1}Ri\right) =f(Ri)$ is a function of the Richardson number only. It is worth noting that under neutral stratification (i.e., $Ri=0$), $E_T/\tau =1/\alpha _B$ in line with results from Monin and Yaglom (1971). Following Zilitinkevich et al. (2013), this last relation remains approximately true for Ri $\le$ 0.1. On the other hand, buoyancy waves are typically observed under stable conditions (especially over sloping terrain), where buoyancy waves are initiated by vertical displacement of the flow streamlines resulting from the interaction with either a physical obstacle (such as topography) or disturbed density interfaces caused by cold pools, density currents, turbulent patches, or convective systems among others (Sun et al. 2015b). For buoyancy waves, an estimation of $E_W$ is given by Gill (1982) as

$$\begin{aligned} E_W=\frac{N^2 H^2}{2}, \end{aligned}$$

(21)

where N is the Brunt–Väisälä frequency and H is the length scale of the streamline vertical displacement. By taking the ratio between Eq. 20 and Eq. 21, we obtain

$$\begin{aligned} R_{T,W}^E=\frac{E_T}{E_W}=2\frac{\tau f(Ri)}{N^2H^2}, \end{aligned}$$

(22)

where $R_{T,W}^E$ is the ratio between the kinetic energies of small-scale turbulence and waves. Below, this ratio is adopted for different quantities and contributions, so that $R_{y{_1},y{_2}}^x$ is the ratio between the quantities $x_{y_1}/x_{y_2}$, with $y_1$ and $y_2$ as K, T, and W, while x can be E, $E_P$, $\tau$, or $\langle w{\Theta }\rangle$. Equation 22 describes a local relationship; herein, the energy ratio, the vertical stress, the Richardson number and the Brunt–Väisälä frequency are all functions of the elevation z. Equation 22 shows that the ratio between the kinetic energy of the small-scale turbulence and the kinetic energy of the waves increases as the shear increases, and decreases with increasing stability. As such, while with decreasing stability we expect a decreasing effect of the waves, this brief discussion concludes that we can observe a progressively smaller influence of waves on the energy budget approaching the ground where the shear is expected to increase and the wave energy is expected to be absorbed/dissipated or reflected.

Fig. 1

Paradigm of turbulent flows in nocturnal SBLs in the presence of waves. The kinetic $E_K$ and potential $E_{PK}$ energies generated within a nocturnal flow (a) involve different contributions of wave and small-scale turbulence in the near-ground (NGS) and far-ground (FGS) sublayers (b), with the latter resulting in the addition of the $\varPi$ terms to the dissipations as a result of the wave and small-scale turbulence interaction (c). The sketch encompasses the example of a nocturnal low-level jet directed along the valley axis, identified with green arrows in (a), under stable stratification

Following these findings, we asked ourselves whether a separation may exist, dividing the atmospheric depth close to the surface into near and far sublayers with respect to the ground. Our question finds an answer in the stable-layer paradigm represented in Fig. 1. As a stably stratified temperature inversion layer grows together with a stratified flow at the surface (usually developing into a low-level jet even on complex terrain), waves and small-scale turbulence develop from different contributions (buoyancy and shear respectively) and interact at the submesoscale. As a consequence, two sublayers can develop at the surface when wave activity is observed in a turbulent flow. The near-ground sublayer (NGS) is the atmospheric depth where the wave impact is smaller (or even negligible) than the small-scale turbulence and the double-decomposition approach satisfies the energy budgets. Specifically, the turbulence energy production is driven by the mean flow and dissipation results from the inertial subrange. Conversely, the far-ground sublayer (FGS) develops above the NGS, where waves and turbulence both contribute to the energy balances, and the triple-decomposition approach is preferred. The turbulence energy production is driven by both the mean flow and waves, and the true dissipation (from the inertial subrange) is enhanced by the energy exchanges with the waves ($\varPi$’s terms in Fig. 1). As a result, the waves can feed or be fed by turbulence.

An estimation of the separation height $z_c$ can be derived from Eq. 17 under well-defined assumptions. If the vertical stress $\tau$ is independent from z, it can be reasonably assumed as equal to the square of the friction velocity $u_*$. Accordingly, the wind profile takes the log-linear form

$$\begin{aligned} \frac{dU}{dz}=\frac{u_*}{\kappa z}\left( 1+\alpha \frac{z}{{\Lambda }}\right) , \end{aligned}$$

(23)

where $\kappa =$ 0.37 is the von Kármán constant, ${\Lambda }$ is the Obukhov length, and $\alpha =$ 4.7. Substituting $\tau =u_*^2$ and Eq. 23 into the term between round brackets of Eq. 17, we obtain

$$\begin{aligned} \left( 1+\frac{\beta \langle w{\Theta }\rangle }{\tau dU/dz}\right) =1-\frac{z}{{\Lambda }}\left( 1+\alpha \frac{z}{{\Lambda }}\right) ^{-1}. \end{aligned}$$

(24)

Thus, Eq. 17 with Eqs. 24 and 18 reads

$$\begin{aligned} u_*^2\left[ 1-\frac{z}{{\Lambda }}\left( 1+\alpha \frac{z}{{\Lambda }}\right) ^{-1}\right] -\alpha _B E_T=0, \end{aligned}$$

(25)

which gives a relation where the small-scale TKE changes with the elevation only

$$\begin{aligned} E_T=\frac{u_*^2}{\alpha _B}\left[ 1-\frac{z}{{\Lambda }}\left( 1+\alpha \frac{z}{{\Lambda }}\right) ^{-1}\right] . \end{aligned}$$

(26)

Similarly, by assuming the investigated atmospheric layer has a constant stability, the Brunt–Väisälä frequency can be approximated by its constant value in this layer. Taking again the ratio between this latest version of the small-scale TKE (Eq. 26) and the wave kinetic energy, we get

$$\begin{aligned} R^E_{T,W}=2\frac{u_*^2}{\alpha _B}\frac{\left[ 1-\frac{z}{{\Lambda }}\left( 1+\alpha \frac{z}{{\Lambda }}\right) ^{-1}\right] }{H^2N^2}. \end{aligned}$$

(27)

Since the separation height $z_c$ determines the borderline between the NGS and FGS, it also identifies where the kinetic energy of the small-scale turbulence equals that of the wave. Therefore, $R_{T,W}^E(z_c)=$ 1. Solving Eq. 27 for $z=z_c$, we can have an estimation of the separation height in the form

$$\begin{aligned} z_c={\Lambda }\left( 2\frac{u_*^2}{\alpha _B}-H^2N^2\right) \left( \alpha N^2H^2+2\frac{u_*^2}{\alpha _B}\right) ^{-1}. \end{aligned}$$

(28)

When the observation height is below the theoretical value ($z<z_c$), $R_{T,W}^E>1$ and the small-scale turbulence dominates over the wave contribution; when $z>z_c$, $R_{T,W}^E<1$ and the wave contribution becomes important. The evaluation of the separation height can also be performed a posteriori from the measurements of the kinetic energies, by visualizing the elevation where $E_T=E_W$.

Finally, by solving Eq. 22 for $z=z_c$, we can estimate the streamline vertical displacement H as

$$\begin{aligned} H=\left( \frac{2f(Ri(z_c))\tau (z_c)}{N(z_c)^2}\right) ^{1/2}, \end{aligned}$$

(29)

and we can argue on the possible form and nature of the wave motions we are dealing with.

3 Data and Methods

3.1 A Case Study from the Sagebrush Field Site

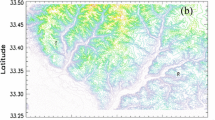
To evaluate the wave–turbulence reciprocal interactions, we selected a specific dataset from the Dugway Valley testbed within the MATERHORN Program (Fernando et al. 2015). Measurements are collected from the flux tower and the tethered balloon located at the Sagebrush field site, located within the valley floor at latitude 40.121360, longitude − 113.129070, and altitude 1316 m (Fig. 2) during the night between the 11–12 May 2013. The tethered-balloon (TTS111, Väisälä, Helsinki, Finland; Fernando 2017) soundings allow the nocturnal-flow profiling within a 400-m atmospheric layer, providing measurements of the wind speed and air temperature (among others) with a vertical resolution of 1 m. The 20-m flux tower (Pace et al. 2017) allows to delve into the near-surface interactions, detailing the nocturnal flows characteristics through five equipped levels (0.5 m, 2 m, 5 m, 10 m, and 20 m) of sonic anemometers (81000, Young Company, Traverse City, U.S.) sampling at 20 Hz, and temperature and relative-humidity probes (HMP45C-L, Campbell Scientific, Logan, U.S.) sampling at 1 Hz. Below, we refer to the atmospheric depth between 0.5 m and 20 m as the observed layer.

Fig. 2

a Sagebrush measurement site (purple star) within the Dugway Valley testbed (Source: https://www.google.com/maps/). b Tethered-balloon and c flux-tower view at the Sagebrush site (photographs source: University of Utah 2017)

The collected data have been preliminarily processed to check the dataset against possible instrumental malfunctioning, non-physical data saving, or instrumental fails. Specifically, a wind velocity value is considered reliable if the measured components range within ±20 m s$^{-1}$; a range of ±40 $^\circ$C is applied to the temperature measurements. The sonic-anemometer measurements are further despiked using a data-removal procedure (Hejstrup 1993) applied to every 30-min data interval (Vickers and Mahrt 1997). This procedure assumes that each interval follows a Gaussian distribution of independent data characterized by a mean (${\overline{x}}$) and a standard deviation ($\sigma$). Values above the threshold $C\sigma$ $=$ 3.5$\sigma$ (Vickers and Mahrt 1997; Schmid et al. 2000) are marked as spikes and replaced by the linearly interpolated value within the same 30-min interval. The despiked wind components are then double-rotated to align the wind vector to the mean streamline direction (McMillen 1988). Finally, tethered-balloon profiles are smoothed with a 10-m running average to filter the small fluctuations in the signal.

Notwithstanding the information we intend to extrapolate from the data, a final 30-min average is applied to the flux-tower measurements, unless specified otherwise. A more detailed description of the averaging procedures complying with the scope of the computations is given in Sect. 3.2. When the investigated quantity is the wind direction, the average is replaced by the mode over the same temporal or spatial intervals. For the whole investigation, UTC is used, but it is worth mentioning the local time is MDT = UTC - 6 h.

Fig. 3

Contour plot of the wind speed (a) and potential temperature (b) linearly interpolated from the tethered-balloon soundings (solid black lines). Dashed black lines identify sunset and sunrise

Fig. 4

5-min-averaged wind speed U (a), potential temperature ${\Theta }$ (b) and wind direction WD evolution from the sonic-anemometer data of the flux-tower (light blue at 0.5 m, red at 2 m, yellow at 5 m, purple at 10 m and green at 20 m). Night is shaded in grey

The period 11–12 May 2013 was classified as quiescent (i.e., wind speed less than 5 m s$^{-1}$ at 700 hPa; Fernando et al. 2015), and no-synoptic forcing is expected within the valley. During the night, the development of a well-stratified valley flow is observed starting at 0300 UTC, resulting in a low-level jet appearing around 0500 UTC and propagating towards the down-valley direction (north-west along the valley axis), with the jet peak reaching its maximum speed at 50 m around 1100 UTC and disappearing almost completely at 1400 UTC (Fig. 3a). The evolution of the low-level jet (i.e., the intensification of the vertical wind-speed gradient, the deepening of the atmospheric layer of the jet peak and the increasing maximum speed) follows the intensification and growth of the temperature inversion layer (Fig. 3b). Beneath the jet peak, oscillatory motions are observed in the wind-speed time series (Fig. 4a), and interpreted as the result of wave activity at the surface. As a local fluctuation of the mean flow, this wave activity can be arguably associated with buoyancy waves (as suggested by Serafin et al. 2018). A verification is provided by Brogno et al. (2021), where an inertial-gravity wave was observed within the same night here investigated. The typical periods $T_W$ of these waves are retrieved from Fig. 4a (as suggested by Sun et al. 2015b) by computing the time differences between each crest and trough observed in the wind-speed time series, and then doubling these values. As a result, these periods are in the range of 10$^3$ s $\le$ $T_W$ $\le$ 3$\times 10^{3}$ s, suggesting the wave activity can be either attributed to inertial-gravity and/or low-frequency internal waves (similar to those observed by Monti et al. 2002). This wave activity is likely caused by the complex interaction between the wind field and the local roughness of the valley, and/or by the entrainment of surface currents within the valley. An example of the second formation mechanism is observed at 0730 UTC and 0930 UTC, when the entrainment of a lateral flow close to the surface (only evident within the first 10 m above the ground, Fig. 4c) causes a sudden decrease of the wind speed (Fig. 4a), which propagates upwards as the valley flow has to readjust to the perturbation. This causes a sudden displacement of the flow streamline triggering the formation of the wave (Brogno et al. 2021). Overall, the wave activity seems not to affect the thermal aspects, as the temperature evolves in an unperturbed thermal inversion lasting through the night (Fig. 4b).

Given this insight on the nature of the observed wave activity, we remark that we are not explicitly computing the wave terms obtained with the triple decomposition, but we used a practical frame to evaluate the wave activity as a non-turbulent perturbation field whose reference time scale is smaller than that of the mean flow. Therefore, the present investigation should be independent from the wave type or characteristics, as long as the waves perturb (and are perturbed by) the turbulence behaviour.

3.2 Evaluation of Wave and Small-Scale Turbulence Contributions

The research of wave-like motions in a time-dependent dataset has been addressed by using specific filters to disaggregate the wave contribution from the mean and turbulence fields. A simple method suggests to use different averaging windows to evaluate an investigated quantity, in order to isolate a specific contribution. As an example, the 30-min average applied to the current nocturnal data allows filtering of the large-scale variability, as the mean flow is close to stationary within this time interval. The same approach is herein used to filter the wave and mean motions from the time series, retaining the small-scale turbulence contribution alone. A certain wave activity has already been discussed in Sect. 3.1 and associated with characteristic wave periods in the range 10$^3$ s $\le$ $T_W$ $\le$ 3$\times 10^{3}$ s. Here we seek a wave-filtering averaging interval within the power spectral variances of the velocity components uu, vv, ww, and potential temperature ${\Theta }^2$, and the vertical covariances wu, wv, and $w{\Theta }$. Power spectra and cospectra are computed from sonic-anemometer measurements at each flux-tower level using the fast-Fourier transform with a hamming window 0500–1200 UTC with no overlap, and their dimensionless forms are plotted as a function of the non-dimensional frequency $n=fzU^{-1}$. The nocturnal subperiod 0500–1200 UTC is chosen throughout the following investigations to avoid transitional dynamics typical at sunrise and sunset (those occurring at 0233 UTC and 1214 UTC respectively), and during the initial growth of the inversion layer between 0233 UTC and 0500 UTC when the valley-flow dynamic is likely to superimpose the wave and small-scale turbulence activities. The non-dimensional form of the spectra allows a direct comparison with the literature (e.g., Kaimal and Finnigan 1994), thus enabling the evaluation of the frequency range exposed to the wave activity. Considering $N_x$ a general normalizing factor and $S_x$ either a variance or a covariance spectra of $x=uu, vv, ww, {\Theta }^2, \tau , w{\Theta }$, the reference spectra read

$$\begin{aligned} \frac{fS_x(f)}{N_x}=\frac{C_x n}{(1+D_x n)^\gamma }, \end{aligned}$$

(30)

where the values of $C_x$ and $D_x$ are taken from the Kansas spectra (Kaimal and Finnigan 1994) and $\gamma$ changes according to the analyzed quantity x, with the exception of the potential-temperature variance for which only the inertial-subrange tendency is given in Kaimal and Finnigan (1994). Therefore, the values of $C_{{\Theta }^2}=$ 28.2 and $D_{{\Theta }^2}=$ 12.3 are obtained by fitting the measured spectra with Eq. 30 and forcing the fit to follow the expected tendency $C_{{\Theta }^2}^S n^{-2/3}$ within the inertial subrange. The specific normalizing factors depend on the analyzed quantity. For the velocity-component variances, $N_{uu,vv,ww}=u_*^2\phi _\epsilon ^{2/3}$ where $\phi _\epsilon =\kappa z\epsilon _T/u_*^3$ is the dimensionless form of the dissipation $\epsilon _T$. Similarly for the potential-temperature variance, $N_{{\Theta }^2}={\Theta }_*^2\phi _N\phi _\epsilon ^{-1/3}$ where ${\Theta }_*=-w{\Theta }/u_*$ and $\phi _N=\kappa z \epsilon _{\Theta }/u_*{\Theta }_*^2$ is the dimensionless form of the potential-temperature dissipation $\epsilon _{\Theta }$. Note that the values of both $\epsilon _T$ and $\epsilon _{\Theta }$ are obtained from the inertial subrange of the along-stream and potential-temperature variance spectra, as described in Sect. 3.3. Finally, for the cospectra of $\tau$ and $w{\Theta }$ the normalizing factors reduce to $N_\tau =u_*^2$ and $N_{w{\Theta }}=u_*{\Theta }_*$, respectively. The measured variance and covariance spectra are shown in Figs. 5 and 6 respectively, along with the respective reference from Eq. 30. Since the analysis of the time series has shown that the characteristic period of the wave activity is likely changing within the 10$^3$ s $\le$ $T_W$ $\le$ 3$\times 10^{3}$ s range, we did not expect an individual spectral peak. Nevertheless, local spectral peaks can be observed at $f\approx 10^{-3}$ s$^{-1}$ in the horizontal-velocity variances and both covariances at 10 m and 20 m, where the wave activity is expected to be more evident. The presence of a certain wave activity is corroborated by behaviour of the observed spectra with respect to the expected ones. Except for the vertical velocity component, two frequency ranges can be recognized. For n $\ge$ 10$^{-2}$, the spectra follow the theoretical ones, revealing the presence of an inertial subrange in the data and suggesting the turbulent nature of the high frequencies. For n < 10$^{-2}$, the spectral levels are larger than expected, suggesting the presence of energetic non-turbulence wave motions. As oftentimes observed in the literature (e.g., Schiavon et al. 2019), the vertical velocity component is marginally modified by the wave activity. The division between low and high frequencies is emphasized by a spectral gap dividing wave and small-scale contributions between $f=6\times 10^{-3}$ s$^{-1}$ and $f=2\times 10^{-2}$ s$^{-1}$ (corresponding to periods in the range 50 $\div$ 167 s), with a characteristic cutting frequency at 1 $\div$ 2$\times 10^{-2}$ s$^{-1}$ (50 $\div$ 100 s). It is worth mentioning that the evidence of a spectral gap persists within smaller intervals (i.e., each 30-min window the night can be divided into), suggesting the low–high frequency separation robustness against typical nocturnal processes. The location of the spectral gap is also in agreement with the Ozmidov frequency $f_{Oz}$ $\approx$ 8.8$\times 10^{-3}$ s$^{-1}$ computed from measurements as

Fig. 5

Non-dimensional spectra of uu (a), vv (b), ww (c), and ${\Theta }^2$ (d) as a function of the non-dimensional frequency for all tower levels (0.5 m in blue, 2 m in red, 5 m in yellow, 10 in purple, and 20 m in green). Black dashed lines represent the reference spectra from Eq. 30. The green vertical bands describe the variability within the 20-m layer of the mean value of the Ozmidov scale through the night

Fig. 6

Non-dimensional spectra of $\tau$ (a) and $w{\Theta }$ (b) as a function of the non-dimensional frequency for all tower levels (0.5 m in blue, 2 m in red, 5 m in yellow, 10 in purple, and 20 m in green). Black dashed lines represent the reference spectra from Eq. 30. The green vertical bands describe the variability within the 20-m layer of the mean value of the Ozmidov scale through the night

$$\begin{aligned} f_{Oz} = \left( \frac{\epsilon _T^{1/2}}{N^{3/2}}\frac{1}{\mid {\varvec{U}}\mid }\right) ^{-1}, \end{aligned}$$

(31)

and averaged over the 0500–1200 UTC time period. The reciprocal time scale $T_{Oz}$ $=$ 114 s suggests that the time scale of the spectral gap is close to 2 min. Note that the Ozmidov frequency is obtained from the Ozmidov wavenumber following the Taylor hypothesis on frozen turbulence. The Ozmidov frequency, together with the evidence of a spectral gap, marks the discontinuity in a bimodal contribution to the flow energy, associated with wave motions (low frequencies) and small-scale turbulence (high frequencies). The use of the reverse of the spectral-gap frequency is a valid option to filter the wave contribution without losing the turbulence one (Smedman 1988), strengthened by the superposition with the Ozmidov scale, which is sometimes suggested as the cut-off frequency even in absence of a spectral gap (as reported by Finnigan 1988). Therefore, we adopted a preliminary 2-min-averaging interval to filter the wave contribution, followed by a 30-min average to align to the original 30-min data average. In the following sections, quantities directly averaged over 30-min intervals (i.e., the total fluctuations sum of wave and small-scale turbulence contributions) are indicated with the subscript K (e.g., the kinetic energy $E_K$), the small-scale turbulence (2-min followed by 30-min averages) with subscript T (e.g., the small-scale TKE $E_T$), and the wave contribution (identified as the difference between K and T quantities) with the subscript W (e.g., wave kinetic energy $E_W$).

3.3 The Dissipation Terms within the Energy Budgets

To evaluate the kinetic-energy dissipation $\epsilon _T$ directly from the energy spectra, we interpolate the common formulation for the along-stream energy spectra $S_u$ within the inertial subrange (e.g., Grachev et al. 2016) with the same interval within the observed spectra. The inertial subrange is identified directly from the observed 30-min spectra in the interval 0500–1200 UTC to estimate the kinetic-energy dissipation for each 30-min record as

$$\begin{aligned} \epsilon _T = \left( \frac{f S_u^{in}}{c^{in}_{uu}\left( \kappa z\right) ^{2/3}n^{-2/3}} \right) ^{3/2} \end{aligned}$$

(32)

where $S_u^{in}$ are the observed spectral values of $S_u$ within the inertial subrange and $c^{in}_{uu}=\alpha _K/(2\pi \kappa )^{2/3}$ $\approx$ 0.31 (with $\alpha _K$ $=$ 0.55 the Kolmogorov constant and $\kappa$ $=$ 0.37 the von Kármán constant). From a linear regression, the optimal value of $\epsilon _T$ is retrieved and used to asses the likelihood of the computation, using the coefficient of determination (for each 30-min spectra between 0500 UTC and 1200 UTC) between $S_u^{in}$ (made explicit from Eq. 32 with the computed $\epsilon _T$) and the observed spectra in the inertial subrange.

The same procedure is adopted to extract the potential-temperature-variance dissipation $\epsilon _{\Theta }$ from the inertial subrange of the potential-temperature energy spectra, so that

$$\begin{aligned} \epsilon _{\Theta } = \frac{f S_{\Theta }^{in}}{c^{in}_{{\Theta }^2}\left( \kappa z\right) ^{2/3}\epsilon _T^{-1/3}n^{-2/3}} \end{aligned}$$

(33)

where $S_{\Theta }^{in}$ is the observed spectrum in the inertial subrange and $c^{in}_{uu}=\beta _K/(2\pi \kappa )^{2/3}$ $\approx$ 0.46, with $\beta _K$ $=$ 0.8 the Kolmogorov (Obukhov–Corrsin) constant. Using the same regression method for the kinetic-energy dissipation, the optimal value of $\epsilon _{\Theta }$ is the best guess of the time-dependent ratio in Eq. 33 evaluated at each frequency.

As a final note, within the inertial subrange the right-hand side of Eq. 30 can be approximated as $C^S_x n^{1-\gamma }$, with $C^S_x \approx C_x/(D_x)^\gamma$ being the slope coefficient. By evaluating the spectra for uu and ${\Theta }^2$ according to the left-hand side of Eq. 30 for the inertial subrange only, we obtain the coefficient values $C^S_{uu}=$ 0.33 and $C^S_{{\Theta }^2}=$ 0.49, respectively. Both values are in line with $c^{in}_{uu}$ and $c^{in}_{{\Theta }^2}$ and with the Kansas spectra (Kaimal and Finnigan 1994), further consolidating the inertial subrange identification.

3.4 A Note on the Equilibrium Between Wave and Small-Scale Turbulence

The presence of wave activity within the flow is typically associated with non-stationary regimes. A typical consequence of non-stationarity is the lack of equilibrium between the turbulent and non-turbulent components of the motions, due to their scale overlap (Mahrt and Bou-Zeid 2020). Commonly, the presence of a spectral gap is necessary to infer local equilibrium conditions. As an example, Vercauteren et al. (2016) observed a spectral gap separating the scales of turbulent and non-turbulent motions, allowing local equilibrium. We can therefore argue that in the presence of a spectral gap we have an equilibrium between different scales if the characteristic times of turbulent and non-turbulent motions are well separated. Considering nocturnal (0500–1200 UTC, identified as $\langle \,\rangle _n$) and vertical (in the atmospheric layer ${\Delta }z=$ 20 − 0.5 m observed by the flux-tower instrumentation, identified as $\langle \,\rangle _{{\Delta }z}$) averages, the characteristic time scale of turbulence,

$$\begin{aligned} T_r = \left\langle \frac{E_K}{\epsilon _T}\right\rangle _{n,{\Delta }z}=15 \,\mathrm{s}, \end{aligned}$$

(34)

is much smaller than the time scales of the mean flow fields, (as computed by Finnigan and Einaudi 1981)

$$\begin{aligned}&T_{{{\Theta }}}=\left\langle \frac{{\Delta }z{\Delta {\Theta }}}{\mid \langle w{\Theta }\rangle \mid }\right\rangle _{n,{\Delta }z}=7\times 10^3 \,\mathrm{s} \qquad \text{ and } \qquad T_{U}=\left\langle \frac{{\Delta }z{\Delta }U}{\tau }\right\rangle _{n,{\Delta }z}=8\times 10^3 \,\mathrm{s}, \end{aligned}$$

(35)

ensuring the equilibrium between turbulence and its largest energy-containing scale. We have already observed that the typical wave period is in the range 10$^3$ s $\le$ $T_W$ $\le$ 3$\times 10^{3}$ s, revealing that turbulence and wave time scales are very well separated, and thus within a state of equilibrium. The evidence of a local equilibrium between the motion scales supports the assumption used to introduce our paradigm (Sect. 2.4) and will help in the resulting discussion.

4 Results

4.1 Near-Ground and Far-Ground Sublayers

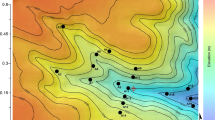
In Sect. 2.4 we hypothesize the existence of a NGS, where the shear-produced turbulence kinetic energy overcomes the wave kinetic energy, and a FGS, where wave and small-scale turbulence both contribute to the energy budget with the first being a dominant factor. Based on the typical dependences of the wave $E_W$ and small-scale turbulence $E_T$ kinetic energies, we evaluate a simple relation (Eq. 28) to compute the separation height $z_c$ where the ratio $R_{T,W}^E$ $=$ 1, i.e., the separation between NGS and FGS. Equation 28 relies on the assumption that both buoyancy and vertical stress (and therefore shear according to the flux-gradient relationship) are constant within the atmospheric layer scanned by the flux-tower instrumentations. This assumption is supported by Fig. 7, where the nocturnal-averaged Brunt–Väisälä frequency $\langle N\rangle _{n}$ shows a constant profile and that of the wind speed $\langle {\Delta }U\rangle _{n}$ (expressed as the difference between the wind speed at each flux-tower level and that at $z_1=$ 0.5 m) is well approximated by the log-linear profile (Eq. 23). Equation 28 further requires an estimation of the vertical displacement H of the flow streamline caused by the driving mechanisms of the wave. On the other hand, the evaluation of H requires the knowledge of $z_c$ (see Eq. 29). To solve this loop, we first evaluate $z_c$ from the nocturnal-averaged profiles of the potential and kinetic energies and with that we compute H according to Eq. 29. Finally, we use Eq. 28 to verify the value of the separation height $z_c$.

Fig. 7

Nocturnal-averaged Brunt–Väisälä frequency $\langle N\rangle _{n}$ (a) and wind speed $\langle {\Delta }U\rangle _{n}$ (b) profiles. The profile of the Brunt–Väisälä frequency is compared with its mean value (dashed black line), while the wind speed is compared to the log-linear profile under stable conditions (Eq. 23, blue line)

Fig. 8

Nocturnal-averaged (0500–1200 UTC) profiles of a the kinetic energy $\langle E\rangle$ and b the potential energy $\langle E_P\rangle$ of the total fluctuations (cyan), wave (green), and small-scale turbulence (orange). The subscript y in both panels stands for K, W, and T. Errorbars are the standard deviations propagated following the error theory. Wave and small-scale turbulence profiles are shifted of 0.4 m downwards and upwards respectively, to avoid symbols superposition. The dashed black lines highlight the interpolated value of the separation height $z_c$

Figure 8a shows the relative impact of each kinetic-energy contribution during the investigated night. While not negligible, the wave contribution decreases towards the ground, becoming predominant only within the FGS, where it is expected to modify the kinetic-energy budget. A similar behaviour is also observed for the potential energy in Fig. 8b, where the wave is the dominant fluctuation within the FGS, while it resembles the small-scale turbulence in the NGS. From the observations so far, we can conclude that the wave has a strong impact on the velocity and temperature variances, drastically modifying the turbulence field away from the ground.

From these averaged profiles, the separation height falls somewhere between 2 m and 5 m, where we have the criss-cross of the wave and small-scale turbulence profiles. By applying a shape-preserving interpolation of the difference between wave and small-scale turbulence profiles, we obtained a rough approximation of the separation height at $z_c\approx$ 3 m. The value of $z_c$ is in line with Fig. 9a, which shows a self-comparison of between the time-dependent kinetic energies of wave and small-scale turbulence. In Fig. 9a, the kinetic energy of the total fluctuations $\langle E_K\rangle$ is displayed as a function of the difference between small-scale turbulence and wave kinetic energies normalized on the total one. For $\langle R_{T,W}^E\rangle$ > 1, (small-scale turbulence larger than wave fluctuations) the abscissa becomes positive as the small-scale turbulence contribute the most to the kinetic-energy budget. For $\langle R_{T,W}^E\rangle$ < 1, (wave larger than small-scale-turbulence fluctuations) the abscissa becomes negative and the wave contribution is no longer negligible. In the first case, measurements are confined at z < $z_c$, while being at z > $z_c$ in the second, confirming the behaviour observed from the profiles. With an estimation of $z_c$, the remaining unknown for the computation of H is f(Ri), which can be evaluated from the ratio $E_T/\tau$ according to Eq. 20. Figure 9b shows that $E_T/\tau$ is mostly independent from the Richardson number, especially for $Ri<$ 0.1 where the 2-m and 5-m measurements are located and their distributions collapse on the expected value $f(Ri)=1/\alpha _B$. Finally, Eq. 29 gives a value of H $=$ $(5 \pm 1)$ m evaluated with the averaged quantities measured at 2 m and 5 m, weighted on the distance to the approximated value of $z_c$. This result is in line with the observations from the time series in Sect. 3.1, where we described the wave activity being triggered by the valley roughness and density currents confined in a few metres above the ground. As a verification, the separation height computed using Eq. 28 with nocturnal- and layer-averaged quantities gives a value of $z_c$ $=$ $(3 \pm 1)$ m.

Fig. 9

a Kinetic energy of the total fluctuations $\langle E_K\rangle$ as a function of the difference between small-scale turbulence $\langle E_T\rangle$ and wave $\langle E_W\rangle$ kinetic energies normalized on $\langle E_K\rangle$. Plus symbols represents the 30-min averages, dots with error bars the nocturnal average over the period 0500–1200 UTC with errors derived from the standard deviations. b Shows the ratio $E_T/\tau$ as a function of Ri. The black dashed line identifies the expected value $f(Ri)=1/\alpha _B$ at Ri $=$ 0. Data are 2-min averaged. In both panels, colours define the sonic levels (0.5 m in cyan, 2 m in red, 5 m in yellow, 10 m in purple, and 20 m in green)

4.2 Wave and Small-Scale Turbulence Fluctuations

The separation height $z_c$ defines the depth of the NGS, where the kinetic energy of the total fluctuations is mostly driven by the small-scale turbulence, and fixes the beginning of the FGS, where waves become the main contributor. Following the recent study by Schiavon (2020), the presence of waves affects the horizontal components of the total fluctuation kinetic energy while leaving the vertical component almost untouched. The spectral analysis performed in Sect. 3.2 aligns with the evidence from this study, despite the fact that we are investigating a flow in complex terrain. Figure 10a, b shows these different behaviours between horizontal $\langle uu_y+vv_y\rangle$ and vertical $\langle ww_y\rangle$ velocity components (with y being alternatively W, T or K), with the first defining the behaviour of the whole kinetic energy already observed in Fig. 9a. Measurements in Fig. 10b are mostly close to the abscissa value of 1, meaning the waves do not affect the vertical component of the TKE. Note that values of Fig. 10b abscissa larger than 1 mean $\langle ww_W\rangle$ < 1 (and $\langle ww_K\rangle$ < $\langle ww_T\rangle$), with the waves inefficiently subtracting vertical momentum from the mean flow.

Fig. 10

a Quadratic sum of the horizontal components of the total fluctuation kinetic energy $\langle uu_K+vv_K\rangle$ as a function of the difference between small-scale turbulence $\langle uu_T+vv_T\rangle$ and wave $\langle uu_W+vv_W\rangle$ quadratic sum of the horizontal components normalized on $\langle uu_K+vv_K\rangle$. b Analogous to panel a for the vertical component $\langle ww_K\rangle$ of the fluctuation kinetic energy. In both panels, plus symbols represents the 30-min averages, dots with error bars the nocturnal average over the period 0500–1200 UTC with errors derived from the standard deviations. Colours define the sonic levels (0.5 m in cyan, 2 m in red, 5 m in yellow, 10 m in purple, and 20 m in green)

Fig. 11

Nocturnal-averaged (0500–1200 UTC) profiles of a the stress tensor $\langle \tau \rangle$ and b the heat flux $\langle w{\Theta }\rangle$ of the total fluctuations (cyan), wave (green), and small-scale turbulence (orange). The subscript y in both panels stands for K, W, and T. Wave and small-scale turbulence profiles are shifted 0.4 m downwards and upwards respectively, to avoid symbols superposition. The dashed black lines highlight the interpolated value of the separation height $z_c$

A different paradigm applies to the vertical covariances, where the wave impact remains small regardless of the sublayer we are supposedly in (as shown in Fig. 11). Over a nocturnal average, the vertical covariances are indeed mostly dominated by the small-scale turbulence. The only exceptions can be found at the 20-m measurement level, where the flow is affected by the largest eddies, and the separation between wave and small-scale turbulence becomes more irrelevant. However, no separation height can be observed in opposition to the variances’ behaviours, allowing the formation of interesting variance–covariance interactions/separations in the budget.

The existence of a variance–covariance activity is a symptom of the different ways waves and small-scale turbulence can interact in such a small atmospheric depth. Figure 12 displays the ratio of the variances as a fuction of the covariance ratios. In other words, Fig. 12 shows the effects of the production/destruction terms of each energy budget on the respective energy. In Fig. 12a, the ratio $\langle R_{K,T}^E\rangle$ is displayed as a function of the stress-tensor and heat-flux ratios $(\langle R_{K,T}^\tau \rangle + \mid \langle R_{K,T}^{w{\Theta }}\rangle \mid )/2$. Similarly, Fig. 12b shows the potential-temperature-variance ratio $\langle R_{K,T}^{\Theta }\rangle$ as a function of the heat-flux ratio $\mid \langle R_{K,T}^{w{\Theta }}\rangle \mid$. The reciprocal behaviour of variances and covariances defines four possible fluctuation regimes. The no-perturbation regime is established for small values of both variances and covariances, meaning the wave effect on the production/destruction terms of the budgets are small/negligible, with the corresponding small/negligible impacts on kinetic and potential energies. Conversely, the perturbation regime occurs where both values of variances and covariances are large, corresponding to a large/dominant wave effect on both production/destruction terms and both energies (small/negligible and large/dominant are intended with respect to the small-scale turbulence). In between, two cross-regimes are also possible, where variances and covariances have an opposite tendency. The variance-perturbed regime corresponds to large variances with small covariances, and describes a large/dominant effect of the wave on the kinetic and potential energies despite a small/negligible impact on the production/destruction terms of the budget. Finally, the covariance-perturbed regime (corresponding to large covariances inducing small variances) describes an increase of the production/destruction terms of the budgets with minimum impact on the kinetic and potential energies. The first two regimes describe a direct correspondence between wave activity and modification of the energy budgets. The wave activity proportionally enhances kinetic and potential energies as well as the production/destruction terms in the respective budget. Within the covariance-perturbed regime, the wave activity only involves the production and loss terms, creating a sort of balance between them, which does not modify the energy amounts. Within the variance-perturbed regime, the energy variations may be induced by external contributions, such as divergences of the third-order moments and flow unsteadiness.

Fig. 12

a Total fluctuation and small-scale turbulence kinetic energy ratio $\langle R_{K,T}^E\rangle$ as a function of the mean production/destruction terms given by stress-tensor and heat-flux ratios $(\langle R_{K,T}^\tau \rangle +\! \mid \langle R_{K,T}^{w{\Theta }}\rangle \mid )/2$. b Total fluctuation and small-scale turbulence potential-temperature-variance ratio $\langle R_{K,T}^{\Theta }\rangle$ as a function of the mean production/destruction term given by the heat-flux ratios $\mid \langle R_{K,T}^{w{\Theta }}\rangle \mid$. Background colours identify the perturbation regimes: no perturbation in green, perturbation in pink, covariance perturbation in blue and variance perturbation in grey. Data colours identify the sonic level (0.5 m in cyan, 2 m in red, 5 m in yellow, 10 m in purple, and 20 m in green). The dashed lines are the regime thresholds

The boundaries of the fluctuation regimes are identified by means of typical values. As far as the kinetic energy is concerned, the variance threshold (separating small from large values of energy variances) is 2$\langle R_{K,T}^{E} \rangle _{n,\varDelta z}$ (twice the ratio of total fluctuation and small-scale turbulence kinetic energies averaged over the night and measured layer). Since $\langle R_{K,T}^{E} \rangle _{n,\varDelta z}$ represents the typical nocturnal contribution of the small-scale turbulence on the total fluctuation kinetic energy, we expect 2$\langle R_{K,T}^{E} \rangle _{n,\varDelta z}$ to be an appropriate threshold as it ensures wave and small-scale turbulence to equally contribute to the kinetic energy of the total fluctuations. The value of $\langle R_{K,T}^{E} \rangle _{n,\varDelta z}$ has been revealed as inadequate for separating the covariances (see discussion on Fig. 11), but we consider twice the nocturnal- and observed-layer-averaged covariance ratios $\langle R_{K,T}^\tau + \mid R_{K,T}^{w{\Theta }}\mid \rangle _{n,\varDelta z}$ to be a more accurate threshold (where the factor 2 is consistent with the previous discussion). In analogy, we consider 2$\langle \mid R_{K,T}^{{\Theta }}\mid \rangle _{n,\varDelta z}$ and 2$\langle \mid R_{K,T}^{w{\Theta }}\mid \rangle _{n,\varDelta z}$ respectively as the variance and covariance thresholds for the potential energy. In particular, the first is considered as accurate in representing the variances threshold for the potential energy, as it identifies where wave and small-scale turbulence has an equal impact on the total potential-temperature fluctuations (and thus corresponding to the wave–turbulence balance observed in the NGS of Fig. 8b).

As evident for both kinetic and potential energies (see Fig. 12), the no-perturbation regime establishes as the most typical, describing the majority of the NGS evolution. Measurements in the FGS also occupy the perturbed regimes. It is not rare to have large covariances leading or not to large kinetic energy, especially in the farthermost measurement level from the ground. On the contrary, several variance-perturbed data are observed as far as the potential temperature is concerned, suggesting the potential temperature may receive a relevant contribution from larger scales (small frequencies) enhancing their variances.

4.3 The Energy Budgets in the Surface-Layer Approximation

To evaluate the kinetic- and potential-energy budgets, we adopt the surface-layer approximation to consider as negligible the horizontal derivatives and the mean vertical component of the wind velocity. Although rough, this approximation allows removal of those terms of the budget that are often rather difficult to evaluate in the field. As such, most field experiments prefer to detail the vertical structure of the surface layer rather than the horizontal one, forcing the computation to be independent of the advection. The negligible mean vertical velocity component is instead a quite gentle approximation as it is typically smaller than the horizontal components. Additionally, we consider stationary conditions and we neglect the divergence of third-order moments of both waves and small-scale turbulence (terms II and III in Eqs. 4, 8, 10, and 14), while we retain the $\varPi$ terms relating to the wave-turbulence interaction (terms VI and VII in Eq. 4, IV and V in Eq. 10, V and IV in Eqs. 8 and 14). The steady-state condition is quite typical within nocturnal periods, and it has been verified for the current case study as both kinetic- and potential-energy tendencies are order of magnitudes smaller than production/destruction terms. The choice on the divergence of third-order moments is twofold: terms involving pressure cannot be computed due to the dataset limitations; most importantly, the observed flow involves an equilibrium state between its motion scales (Sect. 3.4). Moreover, observing the regimes in Fig. 12, they are expected to play a role only for the potential energy, but they will be shown to be ineffective. Applying the aforementioned approximations, the kinetic-energy budget for the total fluctuations (Eq. 8) reduces to

$$\begin{aligned} -\underbrace{\langle u_jw\rangle \frac{d\langle U\rangle }{dz}}_{P} + \underbrace{\beta \langle w{\Theta }\rangle }_{B} + \underbrace{\varPi _W - \varPi _T}_{Re} - \epsilon _T = 0. \end{aligned}$$

(36)

while its counterpart for the small-scale turbulence (Eq. 4) reads

$$\begin{aligned} -\underbrace{\langle u'_jw'\rangle \frac{d\langle U\rangle }{dz}}_{P} + \underbrace{\beta \langle w'{\Theta }'\rangle }_{B} - \underbrace{\varPi - \varPi _T}_{Re} - \epsilon _T = 0. \end{aligned}$$

(37)

With a similar procedure, the potential-energy budgets for the total fluctuations (Eq. 16) and the small-scale turbulence [Eq. 10, multiplied by $\beta (d\langle {\Theta }\rangle /dz)^{-1}$] read, respectively,

$$\begin{aligned} -\underbrace{\beta \langle w{\Theta }\rangle }_{P} + \underbrace{\beta \left( \frac{d\langle {\Theta }\rangle }{dz}\right) ^{-1}\varPi _{{\Theta } W} - \beta \left( \frac{d\langle {\Theta }\rangle }{dz}\right) ^{-1}\varPi _{{\Theta } T}}_{Re} - \epsilon _p = 0 \end{aligned}$$

(38)

and

$$\begin{aligned} -\underbrace{\beta \langle w'{\Theta }'\rangle }_{P} - \underbrace{\beta \left( \frac{d\langle {\Theta }\rangle }{dz}\right) ^{-1}\varPi _{\Theta } - \beta \left( \frac{d\langle {\Theta }\rangle }{dz}\right) ^{-1}\varPi _{{\Theta } T}}_{Re} - \epsilon _p = 0. \end{aligned}$$

(39)

In these equations, Ps are the production terms, Bs the buoyancy, and Res the residuals. To address the effect of the waves on the energy budgets, we compute and compare the approximated budgets in Eqs. 36, 37 and 38, 39 for the total fluctuations and the small-scale turbulence. As argued in Sect. 3.3, the dissipation term we compute for the budget is directly calculated from the inertial subrange of the spectra, and therefore is associated with $\epsilon _T$ and $\epsilon _p$, letting the $\chi _K$ and $\chi _P$ be the residuals. The budgets are integrated on the NGS (0.5–2 m measurement levels) and FGS (5–20 m measurement levels) sublayers, using a weighted average to compute the different quantities of the FGS budget. The budgets are also compared with representative ratios between total fluctuations and small-scale turbulence $\langle R^x_{K,T}\rangle$, such as the energies, the stress tensor, and the heat flux (taken in turns as x).

Fig. 13

Kinetic energy budgets of the total fluctuations in black and small-scale turbulence in red (left y-axis), and ratios $R^x_{K,T}$ of kinetic energy (blue), stress tensor (orange), and heat flux (green) (right y-axis) as a function of time. Panel a shows the NGS, panel b the FGS. The variable y identifies the subscripts K or T, while x stands for the variables E, $\tau$ or $w{\Theta }$

Figure 13 shows the kinetic energy budget, together with the representative ratios, as a function of time. Within the NGS (Fig. 13a), the total fluctuation and small-scale-turbulence budgets are almost perfectly superimposed, with small unbalances around 0945 UTC. The peaks in the $\langle R^x_{K,T}\rangle$ ratios within the interval 0915–0945 UTC are associated with a temporary increase in the wave activity, increasing the surface energy while decreasing the stability (and loss of energy due to buoyancy). As already observed from the regime investigation (see discussion about Fig. 12a), waves do not perturb the kinetic-energy budget, as the wave activity is somehow suppressed and small-scale turbulence becomes the dominant component. With the absence of the variance-perturbed regime (see Fig. 12a), the vertical divergence of the third-order moments are expected to be negligible and the kinetic-energy budgets are closed by the residual terms $\varPi$, $\varPi _W$, and $\varPi _T$ (notwithstanding possible advections). Specifically, since Eqs. 36 and 37 show similar budgets, we must have $\varPi _W - \varPi _T \approx -\varPi - \varPi _T$ and therefore $\varPi _W \approx -\varPi$, suggesting that the wave transport of small-scale turbulence balances the source/sink activity of the small-scale turbulence. In other words, the wave kinetic energy is rapidly suppressed by the small-scale turbulence, in line with the wave absorption observed by Finnigan and Einaudi (1981).

Differences between the total fluctuation and small-scale-turbulence budgets are more evident in the FGS (Fig. 13b), where imbalances also become larger, especially in the total fluctuations. The budget of the small-scale turbulence shows similar oscillations around zero as observed in the NGS, with two negative peaks corresponding to as much relative $\langle R^\tau _{K,T}\rangle$ and $\langle R^E_{K,T}\rangle$ maxima and $\langle R^{w{\Theta }}_{K,T}\rangle$ minima. The imbalances in the total-fluctuations budget are more pronounced than in the NGS, with a tendency towards negative residuals. The peak at 0915–0945 UTC is strongly induced by the wave activity, which turns a NGS dissipation into a production in the FGS (despite the small-scale turbulence budget remains negative). The kinetic-energy budget of the total fluctuations is typically larger than that for the small-scale turbulence ($\langle R^E_{K,T}\rangle$ > 2), corresponding to values of $\langle R^\tau _{K,T}\rangle$ and $\langle R^{w{\Theta }}_{K,T}\rangle$ close to 1, in line with the perturbation regime (wave altering the kinetic energy). In correspondence of the $\langle R^E_{K,T}\rangle$ minima ($\langle R^E_{K,T}\rangle$ $\approx$ 2), $\langle R^\tau _{K,T}\rangle$ $\approx$ $\langle R^\tau _{K,T}\rangle$ $\approx$ 1 and the FGS falls in the no-perturbation regime, coupling the behaviour of the NGS. The balance of the residuals is mostly not achieved, but we mostly expect $\varPi _W - \varPi _T$ $\le$ 0 and $\varPi + \varPi _T$ $\approx$ 0. Transport and advection of small-scale turbulence by the wave have a small effect on the turbulence itself but enhance the fluctuation energy, resulting in the wave feeding energy to the small-scale turbulence (as observed by Finnigan et al. 1984).

Fig. 14

Potential energy budgets of the total fluctuations in black and small-scale turbulence in red (left y-axis), and ratios $R^x_{K,T}$ of potential energy (blue) and heat flux (green) (right y-axis) as a function of time. Panel a shows the NGS, panel b the FGS. The variable y identifies the subscripts K or T, while x stands for the variables $E_P$ or $w{\Theta }$

Similar considerations can be done for the potential-energy budgets in Fig. 14. The total-fluctuation (Eq. 38) and small-scale-turbulence (Eq. 39) budgets in the NGS are well balanced and superimposed (Fig. 14a). Thus, the residuals from both equations are $\varPi _{{\Theta } W} - \varPi _{{\Theta } T}$ $\approx$ $\varPi _{\Theta } + \varPi _{{\Theta } T}$ $\approx$ 0, with no wave–turbulence interaction. The peaks in the potential-energy ratio $\langle R^{E{_P}}_{K,T}\rangle$ (i.e. $\langle E_{PK}\rangle$ > $\langle E_{PT}\rangle$) do not correspond to likewise variations of the forcing ratio $\langle R^{w{\Theta }}_{K,T}\rangle$. The dynamics of the peaks follow the variance-perturbed regime, as unsteadiness and/or transport from upper layers may enhance the potential energy. However, these last contributions (which may be related to the vertical divergence of the third-order moments) do not unbalance the budgets.

Within the FGS (Fig. 14b), the small-scale-turbulence budget alone is balanced while that of the total fluctuations have negative residuals (apart from the peak at 0945 UTC). Therefore, the residual of Eq. 39 gives $\varPi _{\Theta } + \varPi _{{\Theta } T}$ $\approx$ 0, while from Eq. 38 we obtain $\varPi _{{\Theta } W} - \varPi _{{\Theta } T}$ $\le$ 0. Again the potential-energy ratio $\langle R^{E{_P}}_{K,T}\rangle$ $\ge$ 2, with a dynamic that oscillates between the variance-perturbed and the perturbation regimes, both of them implying a wave contribution. Transport and advection of small-scale turbulence by the wave have a small effect on the turbulence itself but enhance the fluctuation energy (in line with the observations by Finnigan et al. 1984).

5 Summary and Conclusions

The presence of waves has been proven ubiquitous within stable boundary layers over complex terrain, where turbulence is typically in a weak but continuous state of activity. The coexistence of waves and turbulence has proven challenging as their interactions can cause additional production/destruction of turbulent energy. A typical approach based on the Reynolds decomposition is inadequate to disaggregate these two contributions, thus causing unbalances in the energy budget equations.

In this article, we adopted the triple-decomposition approach to disaggregate a nocturnal boundary-layer flow into mean, wave, and turbulence contributions, and with that compute the correct kinetic- and potential-energy budgets under the rules of our stable-layer paradigm. Granted by the equilibrium between flow contributions and by the presence of a spectral gap in the power spectra, we identified the buoyancy-driven non-turbulent component (associated with the wave activity) and the inertial turbulent component (the small-scale turbulence) within each variable spectra. To separate waves from turbulence we adopted two time-averaging windows, the shortest of which was evaluated according to the spectral gap of the power spectra and the Ozmidov frequency (which envisages the buoyancy–inertial subrange ratio). This method enables filtering of the wave motion and makes the turbulence explicit. Then, we defined a paradigm using the governing forces supplying the waves (buoyancy) and turbulence (shear) kinetic energies to separate the atmospheric depth close to the surface into two sublayers:

• a near-ground sublayer (NGS) where the wave impact is smaller than turbulence (shear dominates over buoyancy); within this layer, turbulence energy production is driven from the mean flow while dissipation is estimated from the inertial subrange, revealing the double-decomposition approach satisfactory for the energy budgets computation;

• a far-ground sublayer (FGS) above the NGS, where the wave and turbulence both contribute to the energy balances (shear and buoyancy are both important); here the triple-decomposition approach is preferred because it clarifies that the energy production/destruction of the small-scale turbulence does not balance the dissipation due to the additional energy production from wave interaction.

From the comparison between TKE due to shear and that due to waves we also evaluate the separation height between the two sublayers. The proposed investigation is successfully tested on a nocturnal low-level jet case study observed in a wide and gentle-sloping valley during the MATERHORN Program.

The paradigm has proven to efficiently separate a thin layer at the surface where both kinetic and potential energies are turbulence-produced from a thicker layer above where the wave contributions are predominant. On the contrary, shear stresses and heat fluxes (production/destruction terms within the energy budgets) are mostly turbulent-produced, leading to the formation of four regimes of interaction:

• no-perturbation regime, where the wave has a small effect on both energies and their production/destruction terms;

• perturbation regime, where an energy modification caused by the wave corresponds to a variation in the production/destruction terms;

• variance-perturbed regime, where an energy modification caused by the wave does not correspond to a variation in the production/destruction terms;

• covariance-perturbed regime, where a variation of the production/destruction terms caused by the wave does not correspond to a variation of energy.

These regimes proved to be valuable tools to understand and interpret the energy budgets in real environments, where approximations are typically required to overcome the possible lack of data (especially those required to compute horizontal divergences).

The kinetic- and potential-energy budgets were computed for the two sublayers, comparing total fluctuations (wave and turbulence) with the small-scale turbulence alone. Within the NGS, the budgets of total fluctuations are superimposed to the small-scale turbulence, revealing the accuracy of the Reynolds decomposition close to the surface. The balances are almost closed, with a small fraction of small-scale TKE transported by the wave. The discrepancy introduced by the waves became evident in the FGS, with the wave advecting and transporting small-scale turbulence and thus enhancing the total energies. In this sublayer, the triple decomposition provided a better representation of the ongoing interactions.

In conclusion, we have derived a simple paradigm to describe the complexity enclosed in the nocturnal stable boundary layer, establishing a paradigm able to discern and capture the interactions between waves and turbulence. With this study, we encourage novel investigations and applications of this methodology in order to verify its reproducibility in different contexts.

Appendix 1: Derivation of the First-Order Moments under the Triple-Decomposition Framework

The computation of the continuity equation is trivial. Substituting the decomposed velocity in Eq. 2a into Eq. 1a, and applying the phase and time averages we obtain

$$\begin{aligned} \frac{\partial \langle {U}_i\rangle }{\partial x_i}=\frac{\partial {\tilde{u}}_i}{\partial x_i}=\frac{\partial {u'}_i}{\partial x_i}=0. \end{aligned}$$

(40)

To derive the mean velocity $\langle U_i\rangle$ equation, we first apply the phase average and then the time average to the triple-decomposed Eq. 1b so that

$$\begin{aligned} \underbrace{\frac{\mathrm {D} \langle U_i\rangle }{\mathrm {D} t}}_{\mathrm {I}}= -\underbrace{\frac{\partial \langle P\rangle }{\partial x_i}}_{\mathrm {II}}+\underbrace{\beta \langle {\Theta }\rangle \delta _{i3}}_{\mathrm {III}} -\underbrace{\frac{\partial }{\partial x_j}\left[ \langle {\tilde{u}}_j {\tilde{u}}_i \rangle +\langle u'_j u'_i \rangle \right] }_{\mathrm {IV}}, \end{aligned}$$

(41)

where the viscous term has been neglected being in conditions of large Reynolds number. By subtracting Eq. 41 from the phase-averaged triple-decomposed Eq. 1b, we get that for the wave ${\tilde{u}}_i$

$$\begin{aligned} \underbrace{\frac{\mathrm {D} {\tilde{u}}_i}{\mathrm {D} t}}_{\mathrm {I}}= & {} -\underbrace{\frac{\partial {\tilde{p}}}{\partial x_i}}_{\mathrm {II}}+\underbrace{\beta \tilde{{\Theta }} \delta _{i3}}_{\mathrm {III}}+ \nonumber \\&-\underbrace{\frac{\partial }{\partial x_j}\left[ {\tilde{u}}_j \langle U_i\rangle \right] }_{\mathrm {IV}} -\underbrace{\frac{\partial }{\partial x_j}\left[ {\tilde{u}}_j {\tilde{u}}_i -\langle {\tilde{u}}_j {\tilde{u}}_i \rangle \right] }_{\mathrm {V}} -\underbrace{\frac{\partial }{\partial x_j}\left[ \overline{u'_j u'_i}-\langle u'_j u'_i \rangle \right] }_{\mathrm {VI}}, \end{aligned}$$

(42)

where as before the viscous dissipation has been neglected assuming a large Reynolds number estimated on the basis of the wave length and velocity scales. Finally, by subtracting the phase-averaged triple-decomposed Eq. 1b from the triple-decomposed governing equation (Eq. 1b), we obtain for $u'_i$

$$\begin{aligned} \underbrace{\frac{\mathrm {D} u'_i}{\mathrm {D} t}}_{\mathrm {I}}= & {} -\underbrace{\frac{\partial p'}{\partial x_i}}_{\mathrm {II}}+\underbrace{\beta {\Theta }'\delta _{i3}}_{\mathrm {III}}+\underbrace{\nu \frac{\partial ^2 u'_i}{\partial x_j \partial x_j}}_{\mathrm {IV}}+ \nonumber \\&-\underbrace{\frac{\partial }{\partial x_j}\left[ u'_j \langle U_i\rangle \right] }_{\mathrm {V}} -\underbrace{\frac{\partial }{\partial x_j}\left[ u'_j u'_i-\overline{u'_j u'_i}\right] }_{\mathrm {VI}} -\underbrace{\frac{\partial }{\partial x_j}\left[ {\tilde{u}}_j u'_i+u'_j{\tilde{u}}_i\right] }_{\mathrm {VII}}. \end{aligned}$$

(43)

The equations for mean flow, wave, and small-scale turbulence contributions share some similarities: terms I describe the material derivative (tendency and advection), terms II are the pressure divergence, terms III the buoyancy. Coupling terms between different equations can be found as well, but rather similar to that obtained with the Reynolds decomposition. Term IV in Eq. 41 represents the divergence of the wave and small-scale turbulence fluxes, subtracting momentum from the mean flow. Terms IV in Eq. 42 and V in Eq. 43 are the divergence of the mean flow coupled with the wave and the small-scale turbulence respectively. Term IV in Eq. 43 is the viscous dissipation. However new terms also appear as a consequence of the triple decomposition. Term V in Eq. 42 is the divergence of the fluctuation of the instantaneous momentum flux with respect to its mean, while term VI in Eq. 43 is the analogous term concerning the small-scale turbulence and the departure of the flux from its phase average. Terms VI in Eq. 42 and VII in Eq. 43 couple the wave to the small-scale turbulence. In particular, the expression between square brackets in VI (Eq. 42) is referred in the literature as

$$\begin{aligned} {\tilde{r}}_{ij}=\overline{u'_i u'_j} - \langle u'_i u'_j \rangle , \end{aligned}$$

(44)

and is interpreted as the wave-like fluctuation in the small-scale turbulence due to the presence of the waves (for a thorough discussion on ${\tilde{r}}_{ij}$ the reader is referred to Reynolds and Hussain 1972).

Following the same procedure, the potential temperature equation (Eq. 1c) is separated into the mean, wave and small-scale turbulence contributions. Taking the phase average of triple-decomposed Eq. 1c we obtain the equation for $\langle {\Theta }\rangle +\tilde{{\Theta }}$. Taking the time average of this equation we obtain the equation for $\langle {\Theta }\rangle$

$$\begin{aligned} \underbrace{\frac{\mathrm {D} \langle {\Theta }\rangle }{\mathrm {D} t}}_{\mathrm {I}}= -\underbrace{\frac{\partial }{\partial x_j}\left[ \langle {\tilde{u}}_j\tilde{{\Theta }}\rangle +\langle u'_j {\Theta }'\rangle \right] }_{\mathrm {II}}, \end{aligned}$$

(45)

where the viscous term has been neglected. Subtracting Eq. 45 from the equation for $\langle {\Theta }\rangle +\tilde{{\Theta }}$ we get the equation for the wave contribution $\tilde{{\Theta }}$

$$\begin{aligned} \underbrace{\frac{\mathrm {D} \tilde{{\Theta }}}{\mathrm {D} t}}_{\mathrm {I}}= -\underbrace{\frac{\partial }{\partial x_j}\left[ {\tilde{u}}_j \langle {\Theta }\rangle \right] }_{\mathrm {II}} -\underbrace{\frac{\partial }{\partial x_j}\left[ {\tilde{u}}_j \tilde{{\Theta }}-\langle {\tilde{u}}_j \tilde{{\Theta }} \rangle \right] }_{\mathrm {III}} -\underbrace{\frac{\partial }{\partial x_j}\left[ \overline{u^\prime _j {\Theta }^\prime }-\langle u^\prime _j {\Theta }^\prime \rangle \right] }_{\mathrm {IV}}, \end{aligned}$$

(46)

where the viscous term has been neglected as we are in high Reynolds number regimes. By subtracting the equation for ${\Theta }+\tilde{{\Theta }}$ from the triple-decomposed governing potential-temperature equation (Eq. 1c) we obtain the equation for the small-scale turbulence ${\Theta }'$

$$\begin{aligned} \underbrace{\frac{\mathrm {D} {\Theta }'}{\mathrm {D} t}}_{\mathrm {I}}= -\underbrace{\frac{\partial }{\partial x_j}\left[ u'_j \langle {\Theta }\rangle \right] }_{\mathrm {II}}+ \underbrace{\nu _{\Theta } \frac{\partial ^2 {\Theta }'}{\partial x_j \partial x_j}}_{\mathrm {III}} -\underbrace{\frac{\partial }{\partial x_j}\left[ u'_j {\Theta }'-\overline{u'_j {\Theta }'}\right] }_{\mathrm {IV}} -\underbrace{\frac{\partial }{\partial x_j}\left[ {\tilde{u}}_j {\Theta }'+u'_j\tilde{{\Theta }}\right] }_{\mathrm {V}}. \end{aligned}$$

(47)

Again, the equations for the mean, wave, and small-scale turbulence contributions share terms I, describing the material derivative, and terms II, coupling the mean contributions to both wave and small-scale turbulence. Coupling terms between different equations can be found as well, but rather similar to that obtained with the Reynolds decomposition. Term III in Eq. 47 is the viscous dissipation. Terms III in Eq. 46 and IV in Eq. 47 are analogous to term V in Eq. 42 and VI in Eq. 43 respectively, while terms IV in Eq. 46 and V in Eq. 47 couple the wave to the small-scale turbulence. In particular, the expression in square brackets in term IV of Eq. 46 is referred in the literature as

$$\begin{aligned} {\tilde{r}}_{j{\Theta }}=\overline{u^\prime _j {\Theta }^\prime }-\langle u^\prime _j {\Theta }^\prime \rangle , \end{aligned}$$

(48)

interpreted as the wave-like fluctuation in the small-scale turbulence due to the heat-flux variation induced by the wave (Finnigan et al. 1984).

Standard manipulations of the first-order moment and potential-temperature equations enable the computation of the kinetic and potential energy budgets.