The Dynamical Coupling of Wind-Waves and Atmospheric Turbulence: A Review of Theoretical and Phenomenological Models

Abstract

When wind blows over the ocean, short wind-waves (of wavelength smaller than 10 m) are generated, rapidly reaching an equilibrium with the overlying turbulence (at heights lower than 10 m). Understanding this equilibrium is key to many applications since it determines (i) air–sea fluxes of heat, momentum and gas, essential for numerical models; (ii) energy loss from wind to waves, which regulates how swell is generated and how energy is transferred to the ocean mixed layer and; (iii) the ocean surface roughness, visible from remote sensing measurements. Here we review phenomenological models describing this equilibrium: these models couple a turbulence kinetic energy and wave action budget through several wave-growth processes, including airflow separation events induced by breaking waves. Even though the models aim at reproducing measurements of air–sea fluxes and wave growth, some of the observed variability is still unexplained. Hence, after reviewing several state-of-the-art phenomenological models, we discuss recent numerical experiments in order to provide hints about future improvements. We suggest three main directions, which should be addressed both through dedicated experiments and theory: (i) a better quantification of the variability wind-wave growth and of the role played by the modulation of short and breaking wind-waves by long wind-waves; (ii) an improved understanding of the imprint of wind-waves on turbulent coherent structures and; (iii) a quantification of the interscale interactions for a realistic wind-wave sea, where wind-and-wave coupling processes coexist at multiple time and space scales.

1 Introduction

Understanding the properties of atmospheric turbulent motions close to the sea surface is of utmost importance for air–sea interactions, since they determine the air–sea fluxes of momentum, heat, and gases. It is a complex problem, essentially due to the presence of ocean surface waves (see, e.g., the reviews on wind-and-wave interactions in Jones et al. 2001; Janssen 2004; Sullivan and McWilliams 2010; LeMone et al. 2019).

Indeed, field observations (e.g., Edson et al. 2013, reproduced in Fig. 1a) indicate that, in the presence of surface waves and for sufficiently strong winds, the turbulent momentum flux on top of the so-called wave boundary layer (WBL), of height of about 10 m, is increased with respect to a flat surface (for averaging periods of about 30 min, compare solid and dashed lines in Fig. 1a). Thus the disturbances generated by surface waves, whose amplitude is coupled to atmospheric turbulence, result in an overall change in the properties of turbulence in the WBL (see also the experiments of Edson and Fairall 1998; Sjöblom and Smedman 2002). For neutral atmospheric conditions, this translates into a non-linear one-to-one relation between momentum fluxes and 10-m wind (Fig. 1a, black line), which can be interpreted as describing a local wind-over-waves equilibrium: wind-waves, generated by the local winds, come to an equilibrium with near-surface turbulence, as expressed by the 30-min-averaged turbulent momentum flux. This non-linear relation is at the heart of parametrizations of air–sea fluxes used in numerical models, and is reproduced by wind-over-waves phenomenological models (solid line in Fig. 1a).

Fig. 1

Two examples of measurements related to wind-and-wave coupling. a Surface momentum flux versus 10-m neutral wind speed (i.e. for which atmospheric stability effects have been removed). Dots are open-ocean measurements (Edson et al. 2013) and the solid and dashed lines are from a phenomenological wind-over-waves model (Kudryavtsev et al. 2014). The grey horizontal bar exemplifies the wind variability unexplained both by parametrizations and phenomenological models for a fixed momentum flux of 0.35 $\hbox {m}^2$ $\hbox {s}^{-2}$. b Dimensionless wave growth rate versus wave age (the ratio between wave phase speed c and friction velocity $u_*$). Wave growth is defined as $\beta = E^{-1}\hbox {d}E/\hbox {d}t$ where E is the wave energy, and is normalized by $\omega ^{-1}$, the wave orbital frequency. For clarity, the upper axis shows the corresponding wavelength for a 10-m wind speed of 10 m $\hbox {s}^{-1}$ [i.e., $u_*\approx 0.35$ m $\hbox {s}^{-1}$, corresponding to the grey bar in (a)]. Crosses are measurements compiled by Plant (1982), while the two lines represent theories discussed in Sect. 3

However, the data of Fig. 1a also show some scatter around the wind-over-waves equilibrium described by the black curve (take, for example, a momentum flux of 0.35 $\hbox {m}^2$ $\hbox {s}^{-2}$, then the measured winds cover a range of almost 5 m $\hbox {s}^{-1}$, grey interval in Fig. 1a). Besides measurement variability (which is small for 30-min averages), this indicates that other variables might be missing in the description of the wind-over-waves equilibrium. More fundamentally, such a variability reflects missing knowledge about the sources and sinks of wave energy. The life cycle of a wave is indeed very complex, and consists of its generation and maintainment by the wind, and its dissipation by wave breaking and non-linear wave-wave interactions (see e.g., Longuet-Higgins 1987). This complex life cycle has been mathematically described by separating the sources and sinks into distinct physical processes, among them wave growth. Hence wave growth, which in reality encompasses several different physical processes, is at the heart of a proper description of the wind-over-waves equilibrium.

Theories of wind-wave growth are often based on (and validated by) laboratory measurements of the type shown in Fig. 1b. As pointed out by H. Mitsuyasu (Donelan et al. 1991), these data, often “obtained from a very carefully controlled experiment" exhibit a strong scatter (the data are plotted in logarithmic scale, see Fig. 3 for further evidence of this scatter). This shows that “there still remain problems in understanding even such a fundamental process" as wave growth, and its variability. This knowledge gap motivates the present review, which aims at bringing together various phenomenological and theoretical models of the wind-over-waves equilibrium to foster novel ideas and research. What follows is by no means an exhaustive or historical review, but rather one with a specific focus on theoretical and phenomenological studies of the WBL. Note also that in the following we do not discuss stability effects, which are usually accounted for by standard Monin–Obukhov similarity theory (e.g., Edson et al. 2013), as discussed in Ayet et al. (2020a) in the context of phenomenological wind-over-waves modelling.

The difficulty in describing flows over surface waves comes from several aspects, which distinguish this type of flows with respect to flow above hills and fixed wavy boundaries (see also the review by Belcher and Hunt 1998, where both flows are compared, albeit differently than in the following).

First, surface waves are moving multi-scale undulations of the sea surface, which generally follow a dispersion relation. More precisely, the phase speed $c = \omega /k$ of an isolated linear monochromatic wave depends on its wavenumber k and frequency $\omega$, which are linked as $\omega ^2 =g k+ T_\mathrm{sw}k^3$, where g is the acceleration due to gravity and $T_\mathrm{sw}$ is the dynamical surface water tension. The phase speed has a minimum for waves of wavelength ($\lambda = 2\pi /k$) of 1.6 cm, which marks the transition between capillary (smaller) and gravity (longer) waves: the phase speed of gravity waves increases with their size, as opposed to capillary waves. Note that this deep-water dispersion relation is modified for small-scale waves riding on larger-scale waves: the frequency of small-scale waves is Doppler-shifted by the orbital velocity of the longer waves, and heaving effects can impact the local gravity acceleration.

This first feature implies that the impact of waves on atmospheric turbulence should depend not only on their variable geometry, but also on the relative velocity of the wave with respect to the airflow, and hence on the scale of the wave (see for instance Kitaigorodskii 1973, p. 27 to 36, where the surface is modelled as a linear superposition of moving roughness elements). The relative velocity of the wave is termed wave age, $c/u_*$, with $u_*$ the friction velocity (the square root of the momentum-flux magnitude on top of the WBL).

Second, the airflow bottom boundary condition is non-uniform, and strongly depends on the wave steepness. As explained by Kraus (1967), the difference in dynamic viscosity between the air and the water results in the air–sea interface moving at the wave orbital velocity. The wave orbital velocity varies quasi-periodically in the reference frame of the wave, and its magnitude, akc, depends on the wave steepness ak (a is the wave amplitude). As waves grow and decay locally under the action of the wind, non-linear wave-wave interactions and dissipation, their steepness changes (Longuet-Higgins 1987). Hence the airflow bottom boundary condition is non-uniform, stochastic, and is dynamically coupled to the wind and wave fields.

The growth and decay of waves under the action of the wind is also a very complex mechanism. It cannot be simply explained by a Kelvin-Helmoltz-type instability (as originally proposed by Lord Kelvin, Thomson 1871). Indeed a suction on top of wave crests strong enough to overcome the gravity-restoring force would only occur for winds stronger than about 6–7 m $\hbox {s}^{-1}$, while waves are already present at much lower wind speeds (Ursell 1956). Additionally, random wave breaking is an essential component of the sea-surface equilibrium state, associated with transient and intense energy dissipation events from the wave field towards ocean currents, but also to intense ejection events and momentum flux spikes in the atmosphere (Banner and Melville 1976; Kawamura and Toba 1988; Melville 1996).

Finally, a realistic sea surface is described by a broadband wave spectrum: it is a multiscale interface which can be, to some extent, viewed as a sum of individual components, each moving at a different phase speed. This implies three additional difficulties: (i) the roughness properties of waves of different sizes (quantified by, e.g., the roughness Reynolds number) are modulated and span a wide range of regimes, and hence the overall effect of the multiscale sea surface is non-trivial (Kitaigorodskii 1973; ii) the response of a given wave component to the airflow depends on its non-linear interaction with other wave components, which redistributes energy among different wavenumbers (Phillips 1985; iii) the response of the turbulent airflow to a multiscale surface can be qualitatively different from the superposition of responses to individual wave components (Deardorff 1967).

From a practical point of view, it is interesting to length represent the impact of these various features on the atmosphere through a roughness length $z_0$ (the height at which the mean wind speed, following a logarithmic law, becomes zero). A very influential scaling was proposed by Charnock (1955) for sufficiently wind speeds: $z_0 \propto u_*^2/g$. This scaling can be interpreted in light of the observations of Francis (1954) and Munk (1955), which indicate that the wind stress (equivalent to $z_0$) should essentially depend on short wind-wave (of wavelength smaller than one metre). As argued by Phillips (1977) (p. 194), the amplitude of short wind-wave depends on wind-induced surface drift (related to $u_*$) and wave breaking (related to gravity), and hence scales with $u_*^2/g$, explaining the Charnock relation. An important consequence of this argument is that, at a bulk scale, wind stress is related to the mean square slope of the sea surface, which is mainly driven by short wind-wave, and not to its mean square height, which is mainly set by larger, uncoupled waves.

This bulk Charnock scaling, verified experimentally and commonly used in weather-forecast and climate models, gives a first intuition on the fact that the steepness of short wind-waves is important in the coupling of the sea surface with the atmosphere. While this represents an aspect of the coupling, in an averaged sense, it does not highlight the physical processes at stake in the interaction between the highly fluctuating turbulent and wave motions. In the following, we review models that go beyond this description, focusing on theoretical and phenomenological models of a stationary and horizontally-homogeneous WBL, where the turbulent airflow reaches an equilibrium with locally generated wind-waves (i.e., without swell). These hypotheses imply that the WBL is a constant-flux layer, described in Sect. 2. An essential element of this constant-flux layer is wave-induced stress, resulting from wave-coherent perturbations of the airflow moving at the phase speed of the waves. Wave-induced stress is intrinsically related to wave growth, and we discuss its modelling in Sect. 3. The interaction of turbulence with wave-induced motions for a realistic sea surface is then presented in Sect. 4. In what follows we only consider waves aligned with the mean wind direction (denoted by U, in the streamwise, x, direction). In those coordinates, the mean wind speed is zero in the spanwise (y) and vertical (z) directions.

2 Momentum Balance in the Wave Boundary Layer

In the following, we focus on the properties of the stationary and homogeneous WBL, above which the impact of waves on turbulent motions can be regarded as negligible. In this section we discuss its momentum balance.

2.1 Wave-Induced Motions

At the core of the coupling between wind and waves is the existence of perturbations of atmospheric quantities, which are correlated to waves, and that can extract or lose energy either to the mean flow or to turbulent motions, leading to wave growth or decay. As discussed in Stewart (1961), since these motions carry energy down to the surface, their coherency must increase as height decreases, in the sense that the different components of the motions become increasingly correlated (e.g., the covariance between horizontal and vertical velocities). These wave-induced motions are similar to internal waves in stably stratified turbulence (e.g., Zilitinkevich et al. 2008), or to flow over inhomogeneous surfaces, such as forest canopies (see Kaimal and Finnigan 1994, p. 84). Formally, in the presence of ocean waves the flow, for example the streamwise velocity component, is linearly decomposed into a mean component $\langle {\overline{u}} \rangle = U$, a wave-induced component $\overline{u} = u_\mathrm{w}$, and a turbulent component $u'$

$$\begin{aligned} u = U + u_\mathrm{w} + u', \end{aligned}$$

(1)

where $\overline{\text {}\cdot \text {}}$ is a Reynolds average, filtering the turbulent motions, and $\langle \cdot \rangle$ is a wave average, i.e., filtering wave-induced motions (Phillips 1977, p. 118).

Defining wave-induced motions is not a trivial task from a theoretical point of view, and this is even more complicated in data (where all the state variables of the flow are often not observed). For flow over canopies, the existence of a third component in the flow (denoted by $u''$ in, e.g., Kaimal and Finnigan 1994, p. 84) results from the spatial inhomogeneities of the canopy, which are fixed in time (at least on the time scales of turbulence). If an observer was to stand at two different positions in the same horizontal plane, it would hence see differences in the time- (or Reynolds-) averaged flow. Those differences then define a space-dependent deviation of atmospheric quantities from their time and space average [i.e. $\overline{u}(x,y,z) = U(z) + u''(x,y,z)$]. The ocean surface is however non-stationary, and its height is on average zero. Hence the same observer would, in the case of ocean waves, not see differences in the time-averaged flow. The previous definition can thus not be applied in a straightforward manner to wave-induced perturbations of the airflow.

This difficulty has led to the development of several methods to define the wave average $\langle \cdot \rangle$. From a theoretical point of view, considering only a single monochromatic wave propagating in one direction allows analysis of the flow in the frame of reference moving with the wave, where the undulations of the sea surface are stationary. In this reference frame, deviations from a Reynolds-averaged flow, as for flow over canopies, can be identified by defining the wave average $\langle \cdot \rangle$ as a space average in the direction of the wave propagation (Phillips 1977, p. 119). Wave-induced motions are, in this frame of reference, periodic with respect to the wave period. Note that the Reynolds average, although sometimes considered as a time average (Makin et al. 1995; Makin and Mastenbroek 1996; Hara and Belcher 2002, 2004), can also be defined as an average in the direction perpendicular to the wave propagation (Phillips 1977; Kudryavtsev and Makin 2004).

In a realistic setting, the surface is described by a continuous spectrum of waves. Assuming that each wave component generates airflow perturbations travelling at its phase speed, identification of wave–induced motions requires a space–time Fourier transform, to separate Fourier components advected at the flow speed from components travelling at the wave speed, as done in large-eddy simulations by Hao and Shen (2019). In field experiments, simultaneous temporal and spatial measurements of the flow are however seldom available. Cross-correlations between the surface displacement and temporal measurements of the wind field have been used to identify the dominant wave-coherent motions (Hristov et al. 1998, 2003) and, when detailed measurements of the sea surface are available, their frequency spectra (Veron et al. 2007, 2008; Grare et al. 2013, 2018).

2.2 Wave-Induced Stress

The existence of wave-induced motions and of an undulating surface has important consequences on the momentum balance of the mean flow. More precisely, the Reynolds- and wave-averaged horizontal momentum balance can be written, for a stationary and horizontally homogeneous flow, as

$$\begin{aligned} \tau _\mathrm{t}(z) + \tau _\mathrm{w}(z) + \tau _\mathrm{v}(z) = u_{*}^2. \end{aligned}$$

(2)

This equation expresses the momentum conservation in the constant-flux WBL. The total momentum flux divided by air density ($u_*^2$) is split between turbulent ($\tau _\mathrm{t}$), wave-induced ($\tau _\mathrm{w}$), and viscous ($\tau _\mathrm{v}$) stresses (Janssen 1989; Makin et al. 1995). At the top of the WBL, the momentum flux is supported entirely by turbulent stresses ($\tau _\mathrm{w} = \tau _\mathrm{v} = 0$) and, at the surface, the turbulent stress vanishes and the flux is supported by wave-induced and viscous stresses. In the following, we only consider the case of wind-waves, extracting momentum from the mean flow (i.e., no swell), and hence $\tau _\mathrm{w} \ge 0$. The additional stress component $\tau _\mathrm{w}$ is the analogue of the dispersive flux for flows in the roughness sublayer of canopies (Wilson and Shaw 1977).

The presence of an undulating surface implies that the momentum balance should be written in surface following coordinates (see, e.g., Phillips 1977; Chalikov and Makin 1991; Kudryavtsev and Makin 2004; Hara and Sullivan 2015, for several surface-following coordinate choices). In these coordinates, the turbulent and wave-induced stresses are expressed as

$$\begin{aligned}&\tau _\mathrm{t} = - \langle \overline{u'W'}\rangle , \end{aligned}$$

(3a)

$$\begin{aligned}&\tau _\mathrm{w} = - \langle u_\mathrm{w} W_\mathrm{w} \rangle + \rho _\mathrm{a}^{-1}\langle p_\mathrm{w} \partial _x \eta \rangle , \end{aligned}$$

(3b)

where $W = w - (\partial \eta /\partial x)u - (\partial \eta /\partial y)v - (\partial \eta /\partial t)$ is the contravariant vertical velocity ($\eta$ is the sea-surface height displacement, i.e. $\langle \eta \rangle = 0$), $p_\mathrm{w}$ is the wave-induced pressure, and $\rho _\mathrm{a}$ is the air density.

Wave-induced stress (Eq. 3b) contains two terms: correlations between wave-induced motions and correlations between wave-induced pressure and surface slope. At the surface, the main contribution to wave-induced stress is the pressure-slope correlation, termed form drag by Phillips (1977), which is responsible for the wave growth and hence maintenance of wave-induced motions (Makin and Mastenbroek 1996). Longuet-Higgins (1969a) further unveiled that form drag, and hence wave growth, results not only from pressure-slope correlations, but also from wave-induced variations in surface turbulent stress in phase with the wave height (i.e., in quadrature with the wave slope), which were shown to act as wave-induced pressure variations in phase with wave slope. Those are included implicitly in the pressure-slope correlation term at the surface.

2.3 The Viscous Sublayer

In the momentum balance discussed above, the viscous stress $\tau _\mathrm{v}$ acts only at the bottom of the WBL, in the so-called viscous sublayer. In wind-over-wave models of the WBL, described below, it represents the unresolved (small-scale) processes. These small-scale processes include viscous friction, but also wave-induced stresses due to waves too small to be explicitly included in $\tau _\mathrm{w}$, due to lack of exact knowledge about their impact. Historically, the WBL model of Chalikov and Makin (1991) included high-frequency gravity waves in the unresolved processes. They were described through a “background” roughness coefficient, tuned to observations. Following ideas from Janssen (1989), Makin et al. (1995) extended the model, with the hypothesis that all surface undulations can be described by a wave spectrum. This eliminates the need for a background roughness parameter, which was then set to the height of the surface viscous sublayer $z_0^v$

$$\begin{aligned} z_0^v = 0.14 \frac{\nu }{\tau _\mathrm{t}^{1/2}(z_0^v)}. \end{aligned}$$

(4)

Evaluation of Eq. 4 requires specification of the turbulent stress on top of the viscous sublayer $\tau _\mathrm{t}(z_0^v)$. Makin et al. (1995) assumed that wave-induced stress is constant with height in the viscous sublayer [$\tau _\mathrm{w}(z_0^v) = \tau _\mathrm{w}(0)$]. This is equivalent to the assumption that all waves with wavelengths smaller than $z_0^v$ do not contribute to the wave-induced stress. By using Eq. 2 at the top of the viscous sublayer (where the viscous stress vanishes), the surface turbulent stress was then expressed as a function of the surface wave-induced stress, i.e., form drag. Note that it is not expected that the behaviour of the flow in this viscous layer is equivalent to the flow in the viscous layer of smooth-wall flows. In the former, small-scale smooth and breaking waves act as roughness elements, inducing pressure gradients that most likely perturb the turbulent organization present in the latter (streaks, or self-sustaining coherent motions, see, e.g., Jiménez 2012).

To summarize, above the height $z_0^v$, the wave-averaged momentum balance in the WBL is a balance between turbulent and wave-induced stresses, which sum-up to a height-independent total momentum flux ($u_*^2$). Close to the surface, turbulent stress vanishes, and wave-induced stress is responsible for the momentum flux to the waves, through form drag.

3 Theoretical Models of Wave-Induced Stress

The previous section highlighted that the impact of waves on the WBL momentum balance occurs through wave-induced stress. As an energy balance reveals (see Sect. 4), wave-induced stress is related to the extraction of mean-flow energy by waves, and hence to wave growth. Historically, the determination of wave growth begins with the separated sheltering mechanism of Jeffreys (1925), according to which airflow separation on the leeside of the wave leads to a pressure drop and hence to wave growth. However, the growth rates predicted by this mechanism did not match measurements. Phillips (1957) and Miles (1957) proposed two mechanisms which aim at explaining the initial and later stage of wave growth, respectively. The mechanism of Phillips (1957) considers the effect of turbulent pressure fluctuations on the free surface, leading to linear wave growth. The mechanism proposed by Miles (1957) considers the inviscid growth of wave-induced motions and waves in the context of stability analysis and neglects turbulent Reynolds stresses, leading to an exponential wave growth. Belcher and Hunt (1993) later argued that the Miles mechanism might not be valid for short waves, for which the effect of turbulence becomes important. This led to the “non-separated” sheltering mechanism whereby, even without airflow separation (which requires waves to be steep), the presence of waves results in a pressure anomaly correlated to wave slope. In the following, we discuss in more detail the Miles (1993) and Belcher and Hunt (1993) mechanisms, since our interest lies in the description of a stationary wind-over-waves system, and not in the initial stages of wave growth described by Phillips (1957).

To understand the dependence of wave-induced stress on sea state, it is interesting to recast it in terms of vortex force. For a stationary flow, the Reynolds-averaged horizontal momentum balance (before wave averaging) can be written as

$$\begin{aligned} \frac{\partial \overline{u}}{\partial t} = 0 = -\frac{1}{\rho _\mathrm{a}}\frac{\partial p_\mathrm{w}^{\text {tot}}}{\partial x} - {\Omega }_\mathrm{w} w_\mathrm{w} + \frac{1}{\rho _\mathrm{a}}\frac{\partial \eta }{\partial x} \frac{\partial p_\mathrm{w}}{\partial z} + \frac{\overline{\tau }_{x,x_j}}{\partial x_j}, \end{aligned}$$

(5)

where we have introduced $\overline{\tau }_{x_i, x_j}$, the Reynolds-averaged turbulent and viscous stress tensor (such that $\langle \overline{\tau }_{x,z} \rangle = \tau _\mathrm{t} + \tau _\mathrm{v}$), ${\Omega }_\mathrm{w} = \partial _z u_\mathrm{w} - \partial _x w_\mathrm{w}$, the spanwise component of the wave-induced vorticity, and with $p_\mathrm{w}^{tot} = p_\mathrm{w} + \frac{1}{2}(u_\mathrm{w}^2 + w_\mathrm{w}^2)$ the wave-induced total pressure. The term ${\Omega }_\mathrm{w} w_\mathrm{w}$ is called the vortex force (Lighthill 1962).

If Eq. 5 is wave-averaged, the horizontal pressure gradient term cancels, due to the streamwise periodicity of wave-induced motions, and Eq. 2 is obtained, with the vertical gradient of wave-induced stress expressed as

$$\begin{aligned} \frac{\partial \tau _\mathrm{w}}{\partial z} = - \langle {\Omega }_\mathrm{w} w_\mathrm{w} \rangle . \end{aligned}$$

(6)

The effect of wave-induced motions on the mean flow can thus be expressed through the averaged wave-induced vortex force and, in the following, we mainly discuss two models for its computation: Miles (1957) matched layer theory for a laminar flow and Belcher and Hunt (1993) non-separated sheltering mechanism for a turbulent flow. In both cases, the wave-induced motions are computed for a monochromatic wave, of wavenumber k, amplitude a, and phase speed c, travelling in the wind direction, and small slopes are considered ($ak \ll 1$). Airflow separation for steep slopes, along with more recent developments, are discussed in Sect. 3.3.

The notation ${d}_k \langle {\Omega }_\mathrm{w} w_\mathrm{w} \rangle$ is used hereinafter to designate wave-averaged vortex force for a single monochromatic wave, also called spectral density of vortex force. In the case of a realistic sea surface, it corresponds to the wave-averaged vortex for waves of wavenumber between k and $k + {d}k$, and is hence related to the total wave-averaged vortex force as

$$\begin{aligned} \langle {\Omega }_\mathrm{w} w_\mathrm{w} \rangle = \int _k {d}_k \langle {\Omega }_\mathrm{w} w_\mathrm{w} \rangle . \end{aligned}$$

(7)

3.1 The Matched Layer Inviscid Theory

Miles (1957) proposed a laminar and inviscid theory for the generation of the vortex force in the WBL. By considering the growth of wave-induced perturbations generated by a monochromatic wave, he was able, using stability analysis, to derive the wave growth rate, and hence the vortex force. This analysis was rather mathematical, and in a later work, Lighthill (1962) discussed Miles’ results using physical arguments.

It is first instructive to consider the following expression, derived by Davis (1972),

$$\begin{aligned} -k^2 [U(z) - c(k)] \langle {d}_k{\Omega }_\mathrm{w} w_\mathrm{w} \rangle = \left\langle \frac{\partial \mathcal {S} }{\partial x} w_\mathrm{w} \right\rangle , \end{aligned}$$

(8)

which links the wave-averaged vortex force to the variations of the Reynolds stress tensor anisotropy $\mathcal {S}$ [defined as $\mathcal {S}= - (\partial _x^2 - \partial _z^2) \langle \overline{u'w'} \rangle + \partial _x \partial _z(\langle \overline{u'^2} \rangle - \langle \overline{w'^2} \rangle )$]. For a laminar flow, the right-hand side (r.h.s.) of the above equation vanishes and hence wave-averaged vortex force can be non-zero only at the matched height $z_m$, where $U(z_m) = c$. However, for a turbulent flow, vortex force is non-zero within a layer around the matched height. That is why, following Phillips (1977), $z_m$ is termed the matched height instead of the critical height, as originally used by Miles. This emphasizes that, unlike the high-vorticity and thin critical layer of standard laminar instability theory, the thickness and intensity of the vortical layer around the matched height depend on turbulence anisotropy.

For a laminar flow, Miles (1957) found a vortex force of the form

$$\begin{aligned} {d}_k\langle {\Omega }_\mathrm{w} w_\mathrm{w} \rangle |_{\text {Matched}} = \underbrace{- \frac{\pi }{k}\frac{U''(z_m)}{U'(z_m)}}_{\text {I}} \underbrace{\langle w_\mathrm{w}^2 \rangle (z_m)}_{\text {II}}\delta (z - z_m), \end{aligned}$$

(9)

where $\delta$ is the Dirac function. This expression was obtained by assuming a small wave slope ($ak \ll 1$), a wave wavenumber lying between the boundary layer depth ($D_b$) and the matched layer height ($1/D_b \ll k \ll 1/z_m$), and a small friction velocity ($u_* \ll U(1/k)$).

The wave-averaged vortex force is localized at the matched height $z_m$ and is the product of two terms. Term I depends on the mean wind curvature ($U'' = \hbox {d}^2U/\hbox {d}z^2$) and shear ($U' = \hbox {d}U/\hbox {d}z$) at the matched layer height, and reveals that, in order to have a net transfer of momentum from wind to waves (a positive vortex force), their ratio should be positive. This is usually the case in the surface layer, in particular for a logarithmic wind profile. Term II depends on the wave-induced vertical velocity variance at the matched height $\langle w_\mathrm{w}^2 \rangle (z_m)$. An expression for $\langle w_\mathrm{w}^2 \rangle (z_m)$ was obtained by Miles, first by an approximate (Miles 1957) and then by an exact (Miles 1959) solution of the small-perturbation equations. Lighthill (1962) derived a similar expression by using a simple balance between wave-induced pressure perturbations and vortex force. In either case, the resulting vertical velocity was found proportional to the wave amplitude, i.e. $\langle w_\mathrm{w}^2 \rangle (z_m) \propto a^2 \omega ^2/2$, yielding an exponential wave growth, unlike the linear Phillips (1957) mechanism. Note that the matched layer mechanism vortex force was also derived more recently by Hristov and Ruiz-Plancarte (2014), in a more general framework, which includes atmospheric stability effects.

Fig. 2

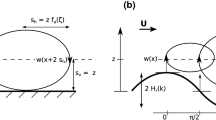
Two models of wind-and-wave interactions. a Laminar and inviscid matched layer mechanism (Miles 1957, drawn here in the wave frame of reference) and b non-separated sheltering mechanism for a turbulent flow (Belcher and Hunt 1993, drawn here in the laboratory frame of reference). a The closed loops formed by the streamlines (solid lines) around the matched height (dashed line) generate pressure-slope correlations due to vertical velocity (red arrows). This results in vortex force at the matched height, and wave growth. b In the inner (turbulent) region, surface undulations modulate turbulent stresses [$\overline{(u'w')}_\mathrm{w}$], causing a displacement of the streamlines downwind. This results in a pressure anomaly at the top of the (inviscid) middle layer, which induces (green arrow) pressure-surface slope correlations at the surface (in red), and a vortex force at the top of the inner region. Note that in b, the matched height lies in the bottommost layer of the flow, called the internal boundary layer. This is because the considered waves are small, and hence slow with respect to the advection velocity of the considered turbulent eddies

The vortex force Eq. 9 results from the dynamical structure of the wave-induced flow around the matched layer, which is described here following Lighthill (1962) and Phillips (1977). Assuming that the flow is two-dimensional (in the x, z plane), streamlines of the wave-induced flow form, in the frame of reference moving with the waves, closed loops (cat’s-eye patterns) centred at the matched height (solid lines in Fig. 2a). Outside of the closed loops, the wave-induced vorticity (${\Omega }_\mathrm{w}$) and vertical velocity ($w_\mathrm{w}$) are in quadrature, and the contribution of those regions to the wave-averaged vortex force is zero (see Lighthill 1962, for more details). Inside the cat’s-eye pattern, fluid elements are trapped and mix the mean flow vorticity $U'$ in the vertical direction (red arrows in Fig. 2a). The resulting vorticity anomaly (the wave-induced vorticity) is proportional to the mean flow curvature $U''$ (appearing in term I) times the vertical width of the cat’s-eye pattern $\delta _m$ (i.e., a first-order Taylor expansion of the vertical variations of mean flow vorticity). The width $\delta _m$ depends on the efficiency of fluid elements to diffuse vorticity inside the closed loop region. A diffusion coefficient can be estimated as $\langle w_\mathrm{w}^2 \rangle /U'$, which explains Eq. 9. Hence Miles’ vortex force can be interpreted as resulting from the mean-flow vorticity variations, transported by fluid elements trapped in the cat’s-eye patterns. It is important to highlight that the above picture should be amended when turbulent motions are considered: turbulence increases vorticity diffusion (increasing vortex force) and decreases the mean vorticity gradient transported by fluid particles (decreasing vortex force) (note, however, that Lighthill 1962 argued that both effects should compensate, and hence that the wave-averaged vortex force should be unchanged). Turbulence also changes the vertical distribution of vortex force which becomes non-zero in a layer around the matched height (Eq. 8). Last but not least, while in the laminar case the streamlines defined above can be interpreted as fluid particle trajectories, this is not true for a turbulent flow.

The time-dependent dynamics of fluid particles inside the cat’s eyes were further analyzed by Reutov (1980). It was argued that the oscillation of the particles inside the cat’s eyes leads to a mixing of vorticity, which causes a decrease in the wave-averaged vortex force over time. This quenching of the momentum transfer from wind to waves leads to a stabilisation of the wind-over-waves coupled system over time. Although in the original analysis of Reutov (1980) the saturated wave amplitude, at equilibrium, was found to be too small compared to observations, this concept was recast by Fabrikant (1976) and Janssen (1982) in their quasi-linear theory of wave growth, explained in Sect. 3.3.

So far, only the wave-averaged vortex force ($\langle {\Omega }_\mathrm{w} w_\mathrm{w}\rangle$) has been discussed. It is however also interesting to discuss the link between wave-induced pressure ($p^w$) and the Reynolds-averaged vortex force (${\Omega }_\mathrm{w} w_\mathrm{w}$). For heights sufficiently far from the wavy surface, Eq. 5 can be simplified by neglecting the pressure-slope term (the third term). Neglecting turbulence (i.e., the fourth term of Eq. 5), the equation is reduced to a balance between the horizontal gradient of wave-induced pressure and the vortex force. Hence, as depicted in Fig. 2a, wave-induced pressure and vortex force should be in quadrature (this is obvious by assuming, e.g., sinusoidal horizontal variations of both quantities). If the vortex force is further approximated, as above, by the product of the wave-averaged shear and the wave-induced vertical velocity (${\Omega }_\mathrm{w} w_\mathrm{w} \sim U'w_\mathrm{w}$), then the wave-induced updrafts and downdrafts should also be in quadrature with wave-induced pressure. For wave-induced streamlines described by Miles’ cat’s-eye pattern, the updrafts and downdrafts are located in between the edges and the middle of the cat’s-eye (vertical red arrows in Fig. 2a). Hence, for Miles’ mechanism to describe wind-waves, i.e., waves that receive momentum from the atmosphere, the centre of the cat’s eyes should be (at least partly) in phase with the wave slope, to induce pressure-slope correlations (see, e.g., Sullivan et al. 2000, for a numerical simulation of this process).

As a final remark, Eq. 9 can be rearranged by (i) introducing the proportionality relation between $\langle w_\mathrm{w}^2 \rangle$ and wave amplitude a mentioned above ($\langle w_\mathrm{w}^2 \rangle (z_m) \propto (akc)^2/2$) and, (ii) using a logarithmic mean wind profile to express $U''/U'$ at the matched height

$$\begin{aligned} {d}_k\langle {\Omega }_\mathrm{w} w_\mathrm{w} \rangle |_{\text {Matched}} \propto \underbrace{\frac{\exp (- \kappa c / u_*)}{z_0 k}}_{\text {I}} \underbrace{\frac{(akc)^2}{2}}_{\text {II}}\delta (z - z_m), \end{aligned}$$

(10)

where $\kappa$ is the von Kármán constant. This expression shows that term I, originating from $U''/U'$, expresses the dependence of the wave-averaged vortex force on wave age: as the underlying wave becomes longer (i.e., faster), the vortex force decreases. Term II originates from $\langle w_\mathrm{w}^2\rangle$, and is related to the wave orbital velocity (akc) which, as mentioned in the introduction, is one of the defining characteristics of surface waves when compared to immobile roughness elements. More importantly, term II also reveals that the wave-averaged vortex force depends on the slope (ak) of the underlying wave, and not on its amplitude. This dependency, formulated by Munk (1955), reflects the increase in contact area between air and water due to the presence of an undulating surface, which increases the momentum flux from wind to waves, and hence vortex force. Note that the assumption that U follows a log profile, which results in the wave-age dependence of term I, is not entirely valid in the WBL (see Sect. 4) and is used here for illustrative purposes only.

3.2 Inclusion of Turbulence: The Non-separated Sheltering Mechanism

The work of Miles (1957) assumed a laminar and inviscid flow. Let us write the momentum balance for wave-induced motions, neglecting the effects of surface curvature, as

$$\begin{aligned} \frac{\hbox {D} u_\mathrm{w}}{\hbox {D}t} = - \frac{1}{\rho _\mathrm{a}}\frac{\partial p_\mathrm{w}}{\partial x} - \frac{\partial \left( \overline{u'w'}\right) _\mathrm{w}}{\partial z}, \end{aligned}$$

(11)

where $\hbox {D}/\hbox {D}t$ denotes the Lagrangian derivative, and $\left( \overline{u'w'}\right) _\mathrm{w} = \overline{u'w'} - \langle \overline{u'w'}\rangle$ the wave-induced variations of turbulent stress (see, e.g., Belcher and Hunt 1998). From the linear analysis, Miles (1957) derived an expression for wave-induced motions from the above balance by neglecting turbulence, i.e. $\partial \left( \overline{u'w'}\right) _\mathrm{w}/\partial z$.

Following this development, several works included turbulent motions in the derivation of the wave-averaged vortex force (Townsend 1972; Jacobs 1987; Van Duin and Janssen 1992; Belcher and Hunt 1993; Belcher 1999). In particular, Belcher and Hunt (1993) found that, for short (young) waves, effects of turbulence overcome Miles’ mechanism in the determination of the vortex force. More precisely, they argued, following Townsend (1972), that there exists a layer close to the surface, called the inner region, in which eddies have a turnover time smaller than their advection time across the wave. In the inner region, of height $l_i$ of about $0.1 k^{-1}$ for a short wave, eddies are in equilibrium with the mean flow and hence wave-induced variations of turbulent stress can be modelled with a mixing-length model

$$\begin{aligned} \left( \overline{u'w'}\right) _\mathrm{w} = 2 \kappa z u_* \frac{\partial u_\mathrm{w}}{\partial z}. \end{aligned}$$

(12)

In the outer region, for heights $z > l_i$, the eddies follow rapid distortion theory, and Belcher and Hunt (1993) found that the flow can be considered as being inviscid (in the sense that $\left( \overline{u'w'}\right) _\mathrm{w} = 0$).

The analysis of Belcher and Hunt (1993) resulted in a mechanism for the generation of wave-averaged vortex force called non-separated sheltering (NSS) mechanism. It is illustrated in Fig. 2b for slow (short) waves. To start with, in the presence of an undulating surface, the streamlines are bent, which creates pressure gradients larger on the crest than on the trough of the wave. In the inner region, as those horizontal pressure gradients develop, they induce vertical gradients of wave-induced turbulent stress (from Eq. 11). This results in higher stress at the surface than at the top of the inner region (bottom-left part of Fig. 2b). Hence, in the inner region, the flow is decelerated as it reaches the surface (from Eq. 5), which causes a displacement of the streamlines downwind by a distance which can be shown to be proportional to $[u_*/U(1/k)]^2$ (middle of Fig. 2b). This sheltering effect of the flow then causes pressure differences in the inviscid outer region, at the so-called middle layer height $l_m$, which are slightly in phase with the wave slope. Those pressure differences affect, at leading order, the pressure at the surface (green arrow in Fig. 2b), causing wave growth, and hence a vortex force. At leading order in $u_*/U(1/k)$, it reads

$$\begin{aligned} {d}_k\langle {\Omega }_\mathrm{w} w_\mathrm{w} \rangle |_{\text {NSS}} = - \underbrace{\mathcal {C}_{\beta }\frac{u_*^2}{c^2}}_{\text {I}} \underbrace{\frac{(akc)^2}{2}}_{\text {II}}\delta (z-l_i), \end{aligned}$$

(13)

where the vortex-force coefficient $\mathcal {C}_{\beta }$ depends on the mean wind speed in the frame of reference of the wave $U_c(z) = U(z) - c$, and is presented as

$$\begin{aligned} \mathcal {C}_{\beta } = \frac{ U_c^2(l_m)}{U_c^2(l_i)}\left( 2 \frac{U_c(l_m)^2}{U_c(l_i)^2} - \frac{U_c^2(l_i)}{U_c^2(l_m)} + 1 \right) . \end{aligned}$$

(14)

The NSS vortex force is localized at the inner layer height, and its magnitude depends on two terms, similar to the matched layer vortex force (Eq. 10). Term I depends on wave age, and on the mean wind shear in the middle layer [through the ratio $U_c(l_m)/U_c(l_i)$]. The quadratic dependence of vortex force on inverse wave age is an important result that was originally proposed by Plant (1982) on the basis of the measurements of Fig. 1b. Term II again expresses the dependence of the vortex force on wave slope. Note that the estimates of $C_{\beta }$ by Plant (1982) are larger than those found from the analytical theory of Belcher and Hunt (1993) by a factor of two (see Fig. 3 and the discussion in Sect. 3.4). Recent works presented below (Kudryavtsev and Chapron 2016) show that this mismatch can be corrected by accounting for short wind-wave modulations by longer waves.

The NSS mechanism is valid for slow $c/u_* < 15$ and fast $c/u_* > 25$ waves (Belcher and Hunt 1993; Belcher 1999). Common to both situations is the matched layer height being markedly distinct from the inner region height. For slow waves, the matched layer lies in the inner layer (see Fig. 2b), where wave-induced variations of turbulent stress are the dominant term in the momentum balance Eq. 11. This is true in particular at the matched height, which is then of little dynamical importance (in the sense that the advection terms, on the left-hand side of Eq. 11, are negligible in the overall balance). For intermediate waves, with $15 \le c/u_* \le 30$, the matched layer and inner region heights are similar. Belcher and Hunt (1993) mention that, for this configuration, the matched layer should be significant in the determination of vortex force, and that the effect of the inner layer dynamics is to tilt the streamlines of the cat’s-eye patterns: streamlines below and above $z_m$ are displaced upwind and downwind, respectively. Note that Janssen (2004) has suggested that the matched height mechanism could be valid for all wave ages. This results from using a different scaling for eddy-turnover time than the one used in the original work of Belcher and Hunt (1993). In the following we focus on slow and short waves which, as mentioned in the introduction, are more determinant in setting the wind-over-waves equilibrium described in Sect. 4. We hence do not discuss the case $c/u_* > 25$.

In addition to wave age, there is another limitation to the NSS mechanism. When the underlying wave is too steep, the downwind thickening of the streamlines can cause a detachment of the flow on the leeside of the wave, similar to the separated sheltering mechanism (Jeffreys 1925). Such airflow separation events, which can occur, e.g., for breaking waves, are discussed below.

3.3 Further Developments

Following the works of Miles (1957) and Belcher and Hunt (1993), other expressions for the vortex force were presented, which we discuss below. These expressions are discussed in the context of a realistic sea surface, for which the amplitude of an individual wave component a can be related to the omnidirectional (i.e., integrated over all angles) wave spectrum S(k) as $a^2 = S(k)k\hbox {d}k$. Upon replacement in Eqs. 10 and 13, the total wave-averaged vortex force for a realistic sea can then be obtained by summation over all wave components (Eq. 7). In addition, for waves whose direction of propagation is at an angle with the mean wind direction, directional dependencies for the vortex force have been proposed (Plant 1982; Mastenbroek et al. 1996) and, for simplicity, are not discussed here.

3.3.1 Quasi-Linear Theory

Following Miles (1965) and the analysis of Reutov (1980), Fabrikant (1976) and Janssen (1982) proposed a quasi-linear theory of wave growth, where a broadband wave spectrum and a time-dependent wind were considered. They considered a continuum of matched layers with random phase, each corresponding to a wave component. The destructive interference between matched layers resulted in a quenching of the vortex force, which was much larger than found by Reutov (1980), and closer to measurements. The numerical studies of Janssen (1982, 1989) further revealed that wave growth was quenched due to the extraction of momentum from the mean component, which reduces the mean wind curvature (term I in Eq. 9): this effect was found to be particularly important for short waves (small $c/u_*$). This is discussed in more details below in the context of the non-separated sheltering mechanism. Note that those numerical simulations were then used in Janssen (1991) to derive a parametrization of vortex force used for the coupling of numerical weather and wave prediction models.

3.3.2 Impact of Longer Waves on the Non-separated Sheltering Mechanism

The analysis of Miles (1965) (which led to the quasi-linear theory) highlighted that the coexistence of multiple wave frequencies could result in a reduction of the vortex forces generated by each of the wave components. More precisely, the existence of a vortex force, and hence of wave-induced stress, results in a change of turbulent stress in the WBL (Eq. 2). Hence the NSS mechanism, which results from variations of turbulent stress in the inner region, should be affected by this modification.

This sheltering effect was formalized by Makin and Kudryavtsev (1999) and later by Belcher (1999). Based on numerical simulations Mastenbroek et al. (1996), Makin and Kudryavtsev (1999) suggested using the local turbulent stress on top of the inner region in place of the friction velocity in the computation of the NSS vortex force (Eq. 13), i.e.,

$$\begin{aligned} {d}_k\langle {\Omega }_\mathrm{w} w_\mathrm{w} \rangle |_{\text {NL-NSS}} = \mathcal {C}_\beta \frac{\tau _\mathrm{t}[l_i(k)]}{c^2(k)} c^2(k) k^2 S(k)\delta [z-l_i(k)]k {d}k, \end{aligned}$$

(15)

where NL-NSS stands for non-linear non-separated sheltering. Hence, as longer waves grow they generate vortex force, and hence wave-induced stress, that shelters the shorter waves, reducing the turbulent stress on top of their inner region. The reduced vortex force of the shorter waves, and hence of their growth leads to a non-linear stabilization of their amplitude, similar to the quenching mechanism put forth by Janssen (1982).

3.3.3 Impact of Breaking Waves

Both the matched layer and the NSS mechanisms require waves that are not steep. For steep waves, airflow separation can occur, which translates in a sharp pressure drop on the forward face of the wave associated with a recirculating pattern in the wind field (see the experimental work by Banner and Melville 1976; Banner 1990; Reul et al. 1999, 2008). Those transient events are associated with waves whose slope is generally confined between 0.1 and 0.5, which are also often breaking waves (Melville 1996). Field measurements indicate that the wave-breaking distribution is strongly correlated with the wind speed and hence that it can be an important parameter in the determination of the wind-and-waves equilibrium (see the measurements of Sutherland and Melville 2013, which cover a wide range of wave scales). Note that recently, Husain et al. (2019) found, using large-eddy simulations and laboratory measurements, that for strong winds, a significant fraction of airflow separation events could also be associated with non-breaking waves.

Airflow separation events have been modelled as additional sources of vortex force by Kudryavtsev and Makin (2001) and later by Kukulka et al. (2007). As the airflow separates over a wave of wavenumber k and of steepness $\epsilon _b = ak$, it creates a pressure difference ${\Delta } p$ between its forward and backward faces. The wind force per unit surface area at the top of the wave is then $- {\Delta } p 2 k \epsilon _b l_b(k)$, where $l_b$ is the length of the breaking crest (i.e., perpendicular to the direction of wave propagation). The resulting vortex force reads

$$\begin{aligned} {d}_k\langle {\Omega }_\mathrm{w} w_\mathrm{w} \rangle |_{\text {AFS}}(z) = \rho _\mathrm{a}^{-1}{\Delta } p 2\epsilon _b \delta (z-\epsilon _bk^{-1}) l_b(k) , \end{aligned}$$

(16)

where AFS stands for “airflow separation". The pressure difference was further parametrized (based on experiments) as a function of a drag coefficient $c_\mathrm{d}^b$, i.e., ${\Delta } p = \rho _\mathrm{a} c_\mathrm{d}^b [U(\epsilon _bk^{-1}) - c(k)]^2$ (and ${\Delta } p = 0$ if the wind on top of the breaking crest, $U(\epsilon _bk^{-1})$, is smaller than the speed of the wave, c). Note that, similarly to the reduction of the NSS sheltering mechanism presented above, Kukulka et al. (2007), Kukulka and Hara (2008b), and Mueller and Veron (2009) proposed a sheltering associated with airflow separation events: smaller waves, on the leeward side of a breaking wave are sheltered from the mean flow, leading to a strong reduction of their vortex force and viscous stress. This sheltering mechanism was found to be important for growing and very young seas, as found mostly in laboratory conditions (Kukulka and Hara 2008b).

For a realistic sea surface, $l_b(k)$ is replaced by $\Lambda (k){d}k$, the length of breaking crests of a given wavenumber per unit area of surface and per unit time. This quantity, introduced by Phillips (1985), represents the scale-dependent distribution of transient wave-breaking events. It is stressed that, even if a small fraction of ocean waves are breaking (5%), their impact on atmospheric turbulence is significant (Banner 1990; Kudryavtsev et al. 2014). In addition, Csanady (1985) argued, on the basis of laboratory measurements of Kawai (1981) and Okuda et al. (1977), that airflow separation on top of centimetre-scale breaking waves could in fact be three-dimensional, due to realistic sea-surface waves being short-crested. This has influences on the properties of the recirculating region, which is no longer isolated from the rest of the flow, but can lead to a reversed-horseshoe kind of motion, with entrained fluid escaping from the sides of the wave before being advected forward again.

Finally, besides supporting the vortex force, airflow separation events also have a profound impact on turbulence spectra. As demonstrated by the large-eddy simulations (LES) of Suzuki et al. (2013), airflow separation events shortcut the inertial-subrange energy cascade through two processes. First, the energy they extract from the mean flow through wake production (see Sect. 4) is directly converted to small-scale eddies instead of being injected at the energy-containing scale. Second, large eddies are shattered into small-scale eddies in the wake of the airflow separation events. Both processes could change the properties of the energy cascade of the inertial subrange in the vicinity of the elements causing airflow separation. While this has been extensively investigated for flow inside canopies and in their roughness sublayer (Finnigan 2000), it remains both a theoretical and experimental challenge for flows over wind-waves.

3.3.4 Impact of Short Wave Modulations

The NSS mechanism (Eq. 13) resulted in a growth coefficient $\mathcal {C}_{\beta }$ which is low, when compared to the measurements compiled by Plant (1982) (dashed line in Fig. 3). Following Longuet-Higgins (1969b) and Davis (1972), Kudryavtsev and Chapron (2016) included the impact of short wave modulations by longer waves in the NSS mechanism to possibly explain this deficiency. Indeed, for a multiscale sea surface, long waves modulate the steepness of shorter waves: it is increased near the crests and decreased in the troughs of the modulating wave. Hence, the short-wave breaking statistics change (wave breaking becomes more intense on the lee side of the wave). This asymmetric variation induces additional turbulent stress variations in the inner region, leading to an enhanced vortex force for the long, modulating wave. Kudryavtsev and Chapron (2016) used a wind-over-waves model (Kudryavtsev et al. 2014) to estimate these variations of short-wave breaking statistics along the longer waves, and found a significant enhancement of the vortex force (dotted-dashed line in Fig. 3).

This indicates that, for a realistic sea surface, the vortex force generated by a single long wave component according to the NSS mechanism is significantly dependent on the existence of shorter waves, modulated by that wave component.

As a final note, it should be stressed that there is increasing evidence that these modulations (which include, more generally, localized patches of transient events with increased roughness related to large scale breakers or wind gusts) are essential not only in the context of the NSS mechanism. First, the intensity of these modulations is strongly dependent on external parameters such as surface currents, fetch and/or complex multi-swell systems, which can cause variability in the overall wind-and-waves system (Ayet et al. 2020a). Second, when recast in the context of Phillips wave-growth theory, these modulations act as a multiplicative random noise in the wave-growth equations and can result in an exponential wave growth, providing another possible mechanism for the wind-and-waves coupling (Farrell and Ioannou 2008).

Fig. 3

Growth-rate coefficient vs. wave age. The coefficient $C_\beta$ is defined as $C_{\beta } = - (c^2/u_*)^2 [(akc)^2/2]\int {d}_k\langle {\Omega }_\mathrm{w} w_\mathrm{w} \rangle dz$. It can be interpreted as a normalized growth rate (Fig. 1b) for which the trend in $u_*^2/c^2$ has been removed. Crosses are the data compiled by Plant (1982) and lines are theoretical models, discussed in Sect. 3

3.4 Discussion

In this section, we have discussed theoretical models describing the emergence of vortex force for slow monochromatic waves (i.e., $c/u_* < 30$). All models result in a vortex force localized either at the matched layer height or at the inner region height. This implies, from Eq. 6, a wave-induced stress, which is constant up to the matched or inner region height. This discontinuous picture must be amended for realistic conditions. As mentioned in Sect. 3.1, inclusion of turbulence in the matched layer formalism broadens the area where the wave-averaged vortex force is non-zero. In the case of the NSS mechanism, numerical simulations have shown that the vertical distribution of wave-induced stress is best described by an exponential function, with a sharp decay on top of the inner region (Mastenbroek et al. 1996). In addition, in the case of a broadband wave spectrum, the total wave-induced stress (Eq. 7) is smoother than contributions from individual wave components, even if those are discontinuous (e.g., Kudryavtsev et al. 2014).

There is no definite consensus on the mechanism responsible for wave-induced stress. However the matched layer mechanism seems to be dynamically important for long waves, while the NSS mechanism is significant for shorter waves. Belcher (1999) defined the transition between the two regimes for waves whose phase speed is $c/u_* = 15$. Kihara et al. (2007) found, using direct numerical simulations (DNS) over a single monochromatic wave, that the transition occurs for $c/u_* \sim 4$, and that for $c/u_* \ge 16$, the NSS mechanism becomes again the dominant mechanism. The authors mention that they expect their results to be significantly sensitive the the Reynolds number of the DNS ($\propto u_*/(k \nu )$), which in their case was $\sim 150$ (consistent with an earlier DNS analysis at similar Reynolds numbers, Sullivan et al. 2000). The Reynolds-number dependence of the vortex force was also discussed by Meirink and Makin (2000) using a second-order turbulence closure. The authors found a strong increase of form drag with decreasing Reynolds number. This was related, among others, to an increase of the inner layer height with viscosity, which in addition results in an increase of the wave-age threshold between NSS and matched layer mechanisms. Finally, a recent LES study by Åkervik and Vartdal (2019) revealed that the wave-induced perturbations to turbulence increase with Reynolds number, which seems to indicate that the NSS mechanism is a high-Reynolds number mechanism, as originally suggested by Belcher and Hunt (1993). This Reynolds-number dependence of processes is not anecdotal. Indeed, as already mentioned in the introduction, in realistic conditions, the Reynolds number associated with different wave components can vary greatly with respect to the overall Reynolds number of the flow.

The matched layer mechanism has been identified in field measurements by Hristov et al. (2003), for waves such that $16< c/u _*< 40$, using the wave-coherent motion extraction technique of Hristov et al. (1998). This result has been confirmed by Grare et al. (2013, 2018) and Buckley and Veron (2016) using the spectral analysis of Veron et al. (2007, 2008). In both cases, two critical features of the matched layer mechanism were identified, as also confirmed by the DNS of Sullivan et al. (2000) over monochromatic waves: (i) a jump in the phase relation between wave-coherent wind components and the surface elevation when the matched layer height is crossed; (ii) a step-like distribution of wave-induced stress, which vanishes very fast above the matched layer height. For smaller waves, the field measurements compiled by Plant (1982) provided a dependence of wave-growth rate with wave age consistent with the NSS mechanism (but with a difference in magnitude, explained by Kudryavtsev and Chapron 2016). These are an indirect test of the NSS mechanism, and direct measurements of the inner region in field conditions remain a formidable challenge, due to its size. The Reynolds-averaged Navier–Stokes equation (RANS) numerical simulations of Makin and Mastenbroek (1996), which included rapid-distortion effects (Launder et al. 1975), also confirmed the NSS mechanism and the vertical distribution of wave-induced perturbations of turbulent stress. As mentioned above, Kihara et al. (2007) also investigated the NSS mechanism using a DNS.

All of these models fall into the range of observed growth rates, as shown in Fig. 3. The observed range is wide, especially for intermediate wind-waves (corresponding to waves larger than one metre, see Fig. 1a). This suggests that additional parameters, besides wave age, are needed to fully describe wave growth. The recent works presented in Sect. 3.3 suggest that these parameters can emerge from the multiscale complexity of a realistic wave field, for which the sheltering and modulation of small waves by long waves, and the transient wave breaking events play an important dynamical role in the total wave-induced stress. This multiscale structure of wave-induced stress further results from the coupling between the broadband wave field and atmospheric turbulence at all heights in the WBL. This is described in the next section in the context of phenomenological wind-over-waves models.

4 Turbulence in the Wave Boundary Layer

As emphasized above, the turbulence equilibrium in the WBL results from a multiscale coupling between wind and waves, through wave-coherent motions, which change the properties of near-surface turbulence. In this section we first briefly discuss wind-over-waves models for the description of this equilibrium (Sect. 4.1), before discussing how the energetic (Sect. 4.2) and instantaneous (Sect. 4.3) properties of turbulence are modified in the WBL.

4.1 Wind-Over-Waves Models and the Equilibrium Range

Several wind-over-waves models have been developed for the description of the local equilibrium between turbulence and and waves in the WBL. Within a one-dimensional vertical column, those models couple an atmospheric component, e.g., a momentum balance and turbulence-kinetic-energy (TKE) equation, to a wave component, i.e., a balance equation describing the evolution of the wave spectrum under the action of the wind. The coupling between those two components occurs through wave-induced stress, which characterizes both the changes in the atmospheric momentum balance (Eq. 2) and the momentum input from the wind to the waves. Assuming that both the wind and wave systems are stationary, wind-over-waves models thus describe the equilibrium between turbulence and locally generated wind-waves. We further term these models as being phenomenological, because they aim at reproducing bulk measurements of the WBL, such as the $U_{10}$-dependence of the surface momentum flux observed in open-ocean measurements, for time averages of about 30 min (Fig. 1a).

More precisely, the range of gravity waves crucial to determine the stationary wind-and-waves system, described by the wave component of the wind-over-waves model, is the so-called equilibrium range. It covers wavelengths between the 10-m scale and the centimetre scale, when surface tension starts to be important (Kitaigorodskii 1983; Phillips 1985). In this range, wind input to the wave field is balanced by dissipation, mainly due to wave breaking. This results in a wave spectrum with a $k^{-4}$ scale dependence (see the theoretical works of Phillips 1958, 1985; Belcher and Vassilicos 1997). More recently, the role of centimetre-to-millimetre waves in the determination of the wind-and-waves equilibrium has been emphasized, as their amplitude is very sensitive to mean wind speed (Yurovskaya et al. 2013), and those scales might support a significant fraction of wave-induced stress (Kudryavtsev et al. 1999, 2014).

For these waves, a statistical equilibrium time scale can be estimated from $\beta ^{-1}(k)$, the inverse of the growth rate, related to wave-induced vortex force ($\beta$, defined in Fig. 1, is a vertical integral of the wave-induced vortex force). The inverse growth rate is an estimate of the wind input duration needed to establish a life cycle of wind-waves, consisting of growth by wind input followed by dissipation due to non-linear interactions or wave breaking (Longuet-Higgins 1987). Hence, for time scales larger than $\beta ^{-1}(k)$, waves of wavelength k can be viewed in a statistical equilibrium when averaging over their life cycle. As show in Fig. 6 for waves in the equilibrium range, the largest equilibrium time scale is of the order of 100 s, well below the averaging time scale of 30 min. Note that this time scale is an estimate from theory, as “no measurements of the relaxation time in the open ocean exist" (Alpers and Hennings 1984). For an extensive discussion, see also section 3 of Kudryavtsev et al. (2005).

On the other end of the spectrum, large waves result mostly from an inverse energy cascade due to wave–wave interactions, and are not directly coupled to the local wind. Their amplitude depends on the history of the wave field (e.g., on fetch). It is out of the scope of this review to discuss the impact that these long gravity waves can have on the atmospheric momentum budget, or their impact on the local wind-over-waves equilibrium through a change in the properties of the overall wave spectrum, the latter being still an open question.

Following the quasi-linear theory of Fabrikant (1976) and Janssen (1982), Janssen (1991) developed a wind-over-waves model, in which a simple spectrum describing the equilibrium range was coupled to an equation describing the atmospheric momentum balance. It was then extended in Janssen (1991) by using a numerical wave-prediction model. More recently, Hristov et al. (2003) followed a similar approach, coupling a linearized atmospheric momentum balance equation with a simplified wave spectrum of the equilibrium range, with some degree of freedom in the slope of the spectrum. In those models, wave-induced stress is described by the matched layer mechanism (and its extension for the quasi-linear theory).

A second set of wind-over-waves models, based on the NSS mechanism, has been proposed, with a focus on obtaining the detailed properties of the sea surface as measured from remote sensing techniques. Those were triggered by the work of Cox and Munk (1954), who made optical measurements of the mean-squared sea-surface slope and found a linear increase with wind speed due to short gravity and capillary waves. Based on these observations, a series of one-dimensional wind-over-waves models were developed (starting from Makin and Kudryavtsev 1999; Kudryavtsev et al. 1999), in which the whole range of wave scales is described with, among others, the constraint of having a mean-squared sea-surface slope consistent with the measurements of Cox and Munk (1954). In these models, wave-induced stress is described by the non-linear NSS mechanism (Eq. 15) with $C_{\beta } = 40$, following measurements by Plant (1982) (Fig. 1b). More recently, Kudryavtsev et al. (2014) included airflow separation (Eq. 16) as an additional source of wave-induced stress, together with a consistent spectral wave balance equation for the description of equilibrium-range and capillary waves, in which the effect of breaking waves is included.

These series of models, although simplified, do not provide an analytical solution to the wind-over-waves equilibrium. Such a solution was obtained by Hara and Belcher (2002, 2004), by including waves smaller than 6 cm in the viscous sublayer (see the discussion at the end of Sect. 2), and by using a different wave spectrum than Kudryavtsev et al. (2014). This allowed Hara and Belcher (2002) to discuss the range of waves that are significantly sheltered by long waves (i.e., for which the Reynolds stress used to compute the vortex force in Eq. 15 is reduced with respect to $u_*^2$). They found that this effect started affecting gravity-range waves for wind speeds of 12 m $\hbox {s}^{-1}$, and could be important for waves up to the metre scale for wind speeds of about 18 m $\hbox {s}^{-1}$. Following those developments, Kukulka et al. (2007) and Kukulka and Hara (2008a, 2008b) included the effect of airflow separation in the wind-over-waves model, which however required the use of numerical methods to solve the coupled system of equations. The Kudryavtsev et al. (2014) and Kukulka and Hara (2008a) models mainly differ in their description of the wave spectra. Additional differences in the atmospheric component of the wind-over-waves models are discussed in Sect. 4.2 below.

Fig. 4

a Comparison of normalized wave-induced stress in the WBL for the matched layer mechanism (solid line), the NSS mechanism (dashed line) and the NSS sheltering mechanism with addition of airflow separation (grey shading). The solid line has been digitized from Janssen (1989), and the dashed line and grey shadings have been computed from the model of Kudryavtsev et al. (2014), both for $u_* = 0.7$ m $\hbox {s}^{-1}$. b Height of the wave-induced vortex force, as a function of the size of the underlying wave. Solid line is the matched layer height for a logarithmic wind profile (with roughness length of about $10^{-3}$), dashed line the inner region height (set to $0.1 k^{-1}$) and dotted line is the top of the breaking wave crest (set to $0.3k^{-1}$). The leftmost vertical bar denotes the wave length of minimum phase velocity (the transition between capillary and gravity waves). The rightmost vertical bar denotes the wave age threshold $c/u_* = 4$ of Kihara et al. (2007) separating domains of validity of the NSS and the matched layer mechanism. The height z is the height from the instantaneous water surface in wave-following coordinates (see, e.g., Makin et al. 1995, for a change of coordinates)

An example of vertical profiles of wave-induced stress from two wind-over-waves models is shown in Fig. 4a, for a prescribed $u_*$ of 0.7 m $\hbox {s}^{-1}$ (corresponding to a 10-m wind of about 16 m $\hbox {s}^{-1}$). Wave-induced stress from the matched layer mechanism (solid line, Janssen 1982) is compared to wave-induced stress from the NSS mechanism (Kudryavtsev et al. 2014), without and with airflow separation (dashed line and grey shading respectively). Wave-induced stress decays fast with height, and is confined within the first metres of atmospheric surface layer (the figure only shows the first 0.5 m for clarity). For heights above 0.1 m (upper panel), the order of magnitude predicted by both models is similar. However, as shown in Fig. 4b, wave-induced stress is not caused by the same range of waves. Waves whose matched layer height lies in the range 0.1-0.5 m (solid line in Fig. 4b) have a wavelength between 30 and 70 m, while waves whose inner region height is in the range 0.1–0.5 m (dashed line in Fig. 4b) have a wavelength between 5 and 20 m.

These differences in wave scale are important when describing the sensitivity of the wind-and-waves system to external parameters such as ocean surface currents, fetch, non-stationary winds or biological slicks, since the response of the wave field to those forcings differs depending on the scale of the waves considered. Note that for the value of $u_*$ considered here, the separation between a regime where NSS or the matched layer are dynamically important is for waves of 5 m (owing to Kihara et al. 2007, vertical line in Fig. 4b) or 85 m (Belcher and Hunt 1998). This shows, as mentioned earlier, that there exists a great range of uncertainty regarding the relative importance of the matched layer and NSS mechanisms in the determination of wave-induced stress.

The model of Kudryavtsev et al. (2014) describes wave-induced stress caused by millimetre-to-metre waves, which is important for heights below 0.1 m. As shown in Fig. 4a (bottom panel), this range of waves support, in the model, a significant fraction of the stress (which can be larger than 60% of the total momentum flux). As further shown in grey shadings, airflow separation (i.e. wave breaking) impacts mainly wave-induced stress for this range of waves (compare top and bottom panels of Fig. 4a), by causing a significant increase in wave-induced stress. It is interesting to note that airflow separation at a given height is associated with a similar but slightly different wavelength than the NSS mechanism (compare dashed and dotted lines in Fig. 4b). This implies, when both effects are included, that the wind field at a given height is coupled with several wave scales.

Thus it is seen that in the above models, the wind-and-wave system results from multiscale interactions between wind and waves, due to the presence of wave breaking and of the competing NSS and matched layer mechanisms. It must be emphasized that these models give an averaged description of the WBL, which, in reality, emerges from the transient coupling between wind and waves, punctuated by wave-breaking events. Before focusing again on the description of the properties of the WBL, it is interesting to highlight that gravity waves coupled to the wind appear to reach saturation very fast, in the sense that their elevation spectrum collapses to the $k^{-4}$ slope for very short fetches, below what is typical of open-ocean conditions (Vandemark et al. 2004). As Banner and Donelan (1992) mention, this saturation, reached both for low and moderate winds, is surprising, since it is unlikely that, in the former regime, gravity-wave breaking plays an important role in maintaining a saturated spectra. This again demonstrates the complexity of the wind-and-wave system, whose transient coupling might be qualitatively different depending on the wind speed. Note that, from a purely atmospheric perspective, for low winds where swell is usually present, Kudryavtsev and Makin (2004) and Jiang et al. (2016) have, among others, shown that there exists an inverse transfer of momentum from the waves to the wind, associated with the emergence of a low-level jet.

4.2 Energy Balances in a Stationary Wave Boundary Layer

Among the quantities characterizing turbulence, turbulence kinetic energy (TKE) is a statistical measure of its intensity. Discussing the impact of waves on TKE requires analyzing the energy balances in the WBL. In wind-over-waves models those balances, and the models chosen for the parametrization of higher order terms, are essential to link turbulent stress to the mean wind speed U(z). Historically, Janssen (1982), Chalikov and Makin (1991), and Makin et al. (1995) used an eddy viscosity model, a first-order closure. However, simulations of Makin and Mastenbroek (1996), using a two-equation eddy viscosity model, showed that this simple closure was not sufficient. Building on these results, Makin and Kudryavtsev (1999) extended the model of Makin et al. (1995) using a TKE budget, which includes the effect of waves. This approach has been used in subsequent work (Hara and Belcher 2002, 2004; Kukulka et al. 2007; Kukulka and Hara 2008a, b; Kudryavtsev et al. 2014; Ayet et al. 2020a) . In the following we discuss the TKE budget to understand some of the statistical properties of turbulence in the WBL.

4.2.1 Mean, Wave-Induced, and Turbulence Kinetic Energy Balances

As discussed in Sect. 2, in the WBL the flow is separated into three components. The kinetic energy balance can be expressed separately for each component: the mean flow kinetic energy $(1/2) U^2$, the wave-induced kinetic energy $(1/2)(u_\mathrm{w}^2 + w_\mathrm{w}^2)$, and the turbulence kinetic energy $(1/2)(u'^2 + w'^2)$ (e.g., Makin and Mastenbroek 1996). The mean energy balance

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}z}(u_*^2U) - P_\mathrm{t} - P_\mathrm{w} = 0 \end{aligned}$$

(17)

is between the divergence of mean energy flux ($u_*^2U$), and the loss of energy to turbulent ($P_\mathrm{t}$) and wave-induced ($P_\mathrm{w}$) motions, where

$$\begin{aligned}&P_\mathrm{t} = \tau _\mathrm{t} \frac{\hbox {d}U}{\hbox {d}z}, \end{aligned}$$

(18a)

$$\begin{aligned}&P_\mathrm{w} = \tau _\mathrm{w} \frac{\hbox {d}U}{\hbox {d}z}. \end{aligned}$$

(18b)

The wave-induced motions energy balance,

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d} z}\Pi _\mathrm{w} + P_\mathrm{w} - D = 0, \end{aligned}$$

(19)

is between vertical transport of wave-induced energy ($\hbox {d}\Pi _\mathrm{w}/\hbox {d}z$), mechanical production ($P_\mathrm{w}$), and energy loss to turbulence (D), where

$$\begin{aligned}&\Pi _\mathrm{w} = \langle u_\mathrm{w} \tau _\mathrm{w} - \rho _\mathrm{a}^{-1} p_\mathrm{w} W_\mathrm{w} \rangle , \end{aligned}$$

(20a)

$$\begin{aligned}&D = \left\langle (\overline{u'w'})_\mathrm{w} \frac{du_\mathrm{w}}{dz} \right\rangle . \end{aligned}$$

(20b)

and $W_w$ is the contravariant wave-induced vertical velocity (see Sect. 2.2). Finally, the TKE balance

$$\begin{aligned} P_\mathrm{t} + D - \epsilon = 0 \end{aligned}$$

(21)

is between mechanical production ($P_\mathrm{t}$), energy uptake from wave-induced motions (D), and TKE dissipation rate ($\epsilon$, discussed below). In this last balance, diffusive fluxes are neglected (in the WBL), following Chalikov and Belevich (1993) and Janssen (1999).

With respect to a stationary and homogeneous surface boundary layer, the presence of wave-induced motions alters the WBL energy balance in three ways. First, there is an additional sink of energy for the mean flow, resulting from wave-induced stress ($P_\mathrm{w}$). Second, there is an additional term (D), accounting for the transfer of energy between TKE and wave-induced energy. This term depends on the vorticity of wave-induced motions and on the wave-induced variations of turbulent stress, showing their importance not only for the NSS mechanism (Sect. 3.2) but also in the energy balance of the WBL. Upon summation of Eqs. 19 and 21, D can be eliminated, and the energy balance for wave-induced and turbulent motions becomes

$$\begin{aligned} (\tau _\mathrm{t} + \tau _\mathrm{w})\frac{\hbox {d}U}{\hbox {d}z}+ \frac{\hbox {d}\Pi _\mathrm{w}}{\hbox {d}z}- \epsilon = 0. \end{aligned}$$

(22)

It reveals that the net effect of wave-induced motions is to act as an additional source for TKE by extracting energy from the mean flow, by a mechanism similar to wake production of TKE over canopies (Kaimal and Finnigan 1994). The last alteration resulting from wave-induced motions is the presence of a flux of wave-induced energy $\Pi _\mathrm{w}$. It is related to the energy loss from wave-induced motions to the waves. More precisely, summation of Eqs. 17, 19 and 21 and integration over the WBL (of height H) results in the following balance (discussed in Hara and Belcher 2004):

$$\begin{aligned} u_*^2 U - \Pi _\mathrm{w}(z = z_0^v) - \int _{z_0^v}^H\epsilon \hbox {d}z = 0. \end{aligned}$$

(23)

This equation describes the balance for the total energy integrated over the WBL, and shows that the flux of energy at the top of the WBL is balanced by the flux to the waves at the surface and TKE dissipation in the WBL (terms from left to right, respectively). The flux of wave-induced energy is usually related to wave-induced stress of individual wave components ${d}_k \tau _\mathrm{w}$ as $\Pi _\mathrm{w} = \int c(k) {d}_k \tau _\mathrm{w}$ and, as mentioned in Sect. 2, is mainly related to the work of wave-induced pressure against the surface vertical velocity $\langle \rho _\mathrm{a}^{-1} p_\mathrm{w} W_\mathrm{w} \rangle$.

Several models for the vertical structure of $\Pi _\mathrm{w}$ have been proposed. Makin and Kudryavtsev (1999) (and subsequent work: Kudryavtsev et al. 2014; Ayet et al. 2020a) , based on the numerical simulations of Mastenbroek et al. (1996), suggested that $\Pi _\mathrm{w}$ is constant within the WBL, and zero above. Hence its divergence is zero in the WBL, and $\Pi _\mathrm{w}$ only appears in the total balance (Eq. 23) and not in the modified TKE balance (Eq. 22). Hara and Belcher (2004) (and subsequent works: Hara and Belcher 2002, 2004; Kukulka et al. 2007; Kukulka and Hara 2008a, b) assumed that $\hbox {d}\Pi _\mathrm{w}/\hbox {d}z$ is important in the TKE balance over the whole WBL due to the decay of $\Pi _\mathrm{w}$ with height that should follow that of wave-induced stress (Belcher 1999). Finally, note that Janssen (1999) and Cifuentes-Lorenzen et al. (2018) considered that, very close to the surface, the divergence of the momentum flux is significant in Eq. 19, and balances the wake production of wave-induced energy $P_\mathrm{w}$, which is then transfered directly to the wave field. Those different choices are related to either numerical or theoretical models and their underlying assumptions. In the next paragraph, and in Fig. 5b, we choose the approach of Makin and Kudryavtsev (1999) to compare the effect of different TKE dissipation-rate parametrizations on the mean wind speed.

To summarize, the presence of wave-induced motions alters the energy budget in the WBL by extracting energy from the mean flow, which is then transfered to turbulent motions and surface waves. In particular, this energy transfer results, for a fixed mean wind speed, in an increase of the turbulent stress at the top of the WBL ($u_*^2$), with respect to a smooth flow, matching open-ocean measurements (Fig. 1a). However, in order to close the balances presented above, a parametrization of the TKE dissipation rate is needed.

4.2.2 Dissipation of Turbulence Kinetic Energy

Several vertical profiles of the the TKE dissipation rate and mean wind speed are shown in Fig. 5. In particular, dashed and dotted lines correspond to two choices of TKE dissipation-rate parametrizations:

$$\begin{aligned}&\epsilon _{\text {Hara}} = (\kappa z)^{-1}\tau _\mathrm{t}^{3/2}, \end{aligned}$$

(24a)

$$\begin{aligned}&\epsilon _{\text {Makin}} = (\kappa z)^{-4}\tau _\mathrm{t}^3 \left( \frac{\hbox {d}U}{\hbox {d}z}\right) ^{-3}, \end{aligned}$$

(24b)

used in the wind-over-waves models of Hara and Belcher (2004) and Makin and Kudryavtsev (1999), respectively. The mean wind speed profile is computed from the modified TKE balance Eq. 22, where $\hbox {d}\Pi _\mathrm{w}/\hbox {d}z$ has been neglected. The turbulent stress, required to compute the mean wind speed, is obtained from the momentum balance Eq. 2 by using a vertical profile of wave-induced stress from the model of Kudryavtsev et al. (2014) (Fig. 4a). Once the mean wind speed profile is computed, TKE dissipation can be diagnosed from the above formulas or from the modified TKE balance.

First, note that in the absence of waves, i.e. when $\tau _\mathrm{t} = u_*^2$ and $\hbox {d}U/\hbox {d}z = u_*/\kappa z$, both TKE dissipation-rate parametrizations are consistent with the logarithmic-law scaling of wall-bounded turbulence (solid line). The two parametrizations of TKE dissipation rate are local, in the sense that they depend on the turbulent stress or turbulent viscosity ($u_*^2(\hbox {d}U/\hbox {d}z)^{-1}$) respectively, and on a mixing length $\kappa z$. Inclusion of waves results in a decrease of TKE dissipation rate, which is slightly weaker for $\epsilon _{\text {Hara}}$ (dashed line) than for $\epsilon _{\text {Makin}}$ (dotted line). This decrease results from the presence of wave-induced stress, which reduces turbulent stress for a fixed $u_*$ (see the momentum balance Eq. 2). The decrease is stronger close to the surface, where wave-induced stress is larger (Fig. 4a).

As a consequence, the mean wind speed is also affected by the presence of waves (Fig. 5b). As found by Stewart (1961) and Miles (1965), in order to reach their equilibrium with the wind, waves extract energy from the mean flow (through $P_\mathrm{w}$) and the wind profile deviates from a logarithmic law towards a linear profile (compare the solid line with the dashed or dotted lines). This deviation is stronger close to the surface, and follows the changes in TKE dissipation. As an example, for $u_* = 0.7$ m $\hbox {s}^{-1}$ Fig. 5b indicates that 10-m wind speed, which is a commonly measured quantity in experiments, ranges from 15 to 20 m $\hbox {s}^{-1}$ depending on the choice of the parametrization for TKE dissipation rate. This shows the importance of choosing an appropriate closure for the TKE budget, to have a realistic description not only of the turbulent statistics but also of the mean flow quantities.

Fig. 5

Comparison of vertical profiles of a TKE dissipation rate and b mean wind speed for three parametrizations of TKE dissipation rate, with wave-induced stress computed from the model of Kudryavtsev et al. (2014) for $u_* = 0.7$ m $\hbox {s}^{-1}$ (Fig. 4a). Dashed lines are the model of Hara and Belcher (2004), dotted lines the model of Makin and Kudryavtsev (1999). Grey shadings are the range of values proposed in Ayet et al. (2020a). The height z is the height from the instantaneous water surface in wave-following coordinates (see, e.g., Makin et al. 1995, for a change of coordinates)

Recently, we suggested that the modulation of short wind-wave steepness by 10-m wavelength wind-waves could change the TKE dissipation rate (Ayet et al. 2020a). Based on the model of Katul et al. (2011), we proposed that the mean size of attached eddies responsible for the dissipation of TKE is impacted in the presence of those modulating waves, which changes the mixing length $\kappa z$. As a consequence, TKE dissipation rate can either increase or decrease depending on environmental conditions (currents, fetch, etc.), to which the modulation process is sensitive. Those variations in the TKE dissipation rate and hence mean wind speed (grey shadings in Fig. 5) occur at greater heights, and are significant with respect to the unperturbed quantities (compare grey shadings and dotted line).

4.2.3 Discussion

To summarize, the presence of waves impacts the production, and hence also the dissipation rate of TKE, with uncertainties on its modelling in the presence of waves. This is further confirmed by the LES of Hara and Sullivan (2015), which show the presence of a TKE dissipation anomaly (excess) in the WBL above a fixed sinusoidal wave (and hence this anomaly cannot result from an input of energy to the wave field). From a spectral perspective, the TKE dissipation rate is related to the turbulence energy cascade, and to the shape of the TKE spectrum. Hence, accurate understanding of these changes is essential both to describe the bulk properties of turbulence, but also to understand the multiscale coupling between the turbulence and wave spectra, which, as pointed out in Benilov et al. (1974) and more recently in Ortiz-Suslow and Wang (2019), is not well understood.

Note that the above discussion has focused on neutral conditions. For a stable or an unstable WBL, measurements show that, to first order, Monin–Obukhov similarity theory functions accurately describe the changes of $\hbox {d}U/\hbox {d}z$ with stability. This result was recovered by Ayet et al. (2020a) using a phenomenological wind-over-waves model in which stability was included (i) as an additional source/sink in the TKE balance, and (ii) in the parametrization of TKE dissipation rate, following recent works of Katul et al. (2011).

Further, the above discussion has focused solely on equilibrium conditions (for time averages of 30 min), meaning that wind and waves are at a statistical one-dimensional equilibrium (i.e. time evolution terms and advection terms are neglected in the above budgets). While this assumption is certainly valid at first order for long enough averaging times, such as those used in typical measurements of air–sea fluxes, variations around this equilibrium could result from external parameters causing an unsteady response of the wind-over-waves system. As an example, this response could emerge from (i) the modulation of short wind-waves by longer, out-of-equilibrium, waves (Ayet et al. 2020a); or (ii) large-scale wind, pressure, or temperature horizontal gradients leading to an unsteady atmospheric boundary layer. Finally, the equilibrium assumption should fail for averaging times shorter than 30 min. All of those points are still open questions.

4.3 Impact of Waves on Turbulent Structures

Following the discussion on the changes of TKE in the presence of waves, below we briefly review some recent numerical experiments on the modulation of instantaneous, coherent turbulent structures by the presence of waves. For a recent and extensive review on numerical simulations of wind-and-wave interactions, the reader is referred to Deskos et al. (2021). The motivation for our review is twofold. First, coherent turbulent structures are important in the determination of the turbulent stress both for smooth-wall ( Robinson 1991; Jiménez 2012, 2018) and rough-wall ( Raupach et al. 1991; Jiménez 2004) flows. A wave-induced change in their properties hence reflects the impact of waves directly on turbulence statistics, and not indirectly as is the case for wave-induced stress (and as put forth in the model of Ayet et al. 2020a). Second, modifications of the properties of turbulent stress impacts vortex force, both when described through the critical layer mechanism (through Eq. 9) or the NSS mechanism (through Eq. 13). Hence an accurate description of the instantaneous properties of the flow could lead to improvements in the description of its averaged properties.

As an example of the importance of coherent structures, it is interesting to consider the case of transitionally rough surfaces. For these surfaces, the Reynolds-number similarity, expected for aerodynamically rough surfaces, is not attained, but the geometry of the roughness elements impacts the flow. For flow over the sea surface, this transition occurs for winds between 3 and 7.5 m $\hbox {s}^{-1}$ (Kitaigorodskii and Donelan 1984), and this results in a minimum of surface drag ($u_*^2/U(10)^2$) for wind speeds of about 3 m $\hbox {s}^{-1}$ (Edson et al. 2013). For generic surfaces, Jiménez (2004) suggested that this minimum could result from two competing mechanisms: (i) an increase of surface drag due to additional form drag from the roughness elements; (ii) a decrease of surface drag due to a randomization of coherent structures in the viscous sublayer which, in the aerodynamically smooth case, act as a source of turbulence for the logarithmic layer (the so-called viscous sublayer cycle, described in Jiménez and Moin 1991 and Jiménez 1999). In the case of transitional surfaces, mechanism (ii) can overcome mechanism (i), explaining the observed decrease of surface drag.

Along these lines, several experiments, including DNS (Sullivan et al. 2000), LES (Sullivan et al. 2014) and observations (Buckley and Veron 2016), reveal that the streaky structure of viscous-layer turbulence above flat walls (e.g., Kline and Runstadler 1959, related to the viscous sublayer cycle) is affected by the presence of waves. Close to the surface, streaks are disrupted, and their length appears to be constrained by the wave size. The use of low-Reynolds-number DNS (Sullivan et al. 2000; Yang and Shen 2009, 2010) allows further investigation of those changes by analysis of coherent structures. For a slow wave ($c/u_* = 2$), Yang and Shen (2009) found that the negative turbulent stress is induced mainly by contributions from sweep events in the trough of the wave, and ejection events on the windward face of the wave. This is consistent with early experimental work of Kawamura and Toba (1988). Those events were associated with reversed horseshoe vortices (for sweeps), and to quasi-streamwise vortices (for bursts). For faster waves, with a thick enough matched layer, near surface coherent structures are advected upwind in the reference frame of the wave. In this situation, quadrant analysis (Sullivan et al. 2000) reveals that positive contributions to turbulent stress become significantly higher (Q3, or inward interactions). Those are associated with the bending of quasi-streamwise vortices as they are advected downwind, which generates vertical vorticity (Yang and Shen 2009). Even though these results provide an indication of the mechanisms at stake, they should however not be readily extrapolated to field-condition flows, due to the low Reynolds number of the simulations.

The impact of wave breaking on coherent structures was analyzed by means of LES by Suzuki et al. (2011, 2013). Suzuki et al. (2011) modeled the effect of a windy sea with breaking wave crests as an anisotropy in surface drag, stronger in the streamwise (perpendicular to the crests) than in the spanwise direction. The authors found an enhancement of the intensity of quasi-streamwise vortices with respect to an isotropic situation, resulting in more intense turbulence mixing. Suzuki et al. (2013) focused on the impact of airflow separation events on turbulence. The simulations revealed that due to the separation of the near-surface sheared boundary layer, near surface streaks (and coherent vortices) were inhibited. Finally, note that the boundary-layer detachments above a breaking crest also result in the creation of vortical structures which are ejected upwards in the fluid (Reul et al. 2008).

These different studies show that waves certainly affect turbulent coherent structures (as summarized in Fig. 6), suggesting that their accurate modelling might improve the understanding of wind-over-wave interactions. We end this review by mentioning two theoretical works. First, Eifler (1993), who developed a theoretical model of the near-surface WBL (with heights from 1 to 10 cm) including instantaneous properties of the turbulent flow and multiscale wave effects. His model was based on the analogy between the WBL flow and flow within the viscous sublayer over a flat wall. The later has been described by Kline and Runstadler (1959) and Blackwelder and Eckelmann (1979) as a sequence of growing and collapsing laminar sublayers, associated with the destabilisation of quasi-streamwise vortices. Those growths and collapses were proposed as a model for observed burst and sweep events. Eifler (1993) discussed how the spatial distribution of those transient events was constrained by the presence of an individual surface wave: as the laminar sublayer grows along the wave, near-surface wind speed increases, generating small wavelets, which act as roughness elements. This triggers the collapse of the sublayer, hence constraining the spatial distribution of burst and sweep events. Along similar lines, the theoretical work of Csanady (1985) emphasized the role of airflow separation events on top of steep and short waves [$\mathcal {O}(10$cm)] for their coupling with wind. The author argued that, following an airflow separation event, the reattachment of the airflow on the windward face of such a wave is necessary to maintain a balance between momentum input to the wave (by means of a shear-stress spike at the point of reattachment, observed by Okuda et al. 1977) and dissipation of wave energy to the near-surface turbulent water field. This allows trains of such small-scale waves to be long-lived, and hence to be coupled by wind through airflow separation. These works, although conceptual, emphasize the role of multiscale and transient coupled processes in the wind-and-waves coupling, which is not covered by the DNS and LES results presented above.

5 Concluding Remarks

In this review we have discussed (i) several theoretical models of the vortex force (or wave-growth rate) associated to short wind-waves (smaller than ten metres) used as building blocks of (ii) phenomenological wind-over-waves models, which describe the averaged properties of turbulence in the atmospheric wave boundary layer (below ten metres, in the atmosphere) when turbulence and wind-waves have reached an equilibrium. Both these models aim at reproducing observations, presented in Fig. 1. There is still a large scatter, in these observations, which is unexplained by theoretical models, suggesting that other processes and variables might be essential for the description of wind-and-wave interactions. Understanding this scatter is essential since the above-mentioned models are at the heart of how parametrizations of air–sea fluxes are built for coupled ocean-atmosphere models, and of how remote sensing measurements of the sea-surface roughness (e.g., scatterometers) are interpreted.

Emphasis was placed on the fact that a realistic sea surface is a multiscale surface, whose roughness can be highly modulated by space–time transient events, both for waves and turbulence. Figure 6 summarizes the multiscale nature of the surface, by showing that depending on the wave size, wave-induced motions and instantaneous turbulence properties can be significantly different. In order to advance our understanding of wind-and-wave interactions, we believe that these multiscale and transient interactions should be better characterized. These involve small-scale roughness modulations and patches of localized small-scale breakers with random length scales and durations, which can be caused by modulating longer waves, large-scale breaking events but also wind gustiness. In Sect. 3.4 we discussed how these roughness modulations could lead to enhanced growth rates. The recent numerical simulations discussed in Sect. 4.3 further suggest that all of these mechanisms could lead to organized three-dimensional flow structures spanning a wide range of spatio–temporal scales, crucially affecting the vortex force (or wave-growth rate): this could help explain differing wave-growth rates and momentum fluxes under comparable wind speeds (see Figs. 1 and 3). Including those processes in theories of wind-wave growth would require accounting for the spanwise extension of waves (which are short-crested), and therefore would also require describing the three-dimensional vortex force in the overlying turbulent flow.

Improving our understanding of how wind-waves are coupled to organized, quasi-instantaneous flow structures (or coherent turbulent structures) would also be beneficial for the description of the averaged properties of the turbulent boundary layer above waves. This involves understanding the three-dimensional coupling between short-crested waves and those structures, a problem which is beginning to be tackled thanks to high resolution numerical simulations (see the review Deskos et al. 2021). More generally, there is a need for understanding how the multiscale interactions that take place in the overlying turbulent flow might be affected by wind-and-wave coupling, a seldom explored question. The discussion of several turbulence closures in Sect. 4.2 also highlighted that uncertainties persist on how to paremterize the different terms in the turbulence budgets, and this could be improved by a spectral description of the turbulent flow in the presence of wind-waves (see the spectral link described in Katul and Manes 2014; Ayet et al. 2020b). The difficulty being that, depending on the wave scale, the wind-and-wave coupling mechanisms mechanisms might be qualitatively different (Fig. 6)

Fig. 6

Summarizing schematic presenting a multiscale and three-dimensional view the dynamical impact of wind-waves on turbulence. For each of the panels, the horizontal scale is the wavelength of the considered waves and the time scale is the inverse of the wave growth rate: and estimate of the life-cycle time scale of the considered waves (see Sect. 4.1). The presence of waves results in both wave-coherent motions (background streamlines) and modification of the instantaneous properties of turbulence (foreground vortex tubes), which are transient events. The latter are deduced from laboratory observations (for the case of breaking waves) and low-Reynolds-number DNS, and are hence possible processes, not observed in field conditions. The drawing is in the reference frame of the moving waves, whose speed increases with wave scale, and the scale of the waves is not respected. Airflow separation events (left) are mainly associated with short-crested breaking waves, resulting in inhibition of near surface streaks downwind of the breaking crest, and ejection of vortical structures in the interior of the fluid. Short waves (middle) are associated with the non-separated sheltering mechanism of vortex force, and to intensified sweeps and ejections on the trough and windward face of the wave. Longer waves (right) are associated with the matched-layer mechanism of vortex force, and to positive contributions to turbulent stress resulting from the horizontal bending of quasi-streamwise vortices (Q3 events). Finally, both vortex-force mechanisms are dependent on the modulation of the steepness of shorter waves along the long wave

Quantification of these multiscale interactions requires advanced experimental set-ups. In particular, those could focus on achieving a joint statistical descriptions of near surface turbulence coupled to short wind-waves, riding on random long waves that can also develop with the fetch. Varying in both time and space, short wind-waves have different wave ages, and differing growth rates, in the course of the long wave development. Advancing the understanding of the overall dynamical coupling of wind-waves and atmospheric turbulence may thus require the combined use of highly-resolved space and time measurements for the sea-surface roughness (Lenain et al. 2019; Laxague and Zappa 2020), therefore extending present laboratory efforts (Yousefi et al. 2020; Buckley et al. 2020) to field measurements. Those efforts should then benefit from joint and dedicated high-resolution numerical simulations to provide a global view of the coupled turbulence-wave dynamics. By ultimately feeding our theoretical understanding of wind-and-wave interactions, these joint efforts will contribute to reduce uncertainties around air–sea flux parametrizations, in the context of (coupled) weather and climate models.