Real-Time Tracer Dispersion Simulations in Oklahoma City Using the Locally Mesh-Refined Lattice Boltzmann Method

Abstract

We present ensemble-based large-eddy simulations based on a lattice Boltzmann method for a realistic urban area. A plume-dispersion model enables a real-time simulation over several kilometres by applying a local mesh-refinement method. We assess plume-dispersion problems in the complex urban environment of Oklahoma City on 16 July using realistic mesoscale velocity boundary conditions produced by the Weather Research and Forecasting model, as well as building structures and a plant-canopy model introduced into the plume-dispersion model. Ensemble calculations are performed to reduce uncertainties in the macroscale boundary conditions due to turbulence, which cannot be determined by the mesoscale model. The statistics of the plume-dispersion field, as well as mean and maximum concentrations, show that ensemble calculations improve the accuracy of the simulations. Factor-of-2 agreement is found between the ensemble-averaged concentrations based on the simulations over a 4.2 × 4.2 × 2.5 km² area with 2-m resolution with the plume-dispersion model and the observations.

1 Introduction

Nuclear security requires the prediction of the environmental dynamics of radioactive substances based on detailed simulations of the airflow and the resulting plume dispersion. These kinds of flow simulations in urban areas are also important tools in designing smart cities. In the past decade, many urban-dispersion models have been developed for emergency-response purposes and validated with respect to field-dispersion experiments (Hanna et al. 2011; Kopka et al. 2019; Hernández-Ceballoset al. 2019a, b). These models can take into account urban buildings and meteorological conditions, but do not compute the detailed airflow, but are much faster than computational fluid dynamics (CFD). However, since the accuracy of the model strongly depends on the model parameters, it is necessary to develop more reliable CFD-based approaches that reduce such uncertainties.

Computational fluid dynamics are a direct approach for evaluating the flow and plume dispersion in a self-consistent manner. Many studies regarding guidelines for urban-flow simulations have been reported (Tominaga and Mochida 2008; Blocken 2015). A CFD method based on the Reynolds-averaged Navier–Stokes (RANS) equations is effective for urban flow simulations (Yoshie et al. 2007; Blocken and Persoon 2009). Since only the mean and time-averaged flow is resolved, while turbulent fluctuations are modelled, the computational cost is lower than direct numerical simulation (DNS). However, the RANS approach often overestimates the turbulent energy dissipation for transient flows, including secondary flows around an object, and thus, more accurate assessment methods are needed.

Large-eddy simulation (LES) based on the Navier–Stokes equations have been widely used in airflow and climate analyses (Shimokawabe et al. 2010; Cheng and Fernando 2015; Nakayama et al. 2016), whereby the flow dynamics of large-scale structures are resolved on a grid scale, and only turbulent fluctuations of the subgrid scale (SGS) are modelled by the turbulent viscosity. However, when trying to understand the detailed dynamics in an urban area, the computational cost becomes extremely large due to the high Reynolds number, making it difficult to achieve real-time or faster-than-real-time simulations, which are required in emergency situations, such as accidental releases of radioactive substances.

The lattice Boltzmann Method (LBM) is one CFD method that solves a discrete-velocity Boltzmann equation, whereby the flow field is expressed by pseudo-particles, which move in a limited number of directions. The discretized velocity vectors of the LBM approach are defined on each Cartesian grid, so that they satisfy conservation laws and Galilean invariance of the Navier–Stokes equations. While the LBM approach was originally developed for the DNS approach at low Reynolds number, SGS models and state-of-the-art collision operators enable turbulent flow simulations at high Reynolds number (Wang and Aoki 2011). The advantage of the LBM approach is that it is suitable for high-performance computing because of its local and continuous memory access. Since the LBM approach is based on a weak compressible formulation, the time integration is calculated explicitly without solving the Poisson equation.

Recently, the LBM approach was successfully applied to large-scale-flow simulations using a realistic urban geometry (Onodera et al. 2013; Inagaki et al. 2017). However, it is difficult to perform such multi-scale simulations with a uniform grid system from the viewpoint of computational resources and a realistic calculation time. A mesh-refinement method for the LBM approach is a key technique for accelerating such multi-scale simulations (Jacob and Sagaut 2018). The locally mesh-refined LBM approach enables real-time flow simulations to be realized for about 2 km² with a 1-m resolution on graphics-processing-unit-based computers (Onodera and Idomura 2018a; Onodera et al. 2018; Lenz et al. 2019).

Here, we perform large-scale plume-dispersion simulations with a dispersion model based on the field experiments conducted during the Joint Urban experimental campaign in 2003 (JU2003, Leach 2005). Realistic flow conditions are reproduced by the Weather Research and Forecasting Model (WRF, Skamarock et al. 2008), and time series of the mesoscale model are combined with the dispersion model through the boundary conditions. The building structures are arranged in the central district of Oklahoma City by a digital surface model. A plant-canopy model (Shaw and Pereira 1982; Kanda et al. 2004; Watanabe 2004) is also applied to the botanical gardens near the plume-release point to improve the flow conditions in the boundary layer accurately. Ensemble calculations are performed to reduce turbulence uncertainties due to macroscopic boundary conditions, which cannot be determined by the WRF model. We evaluate the requirements for detailed physical models and numerical parameters to reproduce the plume-concentration data collected during the JU2003 campaign.

2 The Dispersion Model

2.1 Lattice Boltzmann Method

The lattice Boltzmann equation (LBE) is obtained by reducing the Boltzmann equation to a finite number of discrete velocities. The fluid is represented by pseudo-particles on a uniform Cartesian grid system, and the macroscopic values are defined by the sum of pseudo-particles or the first moment of the velocity distribution function. Since the fluid is assumed to be weakly compressible, the time evolution of the discretized velocity distribution function is calculated with an explicit time integration as

$$ f_{ijk} \left( {\vec{x} + \vec{c}_{ijk} {\Delta }t, t + {\Delta }t} \right) = f_{ijk} \left( {\vec{x}, t} \right) + {\Omega }_{ijk} \left( {\vec{x}, t} \right), $$

(1)

where $\vec{x}$ is the configuration space, ${\Delta }t$ is the time interval, $c_{ijk}$ is the lattice vector of the pseudo particle, $f_{ijk}$ is the velocity distribution function corresponding to the lattice vector, and ${\Omega }_{ijk}$ is the collision operator.

The LBE consists of streaming and collision processes. Since pseudo-particles move onto neighbouring lattice points after one timestep in the streaming process, this process is completed without any error related to interpolations, but it is important to choose a proper lattice-velocity model by taking into account the tradeoff between efficiency and accuracy. The three-dimensional twenty-seven (D3Q27) discrete velocity model is suitable for simulating weakly compressible flows at high Reynolds number of a complex geometry (Kang and Hassan 2013). The components of the velocity vector are defined as

$$ \vec{c}_{ijk} = \left( {ic, jc, kc} \right), i,j,k \in \left\{ { - 1,0,1} \right\} \otimes \left\{ { - 1,0,1} \right\} \otimes \left\{ { - 1,0,1} \right\}, $$

(2)

where the lattice speed is normalized as $c = 1$. Since memory access is simple and continuous, the streaming process is suitable for graphics-processing-unit computing (Onodera and Idomura 2018a).

The macroscopic diffusion is expressed by the local collision process with the lattice BGK model, which is also suitable for high-performance computing. A single-relaxation-time model is widely used in most of the previous studies, because of its simple formulation and low computational cost (Wang and Aoki 2011). The collision operator of the single-relaxation-time model is defined as

$$ \Omega_{ijk} = - \frac{1}{\tau }\left( {f_{ijk} - f_{ijk}^{{{\text{eq}}}} } \right), $$

(3)

$$ \tau = \frac{1}{2} + \frac{3\nu }{{c^{2} {\Delta }t}} , $$

(4)

where $\nu$ is the kinematic viscosity, $\tau$ is the relaxation time normalized by ${\Delta }t$, and $f_{ijk}^{{{\text{eq}}}}$ is a local equilibrium distribution function given as

$$ f_{ijk}^{{{\text{eq}}}} = \omega_{ijk} \rho \left( {1 + \frac{{3\vec{c}_{ijk} \Delta \vec{u}}}{{c^{2} }} + \frac{{9\left( {\vec{c}_{ijk} \Delta \vec{u}} \right)^{2} }}{{2c^{4} }} - \frac{{3\vec{u}^{2} }}{{2c^{2} }}} \right). $$

(5)

Here $\rho$ is the density, $\vec{u}$ is the macroscopic velocity, and $\omega_{ijk}$ is a weighting factor of the D3Q27 discrete velocity model. The single-relaxation-time model may suffer from numerical instability at high Reynolds number because its relaxation time $\tau \to 0.5$, which causes over-relaxation of the velocity distribution function. The single-relaxation-time model requires SGS models with excessive viscosity to suppress unphysical numerical oscillations, but the excessive eddy viscosity often makes the results diffusive. While multiple-relaxation-time models improve computational stability (Kuwata and Suga 2016), they require empirical parameter tuning, and their simulations also require the use of a SGS viscosity for numerical stability at high Reynolds number.

The cumulant-relaxation-time model is one of the most efficient LBM approaches, which satisfies both accuracy and stability (Geier et al. 2015; Geier et al. 2017a, b). The collision process is not calculated in the momentum space, but calculated in the cumulant space. We adopt the original cumulant-relaxation-time model (Geier et al. 2015), in which the equilibria for some higher-order cumulants are zero, to realize the stable long-term calculation of turbulent flows at very high Reynolds number.

2.2 Subgrid-Scale Model

The LES approach resolves the dynamics of large-scale-flow structures on a grid scale, and represents the effect of SGS turbulent flow structures by an eddy viscosity defined as

$$ \nu_{{{\text{SGS}}}} = C{\overline{\Delta }}^{2} \left| {\overline{S}} \right|, $$

(6)

where $C$ is the model coefficient,${\overline{\Delta }}$ is the filter width, and $\left| {\overline{S}} \right|$ is the magnitude of a velocity strain tensor. In the conventional Smagorinsky model (Smagorinsky 1963), the model coefficient is a constant in the entire computational domain, and the SGS viscosity does not describe the correct asymptotic behaviour near the wall.

The dynamic Smagorinsky model overcomes this defect by dynamically calculating the model parameter using two types of grid filters (Germano et al. 1991; Lilly 1992). Although the dynamic Smagorinsky model is the most notable breakthrough in LES investigations, the model parameter requires the average to be taken in the global domain for the sake of numerical stability, which introduces a large simulation duration and makes it difficult to treat complex geometries.

The coherent structure Smagorinsky model (CSM) (Kobayashi et al. 2008) is an eddy-viscosity model which satisfies both stability and accuracy near the wall of complex geometries. The model coefficient $C_{{{\text{CSM}}}}$ is calculated locally by the second invariant of the velocity gradient tensor $Q$ and the magnitude of the velocity gradient tensor $E$ as

$$ C_{{{\text{CSM}}}} = C^{\prime}\left| {Q/E} \right|^{3/2} , $$

(7)

where the model coefficient $C^{\prime} = 1/25$ is a fixed model parameter. Since this eddy viscosity is determined locally and describes a correct asymptotic behaviour near the wall, the CSM approach can treat complex geometries. In applying this to the LBE, the total relaxation time is expressed by the sum of kinematic viscosity and eddy viscosity as

$$ \tau = \frac{1}{2} + \frac{{3\left( {\nu + \nu_{{{\text{SGS}}}} } \right)}}{{c^{2} {\Delta }t}}, $$

(8)

$$ \nu_{{{\text{SGS}}}} = C_{{{\text{CSM}}}} {\overline{\Delta }}^{2} \left| {\overline{S}} \right|. $$

(9)

The velocity strain tensor is directly calculated by the velocity distribution functions as

$$ \overline{S}_{\alpha \beta } = - \frac{3}{{2\rho c^{2} \tau {\Delta }t}} \sum \left( {\frac{{\vec{c}_{ijk} \cdot \vec{c}_{\alpha } }}{c}} \right)\left( {\frac{{\vec{c}_{ijk} \cdot \vec{c}_{\beta } }}{c}} \right)\left( {f_{ijk} - f_{ijk}^{{{\text{eq}}}} } \right). $$

(10)

2.3 Plant-Canopy Model

A plant-canopy model (Shaw and Pereira 1982; Kanda et al. 2004; Watanabe 2004) is important for assessment of the boundary layer near the ground. Plant elements are modelled by the drag force, which is parametrized as

$$ \vec{F}_{d} = - \rho C_{d} a_{f} \left| {\vec{u}} \right|\vec{u}, $$

(11)

where $C_{d}$ is the isotropic drag coefficient, and $a_{f}$ is a one-sided plant-area density. These canopy parameters are given as $C_{d} a_{f} = 0.01$, which is adjusted so that simulations reproduce the observed wind speed in the JU2003 campaign. The drag force is simply introduced to the LBE as an external force as

$$ f_{ijk} \left( {\vec{x} + \vec{c}_{ijk} {\Delta }t,t + {\Delta }t} \right) = f_{iij} \left( {\vec{x}, t} \right) + {\Omega }_{ijk} \left( {\vec{x}, t} \right) + F_{d,ijk} {\Delta }t, $$

(12)

where $F_{d,ijk}$ is an external force on each velocity distribution evaluated as

$$ F_{d,ijk} = 3 \omega_{ijk} \frac{{\left( {\vec{F}_{d} \cdot \vec{c}_{ijk} } \right)}}{{c^{2} }}. $$

(13)

2.4 Thermal Convection Model

Convective heat transfer is simply modelled by an advection–diffusion equation as

$$ \frac{{{\text{D}}T}}{{{\text{D}}t}} = \left( {\chi + \frac{{\nu_{{{\text{SGS}}}} }}{{\Pr_{{{\text{SGS}}}} }}} \right)\nabla^{2} T, $$

(14)

where ${\text{D}}/{\text{D}}t$ is the convective derivative, χ is the thermal diffusivity, and $\Pr_{{{\text{SGS}}}}$ is the turbulent Prandtl number. Although it is also possible to model the convective heat transfer within a pure LBM approach, such an extension requires more pseudo-particles, leading to large memory usage. An advantage of the LBM formulation is that it does not require a iterative calculation in the Poisson equation and the implicit time integration. However, the stability conditions of the advection and diffusion terms in the heat-transfer equation are not so severe at grid resolutions of a few metres, and thus it is also possible to adopt explicit time integration. When Eq. 14 is discretized by a finite-difference method with explicit time integration, the memory usage and the computational cost are significantly lower than LBM-based thermal-convection models. The advection term is discretized by a second-order Taylor expansion in space and time. The SGS viscosity is added to the diffusion term to evaluate the effect of turbulence on the heat transport, and the Prandtl number $\Pr_{{{\text{SGS}}}} = 0.7$.

The Boussinesq approximation is applied to solve non-isothermal flows. Buoyancy is simply introduced to the LBE as an external force,

$$ f_{ijk} \left( {\vec{x} + c_{ijk} \Delta t,t + \Delta t} \right) = f_{iij} \left( {\vec{x}, t} \right) + \Omega_{ijk} \left( {\vec{x}, t} \right) - g_{ijk } \alpha \left( {T - T_{0} } \right)\Delta t, $$

(15)

$$ g_{ijk} = 3\omega_{ijk} \frac{{\left( {\vec{c}_{ijk} \cdot \vec{G}} \right)}}{{c^{2} }}, $$

(16)

where $\vec{G} = \left( {0, \, 0, - 9.8} \right)$ is the acceleration due to gravity, $\alpha$ is the coefficient of thermal expansion, and $T_{0}$ is the reference temperature. A hybrid finite-different method and LBM approach can capitalize on the enhanced calculation speed and reducing memory usage (Onodera and Idomura 2019) compared with the pure LBM approach (Yoshino and Inamuro 2003). The dispersion model has also been validated for simulations of natural convection in two-dimensional cavities and natural convection experiments with Rayleigh numbers up to about 2 × 10⁹ (Onodera et al. 2020).

2.5 Plume-Dispersion Model

The plume density follows a mass-conservation law, which is simply discretized by a finite volume method as

$$ \frac{\partial q}{{\partial t}} + \nabla \cdot \left( {\vec{u} \cdot q} \right) = \nabla \cdot \left( {\frac{{\nu_{{{\text{SGS}}}} }}{{Cq_{{{\text{SGS}}}} }}\nabla q} \right) + s, $$

(17)

where $s$ is a source term, and the parameter $Cq_{{{\text{SGS}}}} = 2$. The convection term is discretized by a second-order Taylor expansion in space and time, and the numerical viscosity of the first-order upwind scheme is added to the advection term to prevent non-physical oscillation originating from point sources. The physical properties of the plume are assumed to be the same as air, and its dynamics do not affect the velocity field. The above coupling of the LBM and finite-volume-method approaches was validated by a plume-dispersion calculation for wind-tunnel experiments with a single object (Onodera and Idomura 2018b).

2.6 Boundary Treatment

The LBM approach is suitable for modelling boundary conditions with complex shapes. The bounce-back scheme and the interpolated bounce-back scheme (Chun and Ladd 2007) make it easy to implement no-slip boundary conditions. Immersed boundary methods (Kim et al. 2001) are also able to handle complex boundary conditions by adding external forces to the LBM approach.

Here, we applied the interpolated bounce-back scheme because of its flexibility and accuracy. The pseudo-particle, which contacts with the solid surface, is simply reflected back to the fluid domain with opposite velocity. The velocity-distribution function in one dimension is expressed as

$$ f_{ - i}^{*} \left( {\vec{x},t + \Delta t} \right) = \left\{ {\begin{array}{*{20}l} {2\phi f_{i} \left( {\vec{x},t} \right) + \left( {1 - 2\phi } \right)f_{i} \left( {\vec{x} - \vec{c}_{i} \Delta t,t} \right) ,} & {\quad \phi < \frac{1}{2} , } \\ {\frac{1}{2\phi }f_{i} \left( {\vec{x},t} \right) + \frac{{\left( {2\phi - 1} \right)}}{2\phi }f_{ - i} \left( {\vec{x},t} \right) ,} & {\quad \phi \ge \frac{1}{2},} \\ \end{array} ,} \right. $$

(18)

where $f_{ - i}^{*} \left( {\vec{x},t + {\Delta }t} \right)$ is the velocity distribution function after reflection, and $\phi$ is a distance function normalized by the grid width ${\Delta }x$. Since the velocity vectors involve diagonal directions, which are not aligned with Cartesian grids, a high-precision analysis can be performed with complex boundary conditions.

The Dirichlet boundary condition of temperature is given by the surface temperature of the building, which is assumed to be the same as the ground temperature given by the mesoscale model. A zero-flux condition of the plume concentration is imposed on the building surface.

2.7 Mesh-Refinement Algorithm

The LBM approach originally solved the fluid flow on a uniform Cartesian grid system, but recently a mesh-refinement method was applied to the LBM approach and multi-scale flow simulations were carried out for urban areas (Jacob and Sagaut 2018; Lenz et al. 2019). High-resolution grids are arranged only in a region with fine-scale flows, and the number of grid points can be reduced dramatically. Since the LBM approach is a dimensionless method in time and space, the timestep width differs for each adaptive-mesh-refinement resolution (Yu et al. 2002), which is a multi-timestep method adopted for the time evolution of the LBM, finite-volume and finite-difference methods.

A cell-based adaptive-mesh-refinement method divides the whole domain into cells, with one cell subdivided into four cells in two dimensions and eight cells in three dimensions. For interpolating a coarse cell value from fine cell values, the latter values are simply averaged over the former cell region. In contrast, for interpolating a fine-cell value from coarse-cell values, the interpolation function is determined over the coarse cells, and we use a quadratic function in three dimensions.

Data structure is very important from the viewpoint of computational efficiency in graphics-processing-unit-based computing. A block-structured adaptive-mesh refinement has an efficient data structure by dividing the whole domain into block units. Since several cells are contained in a block unit, this enables continuous memory access. In the dispersion model, the number of cells in a block unit is set to 4³ by accounting for the tradeoff between adaptivity to physical phenomena and continuity of memory access. Our implementation achieved good scalability up to 200 graphics processing units (Onodera et al. 2018).

3 Multi-scale Flow Simulation with the Mesoscale Model

3.1 Nudging Data Assimilation for the Dispersion Model

As the flow in urban areas is neither uniform nor steady, data assimilation is needed to establish more realistic flow conditions based on observations and/or mesoscale mereological models. Nudging is a continuous data-assimilation method known as Newtonian relaxation (Paniconi et al. 2003; Brian and David 2010), which perturbs the model state towards a target state determined based on observations and/or different models with an empirical relaxation coefficient. By using this technique, a local flow simulation and a mesoscale meteorological simulation are coupled to construct multi-scale flow simulations. The temperature and the velocity distribution functions of the dispersion model are gradually corrected in time and space as

$$ T^{*} \left( {\vec{x},t} \right) = T\left( {\vec{x},t} \right) + w\left( {\hat{T} - T\left( {\vec{x},t} \right)} \right), $$

(19)

$$ f_{ijk}^{*} \left( {\vec{x},t} \right) = f_{ijk} \left( {\vec{x},t} \right) + w\left( {\hat{f}_{ijk}^{{{\text{eq}}}} - f_{ijk} \left( {\vec{x},t} \right)} \right), $$

(20)

$$ \hat{f}_{ijk}^{{{\text{eq}}}} = \omega_{ijk} \hat{\rho }\left( {1 + \frac{{3\vec{c}_{ijk} \Delta \widehat{{\vec{u}}}}}{{c^{2} }} + \frac{{9\left( {\vec{c}_{ijk} \Delta \widehat{{\vec{u}}}} \right)^{2} }}{{2c^{4} }} - \frac{{3\widehat{{\vec{u}}}^{2} }}{{2c^{2} }}} \right), $$

(21)

where $T^{*}$ and $f_{ijk}^{*}$ are the temperature and the equilibrium distribution functions after nudging data assimilation, $\hat{T}$, $\hat{\rho }$, and $\widehat{{\vec{u}}}$ are the temperature, density, and velocity vectors of the observation data or mesoscale simulation data normalized by the lattice speed, $\hat{f}_{ijk}^{{{\text{eq}}}}$ is the equilibrium distribution function, and $w$ is an empirical coefficient in the nudging data-assimilation model. For $w = 1$, nudging data assimilation behaves like a Dirichlet boundary condition. The WRF data is pre-arranged before simulation of the CityLBM dispersion model, and one-way nudging data assimilation is performed at every coarse grid timestep used in the WRF model via hard-disk-drive storage.

3.2 Continuous Boundary Treatment for the dispersion and Mesoscale Models

The mesoscale WRF model can reproduce mesoscale meteorological conditions for hundreds of kilometres and several hours. Since the computational domain of the mesoscale model includes the urban area of several kilometres, it is possible to perform a realistic simulation by using WRF data as the boundary conditions in time and space. The WRF model computes mesoscale quantities such as density, velocity, and temperature based on the RANS equations. Although the WRF results are adjusted to reproduce the mean value of mesoscale meteorological observation data, it does not include high-frequency turbulent fluctuations, which are needed in LES-based CFD models. In the dispersion model, in addition to the equilibrium distribution function $\hat{f}_{ijk}^{{{\text{eq}}}}$, which can be determined from the mesoscale results, it is also important to generate the non-equilibrium distribution function of the turbulent fluctuations.

To solve this problem related to turbulent flow generation, the dispersion model considers an extended turbulent-generation and data-assimilation area around the target city area. Roughness blocks are placed to promote the development of turbulence, and a periodic boundary condition is also imposed in the horizontal directions to maintain the height of the turbulent boundary layer. The height and interval of the roughness blocks are adjusted to reproduce the velocity profiles observed at the upwind side of the city area (station I). The nudging data-assimilation model is applied over an extended outer area surrounding the city with a low nudging coefficient as 10^–3 so that the model state is gradually relaxed to the WRF data while inserting the turbulent fluctuations coming the periodic boundary conditions.

Since grid and time resolutions between the dispersion and mesoscale models are different by two orders of magnitude, the WRF data are linearly interpolated on computational grids in time and space. The wind speed at the ground and building surfaces is given as no-slip boundary conditions, and the surface temperature is given by the ground temperature of the WRF model, which enables multi-scale flow simulations to reflect the complex flow conditions.

4 Validation for the Field Experiments in Oklahoma City

4.1 Field Experimental Conditions

The field experiments of the JU2003 campaign (Leach 2005) were conducted in the city centre of Oklahoma City, U.S.A. from 28 June to 31 July 2003. The focus of these experiments was to understand the atmospheric dispersion process of a tracer gas in urban environments under realistic atmospheric conditions. Sulfur hexafluoride (SF₆) tracer was released as puffs and 30-min continuous releases from one of three release locations during the 10 main intensive observational periods.

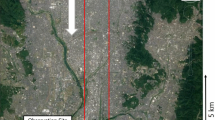
We validate the CityLBM model based on the field experiment on 16 July during intensive observational period 6. The tracer was released continuously from a height of 1.9 m in the botanical gardens at 0900, 1100, and 1300 local time (LT = UTC – 5 h) for 30 min. The concentration data were measured by fast-response tracer analyzers with a time response of approximately 1 Hz by the Lawrence Livermore National Laboratory. These analyzers were located at eight points on the ground, from locations A to H as seen in Fig. 1, mainly above Robinson Avenue and Sheridan Avenue located within 200 m downstream of a point source. The release and measurement points are shown in Fig. 1.

Fig. 1

Locations of the a meteorological stations and b concentration measurement points in the central business district of Oklahoma City. The meteorological data of vertical wind-speed profiles are obtained at stations (St.) I and II. Time series of concentration fluctuations are obtained at the points A–H. The star mark is the release point. A plant-canopy model is applied to the botanical garden (green area)

The vertical profiles of wind speed and direction were measured at stations I and II, which were located 1.8 km south-south-west from the botanical gardens, and in the botanical gardens, respectively. The data obtained at stations I and II were measured by sodar (Pacific Northwest National Laboratory) and by minisodar (Argonne National Laboratory) devices, respectively.

4.2 Mesoscale Meteorological Model

The mesoscale meteorological simulation is conducted by the Advanced Research WRF model version 3.3.1. Full physics processes are included in the present simulation in order to reproduce real meteorological phenomena as shown in a previous study (Nakayama et al. 2016). There are three computational domains connected with two-way nesting, covering 2700 × 2700, 600 × 600, and 150 × 150 km² areas with 4.5, 1.5, and 0.5 km horizontal resolution, respectively. The number of vertical levels is 53, with 12 levels in the lowest 1 km. The terrain data used are the global 30-s data from the United States Geological Survey. The land-use/land-cover information is determined by the 30-s resolution Global Land Cover Characterization dataset.

The simulation covers the experiment period from 1900 LT 14 July to 1900 LT 16 July. The initial and boundary conditions are set based on 6-h Final Analysis data of the US National Centers for Environmental Prediction. The WRF simulation outputs of the innermost domain are pre-arranged with 1-min intervals and 500 × 500 × 500 m³ resolution before acting as input for the CityLBM dispersion simulation.

4.3 Numerical Set-Up

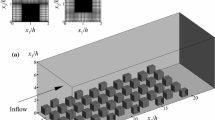
The computational domain covers an area of 4.2 × 4.2 × 2.5 km² as shown in Fig. 2. Three kinds of grid resolutions are set according to the altitude, with the finest grid resolution of 2 m or 4 m near the ground. The building structures are arranged in the central district of Oklahoma City by the use of a digital-surface-model dataset. Roughness blocks are placed outside the central district to maintain urban boundary-layer flows throughout the computational domains. The plant-canopy model is applied up to a height of 16 m in the botanical gardens, which includes the release point and the measurement point of station II. The plant-canopy parameter is determined as $C_{d} a_{f} = 0.01$, which gives velocity distributions comparable to the observations near the ground at station II. The boundary conditions of the temperature and the velocity are given by the WRF data. The nudging data assimilation is applied to a boundary region within 250 m from the horizontal outer boundaries and 500 m from the top boundary, respectively. The nudging coefficient $w = {1 \mathord{\left/ {\vphantom {1 {\left( {60\,{\Delta }t} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {60\,{\Delta }t} \right)}} \approx 10^{ - 3}$, so that its integral over a 1-min interval of WRF data becomes unity. The temperature of the ground and building surfaces are given using the ground temperature of the WRF data.

Fig. 2

Visualization of buildings and computational grids. Three kinds of grid resolution are set according to the height. A nudging region is at the computational boundaries. The locations of the interface ${\Delta }x_{{{\text{fine}}}}$/${\Delta }x_{{{\text{medium}}}}$ and ${\Delta }x_{{{\text{medium}}}}$/${\Delta }x_{{{\text{coarse}}}}$ are 88 and 344 m in the case of ${\Delta }x_{{{\text{fine}}}} = 2$ m, and 240 and 752 m in the case of ${\Delta }x_{{{\text{fine}}}} = 4$ m, respectively

Nine ensemble calculations are performed to account for turbulence uncertainty. Different ensemble conditions are generated by changing the arrangement of roughness blocks. Simulations are carried out from 0700 LT 16 July to 1400 LT 16 July including three release cases as case 1 (0900–0930 LT), case 2 (1100–1130 LT), and case 3 (1300–1330 LT).

4.4 Computational Performance

We evaluate the performance of the CityLBM software on the Artificial Intelligence Bridging Cloud Infrastructure supercomputer at the National Institute of Advanced Industrial Science and Technology in Japan. The CityLBM software is written in the NVIDIA CUDA language, and the graphics-processing-unit kernel is well tuned to achieve high performance on supercomputers (Onodera et al. 2018). The whole computational domain is divided into 6 × 6 sub-domains in the horizontal directions to achieve a real-time simulation. The code is compiled with the NVIDIA CUDA Compiler 9.2 (-O3 -use_fast_math –restrict -Xcompiler fopenmp -gpu-architecture = sm_70 -std = c++ 11) and uses OpenMPI 9.2 software.

Table 1 shows the computational performance of a plume-dispersion simulation in single precision. The computational time includes the central-processing-unit calculations, message-passing-interface communications, and input/output processes for the nudging data assimilation and post-processing. In order to achieve a real-time simulation, the number of cells per graphics processing unit is set to about 10⁷ for the finest case of 2-m grid resolution. Since the number of cells per graphics processing unit is relatively small, the communication time occupies about 30% of the total, and the corresponding performance is about 365 mega-lattice updates per second per graphics processing unit (MLUPS). In the case of the 4-m grid resolution, the performance is about 275 MLUPS, and the communication time occupies about 40% of the total time. The results indicated that real-time simulations are feasible using a 2-m resolution, and beyond real-time simulations are realized using a 4-m resolution.

Table 1 Computational performance of the CityLBM model with the finest grid resolutions of up to 2 m and 4 m, respectively

4.5 Flow Field

Flow fields of the dispersion model are compared with the mesoscale results and the observation data at station I upstream of the release point and station II near the release point, respectively. Station I is located about 500 m from the calculation boundary where the flow is produced through the data-assimilation area and the following roughness block area. Station II is located in the botanical gardens in the city area. The wind-speed profiles are affected by complex buildings and the plant-canopy model. The CityLBM and WRF data are linearly interpolated at each observation point. The mean wind-speed profiles and their standard deviation ($v_{{{\text{mean}}}} \pm \sigma$) of the CityLBM model are evaluated from the ensemble calculations and are shown in Figs. 3 and 4 by a solid line and a filled area, respectively.

Fig. 3

Vertical profiles of wind speed and direction according to the mesoscale (WRF) and dispersion (LBM) models near the ground observed at station I. The 2-m-resolution data with the plant-canopy model are shown

Fig. 4

Vertical profiles of wind speed and direction according to the dispersion model (LBM) with/without the plant-canopy model at station II; 2-m-resolution data are shown for case 1 (0900–0930 LT)

Figure 3 shows vertical profiles of wind speed and direction at station I between the three release times in cases 1–3. The observations were obtained from the ground up to an altitude of z = 500 m. The wind-speed profiles of the CityLBM model show good agreement with the observations for z < 200 m due to the optimized placement of the roughness blocks. Since the vertical grid resolution of the urban model is about 10 times finer than that of the mesoscale model, the calculation of the wind direction is significantly improved near the ground. In contrast, the difference between the urban model and observations reaches a factor of 2 at higher altitudes, because the influence of the mesoscale boundary conditions becomes stronger than that near the ground. In order to improve the accuracy at higher altitude, it may be necessary to use a higher-resolution mesoscale model (Wiersema et al. 2020). The above results indicate that the nudging with the mesoscale model enables the dispersion model to reproduce the observed wind-speed profiles and give reasonable results outside the city central area.

Figure 4 shows vertical profiles of wind speed and direction with and without the plant-canopy model at station II in case 1, where the observations were measured from the ground up to the height z = 120 m. The wind speed and direction of the mesoscale/dispersion model with and without the plant-canopy model, are reasonable compared to the observations. Here, it is very important to predict detailed wind-speed profiles near the ground, which greatly affect the plume dispersion from a point source near the ground. Since the dispersion model can resolve complex structures of buildings and streets at the metre scale, detailed wind-speed profiles for z < 20 m can be directly determined. Despite the fine grid resolution of 2 m, the CityLBM model without the plant-canopy model overestimates the wind speed compared with the observations for z < 20 m, with the dispersion model with the plant-canopy model reproducing the observations well.

In theory, a no-slip boundary condition is valid only for the DNS approach for turbulent flows that resolve the viscous sublayer to about a 1-mm resolution. However, no wall model has been established for complex urban structures. In order to resolve this problem, we introduced the plant-canopy model, and the canopy parameters were adjusted to reproduce the observed wind speed at station II, which may be a useful empirical approach for clarifying the effects of vegetation in the current local flow simulations.

Unlike the wind speed near the ground, there was no significant difference in the wind direction with and without a plant-canopy model. The wind direction near the ground varies rapidly, with none of the models shown in Fig. 4 able to reproduce the observations. To resolve this issue, it is necessary to increase the mesoscale grid resolution. In the future, it may be also effective to introduce a data-assimilation method with detailed observations from urban areas.

4.6 Dispersion Field

The impact of the plant-canopy model is demonstrated here, with Fig. 5 showing horizontal distributions of instantaneous concentration at z = 5 m with and without the plant-canopy model. The concentration is normalized by the initial release concentration. The time evolution of tracer gas is visualized at 5, 15, and 30 min after release in case 1. The tracer gas is released from the botanical gardens and advected to the north-east as indicated by the wind direction in Fig. 5. Comparing the tracer concentration with (Fig. 5a, c, e) and without (Fig. 5b, d, f) the plant-canopy model reveals that the concentration distribution without the plant-canopy model spreads over a wider downstream area. A major difference between the two simulations is that only with the plant-canopy model does the concentration distribution spread into the north-west direction near the measurement point A at 0915 LT (see Fig. 5c).

Fig. 5

Horizontal concentration profiles at z = 5 m with (a, c, e) and without (b, d, f) the plant-canopy model; 2-m-resolution data is shown for case 1 (0900–0930 LT). The release point is indicated by the star symbol. The wind direction is indicated by the arrow

Figure 6 shows vertical profiles of normalized concentration with and without the plant-canopy model at points A–H. Point A is in the north-west area, and Points B–H are in the north-east area (see Fig. 1b). The mean concentration is normalized by the observations and averaged in cases 1–3. These results show that the plume concentration differs depending on the presence of the plant-canopy model, rather than the grid resolution between 2 and 4 m. The simulation with the plant-canopy model enhances vertical mixing due to turbulence near the ground, and a greater fraction of the plume is transported to the north than that without the plant-canopy model, except points A and E. Point A is not downstream of the release point and is not directly affected by vertical mixing, but the concentration has improved to within a factor of 10 of the observations with the plant-canopy model. Point E is located on the north-east corner of the building near the release point. Here, the concentration with the model is higher than that without the model near the ground, and there is no significant difference in the vertical diffusion.

Fig. 6

Vertical profiles of mean plume concentration with/without the plant-canopy model; the 2-m and 4-m-resolution data are shown. The normalized results are averaged for case 1 (0900–0930 LT), case 2 (1100–1130 LT), and case 3 (1300–1330 LT)

Figure 7 presents the mean concentration with and without the plant-canopy model in cases 1–3, respectively, with the solid, dashed, and dotted lines representing perfect agreement, factor-of-2 agreement, and factor-of-10 agreement between the dispersion model and observations, respectively. The symbols represent the measurement points A–H. The ensemble contains all simulations such that the open symbols denote the individual simulations and the solid symbol is the ensemble average. Since airflow in the urban area is characterized by high-Reynolds-number turbulence, open symbols are greatly scattered in each ensemble, making it essential to use ensemble-averaged data in environmental assessment for such highly turbulent data. The ensemble-averaged values denoted by the filled markers are found within a factor of 2 of many of the observation points. Comparing the plume concentration with and without the plant-canopy model, the values without the plant-canopy model overestimate the concentration in the north-east downstream side (B–H), which is consistent with the vertical concentration profiles in Fig. 8. Another clear difference can be seen at the measurement point A in the north-west area. Although simulations with the plant-canopy model reproduce the concentration either within a factor of 2 or 10, simulations without the plant-canopy model underestimate the concentration, which is indicated by the horizontal distribution of concentration at 0915 LT in Fig. 7.

Fig. 7

Scatter plots of mean concentration with (a, c, e) and without (b, d, f) the plant-canopy model. The 2-m-resolution data is shown for case 1 (0900–0930 LT), case 2 (1100–1130 LT), and case 3 (1300–1330 LT). Open and solid symbols denote ensemble and ensemble-averaged data, respectively, at the measurement points indicated in Fig. 1b. The solid, dashed, and dotted lines represent perfect, factor-of-2, and factor-of-10 agreement with the observations, respectively

Fig. 8

Model-performance measures for the a mean and b maximum concentration. Thick horizontal black lines indicate a perfect model score

The prediction capability of each model is quantitatively assessed by the following measures: fraction of predictions within a factor of x (FAC_x), fractional bias (FB), geometric mean bias (MG), and the geometric variance (VG), which are calculated as

$$ {\text{FAC}}_{x} = 1 \;{\text{if}}\; 1/x \le X_{o} /X_{p} \le x \quad {\text{else}}\; 0, $$

(22)

$$ {\text{FB}} = 2\left( { \overline{{X_{o} }} - \overline{{X_{p} }} } \right)/\left( { \overline{{X_{o} }} + \overline{{X_{p} }} } \right), $$

(23)

$$ {\text{MG}} = {\text{exp}}\left( { \overline{{{\text{ln}}X_{o} }} - \overline{{{\text{ln}}X_{p} }} } \right), $$

(24)

$$ {\text{VG}} = {\text{exp}}\left\{ {\overline{{\left[ {{\text{ln}}\left( {X_{o} } \right) - {\text{ln}}\left( {X_{p} } \right)} \right]^{2} }} } \right\}, $$

(25)

respectively. Here, $X_{o}$ is the set of observational data, and $X_{p}$ are the corresponding predictions from the ensemble simulations. An overbar indicates averaging for the seven locations in the north-east downstream side (B–H) and the three periods in the cases 1–3. Point A is excluded because the tendency of concentration is different from the other points and an extremely low concentration of the simulation contaminates the overall model performance, especially for the geometric mean bias and geometric variance. A perfect model would have the values FAC_x = 1, FB = 0, MG = 1, and VG = 1, while a “good” or “acceptable” model as defined by Chang and Hanna (2004) as FAC₂ > 0.5, while the mean bias is within ± 30% (− 0.3 < FB < 0.3 or 0.7 < MG < 1.3).

Figure 8 shows the above performance measures estimated for the mean and maximum concentrations. In order to show the convergence of the dispersion model, we also compare the results with different grid resolutions. The results without the plant-canopy model give poor agreement, and the mean concentration shows FAC₂ = 0.1 with 4-m grid resolution and FAC₂ = 0.19 with a 2-m grid resolution. In contrast, the results with the plant-canopy model are dramatically improved, and the mean concentration with 2-m grid resolution gives FAC₂ and FAC₅ values of 0.76 and 1.0, respectively, with a similar accuracy also observed for the maximum concentration. This performance is comparable to one of the most advanced WRF models (Wiersema et al. 2020) where WRF simulations were performed using a multiscale five-domain nested configuration, spanning horizontal grid resolutions from 6 km to 2 m. Although the observation dates are different, their FAC₂ and FAC₅ values are about 0.58 and 095, respectively, which is the current record score compared with the previous WRF-based simulations (Lundquist et al. 2012; Bao et al. 2018).

The statistics of fractional bias and geometric mean bias indicate a tendency for the dispersion model to overestimate the mean and maximum concentration. The performances are improved by applying the plant-canopy model, which can be confirmed from the vertical concentration profiles in Fig. 6. The statistics of the geometric variance indicate the scatter of the data, and the performances are also improved by the high-resolution simulation with the plant-canopy model. The above statistics indicate that the dispersion model with the plant-canopy model has a good prediction capability for both mean and maximum concentrations.

5 Conclusion

We presented locally mesh-refined LBM-based plume-dispersion simulations using the CityLBM dispersion model. The nudging data-assimilation method was applied to the dispersion model, and multi-scale flow simulations are enabled by combining local flow simulations for resolving the building structures and mesoscale meteorological simulations with the WRF mesoscale model. The plant-canopy model was also applied to evaluate the detailed flow conditions near the ground. The dispersion model was validated with respect to the field experiments of the JU2003 campaign conducted in the city centre of Oklahoma City from 28 June to 31 July 2003. Ensemble calculations were performed to account for the measurement uncertainty. We evaluated the flow field and the dispersion field in comparison with the observations.

Regarding the flow field, vertical profiles of the wind speed and the wind direction give reasonable agreement compared with the observations at stations I and II. In particular, the dispersion model with the plant-canopy model improves the wind speed near the ground at station II, which is close to the tracer-release point.

Regarding the dispersion field, mean and maximum concentrations were compared with the observations at the measurement points A to H. Since airflow in the urban area is characterized by high-Reynolds-number turbulence, mean and maximum concentrations are greatly scattered in each ensemble case. However, the ensemble calculations enable the simulation results to converge within a factor-of-10 agreement with the observations at almost all observation points. Comparisons indicate that the dispersion model with a 2-m resolution and the plant-canopy model achieves good results in terms of the metrics FAC₂, FAC₅, the fractional bias, geometric mean bias and geometric variance. We conclude that the locally mesh-refined LBM approach can simulate plume dispersion with resolved building structures, detailed plant-canopy models, and ensemble LES models.