Characterizing the Coherent Structures Within and Above Large Wind Farms

Abstract

We study large-eddy simulations of coherent structures within and above different wind-farm configurations in a neutral atmospheric boundary layer (ABL) using proper orthogonal decomposition (POD) to improve understanding of the flow structures in both physical and spectral space. We find that the spanwise extent of elongated streamwise counter-rotating rolls is constrained by the spanwise turbine spacings. The very large streamwise extent of the observed POD flow structures in physical space indicates that the interaction between the wind turbines and the ABL also causes large-scale flow organization. Using a spectral POD analysis to characterize the coherent structures at a certain frequency, we find that the flow dynamics for the frequency corresponding to the time a fluid parcel takes to traverse one streamwise turbine spacing is dominated by the wind-turbine wakes. The first POD mode at this frequency indicates that the wakes are spatially correlated. However, the flow dynamics at lower frequencies, corresponding to the longer time a fluid parcel takes to traverse the entire wind farm, are dominated by large flow structures originating from the ABL dynamics. We find that hundreds of POD modes are required to accurately describe the full three-dimensional flow profiles in large wind farms, while even more POD modes are required to accurately describe the Reynolds stresses that are important to describe the momentum exchange between the wind farm and the ABL. This indicates that wind-farm dynamics in the ABL are very complex.

1 Introduction

Wind energy is a very promising renewable-energy source and in recent years the industry has grown tremendously. However, more research is essential to improve understanding of the physical mechanisms affecting the efficiency of large wind farms, which is determined by the interplay between the wind-turbine wakes and the atmospheric boundary layer (ABL) (Sanderse et al. 2011; Sørensen 2011; Stevens and Meneveau 2017). In large wind farms, the wakes from upstream turbines significantly affect the performance of downstream turbines (Barthelmie et al. 2010) and, as the incoming flow energy at hub height is limited, the performance of large wind farms is strongly influenced by the vertical exchange of kinetic energy that transfers high-velocity air from above to hub-height level (Frandsen 1992; Cal et al. 2010; Calaf et al. 2010; Luzzatto-Fegiz and Caulfield 2018; Cheng and Porté-Agel 2018).

To improve understanding of the flow dynamics in large wind farms, extensive wind-tunnel measurements, simulations, and field experiments have been performed (Stevens and Meneveau 2017). Experiments have the advantage that all physical effects are incorporated, while full access to the flow field in simulations enables the detailed study of flow structures. Recently, large-eddy simulation (LES) has become a popular method for studying wind-farm dynamics, as it can handle unsteady, anisotropic turbulent flows dominated by large-scale structures and turbulent mixing well (Mehta et al. 2014; Stevens and Meneveau 2017). Characterizing all spatiotemporal correlations in fully-turbulent flow is a daunting task due to the very large range of length scales involved. Therefore, one aim is to characterize only the dynamically-relevant flow structures by the use of decomposition methods, such as proper orthogonal decomposition (POD), which have been used successfully to characterize the coherent flow structures in turbulent wall-bounded flow, free shear flow, and thermal convection (see Berkooz et al. 1993).

Proper orthogonal decomposition (Holmes et al. 1998) has also been used in several studies to analyze the flow structures within and above wind farms. VerHulst and Meneveau (2014) presented a comprehensive three-dimensional POD study on the flow structures in aligned and staggered periodic wind farms, finding that the streamwise counter-rotating rolls, which generate strong ejection and sweep regions, are the dominant flow structure. It is believed that these rolls play an important role in the kinetic-energy redistribution and, therefore, have a strong influence on the wind-farm efficiency. VerHulst and Meneveau (2014) also showed that more POD modes are needed to represent $40\%$ of the kinetic energy than to reconstruct $40\%$ of the flux of turbulence kinetic energy from the POD modes of the velocity field and the mean flow gradient. Hamilton et al. (2015, 2016) applied a double POD analysis to wind-tunnel measurements obtained at separate streamwise stations inside a model wind farm. The idea of the double POD analysis is to apply an additional POD analysis to the original POD results with the same index. By analyzing the velocity and stress fields, Hamilton et al. (2015, 2016) demonstrated that the streamwise development can be taken into account in the double POD analysis because it collectively evaluates the flow field spanning the rows of the measurement locations. In addition, they showed that the double POD analysis significantly reduces the number of modes required to capture the wind-turbine wakes.

Newman et al. (2014) studied the entrainment process in a three by five array of wind turbines deployed along the streamwise and spanwise directions, respectively, finding a characteristic wavelength of two turbine diameters at the turbine-tip height for the dominant POD modes of the reconstructed Reynolds shear stress, while the most energetic POD modes are associated with larger wavelengths. Andersen et al. (2017) analyzed vertical snapshots of the LES results using a POD analysis, and showed that the dominant length scales responsible for the entrainment process increase with the distance in the wind farm. Inside the wind farm, this length scale is restricted by the streamwise turbine spacing, but above the wind farm, larger structures are observed. Ali et al. (2017) studied the effect of different thermal-stratification conditions on the flow structures in large wind farms, and showed that, in neutral and unstable boundary layers, the large-scale structures related to the ABL dominate over the small-scale structures introduced by the wind-turbine wakes. However, for stable boundary layers, the wind-turbine wakes are the dominant flow structure.

In several studies, the results of a POD analysis have also been coupled with other turbulent-analysis tools such as a multi-fractal analysis (Ali et al. 2016). Bastine et al. (2018) devised a stochastic wake model based on two-dimensional POD modes obtained from LES results, and showed that the large-scale structures are captured well by only a few POD modes, with the small-scale turbulence modelled using an additional homogeneous-turbulence field. Bastine et al. (2018) found that, even though large-scale structures contain the most kinetic energy, the small-scale turbulence plays an important role in the wind-farm dynamics.

Another promising area of research is the use of the POD technique for flow control. A reduced-order model based on a POD analysis is able to predict dynamically the wake position, which can yield improved control strategies. Using the LES results of a wind-farm-flow investigation, Hamilton et al. (2018) constructed such a reduced-order model for the turbulent wake by projecting the POD modes on the velocity snapshots, which produces the dynamic coefficients for each POD mode. The model is dynamically reinitialized with a new initial condition to update the POD mode coefficients. By using dynamic mode decomposition, which is related to the POD technique, Iungo et al. (2015a) constructed a reduced-order model of the wind-turbine wakes embedded in a Kalman filter, and demonstrated the potential of this tool for real-time flow control in large-scale wind farms. Andersen and Sørensen (2018) found that the correlation between the instantaneous turbine performance and the upstream wake position is limited in very large wind farms, which they argue limits the benefits of wake steering as a control strategy, and point out that these results should be extended to cases in which intentional yaw misalignment is considered. In addition, they argued that the potential of induction-based control strategies should be further investigated.

Most of the previous works focused on the POD analysis in physical space in which the POD modes contain information about all dynamically-important frequencies. For the development of wind farm control insight in the wind farm flow dynamics at dynamically critical frequencies is crucial. Dynamic mode decomposition allows us to determine the flow dynamics of specific frequencies, and this has not yet been considered in POD analysis. As POD analysis is very frequently adopted in wind-farm research, we believe its application in spectral space may provide useful new insights.

Here, we extend the previous works on POD analysis to further study the coherent structures in the LES results of large wind farms. Using a very large amount of data generated from high-fidelity LES tools, we perform both conventional POD analysis in three-dimensional physical space, corroborating previous related publications, as well as a new spectral POD analysis to determine the physically-relevant frequencies important for frequency-based wind-farm-flow control. In Sect. 2, we introduce the POD and LES methods, and analyze the main flow structures and Reynolds stress using a POD analysis in Sect. 3. While all POD studies discussed above focus on the spatial structures, we also determine the POD modes in spectral space using a spectral POD analysis (Towne et al. 2018) to characterize the flow dynamics at different frequencies in Sect. 4. This provides insight into the flow modes at dynamically-relevant frequencies, which can be important for the development of frequency-based control strategies in wind farms. We conclude the paper with a discussion in Sect. 5.

2 Problem Formulation and Numerical Methods

2.1 Proper Orthogonal Decomposition

Proper orthogonal decomposition is a powerful post-processing tool for analyzing coherent flow structures in turbulent flows (Holmes et al. 1997, 1998), and can be interpreted as a singular-value decomposition of the flow field in a series of snapshots. For a general introduction to the POD technique, we refer the reader to Sirovich (1987) and Berkooz et al. (1993). It was noted by VerHulst and Meneveau (2014) that, for wind-farm simulations performed in a periodic domain, the POD modes need not be Fourier modes due to the flow inhomogeneity imposed by the wind turbines, which is also an issue discussed in general by George (1999). Below, we present the mathematical formulation of our POD method.

We first use Reynolds decomposition to obtain the corresponding fluctuating components from the mean flow field of which the streamwise, spanwise, and vertical velocity components are denoted by u, v, and w, respectively. For the LES data, we formulate a snapshot matrix $\mathbf {A}$ as

$$\begin{aligned} \mathbf {A}=\begin{bmatrix} \cdot&\cdot&\cdot&\cdot&\ldots&\cdot&\cdot&\cdot \\ \cdot&\cdot&\cdot&\cdot&\ldots&\cdot&\cdot&\cdot \\ \cdot&\cdot&\cdot&\cdot&\ldots&\cdot&\cdot&\cdot \\ \end{bmatrix}_{N_t \times 3N_{xyz} } \end{aligned}$$

(1)

where $N_t$ is the number of snapshots, $N_{xyz}= N_x\times N_y\times N_z$, where $N_x$, $N_y$, and $N_z$ are the number of grid points in the streamwise, spanwise, and vertical directions, respectively, and the factor 3 accounts for the three velocity components considered. By this arrangement, each row of $\mathbf {A}$ represents a snapshot of the flow field at a certain time, with each column giving the time history of a flow variable at a given location. We apply singular-value decomposition to the matrix $\mathbf {A}$ to yield

$$\begin{aligned} \mathbf {A}=\mathbf {U}\varvec{\Sigma } \mathbf {V}^{\dag }, \end{aligned}$$

(2)

where the superscript $^\dag$ represents the transpose conjugate. The unitary matrices $\mathbf {U}$ (of size $N_t\times N_t$) and $\mathbf {V}$ (of size $3N_{xyz}\times 3N_{xyz}$) accommodate, respectively, the left and right singular vectors of $\mathbf {A}$, and $\varvec{\Sigma }$ is a rectangular diagonal matrix whose diagonal entries are the singular values whose physical interpretation is explained below. To obtain these matrices, one forms the correlation matrix $\mathbf {C}=\mathbf {A}\mathbf {A}^\dag$ and poses the corresponding eigenvalue problem as

$$\begin{aligned} \mathbf {C}=\mathbf {A}\mathbf {A}^\dag =\mathbf {U}\varvec{\Sigma }_{N_t\times N_t}^2\mathbf {U}^{\dag }, \end{aligned}$$

(3)

which is the so-called snapshot POD method proposed by Sirovich (1987), whose solution is used to obtain $\mathbf {U}$ and $\varvec{\Sigma }_{N_t\times N_t}$. The POD modes in $\mathbf {V}$ are obtained using Eq. 2 by calculating $\varvec{\Sigma }^{-1}\mathbf {U}^\dag \mathbf {A} = \mathbf {V}^\dag$. Each column of $\mathbf {V}$ spans the entire flow field (u, v, w) and is referred to as a POD mode. The eigenvalues in $\varvec{\Sigma }_{N_{t}\times 3N_{t}}^2$ represent the kinetic energy contained in each POD mode, with $\mathbf {U}$ giving the temporal coefficients for the snapshots in $\mathbf {A}$, constituting the POD modes in $\mathbf {V}$. Finally, as mentioned above, $\mathbf {U}$ and $\mathbf {V}$ are unitary matrices whose columns form an orthonormal set. This property is used for an a posteriori verification of our results in a procedure similar to the one presented by Zhang and Stevens (2017).

We also reconstruct the Reynolds-stress distribution from the POD modes of the velocity fields. For example, for the shear component $\overline{u'w'}$,

$$\begin{aligned} \mathbf {A}_u&= \mathbf {U} \varvec{\Sigma }_{N_t\times N_{xyz}} \mathbf {V}^\dag _u, \end{aligned}$$

(4)

$$\begin{aligned} \mathbf {A}_w&= \mathbf {U} \varvec{\Sigma }_{N_t\times N_{xyz}} \mathbf {V}^\dag _w, \end{aligned}$$

(5)

where $\mathbf {A}_u$ and $\mathbf {A}_w$ represent the part of the matrix $\mathbf {A}$ related to the streamwise and vertical velocity component, respectively, thus the size of $\mathbf {A}_u$ and $\mathbf {A}_w$ is $N_{t} \times N_{xyz}$. The snapshot matrix for the time-averaged Reynolds stress is

$$\begin{aligned} \overline{u'w'}&=\overline{\mathbf {A}_u \mathbf {A}_w}=\frac{1}{N_t}\sum _{i=1}^{N_t} (\mathbf {A}_u \circ \mathbf {A}_w)_{_{i,j}} = \frac{1}{N_t} (\mathbf {A}_w^\dag \mathbf {A}_u)_{_{j,j}} \nonumber \\&= \frac{1}{N_t} (\mathbf {V}_w \varvec{\Sigma }^\dag _{ N_{xyz}\times N_t} \mathbf {U}^\dag \mathbf {U} \varvec{\Sigma }_{N_t\times N_{xyz}} \mathbf {V}^\dag _u)_{_{j,j}} = \frac{1}{N_t} (\mathbf {V}_w \varvec{\Sigma }^2_{ N_{t}\times N_{t}} \mathbf {V}^\dag _u)_{_{j,j}} \nonumber \\&= \frac{1}{N_t} \sum _{j=1}^{N_t} \lambda ^2_j \mathbf {V}^\dag _{w_{:,j}}\mathbf {V}^\dag _{u_{:,j}} \end{aligned}$$

(6)

where the circle is the Hadamard product executing entry-wise multiplication between two matrices. The final formulation is equivalent to Eq. 14 in VerHulst and Meneveau (2014), and indicates that the contribution of the jth POD modes to the Reynolds stress $\overline{u'w'}$ is $\lambda ^2_j \mathbf {V}^\dag _{w_{:,j}}\mathbf {V}^\dag _{u_{:,j}}/N_t$.

2.2 Large-Eddy-Simulation Method

We simulate the ABL and wind-farm flow dynamics in periodic and developing aligned and staggered wind farms using our code to model a neutral pressure-driven ABL flow by solving the filtered, incompressible Navier–Stokes equations without buoyancy, system rotation, or other effects (Calaf et al. 2010; Stevens et al. 2014). In the horizontal directions, a pseudo-spectral discretization with periodic boundary conditions is adopted, and a second-order centred finite-difference scheme is used for the vertical direction. The subgrid stresses are modelled using a scale-dependent Lagrangian dynamic model (Bou-Zeid et al. 2005), the wall stress at the ground is captured by a standard rough-wall model (Moeng 1984) using velocities test-filtered at twice the grid scale, and for the top boundary conditions, we use zero vertical velocity component and shear stress. Time-stepping is performed with a second-order Adams–Bashforth scheme, the turbines are modelled using an actuator disk (Sørensen and Myken 1992), and it is assumed that they are operating in regime II (Johnson et al. 2004) where the thrust coefficient is constant as a function of wind speed by adjustment of the blade rotation frequency to the incoming wind speed. According to Porté-Agel et al. (2013), the turbines operate most of the time in this regime. Here, we use a thrust coefficient $C_T=0.75$ for all turbines. For an overview of wind-farm modelling with the LES technique, we refer the reader to Mehta et al. (2014) and Stevens and Meneveau (2017).

The different simulation cases are indicated in Table 1. We consider first a canonical neutral ABL, and compare the results to those obtained by Shah and Bou-Zeid (2014), and then consider periodic wind farms with $16\times 12$ turbines in the streamwise and spanwise directions, respectively, and finite-size wind farms with 12 rows in the streamwise direction. A comparison of the results for the ABL case with the wind-farm cases reveals the interaction between the large-scale flow modes and the wind farm. To simulate flow above a finite-size wind farm, we use the concurrent precursor inflow method introduced by Stevens et al. (2014). In all simulations, the dimensionless roughness length $z_0/H=10^{-4}$, while the turbine hub height $z_h$ and turbine diameter D are 0.1H. To perform the spectral POD analysis, we use a constant timestep of $5\times 10^{-5}$ non-dimensional time units. To ensure that all the essential flow dynamics are captured, we verified that sampling the velocity field every 15 timesteps is sufficient to capture all energetically-relevant events. For each simulation, we stored 100,000 snapshots to produce a database covering about 75 non-dimensional time units, which is equivalent to about 850 turbine travel times, i.e. the time for a fluid parcel to traverse one streamwise turbine spacing at hub height.

Table 1 Summary of the simulated cases performed on a grid of resolution $512\times 256\times 128$ nodes following the guidelines of Porté-Agel et al. (2013) and Stevens et al. (2014)

Fig. 1

Time-averaged, a streamwise, and b spanwise velocity components at hub height, and c the streamwise and d vertical velocity components in the vertical cross-section intersecting the turbines for a developing aligned wind farm. The velocity components are normalized with the reference velocity $U_a$ (see Eq. 7), and the colour scale of each panel has been adjusted to the corresponding values

3 Results

In Sect. 3.1, we discuss the characteristics of the mean velocity field in wind farms followed by an analysis of the corresponding POD results in Sect. 3.2. In Sect. 3.3, we discuss the POD modes of the Reynolds stress.

3.1 Averaged Wind-Farm Flow Field

Figure 1 shows the time-averaged velocity components in a developing aligned wind farm normalized by the reference flow speed $U_a$ at hub height $z/H=0.1$, which we define as

$$\begin{aligned} U_a=\sqrt{U_\mathrm {hub}^2+V_\mathrm {hub}^2+W_\mathrm {hub}^2}, \end{aligned}$$

(7)

where $U_\mathrm {hub}$, $V_\mathrm {hub}$ and $W_\mathrm {hub}$ are the streamwise, spanwise, and vertical velocity components, respectively. Figure 1a, c clearly reveals the structure of wind-turbine wakes in the field of the streamwise velocity component. Figure 1b shows the spanwise velocity component at hub height, and the regions of positive and negative values indicate the flow around the turbines. The vertical cross-section of the field of the wall-normal velocity component in Fig. 1d also shows the flow around the wind turbines, while Fig. 1c also shows the development of the internal boundary layer, which begins at the start of the wind farm.

3.2 POD Analysis

3.2.1 Convergence Test

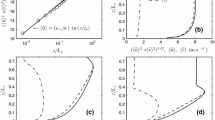
Following Newman et al. (2014), we test the convergence of the POD modes using the $L_2$ norm of the normalized eigenvalue spectrum defined as

$$\begin{aligned} \eta ^{N_t}=\left| \left| \frac{{\varvec{{\Lambda }}}}{\sum _{i=1}^{N_t} \lambda ^2_i} \right| \right| ^2, \end{aligned}$$

(8)

where ${{\varvec{{\Lambda }}}}=\lambda ^2_i (1\le i\le N_t$) are the diagonal terms in the eigenvalue matrix. The relative comparison is defined as

$$\begin{aligned} E(N_t)=\left| 1-\frac{\eta ^{N_t}}{\eta ^{\infty }} \right| , \end{aligned}$$

(9)

where $\eta ^{\infty }$ is based on all 5000 POD modes determined. When we calculate the quantity $E(N_t)$, we keep the considered time interval constant (as close as possible), so the time interval between two consecutive snapshots varies with the value of $N_t$. Figure 2 shows that the value of $E(N_t)$ decreases with the value of $N_t$ for all considered cases, and the small variation for larger $N_t$ values indicates that the eigenvalue spectrum has indeed converged.

Fig. 2

Convergence test for the eigenvalues of the POD modes using Eqs. 8 and 9

Fig. 3

The streamwise velocity component of the first POD mode at hub height in a developing aligned wind farm obtained using a 50, b 500, c 2500 and d 5000 snapshots captured over 75 non-dimensional time units, which is equivalent to about 850 turbine travel times

Figure 3 shows the streamwise velocity component of the first POD mode at hub height based on a different number of flow snapshots over the same time interval. In this and all subsequent figures, the POD mode is normalized by its maximum absolute value. Figure 3 gives additional confidence in the convergence of the results since that obtained using 2500 snapshots is nearly identical to the result obtained using 5000 snapshots. As a similar convergence is found for the other velocity components and cases, we use 5000 snapshots for all analyses.

Fig. 4

The distributions of the eigenvalues of the POD modes (see Eq. 3) for the different cases indicated in the legend. Panel a shows the eigenvalues normalized by the largest eigenvalue ($\lambda _1^2$) and panel b the cumulative eigenvalue normalized by its total sum. Note that the number of modes are shown logarithmically

Figure 4a reveals that the kinetic-energy distribution of the POD modes for the different cases shows a similar trend. Note the POD modes are sorted based on their kinetic-energy content and, therefore, the energy per mode decreases with increasing mode number. For all cases, the smallest eigenvalues are more than two orders of magnitude smaller than the largest eigenvalue, which indicates that the higher POD modes bear less dynamic significance, at least from the point-of-view of the kinetic-energy composition. Figure 4b shows the corresponding cumulative energy distribution as function of mode number. Note that the convex shape is a result of the choice to represent the number of modes logarithmically (VerHulst and Meneveau 2014). This distribution is similar for all cases, but would depend somewhat on the exact number of modes considered. Here, we concentrate on the energetically-dominant POD modes. Figure 4b shows that about 2000 POD modes are required to capture $80\%$ of the total energy in a neutral ABL, while Shah and Bou-Zeid (2014) found by using a two-dimensional snapshot POD that only about 500 POD modes are required to capture $80\%$ of the total energy. This indicates that the total number of modes required to represent the flow increases for a full three-dimensional POD analysis, which we believe is due to the emergence of streamwise-varying POD modes (see Sect. 3.2.2) captured using the three-dimensional analysis, but not using the two-dimensional POD modes.

Fig. 5

a Streamwise velocity component of different POD modes at hub height for the ABL case, and the b vertical cross-section showing the streamwise, spanwise and vertical velocity components of the first POD mode at $x/H=2{\uppi }$

Fig. 6

a Streamwise velocity component of different POD modes at hub height for the periodic aligned wind farm, and b the vertical cross-section showing the streamwise, spanwise and vertical velocity components of the first POD mode at $x/H=2{\uppi }$, which is in between the turbine rows. The open circles indicate the spanwise location of the turbines

3.2.2 Proper Orthogonal Decomposition Modes

Figure 5a shows the streamwise velocity component of different POD modes at hub height for the ABL case. One can easily see that the dominant flow pattern consists of elongated streamwise rolls of limited variation in the streamwise direction and of vertical extent covering the entire boundary layer (see Fig. 5b). The spanwise and vertical velocity components of the first POD mode reveal clockwise (e.g. $2.4< y/H<3$) and counterclockwise (e.g. $3<y/H<3.8$) rolls. In agreement with VerHulst and Meneveau (2014), we see that some of the higher POD modes show streamwise-varying patterns. When only two-dimensional POD modes are considered (Shah and Bou-Zeid 2014), the structure of the streamwise-varying rolls is similar for the lower POD modes, but differences appear for the higher modes due to the streamwise variation captured using the three-dimensional method.

Figure 6 shows that, in the aligned periodic wind farms, the size of the roll structures is clearly delimited by the turbines, and each roll covers one or two turbine columns in the spanwise direction, i.e. the rolls have a spanwise extent of about $2{\uppi } H\times 1/12=0.523H$ or $2{\uppi } H\times 2/12=1.047H$. For the aligned periodic wind farm, the streamwise-varying modes are observed for a lower POD mode than for the ABL case, which indicates that, due to the interaction between the wind turbines and the ABL flow, the kinetic energy is redistributed across the POD modes. The POD modes 7 and 8 show that these streamwise-varying structures have an extent of up to six times the boundary-layer height, which is significantly longer than the structures observed by VerHulst and Meneveau (2014). Newman et al. (2014) and Andersen et al. (2017) used a POD analysis in two-dimensional vertical planes to show that the important characteristic length scales inside the wind farm are restricted by the turbine spacing, while larger structures are found above the turbine-tip height. Our three-dimensional POD modes are dominated by the large flow structures above the wind farm and, therefore, are consistent with the results from Andersen et al. (2017). In agreement with the two-dimensional POD results in Newman et al. (2014) and Andersen et al. (2017), we also find a length scale of the order of turbine spacing above the hub height if we extract from the three-dimensional POD results the velocity signals at the tip of the turbine ($z/H=0.15$) (Zhang and Stevens 2017). At hub height, the characteristic length scales are smaller than above the wind farm due to the turbulent mixing caused by the wind-turbine wakes.

Fig. 7

a Streamwise velocity component of different POD modes at hub height for the periodic staggered wind farm, and b the vertical cross-section showing the streamwise, spanwise and vertical velocity components of the first POD mode at $x/H=2{\uppi }$, which is in between the turbine rows. The open circles indicate the spanwise location of the turbines

Figure 7 shows that the POD modes for the staggered wind farm reveal similar flow structures to those for the aligned wind farm, although more streamwise-varying POD modes are observed. This suggests that large-scale flow structures are mostly determined by the ABL dynamics and the number of wind turbines, while the exact wind-farm layout has a secondary effect in agreement with the observation that the power production in the fully-developed regime of large wind farms also mainly depends on the wind-turbine density and weakly on the exact wind-farm layout (Stevens and Meneveau 2017; Stevens et al. 2016).

Fig. 8

a Streamwise velocity component of different POD modes at hub height for the developing aligned wind farm, and b the vertical cross-section showing the streamwise, spanwise and vertical velocity components of the first POD mode at $x/H=2{\uppi }$, which is in between the turbine rows. The solid circles indicate the turbine locations in this plane

Fig. 9

a Streamwise velocity component of different POD modes at hub height for the developing staggered wind farm, and b the vertical cross-section showing the streamwise, spanwise and vertical velocity components of the first POD mode at $x/H=2{\uppi }$, which is in between the turbine rows. The solid circles indicate the turbine locations in this plane

Fig. 10

Reynolds stresses in periodic (a, b) aligned and (c, d) staggered wind farms. a, c the time average, the first POD mode, and the sum of the first 10 POD modes at hub height, and b, d the corresponding vertical cross-sections at $x/H=2{\uppi }$

Fig. 11

Reynolds stresses in developing (a, b) aligned and (c, d) staggered wind farms. For a, c the time average, the first POD mode, and the sum of the first 10 POD modes at hub height, and b, d the corresponding vertical cross-sections at $x/H=2{\uppi }$

Figures 8 and 9 show that, although the flow structures in the streamwise direction are not periodic for the developing wind farms, the flow is still dominated by streamwise elongated rolls. Similar to the periodic cases, the spanwise extent of the rolls covers 1 or 2 turbine columns in the spanwise direction. For the aligned case (see Fig. 8), the dominance of the streamwise rolls starts to diminish at around POD mode 5 (not shown), while POD modes 6, 7 and 8 reveal streamwise-varying patterns similar to the ones obtained in periodic wind farms. For the staggered case (see Fig. 9), the streamwise-varying modes start to appear at POD mode 9 (not shown), but already appear for POD mode 3 in the periodic staggered wind farm. This suggests that the streamwise-varying structures are dynamically more important in periodic than in developing wind farms, but the exact cause for this is not yet fully understood. Overall, although some differences exist, the main flow structures obtained in the periodic wind farms share most of the same characteristics when compared to the results obtained in the developing wind farms, suggesting periodic wind-farm flows simulated in large domains can capture many of the main flow modes found in developing wind-farm-flow simulations.

3.3 Proper-Orthogonal-Decomposition Modes of the Reynolds Stress

Using Eq. 6, we construct the POD modes of the Reynolds stress from the POD modes of the velocity field for the different wind-farm cases in Figs. 10 and 11. Figure 10 reveals that the horizontal distribution of the Reynolds stress is more uniform in a staggered wind farm than in an aligned one, which indicates that the maximum Reynolds stress is always located directly above the turbines for an aligned wind farm. As the Reynolds stresses due to the wind-turbine wakes reach their maximum about 5 turbine diameters downstream of a wind turbine, the maximum Reynolds stresses are not found above the wind turbines, but in between (see the left panel of Fig. 10d). In addition, Fig. 10 reveals that the maximum in the Reynolds stresses just above the turbines is not captured by the first 10 POD modes, which is the first indication that a significant number of modes is required to capture the overall interaction between the wind farm and the ABL. In the developing wind farms (Fig. 11), the Reynolds stresses increase with increasing distance inside the farm. Figure 12a shows the corresponding vertical kinetic energy flux $\varPhi = - \overline{u} \overline{u'w'}$, where the overbar indicates time averaging, and confirms that the vertical kinetic energy flux is greater in staggered wind farms than in aligned wind farms. Figure 12b shows that the performance in the fully-developed regime of the wind farm is better in a staggered wind farm than in an aligned one in agreement with the results reported by, for example, Chamorro et al. (2011), Wu and Porté-Agel (2013), and Stevens et al. (2016), who show that staggered wind farms are more efficient in terms of momentum transfer from the background flow to the turbines compared with aligned wind farms.

To illustrate the high number of POD modes required to accurately reconstruct the streamwise development of the Reynolds stress, Fig. 13a shows 2000 POD modes are required to reconstruct the main features of the distribution obtained using the information of all 5000 available modes. A particular feature is the increase in the Reynolds stresses around the turbine locations, which is only recovered when $>100$ POD modes are taken into account, and confirms the earlier conjecture that many modes are required to capture this phenomenon. Our results thus indicate that important aspects of the wind-farm dynamics can only be captured by the higher POD modes, illustrating the difficulty in modelling the farm dynamics with a limited number of POD modes.

Fig. 12

a Spanwise-averaged vertical kinetic energy flux, and b normalized power production $P/P_1$ as a function of the downstream position

Fig. 13

a The Reynolds shear stress $\overline{u'w'}$ reconstructed using a different number of modes averaged at the centre of the turbines in the spanwise direction at hub height in the developing aligned wind farm, and b the power spectral density of the streamwise velocity component at hub height for the different cases

4 Coherent Structures in Fourier Space

We have considered above the POD modes in physical space, but to determine which flow structures dominate the flow dynamics at different relevant frequencies, it is important to study the POD modes in spectral space (Towne et al. 2018), which has not been explored in previous POD studies of wind-farm simulations. Figure 13b shows the power spectral density of the streamwise velocity at hub height for the different simulations, revealing a sudden drop of the power spectral density at frequencies about 15 times the frequency corresponding to the turbine travel time, which is the time it takes a fluid parcel to traverse one streamwise turbine distance at hub height; this “cut-off frequency” primarily depends on the grid resolution. The drop in the spectrum is more gradual for the wind-farm cases than for the ABL case due to the spatial-filtering effect of the actuator-disk model at the turbine locations. The spectra also show a peak at a frequency about 16 times lower than the turbine travel-time frequency, which corresponds to the average time it takes a fluid parcel to pass through the entire wind farm (Stevens and Meneveau 2014).

Fig. 14

The distributions of the eigenvalues of the POD modes in a developing aligned wind farm for $f=1$, which corresponds to the time it takes a fluid parcel to traverse one streamwise turbine spacing, and $f=0.06$, which corresponds to the wind-farm flow-through time

Considering the dynamical significance of the turbine travel time and the wind-farm flow-through time, we analyze the flow structures at these two frequencies for the developing aligned wind farm, which Fig. 14 shows has similar eigenspectra for these frequencies. Figure 14a depicts large-scale modes extending the whole wind-farm length, and the first eigenvalue is about twice the second one, whereas Fig. 16b shows the first two eigenvalues are roughly the same for the streamwise turbine spacing travel time. Moreover, Fig. 16b also shows that the kinetic energy associated with the smaller frequency (larger-scale structures) is higher than that related to the structures with larger frequency. Figure 14 also shows a more gradual reduction of the eigenvalues for the POD modes in spectral space than in physical space (see Fig. 4). Figure 15a, b reveals that the wind-turbine wakes are the dominant flow structure at the frequency corresponding to the turbine travel time. Both the complete amplitude field and the amplitude field from the first POD mode reveal a high spatial correlation in the wake areas directly behind the turbines. Figure 15c, d reveals that the flow structures at the frequency corresponding to wind-farm flow-through time are dominated by large-scale structures, which are similar to the lower POD modes observed for the ABL and wind-farm cases. The results for higher frequencies ($f > 1$, but smaller than the cut-off frequency $f\approx 15$) are similar to $f = 1$, but reveal the small-scale turbulent flow structures. Similar flow characteristics are observed for the staggered wind farm and, therefore, are not shown here.

Fig. 15

Spectral POD results for the streamwise velocity component in the developing aligned wind farm. For a, b amplitude of the flow field and amplitude of the first POD mode of the streamwise velocity component for the frequency corresponding to the turbine travel time and c, d the same as panels a and b for the frequency corresponding to the wind-farm flow-through time

Figure 16 shows the results for the spectral POD analysis of the Reynolds stress field determined in a similar way as for Eq. 6 by using

$$\begin{aligned} \overline{u'w'}(f)= \frac{1}{N_{\mathrm{FFT}}} \sum \limits _{j=1}^{N_{\mathrm{FFT}}} \lambda ^2_j (f)\mathbf {V}^\dag _{w_{:,j}}(f)\mathbf {V}^\dag _{u_{:,j}}(f), \end{aligned}$$

(10)

where the Reynolds stress and its spectral POD modes are evaluated at a certain frequency f, and $N_{\mathrm{FFT}}$ is the length of the time signals in the spectral space. Figure 16a, c shows the amplitude of $\overline{u'w'}(f)$, while Fig. 16b, d shows the first-mode reconstruction

$$\begin{aligned} \lambda ^2_1 (f)\mathbf {V}^\dag _{w_{:,1}}(f)\mathbf {V}^\dag _{u_{:,1}}(f)/N_{\mathrm{FFT}}. \end{aligned}$$

(11)

Figure 16 reveals less uniformly distributed regions of the Reynolds stress since less of these high-correlation regions are visible there than for the streamwise velocity profiles shown in Fig. 15, because it is more difficult to obtain good correlations of the second-order statistics. Another observation is that, at a lower frequency, the strongest Reynolds stresses are generated by the large-scale flow structures, while at higher frequencies, most Reynolds stresses result from the wind-turbine wakes. In addition, we see that the first POD mode for the Reynolds stresses only captures a small portion of the total amplitude (see Fig. 16a, c) consistent with the spectral POD results obtained for the mean velocity profiles in Figs. 14 and 15. As with the physical POD results, these results indicate that a larger number of spectral POD models is required to accurately represent the Reynolds stresses at a given frequency, implying that using POD modes to model the relevant dynamics at the most important dynamical frequencies would be challenging, and such an attempt is outside the scope of the present study.

Fig. 16

Spectral POD results for the Reynolds stress in the developing aligned wind farm. a, b Amplitude of the Reynolds stress field and amplitude of the first POD mode of the Reynolds stress for the frequency corresponding to the turbine travel time and c, d the same as panels a and b for the frequency corresponding to the wind-farm flow-through time

5 Discussion and Conclusions

We performed an LES investigation of ABL flow and periodic and developing aligned and staggered wind farms to study the coherent flow structures using the POD technique. Comparison of the three-dimensional POD results with the two-dimensional POD modes reported for the neutral ABL by Shah and Bou-Zeid (2014) reveals that the three-dimensional POD modes are able to capture the streamwise-varying flow modes. Here, we find that, for the three-dimensional POD analysis, the number of important POD modes is higher than for the two-dimensional POD analysis, while Shah and Bou-Zeid (2014) focused on the influence of the thermal stratification on the POD modes and flow physics.

An analysis of the time-averaged results reveals that the flow is partially forced around the turbines modelled as actuator disks facing the atmospheric flow. By comparing the POD results for the wind-farm cases with the ABL case, we find that, due to the interaction between the wind turbines and the atmospheric flow, the kinetic energy among the POD modes is redistributed. We find that the turbines confine the dominant streamwise roll structures such that these rolls consistently span one or two turbine columns in the spanwise direction. It turns out that there are very large streamwise-varying structures with an extent of up to six times the boundary-layer height, indicating a large-scale interaction between the wind turbines and the atmospheric flow above. We find that the POD modes for both the aligned and staggered wind-farm geometry display similar characteristics, which indicates that the large-scale interaction between the turbines and the atmospheric flow is mostly determined by the number of turbines, and not by their exact configuration. An analysis of the POD modes of the Reynolds stresses $u'w'$ reveals that the stress increases as a function of the downstream location in the farm, and that it is more homogeneously distributed in staggered wind farms than in aligned wind farms. Correspondingly, the horizontally-averaged vertical kinetic energy flux is higher for a staggered wind farm than for an aligned one, which results in a better performance in the fully-developed regime of the wind farm when a staggered configuration is used. This observation agrees with the view that a strong vertical kinetic energy flux is important to ensure good performance of large wind farms (Chamorro et al. 2011; Wu and Porté-Agel 2013; VerHulst and Meneveau 2014; Stevens et al. 2016; Stevens and Meneveau 2017). A reconstruction of the downstream development of the Reynolds stress reveals that many POD modes are required to capture this development accurately, which highlights the challenge of modelling wind-farm dynamics using a limited number of POD modes.

To study the flow structures at dynamically-relevant frequencies, we performed a spectral POD analysis. For low frequencies, corresponding to wind-farm flow-through time, we find large-scale structures corresponding to the physical POD modes observed for the ABL and wind-farm cases. However, at higher frequencies, corresponding to the turbine travel time, the wind-turbine wakes are the dominant flow structure. We find that the wakes are highly correlated, which means that a modification of an upstream wake at this frequency influences the dynamics of subsequent downstream wakes. At lower frequencies, the Reynolds stresses mostly originate from the large-scale flow structures, while at frequencies that correspond to the turbine travel time, the Reynolds stresses mostly originate from the wakes behind the wind turbines. Just as for the physical POD modes, we find that a larger number of spectral POD modes is required to accurately capture the Reynolds stresses than to capture the mean flow structures. As capturing these Reynolds stresses accurately is very important to correctly model the momentum exchange between the wind farm and the atmospheric flow above, this seems to indicate the challenge of capturing all these effects in low-dimensional models without any control feedback, with important implications for wind-farm-flow control strategies (Iungo et al. 2015b; Hamilton et al. 2018), which will require further investigations beyond the scope of this paper.