Simplification and Validation of a Spectral-Tensor Model for Turbulence Including Atmospheric Stability

Abstract

A spectral-tensor model of non-neutral, atmospheric-boundary-layer turbulence is evaluated using Eulerian statistics from single-point measurements of the wind speed and temperature at heights up to 100 m, assuming constant vertical gradients of mean wind speed and temperature. The model has been previously described in terms of the dissipation rate $\epsilon$, the length scale of energy-containing eddies $\mathcal {L}$, a turbulence anisotropy parameter $\varGamma$, the Richardson number Ri, and the normalized rate of destruction of temperature variance $\eta _\theta \equiv \epsilon _\theta /\epsilon$. Here, the latter two parameters are collapsed into a single atmospheric stability parameter z / L using Monin–Obukhov similarity theory, where z is the height above the Earth’s surface, and L is the Obukhov length corresponding to $\{Ri,\eta _\theta \}$. Model outputs of the one-dimensional velocity spectra, as well as cospectra of the streamwise and/or vertical velocity components, and/or temperature, and cross-spectra for the spatial separation of all three velocity components and temperature, are compared with measurements. As a function of the four model parameters, spectra and cospectra are reproduced quite well, but horizontal temperature fluxes are slightly underestimated in stable conditions. In moderately unstable stratification, our model reproduces spectra only up to a scale $\sim$ 1 km. The model also overestimates coherences for vertical separations, but is less severe in unstable than in stable cases.

1 Introduction

Atmospheric turbulence causes fluctuating loads on structures, and has dynamic effects on flexible structures such as wind turbines, whose proper design, life assessment, and pitch and yaw control strategies require accurate predictions of the loads due to the turbulence. Therefore, an adequate description of the structure of atmospheric turbulence is important for the calculation of dynamic loads on wind turbines. The spectrum of the force at a point on a wind turbine due to turbulence depends on the spectrum of the fluctuating velocity, i.e. the turbulence. In addition, the spectrum of the fluctuating force on different components of the wind turbine also depends on the cospectrum and cross-spectrum of the velocity components. The dynamic displacements of the wind turbine are functions of the force spectrum, which in turn depend on the spectrum and cross-spectrum of the turbulence (Dyrbye and Hansen 1996).

Turbulence spectra and cospectra refer to the one-point autospectra of, for example, a velocity component, and the spectra of two time series at one point of any two velocity components, respectively. Turbulence cross-spectra are spectra between two points of time series of any two velocity components. Furthermore, two-point, cross-spectral properties are often expressed in terms of the coherence and cross-spectral phases, which are also important for wind engineering (Davenport 1961).

Spectral-tensor models are often used to model the spectra and cross-spectra (Kristensen et al. 1989), and can be used to estimate the loads on wind turbines through simulation of the incoming flow. However, these models must represent the flow structure observed in the atmospheric boundary layer (ABL) adequately, and provide the required turbulence loading for reproduction of a realistic dynamic response of wind turbines during load simulations. Models developed by Kaimal et al. (1972), Veers (1988) (the Sandia method), and Mann (1994b) are commonly used in the wind-energy community.

The International Electrotechnical Commission (IEC 2005) recommends the use of the Mann (1994b) model for the estimation of loads on wind turbines through simulation of the rotor inflow (Mann 1998). The three-dimensional spectral-tensor model of Mann (1994b) incorporates rapid distortion theory (RDT; Townsend 1976; Pope 2000), with the assumption of uniform mean shear, and consideration of the eddy lifetime. The model is applicable for homogeneous, neutral, surface-layer turbulence, and requires three input parameters: the viscous dissipation rate $\epsilon$, a length scale for the energy-containing eddies $\mathcal {L}$, and a non-dimensional, eddy-lifetime parameter $\varGamma$.

An extension to the Mann model by including buoyancy effects is the model of Chougule et al. (2017), which, in addition to $\epsilon$, $\mathcal {L}$, and $\varGamma$, contains two extra input parameters: the gradient Richardson number (Ri) representing the local atmospheric stability, and a parameter proportional to the rate of destruction of temperature variance $\eta _\theta$. The model simulates velocity and temperature spectra, as well as the associated cospectra for the streamwise velocity component and vertical temperature fluxes. The original Mann model provides only velocity spectra and cospectra of the longitudinal and vertical velocity components. The buoyancy model also produces two-point statistics of the coherence and phase for the temperature field.

The turbulence characteristics described above can all be derived from the spectral tensor, which, since it is not directly observable, must be parametrized based on observations. However, the atmospheric stability parameter Ri requires observations from two heights, and the $\eta _\theta$ parameter cannot always be measured due the contamination of the temperature spectra by noise. Therefore, as it is easier to represent the atmospheric stability in terms of the Obukhov length L than the gradient Richardson number Ri, we simplify an existing model of the spectral tensor by replacing Ri and $\eta _\theta$ with L. The simplified model is then evaluated with an extensive dataset, including atmospheric observations at heights relevant for a modern wind turbine.

Here we describe the buoyancy-dependent, spectral-tensor model, but with one less buoyancy parameter based on Monin–Obukhov similarity theory (MOST; Wyngaard and Coté 1972). The model is thus formulated in terms of a reduced set of four parameters. In Sect. 2, we provide the basic theory of the four-parameter model, Sect. 3 describes the experiments, the data, and the methodology used for the model validation, followed by the results and discussion in Sect. 4.

Lack of the temperature-variance parameter $\eta _\theta$ results in the underestimation of the temperature spectrum in the simplified model, which is, however, not important for wind-energy applications. Moreover, as this parameter is inherently noisy, we exclude the temperature spectrum from the modelling. However, the error is reduced in the cospectra between the temperature and the other, less noisy variables, such as the velocity components, which the model reproduces reasonably well. Therefore, we include the temperature fluxes in our analysis, so that the model is applicable for general micrometeorological applications.

Our study differs from Chougule et al. (2017) in the following respects:

• Description of the spectral-tensor model for a reduced set of four parameters (from originally five) using MOST;

• Exclusion of the temperature spectrum in the spectral fitting;

• Validation in terms of spectra and cospectra at heights up to 100 m;

• Validation of the modelled coherence and phase for larger separation distances ($\approx$ 10 times that studied previously);

• Validation from very stable to very unstable stratification; and

• Considering the slope of the inertial subrange of cospectrum between the streamwise velocity component u and potential temperature $\theta$ at heights up to 100 m, including the variation with height.

2 Theory: Spectral-Tensor Modelling

2.1 Preliminaries

The spectral representation of the three-dimensional fluctuating velocity field ${{\varvec{u}}}'({{\varvec{x}}})$ and potential temperature (hereafter temperature) $\theta '({{\varvec{x}}})$, can be given in terms of the Fourier-Stieltjes integral (Pope 2000)

$$\begin{aligned} \mathfrak {I}_{\lambda }'({{\varvec{x}}})= \left\{ \begin{array}{ll} \int \text {e}^{\text {i}{{\varvec{k}}}\cdot {{\varvec{x}}}}\text {d}{} \textit{Z}_{\lambda }({{\varvec{k}}}), &{}\quad \lambda =1, 2, 3,\\ \frac{\text {d}U}{\text {d}z}\left( \frac{g}{\overline{\theta }}\right) ^{-1}\int \text {e}^{\text {i}{{\varvec{k}}}\cdot {{\varvec{x}}}}\text {d}{} \textit{Z}_{\lambda }({{\varvec{k}}}), &{}\quad \lambda =4, \end{array} \right. \end{aligned}$$

(1)

where $\mathfrak {I}'({{\varvec{x}}})\equiv \left\{ {{\varvec{u}}}'({{\varvec{x}}}),\theta '({{\varvec{x}}})\right\}$, ${{\varvec{x}}}=\{x,y,z\}$ is the (longitudinal, lateral, vertical) position vector in space, dU/dz is the mean wind shear with the mean velocity field considered as (U, 0, 0), g is the acceleration due to gravity, $\overline{\theta }$ is the mean temperature, and ${{\varvec{k}}}=(k_1,k_2,k_3)$ is the three-dimensional wavenumber vector. The Greek index $\lambda$ indicates no summation over indices, and the integration in (1) is over the entire wavenumber space (Batchelor 1953).

In homogeneous turbulence, the spectral tensor for the velocity field is defined as

$$\begin{aligned} \varPhi _{ij}({{\varvec{k}}})=\frac{1}{(2\pi )^3}\int R_{ij}({{\varvec{r}}}) \text {e}^{-\text {i}{{\varvec{k}}}\cdot {{\varvec{r}}}}\text {d}{{\varvec{r}}}, \end{aligned}$$

(2)

where $R_{ij}({{\varvec{r}}})$ is the covariance tensor with separation distance ${{\varvec{r}}}$, and $\int \text {d}{{\varvec{r}}}\equiv \int _{-\infty }^{\infty }\int _{-\infty }^{\infty } \int _{-\infty }^{\infty }\text {d}{} \textit{r}_1\text {d}{} \textit{r}_2\text {d}{} \textit{r}_3$. The two-point correlations of the Fourier velocity components $\text {d}Z_i$ are related to the spectral tensor by Wyngaard (2010)

$$\begin{aligned} \varPhi _{ij}({{\varvec{k}}})=\frac{\left\langle \text {d}Z_i^*({{\varvec{k}}})\text {d}Z_j({{\varvec{k}}})\right\rangle }{\text {d}{} \textit{k}_1\text {d}{} \textit{k}_2\text {d}{} \textit{k}_3}, \end{aligned}$$

(3)

where $\langle$ $\rangle$ denotes the ensemble average operator, and the superscript $*$ denotes a complex conjugate.

The indices $i,j=\{1,2,3\}$ denote the velocity components, i.e., $\{u'_1,u'_2,u'_3\}=\{u',v',w'\}$, and the space vector $\{x_1,x_2,x_3\}=\{x,y,z\}$. When the (scalar) temperature is also included, we use the index notation $l,m=\{1,2,3,4\}$ for the three velocity components along with the temperature fluctuations, so the full set $\varPhi _{lm}({{\varvec{k}}})$ in (3) is a matrix, not a tensor.

2.2 Model for the Spectral Tensor Including Buoyancy Effects

The homogeneous spectral tensor in (3) is modelled using RDT (Pope 2000), assuming the evolution from an initial isotropic spectral tensor, and zero initial temperature fluxes. For the initial velocity and temperature fluctuations, we assume the von Kármán energy spectrum and the spectrum proposed by Kaimal and Finnigan (1994) for the isotropic tensor, respectively. Therefore, the spectral tensor becomes a function of a subset of parameters (discussed later) defining the initial energy spectra. Rapid distortion theory assumes a mean lapse rate and uniform shear, which distorts the eddies both spatially and temporally. The time evolution of the tensor in (3) is replaced¹ by a wavenumber evolution through the wavenumber-dependent, eddy-lifetime parametrization of Mann (1994b). Therefore, the equilibrium solution is achieved through a set of parameters based on the initial conditions, the RDT equation, and eddy-lifetime parametrization. The physics of the model are contained in the RDT equations with the initial conditions, which give the initial correlations between the velocity components, as well as maintaining correlations among the velocity components and the temperature through the mean uniform shear and lapse rate. This mechanism is time-limited by replacing the time variable with the non-dimensional eddy lifetime, giving a statistical description of a stationary process, whereby turbulence is generated and turbulent eddies are stretched over a finite extent. One-point observations are input to the tensor model to determine the model parameters by fitting the one-dimensional model spectra and cospectra to the data through a procedure described in Sect. 3.3. The model is now described mathematically.

Due to the mean wind shear dU/dz, the third component of the wavenumber vector is distorted with time and the rate of change of ${{\varvec{k}}}(t)$ to give (Pope 2000)

$$\begin{aligned} \frac{\text {d}k_3}{\text {d}t}=-k_1\frac{\text {d}U}{\text {d}z}, \end{aligned}$$

(4)

with ${{\varvec{k}}}(0)=(k_{10},k_{20},k_{30})$ as an initial wavenumber. Therefore, the final wavenumber using the dimensionless strain time $\xi =(\text {d}U/\text {d}z)t$ gives

$$\begin{aligned} {{\varvec{k}}}(\xi )=(k_{10},k_{20},k_{30}-k_{10}\xi ). \end{aligned}$$

(5)

The equation for the evolution of the Fourier modes $\text {d}{{\varvec{Z}}}({{\varvec{k}}},t)$ in (3) is deduced from momentum and temperature equations according to RDT, and given as²

$$\begin{aligned} \frac{\text {D}}{\text {D} \xi }\text {d}Z_{l}({{\varvec{k}}}(\xi ),\xi )= \text {M}_{lm}({{\varvec{k}}}(\xi ),\xi ) \text {d}Z_{m}({{\varvec{k}}}(\xi ),\xi ), \end{aligned}$$

(6)

where $l,m=1,2,3,4$, and

$$\begin{aligned} \text {M}_{lm}({{\varvec{k}}}(\xi ),\xi ) = \left( \begin{array}{cccc} 0 &{}\quad 0 &{}\quad \frac{2k_{1}^2}{k^2}-1 &{}\quad -\frac{k_{1}k_{3}}{k^2} \\ \\ 0 &{}\quad 0 &{}\quad \frac{2k_{1}k_{2}}{k^2} &{}\quad -\frac{k_{2}k_{3}}{k^2} \\ \\ 0 &{}\quad 0 &{}\quad \frac{2k_{1}k_{3}}{k^2} &{}\quad -\left( \frac{k_{3}^2}{k^2}-1\right) \\ \\ 0 &{}\quad 0 &{}\quad -Ri &{}\quad 0 \end{array}\right) . \end{aligned}$$

(7)

Here, the Richardson number Ri is defined as (Kaimal and Finnigan 1994)

$$\begin{aligned} Ri = \frac{\left( g/\overline{\theta }\right) \text {d}\overline{\theta }/\text {d}z}{\left( \text {d}U/\text {d}z\right) ^2}. \end{aligned}$$

(8)

Neglecting the Coriolis force, viscosity, non-linear terms, and molecular diffusivity, (6) constitutes the governing RDT equations for homogeneous turbulent flow with the assumptions of constant vertical gradients of the mean temperature $(\text {d}\overline{\theta }/\text {d}z)$ and mean wind speed $(\text {d}U/\text {d}z)$ with respect to the vertical z direction (Hanazaki and Hunt 2004; Chougule et al. 2017).

Equation 6 is solved with the initial conditions assuming the state of isotropic turbulence at ${{\varvec{k}}}_0={{\varvec{k}}}(0)$. For the velocity components, the isotropic tensor is given as (Pope 2000)

$$\begin{aligned} \varPhi _{ij}({{\varvec{k}}}_{0})=\frac{E(k)}{4\pi k^2}\left( \delta _{ij}-\frac{k_{i}k_{j}}{k^{2}}\right) . \end{aligned}$$

(9)

We use the form of the energy spectrum E(k) given by von Kármán (1948) as

$$\begin{aligned} E(k)=\alpha \epsilon ^{\frac{2}{3}}\mathcal {L}^{\frac{5}{3}} \frac{(k\mathcal {L})^4}{(1+(k\mathcal {L})^2)^{\frac{17}{6}}}, \end{aligned}$$

(10)

where $\epsilon$ is the rate of viscous dissipation of specific turbulent kinetic energy (TKE), $\mathcal {L}$ is a length scale, and $\alpha \approx 1.7$ is the spectral Kolmogorov constant.

For temperature, the isotropic three-dimensional spectrum is given as

$$\begin{aligned} \varPhi _{\theta \theta }({{\varvec{k}}}_{0})=\frac{S(k)}{4\pi k^2}, \end{aligned}$$

(11)

where S(k) is the potential energy spectrum containing the form of the inertial subrange (Kaimal and Finnigan 1994) as

$$\begin{aligned} S(k)=\beta _{1} \epsilon ^{-1/3}\epsilon _\theta \mathcal {L}^{\frac{5}{3}} \frac{(k\mathcal {L})^2}{(1+(k\mathcal {L})^2)^{\frac{11}{6}}}, \end{aligned}$$

(12)

where $\epsilon _\theta$ is the dissipation rate for half the temperature variance, and $\beta _{1}=0.8$ is a universal constant (Kaimal et al. 1972). From (1), (11), and (12),

$$\begin{aligned} \varPhi _{44}({{\varvec{k}}}_{0})=\frac{S'(k)}{4\pi k^2}, \end{aligned}$$

(13)

where

$$\begin{aligned} S'(k) = \beta \eta _\theta \frac{1+(k\mathcal {L})^2}{(k\mathcal {L})^2}E(k), \end{aligned}$$

(14)

$\beta =\beta _1/\alpha$, and

$$\begin{aligned} \eta _\theta =\frac{\epsilon _\theta }{\epsilon }\left[ \frac{g}{\overline{\theta }}\left( \frac{\text {d}U}{\text {d}z}\right) ^{-1}\right] ^2. \end{aligned}$$

(15)

From (6) and the definitions of E(k) and $S'(k)$, the anisotropic (where $\xi \ne 0$) tensor $\varPhi ({{\varvec{k}}},\xi )$ can be expressed as

$$\begin{aligned} \varPhi ({{\varvec{k}}},\xi )\equiv \varPhi ({{\varvec{k}}},\alpha \epsilon ^{\frac{2}{3}},\mathcal {L},\xi , Ri,\eta _\theta ). \end{aligned}$$

(16)

The spectral tensor in (16) is non-stationary (time dependent via $\xi$), and the stretching of eddies due to shear for an infinitely long time is unrealistic, since stretching must break the eddies at some point, with eddies stretching or compressing depending on their orientation in the plane of uniform shear. To make the spectral tensor stationary, and to account for the eddy size, the general concept of a wavenumber-dependent eddy lifetime from Mann (1994a) is parametrized as

$$\begin{aligned} \tau (k)=\varGamma \left( \frac{\text {d}U}{\text {d}z}\right) ^{-1}(k\mathcal {L})^{-2/3}\left[ { }_{2}F_{1}\left( \frac{1}{3},\frac{17}{6};\frac{4}{3};-(k\mathcal {L})^{-2}\right) \right] ^{-1/2}, \end{aligned}$$

(17)

where $\varGamma$ is a parameter to be determined, and ${}_{2}F_{1}$ is the ‘ordinary’ or ‘Gaussian’ hypergeometric function. The spectral tensor in (16) is made stationary by replacing t in $\xi$ with the wavenumber-dependent eddy lifetime $\tau (k)$ given in (17), so $\xi \rightarrow \varGamma$ in the arguments of $\varPhi$, and the anisotropic spectral tensor $\varPhi$ can be expressed as $\varPhi ({{\varvec{k}}},\alpha \epsilon ^{\frac{2}{3}},\mathcal {L},\varGamma ,Ri,\eta _\theta ).$ Further, using (10)–(14), $\varPhi$ can also be given as

$$\begin{aligned} {\varvec{\Phi }}^{(5)}=\alpha \epsilon ^{\frac{2}{3}}\mathcal {L}^{\frac{11}{3}} \varPhi ({{\varvec{k}}}\mathcal {L},1,1,\varGamma ,Ri,\eta _\theta ), \end{aligned}$$

(18)

where the spectral tensor with a five-parameter input is denoted by ${\varvec{\Phi }}^{(5)}$.

2.3 Reduction of Model Stability Parameters from Two to One

For the parameters Ri and $\eta _\theta$ in (18), we use forms inferred from MOST (Obukhov 1946, 1971; Businger and Yaglom 1971; Foken 2006) to reduce the model parameter set from five to four parameters, i.e. by collapsing {Ri, $\eta _\theta$} to a single stability parameter z / L. We note that this approach, strictly speaking, is only valid in the surface layer (with constant vertical fluxes), the extent of which depends on the ABL depth (which in turn can depend upon surface-layer stability). The Obukhov length L is defined as (Kaimal and Finnigan 1994)

$$\begin{aligned} L=\frac{-{u_{\star }}^{3}}{\kappa \left( g/\overline{\theta }_{0}\right) {\left\langle w^{'}\theta ^{'}\right\rangle _{0}}}, \end{aligned}$$

(19)

where $u_{\star }$ is the friction velocity, $\kappa =0.4$ is the von Kármán constant, $\overline{\theta }_{0}$ is the mean surface-layer temperature, and $\left\langle w'\theta '\right\rangle _{0}$ is the vertical flux of potential temperature in the surface layer.

Formulated in terms of L, empirically determined MOST relationships for Ri and the flux Richardson number $Ri_f$ are given by Kaimal and Finnigan (1994) in terms of z / L as

$$\begin{aligned} Ri(z/L) = \left\{ \begin{array}{ll} z/L, &{}\quad -2\le z/L\le 0,\\ (z/L)(1+5 z/L)^{-1}, &{}\quad 0\le z/L\le 1 \end{array} \right. \end{aligned}$$

(20)

and

$$\begin{aligned} Ri_f(z/L)= \left\{ \begin{array}{ll} (z/L) (1+16|z/L|)^{1/4}, &{}\quad -2\le z/L\le 0,\\ (z/L)(1+5 z/L)^{-1}, &{}\quad 0\le z/L\le 1. \end{array} \right. \end{aligned}$$

(21)

Assuming local equilibrium between energy production and dissipation, while neglecting all transport terms in the stationary equations of TKE and temperature variance, $\eta _\theta$ in (15) can be expressed in terms of Ri and $Ri_f$ by

$$\begin{aligned} \epsilon = -\left\langle u'w'\right\rangle \left( \frac{\text {d}U}{\text {d}z}\right) +\frac{g}{\overline{\theta }} \left\langle w'\theta '\right\rangle , \end{aligned}$$

(22a)

and

$$\begin{aligned} \epsilon _\theta = -\left\langle w'\theta '\right\rangle \left( \frac{\text {d}\overline{\theta }}{\text {d}z}\right) , \end{aligned}$$

(22b)

along with the definition (Eq. 8), and

$$\begin{aligned} Ri_{f}=\frac{\left( g/\overline{\theta }\right) \left\langle w'\theta '\right\rangle }{\left\langle u'w'\right\rangle \left( \text {d}U/\text {d}z\right) }, \end{aligned}$$

(23)

leading to

$$\begin{aligned} \eta _\theta =\frac{Ri}{Ri_{f}^{-1}-1}. \end{aligned}$$

(24)

From (20), (21), and (24), $\eta _\theta$ can also be expressed in terms of MOST as

$$\begin{aligned} \eta _{\theta }(z/L)= \left\{ \begin{array}{ll} \frac{z/L}{(z/L)^{-1} (1+16|z/L|)^{-1/4}-1}, &{}\quad -2\le z/L\le 0,\\ \frac{[(z/L)(1+5 z/L)^{-1}]^{2}}{1-(z/L)(1+5 z/L)^{-1}}, &{}\quad 0\le z/L\le 1 . \end{array} \right. \end{aligned}$$

(25)

Using (20) and (25), the spectral tensor in (18) simplifies to

$$\begin{aligned} {\varvec{\Phi }}^{(4)}=\alpha \epsilon ^{\frac{2}{3}}\mathcal {L}^{\frac{11}{3}} \varPhi ({{\varvec{k}}}\mathcal {L},1,1,\varGamma ,z/L), \end{aligned}$$

(26)

where ${\varvec{\Phi }}^{(4)}$ is the spectral tensor with four input parameters. Therefore, the spectral tensor in (26), including the effect of uniform shear and buoyancy (through a uniform lapse rate), contains four parameters to be determined:

• $\alpha \epsilon ^{\frac{2}{3}}$, where $\epsilon$ is the dissipation rate of TKE, and $\alpha$ is the spectral Kolmogorov constant;

• $\mathcal {L}$, which represents the size of the energy-containing eddies;

• $\varGamma$, a non-dimensional eddy-lifetime parameter;

• z / L, characterizing atmospheric stability.

2.4 Spectra Derived from the Model Spectral Tensor

Following Mann (1994b), the relationship between the components of the spectral tensor matrix and the cross-spectra $\chi$ is

$$\begin{aligned} \chi _{lm}(k_{1},\Delta y,\Delta z) = \int \varPhi _{lm}({{\varvec{k}}})\text {e}^{\mathrm{{i}}(k_{2}\Delta y+k_{3}\Delta z)}\mathrm{{d}}{{{\varvec{k}}}}_{\bot }, \end{aligned}$$

(27)

or, from (26),

$$\begin{aligned}&\chi _{lm}(k_{1},\Delta y,\Delta z;\alpha \epsilon ^{\frac{2}{3}}, \mathcal {L}, \varGamma , z/L) = \nonumber \\&\quad \alpha \epsilon ^{\frac{2}{3}}\mathcal {L}^{\frac{5}{3}} \int \varPhi _{lm}({{\varvec{k}}}\mathcal {L},1,1,\varGamma ,z/L)\text {e}^{\mathrm{{i}}(k_{2}\Delta y+k_{3}\Delta z)}\text {d}({{\varvec{k}}}_\bot \mathcal {L}^2), \end{aligned}$$

(28)

where $\int \mathrm{{d}}{{{\varvec{k}}}}_{\bot }\equiv \int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\mathrm{{d}}k_{2}\mathrm{{d}}k_{3}$, and $\Delta y$ and $\Delta z$ are transverse and vertical separations, respectively. From (26) and (28), $\chi _{lm}$ also becomes a function [($\equiv \chi _{lm}(k_{1},\Delta y,\Delta z;\alpha \epsilon ^{\frac{2}{3}}, \mathcal {L}, \varGamma , z/L)$] of the four model parameters.

For zero separation distance ($\Delta y=\Delta z=0$), the model cross-spectra become one-dimensional spectra and cospectra,

$$\begin{aligned} F_{lm}(k_{1})=\chi _{lm}(k_{1},\Delta y=0,\Delta z=0;\alpha \epsilon ^{\frac{2}{3}}, \mathcal {L}, \varGamma , z/L). \end{aligned}$$

(29)

Examples of ${\varvec{\Phi }}^{(4)}$ model spectra and cospectra are shown in Fig. 1 for both stable ($z/L=0.15$) and unstable ($z/L=-0.03$) stratification, with the values of $\alpha \epsilon ^{\frac{2}{3}}, \mathcal {L}$, and $\varGamma$ as 0.05, 10 and 3.2, respectively.

Fig. 1

The ${\varvec{\Phi }}^{(4)}$ model velocity spectra and cospectra for $uw, u\theta$, and $w\theta$ shown for stable (lines, $z/L=0.15$) and unstable (dashed lines, $z/L=-0.03$) cases, with $\{\alpha \epsilon ^{\frac{2}{3}}, \mathcal {L}, \varGamma \}=\{0.05\,\hbox {m}^{4/3}\,\hbox {s}^{-2},10\,\hbox {m},3.2\}$. Dotted lines are the Mann-model velocity spectra and uw cospectrum for the same parameter values of $\alpha \epsilon ^{\frac{2}{3}}, \mathcal {L}$ and $\varGamma$

Figure 1 also shows the Mann-model velocity spectra and uw cospectrum for the same values of $\{\alpha \epsilon ^{\frac{2}{3}}, \mathcal {L}, \varGamma \}$, whose spectra falls between the ${\varvec{\Phi }}^{(4)}$ model spectra for stable and unstable stratification, while the Mann model does not account for the temperature fluxes. The RDT relations in Eq. 6 are solved numerically using a 4th-order, Runge–Kutta adaptive timestep (Press et al. 2007). The components of the spectral tensor are available in closed form in Hanazaki and Hunt (2004) for w and temperature, and recently in Segalini and Arnqvist (2015) for all three velocity components and temperature. We use our numerical solution, which does not produce non-physical kinks in the spectra (Chougule et al. 2017). Once the individual RDT equations are solved, the spectral tensor is formed using (3), and the cross-spectra in (28) are integrated numerically, with the one-dimensional spectra given at $\Delta y=\Delta z=0$ according to (29).

An increase in $\alpha \epsilon ^{2/3}$ shifts the velocity spectra and cospectra $\left| uw\right| , \left| u\theta \right|$, and $|w\theta |$ upwards along the ordinate. An increase in $\mathcal {L}$ results in the shifting of u-, v- and w-spectra and $|uw|,|u\theta |$, and $|w\theta |$ cospectra to the left along the abscissa (i.e., $\mathcal {L}\propto k_1^{-1}$) and upwards along the ordinate. With an increase in $\varGamma$, the spectral peaks of u-, v-spectra and |uw|, $|u\theta |$ and $|w\theta |$ cospectra shift upwards, but downwards for the w-spectrum. The length scale (corresponding to the spectral peak) of u is greater than that of v, which again is greater than that of w, and higher values of $\varGamma$ imply a larger scale separation between the three velocity components. For stable cases, an increase in z / L (while holding the other parameters constant) results in the shifting of the peaks of the velocity spectra to smaller scales, thereby reducing the peak spectral amplitudes (including the amplitude of the peak of the uw cospectrum), with the u-spectrum more sensitive than the v- and w-spectra. The peak amplitudes of the $u\theta$ cospectrum increase, with the amplitude of (negative) $w\theta$ increasing with stability ($z/L>0$). For unstable cases, an increase in the magnitude of z / L has a similar effect on the $u\theta$ and $w\theta$ cospectra as that for the stable case, whereas the peak magnitudes of velocity spectra increase; the peak of the uw cospectrum shifts downwards to a lower wavenumber.

The model velocity and temperature variances, and $uw, u\theta , w\theta$ covariances can be given as

$$\begin{aligned} \left\langle \mathfrak {I}_{l}^{'}\mathfrak {I}_{m}^{'}\right\rangle =\alpha \epsilon ^{\frac{2}{3}}\mathcal {L}^{\frac{2}{3}}\int _{-\infty }^{\infty }\chi _{lm}(k_{1}\mathcal {L},0,0;1,1,\varGamma ,z/L)\text {d}(k_{1}\mathcal {L}). \end{aligned}$$

(30)

Fig. 2

The normalized ${\varvec{\Phi }}^{(4)}$ model variance and covariances $\left\langle \mathfrak {I}_{l}^{'}\mathfrak {I}_{m}^{'}\right\rangle _N=\left\langle \mathfrak {I}_{l}^{'}\mathfrak {I}_{m}^{'}\right\rangle /\sqrt{\left\langle \mathfrak {I}_{l}^{'}\mathfrak {I}_{l}^{'}\right\rangle _{\text {iso}}\left\langle \mathfrak {I}_{m}^{'}\mathfrak {I}_{m}^{'}\right\rangle _{\text {iso}}}$ (no summation), for stable stratification as a function of $\varGamma$ and z / L, with $\varGamma =0, 1, 2, 2.5, 3, 3.5, 4, 4.5,$ and 5, in the direction of the arrow

In isotropic turbulence, all velocity variances are equal ($\approx 0.688\alpha \epsilon ^{\frac{2}{3}}\mathcal {L}^{\frac{2}{3}}$; Mann 1994b), and covariances are zero. In the buoyant RDT model, the initial temperature fluxes are zero, and the initial temperature variance can be given as $\left<\theta ^2\right>\approx 0.6 (\epsilon _\theta /\epsilon )\alpha \epsilon ^{\frac{2}{3}}\mathcal {L}^{\frac{2}{3}}$, which can be obtained from the initial one-dimensional temperature spectrum using (11), (12) and (27). Figure 2 shows the influence of stability in terms of the ratio $\left\langle \mathfrak {I}_{l}^{'}\mathfrak {I}_{m}^{'}\right\rangle /\sqrt{\left\langle \mathfrak {I}_{l}^{'}\mathfrak {I}_{l}^{'}\right\rangle _{\text {iso}}\left\langle \mathfrak {I}_{m}^{'}\mathfrak {I}_{m}^{'}\right\rangle _{\text {iso}}}$ (no summation) as a function of z / L for different $\varGamma$ values in the stable regime. For highly unstable stratification, the model has deficiencies at low wavenumbers, which limits the prediction of the longitudinal velocity component spectra and associated cospectra; therefore, only stable conditions are shown in Fig. 2. The (co-) variances are shown in the z / L range $0{-}0.25$, where the curves become almost invariant at $z/L\approx 0.25$ and beyond. Previous studies (Mann 1994a; Sathe et al. 2012; Chougule et al. 2015) have shown the value of $\varGamma$ in the neutral ABL to be close to 3, with $\varGamma$ in the range $0{-}5$ here, and $\varGamma =0$ corresponding to isotropic turbulence. The model initially assumes isotropic turbulence, where $\varGamma =0$, leading to ${\sigma }^{2}_{u}={\sigma }^{2}_{v}={\sigma }^{2}_{w}$ and $\left\langle uw\right\rangle =0$. For $\varGamma > 0$, the turbulence is anisotropic, i.e., ${\sigma }^{2}_{u}>{\sigma }^{2}_{v}>{\sigma }^{2}_{w}$ and $\left\langle uw\right\rangle <0$, so $\varGamma$ describes the anisotropic nature of turbulence.

Fig. 3

The effect of input parameter variation on theoretical coherences: row a $\mathcal {L}$, row b $\varGamma$, and row c z / L (keeping the other two parameters constant in each graph with $\{\mathcal {L},\varGamma ,z/L\}=\{40\,\hbox {m}, 3.0, -\,0.03\}$, and $\Delta y_0=\Delta z_0=20$ m)

The cross-spectral properties, the squared coherence and cross-spectral phase spectrum, are defined as

$$\begin{aligned} \text {coh}_{lm}\left( \overline{k_{1}},\Delta y,\Delta z;\overline{\mathcal {L}},\overline{\varGamma },\overline{z/L}\right)= & {} \frac{|\chi _{lm}\left( \overline{k_{1}},\Delta y,\Delta z\right) |^{2}}{F_{ll}\left( k_{1a}\right) F_{mm}\left( k_{1b}\right) }\,(\text {no summation}), \end{aligned}$$

(31)

$$\begin{aligned} \varphi _{lm}\left( \overline{k_{1}},\Delta y,\Delta z;\overline{\mathcal {L}},\overline{\varGamma },\overline{z/L}\right)= & {} \arg \left[ \chi _{lm}\left( \overline{k_{1}},\Delta y,\Delta z\right) \right] , \end{aligned}$$

(32)

respectively, where for non-zero vertical separations, $\overline{k_{1}}=4\pi f/(U_{a}+U_{b})$. The average of the parameters between two points (e.g., a and b) are used as inputs to estimate the model coherence and phase. If we assume the validity of Taylor’s frozen turbulence hypothesis, the time series measured at frequency f can then be related to spatial fluctuations through $k_1= 2\pi f/U$. The model coherence as a function of $\mathcal {L}$, $\varGamma$, and z / L is shown in Fig. 3, where the model phase increases with $\varGamma$, whereas the influence of $\mathcal {L}$ and z / L on the model phase is insignificant. The results from modelling and observations in Chougule et al. (2015) show that the coherence (including phase) is independent from the viscous dissipation rate $\epsilon$, since $\epsilon$ dictates the intensity of the turbulence, provided everything else is left unchanged; the numerator and denominator in the definition of the coherence are each proportional to $\epsilon ^{4/3}$, while the coherence is invariant with respect to a scaling of $\epsilon$.

3 Model Validation

A simple procedure for extracting the parameters of the Mann spectral-tensor model is described in Mann (1994b), including reasons to not follow the method. In our case, in addition to the $\varGamma$ parameter, the (normalized) variances are a function of the parameter z / L (Fig. 2) due to the inclusion of buoyancy. Also, in the diabatic ABL, the length scale $\mathcal {L}$ is affected by the atmospheric stability in terms of the Obukhov length L (Peña and Hahmann 2012; Sathe et al. 2012), so that determining $\varGamma$ and $\mathcal {L}$ using the same method is not straightforward. Therefore, and because of the reasons described in Mann (1994b), we follow the approach of the $\chi ^2$-fit given in Sect. 3.3. We validate the model by following the strategy similar to Mann (1994b) by first determining the four parameters $\alpha \epsilon ^{2/3}, \mathcal {L}, \varGamma$, and z / L, by feeding the tensor with the observed velocity autospectra, and uw, $u\theta$ and $w\theta$ cospectra. Secondly, we predict cross-spectral coherences and phases of velocity and temperature, and then compare the model predicted coherences and phases (i.e. two-point cross-spectra) with the measurements.

The model validation is performed using measurements recorded at the characteristic wind-turbine hub height, and measurements recorded close to the ground ($z\approx 2{-}8\,\hbox {m}$) within the surface layer during the Horizontal Array Turbulence Study field program (HATS; Horst et al. 2004). The data recorded at hub height ($\approx$ 100 m) are from the National Centre for Wind Turbines site at Høvsøre on the west coast of Denmark.

Table 1 Classification of ABL stability

The calculations are performed for diabatic conditions. Each 30-min time series is classified into different atmospheric stability classes based on the range of the Obukhov length L [c.f. Table 1; following Gryning et al. (2007)].

3.1 Horizontal Array Turbulence Study

The HATS experiment was carried out over a relatively flat, homogeneous terrain of unplanted farmland near Kettleman City, California in September 2000. Two horizontal (s and d) arrays of identical Campbell Scientific three-component sonic anemometers, each measuring temperature and the three velocity components at a sampling rate of 20 Hz, were placed at different heights above the ground. The horizontal s-array consists of five sonic anemometers placed at the height $z_{s}$ above the ground, whereas the d-array consists of nine anemometers mounted at the height $z_{d}$ parallel to the s-array. The sonic anemometers in the s- and d-array are horizontally separated by $\Delta y_{s}$ and $\Delta y_{d}$, respectively. In eddy-covariance systems, these measurements can be used to calculate the momentum and temperature fluxes.

Table 2 Single 30-min time series used from the HATS dataset based on the measured atmospheric stability z / L and wind direction (WD) during Pacific daylight time (PDT)

The two lines of anemometers are oriented perpendicular to the prevailing wind direction. For flow not exactly normal to the transverse array, the cross-spectra are rotated into the mean wind direction. However, to avoid any transverse effects, flows almost normal (within $\pm 13^\circ$) to the plane of the sonic s- and d-arrays have been selected. The data have also been selected for their particular stability conditions and heights (up to 8 m; c.f. Table 2). For the cross-spectra analyses, horizontal separations in the d-arrays are used (up to $4\times \Delta y_d$). More information about the HATS experiment can be found in Sullivan et al. (2003) and Horst et al. (2004).

3.2 Høvsøre Data

For the validation at higher altitudes where the surface-layer assumptions leading to a reduction in spectral-tensor parameters may be violated, data are taken from heights of 10, 20, 40, 60, 80, and 100 m at the 116.5-m tall Høvsøre mast equipped with Metek sonic anemometers (Metek USA1 F2901A) measuring velocity and temperature at 20 Hz. The mast is located near the western coast of Denmark, 1.5 km inland from the North Sea. Filtering of the flow allows only the wind-direction sector $60^{\circ }{-}120^{\circ }$ to avoid flow disturbance from the five wind turbines situated over a distance of 1.4 km from the mast to the northern side. To the east, a flat agricultural landscape extends up to 15 km before an extensive forested area ($\approx 12\times 12~\hbox {km}^2$), which may affect the turbulence at larger heights (Chougule et al. 2015).

The analyses are performed for mean wind-speed intervals of 8–9 m s$^{-1}$ at the 80-m height based on previous experience with the Høvsøre data giving similar velocity spectra and cross-spectra results from the other wind speeds (Chougule et al. 2015). Each time series is classified into different stability classes based on the L values measured at 10 m with reference to Table 1.

For the wind-speed interval 8–9 m s$^{-1}$, we obtain n 30-min time series for each stability condition given in Table 3. More details about the location and instrumentation can be found in Peña et al. (2016). Statistical analyses are carried out using seven years of data recorded from 2004 to 2010.

3.3 Method

We estimate velocity autospectra and the uw cospectrum from 30-min time series using

$$\begin{aligned} F_{ij}\left( f, z\right) \equiv \left\langle \hat{u}_{i}(f) \hat{u}_{j}^{*} (f)\right\rangle , \end{aligned}$$

(33)

along with the $u\theta$ and $w\theta$ cospectra calculated as

$$\begin{aligned} F_{i\theta }(f, z)\equiv \left\langle \hat{u}_{i}(f) \hat{\theta }^{*} (f)\right\rangle , \end{aligned}$$

(34)

where $\hat{u}_{i}(f)$ and $\hat{\theta }(f)$ are the complex-valued Fourier transform of the $i\hbox {th}$ velocity component and potential temperature, respectively, measured at the height z.

Table 3 The Høvsøre spectra are averaged over n 30-min time series for each stability class

We select segments of 30-min time series from the Høvsøre dataset according to L (measured at 10 m above ground level). Between the wind-direction sector $60^{\circ }{-}120^{\circ }$, we obtain n number of 30-min segments for each stability class. Spectra and cospectra are estimated for each n ensemble of 30-min duration, where spectra are the average of the absolute square of the Fourier transform over all n ensembles, whereas cospectra (or, cross-spectra) are the ensemble average of the Fourier amplitude of the first time series (at height $z_1$) times the complex conjugate of the second (at height $z_2$).

Single 30-min time series in the HATS dataset are based on the data availability, such that the wind direction should be in the vicinity normal to the plane of the s- and d-array sensors. Furthermore, the five-parameter model was validated with the HATS data in  Chougule et al. (2017), where the spectra were initially estimated from time series at each sonic anemometer in both the arrays, and averaged over the sonic anemometers in each respective (s or d) row. It was noted that there was no significant difference in the model parameter values obtained from single sonic anemometers and those obtained from fitting (spatially) averaged spectra. Because of the assumptions of homogeneity and stationarity, the spectral-tensor model is valid for an ensemble-averaged spectrum.

The relative standard deviation of the spectral estimate is discussed in Mann (1994a), where, for the Høvsøre data here, the number of time series is sufficiently long for the largest relative standard deviation to be $60^{-1/2}=13\%$ for the very unstable case, whereas the smallest is $359^{-1/2}=5\%$ for the stable case. Because of the limited number of n realizations, there is uncertainty in the estimated (cross-) spectra and, hence, in the corresponding coherences and phases. While Kristensen and Kirkegaard (1986) showed that the coherence is systematically overestimated, it is insignificant for the n values here. Spectra are not scaled (or normalized) as we do not compare HATS data with Høvsøre data, but validate the model both close to the ground and at greater heights. The Høvsøre data are analyzed for the wind-speed range 8–9 m s$^{-1}$, whereas each single 30-min HATS time series is analyzed for a given z / L. Therefore, the analyses are not based on the wind-speed aggregation, but z / L. Also, as the model does not have an inherent wind-speed parameter, analyses based on the wind speed are not intended.

To determine the four model parameters $\alpha \epsilon ^{\frac{2}{3}}, \mathcal {L}, \varGamma$, and z / L, we use an automatic procedure of $\chi ^2$-fitting following Mann (1994b), where the model velocity spectra and $uw,u\theta$, and $w\theta$ cospectra are fitted simultaneously with those measured using Taylor’s hypothesis ($k_{1}=2\pi f/U$). The $\chi ^2$-fit equation is

$$\begin{aligned} \chi ^{2}(\alpha \epsilon ^{2/3},\mathcal {L},\varGamma ,z/L)= & {} \sum _{l=1}^{3}\frac{1}{ \left[ k_{1}F_{ll}(k_{1})\right] _{M}}\sum _{n=1}^{N}\left[ k_{n}F_{ll,T}(k_{n})-k_{n}F_{ll}(k_{n})\right] ^2\nonumber \\&+ \, \frac{1}{\mid \left[ k_{1}F_{13}(k_{1})\right] _{M}\mid }\sum _{n=1}^{N}\left[ k_{n}F_{13,T}(k_{n})-k_{n}F_{13 }(k_{n})\right] ^2 \nonumber \\&+ \, \frac{1}{\mid \left[ k_{1}F_{14}(k_{1})\right] _{M}\mid }\sum _{n=1}^{N} \left[ k_{n}F_{14,T}(k_{n})-k_{n}F_{14}(k_{n})\right] ^2\nonumber \\&+ \, \frac{1}{\mid \left[ k_{1}F_{34}(k_{1})\right] _{M}\mid }\sum _{n=1}^{N} \left[ k_{n}F_{34,T}(k_{n})-k_{n}F_{34}(k_{n})\right] ^2, \end{aligned}$$

(35)

where N is the number of logarithmically spaced wavenumbers in the estimated spectra, subscript T refers to the theoretical spectra and cospectra F defined by ( Eq. 29), and $\left[ k_{1}F(k_{1})\right] _{M}$ is the corresponding maximum value in the measured spectra and cospectra. The $\chi ^2$-fit minimizes the sum of squared differences between the theoretical and the estimated spectra and cospectra as given in (35), and thereby defines the optimal input parameter set. Due to the scaling in (1), the model kinematic heat fluxes become

$$\begin{aligned} F_{i\theta }(k_1)=\left[ \frac{g}{\overline{\theta }}\left( \frac{\text {d}U}{\text {d}z}\right) ^{-1}\right] ^{-1}F_{i4}(k_1) \end{aligned}$$

(36)

for $i=\{1,3\}$.

Fig. 4

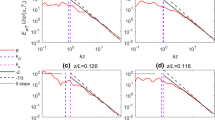
Horizontal Array Turbulence Study stable: example of ${\varvec{\Phi }}^{(4)}$ model spectra and cospectra (solid smooth lines) fitted with observations (ragged lines) at $z=4$ m, for the stability classes a near-neutral stable with $z/L=0.014$, $U\approx 6\,\hbox {m } \hbox {s}^{-1}$; b stable with $z/L=0.07, U=3.5$ m s$^{-1}$; and c very stable with $z/L=0.6, U\approx 2.5$ m s$^{-1}$. Dashed lines are the ${\varvec{\Phi }}^{(5)}$ model fits

Fig. 5

Horizontal Array Turbulence Study unstable: model spectra and cospectra fitted with observations at: $z=6$ m, $z/L=-0.03, U\approx 3.7$ m s$^{-1}$ [near-neutral unstable, (a)]; $z=5$ m, $z/L=-0.08$, $U=3.8$ m s$^{-1}$ [unstable, (b)]; and $z=8$ m, $z/L=-0.09$, $U\approx 4.5\,\hbox {m } \hbox {s}^{-1}$ [very unstable, (c)]. The notation follows Fig. 4

4 Results and Discussion

4.1 Spectra: Quality of Fitting and Resulting Model Parameters

A comparison of the model spectra and cospectra with the HATS data (c.f. Table 2) is shown in Figs. 4 and 5 for stable and unstable stratification, respectively. The model results are fitted to the data using the $\chi ^2$-fit equation given in (35) for velocity spectra and $uw, u\theta , w\theta$ cospectra to obtain the four model parameters given in Table 4, along with the five parameter values determined from fitting the ${\varvec{\Phi }}^{(5)}$ model defined by (18). The results from the fits based on the Høvsøre data at 100 m are shown in Figs. 6 and 7, respectively, for the stable and unstable ABL, with the parameters obtained at each height from the fits shown in Fig. 8a–d. Figure 8 also shows a variation of the parameters obtained from the ${\varvec{\Phi }}^{(5)}$ model fits [see the empty symbols in (a)–(c) and (e)–(f)].

Table 4 Four ${\varvec{\Phi }}^{(4)}$ spectral-tensor parameters obtained from $\chi ^2$-fits of HATS spectra in Figs. 4 (stable) and 5 (unstable) with five ${\varvec{\Phi }}^{(5)}$ spectral-tensor values shown in brackets ‘[ ]’. The z / L parameter from the ${\varvec{\Phi }}^{(4)}$ model fit is used to calculate Ri(z / L) and $\eta _\theta (z/L)$ using (20) and (25)

Fits to HATS data demonstrate no significant difference between the ${\varvec{\Phi }}^{(4)}$ and ${\varvec{\Phi }}^{(5)}$ models, with the exception of the $u\theta$ cospectrum, where $F_{1\theta }(k_1)$ is systematically underestimated when using the ${\varvec{\Phi }}^{(4)}$ model for the HATS (and Høvsøre) data for the stable ABL (the near-neutral stable, stable, and very stable cases). The model spectra and cospectra from the ${\varvec{\Phi }}^{(5)}$ model fits are shown as dashed lines in Figs. 4, 5, 6 and 7. For the HATS stable and very stable cases, as well as Høvsøre stable and near-neutral stable cases, the magnitudes of the ${\varvec{\Phi }}^{(4)}$-modelled u-spectra are slightly larger, and the w-spectra slightly smaller (see Figs. 4, 6), compared with the five-parameter formulation ${\varvec{\Phi }}^{(5)}$. The reason could be that the $\varGamma$ parameters are larger using the four-parameter method (see Fig. 8c), resulting in larger separations between the spectral peaks of $F_{11}$ and $F_{33}$, which is consistent with the theoretical results presented in Fig. 2, where the u-variance increases and w-variance decreases with increasing $\varGamma$. However, the increased $\varGamma$ resulting from the four-parameter method does not cause significant differences in the v-spectra and uw cospectra. We also note from Fig. 2 that, in the range of higher $\varGamma$ and z / L values, $\left\langle vv\right\rangle$ and $\left\langle uw\right\rangle$ become insensitive to $\varGamma$. The dependence of ${\varvec{\Phi }}^{(4)}$ model-predicted $\left\langle u\theta \right\rangle$ increasing with $\varGamma$ (shown in Fig. 2) appears to contradict the fits shown in Figs. 4, 6, where $u\theta$ cospectra are underestimated, yet have larger $\varGamma$ than those resulting from the ${\varvec{\Phi }}^{(5)}$ fits (c.f. Table 4 and Fig. 8c). This can again be due to the fact that the RDT can deviate from MOST, where the $\eta _\theta$ values (as a function of effective z / L obtained from the ${\varvec{\Phi }}^{(4)}$ fit) are much smaller than those from the ${\varvec{\Phi }}^{(5)}$ model fit (see Fig. 8f) for stable regimes. This is also consistent with the effective Ri fit to spectra being much smaller in stable conditions for the four-parameter model than the five-parameter model (Fig. 8e). The RDT modelling of the unstable ABL through the four-parameter MOST application matches well with the five-parameter method, both in terms of the spectral fits (Figs. 5 and 7) as well as parameter values (Table 4; Fig. 8a–c, e). As noted in Chougule et al. (2017), the buoyancy-affected, spectral-tensor model shows limitations in predicting spectra at lower frequencies for increasingly unstable conditions for both the original and new four-parameter approach.

Fig. 6

Høvsøre stable: model spectra and cospectra (smooth lines) fitted with observations (ragged lines) at $z=100$ m for a near-neutral stable; b stable; c very stable cases, and the wind-speed interval 8–9 m s$^{-1}$. Dashed lines are the ${\varvec{\Phi }}^{(5)}$ model fits

Fig. 7

Høvsøre unstable: model spectra and cospectra fitted with observations at $z=100\,\hbox {m}, U=8{-}9\,\hbox {m } \hbox {s}^{-1}$ for: near-neutral unstable (a); unstable (b); and very unstable (c) cases. For notation, see Fig. 6

Fig. 8

Height profiles of the four ${\varvec{\Phi }}^{(4)}$ model parameters (filled symbols) obtained from $\chi ^2$-fits at Høvsøre: a $\alpha \epsilon ^{2/3}$; b $\mathcal {L}$; c $\varGamma$; and d z / L. Open/hollow symbols are model parameters obtained from the ${\varvec{\Phi }}^{(5)}$ model fits. The z / L value from the ${\varvec{\Phi }}^{(4)}$ model fit is used to calculate Ri(z / L) and $\eta _\theta (z/L)$ using (20) and (25), which are compared in (e) and (f), respectively, to Ri and $\eta _\theta$ parameters obtained from the ${\varvec{\Phi }}^{(5)}$ model fits

The difference between the ${\varvec{\Phi }}^{(5)}$ and ${\varvec{\Phi }}^{(4)}$ model performance for the Høvsøre data appears related to the diminished applicability of MOST at heights above the surface layer, which is somewhat supported by the results presented in Fig. 8e, where differences between the two parameter sets seem to increase for heights above the surface layer—i.e. at altitudes exceeding roughly $40\,\hbox {m}$ (Kaimal and Finnigan 1994). For observations well inside the surface layer, it is also interesting to observe that, even in this regime, differences persist between the investigated model parameter sets. The rough compatibility of MOST with the present model has consequences, particularly for the fitting of $\varGamma$, Ri and $\eta _\theta$, whereas the fit-derived values of $\epsilon$ and the turbulence length scale $\mathcal {L}$ are not significantly affected. Typically, the ${\varvec{\Phi }}^{(4)}$ fit in stable ABL results in increased $\varGamma$ values compared with the ${\varvec{\Phi }}^{(5)}$ fit. The last two parameters in the ${\varvec{\Phi }}^{(5)}$ model, Ri and $\eta _\theta$, can also be compared with the MOST estimates as a function of z / L obtained from the ${\varvec{\Phi }}^{(4)}$ spectral fits using (20) and (25), respectively. The Ri and $\eta _\theta$ values obtained as a function of z / L from MOST (shown by the filled symbols) are lower, with $\eta _\theta$ values smaller by a factor of 10 (see Fig. 8e and f).

The parametrized $Ri\,(z/L)$ and $\eta _\theta (z/L)$ are governed (simultaneously) by the MOST-derived expressions Eqs. 20 and 25, and the results confirm that $\eta _\theta$ is not as sensitive as Ri is to z / L. However, in the original spectral-tensor model, Ri and $\eta _\theta$ are unconnected to each other in the same way as that given by MOST, and one can also infer from the figure that for the four-parameter-model fits for stable conditions, larger $\varGamma$ values are found, which compensate for the smaller Ri values compared with the five-parameter results.

Fig. 9

The $u\theta$ cospectrum as a function of height in the stable ABL at Høvsøre with inferred power-law exponents of the ${\varvec{\Phi }}^{(4)}$ model cospectrum (smooth curves). Straight lines indicate the estimated power-law behaviour

4.1.1 On the Power-Law Behaviour of the Inertial Range of $u\theta$

As indicated in earlier studies (Kaimal et al. 1972; Wyngaard and Coté 1972; Chougule et al. 2017), we do not find $F_{1\theta }$ to follow a power-law behaviour, i.e. the spectral ‘slope’ (in logarithmic coordinates) of $u\theta$ is not constant. An averaged exponent of $-\,5/2$ was noted in Kaimal et al. (1972) for stable cases, while Wyngaard and Coté (1972) predicted an exponent of $-\,3$ for the $u\theta$ cospectrum, whereas values from their data fall closer to $-\,7/3$ at a 22.6-m height. Chougule et al. (2017) also predicted an inertial-range exponent of $-\,3$ for the $u\theta$ cospectrum under both stable and unstable stratification. Neither the model nor the observations show a clear power-law behaviour, and the derived spectral slopes depend on the wavenumber interval chosen for the fit as demonstrated in Fig. 9.

Measurements from near-neutral stable and stable cases at Høvsøre show a trend with height in the inertial-range behaviour of $F_{u\theta }$. Surprisingly, the model (based on the $\chi ^2$-fit using Eq. 35) shows a similar trend as shown in Fig. 9, where $k_{1}F_{u\theta }$ exponents from the model and data are shown for the stable case. The $k_{1}F_{u\theta }$ exponent increases with height, with values of $-\,8/3$ at 10 and 20 m, $-\,7/3$ at 40 and 60 m, and $-\,2$ at 80 and 100 m. The model $u\theta$ spectral slopes from the fits for the very stable case show similar values. However, for the very stable case, the data do not show the same slopes because of the noise in the temperature spectra, which significantly contaminates $F_{u\theta }$ in the inertial subrange.

Fig. 10

Comparison of coherences between model predictions (smooth lines) and HATS data (ragged lines) for the stable (S) case for separation distances a $\Delta y_0= 0$; b $\Delta y_0=4.34$; c $\Delta y_0= 8.68$ m, with a vertical separation distance of $\Delta z_0=4$ m. Dashed lines are the coherence predictions of the ${\varvec{\Phi }}^{(5)}$ model

Fig. 11

Modelled coherences compared with HATS data for the very unstable (VU) case for separation distances a $\Delta y_0= 0$; b $\Delta y_0=4.34$; c $\Delta y_0= 8.68$ m, with a vertical separation distance of $\Delta z_0=4$ m. See Fig. 10 for notation

4.2 Cross-Spectra: Evaluation of Model Predictions

The four parameters $\alpha \epsilon ^{2/3}, \mathcal {L}, \varGamma$ and z / L from the $\chi ^2$-fits (Eq. 35) are used as input to calculate the cross-spectral properties of the coherence and phase spectra using (31) and (32), respectively. The model predictions of coherences are compared with the HATS data for stable and very unstable cases in Figs. 10 and 11, respectively. The ${\varvec{\Phi }}^{(4)}$ model predicts identical coherences as the ${\varvec{\Phi }}^{(5)}$ model, except that the predicted stably stratified temperature coherence for ${\varvec{\Phi }}^{(4)}$ is overestimated because $\eta _\theta$, which is responsible for maintaining the initial temperature variance, is much smaller (c.f. Fig. 8f), giving a higher coherence predominantly at lower wavenumbers. The same can be observed from the coherence comparisons for the Høvsøre data shown in Fig. 12a.

Fig. 12

Comparison of model coherence (smooth lines) with Høvsøre data (ragged lines) for a stable and b near-neutral unstable cases with a separation distance $\Delta z_0=40$ m. Dashed lines are the ${\varvec{\Phi }}^{(5)}$ model predictions

Fig. 13

Effects of atmospheric stability on coherences. Ragged lines are the Høvsøre data, and smooth lines are the ${\varvec{\Phi }}^{(4)}$ model predictions

Fig. 14

Comparison of ${\varvec{\Phi }}^{(4)}$ model phases (thin solid lines) with HATS data (thick solid lines) for a stable and b very unstable cases with the separation distance $\Delta z_0=4$ m. Dashed lines are the phase predictions from ${\varvec{\Phi }}^{(5)}$ model fits

Fig. 15

Modelled cross-spectral phases (smooth lines) compared with Høvsøre data (ragged lines) for a stable and b near-neutral unstable cases with the separation distance $\Delta z_0=40$ m. Dashed lines are the ${\varvec{\Phi }}^{(5)}$ model predictions

We note from the HATS results (Figs. 10, 11) that the model overestimates coherence more significantly in stable than in unstable conditions, which, for the same vertical separation distance of 4 m, decreases with the increase in horizontal separation. Moreover, the ${\varvec{\Phi }}^{(4)}$ model gives similar predictions to those of the ${\varvec{\Phi }}^{(5)}$ model, although the number of parameters is reduced from five to four.

The effects of atmospheric stability on the coherence can be seen from the Høvsøre data in Fig. 12, where the coherences are higher in the unstable ABL than those in the stable ABL (Chougule et al. 2015). This is also consistent with the theoretical predictions shown in Fig. 3, whereby the ${\varvec{\Phi }}^{(4)}$ model predicts the buoyancy effects on coherences, as shown in Fig. 12. Figure 3 also shows that the coherences are affected towards high wavenumbers, which is also observed in the Høvsøre data, and more so for the w-coherence. These effects would be clear when the coherences from the data, and the ${\varvec{\Phi }}^{(4)}$ model predictions for the stable and near-neutral unstable cases are presented together, as shown in Fig 13. For the HATS data, however, the stability effects are not predominant, since the measurements are close to the ground, where the eddies have smaller length scales, and are not as affected by buoyancy.

The phases in the modelled cross-spectra are compared with the HATS and Høvsøre data for the non-neutral ABL in Figs. 14 and 15, respectively. For smoother phases in the HATS data, however, we average the cross-spectra calculated from the data over the five sonic anemometers located directly over each other in the s- and d-arrays. The modelling based on the four-parameter input gives similar velocity phases as compared with those using the spectral tensor with five parameters, with the exception of the Høvsøre stable ABL (see Fig. 15a). The temperature phases are smaller in stable cases, however, due to the same reason as discussed previously where the temperature coherences are larger. As noted by Chougule et al. (2012), the w-phase may become zero, which is also predicted by the model as seen in Fig. 15a. We also observed negative w-phases both in the near-neutral stable and very stable cases at the Høvsøre site.

5 Conclusions

A simplified spectral model may be constructed by combining the RDT described in Chougule et al. (2017) with MOST (Obukhov 1946, 1971) to give a spectral tensor (${\varvec{\Phi }}^{(4)}$) accounting for non-neutral stability conditions using only the four parameters $\alpha \epsilon ^{2/3}, \mathcal {L}, \varGamma$ and z / L. These parameters are obtained by fitting the model to measured one-dimensional velocity spectra, and cospectra between horizontal and vertical velocity components, and temperature.

The model spectral fits are presented, with the predictions of cross-spectral coherence and phases compared with ABL data up to 100-m height for stratification varying from very stable to very unstable. The model results are also compared with those obtained from the modelled spectral tensor (${\varvec{\Phi }}^{(5)}$) of Chougule et al. (2017) described in terms of the five parameters $\alpha \epsilon ^{2/3}, \mathcal {L}, \varGamma$, Ri and $\eta _\theta$.

The ${\varvec{\Phi }}^{(4)}$ model described in terms of four parameters generates velocity spectra and cospectra between the longitudinal and the vertical velocity components, as well as that between the temperature and the vertical velocity component. The model systematically underestimates the cospectra between the temperature and the horizontal velocity components in the stably stratified cases, which is also observed for the ${\varvec{\Phi }}^{(5)}$ model. As stated in Chougule et al. (2017), however, excluding the temperature spectrum from the ${\varvec{\Phi }}^{(5)}$ model, as performed here, improves the fitted $u\theta$ cospectrum. With an increase in the value of $\varGamma$, the energy of the u-spectrum increases, whereas that of the w-spectrum decreases, while no significant changes in the v-spectrum and uw cospectrum are observed. Moreover, the u-component is the most important one for wind-loading calculations, and, with the use of the ${\varvec{\Phi }}^{(4)}$ model, the $\varGamma$ value increases the magnitude of the u-spectra, particularly at wind-turbine rotor heights (c.f. Fig. 6), which should give more conservative estimates of turbine loads. There is not any significant difference in the spectral fits of the unstable ABL spectra from the RDT modelling with and without the application of MOST. When comparing the parameters of the ${\varvec{\Phi }}^{(4)}$ and ${\varvec{\Phi }}^{(5)}$ models, it is observed that

• In unstable regimes, no significant difference is evident in the values of $\alpha \epsilon ^{2/3}$, $\mathcal {L}$, $\varGamma$ and Ri (see Fig. 8a–c, e); and

• In stable regimes, the values of $\varGamma$ increase, while Ri and $\eta _\theta$ values decrease (see Fig. 8c, e–f).

The ${\varvec{\Phi }}^{(4)}$ model is able to capture the trend in the $u\theta$ cospectrum slope, which systematically decreases with height in the stable ABL. Further investigation of $u\theta$-slope behaviour is, however, needed.

Our model has deficiencies in reproducing spectra and cospectra in unstable regimes at lower wavenumbers for larger lapse rates. Despite this, the model is able to predict velocity cross-spectra, including those involving temperature, even though the temperature auto-spectra are not included in the fitting. The model overestimates velocity coherence for vertical separations, and these overestimations are smaller in the unstable ABL than in stable cases, and decrease with an increased horizontal separation. The model overestimates temperature coherences in the stable case, but underestimates cross-spectral phases when compared with the ${\varvec{\Phi }}^{(5)}$ model. However, for the unstable case, no significant difference both for the coherence and phase is found. The atmospheric stability has an effect on the low-wavenumber coherence, where the coherences are higher in the unstable, and lower in the stable ABL. However, the simplified spectral-tensor model with the inclusion of buoyancy does model the effects of atmospheric stability on the coherence.

In summary, when compared with results from the five-parameter model, our four-parameter approach produces similar results in terms of the spectra, values of model parameters, including their variation with height, and the cross-spectral properties of coherence and phases for the unstable regime, with slight differences in the stable regime. However, there is a discrepancy between the value of z / L obtained from the model fits and that measured (c.f. Tables 2, 4).

Finally, Fig. 8 serves as a reminder that stability can become altitude dependent above the surface layer. This is an important observation, since ABL stability then affects turbulence and, thus, local wind-turbine loading (Kelly et al. 2014), where conventional turbine rotors often extend beyond the surface layer. As the classic stability measure used here (the Obukhov length L) is defined in the surface layer, and we are using this parameter both in and above the surface layer, one may additionally consider the four-parameter model’s Richardson number Ri as a model parameter. Ongoing work includes the relation of the model’s Ri to the local Obukhov length, which is beyond the scope here.