Abstract
We address the flux footprint for measurement heights in the atmospheric surface layer, comparing eddy diffusion solutions with those furnished by the first-order Lagrangian stochastic (or “generalized Langevin”) paradigm. The footprint given by Langevin models differs distinctly from that given by the random displacement model (i.e. zeroth-order Lagrangian stochastic model) corresponding to its “diffusion limit,” which implies that a well-founded theory of the flux footprint must incorporate the turbulent velocity autocovariance. But irrespective of the choice of the eddy diffusion or Langevin class of model as basis for the footprint, tuning relative to observations is ultimately necessary. Some earlier treatments assume Monin–Obukhov profiles for the mean wind and eddy diffusivity and that the effective Schmidt number (ratio of eddy viscosity to the tracer eddy diffusivity) in the neutral limit \(S_c(0)=1\), while others calibrate the model to the Project Prairie Grass dispersion trials. Because there remains uncertainty as to the optimal specification of \(S_c\) (or a related parameter in alternative theories, e.g. the Kolmogorov coefficient \(C_0\) in Langevin models) it is recommended that footprint models should be explicit in this regard.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The “flux footprint” is the zone of the surface (mostly) upwind from an instrument that contributes to a measured vertical flux (e.g. of water vapour or carbon dioxide) between the ground and the atmosphere: knowledge of that footprint confirms one is correctly attributing the measured flux to the region of the surface whence it derives. Analytical formulae for the footprint are particularly convenient, sparing the flux measurement practitioner the task of numerically solving the turbulent dispersion problem. Existing footprint models applicable to the atmospheric surface layer (ASL) are raw or modified solutions of an advection–diffusion equation, using power laws to represent profiles of mean wind speed \(\overline{u}\) and eddy diffusivity \(K_c\) in lieu of the (actual) Monin–Obukhov profiles.
Here the simplest bases for computing the flux footprint (in the horizontally-homogeneous surface layer) will be briefly reviewed, and the degree of consistency between the resulting footprints examined. It will be shown that the penalty for adopting power-law profiles is not severe, but that there is nonetheless good reason to base the footprint on a generalized Langevin model (i.e. first-order Lagrangian stochastic model) rather than the eddy diffusion paradigm: not only does the generalized Langevin model (hereafter LSM) permit using the “true” Monin–Obukhov (MO) velocity statistics rather than a power-law representation, but more fundamentally the LSM, (i) allows the inclusion of the horizontal velocity fluctuations, long recognized as important (e.g. Rannik et al. 2000), and (ii) corrects what Sawford (2001) has termed the “systematic failure of the diffusion approximation” in strongly inhomogeneous turbulence.
2 Definition of the Flux Footprint
Let \((x,z)\) be the alongwind and vertical coordinates. For steady-state situations with symmetry in the crosswind \((y)\) direction, we may express the vertical mass flux density at an elevated observation point O having coordinates \((x,z_m)\) as a convolution
(Wilson and Swaters 1991; Horst and Weil 1992) of the footprint function \(\varPhi \,({\mathrm {m}}^{-1})\) and the (potentially, spatially-varying) surface emission rate, i.e. surface mass flux density \(F_0\) (e.g., \({\mathrm {kg}}\,{\mathrm {m}}^{-2}\,{\mathrm {s}}^{-1}\)). Setting \(F_0(x')=q \, \delta (x'-0)\) with \(q=1 \, ({\mathrm {kg}}\,{\mathrm {m}}^{-1}\,{\mathrm {s}}^{-1})\) we see that the footprint \(\varPhi (x,z_m)\) is identically the flux at \((x,z_m)\) due to a unit line source at the origin, or in dimensionless terms,
where \({\mathcal {L}}\) is any convenient length scale (chosen below as the aerodynamic roughness length \(z_0\)). That is, the flux footprint is the normalized line-source flux, and it satisfies
3 Kormann–Meixner ( Analytical Flux Footprint
The foundation for existing analytical footprint relations is the steady-state advection–diffusion equation
where \(\overline{c}=\overline{c}(x,z)\) is the mean concentration (here assumed independent of the crosswind coordinate \(y\)), and \(\overline{u}(z)\) and \(K_c(z)\) are the vertical profiles of mean wind speed and eddy diffusivity. If the accepted (Monin–Obukhov) surface-layer profiles are invoked Eq. 4 is intractable, even in the neutral case; however many authors have exploited an exact solution (first obtained, according to Monin and Yaglom 1977, by O. F. T. Roberts) corresponding to power-law profiles, e.g.
The formulae of Kormann and Meixner (2001) provide a concise example of an analytic footprint based on Eqs. 4–6, and the following summary differs from Kormann and Meixner only in one simple (but important) respect: a turbulent Schmidt number is explicitly introduced, whereas Kormann and Meixner had presumed it to be unity. Parameters \(\overline{u}_H, \, K_H, \, m, \, n\) are chosen to reproduce the mean wind speed and eddy diffusivity, and their height gradients, at the reference height \((H)\). Thus,
where \(L\) is the Obukhov length, \(k_v\) is the von Karman constant, and \(\phi _m(z/L)\), \(\phi _c(z/L)\) are respectively the universal MO functions giving the dimensionless gradients in mean wind speed and in tracer concentration (note a trivial difference relative to Kormann and Meixner in the sign convention chosen here for \(\psi _m\) in the mean wind profile). Choosing the MO functions as (Dyer 1974)
(and the Paulson 1970 form for the mean wind profile for \(L<0\), Eqs. 21, 22 below), one obtains Kormann and Meixner’s Eq. 36 for \(m,n\). Then, defining \(r=2+m-n\) and \(\mu =(1+m)/r\), their crosswind-integrated footprint is
where \(\varGamma (\mu )\) is the Gamma function (for which a simple power series representation is given by Abramowitz and Stegun 1953) and
is a transformed height. The origin of this footprint is clear, and it is easy to compute.
4 Footprint from the Random Displacement Model (RDM)
The zeroth-order Lagrangian stochastic model (also known as the random displacement model, RDM) is a Lagrangian (thus, grid free) treatment that is equivalent to eddy diffusion (e.g. Boughton et al. 1987; Wilson and Yee 2007). With the convention of representing Lagrangian variables in upper case, the RDM for stochastic increments in the height \(Z\) of a tracer particle may be written
where \(d \zeta _z\) is a Gaussian random number with variance \(dt\) (i.e. an increment of the Wiener process). The corresponding alongwind step is \(dX = \overline{u}(Z) \, dt\) (one could of course add a correlated turbulent alongwind displacement \(dX'\), and random crosswind displacements \(dY\)).
The profiles \(\overline{u},K_c\) may be specified at will (e.g. power-law or Monin–Obukhov profiles), and, if given the same profiles as used by Kormann and Meixner (2001), the RDM must (in the limit of infinitesimal \(dt\), in any case) yield the same footprint. Here the RDM has been implemented with the same constraint as used in the case of the first-order LS model, viz. \(dt = \gamma \tau \), where \(\gamma \ll 1\) and \(\tau \) is an effective Lagrangian decorrelation time scale, given below. Footprints computed with alternative choices for the \(\overline{u}\), \(K_c\) profiles will be shown, viz.
-
(a)
Those invoked by Kormann and Meixner to calibrate their power-law profiles, i.e. the \(\overline{u}\), \(K_c\) profiles implied by Eqs. 11, 12.
-
(b)
The Monin–Obukhov wind profile \(\overline{u}(z)\), and the far-field eddy diffusivity \(K_{\infty }(z)\) implied (Eqs. 29, 30) by the profiles that calibrate the first-order Lagrangian stochastic model of Sect. 5 to Project Prairie Grass (labelled “WTK profiles”, after Wilson et al. 1981).
5 Footprint from First-Order Lagrangian Stochastic Models (LSM)
Modern Lagrangian stochastic (LS) models (Wilson and Sawford 1996; Thomson and Wilson 2013) provide the state of the art numeric solution for turbulent dispersion, accommodating whatever given statistical information is available regarding the velocity statistics, and correctly treating the non-diffusive near field of sources. The flux footprint is easily derived from an ensemble of trajectories computed by the generalized Langevin model (Thomson 1987),
Here \((a_u,a_w)\) are the components of the conditional mean acceleration (specified below); the coefficient \(b\) of the random forcing terms is given by \(b=\sqrt{C_0 \epsilon }\), where \(\epsilon =\epsilon (z)\) is the turbulent kinetic energy dissipation rate and \(C_0\) is a dimensionless coefficient originally introduced by Kolmogorov; and \((d\zeta _u, d\zeta _w)\) are independent Gaussian random numbers each with variance \(dt\). With the approximations, (i) that the joint probability density function \(g_a\) for the Eulerian velocity fluctuations \((u',w')\) is Gaussian,Footnote 1 and (ii) that the velocity correlation is height invariant \((-\overline{u'w'} \equiv u_*^2)\) throughout the surface layer, and (iii) that the standard deviation of the alongwind velocity fluctuation \(\sigma _u = {\mathrm {constant}}=c_{u}u_{{*}}\) (whereas \(\sigma _w=\sigma _w(z)\)), one obtains the following prescription,
where
The two-dimensional LSM defined by Eqs. 16–20 is a special case of Thomson’s (1987) more general model for vertically-inhomogeneous Gaussian turbulence. Particles are released from the source with a velocity chosen randomly from \(g_a\), i.e. with the correct correlation between \(U', W\). At every step along the trajectory the statistics (\(\sigma _w\), \(\epsilon \), \(\overline{u}\)) appearing in the algorithm are re-evaluated at the particle’s present height \(Z\).
Footprints based on two alternative simplifications of this “2D-LSM” will also be shown: one eliminates the \(U'-W\) correlation, in which case the equation for \(U'\) reduces to the classic Langevin equation; the other entirely suppresses the contribution of \(U'\), in which case the above algorithm reduces to the unique, well-mixed, one-dimensional (1D), first-order LS model for stationary, Gaussian, vertically-inhomogeneous turbulence (simply “LSM,” on diagrams to follow).
5.1 Wind and Turbulence Profiles to Match the Monin–Obukhov Surface Layer
Unless stated otherwise, for LSM simulations the Monin–Obukhov wind profile was specified as
where if \(L<0\)
while, if \(L \ge 0\)
Equations 22, 23 constitute Paulson’s (1970) form for the mean wind profile and the Dyer and Hicks (1970) formulation for the MO dimensionless wind shear function \(\phi _m\).
Wilson et al. (1981) calibrated the 1D (i.e. \(W\) only) version of the above LSM against the Project Prairie Grass profiles (Barad 1958b; Haugen 1959) of crosswind-integrated concentration at radial distance \(x=100\) from a continuous point source of gas, neglecting any possible depositional flux of the PPG “tracer” (sulphur dioxide). Their calibration gives the needed \(C_0 \epsilon \) product as
with \(a=0.5\). Most of the 1D Langevin simulations to be shown below use exactly this prescription, the exception being a single simulation that uses \(a=0.32\) and which corresponds, as will be made clear below, with an assumption that the turbulent Schmidt number in the neutral limit \(S_c(0)=1\).
Along with Eqs. 25, 26 the \(\sigma _w\) profile is prescribed by
with \(c_w=1.25\) (Kaimal and Finnigan 1994). The far-field eddy diffusivity \(K_{\infty }(z)\), implied by the above specification (of \(\sigma _w, \tau \)) in the diffusion limit (Sawford and Guest 1988) is
from which the gradient \(dK_{\infty }/dz\) is readily computed for implementation of the zeroth-order LS model (or RDM) corresponding to this first-order LS model (see Sect. 4). Furthermore the implied Schmidt number (in the neutral limit) is
and so \(a=0.32\) implies \(S_c(0)=1\) and \(C_0=2k_v c_w^3/a=4.9\), while \(a=0.5\) (the calibration of Wilson et al. 1981) implies \(S_c(0)=0.64\) and \(C_0=3.1\).
For the full 2D-LSM, i.e. the Langevin model that includes \(U'\) and its correlation with \(W\), an increased value of \(C_0\) (smaller \(\tau )\) is needed in order that the model imply the same far-field diffusivity (Sawford and Guest 1988 Eq. 20; Sawford 2001 Eq. 6; Wilson et al. 2009 Sect. 4). Hence for such simulations (“2D-LSM”) the time scale \(\tau \) resulting from Eqs. 25, 26 was adjusted by the factor \(c_w^4/(1+c_w^4)=0.71\) (Wilson et al. 2009) (Note: as the LS model has here been formulated explicitly in \(\tau , \sigma _w\) the value of \(C_0\) is cited only as an interpretation).
5.2 Langevin Model with Power-Law Profiles
Of course it is straightforward to implement a 1D (\(W\) only) version of the generalized Langevin model, whose diffusion limit equates (in principle) to a solution of the advection–diffusion equation or RDM. Thus, a first-order LSM related (but, as will be seen, not equivalent) to solutions such as that of Kormann and Meixner (2001) can be obtained by substituting the appropriate power-law for \(\overline{u}\) in lieu of Eqs. 21–24 and by specifying, e.g.,
(\(\sigma _w\) as specified above). This ensures that the far-field eddy diffusivity implied by the 1D Langevin model matches that of the eddy diffusion solution. Surprisingly perhaps, it will be seen that the two solutions are distinct.
5.3 From Forward Trajectories to the Flux Footprint
For the Lagrangian stochastic solutions, sub-ensembles of \(N_P\) (typically here, \(10^5\)) particles are released independently at \((x,z)=(0, z_0)\), each trajectory [\(X=X(t), Z=Z(t)\)] being tracked with time resolution \(dt=\gamma \tau (Z)\), where \(\gamma =0.02\). Upward (downward) crossings of the measurement plane \(z=z_m\) are counted positively (negatively) by accumulators having alongwind span (or resolution) \(\varDelta x\), and subsequently those counts are divided by \(N_P \, \varDelta x\) to provide an estimate of the (dimensional) footprint, i.e. the vertical flux density at \(z=z_m\) due to the unit source at \((0,z_0)\). A standard error is attached to each estimate by repeating this over many (in practice, 19) trials, though (with \(N_P \sim 10^5\)) these proved too small to display on the graphs to follow.
6 Calibration of Dispersion Models for the ASL: An Ambiguity?
Before proceeding to establish similarities and differences between footprints computed along the diverse lines given above, it may be useful to revisit and clarify the notion of calibration of surface-layer dispersion models.
Commencing with Lagrangian models and the prescription of \(C_0 \epsilon \) (or equivalently the parameter \(a\)), recall that Wilson et al. (1981) found \(a=0.5\) is optimal in the 1D-LSM if one interprets the PPG concentration data as being appropriately modelled by a passive tracer (the equivalent inference for eddy diffusion models had been drawn by Wilson 1982). Gryning et al. (1983) have argued, however, that it is necessary to interpret the PPG concentration field as having been affected by a depositional flux.Footnote 2 There are then two possibilities to “fit” the vertical concentration profiles of PPG, which were measured at a single radial distance of 100 m from the source: one may (i) preserve equality of the eddy viscosity and the eddy diffusivity in the neutral limit, i.e. \(S_c(0)=1\), but introduce deposition; or, one may (ii) enhance the eddy diffusivity \((S_c(0)<1)\) and neglect deposition. Examining these options Sawford (2001) found that including deposition (with the deposition velocity \(w_d/u_*=0.05\) suggested by Gryning et al.) “gives almost as good agreement with the data as does increasing the diffusivity,” but also noted that “the resultant streamwise flux is then much lower than is observed.” The underestimated streamwise flux is presumably due to the fact that models with \(S_c=1\) underestimate the mean concentration \(\overline{c}\) (for PPG at \(x=100\) m) at an intermediate range of heights (roughly \(4 \le z \le 11\) m), which error \(\delta \overline{c}\) induces a corresponding error \(\overline{u} \, \delta \overline{c}\) in the streamwise flux density that is accentuated by the larger mean wind speeds aloft than near the surface.
Thus there is an ambiguity as to how best to reconcile models with the Project Prairie Grass data, and that ambiguity flows through to one’s belief as to the optimal calibration of a surface-layer dispersion (or footprint) model. For simplicity we shall label the two interpretations according to their Schmidt number, viz. \(S_c(0)=1\) or \(S_c(0)=0.64\), and note that for the 1D-LSM they correspond respectively to \(a=0.32\) and \(a=0.5\).
Although Project Prairie Grass is not the only tracer dispersion experiment to have been interpreted as implying \(S_c(0)<1\) (e.g. Hassid 1983; Wilson et al. 1984) it is probably true to say that most micrometeorologists would pitch for the \(S_c(0)=1\) interpretation, reflecting the consensus of flux–gradient experiments using natural scalars: for while the Kansas experimenters (Businger et al. 1971) reported the Prandtl number \(P_r(0)\) in the neutral limit as having the value 0.74 (this being analogous to the neutral Schmidt number), subsequent authors find that in the neutral limit the eddy diffusivities and the eddy viscosity are all equal, to within the prevailing experimental uncertainty (e.g. Dyer and Bradley 1982). A more extended discussion of the (tacit) emergence of an \(S_c(0)=1\) consensus is given by Wilson (2013), where it is emphasized there is no requirement a priori that eddy diffusivities for distinct species be equal, nor of course that they be equal to the eddy viscosity. Within the roughness sublayer, certainly \(S_c(0) \ne 1\) and scalar diffusivities are distinct. This does not contradict Hill (1989), whose argument for scalar similarity excludes situations where (in his terminology) the “internal dynamics of the surface itself” may result in concentration (and joint velocity–concentration) statistics that contradict any expectation of scalar-to-scalar similarity.
7 Results
Diverse footprints were computed by the methods outlined above, for each of three combinations \((z_m/z_0,\,z_0/L)\) of the flux measurement height and the stability parameter; unless otherwise specified, the footprint reflects the “\(S_c(0)=0.64\) calibration,” and indeed only the final example (Fig. 3) will show footprints corresponding to \(S_c(0)=1\). For the reasons given above, the predominance here of footprints computed with \(S_c=0.64\) should not be interpreted as implying this is necessarily the “true” option.
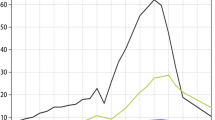
Starting with the neutral case, Fig. 1 compares the footprint as it is given by two categories of model, viz. the eddy diffusion model (solution of the advection–diffusion equation or, equivalently, the random displacement model, RDM) versus the “generalized Langevin” model (LSM). Firstly addressing footprints of the former origin (eddy diffusion), note that the Kormann and Meixner (2001) analytical footprint, which is based on power-law profiles (though here, with \(z_0/L=0\), we have \(n=1\)), is not very sensitive to the choice of reference height \(H\) and that it is exactly consistent (as of course it should be) with the solution given by the RDM, provided the latter is equipped with the same profiles.Footnote 3 As to the penalty paid for adopting a power-law profile for the mean wind, it is apparently not very serious, for while the onset of the footprint given by the RDM with the true (semi-logarithmic) wind profile occurs slightly closer to the flux observation point and has a slightly higher peak than the Kormann and Meixner footprint, those differences are less striking than the difference between the two categories of footprint.
Comparison of computed footprints in the neutral atmospheric surface layer, for measurement height \(z_m/z_0=2000\). “LSM” footprints computed by a first-order forward Lagrangian stochastic model (2D-LSM model includes the horizontal velocity fluctuation \(u'\)). KM identifies the analytical footprint of Kormann and Meixner (2001), while RDM identifies a footprint computed using the random displacement model (equivalent to a solution of the advection–diffusion equation). Where the footprint is based on power-law profiles, the reference height \(H/z_0=100\) unless otherwise stated. All footprints computed according to the “\(S_c(0)=0.64\) calibration”
Turning now to the footprint as given by the LSM (generalized Langevin model), the key facts are that, (i) onset of the LSM footprints occurs farther upwind of the flux measurement point than in the case of the diffusion solutions as a class; and (ii) provided its correlation with the vertical velocity is included, the impact of the alongwind velocity fluctuation \(u'\) is rather significant (as one would expect, and as was earlier established by Rannik et al. 2000). Finally, note that the difference between LSM solutions with the true versus the power-law profile for \(\overline{u}(z)\) is of about the same sense and magnitude as for the diffusion solutions.
Under moderately unstable stratification (see Fig. 2) the footprint computed on the basis of power-law profiles is more sensitive to the choice of the reference level \(H\) than in the neutral case shown above. Otherwise, once again we see the clear separation of footprints based on eddy diffusion and those based on the LSM. Close agreement of RDM footprints with alternatively the power-law profiles or the WTK profiles confirms that the distinction between these two choices is less significant than the distinction between an eddy diffusion paradigm and the generalized Langevin approach.
Comparison of computed footprints in the unstable atmospheric surface layer \((z_0/L=-4\times 10^{-4})\), for measurement height \(z_m/z_0=2000\). Notation and details as per Fig. 1 and again, all footprints were computed according to the “\(S_c(0)=0.64\) calibration”
Differences amongst the various computed footprints for stable stratification (Fig. 3) are qualitatively the same as for neutral and unstable conditions, athough interestingly, in this particular case (and referring to the footprints identified by \(S_c=0.64\)), the 2D-LSM footprint matches the (1D) eddy diffusion footprints rather closely—suggesting that neglect of the alongwind fluctuation has to some extent been compensated by the simplified flux–gradient relationship that defines the eddy diffusion paradigm. The expected consistency between the RDM footprint and the Kormann and Meixner eddy diffusion footprint is again manifest. But most importantly, Fig. 3 emphasizes the significance of one’s specification of the Schmidt number (or, stated more broadly, one’s calibration of the footprint), as indicated by the radical difference between footprints corresponding to \(S_c=0.64\) and those corresponding to \(S_c=1\).
Comparison of computed footprints in the stable atmospheric surface layer \((z_0/L=4\times 10^{-4})\), for measurement height \(z_m/z_0=200\). Unless otherwise indicated, for power-law profiles \(H/z_0=100\). Two clusters of footprints are shown: one group representing \(S_c=0.64\) (not indicated in the legend), and the other \(S_c=1\). The calculation for the Horst–Weil footprint (“HW”) is described in the Appendix. KM is Kormann and Meixner (2001). Further notation and details as on Figs. 1 and 2
It remains to identify the footprint denoted “HW” on Fig. 3. This is one of the flux footprint estimates given by Horst and Weil (1992, 1994) and Horst (1999), and indeed but an approximation to their complete analytical solution: details are given in the Appendix. In short, the curve “HW” reflects (indirectly) an interpretation (by Gryning et al. 1983) that the Project Prairie Grass measurements were affected by deposition to the surface, and with the choices made here for Monin–Obukhov functions it corresponds to \(S_c(0)=1\).
8 Conclusion
Although presumably this can be rendered moot by the step of tuning, it is interesting that the above results suggest the eddy diffusion paradigm misrepresents the flux footprint—relative to the equivalent calculation by the generalised Langevin model. The logic justifying this contention is simplest for the neutral case and with reference to the 1D model (no alongwind fluctuation): then \(\sigma _w={\mathrm {constant}}\) and \(\tau \propto z\), so that the implied far-field eddy diffusivity \(K_c \propto z\) and \(\partial K_c/\partial z={\mathrm {constant}}\). The RDM implementation (equivalent to eddy diffusion) yields a footprint differing from that based on the Langevin model, and agreeing closely (as expected) with the Kormann–Meixner footprint.
Intuition might have suggested that in the context of computing the flux footprint, the distinction between the eddy diffusion model and the LSM would be latent—because for any position of interest in the plume one should effectively be in the far field of the source. However there have been earlier reports (Mooney and Wilson 1993; Sawford 2001; Wilson and Yee 2007) that, even for a surface source, these two classes of models are not equivalent; having computed concentration profiles for the Project Prairie Grass measurements Sawford (2001) stated that the distinction between a LSM solution and the corresponding eddy diffusion solution “is not a near-source effect due to the finite source height, but rather is a systematic failure of the diffusion approximation.”
Tentatively accepting this finding—that in principle an eddy diffusion formulation cannot (fundamentally) describe the flux footprint—then perhaps it can be concluded that the onset region of the flux footprint, where the fetch to the source only just suffices for particles to have had “time to climb” to the flux detector, is strongly affected by extreme or rare trajectories that feature a sustained upward velocity. This would explain the need for a proper representation of the turbulent velocity covariance function, but it raises the question of the adequacy of having (here) based the footprint model on the approximation of a Gaussian velocity distribution (even at the release point, \(z=z_0\)). Physically, it is plausible that the nearby end of the flux footprint would reflect transport by the ejections of the sweep-ejection cycle, so that a good causal footprint model (as opposed to a flexible formula, scaled to fit) would have to include the alongwind fluctuation \(u'\) and its correlation with the vertical velocity.
It bears repetition that all the footprints computed above (barring three exceptions given on Fig. 3) are consistent in regard to their “tuning,” that is, eddy diffusion (and RDM) models feature
while \(a, c_w\) (thus indirectly \(C_0\)) have been prescribed in the Langevin models such that the implied far-field eddy diffusivity also corresponds to \(S_c(0)=0.64\). With \(S_c(0)=1\) (e.g. Kormann and Meixner 2001) the positioning of the footprints is quite different, as indicated by Fig. 3. Although not shown, footprints with \(S_c(0)=(0.64,1)\) differ greatly for all other combinations (\(z_m/z_0\), \(z_0/L\)) investigated. In view of this, and pending resolution of the ambiguity identified in Sect. 6, caution suggests that footprint models be formulated in such a way as to make the Schmidt number (or in Langevin models, \(C_0\)) explicit, thus readily adjustable.
Notes
Note the approximation here that the probability distribution for vertical velocity is Gaussian not only when \(z/L \ge 0\), but also during unstable stratification; the LS model of Horst and Weil (1992) differs in that those authors introduce the skewness of the vertical velocity distribution when \(z/L<0\).
Barad’s (1958a) report states: “there is no evidence of any significant loss of sulphur dioxide due to absorption by vegetation or any other factor.” This was probably based on the demonstrably reasonable agreement of a computed approximation \(\sum \overline{u}_j(z) \, \overline{c}(x,y_i,z_j) \, \varDelta y_i \, \varDelta z_j\) to the total radial mass flux (based on measured \(\overline{c}\) at radius \(x=100\) m) with the actual source strength \(Q\). Uncertainties inherent in the summation, and neglect of the radial eddy flux carried by horizontal velocity fluctuations, would suggest the statement may have been intended to suggest deposition could be neglected as a first approximation.
References
Abramowitz M, Stegun I (1965) Handbook of mathematical functions. Dover Publications, New York, 1046 pp
Barad M (1958a) Project Prairie Grass, a field program in diffusion, vol 1. Technical Report Geophysical Research Papers No. 59, TR-58-235(I). Air Force Cambridge Research Center, Bedford, 280 pp
Barad M (1958b) Project Prairie Grass, a field program in diffusion, vol 2. Technical Report Geophysical Research Papers No. 59, TR-58-235(II). Air Force Cambridge Research Center, Bedford, 209 pp
Boughton B, Delaurentis J, Dunn W (1987) A stochastic model of particle dispersion in the atmosphere. Boundary-Layer Meteorol 40:147–163
Businger J, Wyngaard J, Izumi Y, Bradley E (1971) Flux–profile relationships in the atmospheric surface layer. J Atmos Sci 28:181–189
Dyer A (1974) A review of flux–profile relationships. Boundary-Layer Meteorol 7:363–372
Dyer A, Bradley E (1982) An alternative analysis of flux–gradient relationships at the 1976 ITCE. Boundary-Layer Meteorol 22:3–19
Dyer A, Hicks B (1970) Flux–gradient relationships in the constant flux layer. Q J R Meteorol Soc 96:715–721
Gryning S, Van Ulden A, Larsen S (1983) Dispersion from a continuous ground-level source investigated by a \(K\) model. Q J R Meteorol Soc 109:355–364
Hassid S (1983) Turbulent Schmidt number for diffusion models in the neutral boundary layer. Atmos Environ 17:523–527
Haugen D (1959) Project Prairie Grass, a field program in diffusion, vol 3. Technical Report Geophysical Research Papers No. 59, TR-58-235(III). Air Force Cambridge Research Center, Bedford
Hill R (1989) Implications of Monin–Obukhov similarity theory for scalar quantities. J Atmos Sci 46:2236–2244
Horst T (1999) The footprint for estimation of atmosphere-surface exchange fluxes by profile techniques. Boundary-Layer Meteorol 90:171–188
Horst T, Weil J (1992) Footprint estimation for scalar flux measurements in the atmospheric surface layer. Boundary-Layer Meteorol 59:279–296
Horst T, Weil J (1994) How far is far enough? The fetch requirements for micrometeorological measurement of surface fluxes. J Atmos Ocean Technol 11:1018–1025
Kaimal J, Finnigan J (1994) Atmospheric boundary layer flows. Oxford University Press, Oxford, 289 pp
Kormann R, Meixner F (2001) An analytical footprint model for non-neutral stratification. Boundary-Layer Meteorol 99:207–224
Monin A, Yaglom A (1977) Statistical fluid mechanics. MIT Press, Cambridge, 769 pp
Mooney C, Wilson J (1993) Disagreements between gradient-diffusion and Lagrangian stochastic dispersion models, even for sources near ground. Boundary-Layer Meteorol 64:291–296
Paulson C (1970) The mathematical representation of wind speed and temperature profiles in the unstable atmospheric surface layer. J Appl Meteorol 9:857–861
Rannik U, Aubinet M, Kurbanmuradov O, Sabelfeld K, Markkanen T, Vesala T (2000) Footprint analysis for measurements over a heterogeneous forest. Boundary-Layer Meteorol 97:137–166
Sawford B (2001) Project Prairie Grass—a classic atmospheric dispersion experiment revisited. In: 14th Australian fluid mechanics conference, Adelaide, Dec 2001
Sawford B, Guest F (1988) Uniqueness and universality of Lagrangian stochastic models of turbulent dispersion. Preprints of 8th AMS symposium on turbulence and diffusion, San Diego. American Meteorological Society, Boston, pp 96–99
Thomson D (1987) Criteria for the selection of stochastic models of particle trajectories in turbulent flows. J Fluid Mech 180:529–556
Thomson D, Wilson J (2013) History of the Lagrangian stochastic model for turbulent dispersion. In: Lagrangian models of the atmosphere. Geophysical Monograph 200. American Geophysical Union, Washington, DC, 347 pp
Wilson J (1982) An approximate analytical solution to the diffusion equation for short-range dispersion from a continuous ground-level source. Boundary-Layer Meteorol 23:85–103
Wilson J (2013) Turbulent Schmidt numbers above a wheat crop. Boundary-Layer Meteorol 148:255–268
Wilson J, Thurtell G, Kidd G (1981) Numerical simulation of particle trajectories in inhomogeneous turbulence. III. Comparison of predictions with experimental data for the atmospheric surface layer. Boundary-Layer Meteorol 21:443–463
Wilson J, Swaters G (1991) The source area influencing a measurement in the planetary boundary-layer: the footprint and the distribution of contact distance. Boundary-Layer Meteorol 55:25–46
Wilson J, Sawford B (1996) Review of Lagrangian stochastic models for trajectories in the turbulent atmosphere. Boundary-Layer Meteorol 78:191–210
Wilson J, Clarkson T, Hadfield M (1984) Observations of wind flow and tracer-gas dispersion over sand dunes. N Z J Sci 27:237–242
Wilson J, Yee E (2007) A critical examination of the random displacement model of turbulent dispersion. Boundary-Layer Meteorol 125:399–416
Wilson J, Yee E, Ek N, d’Amours R (2009) Lagrangian simulation of wind transport in the urban environment. Q J R Meteorol Soc 135:1586–1602
Acknowledgments
The author is grateful to Dr. T. W. Horst for his insightful and helpful suggestions in relation to this work, which has been supported by the Natural Sciences and Engineering Research Council of Canada.
Author information
Authors and Affiliations
Corresponding author
Appendix: Horst and Weil Analytic Footprint
Appendix: Horst and Weil Analytic Footprint
Horst and Weil (1994, Eq. A3) and Horst (1999, Eq. 7) give an approximate analytical model for the crosswind-integrated flux footprint. In their own terminology that model is
where \(z_m\) is, of course, the flux measurement height, \(r\) is a (flexible) shape factor for the concentration profile, \(\overline{z}=\overline{z}(x)\) is the height of the centre of mass of the plume off a surface line source, \(c\) is a constrained constant (\(c \overline{z}\) being the height at which the mean wind speed equals the advection speed of the plume), and
Replacing \(z_m\) with \(z_m/z_0\) and \(\overline{z}\) with \(\overline{z}/z_0\) in the expression for \(\overline{f}^y\) automatically makes the latter dimensionless with \(z_0\), i.e. yields the normalized footprint “\(\phi \)”.
To evaluate Eq. 34, which (to be clear) is but an approximation to the full analytical footprint model given by Horst and Weil (1992, Eq. 18; 1994, Eq. A1), one must prescribe \(r\), \(c\) and the MO functions appearing in
controlling the growth of \(\overline{z}\) (in which \(p=1.55\)). Following the pattern of Horst (1999, Eq. 8), the shape factor has here been specified as
which follows from setting \(r=2+m-n\) with the power law indices \(m,n\) fixed by Eqs. 7–10 and the reference height specified as \(c \overline{z}(x)\). Equation 38 differs slightly from Horst’s Eq. 8 in that \(\phi _c\) has been substituted for \(\phi _h\) (but the factor \(k_v \overline{u}(c \overline{z})/u_*\) is equivalent to his \(\ln (c \overline{z}/z_0) - \psi _m(c \overline{z}/L)\)); Horst’s Eq. 8 is in turn a generalization of formulae for \(r\) given by Gryning et al. (1983), in that it allows whatever choices one might wish for the Monin–Obukhov functions.
Here, this Horst–Weil footprint (Eq. 34) has been evaluated only for the case of stable stratification, choosing \(\phi _m(z/L) \equiv \phi _c(z/L)=1+5 z/L\), \(\psi _m(z/L)=-5z/L\), and \(c=0.66\). For each \(x/z_0\), Horst and Weil (1994, Eqs. A4–A7) were solved to provide the value of \(\overline{z}/z_0\) needed for substitution into Eqs. 37 and 34.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Wilson, J.D. Computing the Flux Footprint. Boundary-Layer Meteorol 156, 1–14 (2015). https://doi.org/10.1007/s10546-015-0017-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10546-015-0017-9