Abstract
We propose that flow distortion within a non-orthogonal CSAT3 sonic anemometer is primarily due to transducer shadowing, which is caused by wakes in the lee of the acoustic transducers impinging on their measurement paths. The dependence of transducer shadowing on sonic path geometry, wind direction and atmospheric stability is investigated with simulations that use surface-layer data from the Horizontal Array Turbulence Study (HATS) field program and canopy roughness-sublayer data from the CHATS (Canopy HATS) field program. We demonstrate the efficacy of correcting the CSAT3 for transducer shadowing with measurements of its flow distortion in the NCAR wind tunnel, combined with 6 months of data collected in the atmospheric surface layer with adjacent CSAT3 and orthogonal ATI-K sonic anemometers at the NCAR Marshall field site. CSAT3 and ATI-K measurements of the variance of vertical velocity \(\sigma _w^2\) and the vertical flux of sonic temperature agree within 1 % after correction of both sonics for transducer shadowing. Both the simulations of transducer shadowing and the comparison of CSAT3 and ATI-K field data suggest a simple, approximate correction of CSAT3 surface-layer scalar fluxes with an increase on the order of 4–5 %, independent of wind direction and atmospheric stability. We also find that \(\sigma _w/u_*\) (where \(u_*\) is the friction velocity) and \(r_{uw}\) (the correlation coefficient) calculated with corrected CSAT3 data are insensitive to wind direction and agree closely with known values of these dimensionless variables for neutral stratification, which is evidence for the efficacy of the correction of the horizontal wind components for transducer shadowing as well.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Sonic anemometers, or sonics, have become a common sensor for both micrometeorological research and applied meteorology. Sonics directly measure one, two or three components of the wind vector, as well as the speed of sound and thus the acoustic equivalent of virtual temperature (e.g. Kaimal et al. 1990; Kaimal and Gaynor 1991). Three-component sonic anemometers are commonly used to measure fluxes of momentum and virtual temperature and, when combined with fast-response scalar sensors, vertical fluxes of moisture, \(\hbox {CO}_2\) and other atmospheric constituents. Sonics have many advantages over mechanical anemometers including robustness, good spatial and temporal resolution of the energy-containing range of atmospheric turbulence, a linear calibration that depends only on measurements of path length and acoustic transit time, and calibration stability (Kaimal 1979; Wyngaard 1981a).
There are also some challenges for their design and operation. Uncompensated time delays within the acoustic transducers can produce offsets in the measured values of the wind components. However, these offsets only affect measurements of the mean wind components and not the measurement of turbulent fluctuations and fluxes. Averaging of the wind components and the speed of sound over the finite lengths of the acoustic paths can compromise the measurement of small eddies close to the earth’s surface (e.g. Horst and Oncley 2006). Measurement accuracy is inherently limited by the accuracy to which the lengths of the acoustic paths, the direction cosines of the path geometry, and the acoustic transit times are measured (e.g. Kaimal and Haugen 1969). Finally the sonic array, composed of the acoustic transducers and their support structure, can itself modify the flow that is being measured.
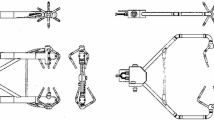
Flow distortion within the sonic array has recently been highlighted by members of the carbon flux community, who have compared sonics with an orthogonal acoustic-path geometry to those with non-orthogonal path geometries (Fig. 1) and find that, in some cases, non-orthogonal sonics underestimate vertical velocity and scalar fluxes compared to orthogonal sonics with a dedicated vertical path (e.g. Kochendorfer et al. 2012; Frank et al. 2013). This attenuation has been attributed to flow distortion within the non-orthogonal sonic-transducer array. Here, we propose a simple correction for flow distortion within a particular commercial, non-orthogonal sonic anemometer, the Campbell Scientific CSAT3, although the flow-distortion mechanism is in principle applicable to all sonic anemometers. The essence of our proposal is that flow distortion in the CSAT3 is dominated by transducer wakes that impinge on their acoustic path and cause a deficit in the path-averaged wind. This is called ‘transducer shadowing’ and is principally a function of the inclination of the wind vector to the sonic path and the ratio between the path length and the transducer diameter (Kaimal 1979). This paper differs from recent approaches in that we invoke a specific physical mechanism for flow distortion, rather than employing an experimental design, either in the atmosphere or in a wind tunnel, with the goal of mapping flow-distortion errors as a function of horizontal wind direction, wind elevation angle, and perhaps also wind speed.
Our paper begins in the next section with evidence of flow distortion of the vertical wind component, obtained by comparing atmospheric measurements by adjacent CSAT3 and orthogonal Applied Technologies ATI-K sonic anemometers. In the subsequent section, we introduce our proposed correction of sonic flow distortion with a short history of sonic anemometer development, followed by CSAT3 wind-tunnel data that support the Kaimal (1979) transducer-shadowing model. Next, in Sect. 4, we investigate the dependence of transducer shadowing on sonic geometry, wind direction, and atmospheric stability by simulating the consequences of sonic flow distortion for wind speed and turbulence variances and covariances, using time series of turbulent wind components measured in the atmospheric surface layer. Then, in Sect. 5, we demonstrate the efficacy of our flow-distortion correction for both vertical and horizontal wind components by applying it to correct the CSAT3 data introduced in Sect. 2. Finally, in Sect. 6 we explore whether transducer shadowing is independent of wind speed, we show that transducer shadowing is also a major component of flow distortion in the non-orthogonal Metek uSonic-3, and we extend our transducer-shadowing simulations to the roughness sublayer within and above an orchard canopy.
2 Observations of Flow Distortion in CSAT3 Sonic Anemometers
In order to investigate flow distortion in the CSAT3 sonic anemometer, we deployed a transverse array of five sonic anemometers at the NCAR Marshall test site from January through August, 2012. The Marshall test site has a uniform fetch of low, arid plants extending 770 m to the south of the array. The sonics were mounted on booms pointing to the south at a height of 3 m and with a lateral spacing of 0.5 m. From west to east, or from left to right in Fig. 1, the sonics will be referred to as \(csatx, atikw, csatva, atike\), and \(csatw\) (additional sonics were mounted to the east and west of these five, whose data are not used herein). Sonics \(csatx\) and \(csatw\) were CSAT3 ‘test’ sonics using Campbell’s Version 3 firmware to avoid the temperature errors found in their Version 4 firmware during high winds (Burns et al. 2012). Sonics \(atikw\) and \(atike\) were orthogonal ATI-K sonics intended as ‘references’ to quantify flow-distortion errors in the CSAT3 sonics, in particular for turbulence statistics that depend on the vertical wind component \(w\). The CSAT3 sonics were factory-calibrated prior to deployment and the ATI-K sonics were user-calibrated as specified by the manufacturer.
Sonic \(csatva\) was a unique CSAT3 sonic with its \(a\)-path vertical and upwind of the other two paths for southerly winds. This sonic was built by Campbell Scientific and provided to NCAR solely to test whether the vertical velocity differences observed between measurements by CSAT3 and vertical-path sonics are caused by differences in their path geometries or by differences in the hardware and firmware used by each manufacturer to measure the transit times of acoustic pulses across the individual paths. This test sonic was not available until February 27 and, by comparing its sonic temperature variance to that of the other sonics, we eventually realized that \(csatva\) was using Version 4 firmware and was averaging the speed-of-sound measured by all three paths, making it dubious to compare its measurement of the kinematic virtual heat flux to that measured by the vertical paths of the ATI-K sonics. However, it was not until July 12 that the original \(csatva\) firmware was replaced by Version 3 firmware and sonic temperature measurement only by the vertical path. Thus most of our sonic comparison analyses use data from February 27 until September 3, while comparisons involving sonic temperature from \(csatva\) only use data beginning on July 12, e.g. Fig. 9.
In addition to flow distortion by the sonics themselves, we must also be concerned with flow distortion by the infrastructure supporting the sensors. The sonic booms were mounted on a horizontal triangular tower section (Fig. 1), which causes flow distortion equivalent to a solid cylinder with an effective radius \(R_{eff} =\) 62 mm (Wucknitz 1980), and the sonic measurement volume was at a distance \(r =\) 1.87 m south of the supporting tower section. For \(r/R_{eff} = 30\), Wyngaard (1981b) finds that the flow distortion error in \(\langle u'u' \rangle \) is on the order of 2 % and the errors in \(\langle w'w' \rangle \) and \(\langle u'w' \rangle \) are on the order of 1 %. Here \(u\) is the component of the horizontal wind normal to the array (from the south) and \(w\) is the vertical wind component, \(\langle x \rangle \) denotes an arithmetic mean of \(x\), and \(x' \equiv x - \langle x \rangle \) denotes turbulent fluctuations of \(x\) with respect to its time mean.
In order to compensate for small differences in the mounting of the sonics within the array, the data from each were rotated into a coordinate system with its vertical axis normal to the mean flow field, using the planar fit technique (Wilczak et al. 2001). Figure 2 shows 5-min-average data samples from sonic \(atike\) prior to coordinate rotation, binned in \(10^\circ \) intervals of wind direction and plotted as the mean of the elevation angle of the wind, \(\phi \equiv \tan ^{-1}(w/\sqrt{u^2 + v^2})\), versus wind direction relative to the \(u\)-axis of the sonic. The sonic \(u\)-axis is positive for the wind from south to north, parallel to the booms on which the sonics are mounted, where positive (negative) wind directions are from the east (west). The vertical ‘whiskers’ for each point denote \(\pm \) the normalized median absolute deviation of the data from the median, \(M(x)\equiv \langle |x - \langle x \rangle |\rangle /0.6745\).Footnote 1 The sinusoidal curve on the plot corresponds to the least-squares planar fit to the data, calculated using data only for wind directions in the range of \(\pm 60^\circ \) in order to avoid contamination by inter-sonic flow distortion. (The \(atike\) pitch angle of \(-2.6^\circ \) was the largest value for all of the sonics; most were on the order of \(-1^\circ \).) Departure of the observations from the planar-fit curve suggests that systematic inter-sonic flow distortion is present outside \(\pm 60^\circ \), but was minimal within that range. Finally, the azimuthal orientation of the data from each of the sonics was adjusted so that the measured wind directions agreed with that of sonic \(csatw\) within \(\pm 0.7^\circ \). These adjustments ranged from \(0.2^\circ \) to \(3.6^\circ \), while most were on the order of \(1^\circ \) or less.
In order to verify the homogeneity of the Marshall test site, proper operation of the sonics, and the accuracy of our post-processing techniques and software, we compared identical sonics by calculating linear fits of variables measured by one with respect to the other for 1225 h of data with acceptable wind directions and wind speeds \(>\)1 \(\hbox {m s}^{-1}\). Recall that the two ATI-K sonics were separated by 1 m, while the CSAT3 sonics were separated by 2 m. The intercepts of the linear fits between identical sonics were negligible and the calculated slopes were within \(\pm \)1 % of unity for wind speed, variances of sonic temperature and the three streamwise wind components, momentum flux, and horizontal and vertical fluxes of sonic temperature.
Figure 3 shows evidence of sonic flow distortion plotted as the ratio of turbulence statistics measured by a CSAT3 to those measured by an adjacent ATI-K sonic, assuming that the vertical wind component measured with a dedicated vertical path is correct. The ratios are plotted as a function of wind direction relative to the sonic \(u\)-axis, with the expectation that flow distortion will be evident as a systematic dependence of the ratio on wind direction (Sect. 4), as well as a departure of the ratios from unity. Each data point in the plot corresponds to the data within a \(5^\circ \) wind direction bin. In Fig. 3 we focus on flow distortion of the second-order moments that depend on the vertical wind component and that have been noted recently to differ between orthogonal and non-orthogonal sonics. These are the standard deviation of vertical velocity fluctuations \(\sigma _w\) and the sonic temperature flux or kinematic virtual heat flux \(\langle w't_{c}' \rangle \), where \(t_c\) denotes sonic temperature derived from the speed of sound.
Linear fits of \(csatw\) versus \(atike\) measurements of \(\sigma _w\) and \(\langle w't_{c}' \rangle \) plotted as a function of wind direction. The ATI-K sonic is corrected for transducer shadowing, but \(m\) is plotted using both corrected and uncorrected CSAT3 data. See the text for detailed explanations of the axis label and legend. Feb. 27–Sept. 3, 2012: 1230 hours of data
This plot format will also be used in Sect. 5 to examine the efficacy of flow-distortion corrections. The legend shows the slopes \(m\) and the normalized mean absolute deviation of the residuals from linear fits to all of the data for both variables within the range of \(\pm 60^\circ \), e.g.
As we have seen in Fig. 2, data outside of this wind direction range may be contaminated by flow distortion between the sonics within the horizontal array. However we show the data for a range of \(\pm 90^\circ \) in order to help judge whether data near the limits of the \(\pm 60^\circ \) range may also be contaminated by inter-sonic flow distortion. The geometry of the CSAT3 repeats at \(120^\circ \) intervals (Fig. 1) so that, with the exception of wind directions from the ‘back’ of the sonic (where it is mounted on its boom), this plot should in principle also apply to the other two sectors. The ordinate has two different scales with identical numerical values. One scale is for \(m\), the (dimensionless) slopes of linear fits with Eq. 1 to the data within each wind direction bin, which we will often refer to simply as a ‘ratio’. The second scale has the dimensions of each particular variable and refers to the magnitude of the vertical ‘whiskers’ for each data point, which correspond to the normalized median absolute deviations of the residuals.
We focus here on the uncorrected CSAT3 data, plotted in red, and we return to this figure in Sect. 5 to discuss the data after correction for flow distortion. Both uncorrected ratios in Fig. 3 have an amplitude \(<\)1 and a systematic dependence on wind direction, with the maximum attenuation occurring near zero degrees as will also be seen in the simulations of Sect. 4. The maximum attenuation occurs when the wind direction is aligned with the CSAT3 \(a\) path, as well as the \(u\)-axis of the sonic. The attenuation of the heat flux by 4–9 % is perhaps at the low end of that previously reported, which might be expected because our Marshall observations are in the surface layer while those of the carbon flux community are often in the roughness sublayer above a forest where vertical gusts are expected to be larger (Sect. 6.3).
3 Proposed Model for CSAT3 Flow Distortion
We now propose a correction for flow distortion within the CSAT3 transducer array. Our proposal is best introduced and understood by a brief review of the history of sonic anemometer development, partially extracted from an account of the evolution of sonic anemometry written by the consummate pioneer in the field, Chandran Kaimal (Kaimal 2013).
Although the concept of an acoustic anemometer was known as early as 1944, the first sonic anemometer to be operated successfully in the atmospheric surface layer was developed by Kaimal as a graduate student under the tutelage of Joost Businger at the University of Washington (Kaimal and Businger 1963a). It was a continuous-wave sonic with a single, 1 m vertical path. The single-path design was chosen for simplicity of development and also because it is the vertical component of velocity that effects the exchange of heat and moisture between the atmosphere and the earth’s surface. This new, fast-response anemometer enabled a significant increase in the understanding of atmospheric turbulent transport (e.g. Kaimal and Businger 1963b).
In 1961 Kaimal joined the Boundary Layer Branch of the Air Force Cambridge Research Laboratory (AFCRL) and worked with several commercial companies to develop a succession of three-component sonic anemometers. The goal of this development was to also measure the horizontal components of turbulence and thus the (kinematic) momentum flux \(\langle u'w' \rangle \)as well as budgets of the second moments of turbulence. These early sonics had a single vertical path and two horizontal paths that were displaced from each other by a distance on the order of the path lengths and had an angular separation of \(120^\circ \). In order to avoid flow distortion by one horizontal path on the other, these sonics had a wind-direction acceptance angle of only \(\pm 45^\circ \) and consequently had to be reoriented whenever there was a significant change in the mean wind direction. Three of these sonics were the backbone of the AFCRL 1968 Kansas field program, which made another leap forward in our understanding of surface-layer turbulence by testing the theoretical ideas of Monin, Obukhov, and Kolmogorov (e.g. Businger et al. 1971; Wyngaard and Cote 1971a; Wyngaard et al. 1971b).
Kaimal (1979) subsequently found that when the wind direction is not normal to a horizontal path, the wakes that form downwind of the transducers impinge on their measurement path and attenuate the path-averaged velocity component. He called this “transducer shadowing” and used both wind-tunnel and atmospheric investigations to examine the dependence of transducer shadowing on the sonic path length \(L\), transducer diameter \(d\), and the angle \(\theta \) between each path and the wind vector. Figure 4a shows the attenuation as a function of \(\theta \), with the maximum attenuation occurring when the wind is aligned with the path and increasing attenuation with decreasing values of \(L/d\). In addition, Kaimal found that the maximum attenuation depends linearly on \(d/L\) (Fig. 4b), for which Wyngaard and Zhang (1985) provide a simple physical explanation. The dependence on \(d/L\) imposes a lower limit on the path length for a given transducer size, which in turn limits the spatial resolution of the sonic and therefore how close to the surface the entire energy-containing range of turbulence that effects vertical transport can be measured.
Dependence of transducer shadowing on a \(\theta \), the angle of the wind vector with respect to the measurement path and b \(d/L\), the ratio of transducer diameter to path length. \(U_L\) is the wind component parallel to the path (Wyngaard and Zhang 1985)
Kaimal et al. (1990) demonstrated the efficacy of correcting the wind components measured by each path for transducer shadowing, using a newly-developed orthogonal, three-component sonic anemometer, the Applied Technologies K-probe (Fig. 1). He did this with a field test using two adjacent ATI-K sonics, mounted at a height of 22 m with one sonic inverted and oriented at \(45^\circ \) with respect to the other, so that the wind direction and elevation angles of the wind relative to one sonic were different from the other. Kaimal’s path-shadowing correction for flow distortion was verified because the horizontal and vertical wind components and the two orthogonal components of the momentum flux as measured by the two sonics agreed very closely with one another.
In the meantime, Joost Businger and Steven Oncley at the University of Washington proposed and built a sonic anemometer with a new path geometry (Zhang et al. 1986), which they named the ‘U.W.’ sonic. It was designed to reduce transducer shadowing for the horizontal wind components, as well as increase the operational range of acceptable wind directions, by having its three acoustic paths oriented at a zenith angle of \(30^\circ \) and with the vertical planes containing each of the paths intersecting the horizontal plane at \(120^\circ \) intervals. Campbell Scientific later adopted the U.W. sonic geometry when they developed the CSAT3 sonic anemometer used today by both the NCAR Earth Observing Laboratory (EOL) and over half of the FLUXNET sites (as of 2012, Nakai et al. 2014). Kaijo-Denki, Gill Instruments, Metek, and R. M. Young have also produced commercial sonics based on the U.W. sonic geometry, but with their paths oriented at a zenith angle of \(45^\circ \), e.g. Fig. 12. Another one-third of FLUXNET sites use sonics with this geometry. However, we note that paths oriented at \(45^\circ \) compromise the intent of the U.W. sonic design to minimize transducer-shadowing errors (Fig. 4a), while also increasing the ratio of noise in the vertical wind component to noise in the horizontal wind components by a factor of \(\sqrt{3}\) (Mann and Dellwik 2014).
Historically, it was thought unnecessary to correct the U.W. and CSAT3 sonics for transducer shadowing, based on the expectation of small flow elevation angles in the atmospheric surface layer. Thus when we learned that scalar fluxes measured by CSAT3 sonics in the roughness sublayer above a forest canopy were observed to be systematically less than fluxes measured by ATI sonics with a dedicated vertical path, our immediate thought was that these differences were simply caused by the fact that the CSAT3 was not corrected for transducer shadowing. This, in turn, motivated our 2012 Marshall sonic intercomparison. Our simple proposal, therefore, is that flow distortion within CSAT3 sonics is dominated by transducer shadowing, and that additional flow distortion by the transducer-supporting infrastructure may well be a second-order effect. The CSAT3 has an \(L/d\) value of 18 or \(d/L = 0.056\) and, from Fig. 4b, we find that this implies a maximum attenuation of 16 % when the wind vector is aligned with one of the paths.
Along with deployment of our sonics at the Marshall test site, we also measured CSAT3 flow distortion in the NCAR/EOL low-speed wind tunnel. This is an open-return wind tunnel that has a cylindrical test section 1.5 m long and 1 m in diameter. The sonic was mounted in the centre of the test section with its \(v\) axis vertical, and we rotated it about that axis in \(10^\circ \) increments in order to simulate a range of wind elevation angles equal to \(\pm 65^\circ \). In this orientation, the wind-tunnel flow is confined to the sonic \(u\)-\(w\) plane and the sonic \(v\)-component is always zero, so that there is no variation in the equivalent horizontal wind direction with respect to the sonic. The measurements were made over a range of flow speeds from 2 to 25 \(\hbox {m s}^{-1}\). Figure 5 is a plot of the difference between the wind components measured along each of the three acoustic paths (\(u_a, u_b\) and \(u_c\)) and the component of the tunnel speed parallel to the path, normalized by the tunnel wind speed. This normalized difference is plotted here as a function of \(\theta \), the angle between each of the three paths and the tunnel axis.
EOL wind-tunnel measurements of CSAT3 transducer shadowing: path wind-speed attenuation, normalized by tunnel speed, versus the angle of the path with respect to the tunnel axis. Model algorithm is proposed by Wyngaard and Zhang (1985)
In general, the normalized measurement errors have minimal dependence on both tunnel speed and the particular path. One exception is path \(a\) measurement errors for \(\theta \ge 170^\circ \), which correspond to negative vertical gusts at elevation angles of \(-50^\circ \) to \(-65^\circ \) that are close to alignment with path \(a\). We have compared our measurements to a transducer-shadowing algorithm suggested by Wyngaard and Zhang (1985), e.g. for CSAT3 path \(a\),
where \(\hat{u}_a\) and \(u_a = S \cos \theta _a\) are the measured and true wind components parallel to the path, \(S\) is the tunnel speed measured with a pitot-static tube, and
Thus the model equation for the ordinate of Fig. 5 is
With the exception of large wind elevation angles, this model provides a good fit to our wind-tunnel data, using the maximum attenuation of 16 % found by interpolation of Kaimal’s (1979) data. One exception is path \(a\) aligned within \(170^\circ \)–\(180^\circ \) of the tunnel axis, as already discussed, and the other is paths \(b\) and \(c\) for \(\theta > 125^\circ \), which again correspond to negative vertical gusts close to alignment with path \(a\) (\(\phi = -60^\circ \) to \(-65^\circ \)) and for which we infer flow distortion by the upper transducer-support infrastructure. The small differences between the model and measurements along paths \(b\) and \(c\) near \(\theta = 90^\circ \) might also indicate some additional flow distortion caused by path \(a\), which is upwind of \(b\) and \(c\).
4 Simulation of Sonic Attenuation by Transducer Shadowing
Wyngaard and Zhang (1985) made a linearized, analytical study of the effects of transducer shadowing on velocity variances, or power spectra, as a function of wind direction, two transducer shapes, \(L/d = \{10, 20, 60\}\), and two sonic geometries: an orthogonal geometry and a geometry with a vertical path and two horizontal paths separated by \(120^\circ \) (the geometry of the sonics used in the 1968 Kansas field program). They found that the variance of a horizontal wind component was maximally attenuated for wind parallel to the corresponding path, but that the attenuation decreased as \(\theta \) increased and the variance could even be amplified by cross-talk between the horizontal paths. As would be expected, these errors decreased with increasing values of \(L/d\).
Zhang et al. (1986) extended this study to the U.W. sonic geometry with a zenith angle of \(30^\circ , L/d = 20.6\) and a maximum transducer-shadow attenuation of 15 %, examining the dependence on wind direction and atmospheric stability of the velocity variances in streamwise coordinates, as well as the shear-stress covariance. They found that the attenuation of each of these second moments has a cyclic dependence on wind direction with a period of \(120^\circ \). For the design values of the transducer array geometry, maximum attenuation again occurs for wind directions aligned with a vertical plane containing one of the three sonic paths. The greatest peak-to-peak amplitudes of the attenuation occur for the shear stress or kinematic momentum flux, \(\langle u'w' \rangle \), and the streamwise velocity variance, \(\langle u'u' \rangle \), which increase with increasing instability for \(\langle u'w' \rangle \) but decrease for \(\langle u'u' \rangle \). The dependence of the cross-stream and vertical wind variances, \(\langle v'v' \rangle \) and \(\langle w'w' \rangle \), on both wind direction and stability was found to be minimal.
Here we use a semi-empirical simulation of transducer shadowing to examine how the flow distortion by transducer-shadowing depends on sonic path geometry, wind direction and atmospheric stability. Transducer shadowing is assumed to be insensitive to wind speed, as shown by the wind-tunnel data discussed in the previous section and discussed further in Sect. 6.1. Our technique is semi-empirical in that we utilize 80 cases of stationary data obtained by a CSAT3 sonic during the Horizontal Array Turbulence Study (HATS) field program, with sonic heights ranging from 3.45 to 8.66 m (Horst et al. 2004). The upwind surface at the HATS field site was covered by low weeds and crop stubble with an aerodynamic roughness length of 20 mm and a displacement height of 0.32 m. Favoured wind directions were from the north-west with a uniform fetch on the order of 6 km.
Our simulations assume that the HATS time series data have representative joint probability distributions of turbulent velocity components and temperature in the atmospheric surface layer. The first step is to transform the measured time series in streamwise coordinates \(\{u, v, w\}\) to path wind components \(\{u_a, u_b, u_c\}\). This step is repeated for \(2^\circ \) increments of wind direction over the entire range of \(\pm 180^\circ \) from the sonic \(u\)-axis. For each wind direction increment, we then attenuate each data sample with transducer shadowing, using Eqs. 2–3. In order to compare geometries on an equal basis, we use the same attenuation coefficient of 0.16 for all sonic geometries, even though those coefficients are likely to be different for the various commercial sonics. Then, we transform the attenuated path winds back to orthogonal wind components, \(\{\hat{u}, \hat{v}, \hat{w}\}\), and calculate various turbulence statistics from the attenuated time series, e.g. \(\langle \hat{w}'\hat{w}'\rangle \). Finally we calculate the ratio of the attenuated statistics to those calculated with the original data, \(\langle w'w' \rangle \), which by our initial assumption represent the true wind components.
Figures 6 and 7 show the effects of transducer shadowing as a function of wind direction for a near-neutral, stably stratified HATS case, \(z/L\!=\!0.03\), where \(z\) is the measurement height and \(L\) is the Obukhov length, and for three sonic geometries: non-orthogonal U.W. geometries with zenith angles of \(30^\circ \) and \(45^\circ \) and an orthogonal geometry. Figure 6 shows three statistics that depend on the vertical wind component, \(\sigma _w\), \(\langle u'w' \rangle \) and \(\langle w't_{c}' \rangle \), while Fig. 7 shows wind speed and the standard deviations of the streamwise horizontal wind components, \(\sigma _u\) and \(\sigma _v\). As predicted, a U.W. sonic with \(45^\circ \) paths has significantly more attenuation than a \(30^\circ \) sonic for both horizontal and vertical wind-component statistics. As might be expected, an orthogonal sonic has the largest attenuation and the largest variation with wind direction for the horizontal statistics, and the U.W. geometries have the largest attenuation and dependence on wind direction for the vertical statistics.
Simulated attenuation by transducer shadowing, as for Fig. 6: wind speed, \(\sigma _u\) and \(\sigma _v\)
The periodicity of the attenuation as a function of wind direction corresponds directly to that of each sonic geometry, i.e. \(120^\circ \) and \(90^\circ \). The maximum (minimum) attenuation for U.W. sonics occurs for wind directions close to negative (positive) alignmentFootnote 2 with one of the vertical planes containing the sonic paths, i.e. \(0^\circ \) and \(\pm 120^\circ \) (\(\pm 60^\circ \) and \(180^\circ \)). For an orthogonal sonic, the maximum attenuation occurs for alignment with one of the horizontal paths and the minimum attenuation occurs for wind directions at \(45^\circ \) to both of the paths (with the exception of \(\sigma _v\), which is \(45^\circ \) out-of-phase with wind speed, \(\sigma _u\) and \(\langle u'w' \rangle \)). Wind speed and \(\sigma _v\) measured by non-orthogonal sonics and \(\sigma _w\) and \(\langle w't_{c}' \rangle \) measured by an orthogonal sonic have no significant dependence on wind direction, while the variation of \(\sigma _w\) for a U.W. sonic with \(30^\circ \) paths is only slightly larger. The variation of the shear stress \(\langle u'w' \rangle \) with wind direction has the largest amplitude of all the non-orthogonal sonic statistics, and even exceeds unity when the wind direction is positively aligned with one of the paths, suggesting that it should be a good diagnostic variable for transducer shadowing. This behaviour was also noted by Zhang et al. (1986), who attributed it to cross-talk between the non-orthogonal sonic paths when the orthogonal wind components are calculated from the path wind components.
Next we examine the dependence of transducer shadowing on stability, using all 80 HATS cases and averaging the statistics over all wind directions for each case. For stable stratification, the turbulence statistics are all minimally dependent on \(z/L\). Like Zhang et al. (1986), we find the dependence on \(z/L\) to be strongest for \(\langle u'w' \rangle \). Figure 8 shows that the attenuation of \(\langle u'w' \rangle \) for non-orthogonal sonics decreases with increasing instability (decreasing \(z/L\)), while for an orthogonal sonic it increases with increasing instability, changing by up to 4–5 % for all three geometries over the range \(-1 \!<\! z/L \!<\! 1.5\). For non-orthogonal sonics, the attenuation of \(\sigma _u\) decreases with increasing instability by perhaps 1 % for unstable stratification (not shown), while for an orthogonal sonic, the attenuation of both \(\sigma _w\) and \(\langle w't_{c}' \rangle \) increases by about 1–2 % with increasing instability (not shown). The dependence on stability of most of the other variances and covariances is 0.5 % or less.
With the exception of those variables in Figs. 6 and 7 that are essentially independent of wind direction, i.e. wind speed and \(\sigma _v\) for non-orthogonal geometries and \(\sigma _w\) and \(\langle w't_{c}' \rangle \) for an orthogonal sonic, the variation of their attenuation with wind direction significantly exceeds the variation with stability. For the variances of most of the three wind components, the amplitude of the variation with wind direction is insensitive to stability. However, for wind speed and \(\sigma _v\) measured by an orthogonal sonic and for \(\langle u'w' \rangle \) and \(\langle w't_{c}' \rangle \) measured by the non-orthogonal sonics (not shown), there is a minor decrease in the amplitude of the variance with wind direction for unstable stratification compared to that for the stable, near-neutral case shown in Figs. 6 and 7.
We are quite surprised by the weak dependence of transducer-shadowing attenuation on stability, since transducer shadowing depends on the instantaneous angle of the wind with respect to the paths and the variance of the elevation angle of the wind increases rapidly with increasing instability. For the HATS data, \(\sigma _\phi \) increases from \(2^\circ \) for strong stable stratification, \(z/L \!\approx \! 1.5\), to \(5^\circ \)–\(7^\circ \) for near-neutral stability and \(6^\circ \)–\(8^\circ \) for \(z/L \approx -0.5\), while \(\sigma _\phi \) is even as high as \(8^\circ \)–\(14^\circ \) for a few unstable cases (not shown). Only orthogonal sonic measurements of \(\sigma _w\), \(\langle u'w' \rangle \) and \(\langle w't_{c}' \rangle \) conform to our expectation, albeit quite weakly compared to the change in \(\sigma _\phi \) with increasing instability, while non-orthogonal sonic measurements of \(\langle u'w' \rangle \) and \(\sigma _u\) act contrary to our expectation.
5 Correction of CSAT3 Sonics for Transducer Shadowing
Next, we demonstrate the efficacy of our flow-distortion proposal by correcting the Marshall CSAT3 wind data for transducer shadowingFootnote 3 and comparing turbulence statistics of the corrected CSAT3 data to those measured by adjacent ATI-K sonics, which have also been corrected for transducer shadowing as specified by the manufacturer. The transducer-shadowing correction is essentially the inverse of that applied to the HATS data in Sect. 4. We transform the measured, attenuated velocity components \(\{\hat{u},\hat{v},\hat{w}\}\) to path components, correct them with the inverse of Eq. 2, and then transform the corrected path components back into orthogonal wind components. In this procedure, we use the measured winds to calculate approximate values for \(\theta \), e.g. for path \(a\),
(For the simulations in Sect. 4, we chose to assume that the HATS data represented true winds in order to preclude the need to approximate \(\theta \).) We find that this first-order approximation is sufficient to keep errors in the corrected path winds to \(<\)0.6 % for an orthogonal sonic and no more than about 1.2 % for a \(45^\circ \) non-orthogonal sonic. The errors are as large as 2.5 % for a \(30^\circ \) non-orthogonal sonic, but exceed 1 % only for \(\theta \!<\! 20^\circ \). The latter is equivalent to a wind elevation angle exceeding \(40^\circ \), which occurs for \(<\)0.1 % of the Marshall data, and therefore the CSAT3 data shown here are corrected using the first-order approximation. Path-wind errors for \(30^\circ \) non-orthogonal sonics can be reduced to \(<\)1 % for all values of \(\theta \) by calculating the angle with one iteration of Eqs. 2 and 5. Finally, we note that the CSAT3 coordinate transformations between orthogonal and path coordinates are done using the coordinate transformation matrices specific to the precise geometry of each sonic, which have been provided by Campbell Scientific, Inc.
We begin by examining whether the differences between CSAT3 and ATI-K sonics could be caused by differences in the hardware and firmware used by each manufacturer to measure the transit times of acoustic pulses across the individual paths. Figure 9 compares the measurements of \(\sigma _w\) and \(\langle w't_{c}' \rangle \) by \(csatva\), the CSAT3 with a dedicated vertical path, to an adjacent ATI-K sonic (displaced by 0.5 m) after both are corrected for transducer shadowing. Both of these statistics averaged over \(\pm 60^\circ \) agree within 1 % between the two sonics, and the variation of the \(\sigma _w\) ratio with wind direction is minimal and even slightly better than a comparison between the two ATI-K sonics or the two CSAT3 sonics (not shown), which are separated by 1 and 2 m, respectively. The dependence of the \(\langle w't_{c}' \rangle \) ratio on wind direction is also small for easterly winds. The cause for the larger variance with wind direction for westerly winds is not immediately obvious, but might be related to the preponderance of stable stratification for westerly windsFootnote 4. Figure 9 demonstrates that it is unlikely that the differences between standard CSAT3 and ATI-K sonics are due to differences in hardware and firmware. Our inference, then, is that the observed differences are due to flow distortion and are primarily caused by the lack of correction of the CSAT3 for transducer shadowing.
Linear fits of \(csatva\) versus \(atikw\) measurements of \(\sigma _w\) and \(\langle w't_{c}' \rangle \) as a function of wind direction, both sonics corrected for transducer shadowing. See the description of Fig. 3 in the text for explanations of the axis labels and the legend. July 12–September 3 2012: 287 hours of data
Figure 3 shows the ratios of CSAT3 to ATI-K data for \(\sigma _w\) and \(\langle w't_{c}' \rangle \) after correction for transducer shadowing. Recall that we are assuming that the vertical path of the ATI-K sonic is a correct reference for measurement of the vertical velocity. The correction of the CSAT3 data has been very effective for \(\sigma _w\) and only slightly less effective for \(\langle w't_{c}' \rangle \). The transducer-shadowing correction has increased the two wind-direction-averaged ratios by similar amounts, 3.5 % for \(\sigma _w\) and 4.0 % for \(\langle w't_{c}' \rangle \), and noticeably decreased the dependence on wind direction, particularly for \(\langle w't_{c}' \rangle \). Recall that the HATS simulation results show the CSAT3 attenuation for these two variables to be essentially identical and on the order of 5 % independent of stability and averaged over all wind directions.
Alternatively, we could also test the CSAT3 transducer-shadowing correction without reference to the ATI-K sonic by plotting a dimensionless variable, for example \(\sigma _w/u_*\), where \(u^2_* \!\equiv \! -\langle u'w' \rangle \), with the expectation that it will be independent of wind direction if the correction is effective. However, many dimensionless turbulence variables are a strong function of stability and therefore, recalling the strong dependence of stability on wind direction at the Marshall site, we limit our analysis of dimensionless variables to near-neutral stratification, \(-0.1 \!<\! z/L \!<\! 0.1\). Figure 10 shows \(\sigma _w/u_*\) for the \(csatw\) sonic both with and without correction for transducer shadowing. The correction is very effective in reducing the dependence on wind direction, but the mean value of 1.16 differs by a disappointing 7 % from the accepted value of \(\sigma _w/u_* \!=\! 1.25\) for neutral stratification (Panofsky and Dutton 1984). One minor contribution to the low overall mean value is the lower values of \(\sigma _w/u_*\) for wind directions of \(40^\circ \) and greater. This appears to be caused, perhaps, by inter-sonic flow distortion from another sonic to the east of \(csatw\), but a second contributing factor may be the weak decrease of \(\sigma _w/u_*\) for unstable stratification (not shown) that predominates for easterly wind directions. Unfortunately, we cannot apply this analysis to \(\langle w't_{c}' \rangle \), i.e. by using the correlation coefficient \(r_{wt_c} \equiv \langle w't_{c}' \rangle /\sigma _w \sigma _{t_c}\), because the difference in sign of the heat flux between stable and unstable stratification causes a strong dependence on stability for near-neutral stratification.
Since we already have confidence in the correction of \(\sigma _w\) as shown in Fig. 3, the mean value of \(\sigma _w/u_*\) in Fig. 10 raises a question about the correction of \(\langle u'w' \rangle \), the third second-order turbulence statistic dependent on measurements of vertical velocity. However, our transducer-shadowing simulations in Figs. 6 and 7 show that an orthogonal sonic has large transducer-shadowing errors for wind speed, \(\sigma _u, \sigma _v\) and \(\langle u'w' \rangle \). Further, our wind-tunnel measurements of CSAT3 flow distortion shown in Fig. 5 suggest that the transducer-shadowing model may underestimate the attenuation for wind directions within \(10^\circ \)–\(15^\circ \) of a path axis, perhaps because of additional flow distortion associated with the transducer-support structures. Consequently we have less confidence in the correction of the horizontal paths of the ATI-K sonic for flow distortion than we do for the vertical wind component. Therefore we examine the efficacy of the CSAT3 transducer-shadowing correction of \(\langle u'w' \rangle \) in Fig. 11 with a plot of the \(u\)–\(w\) correlation coefficient \(r_{uw} \equiv \langle u'w' \rangle /\sigma _u \sigma _w\), independent of the ATI-K data. This is a very demanding test of CSAT3 transducer-shadowing because the \(\langle u'w' \rangle \) attenuation of the \(30^\circ \) non-orthogonal sonic depends strongly on wind direction (Fig. 6), while \(\sigma _w\) (Fig. 6) and \(\sigma _u\) (Fig. 7) have only a weak dependence on wind direction. The correction has again been very effective, in this case essentially eliminating any systematic dependence on wind direction, and the value of \(r_{uw}\) is equal to an accepted, near-neutral value of \(-0.35\) (Kaimal and Finnigan 1994).
As for Fig. 10, for \(|r_{uw}|\)
6 Discussion
6.1 Does Transducer Shadowing Depend on Wind Speed?
By comparing wind-speed measurements made by an ATI-K sonic to those made by an adjacent R. M. Young propeller-vane anemometer, Kaimal et al. (1990) determined that the transducer-shadowing corrections to the sonic horizontal wind components were independent of wind speeds up to 9 \(\hbox {m s}^{-1}\). Our wind-tunnel data find CSAT3 transducer shadowing to be insensitive to tunnel speeds from 2 to 25 \(\hbox {m s}^{-1}\), and our assumption that this is also true in the atmosphere is supported by the successful correction of the CSAT3 turbulence statistics, albeit the median wind speed for the Marshall data is 2.5 \(\hbox {m s}^{-1}\) and only 10 h of data (0.9 %) exceed 10 \(\hbox {m s}^{-1}\). We explore further whether transducer shadowing might be Reynolds-number independent (for a given value of \(d/L\)) by looking at data on the drag coefficients of cylinders, which depend strongly on the wake formed on their lee side. The Reynolds number (Re) of the CSAT3 transducers, based on a diameter of 6.4 mm, is 1280 at 3 \(\hbox {m s}^{-1}\). This falls in the range \(10^3 < Re < 10^4\), where the laminar-flow drag coefficient of a cylinder is insensitive to \(Re\) at the 10 % level (Schlichting 1960). If the boundary layer on the cylinder remains laminar, the drag coefficient is Reynolds-number independent for \(10^4 < Re < 10^5\). However, even in a laminar external flow, the boundary layer undergoes transition from laminar to turbulent around \(Re \approx 2\times 10^5\), and the drag coefficient decreases by a factor of about 4. This transition is likely to occur at a lower \(Re\) when the external flow is turbulent, as in the atmosphere. Thus, whether or not transducer shadowing is Reynolds-number independent in the atmosphere may depend on the \(Re\) value at which the boundary-layer transition occurs. The data used herein only address this question indirectly.
6.2 Transducer Shadowing in the Non-orthogonal Metek uSonic-3
In principle, transducer-shadowing corrections should be applied to all sonic path geometries, although they may not be as dominant a flow-distortion mechanism as for the CSAT3 because of differences in the sonic transducer-support structures. We show evidence for this using wind-tunnel measurements by Metek for their uSonic-3 (formerly USA-1) anemometer, which has a unique geometry of three paths oriented at a zenith angle of \(45^\circ \) (Fig. 12). The wind-tunnel measurements are presented as corrections for wind speed \(s\), horizontal wind direction \(\alpha \), and elevation angle of the wind \(\phi \) (Metek 2004),
where again \(\hat{x}\) denotes the uncorrected data measured by the sonic. The correction functions \(n_c, \alpha _c\) and \(\phi _c\) are calculated with finite Fourier series that depend on the measured wind directions and elevation angles,
where \(C_{f,j}\) and \(S_{f,j}\) are coefficients tabulated as a function of \(\hat{\phi }\), given in steps of \(5^\circ \) ranging from \(-50^\circ \) to \(+45^\circ \). (We note that the uSonic-3 corrections are independent of wind speed.)
We have calculated the dependence of these corrections on \(\theta \), the angle between the wind vector and each path, for horizontal wind directions in \(5^\circ \) steps over the range of \(\pm 180^\circ \) and elevation angles \(\phi \) in \(15^\circ \) steps over the range \(\pm 45^\circ \). Figure 13a shows the attenuation for path \(p1\) and for \(v > 0\) in a format similar to Fig. 5. In this case, path \(p1\) is generally upwind of the rest of the sonic (Fig. 12, inset). In contrast, Fig. 13b is for winds with \(v < 0\). In this case, path \(p1\) is downwind of the rest of the sonic and there appears to be additional flow distortion from upwind paths and/or from the central support bar.
We have fitted the uSonic-3 attenuation for all wind directions to our transducer-shadowing algorithm with a coefficient 0.22, an offset of \(-0.022\), and a normalized mean absolute deviation of the residuals from the fit equal to 0.039. The offset is likely caused by vertical asymmetry due to the extension of the support bar below the three measurement paths (Peters 2014, personal communication). One surprise is that for the \(d/L\) value of the uSonic-3, 0.11, Fig. 4b would imply a maximum attenuation of 0.32 rather than 0.22. However, Fig. 4b is for cylindrical transducers coaxial with their support arms and the acoustic path, whereas the uSonic-3 has its transducer support arms at right angles to the acoustic path and transducers with an aspect ratio on the order of 1 (Fig. 12). Based on only this single example, this suggests that the right-angle support geometry might benefit from 2/3 of the transducer shadowing found in the coaxial transducer-support geometries.
6.3 Simulation of Transducer Shadowing Within and Above a Forest Canopy
The turbulence within and above a forest canopy differs significantly from that in the atmospheric surface layer, resulting from both the canopy-induced inflection-point instability in the wind profile and wakes shed from the canopy elements (e.g. Finnigan 2000; Finnigan et al. 2009). In particular, we expect the root-mean-square elevation angles of the wind to be significantly larger, and thus we might also expect transducer shadowing to be greater, although the HATS surface-layer data did not show a strong correlation between \(\sigma _\phi \) and transducer-shadowing attenuation. In order to investigate this issue, we have repeated the simulations of Sect. 4 using data from the CHATS (Canopy HATS) field program, which took place in a walnut orchard with a canopy height of 10 m and a cumulative plant area index of 2.5 (Patton et al. 2011). The CHATS field program measured the turbulent flow field within and above the orchard from a 30-m tower instrumented with CSAT3 sonic anemometers at six levels within the canopy, one level at the canopy top, and six levels above the canopy. We simulated transducer shadowing using data from all 13 levels of the tower for several cases of stationary turbulence with southerly winds and canopy-top stabilitiesFootnote 5 ranging between \(-0.5 < h/L < 0.5\), where \(h\) is the canopy height and \(L\) is measured at \(z=h\). For southerly winds, there was a uniform upwind fetch of roughly 1500 m.
The CHATS-based transducer-shadowing simulations are qualitatively similar to those presented in Figs. 6 and 7, and thus we have not repeated those plot formats for this dataset. We find again that non-orthogonal sonics have the greatest attenuation and the strongest dependence on wind direction for the vertical statistics, \(\sigma _w\), \(\langle u'w' \rangle \) and \(\langle w't_{c}' \rangle \), and an orthogonal sonic has the largest attenuation and dependence on wind direction for the horizontal statistics, wind speed, \(\sigma _u\) and \(\sigma _v\). And again, wind speed measured by non-orthogonal sonics and \(\sigma _w\) and \(\langle w't_{c}' \rangle \) measured by an orthogonal sonic have no significant dependence on wind direction, while for a U.W. sonic with \(30^\circ \) paths, \(\sigma _v, \sigma _w\) and \(\langle w't_{c}' \rangle \) have only a minor dependence on wind direction. And finally, for non-orthogonal sonics, the strongest dependence on wind direction occurs for \(\langle u'w' \rangle \), while for an orthogonal sonic it occurs for the horizontal wind components.
In Fig. 14, we show CHATS profiles of \(\sigma _\phi \) and CSAT3 transducer-shadowing attenuation for four stability cases and for the same vertical velocity statistics shown in Fig. 6. The attenuation profiles are averages over all wind directions relative to the sonic, as was done previously for Fig. 8, but here horizontal whiskers show the total range of variation with wind direction. This variation is again minor for \(\sigma _w\) and for \(\langle w't_{c}' \rangle \) in near-neutral and unstable stratification, but is quite large for \(\langle u'w' \rangle \) and is shown as a dotted line for cases where the whiskers exceed the limits of the abscissa. (The \(\langle u'w' \rangle \) profile data are plotted as individual points rather than lines because even some of the mean values are off-scale.) The attenuation of \(\langle w't_{c}' \rangle \) is almost identical to that of \(\sigma _w\), and both have minimal dependence on height and stability above the canopy top and only a minor dependence on height and stability within the canopy space. In contrast, the attenuation of \(\langle u'w' \rangle \) depends noticeably on height and stability, particularly within the canopy.
Profiles of \(\sigma _\phi \) and simulated CSAT3 transducer-shadowing attenuation within and above an orchard canopy with \(h \,=\, 10\) m and for four values of stability, \(h/L\). The measured fraction is plotted for: o \(\langle u'w' \rangle \), blue line \(\sigma _w\), and red line \(\langle w't_{c}' \rangle \). Values of attenuation are an average over all wind directions and the horizontal whiskers show the range of variation with wind direction
The CHATS wind elevation-angle fluctuations are significantly larger than those found in the HATS surface-layer data. They increase systematically with increasing instability at all heights, and are on the order of \(10^\circ \)–\(30^\circ \) within the relatively open trunk space, reach a maximum of \(20^\circ \)–\(35^\circ \) within the crown layer, and decrease to \(5^\circ \)–\(25^\circ \) at a height of 5–10 m above the canopy top. These results confirm that the canopy-element wakes and the canopy’s inflection-point instability generate significant turbulent fluctuations. However, as was found for the surface-layer data, \(\sigma _w\) and \(\langle w't_{c}' \rangle \) attenuation are surprisingly insensitive to \(\sigma _\phi \), with the exception of a very minor increase where \(\sigma _\phi \) reaches a maximum within the canopy. The increased attenuation within the canopy is more evident for the \(\langle u'w' \rangle \) attenuation profiles, which are less scattered for near-neutral stability but become more erratic and have a stronger dependence on wind direction for \(h/L = \pm 0.53\). [The attenuation of the 4.5 m \(\langle u'w' \rangle \) measurement near the bottom of the crown space appears to be particularly ill-behaved for all cases.] One caveat to the proceeding is that the transducer-shadowing model may underestimate flow-distortion attenuation for \(\sigma _\phi \) exceeding \(20^\circ \), as seen with our CSAT3 wind-tunnel measurements in Fig. 5.
7 Conclusions
We have proposed that flow distortion within the non-orthogonal CSAT3 sonic anemometer is primarily caused by transducer shadowing, and that flow distortion by the transducer-supporting infrastructure may be no more than a second-order effect, particularly for levels of turbulence in the atmospheric surface layer. We investigated the dependence of transducer shadowing on sonic path geometry, wind direction and atmospheric stability using simulations with both atmospheric surface-layer and canopy roughness-sublayer turbulence data. We find that transducer-shadowing attenuation is greatest for wind speed and the horizontal components of turbulence in orthogonal sonics, whereas the attenuation is greatest for the vertical components of turbulence in non-orthogonal sonics. As expected, we find that transducer-shadowing attenuation is greater in non-orthogonal sonics with paths oriented at zenith angles of \(45^\circ \) than those with paths oriented at \(30^\circ \) as in the U.W. and CSAT3 sonics.
Further, we find that the dependence of the simulated transducer-shadowing attenuation on wind direction is, in general, significantly greater than its dependence on atmospheric stability. The momentum flux attenuation has the greatest dependence on wind direction and even overestimates \(\langle u'w' \rangle \) for the non-orthogonal sonics at wind directions in positive alignment with the azimuths of the measurement paths. The attenuation of \(\sigma _w\) and \(\langle w't_{c}' \rangle \) for an orthogonal sonic and wind speed and \(\sigma _v\) for the non-orthogonal sonics are essentially independent of wind direction. For the CSAT3 path geometry, the variances of the three streamwise wind components and \(\langle w't_{c}' \rangle \) only have a weak dependence on wind direction and stability. However we are surprised that, with the possible exception of \(\langle u'w' \rangle \), transducer shadowing appears to be insensitive to the variance of the vertical attack angle, both in the surface layer and in the roughness sublayer within and above a forest canopy.
We support our proposed correction of flow distortion in the CSAT3 sonic with wind-tunnel measurements of its transducer shadowing and with 6 months of data from adjacent CSAT3 and orthogonal ATI-K sonics at our Marshall field site. By comparing data from a unique CSAT3 with a vertical path to that from an adjacent ATI-K sonic, we establish that the differences between vertical velocities measured by these two sonics are unlikely to be caused by differences in the firmware and hardware used by the two manufacturers to measure the acoustic pulse transit time. Further, measurements of vertical velocity variance and the vertical flux of sonic temperature made by standard CSAT3 sonics, corrected for transducer shadowing, agree within \(\pm \)1 % of measurements by adjacent ATI-K sonic anemometers. In addition, we find that CSAT3 values of \(\sigma _w/u_*\) and \(r_{uw}\), again corrected for transducer shadowing, are insensitive to wind direction and are close to known values of these variables for neutral stratification, which gives confidence in the CSAT3 measurements of the momentum flux independent of the ATI-K sonic. Finally, we demonstrate that transducer shadowing is also quite evident in measurements of flow distortion within the Metek uSonic-3.
The measurement of scalar fluxes is an important application of sonic anemometry, and uncertainty about their measurement with non-orthogonal sonics was a prime motivation for this research. Our simulations of transducer shadowing with the CSAT3 path geometry using the HATS dataset find that the attenuation of \(\langle w't_{c}' \rangle \) averaged over all wind directions equals 5 % independent of stability, and our Marshall sonic intercomparison data suggest an attenuation of 3–4 % averaged over 6 months of data. The variation of simulated \(\langle w't_{c}' \rangle \) attenuation with wind direction decreases from \(\pm \)2 % for stable and near-neutral stratification to \(\pm \)1 % for \(z/L < -0.2\). Thus for practical purposes, \(\langle w't_{c}' \rangle \) and other surface-layer scalar fluxes measured by the CSAT3 might reasonably be corrected by an overall increase of 4–5 %. This approximate correction could be applied to fluxes for which the investigator is unable to apply sample-by-sample transducer-shadowing corrections as done here. However, this simple correction does not apply to non-orthogonal sonics with a \(45^\circ \) path geometry, for which the \(\langle w't_{c}' \rangle \) attenuation in stable conditions varies by \(\pm \)8 % for a wind direction change of \(60^\circ \), and also may not apply to flux measurements in the roughness sublayer of a forest canopy.
The principal shortcoming of our research is the dependence of the results on a comparison between sonics and on the correction of dimensionless turbulence statistics, as well as the limited wind-direction range of our wind-tunnel and field data. Thus the supporting evidence for our proposed correction is somewhat indirect and incomplete. We have assumed that vertical velocity measurements made with a dedicated vertical path, such as with the ATI-K sonic, are a valid reference standard for the CSAT3 measurements. In addition, we rely on plots of dimensionless variables measured by the CSAT3 to verify the efficacy of the transducer-shadowing correction for the momentum flux, and there will likely be some cancellation of flow distortion in the calculation of those dimensionless ratios. Finally, our wind-tunnel measurements apply directly only for winds confined to the vertical plane containing path \(a\) of the CSAT3 sonic (i.e. \(v=0\) in sonic coordinates), and the analysis of our Marshall data is confined to only one of the three \(120^\circ \) sectors of the sonic, with the assumption that the results will also apply for the other two, geometrically identical sectors. The ideal evidence for our proposal would be a comparison of sonic anemometer measurements to a reference that is free from flow distortion. One promising technique is that employed by Dellwik et al. (2015), who made simultaneous velocity measurements with a CSAT3 and with a three-component Doppler lidar system focused at a point 0.8 m ‘in front of’ the sonic.
Notes
The factor 0.6745 normalizes the mean absolute deviation so that \(M\) equals the standard deviation of the data if its frequency distribution is Gaussian.
‘Positive’ or ‘negative’ alignment refers to the sign of the wind measured along the path. Our convention is that positive winds are directed from the lower to the upper transducer of each path.
A minor transducer-shadowing correction is also applicable to sonic temperature because of the path-curvature correction to the measured speed of sound, see the Appendix.
75 % of the winds from \(120^\circ \)–\(180^\circ \) (positive wind directions in sonic coordinates) are unstably stratified, daytime winds and 78 % of the winds from \(180^\circ \)–\(240^\circ \) (negative wind directions in sonic coordinates) are stably stratified, nighttime winds, suggesting a strong influence by anabatic and katabatic flows associated with the mountain foothills to the west.
The distributed canopy elements absorb/scatter/emit incident radiation, which prevent a portion of the incoming solar radiation or emitted longwave radiation from passing through the canopy. Depending on the distribution of those elements, some regions of the canopy absorb (and re-emit) more radiation than others, thereby warming or cooling within-canopy air in a distributed fashion through sensible heat exchange. Therefore, canopy-top stability \(h/L\), which has been used to characterize the flow regime, may not properly characterize the stability throughout the canopy layers (Patton and Finnigan 2012).
The CSAT3 sets an error flag if \(\hat{c}_i\) differ by more than 2.36 \(\hbox {m s}^{-1}\)(Campbell Scientific 2012), but that limit corresponds to a 1.4 % uncertainty in \(t_{c_{i}}'\).
References
Burns SP, Horst TW, Jacobsen L, Blanken PD, Monson RK (2012) Using sonic anemometer temperature to measure sensible heat flux in strong winds. Atmos Meas Tech 5:2095–2111
Businger JA, Wyngaard JC, Izumi Y, Bradley EF (1971) Flux–profile relationships in the atmospheric surface layer. J Atmos Sci 28:181–189
Campbell Scientific (2012) CSAT3 three dimensional sonic anemometer instruction manual. Campbell Scientific Inc., Logan, 63 pp
Dellwik E, Mann J, Sjoholm M, Angelou N, Mikkelsen T (2015) Comparison of three-dimensional wind measurements by wind-LIDARS and a sonic anemometer. In: European Meteorological Society annual meeting, 7–11 Sept 2015, Sofia
Frank JM, Massman W, Ewers BE (2013) Underestimation of sensible heat flux due to vertical velocity measurement errors in non-orthogonal sonic anemometers. Agric For Meteorol 171–172:72–81
Finnigan J (2000) Turbulence in plant canopies. Annu Rev Fluid Mech 32:519–571
Finnigan J, Shaw RH, Patton EG (2009) Turbulent structure above a vegetation canopy. J Fluid Mech 637:387–424
Horst TW, Kleissl J, Lenschow DH, Meneveau C, Moeng C-H, Parlange MB, Sullivan PP, Weil JC (2004) HATS: field observations to obtain spatially filtered turbulence fields from crosswind arrays of sonic anemometers in the atmospheric surface layer. J Atmos Sci 61:1566–1581
Horst TW, Oncley SP (2006) Corrections to inertial-range power spectra measured by CSAT3 and solent sonic anemometers, 1. Path-average errors. Boundary-Layer Meteorol 119:375–395
Kaimal JC (1979) Sonic anemometer measurement of atmospheric turbulence. In: Proceedings of the dynamic flow conference, Skovlunde. DISA Electronic A/S, pp 551–565
Kaimal JC (2013) Advances in meteorology and the evolution of sonic anemometry. Applied Technologies, Inc., 7 pp. http://www.apptech.com
Kaimal JC, Businger JA (1963a) A continuous wave sonic anemometer–thermometer. J Appl Meteorol 2:156–164
Kaimal JC, Businger JA (1963b) Preliminary results obtained with a sonic anemometer–thermometer. J Appl Meteorol 2:180–186
Kaimal JC, Haugen DA (1969) Some errors in the measurement of Reynolds stress. J Appl Meteorol 8:460–462
Kaimal JC, Finnigan J (1994) Atmospheric boundary layer flows. Oxford University Press, New York, 289 pp
Kaimal JC, Gaynor E, Zimmerman HA, Zimmerman GA (1990) Minimizing flow distortion errors in a sonic anemometer. Boundary-Layer Meteorol 53:103–115
Kaimal JC, Gaynor E (1991) Another look at sonic thermometry. Boundary-Layer Meteorol 56:401–410
Kochendorfer J, Meyers TP, Heuer MW (2012) How well can we measure the vertical wind speed? Implications for fluxes of energy and mass balance. Boundary-Layer Meteorol 145:383–398
Mann J, Dellwik E (2014) Sonic anemometer noise. Denmark Technical University, Roskilde, 1 pp
Metek GmbH (2004) Flow distortion corrections for 3-D flows as measured by METEK’s ultrasonic anemometer USA-1. METEK GmbH, Elmshorn, 11 pp
Nakai T, Hiroke I, Harazono Y, Masahito U (2014) An intercomparison between Gill and Campbell sonic anemometers. Agric For Meteorol 195–196:123–131
Panofsky HA, Dutton JA (1984) Atmospheric turbulence. Wiley Interscience, New York, 397 pp
Patton EG, Horst TW, Sullivan PP, Lenschow DH, Oncley SP, Brown WOJ, Burns SP, Guenther AB, Held A, Karl T, Mayor SD, Rizzo LV, Spuler SM, Sun J, Turnipseed AA, Allwine EJ, Edburg SL, Lamb BK, Avissar R, Calhoun RJ, Kleissl J, Massman WJ, Paw UKT, Weil JC (2011) The canopy horizontal array turbulence study. Bull Am Meteorol Soc 92:593–611
Patton EG, Finnigan J (2012) Canopy turbulence, Chap. 24. In: Fernando HJS (ed) Handbook of environmental fluid dynamics, vol 1. CRC Press, Boca Raton, pp 311–328
Schlichting H (1960) Boundary-layer theory. McGraw-Hill, New York, 647 pp
Schotanus P, Nieuwstadt FTM, De Bruin HAR (1983) Temperature measurement with a sonic anemometer and its application to heat and moisture fluxes. Boundary-Layer Meteorol 26:81–93
Wilczak JM, Oncley SP, Stage SA (2001) Sonic anemometer tilt correction algorithms. Boundary-Layer Meteorol 99:127–150
Wucknitz J (1980) Flow distortion by supporting structures. In: Dobson F, Hasse L, Davis R (eds) Air–sea interaction instruments and methods. Plenum Press, New York, pp 605–626
Wyngaard JC (1981a) Cup, propellor, vane, and sonic anemometers in turbulence research. Annu Rev Fluid Mech 13:399–423
Wyngaard JC (1981b) The effects of probe-induced flow distortion on atmospheric turbulence measurements. J Appl Meteorol 20:784–794
Wyngaard JC, Cote OR (1971a) The budgets of turbulent kinetic energy and temperature variance in the atmospheric surface layer. J Atmos Sci 28:190–201
Wyngaard JC, Cote OR, Izumi Y (1971b) Local free convection, similarity, and the budgets of shear stress and heat flux. J Atmos Sci 28:1171–1182
Wyngaard JC, Zhang SF (1985) Transducer shadow effects on turbulence spectra measured by sonic anemometers. J Atmos Ocean Technol 2:548–558
Zhang SF, Wyngaard JC, Businger J, Oncley SP (1986) Response characteristics of the U.W. sonic anemometer. J Atmos Ocean Technol 3:316–323
Acknowledgments
The authors are grateful to the NCAR Integrated Surface Flux System staff for their skillful assistance in collecting the wind-tunnel and field measurements presented here, as well as to Campbell Scientific Inc. for providing the vertical-path CSAT3 and for calibrating the CSAT3 sonics prior to our Marshall field measurements. We also appreciate helpful discussions of this research with Chandran Kaimal, our NCAR colleagues Ned Patton, Peter Sullivan, Steve Oncley, Don Lenschow and Steve Cohn, Ebba Dellwik and Jakob Mann at the Denmark Technical University, and Gerhard Peters at Metek. The National Center for Atmospheric Research is funded by the U.S. National Science Foundation.
Author information
Authors and Affiliations
Corresponding author
Appendix: Flow Distortion Error for Sonic Temperature
Appendix: Flow Distortion Error for Sonic Temperature
In addition to measuring wind components, sonic anemometers commonly also measure the speed of sound, from which an acoustic equivalent of virtual temperature can be calculated (e.g. Kaimal and Gaynor 1991). The speed-of-sound measurement has an error caused by the wind normal to the path advecting the sound pulse out of the path. This error, or the associated correction, has various names and the most descriptive is perhaps ‘path curvature’ error or correction. For example, for the CSAT3 path \(a\),
where \(c\) is the speed of sound, \(\hat{c}\) is its measured value, and \(u_{a\bot }\) is the wind component normal to path \(a\). The CSAT3 and ATI-K sonics correct the measured speed of sound in their firmware using Eq. 10 with \(u_{a\bot } \approx \hat{u}_{a\bot }\).
Obviously, transducer shadowing will alter the measured value of \(u_{a\bot }\). However, the path curvature correction is a small percentage of the speed of sound and the transducer-shadowing error is a small percentage of \(u_a\), so we suspect that the error in the sonic temperature may be negligible. The temperature errors are of particular interest for measurements of \(\langle t_{c}'t_{c}' \rangle \), \(\langle w't_{c}' \rangle \) and \(\langle u't_{c}' \rangle \). Since it is possible for the wind direction to be normal to any one of the paths, upper limits for the path curvature errors can be approximated as,
where \(T_c\) and \(U\) are the mean values of sonic temperature and horizontal wind speed (Schotanus et al. 1983; Kaimal and Gaynor 1991). We have calculated these limits for the HATS data and find that, for unstable stratification, they are on the order of 1–5 % for \(\langle t_{c}'t_{c}' \rangle \) and \(\langle w't_{c}' \rangle \), but as large as 5–20 % for \(\langle u't_{c}' \rangle \). For stable stratification, they are generally not proportional errors, but range up to 0.005 \(\hbox {K}^2\) for \(\langle t_{c}'t_{c}' \rangle \), \(-0.005\hbox { m s}^{-1}\) K for \(\langle w't_{c}' \rangle \), and 0.04 m \(\hbox {s}^{-1}\) K for \(\langle u't_{c}' \rangle \). The additional errors due to transducer shadowing are greatest for the orthogonal sonic, but are generally \(<\)1 % for \(\langle t_{c}'t_{c}' \rangle \) and \(\langle w't_{c}' \rangle \) and on the order of 0.01 m \(\hbox {s}^{-1}\) K for \(\langle u't_{c}' \rangle \).
The procedure to correct the sonic temperature for transducer shadowing is to simply evaluate Eq. 10 with the corrected path-normal wind component \({u}_\bot \). This would be trivial in the sonic firmware at the time of the measurement, but is complicated for post-processing of the CSAT3 data because the CSAT3 sonic produces a value of the speed of sound equal to the average of \(c_i\) measured on all three of the paths. Therefore the value of \(\hat{c}_i\) for each path is unknownFootnote 6 and for that reason, as well as the small value of the temperature path-shadowing error for \(\langle t_{c}'t_{c}' \rangle \) and\(\langle w't_{c}' \rangle \), we have made this correction for the vertical-path sonics, but not for the CSAT3 sonics.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Horst, T.W., Semmer, S.R. & Maclean, G. Correction of a Non-orthogonal, Three-Component Sonic Anemometer for Flow Distortion by Transducer Shadowing. Boundary-Layer Meteorol 155, 371–395 (2015). https://doi.org/10.1007/s10546-015-0010-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10546-015-0010-3