Well-posedness and finite element approximation of mixed dimensional partial differential equations

Abstract

In this article, a mixed dimensional elliptic partial differential equation is considered, posed in a bulk domain with a large number of embedded interfaces. In particular, well-posedness of the problem and regularity of the solution are studied. A fitted finite element approximation is also proposed and an a priori error bound is proved. For the solution of the arising linear system, an iterative method based on subspace decomposition is proposed and analyzed. Finally, numerical experiments are presented and rapid convergence using the proposed preconditioner is achieved, confirming the theoretical findings.

1 Introduction

Numerical simulation of diffusion processes in heterogeneous materials is computationally challenging since the data variation needs to be resolved. Thin structures like cracks, fractures, and reinforcements are particularly difficult to handle. It is often advantageous to instead model thin structures as lower dimensional interfaces, embedded in a bulk domain. Mathematically, this results in a mixed dimensional partial differential equation (PDE), where the solution has bulk and interface components that are coupled weakly. The aim of the paper is to study well-posedness and regularity of mixed dimensional PDEs, construct and analyze a finite element method for solving the problem, and to develop and implement a preconditioner for efficient numerical solution of the resulting linear system.

Numerical solution to PDEs posed on surfaces is a well established field. An early contribution to finite element approximation of the Laplace–Beltrami equation on surfaces is due to Dziuk in [8], where a finite element approximation is constructed on a polyhedral approximation of the surface. Other approaches include trace based methods as in [5, 6, 18], where functions in the surface are represented by traces of functions in the ambient space of higher dimension. The review articles [2, 9] survey several methods for solving PDEs on surfaces. Finite element methods for coupled bulk and interface problems are also well studied, see e.g., [10, 15].

Flow in porous media is probably the most prominent application for mixed dimensional PDEs, see [1, 3, 7, 12, 15] and references therein. These methods are fitted, meaning that the full geometry is resolved by the mesh. The bulk is three dimensional and the interfaces are two dimensional surfaces representing fractures. There is also related work treating three dimensional bulk domains with one dimensional embedded structures. Such models include blood vessels embedded in tissue, see [11].

In this paper, we consider an elliptic mixed dimensional model problem with a large number of interfaces. The interface model is inspired by the works [3, 17], where a general framework for multidimensional representations of fractured domains is developed, and the work [15], where Robin-type couplings between the bulk and interface are studied. In the bulk and interfaces, we consider Poisson’s equation in d and $d-1$ dimensions, respectively. In both cases, we use its primal form. We show that the model is well-posed and pay particular attention to problems with a large number of embedded interfaces and how that affects the coercivity bound of the variational formulation of the problem. We further formulate a fitted finite element method and prove a priori error bounds. Additionally, we propose a domain decomposition method based on subspace correction, allowing for efficient numerical solution of problems with complex coupled interface structures. In this part, we take inspiration from recently developed subspace decomposition algorithms for spatial network models, see [13, 14]. We formulate the Schur complement on the union of interfaces and introduce coarse subspaces, using coarse finite element spaces in the bulk interpolated onto the interfaces. Finally, we present numerical examples in two spatial dimensions together with regularity analysis.

Outline: In Sect. 2, we present the problem formulation and in Sect. 3, we formulate a fitted finite element method and derive an a priori error bound. Section 4 is devoted to an iterative method for efficient solution of the resulting linear system. Finally, in Sect. 5, we present numerical results.

2 Problem formulation

We consider Poisson’s equation in the bulk as well as in the interfaces and couple the solutions in bulk and interfaces by Robin conditions. We are interested in the case when there is a large number of interfaces in the domain. Next follows a description of the geometrical setting to accommodate for this partitioning. Then, we present the model problem in weak form and establish its well-posedness.

2.1 Mixed dimensional geometry

We consider an open and connected domain $\Omega$ of $\mathbb {R}^d$ ($d=2$ or 3) that is partitioned into $d+1$ (not necessarily connected) subdomains of different dimensionalities:

$$\begin{aligned} \Omega = \Omega ^0 \cup \cdots \cup \Omega ^d, \end{aligned}$$

(1)

where each $\Omega ^c$ ($0 \le c \le d$ is the codimension) in turn is composed into a finite number of disjoint and connected subdomain segments defined by a set $L_c$,

$$\begin{aligned} \Omega ^c = \bigcup _{\ell \in L_c} \Omega ^c_\ell , \end{aligned}$$

(2)

each of which is a planar hypersurface of codimension c.

In the following, we put some requirements on this decomposition of $\Omega$. We define topological subspaces $X^c$ of $\mathbb {R}^d$ for subdomains in codimension c and topological properties such as dense, closed, open, and operators such as closure (${{\,\textrm{cl}\,}}$), boundary ($\partial$) and interior (${{\,\textrm{int}\,}}$) for subdomains of codimension c should be interpreted in the subspace topology of $X^c$. For a set $\omega$, the notation ${\bar{\omega }}$ denotes the closure of $\omega$ in $\mathbb {R}^d$.

For codimension $c = 0$, we let $X^0 = \Omega$, while for $c > 0$, we define the subspaces $X^c = X^{c-1} \setminus \Omega ^{c-1}$. We assume that for all $\ell \in L_c$, the subdomain segment $\Omega ^c_\ell$ is open and that their union $\Omega ^c$ is dense. We add the requirement that either $\Omega ^{c+1}_j \subseteq \partial \Omega ^{c}_i$ or $\Omega ^{c+1}_j \cap \bar{\Omega ^{c}_i} = \emptyset$. This makes it possible to define the adjacency relation ${E}_{c}$ between subdomain segments $i \in L_{c}$ and $j \in L_{c+1}$ by

$$\begin{aligned} \begin{aligned} (i, j) \in E_{c} \qquad&\text {if } \Omega ^{c+1}_{j} \subseteq \partial \Omega ^{c}_{i}. \end{aligned} \end{aligned}$$

(3)

This requirement admits a dense partitioning of a subdomain segment by subdomain segments of one codimension higher. Thus subdomain segment boundary integrals can be expressed as sums of integrals over other subdomain segments.

We focus entirely on the subdomains of codimension 0, 1 and 2. To simplify notation, we introduce $I = L_0$, $J = L_1$, and $K = L_2$. To reduce the complexity of the model, we have chosen to work in a simplified setting: We assume that all subdomains segments $\Omega ^c_\ell$ are planar and polyhedrons, polygonals, lines or points, whichever applies in their respective dimension, and that they have Lipschitz boundary. Lipschitz boundary rules out slit domains and means that, for example, an interface cannot end inside a bulk without connecting to another interface. These assumptions can be relaxed at the cost of a more detailed treatment of the interfaces as is done in [3, 17]. To handle curved interfaces, it is possible to consider the planar setting here as an approximation of the curved case. For sufficiently smooth curved interfaces, lift operators on both bulk and interfaces exist that enable an estimate of the error due to such a variational crime, see [10].

In Fig. 1, we see an example of a domain fulfilling our requirements.

Fig. 1

An example of a domain $\Omega$ fulfilling our requirements

2.2 Model problem

Denote the $L^2$-inner product and norm $(u, v)_\omega = \int _\omega uv\,\textrm{d}x$, $\Vert v\Vert _{L^2(\omega )} = (u, v)_\omega ^{1/2}$, and let $L^2(\omega )$ and $H^1(\omega )$ be the usual Sobolev spaces of $L^2$-integrable functions and weak derivatives. If $\omega$ is a subdomain segment of codimension greater than 0, then we interpret $H^1(\omega )$ as $H^1({\widehat{\omega }})$ after a rigid coordinate transformation of $\omega$ to a subset ${\widehat{\omega }} \subset \mathbb {R}^{d-c}$ where the gradient operator, Poincaré inequalites, Green’s theorem, and trace theorems in this lower dimensional space $\mathbb {R}^{d-c}$ can be applied. For clarity, the symbol $\nabla _\tau$ is used to denote the gradient operator on subdomain segments of codimension 1.

For functions in the bulk of the domain, we define the Hilbert space

$$\begin{aligned} V^0 = H^1(\Omega ^0) = \prod _{i\in I} H^1(\Omega ^0_i). \end{aligned}$$

Occasionally, we refer to components $v^0_i$ of $v^0 \in V^0$ defined as the restriction of $v^0$ to $\Omega ^0_i$. Note that the domain $\Omega ^0$ consists of the disconnected union of $\Omega ^0_i$ for $i \in I$ and no continuity between the subdomain segments is assumed. Further, $V^0_0 = \{ v \in V^0 \,:\, v|_{\partial \Omega } = 0 \}$ is the space of functions satisfying homogeneous Dirichlet boundary conditions.

For the functions in codimension 1, we define $V^1$ as follows. The functions in $V^1$ are strongly enforced to be continuous over common domains of codimension 2. Let $V^1_{\text{ b }} = H^1(\Omega ^1) = \prod _{j\in J} H^1(\Omega ^1_j)$ be a “broken” space and $v^1 = (v^1_j)_{j\in J} \in V^1_{\text{ b }}$ be any function with each $v^1_j$ being the restriction of $v^1$ to $\Omega ^1_j$. Then we define the constrained space

$$\begin{aligned} V^1 = \{ v^1 \in V^1_{\text{ b }} :\, v^1_j|_{\Omega ^2_k} - v^1_{j'}|_{\Omega ^2_k} = 0 \text { for all pairs } (j, k), (j', k) \in {E_1}\}. \end{aligned}$$

(4)

We note that $V^1$ is a Hilbert space, since it is the kernel of the bounded and linear trace operator on the Hilbert space $V^1_{\text{ b }}$. Finally, we define $V^1_0 = \{ v \in V^1 \,:\, v|_{\partial \Omega } = 0 \}$, and $V = V^0 \times V^1$ and $V_0 = V^0_0 \times V^1_0$ with norm

$$\begin{aligned} \Vert v\Vert _V = \left( \Vert v^0\Vert _{H^1(\Omega ^0)}^2 + \Vert v^1\Vert _{H^1(\Omega ^1)}^2\right) ^{1/2}. \end{aligned}$$

In the bulk domains $i \in I$, let $A_i \in L^{\infty }(\Omega ^0_i)$ with bounds $0< \underline{\alpha } \le A_i \le \bar{\alpha } < \infty$. In the interfaces $j \in J$, let $A_j \in L^{\infty }(\Omega ^1_j)$ with bounds $\underline{\alpha } \le A_j \le \bar{\alpha }$, and $B_j \in L^{\infty }(\Omega ^1_j)$ with bounds $0< \underline{\beta } \le B_j \le \bar{\beta } < \infty$. With the definition of the symmetric bilinear form a,

$$\begin{aligned} \begin{aligned} a(v, w) =&\sum _{i \in I} ( A_i \nabla v^0_i, \nabla w^0_i )_{\Omega ^0_i} + \sum _{j \in J} ( A_j \nabla _\tau v^1_j, \nabla _\tau w^1_j )_{\Omega ^1_j} \\&+ \sum _{(i, j) \in E_0} ( B_j (v^0_i - v^1_j), w^0_i - w^1_j )_{\Omega ^1_j}, \\ \end{aligned} \end{aligned}$$

and a right hand side functional $F \in V_0^*$ (in the dual space of $V_0$), the model problem can be stated as to find $u \in V_0$ such that for all $v \in V_0$,

$$\begin{aligned} \begin{aligned} a(u,v) = F(v). \end{aligned} \end{aligned}$$

(5)

The bulk and the interfaces are coupled by a Robin-type boundary condition, continuity of the solution between the interface segments is enforced, and a Kirchoff’s law type equation for the flux between interface segments applies. Non-homogeneous Dirichlet boundary conditions defined on $\partial \Omega$ can be handled by picking any function $g \in V$ satisfying the boundary conditions, setting $F(v) = a(-g, v)$, solving (5), and obtaining the solution as $u + g$.

Remark 1

(Bulk-interface coupling) For the bulk-interface coupling, we use boundary conditions III as presented in [15] in a porous media flow setting. The interface parameters $A_j$ and $B_j$ translate to tangential and normal interface permeabilities $K^1_\tau$ and $K^1_n$, and thickness t of the interface as follows: $A_j = K^1_\tau t$ and $B_j = K^1_n/t$.

If the solution is sufficiently smooth, and if $f_i \in L^2(\Omega ^0_i)$, $f_j \in L^2(\Omega ^1_j)$, and

$$\begin{aligned} F(w) = \sum _{i \in I} ( f_i, w^0_i )_{\Omega ^0_i} + \sum _{j \in J} ( f_j, w^1_j )_{\Omega ^1_j}, \end{aligned}$$

then the weak formulation in (5) corresponds to the strong problem of finding $u \in V_0$ such that

$$\begin{aligned} \begin{aligned} - div A_i \nabla u^0_i&= f_i{} & {} \text { in } \Omega ^0_i, \\ - div_{\tau } A_j \nabla _{\tau } u^1_j - \sum _{i :\, (i,j) \in E_0} B_j(u^0_i - u^1_j)&= f_j{} & {} \text { in } \Omega ^1_j, \end{aligned} \end{aligned}$$

with boundary conditions

$$\begin{aligned} \begin{aligned} u^0_i&= 0{} & {} \text { on } \bar{\Omega }^0_i \cap \partial \Omega ,\\ u^1_j&= 0{} & {} \text { on } \bar{\Omega }^1_j \cap \partial \Omega ,\\ n_{\Omega ^0_i} \cdot A_i \nabla u^0_i + B_j u^0_i&= B_j u^1_{j}{} & {} \text { on } \partial \Omega ^0_i \cap \Omega ^1_j, \\ u^1_j&= u^1_{j'}{} & {} \text { on } \partial \Omega ^1_j \cap \partial \Omega ^1_{j'},\\ \sum _{\{j:\,(j, k) \in E_1\}} n_{\Omega ^1_{j}} \cdot A_{j} \nabla _{\tau } u^1_{j}&= 0{} & {} \text { on } \partial \Omega ^1_{j} \cap \Omega ^2_k. \end{aligned} \end{aligned}$$

Here $n_{\omega }$ is the outward normal defined on the boundary of the subdomains $\omega$.

2.3 Well-posedness

To prove existence and uniqueness of solution for the problem (5), we prove that a is coercive and bounded on $V_0$ and apply the Lax–Milgram theorem. Coercivity cannot be shown directly by a Poincaré or Friedrichs inequality since the subdomain segments are disconnected and not all of them necessarily intersect the domain boundary. We establish coercivity by an iterative procedure, starting to bound norms over subdomain segments far from the domain boundary in norms over subdomain segments, and proceed until we reach subdomain segments for which a Friedrichs inequality can be used.

Lemma 1

The bilinear form a is coercive on $V_0$, i.e., there is a $C > 0$ such that for all $v \in V_0$,

$$\begin{aligned} a(v,v) \ge C ({\underline{\alpha }}^{-1} + {\underline{\beta }}^{-1})^{-1} \Vert v\Vert _V^2, \end{aligned}$$

and C depends only on the geometry of the subdomain segments $\{\Omega ^c_\ell \}_{c, \ell }$.

Proof

In the following, C denotes a constant that is independent of the arbitrary function $v = (v^0, v^1) \in V_0 = V^0_0 \times V^1_0$. The value of the constant is generally not tracked between inequalities. Let $i_0 \in I$ be a subdomain segment that intersects the domain boundary so that there is a Friedrichs inequality

$$\begin{aligned} \Vert v^0_{i_0}\Vert _{L^2(\Omega ^0_{i_0})} \le C |v^0_{i_0}|_{H^1(\Omega ^0_{i_0})}. \end{aligned}$$

(6)

We note that $G = (I, J, E_0)$ defines a bipartite undirected graph, where the subdomain segments of codimensionality 0 and 1 (I and J) constitute the vertices and the edges $E_0$ are the adjacency relations between subdomain segments. It is bipartite because the edges connect vertices in I only with vertices in J and vice versa. Since $\Omega$ is connected, $i_0$ is reachable from all vertices in G. Then it is possible to define a walk through G beginning at an arbitrary $i_N \in I$ and ending at $i_0$. We express the walk as the sequence of vertices it visits by $(i_N, j_{N}, i_{N-1}, j_{N-1},\ldots , j_1, i_0)$ and require that all vertices in G are visited at least once by the walk. We allow the same vertex to be visited multiple times to guarantee the existence of such a sequence.

We make use of the following inequality, proven in e.g., [4, Eq. (5.3.3)], valid for any $v^0_i \in H^1(\Omega ^0_i)$ and j such that $(i, j) \in E_0$,

$$\begin{aligned} \begin{aligned} \Vert v^0_i \Vert _{L^2(\Omega ^0_i)} \le C \left( \left| \int _{\Omega ^1_j} v^0_i\, \textrm{d}s\right| + | v^0_i |_{H^1(\Omega ^0_i)}\right) . \end{aligned} \end{aligned}$$

(7)

Further, we note that by Hölder’s inequality, we have

$$\begin{aligned} \left| \int _{\Omega ^1_j} v^0_i\, \text {d}s\right| \le |\Omega ^1_j|^{1/2} \Vert v^0_i\Vert _{L^2(\Omega ^1_j)}, \end{aligned}$$

(8)

which together with (7) gives

$$\begin{aligned} \begin{aligned} \Vert v^0_i \Vert _{L^2(\Omega ^0_i)} \le C \left( \Vert v^0_i \Vert _{L^2(\Omega ^1_j)} + | v^0_i |_{H^1(\Omega ^0_i)}\right) . \end{aligned} \end{aligned}$$

(9)

The following trace inequality will be used, valid for $v^0_i \in H^1(\Omega ^0_i)$ for which $(i, j) \in E_0$,

$$\begin{aligned} \begin{aligned} \Vert v^0_i \Vert _{L^2(\Omega ^1_j)} \le C \left( \Vert v^0_i \Vert _{L^2(\Omega ^0_i)} + | v^0_i |_{H^1(\Omega ^0_i)}\right) . \end{aligned} \end{aligned}$$

(10)

For $i \in I$, we have

$$\begin{aligned} \Vert v^0_i \Vert ^2_{H^1(\Omega ^0_i)}{} & {} = | v^0_i |^2_{H^1(\Omega ^0_i)} + \Vert v^0_i \Vert ^2_{L^2(\Omega ^0_i)} \nonumber \\{} & {} {\mathop {\le }\limits ^{(9)}} C\left( | v^0_i |^2_{H^1(\Omega ^0_i)} + \Vert v^0_i \Vert ^2_{L^2(\Omega ^1_j)}\right) \nonumber \\{} & {} \le C\left( | v^0_i |^2_{H^1(\Omega ^0_i)} + \Vert v^0_i - v^1_j \Vert ^2_{L^2(\Omega ^1_j)} + \Vert v^1_j \Vert ^2_{L^2(\Omega ^1_j)}\right) . \end{aligned}$$

(11)

We also have

$$\begin{aligned} \Vert v^1_j \Vert ^2_{L^2(\Omega ^1_j)}{} & {} \le 2\Vert v^1_j - v^0_i \Vert ^2_{L^2(\Omega ^1_j)} + 2\Vert v^0_i \Vert ^2_{L^2(\Omega ^1_j)} \nonumber \\{} & {} {\mathop {\le }\limits ^{(10)}} 2\Vert v^1_j - v^0_i \Vert ^2_{L^2(\Omega ^1_j)} + C\Vert v^0_i \Vert ^2_{H^1(\Omega ^0_i)}. \end{aligned}$$

(12)

Since the sequence $(i_N, j_N, \ldots , i_0)$ contains all elements in both I and J, we can rewrite the V-norm of v as follows,

$$\begin{aligned} \Vert v\Vert _V^2{} & {} = \sum _{i \in I} \Vert v^0_i\Vert _{H^1(\Omega ^0_i)}^2 + \sum _{j \in J} \Vert v^1_j\Vert _{H^1(\Omega ^1_j)}^2 \nonumber \\{} & {} \le \Vert v^0_{i_N}\Vert _{H^1(\Omega ^0_{i_N})}^2 + \Vert v^1_{j_N}\Vert _{H^1(\Omega ^1_{j_N})}^2 + \Vert v^0_{i_{N-1}}\Vert _{H^1(\Omega ^0_{i_{N-1}})}^2 + \cdots + \Vert v^0_{i_{0}}\Vert _{H^1(\Omega ^0_{i_{0}})}^2\nonumber \\{} & {} {\mathop {\le }\limits ^{(11)}} C \left( |v^0_{i_N}|_{H^1(\Omega ^0_{i_N})}^2 + \Vert v^0_{i_N} - v^1_{j_N}\Vert _{L^2(\Omega ^1_{j_N})}^2\right) + (C + 1)\Vert v^1_{j_N}\Vert _{H^1(\Omega ^1_{j_N})}^2 {} \nonumber \\{} & {} \qquad + \Vert v^0_{i_{N-1}}\Vert _{H^1(\Omega ^0_{i_{N-1}})}^2 + \cdots + \Vert v^0_{i_{0}}\Vert _{H^1(\Omega ^0_{i_{0}})}^ 2\nonumber \\{} & {} {\mathop {\le }\limits ^{(12)}} C \left( |v^0_{i_N}|_{H^1(\Omega ^0_{i_N})}^2 + \Vert v^0_{i_N} - v^1_{j_N}\Vert _{L^2(\Omega ^1_{j_N})}^2\right) + (C + 1)|v^1_{j_N}|_{H^1(\Omega ^1_{j_{N}})}^2 {}\nonumber \\{} & {} \qquad + 2(C+1)\Vert v^1_{j_N} - v^0_{i_{N-1}}\Vert _{L^2(\Omega ^1_{j_N})}^2 + (C(C + 1) + 1)\Vert v^0_{i_{N-1}}\Vert _{H^1(\Omega ^0_{i_{N-1}})}^2 {} \nonumber \\{} & {} \qquad + \Vert v^1_{j_{N-1}}\Vert _{H^1(\Omega ^1_{j_{N-1}})}^2 + \cdots + \Vert v^0_{i_{0}}\Vert _{H^1(\Omega ^0_{i_{0}})}^2. \end{aligned}$$

(13)

This procedure is then iterated, using (11) and (12). For the last term $\Vert v^0_{i_{0}}\Vert _{H^1(\Omega ^0_{i_{0}})}^2$, we use Friedrichs inequality to bound it by $C |v^0_{i_{0}}|_{H^1(\Omega ^0_{i_0})}$. The walk visits the vertices and edges in the graph at most N times, and since we have iterated the steps N times, we get

$$\begin{aligned} \begin{aligned} \Vert v\Vert _V^2&\le NC^{N}\left( \sum _{i \in I} |v^0_i|_{H^1(\Omega ^0_i)}^2 + \sum _{(i, j) \in E_0} \Vert v^0_i - v^1_j\Vert _{L^2(\Omega ^1_j)}^2 + \sum _{j \in J} |v^1_j|_{H^1(\Omega ^1_j)}^2\right) , \end{aligned} \nonumber \\ \end{aligned}$$

(14)

where we have added the terms for the edges from $E_0$ that were not part of the walk. The constant N is the length of the walk and depends on how the subdomain segments are connected with each other and is thus also a constant depending on the geometry of the problem. In the following, we do not track N and let C absorb it.

Finally, to obtain the coercivity bound, we use that $\underline{\alpha }\le A_i$, ${\underline{\alpha }} \le A_j$ and ${\underline{\beta }} \le B_j$ for all $i \in I$ and $j \in J$, and obtain from (14) and the definition of a that

$$\begin{aligned} \Vert v\Vert _V^2 \le C ({\underline{\alpha }}^{-1} + \underline{\beta }^{-1})a(v, v). \end{aligned}$$

$\square$

Lemma 2

The bilinear form a is bounded on V, i.e., there exists a $C < \infty$ such that for all $v \in V$,

$$\begin{aligned} a(v, w) \le C (\bar{\alpha } + \bar{\beta }) \Vert v \Vert _V \, \Vert w\Vert _V, \end{aligned}$$

and C depends only on the geometry of the subdomain segments $\{\Omega ^c_\ell \}_{c, \ell }$.

Proof

Studying the first two sums of a, we note that

$$\begin{aligned}{} & {} \sum _{i \in I} ( A_i \nabla v^0_i, \nabla w^0_i )_{\Omega ^0_i} + \sum _{j \in J} ( A_j \nabla _\tau v^1_j, \nabla _\tau w^1_j )_{\Omega ^1_j} \nonumber \\{} & {} \qquad {} \le \bar{\alpha } \left( \Vert v^0 \Vert _{H^1(\Omega ^0)} \Vert w^0 \Vert _{H^1(\Omega ^0)} + \Vert v^1\Vert _{H^1(\Omega ^1)} \Vert w^1 \Vert _{H^1(\Omega ^1)} \right) \nonumber \\{} & {} \qquad {} \le \bar{\alpha } \left( \Vert v^0 \Vert _{H^1(\Omega ^0)} + \Vert v^1 \Vert _{H^1(\Omega ^1)} \right) \left( \Vert w^0 \Vert _{H^1(\Omega ^0)} + \Vert w^1 \Vert _{H^1(\Omega ^1)} \right) \nonumber \\{} & {} \qquad {} \le 2 \bar{\alpha } \, \Vert v \Vert _V \, \Vert w\Vert _V. \end{aligned}$$

(15)

The trace inequality from Eq. (10) gives us that for $(i, j) \in E_0$,

$$\begin{aligned} \begin{aligned} \Vert v^0_i - v^1_j\Vert _{L^2(\Omega ^1_j)}&\le \Vert v^0_i\Vert _{L^2(\Omega ^1_j)} + \Vert v^1_j\Vert _{L^2(\Omega ^1_j)} \\&\le \Vert v^1_j\Vert _{L^2(\Omega ^1_j)} + C \Vert v^0_i \Vert _{H^1(\Omega ^0_i)}. \end{aligned} \end{aligned}$$

Using this, we can conclude that the third sum of a satisfies

$$\begin{aligned} \begin{aligned}&\sum _{(i, j) \in E_0} ( B_j (v^0_i - v^1_j), w^0_i - w^1_j )_{\Omega ^1_j} \\&\qquad {} \le \sum _{(i,j) \in E_0} C \bar{\beta } \left( \Vert v^0_i \Vert _{H^1(\Omega ^0_i)} + \Vert v^1_j \Vert _{H^1(\Omega ^1_j)} \right) \left( \Vert w^0_i \Vert _{H^1(\Omega ^0_i)} + \Vert w^1_j \Vert _{H^1(\Omega ^1_j)} \right) \\&\qquad {} \le C \bar{\beta } \, \Vert v \Vert _V \, \Vert w \Vert _V, \end{aligned}\nonumber \\ \end{aligned}$$

(16)

where the constant C also depends on the maximum number of interfaces surrounding the subdomains. $\square$

Theorem 1

Under the above assumptions, Eq. (5) has a unique solution $u\in V_0$.

Proof

Since $V_0$ is a Hilbert space, Lemmas 1 and 2 give coercivity and boundedness of the bilinear form, and the right hand side F is assumed to be a bounded linear functional on $V_0$, the Lax–Milgram theorem guarantees existence of a unique solution $u\in V_0$. $\square$

3 Fitted finite element method

In this section, we introduce a fitted finite element discretization of the mixed dimensional model problem and prove an a priori error bound.

3.1 Discretization

We let $\mathcal {T}^1_{h,j}$ be a quasi-uniform and shape-regular partition of $\bar{\Omega }^1_j$, containing closed simplices of diameter no greater than h, with $\mathcal {T}^1_h = \bigcup _{j \in J} \mathcal {T}^1_{h,j}$. Further, we let $\mathcal {T}^0_{h,i}$ be a corresponding partition of $\bar{\Omega }^0_i$, with $\mathcal {T}^0_h = \bigcup _{i \in I} \mathcal {T}^0_{h,i}$ and such that the simplices of $\mathcal {T}^1_h$ constitute the sides of some of the simplices in $\mathcal {T}^0_h$. That is, if $\mathcal {T}^1_h = \{K^1_{\hat{\jmath }}\}_{\hat{\jmath }}$ and $\mathcal {T}^0_h = \{K^0_{\hat{\imath }}\}_{\hat{\imath }}$, then for each pair $\hat{\imath }, \hat{\jmath }$, either

• $K^0_{\hat{\imath }} \cap K^1_{\hat{\jmath }} = \emptyset$,

• $K^0_{\hat{\imath }} \cap K^1_{\hat{\jmath }} = K^1_{\hat{\jmath }}$ or

• $K^0_{\hat{\imath }} \cap K^1_{\hat{\jmath }} \in \partial K^1_{\hat{\jmath }}$.

Similarly to what we did in Sect. 2.2, for the functions on the interface partition, $\mathcal {T}^1_h$, we define

$$\begin{aligned} \begin{aligned}&V^1_{\textrm{b},h} = \prod _{j \in J} \{ v^1 \in C(\bar{\Omega }^1_j): v^1 \text { piecewise linear functions on }\mathcal {T}^1_{h,j}, \, v^1 = 0 \text { on } \partial \Omega \}, \text { and} \\&V^1_h = \{v^1 \in V^1_{\textrm{b},h}: v^1_j |_{\Omega ^2_k} - v^1_{j'} |_{\Omega ^2_k} = 0 \text { for all pairs } (j,k), (j',k) \in E_1\}. \end{aligned} \end{aligned}$$

For the functions on the bulk partition, $\mathcal {T}^0_h$, we define

$$\begin{aligned} V^0_h = \prod _{i \in I} \{ v^0 \in C(\bar{\Omega }^0_i): v^0 \text { piecewise linear functions on }\mathcal {T}^0_{h,i}, \, v^0 = 0 \text { on } \partial \Omega \}, \end{aligned}$$

and use these definitions to define $V_h = V^0_h \times V^1_h$. Then the finite element problem reads: find $u_h \in V_h$ such that

$$\begin{aligned} a(u_h, v_h) = F(v_h) \qquad \text { for all } v_h \in V_h. \end{aligned}$$

(17)

We note that $V^0_h \subset V^0$ and $V^1_h \subset V^1$ are also Hilbert spaces and the argumentation in Sect. 2.3 holds for the discretized equation as well. Thus, Lax–Milgram guarantees the existence and uniqueness of a solution to (17).

3.2 Interpolation estimates

In this section, we introduce an interpolation operator $\mathcal {I}_h: V_0 \rightarrow V_h$ defined componentwise $\mathcal {I}_h(v^0, v^1) = (\mathcal {I}^0_h v^0, \mathcal {I}^1_h v^1)$, where $\mathcal {I}^0_h$ and $\mathcal {I}^1_h$ are Scott–Zhang [19] interpolation operators onto $V^0_h$ and $V^1_h$, respectively.

For each degree of freedom k (enumerating the Lagrange basis functions $\{\varphi ^0_k\}$ of $V^0_h$), we choose an edge (or face if $d=3$, etc.) ${\tilde{K}}_k$ in the support of $\varphi ^0_k$ such that the mesh vertex associated with k is contained in $\tilde{K}_k$. Let $\psi ^0_k$ be the $L^2(\tilde{K}_k)$-dual basis, i.e.,

$$\begin{aligned} \int _{\tilde{K}_k} \varphi ^0_{k'} \psi ^0_{k} \textrm{d}x = {\left\{ \begin{array}{ll}1 &{} \text { if } k=k', \\ 0 &{} \text { otherwise,}\end{array}\right. } \end{aligned}$$

and define

$$\begin{aligned} \mathcal {I}^0_h v^0 = \sum _{k} \left( \int _{\tilde{K}_k} v^0 \psi ^0_{k} \textrm{d}x\right) \varphi ^0_k. \end{aligned}$$

The interface interpolation operator $\mathcal {I}^1_h$ is defined analogously.

In the V-norm, we obtain the interpolation error estimate, for $v \in V_0$,

$$\begin{aligned} \left| \left| v - \mathcal {I}_h v\right| \right| _V \le Ch\left( \left| \left| D^{2} v^0\right| \right| _{L^2(\Omega ^0)} + \left| \left| D^{2} v^1\right| \right| _{L^2(\Omega ^1)} \right) . \end{aligned}$$

(18)

For proofs and further details on this interpolation, we refer to [4, 19].

3.3 A priori error estimate

In order to derive an a priori estimate, we use coercivity and boundedness (Lemmas 1 and 2) together with Galerkin orthogonality. For $v \in V_h$, it holds that

$$\begin{aligned} \begin{aligned} \frac{1}{C(\underline{\alpha }^{-1} + \underline{\beta }^{-1})} \left| \left| u - u_h\right| \right| _V^2&\le a(u - u_h, u - u_h) = a(u - u_h, u - v) \\&\le \tilde{C} \left( \bar{\alpha } + \bar{\beta } \right) \, \Vert u - u_h \Vert _V \, \Vert u - v \Vert _V. \end{aligned} \end{aligned}$$

Thus we obtain

$$\begin{aligned} \left| \left| u - u_h\right| \right| _V \le C \left( \underline{\alpha }^{-1} + \underline{\beta }^{-1} \right) \left( \bar{\alpha } + \bar{\beta } \right) \left| \left| u - v\right| \right| _{V}. \end{aligned}$$

(19)

By choosing $v = \mathcal {I}_h u$, and combining (18) and (19), we can thus state the following theorem.

Theorem 2

(A priori error estimate.) Let $u_h \in V_h$ and $u \in V$ be the solutions of (17) and (5). Assume that $u^0_i \in H^2(\Omega ^0_i)$ and $u^1_j \in H^2(\Omega ^1_j)$. Then

$$\begin{aligned} \begin{aligned} \left| \left| u - u_h\right| \right| _V&\le C h \left( \underline{\alpha }^{-1} + \underline{\beta }^{-1} \right) \left( \bar{\alpha } + \bar{\beta } \right) \left( \left| \left| D^{2} u^0\right| \right| _{L^2(\Omega ^0)} + \left| \left| D^{2} u^1\right| \right| _{L^2(\Omega ^1)} \right) . \end{aligned}\end{aligned}$$

4 Iterative solution based on subspace decomposition

Since the bulk domains are only connected through the interfaces, it is natural to consider a Schur complement formulation. We propose an iterative solver of the Schur complement equation that is based on subspace decomposition. The subspaces are introduced using an artificial coarse mesh on top of the computational domain, see Fig. 5 for an illustration and [13, 14] for more details. Given the subdomains, we use an additive Schwarz preconditioner to solve for the Schur complement. Given the solution on the interfaces, we solve for the decoupled bulk regions, using a direct solver in parallel.

4.1 Schur complement

We let $\{\varphi ^0_{k}\}$ and $\{\varphi ^1_{\ell }\}$ be the standard Lagrange bases of $V^0_h$ and $V^1_h$ respectively. Thus the finite element solution $u_h \in V_h$ consists of the two parts $u^0_h = \sum _{k} U^0_{k} \varphi ^0_{k}$ and $u^1_h = \sum _{\ell } U^1_{\ell } \varphi ^1_{\ell }$. We denote by $U_0$ and $U_1$ the vectors $(U^0_k)_k$ and $(U^1_\ell )_\ell$, respectively.

Let A and b be the resulting matrix and load vector from (17), using the above mentioned basis. Then the system $AU = b$ can be divided into

$$\begin{aligned} \left[ \begin{array}{c | c} A_{00} &{} A_{01} \\ \hline A_{10} &{} A_{11} \end{array} \right] \begin{bmatrix} U_0 \\ U_1 \end{bmatrix} = \begin{bmatrix} b_0 \\ b_1 \end{bmatrix}, \end{aligned}$$

(20)

where $A_{00}$ and $A_{11}$ correspond to the degrees of freedom in the bulk and interfaces respectively. The submatrices $A_{01}$ and $A_{10} = A_{01}^\top$ describe the connections between the interfaces and bulk regions. We form the Schur complement of the submatrix $A_{00}$ and note that $U_1$ solves

$$\begin{aligned} {\tilde{A}}_{11}U_1:=\big (A_{11} - A_{10}A_{00}^{-1}A_{01}\big ) U_1 = b_1 - A_{10}A_{00}^{-1} b_0=:{\tilde{b}}_1. \end{aligned}$$

(21)

The submatrix $A_{00}$ is block diagonal which means that linear systems involving this matrix can be solved in parallel using standard techniques. We therefore focus on how to solve the Schur complement Eq. (21) efficiently.

4.2 Preconditioner based on subspace decomposition

The goal is to define a preconditioner for Eq. (21). Inspired by [13, 14], we introduce an artifical quasi-uniform coarse ($H>h$) finite element mesh $\mathcal {T}_H$ of the computational domain with corresponding Q1-finite element space $W_H$, see Fig. 5. We let $\{\phi _j\}_{j=1}^n$ be the set of bilinear (or trilinear) Lagrangian basis functions spanning $W_H$. The mesh $\mathcal {T}_H$ is independent of the meshes $\mathcal {T}^0_h$ and $\mathcal {T}^1_h$ and thereby independent of the location of the interfaces. Next, we let $\mathcal {I}_h^\text {nodal}$ be the nodal interpolant onto $V^1_h$, which is the finite element space for the interfaces on which the Schur complement equations are posed. We define the coarse space

$$\begin{aligned} W_0=\mathcal {I}_h^\text {nodal} W_H\subset V^1_h. \end{aligned}$$

Furthermore, we define for $j = 1, \ldots , n$,

$$\begin{aligned} W_j=\{v\in V^1_h:\text {supp}(v)\subset \text {supp}(\phi _j)\}\subset V^1_h. \end{aligned}$$

Thereby, we have created a subspace decomposition of $V^1_h$, i.e., any $v\in V^1_h$ can be written as a sum $v=\sum _{j=0}^n v_j$ with $v_j\in W_j$.

In the remainder of this section, we use matrix representations for functions and operators on the interfaces. The functions $\{\varphi ^1_\ell \}_{\ell =1}^m$ are used as basis in $V^1_h$ and the matrices $Q_j \in \mathbb {R}^{m \times m_j}$ are prolongation matrices mapping from functions in $W_j$ to $V^1_h$. As basis in $W_j$, for $j = 0$, the functions $\{\mathcal {I}_h^\text {nodal}\phi _j\}_{j=1}^n$ are used (i.e., $m_0 = n$), while for $j \ge 1$, we choose the smallest subset of $\{\varphi ^1_\ell \}_{\ell =1}^m$ spanning $W_j$, whose size we denote by $m_j$.

We now introduce the matrices

$$\begin{aligned} T_j = (Q_j^\top {\tilde{A}}_{11} Q_j )^{-1} Q_j^\top \in \mathbb {R}^{m_j \times m} \end{aligned}$$

and form the full preconditioner by the sum,

$$\begin{aligned} T=\sum _{j=0}^n Q_j T_j \in \mathbb {R}^{m \times m}. \end{aligned}$$

(22)

The matrix T is a preconditioner to (21),

$$\begin{aligned} T\tilde{A}_{11}U_1=T{\tilde{b}}_1. \end{aligned}$$

Note that in order to compute one application of the preconditioner T, we need to solve one global coarse scale problem (for $j = 0$, on the subspace $W_0$) and n independent local problems (for $j \ge 1$, on the subspaces $W_j$). All these solves are done using a direct solver, which means that the technique we propose is semi-iterative. Under some assumptions of the geometry of the interfaces, it is possible to show optimal convergence properties of this preconditioner, in the meaning that the convergence rate is independent of the fine scale mesh size h and the coarse scale mesh size H.

4.3 Convergence of the preconditioned conjugate gradient (PCG) method

This preconditioner has been thoroughly analyzed for spatial network problems in [13]. In order to apply the convergence analysis presented there, we need to formulate our Schur complement equation as an equation posed on a graph. We limit ourselves to the case $d=2$, so that the interfaces are one-dimensional. We let $\mathcal {N}$ be the set of nodes in the interface finite element mesh $\mathcal {T}^1_h$ and let $\mathcal {E}$ be the set of edges connecting two nodes, where an edge connecting two nodes x and y is represented by an unordered pair $\{x, y\}$. This forms the graph $\mathcal {G}=(\mathcal {N},\mathcal {E})$. In [13], two operators are used in the analysis: a weighted graph Laplacian L and a diagonal mass matrix M. They are both symmetric and thereby uniquely defined by their corresponding quadratic forms:

$$\begin{aligned} \begin{aligned} (L v_1,v_1)&=\frac{1}{2}\sum _{x\in \mathcal {N}}\sum _{\{x,y\}\in \mathcal {E}}\frac{(v_1(x)-v_1(y))^2}{|x-y|},\\ (M v_1,v_1)&=\frac{1}{2}\sum _{x\in \mathcal {N}}\sum _{\{x,y\}\in \mathcal {E}}v_1(x)^2 |x-y|, \end{aligned} \end{aligned}$$

for all $v_1 \in V^1_h$, using the notation $(v,w)=\sum _{x\in \mathcal {N}}v(x)w(x)$. In the following, we overload the notation for L, M, $v \in V_h$ and $v_1 \in V^1_h$ with their matrix representations compatible with (20).

Theorem 3

If $d = 2$ and the Poincaré type inequality $v_1^\top M v_1 \le D v_1^\top L v_1$ holds for all $v_1\in \mathbb {R}^m$ and some $D < \infty$, then there exist constants $c_1,c_2>0$ such that

$$\begin{aligned} c_1 v_1^\top L v_1 \le v_1^\top {\tilde{A}}_{11}v_1\le c_2 v_1^\top L v_1. \end{aligned}$$

Proof

We start with the second inequality. From the construction of $A_{11}$, it follows that

$$\begin{aligned} {\underline{\alpha }} v_1^\top L v_1 \le v_1^\top A_{11}v_1\le {\bar{\alpha }} v_1^\top L v_1+ {\bar{\beta }} v_1^\top M v_1. \end{aligned}$$

Since $A_{00}$ is symmetric and positive definite, $v_0^\top A_{00}^{-1}v_0>0$ and therefore

$v_1^\top A^\top _{01}A_{00}^{-1}A_{01} v_1\ge 0$. We conclude

$$\begin{aligned} v_1^\top {\tilde{A}}_{11} v_1\le {\bar{\alpha }} v_1^\top L v_1+ {\bar{\beta }} v_1^\top M v_1\le ({\bar{\alpha }}+D{\bar{\beta }}) v_1^\top L v_1=: c_2v_1^\top L v_1. \end{aligned}$$

To prove the first inequality, we use that for $v \in V_h$,

$$\begin{aligned} v^\top A v \ge \frac{1}{C(\underline{\alpha }^{-1} + \underline{\beta }^{-1})}\left| \left| v\right| \right| _V^2=:c_1 \left| \left| v\right| \right| _V^2. \end{aligned}$$

Specifically, it holds for $v = [-A_{00}^{-1}A_{01}v_1, v_1]^\top$. Thus,

$$\begin{aligned} v_1^\top (A_{11} - A_{10}A_{00}^{-1}A_{01})v_1 = v^\top A v \ge c_1 \left| \left| v\right| \right| _V^2 \ge c_1 v^\top _1 L v_1. \end{aligned}$$

$\square$

The assumption $v_1^\top M v_1 \le D v_1^\top L v_1$ is fulfilled under assumptions of locality, homogeneity and connectivity of the graph $\mathcal {G}$ on a scale $R_0$. Locality means that all the edges of the network are shorter than $R_0$, homogeneity means that the variations in total length of the subnetwork contained on a square with side length greater than or equal to $2R_0$, are bounded by a constant, and connectivity means that for any subnetwork contained in a square of size $R\ge R_0$, there is a connected subnetwork contained in an extended square of side length $2R+2R_0$. The precise assumptions can be found in Assumption 3.4 in [13]. In short, the theory is applicable if the interfaces are connected and sufficiently dense in the computational domain. We have observed that the preconditioner is still applicable and may give rapid convergence even if these assumptions are not fulfilled.

Under Assumption 3.4 in [13], Theorem 3 holds. Moreover, with $H\ge R_0$, Theorem 4.3 in [13] guarantees convergence of the conjugate gradient method for solving ${\tilde{A}}_{11}U_1={\tilde{b}}_1$ with preconditioner T, defined by Eq. (22). We let $U_1^{(\ell )}$ denote the approximate solution after $\ell$ iterations and let $|v|^2_{\tilde{A}_{11}}=v^T\tilde{A}_{11}v$. Then the following error bound holds,

$$\begin{aligned} |U_1-U_1^{(\ell )}|_{\tilde{A}_{11}}\le 2\left( \frac{\sqrt{\kappa }-1}{\sqrt{\kappa }+1}\right) ^{\ell }|U_1-U_1^{(0)}|_{\tilde{A}_{11}}, \end{aligned}$$

where $\kappa$ is the condition number of $T\tilde{A}_{11}$. Expressed in the $V^1$-norm, we have

$$\begin{aligned} \Vert u^1_h-u^{1,{(\ell )}}_h\Vert _{V^1} \le C\left( \frac{\sqrt{\kappa }-1}{\sqrt{\kappa }+1}\right) ^{\ell }\Vert u^1_h-u^{1,{(0)}}_h\Vert _{V^1}, \end{aligned}$$

where $u^{1,{(\ell )}}_h \in V^1_h$ is the function corresponding to the vector $U_1^{(\ell )}$. We note that C only depends on upper and lower bounds of the coefficients in Eq. (5), and have from [13] that $\kappa$ is independent of the mesh sizes h and H. Once the interface component $U_1^{(\ell )}$ has been computed, the bulk component $U_0^{(\ell )}$ can be solved from

$$\begin{aligned} A_{00} U_0^{(\ell )} = b_0 - A_{01} U_1^{(\ell )}. \end{aligned}$$

Since $A_{00}$ is block diagonal and each block corresponds to a finite element problem on a bulk subdomain, standard techniques can be applied. We use a direct solver in the numerical examples.

5 Numerical examples

We start by investigating the convergence theoretically and numerically for the proposed method for some example problems. We then examine the number of iterations needed for the preconditioned conjugate gradient method to converge, for two different test cases. All numerical examples are two dimensional, $d=2$, and posed on the unit square.

5.1 Regularity and convergence

The solutions $u^0_i$ on the bulk domains $\Omega _i^0$ to Eq. (5) have $H^{{3}/{2}}$-regularity. If the bulk domain is convex it has $H^2$-regularity. We formulate this result as a theorem and leave the proof to Appendix A.

Theorem 4

Let $\Omega \subset \mathbb {R}^2$. Assume $A_i \in C^\infty (\bar{\Omega }^0_i)$, $A_j \in C^\infty (\bar{\Omega }^1_j)$, $B_j \in C^\infty (\Omega ^1_j)$ and $f_i \in L^2(\Omega _i^0)$ for all $i \in I$ and $j \in J$. Then $u_i^0 \in H^{{3}/{2}}(\Omega _i^0)$ and $u_j^1\in H^2(\Omega _j^1)$. If all subdomains are convex, then additionally $u_i^0 \in H^{2}(\Omega _i^0)$.

We note that for convex domains, Theorem 4 guarantees that the assumptions of Theorem 2 are satisfied and we can expect linear convergence in the energy norm. In order to ensure that the method converges according to the theory, we solve a few problems with several different mesh sizes h. The problems we choose for this analysis are a domain with eight infinite interfaces and a domain with 27 finite interfaces, see Fig. 2. Infinite interfaces here means straight lines that pass through the entire domain, leading to convex subdomains, while finite lines leads to non-convex subdomains. For these cases, we let $A_i = 1$, $A_j = 1$, $B_j = 1$ and $f = e^{-10 \sqrt{(x_1 - \frac{1}{2})^2 + (x_2 - \frac{1}{2})^2}}$ on both the interfaces and the bulk areas. The mesh edges are split in two in each refinement of the mesh. The solution using eight interfaces is presented in Fig. 4.

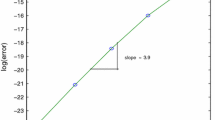
The energy norm $a(u_{\text {ref}}, u_{\text {ref}})^{1/2}$ of the reference solution $u_{\text {ref}}$ is then calculated for each setup and compared to the finite element approximations using different levels of refinement. The initial mesh is fitted to the interfaces and minimal in the sense that interfaces are not refined. We then refine the initial mesh uniformly, using regular refinement, four times. The reference solution is constructed using five uniform refinements. The convergence result is presented in Fig. 3. We detect a linear convergence rate, which agrees with the theory for the case of convex subdomains, and a convergence rate (0.76) that exceeds the predicted one for the case of non-convex subdomains.

Fig. 2

Domains in Sect. 5.1 on which the convergence analysis is performed

Fig. 3

The energy norm of the error between approximations $u_h$ and the reference solution $u_\text {ref}$

Fig. 4

The reference solution $u_\text {ref}$ to the first numerical example with eight interfaces

5.2 Convergence of the iterative solver

We solve Eq. (5) on a unit square with roughly 200 infinite interfaces, using a fine-scale mesh that is uniformly refined once, and using parameters $A_i = 1$ and ${f = e^{-10 \sqrt{(x_1 - \frac{1}{2})^2 + (x_2 - \frac{1}{2})^2}}}$ on both the interfaces and the bulk areas. See Fig. 5 for an illustration of the domain. The effect of varying the coefficients $A_j$ and $B_j$ are tested for two and three different cases respectively. The coefficients $B_j$, describing the coupling between the bulk and interface subdomains, either all have the value 0.01 (weakly coupled), 1 (moderately coupled), or 100 (strongly coupled). The coefficients $A_j$ either all have the value 1, or are uniformly distributed random numbers in the interval [0.01, 1] on the different interface mesh edges. For these setups, the condition numbers of the full matrix varies in the range $10^{11}$ to $10^{15}$. Therefore, solving the system iteratively, without a preconditioner, leads to very poor convergence (around 5 000 – 10 000 iterations in the presented examples).

The number of iterations needed to reach convergence using the preconditioner presented in Sect. 4 for $H=1/8$ (the grid in Fig. 5) and $H=1/16$ are shown in Table 1. We see rapid convergence of the conjugate gradient method given the high condition number for the initial system matrix. We note that a higher number of iterations for the case $B_j=100$, corresponding to strong coupling, is needed. The convergence rate seems to be independent of, or only depend weakly on H, as suggested in the theory. The dense distribution of interfaces and the rapid convergence suggests that Theorem 3 is applicable. It is however difficult to prove this statement since it depends on the exact connectivity and density properties on the network of interfaces.

We also solve the problem on a domain with finite lines, leading to non-convex subdomains. We do this for roughly 200 lines of length $\le 0.2$. The parameters are the same as in the case of infinite interfaces, so we examine weakly, moderately and strongly coupled cases where $A_j$ is either constantly 1 or uniformly distributed between 0.01 and 1. The condition numbers of the full matrix vary in the range $10^8$ to $10^{13}$. The number of iterations using a preconditioner are shown in Table 2. Again, we notice that the preconditioner does a very good job and that the convergence rate is independent or only weakly dependent on the method parameter H. We again need a higher number of iterations for the case $B_j=100$ corresponding to strong coupling.

Fig. 5

Domains in Sect. 5.2 using coarse grid mesh size $H=1/8$ for the subspace correction

Table 1 Number of iterations until convergence using the preconditioner, on a domain with approximately 200 infinite interfaces

Table 2 Number of iterations until convergence using the preconditioner, on a domain with approximately 200 finite interfaces

A Regularity

In this section, we prove that the regularity of a solution to Eq. (5) posed on a two dimensional polygonal Lipschitz domain is $H^{{3}/{2}}$ in the bulk regions in general and $H^2$ in case of convex subdomains. We also show that we have $H^2$-regularity on the interface segments.

The strong formulation of the problem posed on $\Omega _i^0$ reads

$$\begin{aligned} \begin{aligned} - div A_i \nabla u_i^0&= f_i,{} & {} \text { in } \Omega ^0_i, \\ u_i^0&= 0,{} & {} \text { on } \bar{\Omega }_i^0 \cap \partial \Omega , \\ n_{\Omega _i^0} \cdot A_i \nabla u_i^0 + B_j u_i^0&= B_j u_j^1,{} & {} \text { on } \partial \Omega _i^0 \cap \Omega _j^1. \end{aligned} \end{aligned}$$

With the help of the product rule and the fact that $A_i \ge \underline{\alpha } > 0$, this problem can be rewritten as

$$\begin{aligned} \begin{aligned} - \Delta u_i^0&= \frac{f_i + \nabla A_i \cdot \nabla u_i^0}{A_i},{} & {} \text { in } \Omega ^0_i, \\ u_i^0&= 0,{} & {} \text { on } \bar{\Omega }_i^0 \cap \partial \Omega , \\ n_{\Omega _i^0} \cdot \nabla u_i^0 + \frac{B_j}{A_i} u_i^0&= \frac{B_j}{A_i} u_j^1,{} & {} \text { on } \partial \Omega _i^0 \cap \Omega _j^1. \end{aligned} \end{aligned}$$

(23)

We allow the subdomain $\Omega ^0_i$ to be non-convex, but assume $\Omega$ to be convex. We let $\Gamma _k$ denote the segments of the boundary of $\Omega ^0_i$. We let $\omega _k$ denote the internal angle at corner $P_k$, between $\Gamma _k$ and $\Gamma _{k+1}$. Further, we let D be the set of indices of boundary segments that have Dirichlet boundary conditions, i.e., the segments from $\partial \Omega$. Similarly, we let R be the set of indices of the boundary segments equipped with Robin boundary conditions. We let S be the set of indices k for which $\Gamma _k$ and $\Gamma _{k+1}$ both belong to either D or R, and M be the set of indices k for which $\Gamma _k$ and $\Gamma _{k+1}$ belong to one each of them.

We have that $\omega _k < \pi$, $k \in D \cup M$, because of our assumption that $\Omega$ is convex. We also have that $\omega _k < 2 \pi$ for all other k. In Fig. 6, we visualize an example of a subdomain $\Omega ^0_i$.

Fig. 6

An example of a subdomain $\Omega ^0_i$. Angles between different types of boundary conditions have to be smaller than $\pi$, while other angles have to be smaller than $2 \pi$

We are now ready to prove Theorem 4.

Proof

From Lax-Milgram we have that $u^0_i \in H^1(\Omega ^0_i)$ and $u^1_j \in H^1(\Omega ^1_j)$. Since $u^0_i \in H^1(\Omega ^0_i)$, along with the assumptions that $f_i \in L^2(\Omega ^0_i)$ and $A_i$ is smooth and positive, we have that $\left( f_i + \nabla A_i \cdot \nabla u_i^0 \right) /A_i \in L^2(\Omega ^0_i)$. Further, we have that $B_j/A_i \in C^\infty (\partial \Omega _i^0 \cap \Omega _j^1)$, $B_j/A_i> \underline{\beta } / \left| \left| A_i\right| \right| _{\infty } > 0$ and $B_j u_j^1 /A_i \in L^2(\partial \Omega _i^0 \cap \Omega _j^1)$. We have that $\omega _k/(2 \pi ) \notin \mathbb {N}$ for $k \in S$ and $\omega _k/(2 \pi ) + 1/2 \notin \mathbb {N}$ for $k \in M$. Thus, all the requirements of Theorem 2.1 and Proposition 3.1 from [16] are fulfilled for our problem (23) and hence there exist constants $\alpha ^\ell _k$ depending on $f_i$, $A_i$, $B_j$ and $u_j^1$, such that

$$\begin{aligned} u_i^0 - \sum _{0< \lambda _{k,\ell } < 1} \alpha ^\ell _k u^{(0)}_{k,\ell } \in H^2(\Omega ^0_i), \end{aligned}$$

(24)

where

$$\begin{aligned} \lambda _{k,\ell } = {\left\{ \begin{array}{ll} \frac{\ell \pi }{\omega _k}, &{}k \in S,\\ \left( \ell - \frac{1}{2} \right) \frac{\pi }{\omega _k}, &{}k \in M, \end{array}\right. } \qquad \ell = 1,2,3,... \end{aligned}$$

(25)

and

$$\begin{aligned} u^{(0)}_{k,\ell }(r, \theta ) = {\left\{ \begin{array}{ll} r^{\lambda _{k,\ell }} \sin \left( \lambda _{k,\ell } \theta \right) , \qquad k \in D \cap S \text { or } R \cap M,\\ r^{\lambda _{k,\ell }} \cos \left( \lambda _{k,\ell } \theta \right) , \qquad k \in R \cap S \text { or } D \cap M, \end{array}\right. } \end{aligned}$$

(26)

if $\lambda _{k,\ell } \notin \mathbb {N}$, which is the only case present in (24). The variables r and $\theta$ are the local polar coordinates such that $P_k = (0,0)$, $\theta = 0$ along $\Gamma _{k+1}$ and $\theta = \omega _k$ along $\Gamma _k$.

For both $k \in S$ and $k \in M$, we have that $\lambda _{k,l} > \frac{1}{2}$. With $\frac{1}{2}< \lambda _{k,l} < 1$, we have that $u_{k,l}^{(0)} \in H^{{3}/{2}}(\Omega _i^0)$. Thus, we conclude that $u_i^0 \in H^{{3}/{2}}(\Omega ^0_i)$. If all subdomains $\Omega _i^0$ are convex and the requirements of Theorem 4 are fulfilled, we see from Eq. (23) that $u_i^0 \in H^2(\Omega ^0_i)$.

Isolating one interface segment $\Omega _j^1$, one gets the partial differential equation:

$$\begin{aligned} \begin{aligned} - div_{\tau } A_j \nabla _{\tau } u^1_j - \sum _{i :\, (i,j) \in E_0} B_j(u^0_i - u^1_j)&= f_j,{} & {} \Omega ^1_j, \\ u_j^1&= 0,{} & {} \bar{\Omega }^1_j \cap \partial \Omega , \\ u^1_j&= u^1_{j'},{} & {} \partial \Omega ^1_j \cap \partial \Omega ^1_{j'}, \\ \sum _{(j,k) \in E_1} n_{\Omega ^1_j} \cdot A_j \nabla _\tau u^1_j&= 0,{} & {} \partial \Omega ^1_j \cap \Omega ^2_k, \end{aligned} \end{aligned}$$

which, with $\Omega \subset \mathbb {R}^2$, becomes:

$$\begin{aligned} \begin{aligned} -\frac{\textrm{d}^2}{\textrm{d}x^2} u_j^1&= \frac{ f_j + \sum _{i :\, (i,j) \in E_0} B_j (u_i^0 - u_j^1)+ \frac{\textrm{d}}{\textrm{d}x} A_j \frac{\textrm{d}}{\textrm{d}x} u_j^1 }{A_j},{} & {} \Omega ^1_j, \\ u_j^1&= 0,{} & {} \bar{\Omega }^1_j \cap \partial \Omega , \\ u^1_j&= u^1_{j'},{} & {} \partial \Omega ^1_j \cap \partial \Omega ^1_{j'}, \\ \sum _{(j,k) \in E_1} A_j \frac{\textrm{d}}{\textrm{d}x} u^1_j&= 0,{} & {} \partial \Omega ^1_j \cap \Omega ^2_k, \end{aligned} \end{aligned}$$

where x is a parametrisation of the interface segment.

Since $f_j \in L^2(\partial \Omega ^0_i \cap \Omega ^1_j)$, and $B_j$ and $A_j$ are smooth, we can conclude that $u_j^1 \in H^2( \Omega ^1_j)$.

$\square$