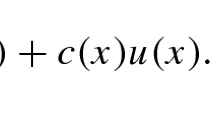Abstract
We consider stochastic differential equations driven by a general Lévy processes (SDEs) with infinite activity and the related, via the Feynman–Kac formula, Dirichlet problem for parabolic integro-differential equation (PIDE). We approximate the solution of PIDE using a numerical method for the SDEs. The method is based on three ingredients: (1) we approximate small jumps by a diffusion; (2) we use restricted jump-adaptive time-stepping; and (3) between the jumps we exploit a weak Euler approximation. We prove weak convergence of the considered algorithm and present an in-depth analysis of how its error and computational cost depend on the jump activity level. Results of some numerical experiments, including pricing of barrier basket currency options, are presented.
Similar content being viewed by others
1 Introduction
Stochastic differential equations driven by Lévy processes (SDEs) have become a very important modelling tool in finance, physics, and biology (see e.g. [1, 4, 6, 24]). Successful use of SDEs relies on effective numerical methods. In this paper, we are interested in weak-sense approximation of SDEs driven by general Lévy processes in which the noise has both the Wiener process and Poisson processes components including the case of infinite jump activity.
Let G be a bounded domain in \(\mathbb {R}^{d}\), \(Q=[t_{0},T)\times G\) be a cylinder in \(\mathbb {R}^{d+1},\) \(\Gamma =\bar{Q}\,{\setminus }\,Q\) be the part of the cylinder’s boundary consisting of the upper base and lateral surface, \( G^{c}=\mathbb {R}^{d}\setminus Q\) be the complement of G and \( Q^{c}:=(t_{0},T]\times G^{c}\cup \{T\}\times \bar{G}.\) Consider the Dirichlet problem for the parabolic integro-differential equation (PIDE):
where the integro-differential operator L is of the form
\(a(t,x)=\left( a^{ij}(t,x)\right) \) is a \(d\times d\)-matrix; \( b(t,x)=(b^{1}(t,x),\ldots ,b^{d}(t,x))^{\top }\) is a d-dimensional vector; c(t, x), g(t, x), and \(\varphi (t,x)\) are scalar functions; \(F(t,x)=\left( F^{ij}(t,x)\right) \) is a \(d\times m\)-matrix; and \(\nu (z),\) \(z\in \mathbb {R} ^{m},\) is a Lévy measure such that \(\int _{\mathbb {R}^{m}}(|z|^{2}\wedge 1)\nu (\mathrm {d}z)<\infty .\) We allow \(\nu \) to be of infinite intensity, i.e. we may have \(\nu \big (B(0,r)\big )=\infty \) for some \(r>0\), where as usual for \(x\in \mathbb {R}^{d}\) and \(s>0\) we write B(x, s) for the open ball of radius s centred at x.
The Feynman–Kac formula provides a probabilistic representations of the solution u(t, x) to (1.1) in terms of a system of Lévy-driven SDEs (see Sect. 2), which can be viewed as a system of characteristics for this PIDE. A weak-sense approximation of the SDEs together with the Monte Carlo technique gives us a numerical approach to evaluating u(t, x), which is especially effective in higher dimensions.
There has been a considerable amount of research on weak-sense numerical methods for Lévy-type SDEs of finite and infinite activity (see e.g. [10,11,12, 14, 15, 17, 20,21,22,23] and references therein). Our approach is most closely related to [12]. As in [3, 11, 12], we replace small jumps with an appropriate Brownian motion, which makes the numerical solution of SDEs with infinite activity of the Lévy measure feasible in practice. There are three main differences between our approach and that of [12]. First, we use restricted jump-adapted time-stepping while in [12] jump-adapted time-stepping was used. Here by jump-adapted we mean that time discretization points are located at jump times \(\tau _{k}\) and between the jumps the remaining diffusion process is effectively approximated [11, 12]. By restricted jump-adapted time-stepping, we understand the following. We fix a time-discretization step \(h>0\). If the jump time increment \(\delta \) for the next time step is less than h, we set the time increment \(\theta =\delta ,\) otherwise \(\theta =h,\) i.e., our time steps are defined as \(\theta =\delta \wedge h.\) We note that this is a different time-stepping strategy to commonly used ones in the literature including the finite-activity case (i.e., jump-diffusion). For example, in the finite activity case it is common [14, 20, 21] to simulate \(\tau _{k}\) before the start of simulations and then superimpose those random times on a grid with some constant or variable finite, small time-step h. Our time-stepping approach is more natural for the problem under consideration than both commonly used strategies; its benefits are discussed in Sect. 3, with the infinite activity case considered in more detail in Sects. 3.5 and 4.2. Restricting \(\delta \) by h is beneficial for accuracy when jumps are rare (e.g. in the jump-diffusion case) and it is also beneficial for convergence rates (measured in the average number of steps) in the case of \(\alpha \)-stable Lévy measure with \(\alpha \in (1,2)\) (see Sects. 3 and 4). Second, in comparison with [12] we explicitly show (singular) dependence of the numerical integration error of our algorithm on the parameter \(\epsilon \) which is the cut-off for small jumps replaced by the Brownian motion. Third, in comparison with the literature we consider the Dirichlet problem for PIDEs, though we also comment on the Cauchy case in Sect. 3.4, which is novel with respect to the use of restricted time-stepping and dependence of the algorithm’s error on \(\epsilon \).
The paper is organised as follows. In Sect. 2, we write down a probabilistic representation for the solution \(u(t,x)\ \)of (1.1), we state assumptions used throughout the paper, and we consider the approximation \(u^{\epsilon }(t,x)\) that solves an auxiliary Dirichlet problem corresponding to the system of characteristics with jumps cut-off by \(\epsilon \). In Sect. 3, we introduce the numerical algorithm which approximates \(u^{\epsilon }(t,x).\) The algorithm uses the restricted jump-adapted time-stepping and approximates the diffusion by a weak Euler scheme. In this section we also obtain and discuss the weak-sense error estimate for the algorithm. In Sect. 4, we illustrate our theoretical findings by three numerical examples, including an application of our algorithm to pricing an FX barrier basket option whose underlyings follow an exponential Lévy model.
2 Preliminaries
Let \((\Omega ,\mathcal {F},\left\{ \mathcal {F}_{t}\right\} _{t_{0}\le t\le T},P)\) be a filtered probability space satisfying the usual hypotheses. The operator L defined in (1.2), on an appropriate domain, is the generator of the d-dimensional process \(X_{t_{0},x}(t)\) given by
where the \(d\times d\) matrix \(\sigma (s,x)\) is defined through \(\sigma (s,x)\sigma ^{\top }(s,x)=a(s,x);\) \(w(t)=(w^{1}(t),\ldots ,w^{d}(t))^{\top }\) is a standard d-dimensional Wiener process; and \(\hat{N}\) is a Poisson random measure on \([0,\infty )\times \mathbb {R}^{m}\) with intensity measure \( \nu (\mathrm {d}z)\times \mathrm {d}s\), \(\int _{\mathbb {R}^{m}}(|z|^{2}\wedge 1)\nu (\mathrm {d}z)<\infty ,\) and compensated small jumps, i.e.,
Remark 2.1
Often [2, 22] a simpler model of the form
where Z(t), \(t\ge t_{0},\) is an m-dimensional Lévy process with the characteristic exponent
is considered instead of the general SDEs (2.1). The Eq. (2.2) is obtained as a special case of (2.1) by setting \(b(t,x)=\mu F(t,x)\) and \(\sigma (t,x)=\sigma F(t,x)\).
When the solution u of (1.1) is regular enough, for example \( u\in C^{1,2}\left( [t_{0},T]\times \mathbb {R}^{d}\right) \), it can be shown that u has the following probabilistic representation
where \((X_{t,x}(s),Y_{t,x,y}(s),Z_{t,x,y,z}(s))\) for \(s\ge t\), solves the system of SDEs consisting of (2.1) and
and \(\tau _{t,x}=\inf \{s\ge t:(s,X_{t,x}(s))\notin Q\}\) is the fist exit-time of the space-time Lévy process \((s,X_{t,x}(s))\) from the space-time cylinder Q. To see why this holds, one may apply Ito’s lemma, see e.g. [2, Theorem 4.4.7], and the fact that u solves (1.1) to prove that the process
is a martingale. The claimed formula follows by letting \(t\rightarrow \infty \).
If one can simulate trajectories of \( \{(s,X_{t,x}(s),Y_{t,x,1}(s),Z_{t,x,1,0}(s));s\ge 0\}\) then the solution of the Dirichlet problem for PIDE (1.1) can be estimated by applying the Monte Carlo technique to (2.3). This approach however is not generally implementable for Lévy measures of infinite intensity, that is when \(\nu \big (B(0,r)\big )=\infty \) for some \(r>0\). The difficulty arises from the presence of an infinite number of small jumps in any finite time interval, and can be overcome by replacing these small jumps by an appropriate diffusion exploiting the idea of the method developed in [3, 11], which we apply here. Alternatively, the issue can be overcome if one can simulate directly from the increments of Lévy process. We will not discuss this case in this paper as we only assume that one has access to the Lévy measure.
2.1 Approximation of small jumps by diffusion
We will now consider the approximation of (2.1) discussed above, where small jumps are replaced by an appropriate diffusion. In the case of the whole space (the Cauchy problem for a PIDE) such an approximation was considered in [3, 11], see also Sect. 3.4 here.
Let \(\gamma _{\epsilon }\) be an m-dimensional vector with the components
and \(B_{\epsilon }\) is an \(m\times m\) matrix with the components
while \(\beta _{\epsilon }\) be obtained from the formula \(\beta _{\epsilon }\beta _{\epsilon }^{\top }=B_{\epsilon }.\) Note that \(|B_{\epsilon }^{ij}|\) (and hence also the elements of \(\beta _{\epsilon })\) are bounded by a constant independent of \(\epsilon \) thanks to the Lévy measure definition.
Remark 2.2
In many practical situations (see e.g. [6]), where the dependence among the components of X(t) introduced through the structure of the SDEs is enough, we can allow the components of the driving Poisson measure to be independent. This amounts to saying that \(\nu \) is concentrated on the axes, and as a result \(B_{\epsilon }\) will be a diagonal matrix.
We shall consider the modified jump-diffusion \(\widetilde{X}_{t_{0},x}(t)=\widetilde{ X}_{t_{0},x}^{\epsilon }(t)\) defined as
where W(t) is a standard m-dimensional Wiener process, independent of N and w. We observe that, in comparison with (2.1), in (2.8) jumps less than \(\epsilon \) in magnitude are replaced by the additional diffusion part. In this way, the new Lévy measure has finite activity allowing us to simulate its events exactly, i.e. in a practical way.
Consequently, we can approximate the solution of u(t, x) the PIDE (1.1) by
where \(\widetilde{\tau }_{t,x}=\inf \{s\ge t:(s,\widetilde{X}_{t,x}(s))\notin Q\}\) is the fist exit time of the space-time Lévy process \((s,\widetilde{X} _{t,x}(s))\) from the space-time cylinder Q and \(\left( \widetilde{X}_{t,x}(s), \widetilde{Y}_{t,x,y}(s),\widetilde{Z}_{t,x,y,z}(s)\right) _{s\ge 0}\) solves the system of SDEs consisting of (2.8) along with
Since the new Lévy measure has finite activity, we can derive a constructive weak scheme for (2.8), (2.10)–(2.11) (see Sect. 3). By using this method together with the Monte Carlo technique, we will arrive at an implementable approximation of \(u^{\epsilon }(t,x)\) and hence of u(t, x).
We will next show that indeed \(u^{\epsilon }\) defined in (2.9) is a good approximation to the solution of (1.1). Before proceeding, we need to formulate appropriate assumptions.
2.2 Assumptions
First, we make the following assumptions on the coefficients of the problem (1.1) which will guarantee, see e.g. [2], that the SDEs (2.1), (2.4)–(2.5) and (2.8), (2.10)–(2.11) have unique adapted, càdlàg solutions with finite moments.
Assumption 2.1
(Lipschitz condition) There exists a constant \(K>0\) such that for all \(x_{1},\) \(x_{2}\in \mathbb {R}^{d}\) and all \(t\in [t_{0},T]\),
Assumption 2.2
(Growth condition) There exists a constant \(K>0\) such that for all \(x\in \mathbb {R}^{d}\) and all \(t\in [t_{0},T]\),
Remark 2.3
Since G is bounded, in practice the above assumptions in the space variable are only required in \(\bar{G}\). We chose to impose them in \(\mathbb {R}^{d}\) to simplify the presentation as it allows us to construct a global solution to the SDEs (2.8), rather than having to deal with local solutions built up to the exit time from the domain. In practice the assumption can be bypassed by multiplying the coefficients with a bump function that vanishes outside G, without affecting the value of (2.3).
In order to streamline the presentation and avoid lengthy technical discussions (see Remarks 2.4 and 2.5), we will make the following assumption regarding the regularity of solutions to (1.1).
Assumption 2.3
The Dirichlet problem (1.1) admits a classical solution \(u(\cdot ,\cdot )\in C^{l,n}([t_{0},T]\times \mathbb {R}^{d})\) with some \(l\ge 1\) and \(n\ge 2\).
In addition to the PIDE problem (1.1), we also consider the PIDE problem for \(u^{\epsilon }\) from (2.9):
where
Again, for simplicity (but see Remark 2.4), we impose the following conditions on the solution \(u^{\epsilon }\) of the above Dirichlet problem.
Assumption 2.4
The auxiliary Dirichlet problem (2.15) admits a classical solution \(u^{\epsilon }(\cdot ,\cdot )\in C^{l,n}([t_{0},T]\times \mathbb {R}^{d})\) with some \(l\ge 1\) and \(n\ge 2\).
Finally, we also require that \(u^{\epsilon }\) and its derivatives do not grow faster than a polynomial function at infinity.
Assumption 2.5
(Smoothness and growth) There exist constants \(K>0\) and \(q\ge 1\) such that for all \(x\in \mathbb {R}^{d}\), all \(t\in [t_{0},T]\) and \( \epsilon >0\), the solution \(u^{\epsilon }\) of the PIDE problem (2.15) and its derivatives satisfy
where \(0\le 2l+j\le 4,\ \sum _{k=1}^{j}i_{k}=j,\) and \(i_{k}\) are integers from 0 to d.
Remark 2.4
Sufficient conditions guaranteeing Assumptions 2.3, 2.4 and 2.5 consist in sufficient smoothness of the coefficients, the boundary \(\partial G,\) and the function \(\varphi \) and in appropriate compatibility of \(\varphi \) and g and also of the integral operator (see e.g. [8, 9, 16]).
Remark 2.5
The main goal of the paper is to present the numerical method and study its convergence under ‘good’ conditions when its convergence rates are optimal (i.e., highest possible). As usual, in these circumstances, the conditions (here Assumptions 2.3, 2.4, and 2.5) are somewhat restrictive. See Theorem 3.3 in [8, p. 93], which indicates sufficient conditions for Assumption 2.3 to hold. If one drops the compatibility condition (3.11) in Theorem 3.3 of [8, p. 93], then, as in the diffusion case, the smoothness of the solution will be lost through the boundary of Q at the terminal time \(T.\ \)This affects only the last step of the method and the proof can be modified (see such a recipe in the case of the Neumann problem and diffusion in e.g. [13]), but we do not include such complications here for transparency of the proofs. Further, in the case of an \(\alpha \)-stable Lévy process with \( \alpha \in (1,2)\) spatial derivatives of u(t, x) may blow up near the boundary \(\partial G,\) the blow up is polynomial with the power dependent on \(\alpha \) if the integral operator does not satisfy some compatibility conditions (see the discussion in [8, p. 96]). This situation requires further analysis of the proposed method, which is beyond the scope of the present paper. At the same time, the method can be successfully used when the assumptions stated in this section are not satisfied as demonstrated in our numerical experiments (see Sect. 4.3).
2.3 Closeness of \(u^{\epsilon }(t,x)\) and u(t, x)
We now state and prove the theorem on closeness of \(u^{\epsilon }(t,x)\) and u(t, x). In what follows we use the same letters K and C for various positive constants independent of x, t, and \(\epsilon .\)
Theorem 2.1
Let Assumptions 2.1, 2.2 and 2.3 hold, the latter with \(l=1\) and \(m=3\). Then for \(0\le \epsilon <1\)
where \(K>0\) does not depend on \(t, x, \epsilon \).
Proof
We have \(\big (\widetilde{\tau }_{t,x},\widetilde{X}_{t,x}(\widetilde{\tau }_{t,x})\big )\in Q^{c}\) and \(\varphi \big (\widetilde{\tau }_{t,x},\widetilde{X}_{t,x}(\widetilde{\tau } _{t,x})\big )=u\big (\widetilde{\tau }_{t,x},\widetilde{X}_{t,x}(\widetilde{\tau }_{t,x}) \big ),\) and
By Ito’s formula, we get
Since u(t, x) solves (1.1) and recalling (2.6), we obtain from (2.20):
Replacing s with the stopping time \(\widetilde{\tau }_{t,x}\) in (2.21) (cf. (2.19)), taking expectations of the resulting left- and right-hand sides of (2.21) and using the martingale property and (2.7), we arrive at
By Taylor’s expansion, we get for some \(\theta \in [0,1]\) which may depend on the randomness,
where to obtain inequality (2.24) we used the fact that by definition of \(\widetilde{\tau }_{t,x}\), \(\widetilde{X}_{t,x}(s-)\in G\) for \(s\le \widetilde{\tau }_{t,x}\), and therefore we have for some \(K>0\) that does not depend on \(\epsilon , t, x, s\),
after noting that \(|z|<\epsilon \). Using Assumption 2.3 and combining (2.22)–(2.24) and since \(\widetilde{Y}_{t,x,1}(\cdot ) \ge 0\), we arrive at
Since \(c\big (s,\widetilde{X}_{t,x}(s)\big )\) is bounded on the set \(\{\widetilde{\tau }_{t,x}>s\},\) \(\mathbb {E}\left[ \widetilde{Y}_{t,x,1}(s){\mathbf{I}}(\widetilde{\tau }_{t,x}>s) \right] \) is bounded which together with (2.26) implies (2.18). \(\square \)
Example 2.1
(Tempered \(\alpha \)-stable Process) For \(\alpha \in (0,2)\) and \(m=1,\) consider an \( \alpha \)-stable process with Lévy measure given by \(\nu (\mathrm {d} z)=|z|^{-1-\alpha }\mathrm {d}z\). Then
Similarly, for a tempered stable distribution which has Lévy measure given by
for \(\alpha \in (0,2)\) and \(C_{+},\) \(C_{-},\) \(\lambda _{+},\) \(\lambda _{-}>0\) we find that the error from approximating the small jumps by diffusion as in Theorem 2.1 is of the order \(O(\epsilon ^{3-\alpha })\).
3 Weak approximation of jump-diffusions in bounded domains
In this section we propose and study a numerical algorithm which weakly approximates the solutions of the jump-diffusion (2.8), (2.10)–(2.11) with finite intensity of jumps in a bounded domain, i.e., approximates \(u^{\epsilon }(t,x)\) from (2.9). In Sect. 3.1 we formulate the algorithm based on a simplest random walk. We analyse the one-step error of the algorithm in Sect. 3.2 and the global error in Sect. 3.3. In Sect. 3.4 we comment on how the global error can be estimated in the Cauchy case. In Sect. 3.5 we combine the convergence result of Sect. 3.3 with Theorem 2.1 to get error estimates in the case of infinite activity of jumps.
3.1 Algorithm
In what follows we also require the following to hold.
Assumption 3.1
(Lévy measure) There exists a constant \(K>0\)
for up to a sufficiently large \(p\ge 2.\)
This is a natural assumption since Lévy measures of practical interest (see e.g. [6] and also examples here of Example 2.1 and Sect. 4) have this property.
Let us describe an algorithm for simulating a Markov chain that approximates a trajectory of (2.8), (2.10)–(2.11). In what follows we assume that we can exactly sample the intervals \(\delta \) between consecutive jump times with the intensity
and jump sizes \(J_{\epsilon }\) distributed according to the density
Remark 3.1
There are known methods for simulating jump times and sizes for many standard distributions. In general, if there exists an explicit expression for the jump size density, one can construct a rejection method to sample jump sizes. An overview with regard to simulation of jump times and sizes can be found in [6, 7].
Thanks to Assumption 3.1, we have
with \(K>0\) being independent of \(\epsilon \) and \(p\ge 2.\) We also note that
where \(K>0\) is a constant independent of \(\varepsilon \), since by the Cauchy-Schwarz inequality
thanks to the Lévy measure definition.
We now describe the algorithm. Fix a time-discretization step \(h>0\) and suppose the current position of the chain is (t, x, y, z). If the jump time increment \(\delta <h\), we set \(\theta =\delta \), otherwise \(\theta =h\), i.e. \(\theta =\delta \wedge h\).
In the case \(\theta =h\), we apply the weak explicit Euler approximation with the simplest simulation of noise to the system (2.8), (2.10)–(2.11) with no jumps:
where \(\xi =(\xi ^{1},\ldots ,\xi ^{d})^{\intercal }\), \(\eta =(\eta ^{1},\ldots ,\eta ^{m})^{\intercal }\), with \(\xi ^{1}, \dots , \xi ^{d}\) and \( \eta ^{1}, \dots , \eta ^{m}\) mutually independent random variables, taking the values \(\pm 1\) with equal probability. In the case of \(\theta <h\), we replace (3.5) by the following explicit Euler approximation
Let \((t_{0},x_{0})\in Q\). We aim to find the value \(u^{\epsilon }(t_{0},x_{0})\), where \(u^{\epsilon }(t,x)\) solves the problem (2.15). Introduce a discretization of the interval \(\left[ t_{0},T\right] \), for example the equidistant one:
To approximate the solution of the system (2.8), we construct a Markov chain \((\vartheta _{k},X_{k},Y_{k},Z_{k})\) which stops at a random step \(\varkappa \) when \((\vartheta _{k},X_{k})\) exits the domain Q. The algorithm is formulated as Algorithm 1 below.
Remark 3.2
If \(\lambda _{\epsilon }\) is large so that \(1-e^{-\lambda _{\epsilon }h}\) is close to 1, then \(I_{k}=1\) (i.e., jump happens) is almost on every time step. In this situation it is computationally beneficial to modify Algorithm 1 in the following way: instead of sampling both \(I_{k}\) and \(\theta _k\), sample \(\delta _k\) according to the exponential distribution with parameter \(\lambda _{\epsilon }\) and set \(\theta _k=\delta _k \wedge h\) and \(I_{k}=1\) if \(\theta _k< h\), else \(I_{k}=0\).
Remark 3.3
We note [18, 19] that in the diffusion case (i.e., when there is no jump component in the noise which drives SDEs) solving Dirichlet problems for parabolic or elliptic PDEs requires to complement a random walk inside the domain G with a special approximation near the boundary \(\partial G\). In contrast, in the case of Dirichlet problems for PIDEs we do not need a special construction near the boundary since the boundary condition is defined on the whole complement \(G^{c}.\) Here, when the chain \(X_{k}\) exits G, we know the exact value of the solution \(u^{\epsilon }(\bar{\vartheta } _{\varkappa },X_{\varkappa })=\varphi (\bar{\vartheta }_{\varkappa },X_{\varkappa })\) at the exit point \((\bar{\vartheta }_{\varkappa },X_{\varkappa })\), while in the diffusion case when a chain exits G, we do not know the exact value of the solution at the exit point and need an approximation. Due to this fact, Algorithm 1 is somewhat simpler than algorithms for Dirichlet problems for parabolic or elliptic PDEs (cf. [18, 19] and references therein).
3.2 One-step error
In this section we consider the one-step error of Algorithm 1. The one step of this algorithm takes the form for \((t,x)\in Q\):
Before we state and prove an error estimate for the one-step of Algorithm 1, we need to introduce some additional notation. For brevity let us write \(b=b(t,x)\), \(\sigma =\sigma (t,x)\), \(F=F(t,x)\), \(g=g(t,x)\), \( c=c(t,x)\), \(J=J_{\epsilon }\). Let us define the intermediate points \(Q_{i}\) and their differences \(\Delta _{i}\), for \(i=1,\ldots ,4\):
where \(x\in G.\) Note that \(Q_{i}\), \(i=1,\ldots ,3,\) can be outside G.
Lemma 3.1
(Moments of intermediate points \(Q_{i}\)) Under Assumptions 2.1 and 3.1, there is \(K>0\) independent of \(\epsilon \) and h such that for \(p\ge 1\):
where \(Q_{i}\) are defined in (3.12).
Proof
It is not difficult to see that the points \(Q_{i},\) \(i=1,2,\) are of the following form
where \(c_{1}\) is either 0 or 1. It is obvious that \(\xi \) and \(\eta \) and their moments are all bounded. The functions b(t, x), \(\sigma (t,x)\) and F(t, x) are bounded as \((t,x)\in Q\), and for \(x\in G\), \(|x|^{2p}\) is also bounded. Recall that sufficiently high moments of \(J_{\epsilon }\) are bounded as in (3.3). Then, using the Cauchy-Schwarz inequality, we can show that
Hence, we obtained (3.13). The bound (3.14) is shown analogously. \(\square \)
We will need the following technical lemma.
Lemma 3.2
(Moments of \(\theta \)) For integer \(p\ge 2,\) we have
where \(K>0\) depends on p but is independent of \(\lambda _{\epsilon }\) and h.
Proof
The proof is by induction. By straightforward calculations, we get
Then assuming that (3.15) is true for all integer \(p\ge 2,\) we obtain
\(\square \)
Now we prove an estimate for the one-step error.
Theorem 3.1
(One–step error of Algorithm 1) Under Assumption 2.4 with \(l=2, n=4\) and Assumptions 2.1, 2.5 and 3.1 the one–step error of Algorithm 1 given by
satisfies the bound
where \(K>0\) is a constant independent of h and \(\epsilon \).
Proof
For any smooth function v(t, x), we write \(D_{l}v_{n}=(D_{l}v)(t,Q_{n})\) for the l-th time derivative and \((D_{l}^{k}v)(t,x)[f_{1},\ldots ,f_{k}]\) for the l-th time derivative of the k-th spatial derivative evaluated in the directions \(f_{j}\). For example, if \(k=2\) and \(l=1\),
We will also use the following short notation
The final aim of this theorem is to achieve an error estimate explicitly capturing the (singular) dependence of the one-step error on \(\epsilon \). To this end, we split the error into several parts according to the intermediate points \(Q_{i}\) defined in (3.12).
Using (3.9) and (3.12), we have
To precisely account for the factor \(\gamma _{\epsilon }\) and powers of \( \theta \) in the analysis of the one-step error, we use multiple Taylor expansions of \(u^{\epsilon }(t+\theta ,X).\) We obtain
where the remainders are as follows
Using (3.17), (3.10)–(3.11), and the fact that \(\xi \) and \(\eta \) have mean zero and that components of \(\xi ,\) \(\eta ,\) \(\theta ,\) J are mutually independent, we obtain
The following elementary formulas are needed for future calculations:
Also, \(\mathbb {E}v(J)\) for some v(z) will mean
Noting that \(u_{4}^{\epsilon }=u^{\epsilon }(t,x)=u^{\epsilon }\) and using ( 3.18), (3.12), (3.19) and (2.15), we obtain
where
and
It is clear that many of the terms in R are only non–zero in the case \( \theta <h\), i.e. when a jump occurs. We rearrange the terms in \(R_{0}\) according to their degree in \(\theta \):
Now to estimate the terms in the error \(R_{0},\) we observe that (i) \( \int _{|s|>\epsilon }s\nu (ds)=\gamma _{\epsilon }+\int _{|s|>1}s\nu (ds)\) with the latter integral bounded and, in particular, \(|\mathbb {E}[J]|\le K(1+|\gamma _{\epsilon }|)/\lambda _{\epsilon };\) (ii) \(\mathbb {E}\left[ |J|^{2p}\right] \), \(p\ge 1,\) are bounded by \(K/\lambda _{\epsilon }\) (see (3.3)); (iii) the terms \(R_{17}\), \(R_{18}\), \(R_{19},\) \(R_{21}\) and \(R_{22}\) contain derivatives of \(u^{\epsilon }\) evaluated at or between the points \( Q_{3}\) and \(Q_{4}\) and in their estimation Assumption 2.5 and (3.14) from Lemma 3.1 are used; (iv) the terms \(R_{11}\), \(R_{12}\) , \(R_{13}\), \(R_{14}\), \(R_{15}\) and \(R_{16}\) contain derivatives of \( u^{\epsilon }\) evaluated at or between the points \(Q_{1}\) and \(Q_{2}\) and in their estimation Assumption 2.5, (3.13) from Lemma 3.1, and Lemma 3.2 are used; (v) \(\gamma _{\epsilon }^{2}/\lambda _{\epsilon }\) is bounded by a constant independent of \(\epsilon .\) As a result, we obtain
and
where all constants \(K_{i}>0\) are independent of h and \(\epsilon \) and \( q\ge 1\).
Overall we obtain
\(\square \)
Remark 3.4
We note the following two asymptotic regimes for the one-step error (3.16). For \(\lambda _{\epsilon }h<1\) (in practice, this occurs only when \(\lambda _{\epsilon }\) is small or moderate like it is in jump-diffusions), we can expand the exponent in (3.16) and obtain that the one-step error is of order \(O(h^{2}):\)
When \(\lambda _{\epsilon }\) is very large (e.g., for small \(\epsilon \) in the infinite activity case) then the term with \(e^{-\lambda _{\epsilon }h}\) can be neglected and we get
The usefulness of a more precise estimate (3.16) is that it includes situations in between these two asymptotic regimes and also allows to consider an interplay between h and \(\epsilon \) (see Sect. 3.5).
3.3 Global error
In this section we obtain an estimate for the global weak-sense error of Algorithm 1. We first estimate average number of steps \(\mathbb {E} \left[ \varkappa \right] \) of Algorithm 1.
Lemma 3.3
(Number of steps) The average number of steps \(\varkappa \) for the chain \( X_{k}\) from Algorithm 1 satisfies the following bound
Proof
It is obvious that if we replace the bounded domain G in Algorithm 1 with the whole space \(\mathbb {R}^{d}\) (i.e., replace the Dirichlet problem by the Cauchy one), then the corresponding number of steps \( \varkappa ^{\prime }\) of Algorithm 1 is not less than \(\varkappa .\) Hence it is sufficient to get an estimate for \(E\left[ \varkappa ^{\prime } \right] .\) Let \(\delta _{1},\delta _{2},\dots \) be the interarrival times of the jumps, \(\theta _{i}=\delta _{i}\wedge h\) for \(i\ge 0,\) and \( S_{k}=\sum _{i=0}^{k-1}\theta _{i}\) for \(k\ge 0\). Then
Introduce the martingale: \(\widetilde{S}_{0}=0\) and \(\widetilde{S}_{k}:=S_{k}-k \mathbb {E}\left[ \theta \right] \) for \(k\ge 1\). Since \(\theta _{i}\le h\) we have that \(\widetilde{S}_{\varkappa ^{\prime }-1}\le S_{\varkappa ^{\prime }-1}<T-t_{0}\) almost surely and thus by the optional stopping theorem we obtain
Therefore
and we conclude
\(\square \)
We also need the following auxiliary lemma.
Lemma 3.4
(Boundedness of \(Y_{k}\) in Algorithm 1) The chain \(Y_{k}\) defined in (3.6) is uniformly bounded by a deterministic constant:
where \(\bar{c}=\max _{(t,x)\in \bar{Q}}c(t,x)\).
Proof
From (3.6), we can express \(Y_{k}\) via previous \(Y_{k-1}\) and get the required estimate as follows:
\(\square \)
Now we prove the convergence theorem for Algorithm 1.
Theorem 3.2
(Global error of Algorithm 1) Under Assumption 2.4 with \(l=2,\) \( m=4\) and Assumptions 2.1, 2.5 and 3.1, the global error of Algorithm 1 satisfies the following bound
where \(K>0\) is a constant independent of h and \(\epsilon .\)
Proof
Recall (see (2.9)):
The global error
can be written as
Using Lemma 3.4, Assumption 2.5 and Lemmas 3.1 and 3.2 as well as that \(\bar{\vartheta }_{\varkappa }-\vartheta _{\varkappa }\le \theta _{\varkappa }\), we have for the first term in (3.21):
where \(K>0\) does not depend on h or \(\varepsilon .\)
For the second term in (3.21), we exploit ideas from [19] to re-express the global error. We get using Theorem 3.1 and Lemmas 3.4 and 3.3:
where, as usual constants \(K>0\) are changing from line to line. Combining ( 3.21)–(3.23), we arrive at (3.20). \(\square \)
Remark 3.5
(Error estimate and convergence) Note that the error estimate in Theorem 3.2 gives us the expected results in the limiting cases (see also Remark 3.4). If \(\lambda _{\epsilon }h<1\), we obtain:
which is expected for weak convergence in the jump-diffusion case.
If \(\lambda _{\epsilon }\) is large (meaning that almost always \(\theta <h\)), the error is tending to
as expected (cf. [11]).
We also remark that for any fixed \(\lambda _{\epsilon }\), we have first order convergence when \(h\rightarrow 0.\)
Remark 3.6
In the case of symmetric measure \(\nu (z)\) we have \(\gamma _{\epsilon }=0\) and hence the global error (3.20) becomes
3.4 Remark on the Cauchy problem
Let us set \(G=\mathbb {R}^{d}\) in (2.15) and hence consider the Cauchy problem for the PIDE:
In this case Algorithm 1 stops only when \(\vartheta _{\varkappa }\ge T\) as there is no spatial boundary (and hence we write \(u^{\epsilon }(T,x)=\varphi (x)\) instead of \(u^{\epsilon }(T,x)=\varphi (T,x))\). Theorem 3.1 remains valid for the Cauchy problem, although in this case one should replace the constant K in the right-hand side of the bound (3.16) with a function \(K(x)>0\) satisfying
with some constants \(\widetilde{K}>0\) and \(q\ge 1.\) Consequently, to prove an analogue of the global convergence Theorem 3.2, we need to prove boundedness of moments \(\mathbb {E}\left[ X_{k}^{2p}\right] .\) Let
Lemma 3.5
Under Assumptions 2.1, 2.2, and 3.1, we have for \(X_{k}\) from Algorithm 1:
with some constants \(K>0\) and \(p\ge 1.\)
Proof
As usual, in this proof \(K>0\) is a constant independent of \(\epsilon \) and h which can change from line to line in derivations. We first prove the lemma for an integer \(p\ge 1.\)
Noting (3.26), we have
For \(\varkappa >k\):
Then
where we used
Then, by the linear growth Assumption 2.2, we get
using that \(\mathbb {E}\left[ \mathbf {I}(\varkappa>k)|X_{k}|^{2p-2}\right] \le K\left( 1+\mathbb {E}\left[ \mathbf {I}(\varkappa >k)|X_{k}|^{2p}\right] \right) \) by Young’s inequality.
For the last term in (3.28), using the linear growth Assumptions 2.2 and 3.1, we get for \(l=2,\ldots ,2p\):
where to obtain the last line we used that \(\theta _{k+1}^{l/2}\) for odd l is estimated by \(K(\theta _{k+1}^{(l-1)/2}+\theta _{k+1}^{(l+1)/2})\) and exploited Lemma 3.2, boundedness of \(\dfrac{|\gamma _{\epsilon }|^{l}}{\lambda _{\epsilon }^{l/2}}\) and (3.3). Then
and
Combining (3.28)–(3.30), we get
whence
Introduce a continuous time piece-wise constant process
and
Then we can write (3.31) as
By Gronwall’s inequality, we get
implies (3.27) for integer \(p\ge 1\). Then, by Jensen’s inequality, (3.27) holds for non-integer \(p\ge 1\) as well. \(\square \)
Based on the discussion before Lemma 3.5 and on the moments estimate (3.27) of Lemma 3.5, it is not difficult to show that the global error estimate (3.20) for Algorithm 1 also holds in the Cauchy problem case.
3.5 The case of infinite intensity of jumps
In this section we combine the previous results, Theorem 2.1 and 3.2, to obtain an overall error estimate for solving the problem (1.1) in the case of infinite intensity of jumps by Algorithm 1. We obtain
where \(K>0\) is independent of h and \(\epsilon .\)
Let us consider an \(\alpha \)-stable process in which the Lévy measure has the following singular behaviour near zero
i.e., we are focusing our attention here on the singularity near zero only and the sign \(\sim \) means that the limit of the ratio of both sides equals to some positive constant. Consequently, all calculations are done in this section up to positive constant factors independent of \(\epsilon \) and h. The behaviour (3.33) is typical for m-dimensional Lévy measures near zero (see e.g. [2, p. 37] and also the one-dimensional Example 2.1). Then
Hence
Let us measure the computational cost of Algorithm 1 in terms of the average number of steps (see Lemma 3.3). Since
we choose to use the cost associated with the average number of steps as
We fix a tolerance level \(\rho _{tol}\) and require \(\epsilon \) and h to be so that
Note that since we are using the Euler scheme for SDEs’ approximation, the decrease of \(\rho _{tol}\) in terms of cost cannot be faster than linear. We now consider three cases of \(\alpha .\)
The case \(\alpha \in (0,1)\) We have
and, by choosing sufficiently small \(\epsilon \), we can reach the required \( \rho _{tol}.\) It is optimal to take \(h=\infty \) (in practice, taking \( h=T-t_{0})\) and the cost is then \(C=1/\epsilon ^{\alpha } .\) Hence \(\rho _{tol}\) is inversely proportional to C, and convergence is linear in cost (to reduce \( \rho _{tol}\) twice, we need to double C).
The case \(\alpha =1\) We have
i.e. convergence is almost linear in cost.
The case \(\alpha \in (1,2)\) If we take \(h=\infty ,\) then \(\rho (\epsilon ,h)=O(\epsilon ^{2-\alpha })\) and the convergence order in terms of cost is \(2/\alpha -1,\) which is very slow (e.g., for \(\alpha =3/2,\) the order is 1/3 and for \(\alpha =1.9,\) the order is \(\approx 0.05\)). Let us now take \(h=\epsilon ^{\ell }\) with \(\ell \ge \alpha .\) Then
and \(C\approx 1/h=\epsilon ^{-\ell }.\) The optimal \(\ell =1+\alpha ,\) for which \(\rho (\epsilon ,h)=O(\epsilon ^{3-\alpha })\) and the convergence order in terms of cost is \((3-\alpha )/(1+\alpha ),\) which is much better (e.g., for \(\alpha =3/2,\) the order is 3/5 and it cannot be smaller than 1/3 for any \(\alpha \in (1,2)\)). Note that in the case of symmetric measure \(\nu (z)\) (see Remark 3.6), convergence is linear in cost for \( \alpha \in (1,2).\)
To conclude, for \(\alpha \in (0,1)\) we have first order convergence and there is no benefit of restricting jump adapted steps by h (see a similar result in the case of the Cauchy problem and not restricted jump-adapted steps in [12]). However, in the case of \(\alpha \in (1,2),\) it is beneficial to use restricted jump-adapted steps to get the order of \( (3-\alpha )/(1+\alpha ).\) We also recall that restricted jump-adapted steps should typically be used for jump-diffusions (the finite activity case when there is no singularity of \(\lambda _{\epsilon }\) and \(\gamma _{\epsilon }\)) because jump time increments \(\delta \) typically take too large values and to control the error at every step we should truncate those times at a sufficiently small \(h>0\) for a satisfactory accuracy.
4 Numerical experiments
In this section we illustrate the theoretical results of Sect. 3. In particular, we display the behaviour in the case of infinite intensity of jumps for different regimes of \(\alpha \). We showcase numerical tests of Algorithm 1 in four different examples: (i) a non-singular Lévy measure (Example 4.1), (ii) a singular Lévy measure which is similar to that of Example 2.1 (see Example 4.2), and (iii) pricing a foreign-exchange (FX) barrier basket option where the underlying model is of exponential Lévy-type (Example 4.3) and (iv) pricing a FX barrier option showing that the convergence orders hold (Example 4.4).
As it is usual for weak approximation (see e.g. [19]), in simulations we complement Algorithm 1 by the Monte Carlo techniques and evaluate \(u(t_{0},x)\) or \(u^{\epsilon }(t_{0},x)\) as
where \((\bar{\vartheta }_{\varkappa }^{(m)},X_{\varkappa }^{(m)},Y_{\varkappa }^{(m)},Z_{\varkappa }^{(m)})\) are independent realisations of \((\bar{ \vartheta }_{\varkappa },X_{\varkappa },Y_{\varkappa },Z_{\varkappa })\). The Monte Carlo error of (4.1) is
where
and \(\Xi ^{(m)}=\varphi \left( \bar{\vartheta }_{\varkappa }^{(m)},X_{\varkappa }^{(m)}\right) Y_{\varkappa }^{(m)}+Z_{\varkappa }^{(m)}.\) Then \(\bar{u}(t_{0},x)\) falls in the corresponding confidence interval \(\hat{u}\pm 2\sqrt{\bar{D}_{M}}\) with probability 0.95.
4.1 Example with a non-singular Lévy measure
In this subsection, we illustrate Algorithm 1 in the case of a simple non-singular Lévy measure (i.e., the jump-diffusion case), where there is no need to replace small jumps and hence we directly approximate \(u(t_{0},x)\) rather than \(u^{\epsilon }(t_{0},x).\) Consequently, the numerical integration error does not depend on \(\epsilon \). We recall (see Theorem 3.2) that Algorithm 1 has first order of convergence in h.
Example 4.1
(Non-singular Lévy measure) To construct this and the next example, we use the same recipe as in [18, 19]: we choose the coefficients of the problem (1.1) so that we can write down its solution explicitly. Having the exact solution is very useful for numerical tests.
Consider the problem (1.1) with \(d=3,\) \(G=U_{1}\) which is the open unit ball centred at the origin in \(\mathbb {R}^{3},\) and with the coefficients
with the boundary condition
and with the Lévy measure density
where \(C_{-}\) and \(C_{+}\) are some positive constants. Note that, keeping in mind Remark 2.3, the coefficients from (4.2)–(4.4) satisfy Assumptions 2.1–2.2.
It is not difficult to verify that this problem has the solution
and we also find
We simulated jump sizes by analytically inverting the cumulative distribution function corresponding to the density \(\rho (z)\) and making use of uniform random numbers in the standard manner.
Here the absolute error e is given by
where the true solution for the point (0, 0) is \( u=u(0,0)\approx 0.987433\). The expected convergence order O(h) can be clearly seen in Fig. 1 and Table 1.
Non-singular Lévy measure example: dependence of the error e on h, the error bars show the Monte Carlo error. The parameters used are \(T=1, C_{+}=30, C_{-}=1.0, \mu = 3.0, f=0.1, M = 40{,}000{,}000\) and \({\hat{u}}\) is evaluated at the point (0, 0)
4.2 Example with a singular Lévy measure
In this subsection, we confirm dependence of the error of Algorithm 1 on the cut-off parameter \(\epsilon \) for jump sizes and on the parameter \(\alpha \) of the Lévy measure as well as associated computational costs which were derived in Sect. 3.5.
Example 4.2
(Singular Lévy measure) Consider the problem (1.1) with \( d=3,\) \(G=U_{1}\) which is the open unit ball centred at the origin in \( \mathbb {R}^{3},\) and with the coefficients as in (4.2), (4.3), and
with the boundary condition (4.5), and with the Lévy measure density
where \(C_{-},\) \(C_{+},\) and \(\mu \) are some positive constants and \(\alpha \in (0,2)\).
We observe that \(C_{-}\ne C_{+}\) gives an asymmetric jump measure and the Lévy process has infinite activity and, if \(\alpha \in [1,2),\) infinite variation. Note that, keeping in mind Remark 2.3, the coefficients from (4.2), ( 4.3), (4.7) satisfy Assumptions 2.1–2.2.
Singular Lévy measure example, the case \(\alpha =0.5\): dependence of the error e on \(\epsilon \), the error bars show the Monte Carlo error. The parameters used are \(T=1, C_{+}=0.1, C_{-}=1.0, \mu = 3.0, f=0.2, M = 40{,}000{,}000\) and \({\hat{u}}\) is evaluated at the point (0, 0)
It is not difficult to verify that this problem has the following solution
Other quantities needed for the algorithm take the form
In this example, the absolute error e is given by
For the case of \(\alpha =0.5\), we can clearly see in Fig. 2 and Table 2 that the error is of order \(O(\epsilon ^{\alpha })=O(\epsilon ^{0.5})\) as expected. We also observe linear convergence in computational cost (measured in average number of steps). In addition we note that choosing a smaller time step, e.g. \(h=0.1,\) does not change the behaviour in this case which is in accordance with our prediction of Sect. 3.5 (Fig. 3).
Numerical results for the case \(\alpha =1.5\) are given in Figs. 4 and 5 and Tables 3 and 4. As is shown in Sect. 3.5, convergence (in terms of computational costs) can be improved in the case of \(\alpha \in (1,2)\) by choosing \(h=\epsilon ^{1+\alpha }\). In Fig. 5, for all \(\epsilon \) it can be seen that choosing a smaller (but optimally chosen) step parameter h results in quicker convergence (i.e., for the same cost, we can achieve a better result if h is chosen in an optimal way) and naturally in a smaller error.
We recall that if the jump measure is symmetric, i.e. \(C_{-}=C_{+}\) in the considered example, then \(\gamma _{\epsilon }=0\) and the numerical integration error of Algorithm 1 is no longer singular (see Theorem 3.2 and Remark 3.6). Consequently (see Sect. 3.5), in this case the computational cost depends linearly on \(\epsilon \) even for \(\alpha =1.5,\) which is confirmed on Fig. 6.
Singular Lévy measure example, the case \(\alpha =0.5\): dependence of the error e on the average number of steps (computational costs). The parameters are the same as in Fig. 2
Singular Lévy measure example, the case \(\alpha =1.5\): dependence of the error e on \(\epsilon \), the error bars show the Monte Carlo error. The parameters used are \(T=1, C_{+}=1.0, C_{-}=25.0, \mu = 3.0, f=1.0, M = 100{,}000{,}000\) and \({\hat{u}}\) is evaluated at the point (0, 0)
Singular Lévy measure example, the case \(\alpha =1.5\): dependence of the error e on the average number of steps (computational costs), the error bars show the Monte Carlo error. The parameters are the same as in Fig. 4
4.3 FX option pricing under a Lévy-type currency exchange model
In this subsection, we demonstrate the use of Algorithm 1 for pricing financial derivatives where underliers follow a Lévy process. We apply the algorithm to estimate the price of a foreign exchange (FX) barrier basket option. A barrier basket option gives the holder the right to buy or sell a certain basket of assets (here foreign currencies) at a specific price K at maturity T in the case when a certain barrier event has occurred. The most used barrier-type options are knock-in and knock-out options. This type of option becomes active (or inactive) in the case of the underlying price S(t) reaching a certain threshold (the barrier) B before reaching its maturity. In most cases barrier option prices cannot be given explicitly and therefore have to be approximated. We illustrate that the algorithm successfully works in the multidimensional case in Example 4.3 and also experimentally demonstrate the convergence orders in Example 4.4, where Assumptions 2.3–2.5 do not hold.
Dependency of \(\epsilon \) on error plot for a simulation example with symmetric singular Lévy measure for \(\alpha =1.5\). The parameters used are \(T=1, C_{+}=0.5, C_{-}=0.5, \mu = 3.0, f=1.0, M = 100{,}000{,}000\) and \({\hat{u}}\) is evaluated at the point (0, 0)
Example 4.3
(Barrier basket option pricing) Let us consider the case with five currencies: GBP, USD, EUR, JPY and CHF, and let us assume that the domestic currency is GBP. We denote the corresponding spot exchange rates as
where \(S_{FORDOM}(t)\) describes the amount of domestic currency DOM one pays/receives for one unit of foreign currency FOR (for more details see [5, 25]). We assume that under a risk-neutral measure \( \mathbb {Q}\) the dynamics for the spot exchange rates can be written as
where \(r_{i}\) are the corresponding short rates of USD, EUR, JPY, CHF and \( r_{GBP}\) is the short rate for GBP, which are for simplicity assumed to be constant; and X(t) is a 4-dimensional Lévy process similar to (2.1) with a single jump noise:
Here \(w(t)=(w_{1}(t),w_{2}(t),w_{3}(t),w_{4}(t))^{\top }\) is a 4-dimensional standard Wiener process. As \(\nu (z),\) we choose the Lévy measure with density (4.8) as in Example 4.2 and we take \( F(t,x)=(f_{1},f_{2},f_{3},f_{4})^{\top }\). We also assume that \(\sigma (s,x)\) is a constant \(4\times 4\) matrix.
The risky asset for a domestic GBP business are the foreign currencies \(Y_{i}(t)=B_{i}(t)\cdot S_{i}(t)\), where \(B_{i}(t)\) denotes the foreign currency (account). Under the measure \(\mathbb {Q}\) all the discounted assets \(\widetilde{Y}_{i}(t)=e^{(r_{i}-r_{GBP})(t-t_{0})}S_{i}(t)=S_{i}(t_{0})\exp (X_{i}(t))\) have to be martingales on the domestic market (therefore discounted by the domestic interest rate) to avoid arbitrage. Using the Ito formula for Lévy processes, we can derive the SDEs for \( \widetilde{Y}_{i}\) (see e.g. [2, p. 288]):
Hence, for all \(\widetilde{Y}_{i}\) to be martingales, the drift component \(b_{i}\) has to be so that
where
We also note that
is satisfied by (4.8) if \(f_{i}<\mu \).
Let us consider a down-and-out (DAO) put option, which can be written as
where \(\mathbf {I}\left( \min \limits _{t_{0}\le t\le T}S(t)>B\right) =1 \) if for any of the underlying exchange rates \(S_{i}(t)>B_{i},\ t_{0}\le t\le T\) , otherwise it is zero.
We use Algorithm 1 (the algorithm is applied to X from (4.10) and then S is computed as \(\exp (X)\) to achieve higher accuracy) together with the Monte Carlo technique to evaluate this barrier basket option price (4.13). In Table 5, market data for the 4 currency pairs are given, and in Table 6 the option and model parameters are provided, which are used in simulations here.
To find the matrix \(\sigma =\{\sigma _{ij}\}\) used in the model (4.10), we form the matrix a using the volatility \(\sigma _{i}\) and correlation coefficient data from Table 5 in the usual way, i.e., \(a_{ii}=\sigma _{i}^{2}\) and \(a_{ij}=\sigma _{i}\sigma _{j}\rho _{ij}\) for \(i\ne j.\) Then the matrix \(\sigma \) is the solution of \(\sigma \sigma ^{\top }=a\) obtained by the Cholesky decomposition.
The results of the simulations are presented in Fig. 7 for different choices of \(\epsilon \) and different choices of h. In Fig. 8, it can be seen that (similar to Example 4.2) by choosing the step size h optimally results in a better approximation for the same cost.
Dependence of the approximate price of the FX barrier basket option on \(\epsilon \) for different choices of h. The error bars show the Monte Carlo error
Dependence of the approximate price of the FX barrier basket option on average number of steps (computational costs) for different choices of h. The error bars show the Monte Carlo error
In this example we demonstrated that Algorithm 1 can be successfully used to price a FX barrier basket option involving 4 currency pairs following an exponential Lévy model despite the considered problem not satisfying Assumptions 2.3–2.5 of Sect. 2.2. In particular, we note that the algorithm is easy to implement and it gives sufficient accuracy with relatively small computational costs. Moreover, application of Algorithm 1 can be easily extended to other multi-dimensional barrier option (and other types of options and not only on FX markets), while other approximation techniques such as finite difference methods or Fourier transform methods typically cannot cope with higher dimensions.
Example 4.4
(Barrier option pricing: one currency pair) In this example, we demonstrate that the convergence orders and computational costs discussed in Sect. 3.5 appear to hold, despite the considered problem not satisfying Assumptions 2.3–2.5 of Sect. 2.2.
Let us consider the case with two currencies: GBP and USD. As before, we assume that the domestic currency is GBP. The corresponding spot exchange rate is
We assume the same dynamics under a risk-neutral measure \(\mathbb {Q}\) for the spot exchange rates as in Example 4.3. Moreover, X(t) is a 1-dimensional Lévy process as defined in (4.10) but for one dimension only. Following the same fashion as in Example 4.3, the risky asset for a domestic GBP business is the foreign currency \(Y(t)=B(t)\cdot S(t)\), where B(t) denotes the foreign currency (account) and under the measure \(\mathbb {Q}\) the discounted asset \(\widetilde{Y}(t)\) has to be a martingale on the domestic market to avoid arbitrage. Using the Ito formula for Lévy processes, we can derive the SDE for \(\widetilde{Y}\) as we did in (4.11)–(4.12). We compute the value for a DAO put option (cf. (4.13)):
The approximate solution \(\hat{P}=\hat{P}_{t_{0}}(T,K)\) is obtained by applying Algorithm 1 directly to the SDE for S(t). To study the dependence of the error of Algorithm 1 on the cut-off parameter \( \epsilon \) for jump sizes and on the parameter \(\alpha \) of the Lévy measure as well as associated computational costs, we need to compare the approximation \(\hat{P}\) with the true price \(P_{t_{0}}(T,K)\). However, in this example, we do not have the exact price, and therefore need to accurately simulate a reference solution. To this end, as in Example 4.3, we apply Algorithm 1 to X(t) and use a sufficiently small \(\epsilon \) and h and also a large number of Monte Carlo simulations M (see Tables 9 and 13). We denote this reference solution as \(\hat{P}^{ref}=\hat{P} _{t_{0}}^{ref}(T,K)\). In this example the absolute error \(e_{ref}\) of Algorithm 1 is evaluated as
In Table 7, market data for the currency pair are given, and in Table 8 the option and model parameters are provided, which are used in simulations here (Table 9).
The results of the simulations for \(\alpha =0.5\) are presented in Figs. 9 and 10 and in Tables 10 and 11 for different choices of \(\epsilon \) and fixed \(h=1.0\) and \(h=0.1\). We can clearly see that the error is of order \(O(\epsilon ^{\alpha })=O(\epsilon ^{0.5})\) as expected. We also observe linear convergence in computational cost (measured in average number of steps).
FX barrier option example, the case \(\alpha =0.5\): dependence of the error on \(\epsilon \) for different choices of h. The error bars show the Monte Carlo error
FX barrier option example, the case \(\alpha =0.5\): dependence of the error e on the average number of steps
FX barrier option example, the case \(\alpha =1.5\): dependence of the error e on \(\epsilon \), the error bars show the Monte Carlo error
FX barrier option example, the case \(\alpha =1.5\): dependence of the error e on the average number of steps
Numerical results for the case \(\alpha =1.5\) are given in Figs. 11 and 12 and in Tables 12, 13 and 14. We observe the expected orders of convergence as given in Sect. 3.5.
In this example, we experimentally demonstrated that convergence orders and computational cost for Algorithm 1 are consistent with predictions of Sect. 3.5 despite the considered problem not satisfying assumptions of Sect. 2.2.
References
Allen, L.J.S.: An Introduction to Stochastic Processes with Applications to Biology. CRC Press, Boca Raton (2003)
Applebaum, D.: Lévy Processes and Stochastic Calculus. Cambridge University Press, Cambridge (2009)
Asmussen, S., Rosiński, J.: Approximations of small jumps of Lévy processes with a view towards simulation. J. Appl. Probab. 38(2), 482–493 (2001)
Barndorff-Nielsen, O.E., Mikosch, T., Resnick, S.I. (eds.): Lévy Processes: Theory and Applications. Birkhäuser, Boston (2001)
Castagna, A.: FX Options and Smile Risk. Wiley, Hoboken (2010)
Cont, R., Tankov, P.: Financial Modelling with Jump Processes. Chapman & Hall/CRC, Boca Raton (2004)
Devroye, L.: Non-uniform Random Variate Generation. Springer, New York (1986)
Garroni, M.G., Menaldi, J.L.: Green Functions for Second Order Parabolic Integro-differential Problems, Pitman Research Notes in Mathematics Series, vol. 275. Longman Scientific & Technical, Harlow (1992)
Jacob, N.: Pseudo Differential Operators and Markov Processes, vol. III. Imperial College Press, London (2005)
Jacod, J., Kurtz, T.G., Méléard, S., Protter, P.: The approximate Euler method for Lévy driven stochastic differential equations. Annales de l’Institut Henri Poincare (B) Probability and Statistics 41(3), 523–558 (2005)
Kohatsu-Higa, A., Tankov, P.: Jump-adapted discretization schemes for Lévy-driven SDEs. Stoch. Process. Appl. 120(11), 2258–2285 (2010)
Kohatsu-Higa, A., Ortiz-Latorre, S., Tankov, P.: Optimal simulation schemes for Lévy driven stochastic differential equations. Math. Comp. 83(289), 2293–2324 (2013)
Leimkuhler, B., Sharma, A., Tretyakov, M.V.: Simplest random walk for approximating Robin boundary value problems and ergodic limits of reflected diffusions. arXiv: 2006.15670 (2020)
Liu, X.Q., Li, C.W.: Weak approximation and extrapolations of stochastic differential equations with jumps. SIAM J. Numer. Anal. 37(6), 1747–1767 (2000)
Mikulevicius, R., Platen, E.: Time discrete Taylor approximations for Ito processes with jump component. Math. Nachr. 138(6), 93–104 (1988)
Mikulevicius, R., Pragarauskas, H.: On Cauchy–Dirichlet problem in half-space for linear integro-differential equations in weighted Hölder spaces. Electron. J. Probab. 10, 1398–1416 (2005)
Mikulevicius, R., Zhang, C.: Weak Euler scheme for Levy-driven stochastic differential equations. Theory Probab. Appl. 63, 346–366 (2018)
Milstein, G., Tretyakov, M.: The simplest random walks for the Dirichlet problem. Theory Probab. Appl. 47(1), 53–68 (2002)
Milstein, G., Tretyakov, M.: Stochastic Numerics for Mathematical Physics. Springer, Berlin (2004)
Mordecki, E., Szepessy, A., Tempone, R., Zouraris, G.E.: Adaptive weak approximation of diffusions with jumps. SIAM J. Numer. Anal. 46(4), 1732–1768 (2008)
Platen, E., Bruti-Liberati, N.: Numerical Solution of Stochastic Differential Equations with Jumps in Finance. Springer, Berlin (2010)
Protter, P., Talay, D.: The Euler scheme for Lévy driven stochastic differential equations. Ann. Probab. 25(1), 393–423 (1997)
Rubenthaler, S.: Numerical simulation of the solution of a stochastic differential equation driven by a Lévy process. Stoch. Process. Appl. 103(2), 311–349 (2003)
van Kampen, N.G.: Stochastic Processes in Physics and Chemistry, 3rd edn. North Holland, Amsterdam (2007)
Wystup, U.: FX Options and Structured Products. Wiley, Hoboken (2007)
Acknowledgements
The authors thank anonymous referees for useful suggestions which improved the manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by David Cohen.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Deligiannidis, G., Maurer, S. & Tretyakov, M.V. Random walk algorithm for the Dirichlet problem for parabolic integro-differential equation. Bit Numer Math 61, 1223–1269 (2021). https://doi.org/10.1007/s10543-021-00863-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10543-021-00863-2
Keywords
- SDEs driven by Lévy processes
- Jump processes
- Integro-differential equations
- Feynman–Kac formula
- Weak approximation of stochastic differential equations