Exact formulae and matrix-less eigensolvers for block banded symmetric Toeplitz matrices

Abstract

Precise asymptotic expansions for the eigenvalues of a Toeplitz matrix $T_n(f)$, as the matrix size n tends to infinity, have recently been obtained, under suitable assumptions on the associated generating function f. A restriction is that f has to be polynomial, monotone, and scalar-valued. In this paper we focus on the case where $\mathbf {f}$ is an $s\times s$ matrix-valued trigonometric polynomial with $s\ge 1$, and $T_n(\mathbf {f})$ is the block Toeplitz matrix generated by $\mathbf {f}$, whose size is $N(n,s)=sn$. The case $s=1$ corresponds to that already treated in the literature. We numerically derive conditions which ensure the existence of an asymptotic expansion for the eigenvalues. Such conditions generalize those known for the scalar-valued setting. Furthermore, following a proposal in the scalar-valued case by the first author, Garoni, and the third author, we devise an extrapolation algorithm for computing the eigenvalues of banded symmetric block Toeplitz matrices with a high level of accuracy and a low computational cost. The resulting algorithm is an eigensolver that does not need to store the original matrix, does not need to perform matrix-vector products, and for this reason is called matrix-less. We use the asymptotic expansion for the efficient computation of the spectrum of special block Toeplitz structures and we provide exact formulae for the eigenvalues of the matrices coming from the $\mathbb {Q}_p$ Lagrangian Finite Element approximation of a second order elliptic differential problem. Numerical results are presented and critically discussed.

Introduction

A matrix $\mathbf A _n$ of the form

$$\begin{aligned} \mathbf A _n=\left[ A_{i-j}\right] _{i,j=1}^{n}=\left[ \begin{array}{cccccc} A_0\quad &{}\quad A_{-1} &{}\quad A_{-2} &{}\quad \cdots &{}\quad \cdots &{}\quad A_{-(n-1)} \\ A_1 &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad &{}\quad \vdots \\ A_2 &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \vdots \\ \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{} \quad \ddots &{}\quad A_{-2}\\ \vdots &{}\quad &{} \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad A_{-1}\\ A_{n-1} &{}\quad \cdots &{}\quad \cdots &{}\quad A_2 &{}\quad A_1 &{}\quad A_0 \end{array}\right] , \end{aligned}$$

where $A_{-(n-1)},\ldots ,A_{n-1}$ are blocks in $\mathbb {C}^{s\times s}$, is said to be a block Toeplitz matrix. Note that the size of $\mathbf A _n$ is $N(n,s)=sn$.

We say that $\phi :[-\,\pi ,\pi ]\rightarrow \mathbb C^{s\times s}$ is a complex matrix-valued Lebesgue integrable function if all its components $\phi _{i,j}:[-\,\pi ,\pi ]\rightarrow \mathbb {C}$, $i,j=1,\dots , s$, are complex-valued Lebesgue integrable functions. The nth block Toeplitz matrix generated by $\phi$ is defined as

$$\begin{aligned} T_n(\phi )=\bigl [\hat{\phi }_{i-j}\bigr ]_{i,j=1}^n, \end{aligned}$$

where the quantities $\hat{\phi }_k \in \mathbb {C}^{s\times s}$ are the Fourier coefficients of $\phi$, that is,

$$\begin{aligned} \hat{\phi }_{k}=\frac{1}{2\pi }\int _{-\pi }^{\pi }\phi (\theta )\,\mathrm{e}^{-\mathbf {i}k\theta }\mathrm{d}\theta ,\quad k\in \mathbb Z. \end{aligned}$$

(1.1)

We refer to $\{T_n(\phi )\}_n$ as the block Toeplitz sequence generated by $\phi$, which in turn is called the generating function or the symbol of $\{T_n(\phi )\}_n$. Such type of matrix sequences have been studied, especially for $s=1$, by many authors including Szegö, Avram, Böttcher, Parter, Sibermann, Tilli, and Tyrtyshnikov (see e.g. [17, 22] and references therein).

Furthermore, if $\phi$ is Hermitian almost everywhere then, by (1.1), $\hat{\phi }_{-k}=\hat{\phi }_{k}^*$ for every $k\in \mathbb Z$ and therefore each $T_n(\phi )$ is Hermitian. As a consequence, the spectrum of $T_n(\phi )$ is real. Moreover, the analytical properties of $\phi$ decide many delicate features of the eigenvalues of $T_n(\phi )$ such as distribution, clustering, and localization, as we briefly describe below without entering into technical details.

Distribution. :

In [22] it was proved that $\{T_n(\phi )\}_n$ has an asymptotic spectral distribution, in the Weyl sense, described by $\phi (\theta )$, under the assumption that $\phi (\theta )$ is a Lebesgue integrable matrix-valued function which is Hermitian almost everywhere. An extension to the non-Hermitian case was given in [11], by adapting the tools introduced by Tilli in [23] for complex-valued generating functions.

When the symbol $\phi$ is also continuous, i.e., each component $\phi _{i,j}$ is continuous, the present distribution result can be described as follows: for sufficiently large n, up to a small number of possible outliers, the eigenvalues of $T_n(\phi )$ can be grouped into s “branches” having approximate cardinality n and for each $q=1,\ldots ,s$ the eigenvalues belonging to the qth branch are approximately given by the samples over a certain uniform grid in $[-\,\pi ,\pi ]$ of the qth eigenvalue function $\lambda ^{(q)}(\phi )$.

Clustering. :

For any $\epsilon >0$, take an $\epsilon$-neighborhood of the set ${\mathcal R}_\phi$, which is defined as the union of the essential ranges of the eigenvalue functions $\lambda ^{(q)}(\phi )$. Then the spectrum of $\{T_n(\phi )\}_n$ is clustered at ${\mathcal R}_\phi$ in the sense that the number of the eigenvalues of $T_n(\phi )$ that do not belong to the $\epsilon$-neighborhood of ${\mathcal R}_\phi$ is o(n) as n tends to infinity. If $\phi$ is a Hermitian-valued trigonometric polynomial, then the number of such outliers is O(1) and it is at most linearly depending on s and on the degree of the polynomial. Such clustering results are consequences of the distribution result. For the case of trigonometric polynomials, on which the present work is focused, see also Appendix A.

Localization. :

Assume that $\lambda ^{(q)}(\phi )$, $q=1,\dots ,s$, are sorted in non-decreasing order, that is, $\lambda ^{(1)}(\phi )\le \lambda ^{(2)}(\phi )\le \cdots \le \lambda ^{(s)}(\phi )$. Then, for all n, the eigenvalues of $T_n(\phi )$ belong to the interval $[m_\phi ,M_\phi ]$, where $m_\phi ={{\mathrm{ess\,inf}}}_{\theta \in [-\pi ,\pi ]} \lambda ^{(1)}(\phi )$ and $M_\phi ={{\mathrm{ess\,sup}}}_{\theta \in [-\pi ,\pi ]}\lambda ^{(s)}(\phi )$. Moreover, if the function $\lambda ^{(1)}(\phi )$ is not essentially constant, then the eigenvalues of $T_n(\phi )$ belong to $(m_\phi ,M_\phi ]$, and, if the function $\lambda ^{(s)}(\phi )$ is not essentially constant, then the eigenvalues of $T_n(\phi )$ belong to $[m_\phi ,M_\phi )$. For such results refer to [19, 20].

Remark 1.1

Part 1.  When the symbol $\phi$ is continuous, then each eigenvalue function $\lambda ^{(q)}(\phi )$, $q=1,\dots , s$, is continuous and therefore the essential infimum becomes a minimum and the essential supremum becomes a maximum (because the interval $[-\,\pi ,\pi ]$ is a compact set), while the essential range is the standard range. Part 2.  Finally the interval $[-\,\pi ,\pi ]$ can be replaced by the interval $[0,\pi ]$ when $\phi (-\,\theta )=\phi (\theta )^T$: this is precisely the case we consider, see (1.3).

In this paper we focus on the case where the symbol is a Hermitian matrix-valued trigonometric polynomial (HTP) $\mathbf {f}$ with Fourier coefficients $\hat{\mathbf {f}}_{0},\hat{\mathbf {f}}_{1},\ldots ,\hat{\mathbf {f}}_{m}\in \mathbb R^{s\times s}$, that is, a function of the form

$$\begin{aligned} \mathbf {f}(\theta )=\sum _{k=-m}^m\hat{\mathbf {f}}_{k} \mathrm{e}^{\mathbf {i}k\theta }=\hat{\mathbf {f}}_{0}+\sum _{k=1}^m\left( \hat{\mathbf {f}}_{k} \mathrm{e}^{\mathbf {i}k\theta }+\hat{\mathbf {f}}_{k}^T \mathrm{e}^{\mathbf {-i}k\theta }\right) ,\quad m=\deg \left( \mathbf {f}(\theta )\right) \in \mathbb N, \end{aligned}$$

where we set

$$\begin{aligned} \hat{\mathbf {f}}_{-k}=\hat{\mathbf {f}}_{k}^T, \quad k=0,\dots ,m. \end{aligned}$$

(1.2)

The assumptions on $\mathbf {f}(\theta )$ imply that $T_n(\mathbf {f})$ is a real symmetric block banded matrix with “block bandwidth” $2m+1$, of the form

Note that from (1.2) we have

$$\begin{aligned} \mathbf { f}(\theta )^T={\hat{\mathbf {f}}}_0+\sum _{k=1}^m\left( {\hat{\mathbf {f}}}_k^T \mathrm{e}^{\mathbf {i}k\theta }+{\hat{\mathbf {f}}}_{-k}^T \mathrm{e}^{\mathbf {-i}k\theta }\right) ={\hat{\mathbf {f}}}_0+\sum _{k=1}^m\left( {\hat{\mathbf {f}}}_{-k} \mathrm{e}^{\mathbf {i}k\theta }+{\hat{\mathbf {f}}}_{k} \mathrm{e}^{\mathbf {-i}k\theta }\right) =\mathbf { f}(-\theta ), \end{aligned}$$

(1.3)

$$\begin{aligned} \mathbf {f}(\theta )^*={\hat{\mathbf {f}}}_0+\sum _{k=1}^m\left( {\hat{\mathbf {f}}}_k^T \mathrm{e}^{-\mathbf {i}k\theta }+{\hat{\mathbf {f}}}_{-k}^T \mathrm{e}^{\mathbf {i}k\theta }\right) ={\hat{\mathbf {f}}}_0+\sum _{k=1}^m\left( {\hat{\mathbf {f}}}_{-k} \mathrm{e}^{\mathbf {-i}k\theta }+{\hat{\mathbf {f}}}_{k} \mathrm{e}^{\mathbf {i}k\theta }\right) =\mathbf { f}(\theta ), \end{aligned}$$

(1.4)

and hence $\mathbf {f}(\theta )$ has the same eigenvalues as $\mathbf {f}(-\,\theta )$. Thus, each eigenvalue function $\lambda ^{(q)}(\mathbf {f})$ is even and we can therefore simply focus on its restriction $\lambda ^{(q)}(\mathbf {f}):[0,\pi ]\rightarrow \mathbb R^{s\times s}$ (in accordance with the second part of Remark 1.1).

In view of the above distribution, clustering, and localization results, up to O(1) possible outliers, the eigenvalues of the symmetric matrix $T_n(\mathbf {f})$ can be partitioned in s subsets (or “branches”) of approximately the same cardinality n; and the eigenvalues belonging to the qth branch are approximately equal to the samples of the qth eigenvalue function $\lambda ^{(q)}(\mathbf f)$ over a uniform grid in $[0,\pi ]$.

In this paper we show that the different branches have a much finer structure and that, under mild restrictions, there exists a hierarchy of symbols which allow us to design extremely economical procedures for the computation of the eigenvalues of the matrices $T_n(\mathbf { f})$. In particular, we conjecture on the basis of numerical experiments that for every integer $\alpha \ge 0$, every $s\ge 1$, and every $q\in \{1,\dots ,s\}$, the following asymptotic expansion holds under the specific local condition and global condition that will be discussed below: for all $n\in \mathbb N$ and $j=1,\ldots ,n$,

$$\begin{aligned} \lambda _\gamma (T_n(\mathbf { f}))=\lambda ^{(q)}(\mathbf { f}(\theta _{j,n}))+\sum _{k=1}^{\alpha }c_k^{(q)}(\theta _{j,n})h^k+E_{j,n,\alpha }^{(q)}\, , \end{aligned}$$

(1.5)

where:

• $\gamma =\gamma (q,j)=(q-1)n+j$;

• $\lambda _k(T_n(\mathbf {f}))$, $k\in \{1,\dots ,N(n,s)\}$, are the eigenvalues of $T_n(\mathbf { f})$, which are sorted so that, for each fixed $\bar{q}\in \{1,\dots , s\}$, the eigenvalues $\lambda _{(\bar{q}-1)n+j}(T_n(\mathbf { f}))$, for $j=1,\ldots ,n$, are arranged in non-decreasing or non-increasing order, depending on whether $\lambda ^{(\bar{q})}(\mathbf { f})$ is increasing or decreasing (this can be seen using the local or the global condition below);

• $\{c_k^{(q)}\}_{k=1,\ldots ,\alpha }$ is a sequence of functions from $[0,\pi ]$ to $\mathbb R$ which depends only on $\mathbf {f}$;

• $h=\frac{1}{n+1}$ and $\theta _{j,n}=\frac{j\pi }{n+1}=j\pi h$, $j=1,\ldots , n$;

• $E_{j,n,\alpha }^{(q)}=O(h^{\alpha +1})$ is the remainder (the error), which satisfies the inequality $|E_{j,n,\alpha }^{(q)}|\le C_\alpha h^{\alpha +1}$ for some constant $C_\alpha$ depending only on $\alpha$ and $\mathbf {f}$.

We note that in the scalar-valued case $s=1$, several theoretical and computational results are available in support of the above expansion [2, 5, 6, 9, 14,15,16], including also extensions to preconditioned matrices and matrices arising in a differential context [1, 13].

Unfortunately, as already shown in [2, 15, 16], the expansion (1.5) is not always satisfied even for $s=1$. Below we give two conditions which ensure that the expansion holds.

Local condition. :

The eigenvalue $\lambda _\gamma (T_n(\mathbf { f}))$ can be expanded as in (1.5) if there exists $\bar{\epsilon }>0$ such that, for all $\epsilon \in (0,\bar{\epsilon })$ and all $y\in (\lambda _\gamma (T_n(\mathbf { f}))-\epsilon ,\lambda _\gamma (T_n(\mathbf { f}))+\epsilon )$, there exists a unique $q\in \{1,\ldots ,s\}$ and a unique $\bar{\theta }\in [0,\pi ]$ for which

$$\begin{aligned} y=\lambda ^{(q)}(\mathbf { f}(\bar{\theta })). \end{aligned}$$

(1.6)

Global condition. :

A trivial global condition is obtained by imposing that the local condition is satisfied for every eigenvalue which is not an outlier (if the eigenvalue $\lambda _\gamma (T_n(\mathbf { f}))$ is an outlier, then, by definition, it does not belong to the range of $\mathbf { f}$ and consequently relation (1.6) cannot be satisfied). A simple general assumption, which is equivalent to the trivial global condition, is that each $\lambda ^{(q)}(\mathbf { f})$, $q=1,\dots , s$, is monotone (non-increasing or non-decreasing) over the interval $[0,\pi ]$ and

$$\begin{aligned} \max _{\theta \in [0,\pi ]} \lambda ^{(q)}(\mathbf { f})< \min _{\theta \in [0,\pi ]}\lambda ^{(q+1)}(\mathbf { f}) \end{aligned}$$

for $q=1,\dots ,s-1$. In other words, the global condition can be summarized as follows: strict monotonicity of every eigenvalue function and the intersection of the ranges of two eigenvalue functions $\lambda ^{(j)}(\mathbf {f})$ and $\lambda ^{(k)}(\mathbf { f})$ is empty for every pair of indices $j,k\in \{1,\ldots ,s\}$ such that $j\ne k$. This version of the global condition is of course much simpler to verify. Moreover, in the case $s=1$ it reduces to the monotonicity condition already used in the literature; see [2, 5, 6, 9, 15, 16] and references therein.

In [15], the authors employed the asymptotic expansion (1.5) with $s=1$ for computing an accurate approximation of $\lambda _j(T_n(\mathbf { f}))$ for very large n, if the values $\lambda _{j_1}(T_{n_1}(\mathbf { f})), \ldots ,\lambda _{j_k}(T_{n_k}(\mathbf { f}))$ are available for moderately sized $n_1,\ldots ,n_k$ such that $\theta _{j_1,n_1}=\cdots =\theta _{j_k,n_k}=\theta _{j,n}$. We stress that the algorithm was developed in [15] and then improved in [1, 12, 14], while the mathematical foundations of the considered expansions and few numerical tests were already present in [5].

The purpose of this paper is to carry out this idea and to support it by numerical experiments accompanied by an appropriate error analysis in the more general case where $s>1$. In particular, we devise an algorithm to compute $\lambda _j(T_n(\mathbf { f}))$ with a high level of accuracy and a relatively low computational cost. The algorithm is completely analogous to the extrapolation procedure [21, Section 3.4], which is employed in the context of Romberg integration to obtain high precision approximations of an integral from a few coarse trapezoidal approximations. In this regard, the asymptotic expansion (1.5) plays here the same role as the Euler-Maclaurin summation formula [21, Section 3.3].

The paper is organized as follows. In Sect. 2, assuming the asymptotic eigenvalue expansion (1.5), we present our extrapolation algorithm for computing the eigenvalues of the $s\times s$ block matrix $T_n(\mathbf { f})$ for $s>1$. In Sect. 3 we provide numerical experiments in support of the asymptotic eigenvalue expansion (1.5) in different cases and we derive exact formulae for the eigenvalues in some practical examples and for matrices coming from order p Lagrangian Finite Element approximations of a second order elliptic differential problem, which are denoted as $\mathbb {Q}_p$. In Sect. 4 we draw conclusions and we outline future lines of research. In “Appendix A” we formally prove (1.5) in the basic case $\alpha =0$, and in “Appendix B” we report in detail the mass and stiffness $\mathbb {Q}_p$ elements for $p=2,3,4$.

Algorithm for computing the eigenvalues of $T_n(\mathbf { f})$ for $s>1$

Assuming that the expansion (1.5) holds true and taking inspiration from [14], in the present section we propose an interpolation–extrapolation algorithm for computing the eigenvalues of $T_n(\mathbf { f})$. In what follows, for each positive integer $n\in \mathbb N=\{1,2,3,\ldots \}$ and each $s>1$ we define $N(n,s)=sn$. Moreover, with each positive integer n we associate the stepsize $h=1/(n+1)$ and the grid points $\theta _{j,n}=j\pi h$, $j=1,\ldots ,n$. For notational convenience, unless otherwise stated, we will always denote a positive integer and the associated stepsize in a strongly related way. For example, if the positive integer is n, then the associated stepsize is h; if the positive integer is $n_1$, then the associated stepsize is $h_1$; if the positive integer is $\bar{n}$, then the associated stepsize is $\bar{h}$; etc. Throughout this section, we make the following assumptions.

• $s>1$ and $n,n_1,\alpha \in \mathbb N$ are fixed parameters.

• $n_k=2^{k-1}(n_1+1)-1$ for $k=1,\ldots ,\alpha$.

• $j_k=2^{k-1}j_1$ where $j_1=\{1,\ldots ,n_1\}$ and $k=1,\ldots ,\alpha$; $j_k$ are the indices such that $\theta _{j_k,n_k}=\theta _{j_1,n_1}$.

A graphical representation of the grids $\theta _{[n_k]}=\{\theta _{j_k,n_k}:\ j_k=1,\ldots ,n_k\}$, for $k=1,\ldots ,\alpha$, is shown in Fig. 1 for $n_1=5$ and $\alpha =4$.

Fig. 1

Representation of the grids $\theta _{[n_k]}$, $k=1,\ldots ,\alpha$, for $n_1=5$ and $\alpha =4$. Red diamonds represent the grid points $\theta _{j_k,n_k}$ and black diamonds represent the rest of the grid points of $\theta _{[n_k]}$ (color figure online)

For each choice of fixed $j_1=\{1,\ldots ,n_1\}$ we apply $\alpha$ times the expansion (1.5) with $n=n_1,n_2,\ldots ,n_\alpha$ and $j=j_1,j_2,\ldots ,j_\alpha$. Since $\theta _{j_1,n_1}=\theta _{j_2,n_2}=\ldots =\theta _{j_\alpha ,n_\alpha }$ (by definition of $j_2,\ldots ,j_\alpha$), we obtain, for $q=1,\dots ,s$,

$$\begin{aligned} \left\{ \begin{aligned} E_{j_1,n_1,0}^{(q)}&=c_1^{(q)}(\theta _{j_1,n_1})h_1+c_2^{(q)}(\theta _{j_1,n_1})h_1^2+\cdots +c_\alpha ^{(q)}(\theta _{j_1,n_1})h_1^\alpha +E_{j_1,n_1,\alpha }^{(q)},\\ E_{j_2,n_2,0}^{(q)}&=c_1^{(q)}(\theta _{j_1,n_1})h_2+c_2^{(q)}(\theta _{j_1,n_1})h_2^2+\cdots +c_\alpha ^{(q)}(\theta _{j_1,n_1})h_2^\alpha +E_{j_2,n_2,\alpha }^{(q)},\\ \vdots \qquad&\\ E_{j_\alpha ,n_\alpha ,0}^{(q)}&=c_1^{(q)}(\theta _{j_1,n_1})h_\alpha +c_2^{(q)}(\theta _{j_1,n_1})h_\alpha ^2+\cdots +c_\alpha ^{(q)}(\theta _{j_1,n_1})h_\alpha ^\alpha +E_{j_\alpha ,n_\alpha ,\alpha }^{(q)},\\ \end{aligned}\right. \end{aligned}$$

(2.1)

where

$$\begin{aligned} E_{j_k,n_k,0}^{(q)}=\lambda _{\gamma _k}(T_{n_k}(\mathbf { f}))-\lambda ^{(q)}(\mathbf { f}(\theta _{j_1,n_1})),\qquad k=1,\ldots ,\alpha , \qquad \gamma _k=(q-1)n_k+j_k \end{aligned}$$

and

$$\begin{aligned} \left| E_{j_k,n_k,\alpha }^{(q)}\right| \le C_\alpha ^{(q)} h_k^{\alpha +1},\qquad k=1,\ldots ,\alpha . \end{aligned}$$

(2.2)

For $q=1,\dots ,s$, let $\tilde{c}_1^{(q)}(\theta _{j_1,n_1}),\ldots ,\tilde{c}_\alpha ^{(q)}(\theta _{j_1,n_1})$ be the approximations of $c_1^{(q)}(\theta _{j_1,n_1}),\ldots ,c_\alpha ^{(q)}(\theta _{j_1,n_1})$ obtained by removing all the errors $E_{j_1,n_1,\alpha }^{(q)},\ldots ,E_{j_\alpha ,n_\alpha ,\alpha }^{(q)}$ in (2.1) and by solving the resulting linear system:

$$\begin{aligned} \left\{ \begin{aligned} E_{j_1,n_1,0}^{(q)}&=\tilde{c}_1^{(q)}(\theta _{j_1,n_1})h_1+\tilde{c}_2^{(q)}(\theta _{j_1,n_1})h_1^2+\cdots +\tilde{c}_\alpha ^{(q)}(\theta _{j_1,n_1})h_1^\alpha ,\\ E_{j_2,n_2,0}^{(q)}&=\tilde{c}_1^{(q)}(\theta _{j_1,n_1})h_2+\tilde{c}_2^{(q)}(\theta _{j_1,n_1})h_2^2+\cdots +\tilde{c}_\alpha ^{(q)}(\theta _{j_1,n_1})h_2^\alpha ,\\ \vdots \qquad&\\ E_{j_\alpha ,n_\alpha ,0}^{(q)}&=\tilde{c}_1^{(q)}(\theta _{j_1,n_1})h_\alpha +\tilde{c}_2^{(q)}(\theta _{j_1,n_1})h_\alpha ^2+\cdots +\tilde{c}_\alpha ^{(q)}(\theta _{j_1,n_1})h_\alpha ^\alpha .\\ \end{aligned}\right. \end{aligned}$$

(2.3)

Note that this way of computing approximations for $c_1^{(q)}(\theta _{j_1,n_1}),\ldots ,c_\alpha ^{(q)}(\theta _{j_1,n_1})$ is completely analogous to the Richardson extrapolation procedure that is employed in the context of Romberg integration to accelerate the convergence of the trapezoidal rule [21, Section 3.4], with the asymptotic expansion (1.5) playing here the same role as the Euler–Maclaurin summation formula [21, Section 3.3]. For more advanced studies on extrapolation methods, we refer the reader to the classical book by Brezinski and Redivo-Zaglia [8]. The next theorem shows that, for $q=1,\dots ,s$, the approximation error $\left| c_k^{(q)}(\theta _{j_1,n_1})-\tilde{c}_k^{(q)}(\theta _{j_1,n_1})\right|$ is $O(h_1^{\alpha -k+1})$.

Theorem 2.1

There exists a constant $A_\alpha ^{(q)}$ depending only on $\alpha$ and $q=1,\dots , s$ such that, for $j_1=1,\ldots ,n_1$ and $k=1,\ldots ,\alpha$,

$$\begin{aligned} \left| c_k^{(q)}(\theta _{j_1,n_1})-\tilde{c}_k^{(q)}(\theta _{j_1,n_1})\right| \le A_\alpha ^{(q)} h_1^{\alpha -k+1}, \quad q=1,\dots ,s. \end{aligned}$$

(2.4)

Proof

It is a straightforward adaptation of the proof given in [14, Theorem 1].

Take an $n\gg n_1$ and fix an index $j\in \{1,\ldots ,n\}$. We henceforth assume that $q\in \{1,2,\dots ,s\}$. To compute an approximation of $\lambda _\gamma (T_n(\mathbf { f}))$, $\gamma =(q-1)n+j$, through the expansion (1.5) we need the value $c_k^{(q)}(\theta _{j,n})$ for each $k=1,\ldots ,\alpha$. Of course, $c_k^{(q)}(\theta _{j,n})$ is not available in practice, but we can approximate it by interpolating and extrapolating the values $\tilde{c}_k^{(q)}(\theta _{j_1,n_1})$, $j_1=1,\ldots ,n_1$. For example, we may define $\tilde{c}_k^{(q)}(\theta )$ as the interpolation polynomial of the data $(\theta _{j_1,n_1},\tilde{c}_k^{(q)}(\theta _{j_1,n_1})),\hbox { for } j_1=1,\ldots ,n_1$,—so that $\tilde{c}_k^{(q)}(\theta )$ is expected to be an approximation of $c_k^{(q)}(\theta )$ over the whole interval $[0,\pi ]$—and take $\tilde{c}_k^{(q)}(\theta _{j,n})$ as an approximation to $c_k^{(q)}(\theta _{j,n})$. It is known, however, that interpolating over a large number of uniform nodes is not advisable, as it may give rise to spurious oscillations (Runge’s phenomenon). It is therefore better to adopt another kind of approximation. An alternative could be the following: we approximate $c_k^{(q)}(\theta )$ by the spline function $\tilde{c}_k^{(q)}(\theta )$ which is linear on each interval $[\theta _{j_1,n_1},\theta _{j_1+1,n_1}]$ and takes the value $\tilde{c}_k^{(q)}(\theta _{j_1,n_1})$ at $\theta _{j_1,n_1}$ for all $j_1=1,\ldots ,n_1$. This strategy removes for sure any spurious oscillation, yet it is not accurate. In particular, it does not preserve the accuracy of approximation at the nodes $\theta _{j_1,n_1}$ established in Theorem 2.1, i.e., there is no guarantee that $|c_k^{(q)}(\theta )-\tilde{c}_k^{(q)}(\theta )|\le B_\alpha ^{(q)} h_1^{\alpha -k+1}$ for $\theta \in [0,\pi ]$ or $|c_k^{(q)}(\theta _{j,n})-\tilde{c}_k^{(q)}(\theta _{j,n})|\le B_\alpha ^{(q)} h_1^{\alpha -k+1}$ for $j=1,\ldots ,n$, with $B_\alpha ^{(q)}$ being a constant depending only on $\alpha$ and q. As proved in Theorem 2.2, a local approximation strategy that preserves the accuracy (2.4), at least if $c_k^{(q)}(\theta )$ is sufficiently smooth, is the following: let $\theta ^{(1)},\ldots ,\theta ^{(\alpha -k+1)}$ be $\alpha -k+1$ points of the grid $\{\theta _{1,n_1},\ldots ,\theta _{n_1,n_1}\}$ which are closest to the point $\theta _{j,n}$,¹ and let $\tilde{c}_{k,j}^{(q)}(\theta )$ be the interpolation polynomial of the data $(\theta ^{(1)},\tilde{c}_k^{(q)}(\theta ^{(1)})),\ldots ,(\theta ^{(\alpha -k+1)},\tilde{c}_k^{(q)}(\theta ^{(\alpha -k+1)}))$; then, we approximate $c_k^{(q)}(\theta _{j,n})$ by $\tilde{c}_{k,j}^{(q)}(\theta _{j,n})$. Note that, by selecting $\alpha -k+1$ points from $\{\theta _{1,n_1},\ldots ,\theta _{n_1,n_1}\}$, we are implicitly assuming that $n_1\ge \alpha -k+1$.

Theorem 2.2

Let $1\le k\le \alpha$, and suppose $n_1\ge \alpha -k+1$ and $c_k^{(q)}\in C^{\alpha -k+1}[0,\pi ]$. For $j=1,\ldots ,n$, if $\theta ^{(1)},\ldots ,\theta ^{(\alpha -k+1)}$ are $\alpha -k+1$ points of $\{\theta _{1,n_1},\ldots ,\theta _{n_1,n_1}\}$ which are closest to $\theta _{j,n}$, and if $\tilde{c}_{k,j}^{(q)}(\theta )$ is the interpolation polynomial of the data $(\theta ^{(1)},\tilde{c}_k^{(q)}(\theta ^{(1)})),\ldots ,(\theta ^{(\alpha -k+1)},\tilde{c}_k^{(q)}(\theta ^{(\alpha -k+1)}))$, then

$$\begin{aligned} \left| c_k^{(q)}(\theta _{j,n})-\tilde{c}_{k,j}^{(q)}(\theta _{j,n})\right| \le B_\alpha ^{(q)} h_1^{\alpha -k+1} \end{aligned}$$

(2.5)

for some constant $B_\alpha ^{(q)}$ depending only on $\alpha$ and q.

Proof

It is a straightforward adaptation of the proof of [14, Theorem 2].

We are now ready to formulate our algorithm for computing the eigenvalues of $T_n(\mathbf { f})$.

Remark 2.1

Algorithm 1 is specifically designed for computing $\lambda _\gamma (T_n(\mathbf { f}))$ in the case where n is quite large. When applying this algorithm, it is implicitly assumed that $n_1$ and $\alpha$ are small (much smaller than n), so that each $n_k=2^{k-1}(n_1+1)-1$ is small as well and the computation of the eigenvalues $\tilde{\lambda }_\gamma (T_n(\mathbf { f}))$—which is required in the first step—can be efficiently performed by any standard eigensolver (e.g., the Matlab eig function).

The last theorem of the current section provides an estimate for the approximation error made by Algorithm 1.

Theorem 2.3

Let $n\ge n_1\ge \alpha$ and $c_k^{(q)}\in C^{\alpha -k+1}[0,\pi ]$ for $k=1,\ldots ,\alpha$. Let

$$\begin{aligned} (\tilde{\lambda }_{(q-1)n+1}(T_n(\mathbf { f})), \tilde{\lambda }_{(q-1)n+2}(T_n(\mathbf { f})) \ldots ,\tilde{\lambda }_{qn}(T_n(\mathbf { f})) \end{aligned}$$

be the approximation of $(\lambda _{(q-1)n+1}(T_n(\mathbf { f})), \lambda _{(q-1)n+2}(T_n(\mathbf { f})) \ldots ,\lambda _{qn}(T_n(\mathbf { f}))$ computed by Algorithm 1. Then, there exists a constant $D_\alpha ^{(q)}$ depending only on $\alpha$ and s such that, for $j=1,\ldots ,n$, $\gamma =(q-1)n+j,$

$$\begin{aligned} \left| \lambda _\gamma (T_n(\mathbf { f}))-\tilde{\lambda }_\gamma (T_n(\mathbf { f}))\right| \le D_\alpha ^{(q)} hh_1^\alpha . \end{aligned}$$

(2.6)

Proof

By (1.5) and Theorem 2.2,

$$\begin{aligned} \left| \lambda _\gamma (T_n(\mathbf { f}))-\tilde{\lambda }_\gamma (T_n(\mathbf { f}))\right|&=\left| \lambda ^{(q)}(\mathbf { f}(\theta _{j,n}))+\sum _{k=1}^\alpha c_k^{(q)}(\theta _{j,n})h^k+E_{j,n,\alpha }^{(q)}-\lambda ^{(q)}(\mathbf { f}(\theta _{j,n}))\right. \\&\quad \left. -\sum _{k=1}^\alpha \tilde{c}_{k,j}^{(q)}(\theta _{j,n})h^k\right| \nonumber \\&\le \sum _{k=1}^\alpha \left| c_k^{(q)}(\theta _{j,n})-\tilde{c}_{k,j}^{(q)}(\theta _{j,n})\right| h^k+\left| E_{j,n,\alpha }^{(q)}\right| \nonumber \\&\le B_\alpha ^{(q)}\sum _{k=1}^\alpha h_1^{\alpha -k+1}h^{k}+C_\alpha ^{(q)} h^{\alpha +1}\le h \left( \alpha B_\alpha ^{(q)}h_1^\alpha +C_\alpha ^{(q)}h_1^\alpha \right) \\&\le D_\alpha ^{(q)} h_1^\alpha h, \end{aligned}$$

where $D_\alpha ^{(q)}=(\alpha +1)\max (B_\alpha ^{(q)},C_\alpha ^{(q)})$.

Numerical experiments

In the current section we present a selection of numerical experiments to validate the algorithms based on the asymptotic expansion (1.5) in different cases where $\mathbf {f}$ is matrix-valued, and we give exact formulae for the eigenvalues in some examples of practical interest.

Description

We test the asymptotic expansion and the interpolation–extrapolation algorithm in Sect. 2 in order to obtain an approximation of the eigenvalues $\lambda _\gamma ({T_n(\mathbf {f})})$, for $\gamma =1,\dots ,sn$, for large n.

• Example 1. We show that the expansion and the associated interpolation–extrapolation algorithm can be applied to the whole spectrum, since the symbol satisfies the global condition.

• Example 2. We show that the expansion and the interpolation–extrapolation algorithm can be locally applied for computing the approximation of the eigenvalues verifying the local condition. In this particular case, the global condition does not hold because the intersection of ranges of two eigenvalue functions is a nontrivial interval and in addition there exists an index $q \in \{1,\dots , s\}$ such that $\lambda ^{(q)}(\mathbf {f})$ is non-monotone.

• Example 3. We show that the expansion and interpolation–extrapolation algorithm can be locally applied for the computation of the eigenvalues satisfying the local condition. For the specific example, the global condition does not hold since there exists an index $q \in \{1,\dots , s\}$ such that $\lambda ^{(q)}(\mathbf {f})$ is non-monotone either globally on $[0,\pi ]$ or just on a subinterval contained in $[0,\pi ]$.

• Example 4. We show how to bypass the local condition in a few special cases: in fact, using different sampling grids, we can recover exact formulas for parts of the spectrum, where the assumption of monotonicity is violated.

• Example 5. We give a close formula for the eigenvalues of matrices arising from the rectangular Lagrange Finite Element method with polynomials of degree $p>1$, usually denoted as $\mathbb {Q}_p$ elements. The number of the eigenvalue functions, which verify the global condition, depends on the order of the $\mathbb {Q}_p$ elements. In this specific setting we have $s=p$.

Experiments

In Examples 1–3 we do not compute analytically the eigenvalue functions of $\mathbf {f}$, but, for $q=1,\dots s$, we are able to provide an ’exact’ evaluation of $\lambda ^{(q)}(\mathbf {f})$ at $\theta _{j_k,n_k}$, $j_k=1,\dots , n_k,$ by exploiting the following procedure:

• sample $\mathbf {f}$ at $\theta _{j_k,n_k}$, $j_k=1,\dots , n_k$, obtaining $n_k$ $s\times s$ matrices, $M_{j_k};$

• for each $j_k=1,\dots , n_k$, compute the s eigenvalues of $M_{j_k}$, $\lambda _q(M_{j_k})$, $q=1,\dots ,s$;

• for a fixed $q=1,\dots s$, the evaluation of $\lambda ^{(q)}(\mathbf {f})$ at $\theta _{j_k,n_k}$, $j_k=1,\dots , n_k,$ is given by $\lambda _q(M_{j_k})$, $j_k=1,\dots ,n_k$.

This procedure is justified by the fact that here $\mathbf {f}$ is a trigonometric polynomial and, denoting by $C_{n_k}(\mathbf {f})$ the circulant matrix generated by $\mathbf {f}$, the eigenvalues of $C_{n_k}(\mathbf {f})$ are given by the evaluations of $\lambda ^{(q)}(\mathbf {f})$ at the grid points $\theta _{r,n_k}=2\pi \frac{r}{n_k}$, $r=0,\dots ,n_k-1$, since

$$\begin{aligned} C_{ n_k}(\mathbf {f})=(F_{n_k}\otimes I_s) D_{ n_k}(\mathbf {f}) (F_{ n_k}\otimes I_s)^*, \end{aligned}$$

where

$$\begin{aligned} D_{n_k}(\mathbf {f}) =\mathrm{diag}_{ 0\le r\le n_k- 1}\left( \mathbf {f}\left( \theta _{ r,n_k}\right) \right) , \quad \theta _{ r,n_k}=2\pi \frac{ {r}}{{ n_k}}, \quad F_{n_k}=\frac{1}{\sqrt{ n_k}} \left( \mathrm{e}^{-i2\pi \frac{j r}{n_k}}\right) _{ j, r=0}^{n_k-1}, \end{aligned}$$

and $I_s$ the $s \times s$ identity matrix [18]. Furthermore, by exploiting the localization results [19, 20] stated in the introduction, we know that each eigenvalue of $T_n(\mathbf {f})$, for each n, belongs to the interval

$$\begin{aligned} \left( \min _{\theta \in [0,\pi ]} \lambda ^{(1)}(\mathbf {f}), \max _{\theta \in [0,\pi ]}\lambda ^{(s)}(\mathbf {f})\right) . \end{aligned}$$

Example 1

In this example we have block size $s=3$, and each eigenvalue function $\lambda ^{(q)}(\mathbf {f}), q=1,2,3$, is strictly monotone over $[0,\pi ]$. The eigenvalue functions satisfy

$$\begin{aligned} \max _{\theta \in [0,\pi ]} \lambda ^{(1)}(\mathbf {f})&< \min _{\theta \in [0,\pi ]}\lambda ^{(2)}(\mathbf {f}),\\ \max _{\theta \in [0,\pi ]} \lambda ^{(2)}(\mathbf {f})&< \min _{\theta \in [0,\pi ]}\lambda ^{(3)}(\mathbf {f}). \end{aligned}$$

In top left panel of Fig. 2 the graphs of the three eigenvalue functions are shown.

The Toeplitz matrix generated by $\mathbf {f}$ is a pentadiagonal block matrix, $T_n(\mathbf {f})\in \mathbb {R}^{N\times N}$, where $N=3n$, and all the blocks belong to $\mathbb {R}^{3\times 3}$, that is

$$\begin{aligned} T_n(\mathbf {f})&=\left[ \begin{array}{cccccc} \hat{\mathbf {f}}_0&{}\quad \hat{\mathbf {f}}_1&{}\quad \hat{\mathbf {f}}_2&{}\quad &{}\quad &{}\quad \phantom {\ddots }\\ \hat{\mathbf {f}}_1&{}\quad \ddots &{}\quad \ddots &{}\quad \ddots \\ \hat{\mathbf {f}}_2&{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots \\ &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \hat{\mathbf {f}}_2\\ &{}\quad &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \hat{\mathbf {f}}_1\\ \phantom {\ddots }&{}\quad &{}\quad &{}\quad \hat{\mathbf {f}}_2&{}\quad \hat{\mathbf {f}}_1&{}\quad \hat{\mathbf {f}}_0 \end{array} \right] ,\quad \hat{\mathbf {f}}_0=\left[ \begin{array}{rrr} 50&{}\quad 2&{}\quad 0\\ 2&{}\quad -\,55&{}\quad 2\\ 0&{}\quad 2&{}\quad 10 \end{array}\right] , \\ \hat{\mathbf {f}}_1&=\left[ \begin{array}{rrr} 11&{}\quad -\,1&{}\quad 0\\ -\,1&{}\quad -\,6&{}\quad -\,1\\ 0&{}\quad -\,1&{}\quad 9 \end{array}\right] , \quad \hat{\mathbf {f}}_2=\begin{bmatrix} 1&\quad 0&\quad 2\\ 0&\quad 1&\quad 0\\ 2&\quad 0&\quad 1 \end{bmatrix}. \end{aligned}$$

Here $\mathbf {f}$ is such that the global condition is satisfied. Hence we can use the asymptotic expansion and Algorithm 1 to get an accurate approximation of the eigenvalues of $T_n(\mathbf {f})$ for a large n. Solving system (2.3) with $\alpha =4$ and $n_1=100$, we obtain the approximation of $c^{(q)}_k(\theta _{j_1,n_1})$, $k=1,\ldots ,\alpha$. In Fig. 2, in the top right and bottom panels, the approximated expansion functions $\tilde{c}^{(q)}_k(\theta _{j_1,n_1})$, $k=1,\ldots ,\alpha$, $q=1,\dots ,s$ are shown for each eigenvalue function. For a fixed $q=1,\dots , s$, the values $\tilde{c}^{(q)}_k(\theta _{j_1,n_1})$, $k=1,\ldots ,\alpha$, $j_1=1,\dots ,n_1$ are known, and finally we can compute $\tilde{\lambda }_\gamma (T_n(\mathbf { f}))$ for $n=10000$, by using (1.5). For simplicity we plot the eigenvalue functions and also the expansion errors, $E^{(q)}_{j_1,n_1,0}$, for $q=1,2,3$. In the right panel of Fig. 3 (in black) we show the errors, $E_{j,n,0}^{(q)}$, $q=1,\dots ,3$, versus $\gamma$, from direct calculation of

$$\begin{aligned} \lambda _\gamma (T_n(\mathbf { f}))-\lambda ^{(q)}(\mathbf { f}(\theta _{j,n})), \end{aligned}$$

for $j=1,\dots ,n$, $q=1,\dots ,3$. As expected, with $\alpha =0$, the errors $E_{j,n,0}^{(q)}$, $q=1,\dots ,3$, are rather large. In the right panel of Fig. 3, comparing $E_{j,n,0}^{(q)}$ with errors $\tilde{E}_{j,n,\alpha }^{(q)}$, $q=1,\dots ,3$, we see the errors are significantly reduced if we calculate $\tilde{\lambda }_\gamma (T_n(\mathbf { f}))$, $\gamma =1,\dots ,3n$, shown in the left panel of Fig. 3, using Algorithm 1, with $\alpha =4$, $n_1=100$, and $n=10000$. Furthermore, a careful study of the left panel of Fig. 3 (coloured) also reveals that, for $q=1,\dots ,s$, $\tilde{E}_{j,n,\alpha }^{(q)}$ have local minima, attained when $\theta _{j,n}$ is approximately equal to some of the coarse grid points $\theta _{j_1,n_1},\ j_1=1,\ldots ,n_1$. This is no surprise, because for $\theta _{j,n}=\theta _{j_1,n_1}$ we have $\tilde{c}_{k,j}^{(q)}(\theta _{j,n})=\tilde{c}_k^{(q)}(\theta _{j_1,n_1})$ and $c_k^{(q)}(\theta _{j,n})=c_k^{(q)}(\theta _{j_1,n_1})$, which means that the error of the approximation $\tilde{c}_{k,j}^{(q)}(\theta _{j,n})\approx c_k^{(q)}(\theta _{j,n})$ reduces to the error of the approximation $\tilde{c}_k^{(q)}(\theta _{j_1,n_1})\approx c_k^{(q)}(\theta _{j_1,n_1})$. The latter implies that we are not introducing further errors due to the interpolation process.

Fig. 2

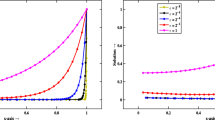
Example 1: Computations made with $n_1=100$, $\alpha =4$. Top Left: The three eigenvalue functions, $\lambda ^{(q)}({\mathbf {f}}), q=1,2,3$. Top Right: Approximations $\tilde{c}_k(\theta _{j_1,n_1})$ for $\lambda ^{(1)}({\mathbf {f}})$. Bottom Left: Approximations $\tilde{c}_k(\theta _{j_1,n_1})$ for $\lambda ^{(2)}({\mathbf {f}})$. Bottom Right: Approximations $\tilde{c}_k(\theta _{j_1,n_1})$ for $\lambda ^{(3)}({\mathbf {f}})$

Fig. 3

Example 1: Left: Errors $\log _{10}|\tilde{E}_{j,n,\alpha }^{(q)}|$, with $\alpha =4$, and errors $\log _{10}|E_{j,n,0}^{(q)}|$ , $q=1,2,3$, versus $\gamma$ for $\gamma =1,\ldots ,3n$. Computations made with $n_1=100$ and $n=10000$. Right: Approximated eigenvalues $\tilde{\lambda }_\gamma (T_n(\mathbf {f}))$, sorted in non-decreasing order. Computation made with the interpolation–extrapolation algorithm, with $\alpha =4$, $n_1=100$ and $n=10000$

Example 2

In the present example we choose block size $s=3$, with eigenvalue functions $\lambda ^{(1)}({\mathbf {f}})$ and $\lambda ^{(3)}({\mathbf {f}})$ being strictly monotone on $[0,\pi ]$. The second eigenvalue function, $\lambda ^{(2)}({\mathbf {f}})$, is non-monotone on a small subinterval of $[0,\pi ]$. Furthermore the range of $\lambda ^{(2)}({\mathbf {f}})$ intersects that of $\lambda ^{(3)}({\mathbf {f}})$, that is

$$\begin{aligned} \max _{\theta \in [0,\pi ]} \lambda ^{(1)}(\mathbf {f})&< \min _{\theta \in [0,\pi ]}\lambda ^{(2)}(\mathbf {f}),\\ \max _{\theta \in [0,\pi ]} \lambda ^{(2)}(\mathbf {f})&> \min _{\theta \in [0,\pi ]}\lambda ^{(3)}(\mathbf {f}). \end{aligned}$$

When comparing with Example 1, the only difference in forming the matrix $T_n({\mathbf {f}})$ consists in the first Fourier coefficient which is defined as

$$\begin{aligned} \hat{\mathbf {f}}_0=\left[ \begin{array}{rrr} 12&{}\quad 2&{}\quad 0\\ 2&{}\quad -\,55&{}\quad 2\\ 0&{}\quad 2&{}\quad 10 \end{array}\right] . \end{aligned}$$

In this example we want to show that it is possible to give an approximation of the eigenvalues $\lambda _\gamma (T_n({\mathbf {f}}))$, $n=10000$, satisfying the local condition.

From the top left panel of Fig. 4, where the graphs of the three eigenvalue functions are displayed, we notice that

• $\lambda ^{(1)}(\mathbf {f})$ is monotone non-decreasing and its range does not intersect that of $\lambda ^{(q)}(\mathbf {f})$, $q=2,3$. Hence, using the asymptotic expansion in (1.5), we expect that it is possible to give an approximation of the first n eigenvalues $\lambda _\gamma (T_n(\mathbf {f}))$, for $j=1,\dots , n$;

• $\lambda ^{(3)}(\mathbf {f})$ is monotone non-increasing and there exist $\hat{\theta }_1$, $\hat{\theta }_2 \in [0,\pi ]$ such that, $\forall$ $\theta \in [0,\hat{\theta }_1)\cup (\hat{\theta }_2,\pi ]$,

  $$\begin{aligned} (\lambda ^{(3)}(\mathbf {f}))(\theta )\not \in \mathrm{Range}(\lambda ^{(2)}(\mathbf {f})). \end{aligned}$$

  Hence, of the remaining 2n eigenvalues, we expect that it is possible to give a fast approximation just of those eigenvalues $\lambda _\gamma (T_n(\mathbf {f}))$ verifying local condition, that is those satisfying the relation below

  $$\begin{aligned} \lambda _\gamma (T_n(\mathbf {f}))\in {\Biggl [}(\lambda ^{(3)}(\mathbf {f}))(\pi ),(\lambda ^{(3)}(\mathbf {f}))(\hat{\theta }_2){\Biggl )}\quad \bigcup \quad {\Biggl (}(\lambda ^{(3)}(\mathbf {f}))(\hat{\theta }_1),(\lambda ^{(3)}(\mathbf {f}))(0){\Biggl ]}. \end{aligned}$$

  (3.1)

We fix $\alpha =4$, $n_1=100$ and we proceed to calculate the approximation of $c^{(q)}_k(\theta _{j_1,n_1}), k=1,\ldots ,\alpha$, as in the previous example. As expected, the graph of $\tilde{c}^{(1)}_k(\theta _{j_1,n_1}),\, k=1,\ldots ,4$, shown in the top right panel of Fig. 4, reveals that we can compute $\tilde{\lambda }_\gamma (T_n(\mathbf { f}))$, for $q=1$ and $j=1,\dots ,n$, using (1.5). In other words the first n eigenvalues of $T_n(\mathbf { f})$ can be computed using our matrix-less procedure.

Fig. 4

Example 2: Top Left: The eigenvalue functions, $\lambda ^{(q)}({\mathbf {f}})$, $q=1,2,3$. Top Right: Approximations $\tilde{c}_k(\theta _{j_1,n_1})$ for $\lambda ^{(1)}({\mathbf {f}})$. Bottom Left: Approximations $\tilde{c}_k(\theta _{j_1,n_1})$ for $\lambda ^{(2)}({\mathbf {f}})$. Bottom Right: Approximations $\tilde{c}_k(\theta _{j_1,n_1})$ for $\lambda ^{(3)}({\mathbf {f}})$. Computations made with $n_1=100$ and $\alpha =4$

For $q=2$ no extrapolation procedure can be applied with $\tilde{c}^{(2)}_k(\theta _{j_1,n_1}), \hbox { for } k=1,\ldots ,4$, as we can see from the oscillating and irregular graph in the bottom left panel of Fig. 4. Concerning Fig. 5 the chaotic behavior of $\tilde{c}^{(2)}_k(\theta _{j_1,n_1}), \, k=1,\ldots ,4$ corresponds to the rather large and oscillating errors $E_{j,n,0}^{(2)}$ and $\tilde{E}_{j,n,\alpha }^{(2)}$. On the other hand for $q=3$ we can use the extrapolation procedure and the underlying asymptotic expansion with $\tilde{c}^{(3)}_k(\theta _{j_1,n_1}), k=1,\ldots ,4$ for $\theta _{j_1,n_1}\in [0,\hat{\theta }_1)\cup (\hat{\theta }_2,\pi ],\,$ $j_1=1,\dots ,n_1$.

As a consequence we compute the approximation of the first n eigenvalues $\lambda _\gamma (T_n(\mathbf { f}))$, for $\gamma =1,\dots ,n$ and that of other $\hat{n}_1+\hat{n}_2$, that verify (3.1). For simplicity, in the right panel of Fig. 5, we visualize them by using the non-decreasing order instead of the computational one.

The good approximation of the $\hat{n}_1+\hat{n}_2$ eigenvalues belonging to

$$\begin{aligned} {\Biggl [}(\lambda ^{(3)}(\mathbf {f}))(\pi ),(\lambda ^{(3)}(\mathbf {f}))(\hat{\theta }_2){\Biggl )}\quad \bigcup \quad {\Biggl (}(\lambda ^{(3)}(\mathbf {f}))(\hat{\theta }_1),(\lambda ^{(3)}(\mathbf {f}))(0){\Biggr ]} \end{aligned}$$

is confirmed by the error $\tilde{E}_{j,n,\alpha }^{(3)}$ in the left panel of Fig. 5. In fact the error is quite high for $\gamma =2n+\hat{n}_1+1,\dots ,3n-\hat{n}_2$, but it becomes sufficiently small for $\gamma =2n+1,\dots , 2n+\hat{n}_1$ and $\gamma =3n-\hat{n}_2+1,\dots ,3n$.

Fig. 5

Example 2: Left: Errors $\log _{10}|\tilde{E}_{j,n,\alpha }^{(q)}|$, with $\alpha =4$, and errors $\log _{10}|E_{j,n,0}^{(q)}|$ , $q=1,2,3$, versus $\gamma$ for $\gamma =1,\ldots ,3n$. Computations made with $n_1=100$ and $n=10000$. Right: Approximated eigenvalues $\tilde{\lambda }_\gamma (T_n(\mathbf {f}))$, sorted in non-decreasing order, for $\gamma =1,\dots , n$ and for $\gamma$ such that $\lambda _\gamma (T_n(\mathbf { f}))$ verifies (3.1). Computation made with the interpolation–extrapolation algorithm, with $\alpha =4$, $n_1=100$ and $n=10000$

Example 3

In this example we set the block size $s=3$, and the eigenvalue functions $\lambda ^{(q)}(\mathbf {f}), q=1,2,3$, satisfy

$$\begin{aligned} \max _{\theta \in [0,\pi ]} \lambda ^{(1)}(\mathbf {f})&< \min _{\theta \in [0,\pi ]}\lambda ^{(2)}(\mathbf {f}),\\ \max _{\theta \in [0,\pi ]} \lambda ^{(2)}(\mathbf {f})&< \min _{\theta \in [0,\pi ]}\lambda ^{(3)}(\mathbf {f}). \end{aligned}$$

See the top left panel of Fig. 6 for the plot of $\lambda ^{(q)}(\mathbf {f}), \,q=1,2,3$.

Fig. 6

Example 3: Top Left: Eigenvalue functions $\lambda ^{(q)}({\mathbf {f}})$, $q=1,2,3$. Top Right: Approximations $\tilde{c}_k(\theta _{j_1,n_1})$ for $\lambda ^{(1)}({\mathbf {f}})$. Bottom Left: Approximations $\tilde{c}_k(\theta _{j_1,n_1})$ for $\lambda ^{(2)}({\mathbf {f}})$. Bottom Right: Approximations $\tilde{c}_k(\theta _{j_1,n_1})$ for $\lambda ^{(3)}({\mathbf {f}})$. Computations made with $n_1=100$ and $\alpha =4$

The matrix $T_n(f)\in \mathbb {R}^{N\times N}$, $N=3n$, shows a pentadiagonal block structure, and all the blocks belongs to $\mathbb {R}^{3\times 3}$, that is

$$\begin{aligned} T_n({\mathbf {f}})&=\left[ \begin{array}{cccccc} \hat{\mathbf {f}}_0&{}\quad \hat{\mathbf {f}}_1^T&{}\quad \hat{\mathbf {f}}_2^T&{}\quad &{}\quad &{}\quad \phantom {\ddots }\\ \hat{\mathbf {f}}_1&{}\quad \ddots &{}\quad \ddots &{}\quad \ddots \\ \hat{\mathbf {f}}_2&{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots \\ &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \hat{\mathbf {f}}_2^T\\ &{}\quad &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \hat{\mathbf {f}}_1^T\\ \phantom {\ddots }&{}\quad &{}\quad &{}\quad \hat{\mathbf {f}}_2&{}\quad \hat{\mathbf {f}}_1&{}\quad \hat{\mathbf {f}}_0 \end{array}\right] , \hat{\mathbf {f}}_0= \frac{1}{5}\left[ \begin{array}{rrr} 16 &{}\quad -\,12 &{} \quad 5 \\ -\,12 &{}\quad 34 &{}\quad -\,10 \\ 5 &{}\quad -\,10 &{}\quad 100\\ \end{array}\right] ,\\ \hat{\mathbf {f}}_1&= \frac{1}{10}\left[ \begin{array}{rrr} -\,4 &{}\quad 7 &{} \quad 0 \\ 8&{} \quad -\,16 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad -\,10 \\ \end{array}\right] , \hat{\mathbf {f}}_2 = \frac{1}{20}\left[ \begin{array}{rrr} -\,12 &{}\quad -\,12 &{} \quad 0 \\ -\,16&{} \quad 12&{} \quad 1\\ 0 &{}\quad 2 &{} \quad 0 \\ \end{array}\right] . \end{aligned}$$

In analogy with Example 2, we want to give an approximation of $\lambda _\gamma (T_n({\mathbf {f}}))$, for $n=10000$, in case that the global condition is not satisfied.

Although the intersection of the ranges of $\lambda ^{(j)}(\mathbf { f})$ and $\lambda ^{(k)}(\mathbf { f})$ is empty for every pair (j, k), $j\ne k$, $j,k\in \{1,2,3\}$, the assumption of monotonicity is violated either globally on $[0,\pi ]$ or on a subinterval in $[0,\pi ]$.

In detail:

• $\lambda ^{(1)}({\mathbf {f}})$, is fully non-monotone on $[0,\pi ]$, hence we expect that no fast approximation can be given on first n eigenvalues, $\lambda _\gamma (T_n(\mathbf {f}))$, for $\gamma =1,\dots , n$;

• $\lambda ^{(3)}(\mathbf {f})$ is monotone non-decreasing and its range does not intersect that of $\lambda ^{(q)}(\mathbf {f})$, $q=1,2$. Hence we can provide an approximation, of the last n eigenvalues $\lambda _\gamma (T_n(\mathbf {f}))$ for $\gamma =2n+1,\dots , 3n$, (analogously with what we did for treating the first n eigenvalues in Example 2);

• $\lambda ^{(2)}({\mathbf {f}})$ is non-monotone on a subinterval $[0,\hat{\theta }_1]$ in $[0,\pi ]$ and monotone non-decreasing on the remaining subinterval, $(\hat{\theta }_1,\pi ]$. Hence we are able to efficiently compute also the eigenvalues that verify the following relation

  $$\begin{aligned} \lambda _\gamma (T_n(\mathbf {f}))\in {\Biggl (}(\lambda ^{(2)}(\mathbf {f}))(\hat{\theta }_1),(\lambda ^{(2)}(\mathbf {f}))(\pi ){\Biggr ]}. \end{aligned}$$

  (3.2)

We set for computation $\alpha =4$ and $n_1=100$ and we proceed, as in the previous examples, to calculate first the approximation of $c^{(q)}_k(\theta _{j_1,n_1}), k=1,\ldots ,\alpha$ .

In the top right image of Fig. 6 we display the resulting chaotic graph of $\tilde{c}^{(1)}_k(\theta _{j_1,n_1}), k=1,\ldots ,4$. The graph confirms that, for $q=1$, the interpolation–extrapolation algorithm cannot be used and, consequently, the first n eigenvalues, $\lambda _\gamma (T_n(\mathbf {f}))$, $q=1$, $j=1,\dots ,n$, cannot be efficiently computed using (1.5): the latter is confirmed by the errors $\tilde{E}_{j,n,\alpha }^{(1)}$ and $E_{j,n,0}^{(1)}$, in Fig. 5.

The chaotic behaviour is also present in the values $\tilde{c}^{(2)}_k(\theta _{j_1,n_1}), k=1,\ldots ,4$, see the bottom left panel of Fig. 6, in the subinterval $[0,\hat{\theta }_1]$ of $[0,\pi ]$, that coincides with same subinterval where $\lambda ^{(2)}({\mathbf {f}})$ is non-monotone.

Hence, if we restrict to $[0,\hat{\theta }_1]$, the extrapolation procedure can be used again on $\tilde{c}^{(2)}_k(\theta _{j_1,n_1}), k=1,\ldots ,4$, for $\theta _{j_1,n_1}\in (\hat{\theta }_1,\pi ],\,$ $j_1=1,\dots ,n_1$. Consequently we obtain a good approximation of $\lambda _\gamma (T_n(\mathbf {f}))$, for $q=2$, $j=\hat{j},\dots ,n$. Notice that $\hat{j}$ is the first index in $\{1,\dots ,n\}$ such that ${\hat{j}\pi }/({n+1})\in (\hat{\theta }_1,\pi ]$, that is we can compute the eigenvalues belonging to the interval reported in (3.2). This is reflected, in Fig. 7, in the gradual reduction of the errors $\tilde{E}_{j,n,\alpha }^{(2)}$ and $E_{j,n,0}^{(2)}$, for indices larger than $\hat{n}_1=n+\hat{j}$.

Finally, the remaining n eigenvalues can be well reconstructed with a standard matrix-less procedure, using the values of $\tilde{c}^{(3)}_k(\theta _{j_1,n_1}), k=1,\ldots ,4$, shown in the top right panel of Fig. 6. The errors related to latter approximation, $\tilde{E}_{j,n,\alpha }^{(3)}$, are shown in Fig. 7.

In total, $3n-\hat{j}+1$ eigenvalues of $T_n(\mathbf {f})$ can be computed and plotted (in non-decreasing order) in Fig. 7.

Fig. 7

Example 3: Left: Errors $\log _{10}|\tilde{E}_{j,n,\alpha }^{(q)}|$, with $\alpha =4$, and errors $\log _{10}|E_{j,n,0}^{(q)}|$ , $q=1,2,3$, versus $\gamma$ for $\gamma =1,\ldots ,3n$. Computations made with $n_1=100$ and $n=10000$. Right: Approximated eigenvalues $\tilde{\lambda }_\gamma (T_n(\mathbf {f}))$, sorted in non-decreasing order, for $\gamma =2n+1,\dots , 3n$ and for $\gamma$ such that $\lambda _\gamma (T_n(\mathbf { f}))$ verifies (3.2). Computation made with the interpolation–extrapolation algorithm, with $\alpha =4$, $n_1=100$ and $n=10000$

Example 4

In this further example we consider three trigonometric polynomials,

$$\begin{aligned} p^{(1)}(\theta )&=2-2\cos (\theta ),\\ p^{(2)}(\theta )&=7-2\cos (2\theta ),\\ p^{(3)}(\theta )&=16-8\cos (\theta )+2\cos (2\theta )=10+(p^{(1)}(\theta ))^2, \end{aligned}$$

with the aim of approximating the eigenvalues of a block banded Toeplitz matrix, with matrix-valued generating function ${\mathbf {f}}(\theta )$, such that $\lambda ^{(q)}({\mathbf {f}})=p^{(q)}$ for $q=1,2,3$. We choose $s=3$ but obviously the following procedure holds for any $s\in \mathbb {Z}_+$ and for any chosen s trigonometric polynomials, $p^{(1)}(\theta ),p^{(2)}(\theta ),\ldots ,p^{(s)}(\theta )$, such that

$$\begin{aligned} \max _{\theta \in [0,\pi ]} p^{(q)}(\theta )< \min _{\theta \in [0,\pi ]}p^{(q+1)}(\theta ) \end{aligned}$$

for $q=1,\dots ,s-1$. We can define

$$\begin{aligned} {\mathbf {f}}(\theta )=Q_3 \begin{bmatrix} p^{(1)}(\theta )&\quad 0&\quad 0\\ 0&\quad p^{(2)}(\theta )&\quad 0\\ 0&\quad 0&\quad p^{(3)}(\theta ) \end{bmatrix} Q_3^{\mathrm {T}}, \end{aligned}$$

where $Q_3$ is any orthogonal matrix in $\mathbb {R}^{3\times 3}$. For the current example we choose

$$\begin{aligned} Q_3=\begin{bmatrix} 1&\quad 0&\quad 0\\ 0&\quad \cos (\pi /3)&\quad -\,\sin (\pi /3)\\ 0&\quad \sin (\pi /3)&\quad \cos (\pi /3) \end{bmatrix}= \frac{1}{2}\begin{bmatrix} 2&\quad 0&\quad 0\\ 0&\quad 1&\quad -\,\sqrt{3}\\ 0&\quad \sqrt{3}&\quad 1 \end{bmatrix}. \end{aligned}$$

Now we define the Fourier coefficients of $\mathbf {f}(\theta )$, that is

$$\begin{aligned} \hat{\mathbf {f}}_{k}= Q_3\begin{bmatrix} \hat{p}_k^{(1)}&\quad 0&\quad 0\\ 0&\quad \hat{p}_k^{(2)}&\quad 0\\ 0&\quad 0&\quad \hat{p}_k^{(3)} \end{bmatrix}Q_3^{\mathrm {T}}=Q_3\hat{D}_kQ_3^T, \end{aligned}$$

(3.3)

where $\hat{p}_k^{(q)}$ is the kth Fourier coefficient of the eigenvalue function $p^{(q)}(\theta )$, and $k=-m,\ldots ,m$, where $m=\max _{q=1,\dots , s}\mathrm{deg}(p^{(q)}(\theta )$. In our example $m=2$, for $p^{(2)}(\theta )$ and $p^{(3)}(\theta )$ and $m=1$ for $p^{(1)}(\theta )$. Each $p^{(q)}(\theta )$ is a real cosine trigonometric polynomial (RCTP), so ${\mathbf {f}}(\theta )$ is a symmetric matrix-valued function with Fourier coefficients

$$\begin{aligned} \hat{\mathbf {f}}_0&= \frac{1}{4}\left[ \begin{array}{rrr} 8&{}\quad 0&{}\quad 0\\ 0&{}\quad 55&{}\quad -\,9\sqrt{3}\\ 0&{}\quad -\,9\sqrt{3}&{}\quad 37 \end{array}\right] ,\quad \hat{\mathbf {f}}_1= \left[ \begin{array}{rrr} -\,1&{}\quad 0&{}\quad 0\\ 0&{}\quad -\,3&{}\quad \sqrt{3}\\ 0&{}\quad \sqrt{3}&{}\quad -\,1 \end{array}\right] ,\\ \hat{\mathbf {f}}_2&= \frac{1}{2}\left[ \begin{array}{rrr} 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad -\,\sqrt{3}\\ 0&{}\quad -\,\sqrt{3}&{}\quad -\,1 \end{array}\right] , \end{aligned}$$

where $\hat{\mathbf {f}}_{-k}=\hat{\mathbf {f}}_{k}^T=\hat{\mathbf {f}}_{k}$, $k=0,1,2$.

The resulting block banded Toeplitz matrix is the following matrix

$$\begin{aligned} T_n({\mathbf {f}})= \left[ \begin{array}{ccccc} \hat{\mathbf {f}}_{0}&{}\quad \hat{\mathbf {f}}_{-1}&{}\quad \hat{\mathbf {f}}_{-2}&{}\quad &{}\\ \hat{\mathbf {f}}_{1}&{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\\ \hat{\mathbf {f}}_{2}&{}\ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \hat{\mathbf {f}}_{-2}\\ &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \hat{\mathbf {f}}_{-1}\\ &{}\quad &{}\quad \hat{\mathbf {f}}_{2}&{}\quad \hat{\mathbf {f}}_{1}&{}\quad \hat{\mathbf {f}}_{0} \end{array}\right] , \end{aligned}$$

with symbol

$$\begin{aligned} {\mathbf {f}}(\theta )=\hat{\mathbf {f}}_0+\sum _{k=1}^{2}\left( \hat{\mathbf {f}}_{k}e^{\mathbf {i}k\theta }+\hat{\mathbf {f}}_{-k}e^{-\mathbf {i}k\theta }\right) =\hat{\mathbf {f}}_0+2\hat{\mathbf {f}}_1\cos (\theta )+2\hat{\mathbf {f}}_2\cos (2\theta ) . \end{aligned}$$

We want to approximate the eigenvalues of $T_n({\mathbf {f}})$, where $\mathbf {f}(\theta )$ is constructed from $p^{(q)}(\theta )$, $q=1,2,3$. For the graph of the chosen polynomials see the top left panel of Fig. 8.

Due to the special structure of all $\hat{\mathbf {f}}_{k}$, see (3.3), we have

$$\begin{aligned} T_n({\mathbf {f}})= I_n\otimes Q_3 \left[ \begin{array}{ccccc} \hat{D}_{0}&{}\quad \hat{D}_{-1}&{}\hat{D}_{-2}&{}\quad &{}\\ \hat{D}_{1}&{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\\ \hat{D}_{2}&{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \hat{D}_{-2}\\ &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \hat{D}_{-1}\\ &{}\quad &{}\quad \hat{D}_{2}&{}\quad \hat{D}_{1}&{}\quad \hat{D}_{0} \end{array}\right] I_n\otimes Q_3^T. \end{aligned}$$

Therefore $T_n({\mathbf {f}})$ is similar to the matrix

$$\begin{aligned} \begin{bmatrix} T_n(p^{(1)}(\theta ))&\quad 0&\quad 0\\ 0&\quad T_n(p^{(2)}(\theta ))&\quad 0\\ 0&\quad 0&\quad T_n(p^{(3)}(\theta )) \end{bmatrix}, \end{aligned}$$

and finally it is trivial to see that the block case, in this setting, is reduced to 3 different scalar problems, which can be treated separately.

Fig. 8

Example 4: Top Left: Constructed eigenvalue functions. Top Right: Errors of the three eigenvalue functions, presented on global indices $\gamma$, when using grid $\theta _{j_1,n_1}=\frac{\pi j_1}{n_1+1}$, $j_1=1,\dots ,n_1$, $q=1,2,3$. Bottom Left: Errors of the three eigenvalue functions, when using grid defined in (3.4). Bottom Right: Error expansion for the third eigenvalue function. Computations made with $n_1=100$ and $\alpha =4$

Differently from previous examples, here the analytical expressions of the eigenvalue functions of $\mathbf {f}(\theta )$ are known, since they coincide, by construction, with $p^{(q)}(\theta )$, for $q=1,2,3$. So we will describe the spectrum of $T_n( {\mathbf {f}})$, approximating or calculating exactly the 3n eigenvalues, treating separately the 3 different scalar problems.

For the first n eigenvalues it is known that they can be calculated exactly, sampling $p^{(1)}$ with grid $\theta _{j,n}={j\pi }/({n+1}),\, j=1, \dots , n$. Analogously, the n eigenvalues can be found exactly by sampling $p^{(2)}$ on a special grid defined in [16]. For the last n eigenvalues, the grid that gives exact eigenvalues is not known, but $p^{(3)}$ is monotone non-decreasing and consequently we can use asymptotic expansion in the scalar case.

We set the parameters as previous cases: $n_1=100$ and $n=10000$.

In the top right panel of Fig. 8 we report the expansion errors $E^{(q)}_{j_1,n_1,0}$, calculated using grid $\theta _{j_1,n_1}={j_1\pi }/({n_1+1})$, $j_1=1,\dots ,n_1$, $q=1,2,3$. There is no surprise that in the first region of the graph (green area) the error is zero, since the first $n_1$ eigenvalues are exactly given, sampling $p^{(1)}$ on standard $\theta _{j_1,n_1}$ grid.

In yellow area we see the result of direct calculation of

$$\begin{aligned} \lambda _\gamma (T_{n_1}(\mathbf { f}))-\lambda ^{(3)}(\mathbf { f}(\theta _{j_1,n_1})), \end{aligned}$$

for $j_1=1,\dots ,n_1$, $q=3$, as we are using asymptotic expansion with $\alpha =0$.

The green area, containing the errors related to $p^{(2)}(\theta )$, is obviously chaotic since $p^{(2)}(\theta )$ is non-monotone.

Following the notation and the analysis in [16], since $p^{(2)}=7-2\cos (2\theta )$ and $n_1=100$, we have two changes of monotonicity which we collect in the parameter $\omega$. As a consequence, in accordance with the study in [16], we choose

$$\begin{aligned} \omega =2,\quad \beta&=\mathrm {mod}(n_1,\omega )=0, \quad n_\omega =(n_1-\beta )/\omega =50,\\ \theta _{n_\omega }^{(1)}&=\frac{j\pi }{n_\omega +1},\quad j=1,\ldots n_\omega ,\\ \theta _{n_\omega +1}^{(2)}&=\frac{j\pi }{n_\omega +2},\quad j=1,\ldots n_\omega +1. \end{aligned}$$

To map the two grids above to match the given symbol $\mathbf {f}(\theta )$ we construct $\theta _{n_1}$ by

$$\begin{aligned} \theta _{n_1}=\left\{ \frac{1}{2}\theta _{n_\omega }^{(1)},\frac{1}{2}\theta _{n_\omega +1}^{(2)}+\frac{\pi }{2}\right\} . \end{aligned}$$

A more general formula to match grids $\theta _{n_\omega }^{(1)}$ and $\theta _{n_\omega +1}^{(2)}$ to be evaluated on the standard symbol is

$$\begin{aligned} \theta _{n}=\frac{1}{\omega }\left\{ \bigcup _{r_1=1}^{\omega -\beta }\left( \theta _{n_\omega }^{(1)}+(r_1-1)\pi \right) ,\bigcup _{r_2=1}^{\beta }\left( \theta _{n_\omega +1}^{(2)}+(r_2-1)\pi +(\omega -\beta )\pi \right) \right\} . \end{aligned}$$

(3.4)

In the left bottom panel of Fig. 8 we report the global expansion errors $E^{(q)}_{j_1,n_1,0}$, calculated using grid described above. In this way the region where the error is 0 is the second (red area), since the eigenvalues are calculated exactly, by sampling $p^{(2)}(\theta )$. Furthermore, in the green and in the yellow areas we see the result of the direct calculation of

$$\begin{aligned} \lambda _\gamma (T_{n_1}(\mathbf { f}))-\lambda ^{(q)}(\mathbf { f}(\theta _{j_1,n_1})), \end{aligned}$$

for $j_1=1,\dots ,n_1$, $q=1,3$, as we are using asymptotic expansion with $\alpha =0$.

Hence, the first n eigenvalues of $T_n( {\mathbf {f}})$ can be calculated exactly sampling $p^{(1)}$ with grid $\theta _{j,n}={j\pi }/({n+1}),\, j=1, \dots , n$ and n exact eigenvalues can be found sampling $p^{(2)}$ on grid (3.4). For the computation of the last n eigenvalues, we use the matrix-less procedure in the scalar setting, passing through the approximation of $c^{(3)}_k(\theta _{j_1,n_1}), k=1,\ldots ,\alpha$, for $\alpha =4$, see the bottom right panel of Fig. 8.

In fact, for $\alpha =4$ we ignore the first two evaluations of $c_4^{(3)}$ at the initial points $\theta _{1,n}$ and $\theta _{2,n}$, because their values behave in a erratic way. This problem has been emphasized in [2] and it is due to the fact that the first and second derivative of $p^{(3)}(\theta )$ at $\theta =0$ vanish simultaneously. However, we have to make two observations for clarifying the situation

• The present pathology is not a counterexample to the asymptotic expansion (1.5) since we take $\theta$ fixed and all the pairs j, n such that $\theta _{j,n}=\theta$: in the current case and in that considered in [2] in the scalar-valued setting, we have j fixed and n grows so that the point $\theta$ is not well defined.

• There are simple ways for overcoming the problem and then for computing reliable evaluations of $c_4^{(3)}$ at those bad points $\theta _{1,n}$ and $\theta _{2,n}$. One of them is described in [12] and consists in choosing a sufficiently large $\alpha >4$ and in computing $c_k^{(3)}$, for $k=1,2,3,4$. Using this trick, the $c_4^{(3)}$ at the initial points $\theta _{1,n}$ and $\theta _{2,n}$ have the expected behavior. In addition we stress the fact that this behavior has little impact on the numerically computed solution. Assuming double precision computations, the contribution to the error deriving from $c_4^{(3)}(\theta _{j,n})h^4$ will be numerically negligible, even for moderate n. Further discussions on the topic are presented in [12].

Example 5

Consider the $\mathbb {Q}_p$ Lagrangian Finite Element approximation, of the second order elliptic differential problem

$$\begin{aligned} {\left\{ \begin{array}{ll} - \varDelta u+\beta \cdot \nabla u + \gamma u=f, &{} \text { in }\varOmega =(0,1)^d,\\ u=0, &{} \text { on }\partial \varOmega , \end{array}\right. } \end{aligned}$$

(3.5)

in one dimension with $\beta =\gamma =0$, and $f\in L^2(\varOmega )$. The resulting stiffness matrix is $A_n^{(p)}=nK_n^{(p)}$, where $K_n^{(p)}$ is a $(pn-1)\times (pn-1)$ block matrix. The construction of the matrix and the symbol is given in [18]. The $p\times p$ matrix-valued symbol of $K_n^{(p)}$ is

$$\begin{aligned} {\mathbf {f}}(\theta )=\hat{\mathbf {f}}_0+\hat{\mathbf {f}}_1e^{\mathbf {i}\theta }+\hat{\mathbf {f}}_1^{\mathrm {T}}e^{-\mathbf {i}\theta }. \end{aligned}$$

We have

$$\begin{aligned} K_n^{(p)}=T_n({\mathbf {f}})_-, \end{aligned}$$

where the subscript − denotes that the last row and column of $T_n({\mathbf {f}})$ are removed. This is due to the homogeneous boundary conditions. For detailed expressions of $\hat{\mathbf {f}}_0$ and $\hat{\mathbf {f}}_1$ in the particular case $p=2,3,4$, see “Appendix B”.

In Table 1, we list seven examples of uniform grids, with varying n. The general notation for a grid, where the type is defined by context, is $\theta _{j,n}$, where n is the number of grid points, and j is the indices $j=1,\ldots ,n$. The grid fineness parameter h, for the respective grids, is also presented in Table 1. The names of the different grids are chosen in view of their relations with the $\tau$-algebras [7] [see specifically equations (19), (22), and (23) therein].

Table 1 Seven examples of uniform grids

In Example 1 of [18] the case $p=2$ is considered, and explicit formulas for the two eigenvalue functions are given, with their notation,

$$\begin{aligned} \lambda _1(\mathbf {f}_2(\theta ))&=5+\frac{1}{3}\cos (\theta )+\frac{1}{3}\sqrt{129+126\cos (\theta )+\cos ^2(\theta )},\\ \lambda _2(\mathbf {f}_2(\theta ))&=5+\frac{1}{3}\cos (\theta )-\frac{1}{3}\sqrt{129+126\cos (\theta )+\cos ^2(\theta )}. \end{aligned}$$

Here we present the two grids used to sample the two eigenvalue functions in order to attain exact eigenvalues,

$$\begin{aligned} \lambda _1(\mathbf {f}_2(\theta _{j_1,n-1}^{(1)})),&\quad \theta _{j_1,n-1}^{(1)}=\frac{j_1\pi }{n},\quad j_1=1,\ldots , n-1,\\ \lambda _2(\mathbf {f}_2(\theta _{j_2,n}^{(2)})),&\quad \theta _{j_2,n}^{(2)}=\frac{j_2\pi }{n},\quad j_2=1,\ldots , n. \end{aligned}$$

With the notation in Table 1, we use the grid $\tau _{n-1}$ for the first eigenvalue function, and grid $\tau _{n-1}^\pi$ for the second. Since for $p>2$ the analytical expression of the the eigenvalue functions can not be computed easily, the following four steps algorithm can be used to obtain the exact eigenvalues for any p.

The mass matrix, of the system (3.5) (that is, $\gamma =1$), is $B_n^{(p)}=n^{-1}M_n^{(p)}$, where $M_n^{(p)}=T_n(\mathbf {g})_-$ is the scaled mass matrix.

The $p\times p$ matrix-valued symbol of $M_n^{(p)}$ is given by

$$\begin{aligned} {\mathbf {g}}(\theta )=\hat{\mathbf {g}}_0+\hat{\mathbf {g}}_1e^{\mathbf {i}\theta }+\hat{\mathbf {g}}_1^{\mathrm {T}}e^{-\mathbf {i}\theta }. \end{aligned}$$

For detailed expressions of $\hat{\mathbf {g}}_0$ and $\hat{\mathbf {g}}_1$ in the particular case $p=2,3,4$, see Appendix B. The algorithm for writing the exact eigenvalues of $M_n^{(p)}$ for p even is the same as the one described for $K_n^{(p)}$ above, just replacing $\mathbf {f}(\theta )$ with $\mathbf {g}(\theta )$. However, for $p>1$ odd, we have a slight modification:

If $(p+1)/2$ is odd, that is $p=5,9,13,\ldots$, define $\hat{p}=p$. If $(p+1)/2$ is even, that is $p=3,7,11,\ldots$, define $\hat{p}=p-2$. In summary, to obtaining the exact eigenvalues of $M_n^{(p)}$, the algorithm becomes:

In Fig. 9 we present the appropriate grids, defined in Table 1, for the exact eigenvalues of $K_n^{(p)}$ and $M_n^{(p)}$ with $n=6$ and $p=5$.

Fig. 9

Example 5: Grids for the exact eigenvalues of $K_n^{(p)}$ and $M_n^{(p)}$, with $n=6$ and $p=5$. Left: Grids chosen for each eigenvalue functions of $\mathbf {f}(\theta )$, for $q=1,\ldots ,5$, according to Algorithm 2. Right: Grids chosen for each eigenvalue function of $\mathbf {g}(\theta )$, for $q=1,\ldots ,5$, according to Algorithm 3

Conclusions and future work

In this paper we considered the case of $\mathbf {f}$ being a $s\times s$ matrix-valued trigonometric polynomial, $s\ge 1$, and $\{T_n(\mathbf {f})\}_n$ a sequence of block Toeplitz matrix generated by $\mathbf {f}$, with $T_n(\mathbf {f})$ of size $N(n,s)=sn$. We numerically observed conditions insuring the existence of an asymptotic expansion generalizing the assumptions known for the scalar-valued setting. Furthermore, following a proposal in the scalar-valued case by the first author, by Garoni, and by the third author, we devised an extrapolation algorithm for computing the eigenvalues in the present setting regarding banded symmetric block Toeplitz matrices, with a high level of accuracy and with a low computational cost. The resulting algorithm is an eigensolver that does not need to store the original matrix and does not need to perform matrix-vector products: for this reason we call it matrix-less

We have used the asymptotic expansion for the efficient computation of the spectrum of special block Toeplitz structures and we have shown exact formulae for the eigenvalues of the matrices coming from the $\mathbb {Q}_p$ Lagrangian Finite Element approximation of a second order elliptic differential problem.

A lot of open issues remain, including a formal proof of the asymptotic expansion clearly indicated by the numerical experiments at least under the global assumption of monotonicity and pair-wise separation of the eigenvalue functions.

Appendices

Appendix

Appendix A

Theorem 5.1

Let $s>1$, $N=N(n,s)=sn$ and $\mathbf {f}$ be an Hermitian matrix-valued trigonometric polynomial (HTP) with Fourier coefficients ${\hat{\mathbf {f}}}_0,{\hat{\mathbf {f}}}_1,\ldots ,{\hat{\mathbf {f}}}_m\in \mathbb R^{s\times s}$. Suppose that $\mathbf {f}$ is of the form

$$\begin{aligned} \mathbf { f}(\theta )=\sum _{k=-m}^m{\hat{\mathbf {f}}}_k \mathrm{e}^{\mathbf {i}k\theta }={\hat{\mathbf {f}}}_0+\sum _{k=1}^m\left( {\hat{\mathbf {f}}}_k \mathrm{e}^{\mathbf {i}k\theta }+{\hat{\mathbf {f}}}_k^T \mathrm{e}^{\mathbf {-i}k\theta }\right) ,\qquad m=\deg \left( \mathbf { f}(\theta )\right) \in \mathbb N, \end{aligned}$$

such that

$$\begin{aligned} \begin{aligned} {\hat{\mathbf {f}}}_{-k}=&{\hat{\mathbf {f}}}^T_k \quad k=0,\dots ,m. \end{aligned} \end{aligned}$$

(5.1)

Suppose that the eigenvalue functions of $\mathbf { f}$, $\lambda ^{(q)}(\mathbf { f}):[0,\pi ]\rightarrow \mathbb R^{s\times s}$, $q=1,\dots , s$, are monotone on $[0,\pi ]$ and such that

$$\begin{aligned} \max _{\theta \in [0,\pi ]} \lambda ^{(q)}(\mathbf { f})< \min _{\theta \in [0,\pi ]}\lambda ^{(q+1)}(\mathbf { f}) \end{aligned}$$

(5.2)

$q=1,\dots ,s-1$, then, fixed $q\in \{1,\dots ,s\}$,

$$\begin{aligned} \left| \lambda _\gamma (T_n(\mathbf { f})) - \lambda ^{(q)} \left( \mathbf { f}\left( \theta _{j,n}\right) \right) \right| \le C h \end{aligned}$$

(5.3)

$\forall \, n$, for $j=1,\dots ,n$, and $\gamma =\gamma (q,j)=(q-1)n+j$, where

• $\lambda _\gamma (T_n(\mathbf { f}))$, $\gamma \in \{1,\dots ,N\}$, are the eigenvalues of $T_n(\mathbf { f})$, such that, for a fixed $\bar{q}\in \{1,\dots , s\}$, $\lambda _{(\bar{q}-1)n+j}(T_n(\mathbf { f}))$ are arranged in non-decreasing or non-increasing order, depending on whether $\lambda ^{(\bar{q})}(\mathbf { f})$ is increasing or decreasing.

• $h=\frac{1}{n+1}$ and $\theta _{j,n}=\frac{j\pi }{n+1}=j\pi h$, $j=1,\ldots , n$;

Proof

For the sake of simplicity, we assume that for $q=1,\dots , s$, $\lambda ^{(q)}(\mathbf { f})$ is monotone non-decreasing (the other cases have a similar proof).

Notice that the conditions on $\mathbf {f}$ imply that the $N \times N$ block Toeplitz matrix generated by $\mathbf { f}$, $T_n(\mathbf { f})$, is Hermitian positive definite so we can order its eigenvalues in non-decreasing order of as follows

$$\begin{aligned} \left\{ \left\{ \lambda _{(q-1)n+j}(T_n(\mathbf { f}))\right\} _{j=1}^{n}\right\} _{q=1}^s \end{aligned}$$

(5.4)

We remark that

$$\begin{aligned} \begin{aligned} T_n(\mathbf { f})&= \tau _N(\mathbf { f})+ H_N(\mathbf { f}),\\ \end{aligned} \end{aligned}$$

(5.5)

where, for $\psi$ (HTP) of degree m and $Q=\left( \sqrt{\frac{2}{n+1}} \sin \left( \frac{ij\pi }{n+1}\right) \right) _{i,j=1}^n$, $\tau _N(\psi )$ is the following $\tau$ matrix [4] of size N generated by $\psi$

$$\begin{aligned} \tau _N(\psi )=(Q\otimes I_s) \underset{{1 \le j \le n}}{{{\mathrm{diag}}}}{\left( \psi \left( \frac{j\pi }{n+1}\right) \right) }(Q\otimes I_s),\, \quad Q=Q^T=Q^{-1}, \end{aligned}$$

where $I_s$ is the $s\times s$ identity matrix, and $H_N(\psi )$ is the Hankel matrix

with $\nu :=\nu (s,m)=\mathrm {rank}(H_N(\psi ))\le 2s(m-1)$.

For $q=1,\dots , s$, $j=1,\dots , n$, setting $\gamma =(q-1)n+j$, we find

$$\begin{aligned} \lambda _\gamma ( \tau _N(\mathbf { f}))=\lambda ^{(q)}\left( \mathbf { f}\left( \frac{j\pi }{n+1}\right) \right) . \end{aligned}$$

(5.6)

Note that $T_n(\mathbf { f})$ is similar to the matrix

$$\begin{aligned} \tilde{T}_n(\mathbf { f})=(Q\otimes I_s)T_n(\mathbf { f})(Q\otimes I_s)= & {} \underset{{1 \le j \le n}}{{{\mathrm{diag}}}}{\left( \mathbf { f}\left( \frac{j\pi }{n+1}\right) \right) }+(Q\otimes I_s)H_N(\mathbf { f})(Q\otimes I_s)\\= & {} \underset{{1 \le j \le n}}{{{\mathrm{diag}}}}{\left( \mathbf { f}\left( \frac{j\pi }{n+1}\right) \right) }+\tilde{H_{\nu }}, \end{aligned}$$

with $\mathrm {rank}(\tilde{H_{\nu }})=\nu$, so $T_n(\mathbf { f})$ and $\tilde{T}_n(\mathbf { f})$ have the same eigenvalues.

Using the MinMax spectral characterization for Hermitian matrices [3], we obtain, for $\gamma =(q-1)n+j\in \{\nu +1,\dots ,N-\nu \}$,

$$\begin{aligned} \lambda _{\gamma -\nu }(\tau _N(\mathbf { f}))&= \lambda ^{(q)} \left( \mathbf { f}\left( \frac{(j-\nu )\pi }{n+1}\right) \right) \le \lambda _\gamma (T_n(\mathbf { f}) )\le \lambda _{\gamma +\nu }(\tau _N(\mathbf { f}))\nonumber \\&=\lambda ^{(q)}\left( \mathbf { f}\left( \frac{(j+\nu )\pi }{n+1}\right) \right) . \end{aligned}$$

(5.7)

The eigenvalue functions $\lambda ^{(q)}(\mathbf { f})$ are monotone non-decreasing function so we have, $\forall \, n$ and for $\gamma =(q-1)n+j\in \{\nu +1,\dots ,N-\nu \}$,

$$\begin{aligned}&\lambda _\gamma (T_n(\mathbf { f}) )-\lambda ^{(q)}\left( \mathbf { f}\left( \frac{j\pi }{n+1}\right) \right) \le \lambda ^{(q)}\left( \mathbf { f}\left( \frac{(j+\nu )\pi }{n+1}\right) \right) - \lambda ^{(q)}\left( \mathbf { f}\left( \frac{j\pi }{n+1}\right) \right) \nonumber \\&\quad =\left( \lambda ^{(q)}(\mathbf { f}( \bar{\theta }))\right) ' \frac{\nu \pi }{n+1}\le \left\| \left( \lambda ^{(q)}(\mathbf { f})\right) '\right\| _{\infty } \frac{\nu \pi }{n+1}, \end{aligned}$$

(5.8)

with $\bar{\theta }\in \left( \frac{j\pi }{n+1},\frac{(j+\nu )\pi }{n+1}\right)$ and

$$\begin{aligned} \lambda _\gamma (T_n(\mathbf { f}) )-\lambda ^{(q)}\left( \mathbf { f}\left( \frac{j\pi }{n+1}\right) \right)&\ge \lambda ^{(q)}\left( \mathbf { f}\left( \frac{(j-\nu )\pi }{n+1}\right) \right) - \lambda ^{(q)}\left( \mathbf { f}\left( \frac{j\pi }{n+1}\right) \right) \nonumber \\&\ge - \left\| \left( \lambda ^{(q)}(\mathbf { f})\right) '\right\| _{\infty } \frac{\nu \pi }{n+1}. \end{aligned}$$

(5.9)

By setting $C=\left\| \left( \lambda ^{(q)}(\mathbf { f})\right) '\right\| _{\infty } \nu \pi$, for $\gamma =(q-1)n+j\in \{\nu +1,\dots ,N-\nu \}$, we obtain

$$\begin{aligned} \left| \lambda _\gamma (T_n(\mathbf { f}) )-\lambda ^{(q)}\left( \mathbf { f}\left( \frac{j\pi }{n+1}\right) \right) \right| \le C h. \end{aligned}$$

(5.10)

Furthermore, from [10] $\forall \, \gamma =1, \dots , N$, we know that

$$\begin{aligned} m_{\mathbf { f}} \le \lambda _\gamma (T_n(\mathbf { f}) )\le M_{\mathbf { f}}, \end{aligned}$$

where

$$\begin{aligned} m_{\mathbf { f}}= \min _{\theta \in [0, \pi ]} \left( \lambda ^{(1)}(\mathbf { f}(\theta ))\right) ; \quad M_{\mathbf { f}}=\max _{\theta \in [0,\pi ]} \left( \lambda ^{(s)}(\mathbf { f}(\theta ))\right) , \end{aligned}$$

with strict inequalities that is $m_{\mathbf { f}}< \lambda _\gamma (T_n(\mathbf { f}) ) < M_{\mathbf { f}}$ since, by the assumptions, the extreme eigenvalue functions are not constant. Hence for $N-\nu < \gamma \le N$

$$\begin{aligned} \left| \lambda ^{(s)}\left( \mathbf { f}\left( \frac{j\pi }{n+1} \right) \right) -\lambda _\gamma (T_n(\mathbf { f}) ) \right|\le & {} \left| \lambda ^{(s)}\left( \mathbf { f}\left( \frac{j\pi }{n+1}\right) \right) - \lambda ^{(s)}\left( \mathbf { f}\left( \frac{n\pi }{n+1} \right) \right) \right| \\\le & {} \left| \left( \lambda ^{(s)}\left( \mathbf { f}\left( \bar{\theta } \right) \right) \right) ' \right| \left| \frac{(n-j) \pi }{n+1}\right| , \end{aligned}$$

where $\bar{\theta }\in \left( \frac{j\pi }{n+1},\frac{n\pi }{n+1}\right)$. If $N-\nu < \gamma \le N$ then $|N-\nu |<|(s-1)n+j|\rightarrow |n-j|<\nu$, so that

$$\begin{aligned} \left| \lambda ^{(s)}\left( \mathbf { f}\left( \frac{j\pi }{n+1} \right) \right) -\lambda _\gamma (T_n(\mathbf { f}) ) \right| \le \left\| \left( \lambda ^{(s)}\left( \mathbf { f}\right) \right) ' \right\| _{\infty }\frac{\nu \pi }{n+1} =C h. \end{aligned}$$

For $1\le \gamma <\nu +1$

$$\begin{aligned} \left| \lambda ^{(1)}\left( \mathbf { f}\left( \frac{j\pi }{n+1} \right) \right) -\lambda _\gamma (T_n(\mathbf { f}) ) \right|&\le \left| \lambda ^{(1)}\left( \mathbf { f}\left( \frac{j\pi }{n+1}\right) \right) - \lambda ^{(1)}\left( \mathbf { f}\left( \frac{\pi }{n+1} \right) \right) \right| \\&\le \left| \left( \lambda ^{(1)}\left( \mathbf { f}\left( \bar{\theta } \right) \right) \right) ' \right| \left| \frac{(j-1) \pi }{n+1}\right| , \end{aligned}$$

where $\bar{\theta }\in \left( \frac{\pi }{n+1},\frac{j\pi }{n+1}\right)$. If $1\le \gamma <\nu +1$ then $\left| j\right| >\left| \nu +1\right| \Rightarrow \left| j-1\right| <\nu$, so

$$\begin{aligned} \left| \lambda ^{(1)}\left( \mathbf { f}\left( \frac{j\pi }{n+1} \right) \right) -\lambda _\gamma (T_n(\mathbf { f}) ) \right| \le \left\| \left( \lambda ^{(1)}\left( \mathbf { f}\right) \right) ' \right\| _{\infty }\frac{\nu \pi }{n+1}=C h. \end{aligned}$$

Hence for $q=1,\dots ,s$, $j=1,\dots ,n$, $\gamma =(q-1)n+j\in \{1,\dots ,N\}$,

$$\begin{aligned} \left| \lambda _\gamma (T_n(\mathbf { f})) - \lambda ^{(q)}\left( \mathbf { f} \left( \frac{j\pi }{n+1}\right) \right) \right| \le C h. \end{aligned}$$

Remark 5.1

With regard to Theorem 5.1, for $q=1,\dots ,s$, the case where $\lambda ^{(q)}(\mathbf { f})$ are bounded and non-monotone is even easier. If we consider $\hat{\lambda }^{(q)}(\mathbf { f})$, the monotone non-decreasing rearrangement of $\lambda ^{(q)}(\mathbf { f})$ on $[0,\pi ]$, taking into account that the derivative of $\lambda ^{(q)}(\mathbf { f})$ has at most a finite number S of sign changes, we deduce that $\hat{\lambda }^{(q)}(\mathbf { f})$ is Lipschitz continuous and its Lipschitz constant is bounded by $\Vert \left( \lambda ^{(q)}(\mathbf { f})\right) '\Vert _\infty$ (notice that $\hat{\lambda }^{(q)}(\mathbf { f})$ is not necessarily continuously differentiable but the derivative of $\hat{\lambda }^{(q)}(\mathbf { f})$ has at most S points of discontinuity). Furthermore the eigenvalues $\lambda _\gamma ( \tau _N(\mathbf { f}))$, $g=(q-1)n$ are exactly given by

$$\begin{aligned} \lambda ^{(q)}\left( \mathbf { f}\left( \frac{j\pi }{n+1}\right) \right) \end{aligned}$$

so that, by ordering these values non-decreasingly, we deduce that they coincide with $\hat{\lambda }^{(q)}\left( \mathbf { f}\left( x_{j,n}\right) \right)$, with $x_{j,n}$ of the form $\frac{j\pi }{n+1}(1+o(1))$. With these premises, the proof follows exactly the same steps as in Theorem 5.1, using the MinMax characterization and the interlacing theorem for Hermitian matrices.

Appendix B

Recall that the $p\times p$ matrix-valued symbols of $K_n^{(p)}$ and $M_n^{(p)}$ are

$$\begin{aligned} {\mathbf {f}}(\theta )=\hat{\mathbf {f}}_0+\hat{\mathbf {f}}_1e^{\mathbf {i}\theta }+\hat{\mathbf {f}}_1^{\mathrm {T}}e^{-\mathbf {i}\theta } \end{aligned}$$

and

$$\begin{aligned} {\mathbf {g}}(\theta )=\hat{\mathbf {g}}_0+\hat{\mathbf {g}}_1e^{\mathbf {i}\theta }+\hat{\mathbf {g}}_1^{\mathrm {T}}e^{-\mathbf {i}\theta } \end{aligned}$$

respectively. The detailed expressions of $\hat{\mathbf {f}}_0$, $\hat{\mathbf {f}}_1$ and $\hat{\mathbf {g}}_0$, $\hat{\mathbf {g}}_1$ for the particular degrees $p=2,3,4$ are given below.

For $p=2$,

$$\begin{aligned} \hat{\mathbf {f}}_0&=\frac{1}{3} \left[ \begin{array}{rr}16&{}\quad -\,8\\ -8&{}\quad 14 \end{array}\right] ,\quad \hat{\mathbf {f}}_1=\frac{1}{3} \left[ \begin{array}{rr} 0&{}\quad -\,8\\ 0&{}\quad 1 \end{array}\right] ,\\ \hat{\mathbf {g}}_0&=\frac{1}{30} \left[ \begin{array}{rr} 16&{}\quad 2\\ 2&{}\quad 8 \end{array}\right] ,\quad \hat{\mathbf {g}}_1=\frac{1}{30} \left[ \begin{array}{rr} 0&{}\quad 2\\ 0&{}\quad -\,1 \end{array}\right] . \end{aligned}$$

For $p=3$,

$$\begin{aligned} \hat{\mathbf {f}}_0&=\frac{1}{40} \left[ \begin{array}{rrr} 432 &{}\quad -\,297 &{}\quad 54 \\ -\,297 &{}\quad 432 &{}\quad -\,189 \\ 54 &{} \quad -\,189 &{} \quad 296 \end{array}\right] ,\quad \hat{\mathbf {f}}_1=\frac{1}{40} \left[ \begin{array}{rrr} 0 &{}\quad 0 &{}\quad -\,189 \\ 0 &{} \quad 0 &{} \quad 54 \\ 0 &{} \quad 0 &{}\quad -\,13 \end{array}\right] ,\\ \hat{\mathbf {g}}_0&=\frac{1}{1680} \left[ \begin{array}{rrr} 648 &{}\quad -\,81 &{}\quad -\,36 \\ -\,81 &{}\quad 648 &{} \quad 99 \\ -\,36 &{}\quad 99 &{} \quad 256 \end{array}\right] ,\quad \hat{\mathbf {g}}_1=\frac{1}{1680} \left[ \begin{array}{rrr} 0 &{} \quad 0 &{} \quad 99 \\ 0 &{} \quad 0 &{} \quad -\,36 \\ 0 &{} \quad 0 &{} \quad 19 \end{array}\right] . \end{aligned}$$

For $p=4$,

$$\begin{aligned} \hat{\mathbf {f}}_0&=\frac{1}{945} \left[ \begin{array}{rrrr} 16640 &{}\quad -\,14208 &{} \quad 5888 &{} \quad -\,1472 \\ -\,14208 &{} \quad 22320 &{} \quad -\,14208 &{} \quad 3048 \\ 5888 &{}\quad -\,14208 &{} \quad 16640 &{} \quad -\,6848 \\ -\,1472 &{} \quad 3048 &{} \quad -\,6848 &{} \quad 9850 \end{array}\right] ,\quad \hat{\mathbf {f}}_1=\frac{1}{945} \left[ \begin{array}{rrrr} 0 &{} \quad 0 &{} \quad 0 &{} \quad -\,6848 \\ 0 &{} \quad 0 &{} \quad 0 &{}\quad 3048 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad -\,1472 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad 347 \end{array}\right] ,\\ \hat{\mathbf {g}}_0&=\frac{1}{5670} \left[ \begin{array}{rrrr} 1792 &{} \quad -\,384 &{}\quad 256 &{} \quad 56 \\ -\,384 &{} \quad 1872 &{} \quad -\,384 &{}\quad -\,174 \\ 256 &{} \quad -\,384 &{} \quad 1792 &{} \quad 296 \\ 56 &{} \quad -\,174 &{} \quad 296 &{} \quad 584 \end{array}\right] ,\quad \hat{\mathbf {g}}_1=\frac{1}{5670} \left[ \begin{array}{rrrr} 0 &{} \quad 0 &{} \quad 0 &{} \quad 296 \\ 0 &{}\quad 0 &{} \quad 0 &{}\quad -\,174 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad 56 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad -\,29 \end{array}\right] . \end{aligned}$$