Additive Schwarz preconditioner for the finite volume element discretization of symmetric elliptic problems

Abstract

A symmetric and a nonsymmetric variant of the additive Schwarz preconditioner are proposed for the solution of a class of finite volume element discretization of the symmetric elliptic problem in two dimensions, with large jumps in the entries of the coefficient matrices across subdomains. It is shown that the convergence of the preconditioned generalized minimal residual iteration using the proposed preconditioners depends polylogarithmically, in other words weakly, on the mesh parameters, and that they are robust with respect to the jumps in the coefficients.

1 Introduction

We consider the classical finite volume element discretization of the second-order elliptic partial differential equation, where we seek for the discrete solution in the space of standard $P_1$ conforming finite element functions, or the space of continuous and piecewise linear functions, cf. [17, 20]. We further consider the second-order elliptic partial differential equation to have coefficients that may have large jumps across subdomains. Due to the finite volume discretization, the resulting systems are in general nonsymmetric, which become increasingly nonsymmetric for coefficients varying increasingly inside the finite elements. All of these make the problem hard to solve in a reasonable amount of time, particularly in large scale computations. Robust and efficient algorithms for the numerical solution of such systems are therefore needed. The design of such algorithms is often challenging, particularly their analysis which is not as well understood as it is for the symmetric system. The main objective of this paper is to design and analyze a class of robust and scalable preconditioners based on the additive Schwarz domain decomposition methodology, cf. [30, 32], using them in the preconditioned generalized minimal residual (GMRES) iteration based on minimizing the energy norm of the residual, cf. [9, 29], for solving the system.

The finite volume element method or the FVE method, also known in the literature as the control volume finite element method or the CVFE, provides a systematic approach to construct a finite volume or a control volume discretization of the differential equations using a finite element approximation of the discrete solution. The method has drawn much interest in the scientific communities over the years. It has both the flexibility of a finite element method to easily adapt to any geometry, and the property of a finite volume discretization of being locally conservative, like conservation of mass, conservation of energy, etc. For a quick overview of the existing research on the methodology, we refer to [1–4, 11, 12, 17, 20, 23, 34].

Additive Schwarz methods have been studied extensively in the literature, see [30, 32] and the references therein. When it comes to solving second-order elliptic problems, the general focus has been on solving symmetric systems resulting from the finite element discretization of the problem. Despite the growing interest for finite volume elements, the research on fast methods for the numerical solution of nonsymmetric systems resulting from the finite volume element discretization has been very limited. In particular methods like the domain decomposition, which are considered among the most powerful methods for large scale computation, have rarely been tested on finite volume elements. Among the few existing works which can be found in the literature, are the works of [13, 35] based on the overlapping partition of the domain, and the works of [27, 33] based on the nonoverlapping partition of the domain. The latter ones are given without the convergence analysis.

In this paper, we propose nonoverlapping domain decomposition methods for the finite volume element, which are based on substructuring, and formulate them as additive Schwarz methods. We show that their convergence is robust with respect to jumps in the coefficients across subdomains, and depends poly-logarithmically on the mesh parameter when used as preconditioners in the GMRES iteration. For an overview of important classes of iterative substructuring methods we refer to [32, chapters 4–6] for symmetric and positive definite systems, and [32, Chapter 11.3] for their extension to nonsymmetric systems. We restrict ourselves to problems in 2D; extension to 3D is possible and will be investigated in the future. Also, since the present work is an attempt to develop a first analysis of iterative substructuring type domain decomposition methods for the finite volume element, we limit ourselves to coefficients that may have jumps only across subdomain boundaries. However, by modifying the coarse space, e.g. using oscillatory boundary conditions instead of the linear boundary conditions for the basis functions, cf. [18, 19, 27], or by enriching the coarse space with eigenfunctions from local eigenvalue problems, cf. [10, 14, 21, 31], it will be possible to extend the methods to effectively deal with highly heterogeneous coefficients.

For the general purpose of designing additive Schwarz preconditioners for a finite volume element discretization in this paper, we have formulated an abstract framework which is then later used in the analysis of the preconditioners proposed in the paper. The framework borrows the basic ingredients of the abstract Schwarz framework for additive Schwarz methods, cf. [30, 32], while the analysis follows the work of [9] where additive Schwarz methods were considered for the advection-diffusion problem. The framework has already been used in two of authors recent papers on the Crouzeix–Raviart finite volume element, cf. [24, 25], demonstrating its usefulness in the design and analysis of new and effective preconditioners for the finite volume element discretization of elliptic problems.

For further information on domain decomposition methods for nonsymmetric problems in general, we refer to [26, 30, 32] and references therein.

The paper is organized as follows: in Sect. 2, we present the differential problem, and in Sect. 3, its finite volume element discretization. In Sect. 4, we present the two variants of the additive Schwarz preconditioners and the two main results, Theorems 4.1 and  4.2. The complete analysis is provided in the next two sections, the abstract framework in Sect. 5, and the required estimates in Sect. 6. Finally, numerical results are provided in Sect. 7.

Throughout this paper, we use the following notations: $x\lesssim y$ and $w\gtrsim z$ denote that there exist positive constants c, C independent of mesh parameters and the jump of coefficients such that $x\le c y$ and $w\ge C z$, respectively.

2 The differential problem

Given $\varOmega$, a polygonal domain in the plane, and $f \in L^2(\varOmega )$, the purpose is to solve the following differential equation,

where $A \in (L^\infty (\varOmega ))^{2\times 2}$ is a symmetric matrix valued function satisfying the uniform ellipticity as follows,

where $|\xi |_2^2=\xi _1^2+\xi _2^2$. Further we consider $\alpha$ equal to 1 which can be always obtained by scaling the original problem by $\alpha ^{-1}$. We assume that $\varOmega$ is decomposed into a set of disjoint polygonal subdomains $\{D_j\}$ such that, in each subdomain $D_j$, A(x) is continuous and smooth in the sense that

$$\begin{aligned} |A|_{W^{1,\infty }(D_i)}\le C_\varOmega , \end{aligned}$$

(2.1)

where $C_\varOmega$ is a positive constant. We also assume that

$$\begin{aligned} \exists \, \lambda _j >0 \quad \text{ such } \text{ that } \quad \xi ^T A(x)\xi \ge \lambda _j |\xi |_2^2 \ge |\xi |_2^2 \quad \forall x \in D_j\quad \text{ and } \quad \forall \xi \in \mathbb {R}^2. \end{aligned}$$

Due to $A\in (L^\infty (D_j))^{2\times 2}$, we have the following,

$$\begin{aligned} \exists \, \Lambda _j >0 \text{ such } \text{ that } \quad | \nu ^T A(x)\xi | \le \Lambda _j| \nu |_2 |\xi |_2 \quad \forall x \in D_j\quad \text{ and } \quad \forall \xi ,\nu \in \mathbb {R}^2. \end{aligned}$$

We also assume that $\Lambda _j\lesssim \lambda _j$. We then have

$$\begin{aligned} \lambda _j |u|_{H^1(D_j)}^2\le \int _{D_j} \nabla u^TA(x)\nabla u \,d x \le \Lambda _j |u|_{H^1(D_j)}^2 \quad \forall u \in H^1(D_j). \end{aligned}$$

(2.2)

In the weak formulation, the differential problem is then to find $u\in H^1_0(\varOmega )$ such that

$$\begin{aligned} a(u,v)=f(v) \quad \forall v \in H^1_0(\varOmega ), \end{aligned}$$

(2.3)

where

$$\begin{aligned} a(u,v) = \int _{\varOmega } \nabla u^T A(x) \nabla v \,d x \quad \text{ and } \quad f(v)=\int _{\varOmega }f v \,d x. \end{aligned}$$

3 The discrete problem

For the discretization, we use a finite volume element discretization where the Eq. (2.3) is discretized using the standard finite volume method on a mesh which is dual to the primal mesh, and where the finite element space or the solution space is defined on the primal mesh, see for instance in [16, 17, 20]; for an overview of finite volume element methods we refer to [23].

Let $T_h=T_h(\varOmega )$ be be a shape regular triangulation of $\varOmega$, cf. [8] or [6], hereon referred to as the primal mesh consisting of triangles $\{\tau \}$ with the size parameter $h=\max _{\tau \in T_h} \mathrm {diam}(\tau )$, and let $\varOmega _h$, $\partial \varOmega _h$, and $\overline{\varOmega }_h$ be the sets of triangle vertices corresponding to $\varOmega$, $\partial \varOmega$, and $\overline{\varOmega }$, respectively. We assume that each $\tau \in T_h$ is contained in one of $D_j$.

Define $V_h$ as the conforming linear finite element space consisting of functions which are continuous piecewise linear over the triangulation $T_h$, and are equal to zero on $\partial \varOmega$.

Now, let $T_h^* = T_h^*(\varOmega )$ be the dual mesh corresponding to $T_h$. For simplicity we use the so called Donald mesh for the dual mesh. For each triangle $\tau \in T^h$, let $c_{\tau }$ be the centroid, $x_j, \; j=1,2,3$ the three vertices, and $m_{k l}=m_{l k}, \; k,l=1,2,3$ the three edge midpoints. Divide each triangle $\tau$ into three polygonal regions inside the triangle by connecting its edge midpoints $m_{k l}=m_{l k}$ to its centroid $c_{\tau }$ with straight lines. One such polygonal region $\omega _{\tau ,x_1}\subset \tau$, associated with the vertex $x_1$, as illustrated in Fig. 1, is the region which is enclosed by the line segments $\overline{c_{\tau }m_{13}}, \overline{m_{13}x_1}, \overline{x_1m_{12}}$, and $\overline{m_{12}c_{\tau }}$, and whose vertices are $c_{\tau }, m_{13}, x_1$, and $m_{12}$. Now let $\omega _{x_k}$ be the control volume associated with the vertex $x_k$, which is the sum of all such polygonal regions associated with the vertex $x_k$, i.e.

$$\begin{aligned} \omega _{x_k}=\bigcup _{\{\tau \in T_h: \, x_k \text{ is } \text{ a } \text{ vertex } \text{ of } \tau \}} \omega _{\tau ,x_k} \end{aligned}$$

The set of all such control volumes form our dual mesh, i.e. $T_h^*=T_h^*(\varOmega )=\{\omega _x\}_{x \in \overline{\varOmega }_h}$. A control volume $\omega _{x_k}$ is called a boundary control volume if $x_k\in \partial \varOmega _h$.

Fig. 1

Showing $\omega _{\tau ,x_1}$ (shaded region) which is part of the control volume $\omega _{x_1}$ restricted to the triangle $\tau$. The control volume is associated with the vertex $x_1$

Let $V_h^*$ be the space of piecewise constant functions over the dual mesh $T_h^*$, which have values equal to zero on $\partial \varOmega _h$. We let the nodal basis of $V_h$ be $\{\phi _x\}_{x\in \varOmega _h}$, where $\phi _x$ is the standard finite element basis function which is equal to one at the vertex x and zero at all other vertices. Analogously, the nodal basis of $V_h^*$ is $\{\psi _x\}_{x\in \varOmega _h}$ where $\psi _x$ is a piecewise constant function which is equal to one over the control volume $\omega _x$ associated with the vertex x, and is zero elsewhere.

The two interpolation operators, $I_h$ and $I_h^*$, are defined as follows. $I_h:C(\varOmega )+V_h^*\rightarrow V_h$ and $I_h^*:C(\varOmega )\rightarrow V_h^*$ are given respectively as

$$\begin{aligned} I_h^* v=\sum _{x\in \varOmega _h} v(x)\psi _x \quad \text{ and } \quad I_h v=\sum _{x\in \varOmega _h} v(x)\phi _x. \end{aligned}$$

We note here that $I_hI_h^*v=v$ for $v \in V_h$, as well as $I_h^* I_h u=u$ for $u \in V_h^*$.

Let the finite volume bilinear form be defined on $V_h\times V_h^*$ as $a_{FV}: V_h\times V_h^*\rightarrow \mathbb {R}$ such that

$$\begin{aligned} a_{FV}(u,v)=-\sum _{x_i\in \varOmega _h}v(x_i) \int _{\partial \omega _{x_i}}A \nabla u \mathbf n ds \quad u\in V_h, \; v\in V_h^*, \end{aligned}$$

or equivalently on $V_h\times V_h$ as $a_h: V_h\times V_h\rightarrow \mathbb {R}$ such that

$$\begin{aligned} a_h(u,v)=a_{FV}(u,I_h^* v) \end{aligned}$$

(3.1)

for $u,v\in V_h$. We note here that $a_h(\cdot ,\cdot )$ is a nonsymmetric bilinear form in general, while $a(\cdot ,\cdot )$ is a symmetric bilinear form. The discrete problem is then to find $u_h \in V_h$ such that

$$\begin{aligned} a_{FV}(u_h,v)=f(v) \quad \forall v \in V_h^*, \end{aligned}$$

(3.2)

or equivalently $a_h(u_h,v)=f(I_h^* v) \quad \forall v \in V_h .$ The problem has a unique solution for h sufficiently small, which follows from the fact that (5.2) holds, cf. Proposition 6.1, leading to the fact that $a_h(u,u)$ is $V_h$-elliptic, cf. Lemma 5.2. An error estimate in the norm induced by a(u, v) can also be given, cf. e.g. [17, § 3],

We close this section with the following remark. Note that in some cases, the bilinear form $a_h(\cdot ,\cdot )$ may equal the symmetric bilinear form $a(\cdot ,\cdot )$, as for instance in the case when the matrix A is piecewise constant over the subdomains $\{D_j\}$. This may not be true if we choose to use a different dual mesh or if A is not piecewise constant. In this paper, we only consider the case when the bilinear form $a_h(\cdot ,\cdot )$ is nonsymmetric.

4 An edge based additive Schwarz method

We propose in this section two variants of the edge based additive Schwarz method (ASM) for the discrete finite volume element problem of the previous section. They are constructed in the same way as it is done in the standard case using the classical abstract framework of additive Schwarz methods, cf. [26, 30, 32]. The convergence analysis of the methods is however based on the abstract framework which will be developed in Sect. 5. The new framework is an extension of the classical framework, and is based on three key assumptions. We validate those assumptions for the proposed methods in Sect. 6, thereby completing the analysis.

We assume that we have a partition of $\varOmega$ into the set of N nonoverlapping polygonal subdomains $\{\varOmega _j\}_{j=1}^N$, such that they form a shape regular coarse partition of $\varOmega$, as described in [7]. Accordingly, we assume that the intersection between two subdomains is either a vertex, an edge, or the empty set, and that there is a fixed number (M) of reference polygonal domains $E_k$ ($1 \le k \le M$) of diameter one each, such that for each subdomain $\varOmega _j$ there is an invertible affine map $\mu _j(x)=B_jx+b_j$ which maps $\varOmega _j$ to one of the reference domains $E_{k(j)}$ ($1\le k(j) \le M$). Here $B_j$ is a $2\times 2$ nonsingular matrix and $b_j$ a $2\times 1$ vector, and

$$\begin{aligned} \Vert B_j\Vert _\infty \lesssim H_j^{-1}, \qquad \Vert B_j^{-1}\Vert _\infty \lesssim H_j, \end{aligned}$$

where $H_j=\mathrm {diam}(\varOmega _j)$.

We assume that each subdomain $\varOmega _k$ lies in exactly one of the polygonal subdomains $\{D_j\}$ described earlier, and that none of their boundaries cross each other. The interface

$$\begin{aligned} \varGamma =\bigcup _{k=1}^N \partial \varOmega _k{\setminus } \partial \varOmega , \end{aligned}$$

which is the sum of all subdomain edges and subdomain vertices not lying on the boundary $\partial \varOmega$, or crosspoints, plays a crucial role in the design of our preconditioner. We also assume that the primal mesh $T_h$ is perfectly aligned with the partitioning of $\varOmega$, in other words, no edges of the primal mesh cross any edge of the coarse substructure. As a consequence, the coefficient matrix A(x) restricted to a subdomain $\varOmega _k$ is in $(W^{1,\infty }(\varOmega _k))^{2 \times 2}$, and hence (cf. (2.1))

$$\begin{aligned} |A|_{W^{1,\infty }(\varOmega _k)}\le |A|_{W^{1,\infty }(D_j)}\le C_\varOmega . \end{aligned}$$

Each subdomain $\varOmega _k$ inherits its own local triangulation from the $T_h$, denote it by $T_h(\varOmega _k)=\{\tau \in T_h: \tau \subset \varOmega _k \}$. Let $V_h(\varOmega _k)$ be the space of continuous and piecewise linear functions over the triangulation $T_h(\varOmega _k)$, which are zero on $\partial \varOmega \cap \partial \varOmega _k$, and let $V_{h,0}(\varOmega _k):=V_h(\varOmega _k)\cap H^1_0(\varOmega _k)$. The local spaces are equipped with the bilinear form

$$\begin{aligned} a_k(u,v)=\int _{\varOmega _k } \nabla u^T A(x) \nabla v\,dx. \end{aligned}$$

We define the local projection operator $\mathscr {P}_k: V_h(\varOmega _k)\rightarrow V_{h,0}(\varOmega _k)$ such that

$$\begin{aligned} a_k(\mathscr {P}_ku,v)=a_k(u,v)\qquad \forall v\in V_{h,0}(\varOmega _k) \end{aligned}$$

and the local discrete harmonic extension operator $\mathscr {H}_k: V_h(\varOmega _k)\rightarrow V_h(\varOmega _k)$ such that

$$\begin{aligned} \mathscr {H}_k u =u- \mathscr {P}_k u. \end{aligned}$$

Note that $\mathscr {H}_ku$ is equal to u on the boundary $\partial \varOmega _k$, and discrete harmonic inside $\varOmega _k$ in the sense that

$$\begin{aligned} a_k(\mathscr {H}_ku, v)=0 \quad \forall v\in V_{h,0}(\varOmega _k). \end{aligned}$$

The local and global spaces of discrete harmonic functions are then defined as

$$\begin{aligned} W_k=\mathscr {H}_k V_h(\varOmega _k) \quad \text{ and } \quad W=\mathscr {H}V_h=\{u \in V_h: u_{|\varOmega _k}=\mathscr {H}_k u_{|\varOmega _k}\}, \end{aligned}$$

respectively.

We now define the subspaces required for the ASM preconditioner, cf. [26, 30, 32]. For each subdomain $\varOmega _k$, the local subspace $V_k\subset V_h$ is defined as $V_{h,0}(\varOmega _k)$ extending it by zero to the rest of the subdomains, i.e.

$$\begin{aligned} V_k = \{v\in V_h: v_{|\overline{\varOmega }_k}\in V_{h,0}(\varOmega _k) \quad \text{ and } \quad v_{|\varOmega {\setminus } \overline{\varOmega }_k}=0 \} \end{aligned}$$

The coarse space $V_0\subset W$ is defined as the space of discrete harmonic functions which are piecewise linear over the subdomain edges (i.e. linear along each subdomain edge and discrete harmonic inside each subdomain). Its degrees of freedom are associated with the subdomain vertices lying inside the domain $\varOmega$, i.e. the crosspoints, and hence the dimension equals the cardinality of $\mathscr {V}=\bigcup _k \mathscr {V}_k$, where $\mathscr {V}_k$ is the set of all subdomain vertices which are not on the boundary $\partial \varOmega$. For an analogous coarse space, we refer to [32, §5.4] where 3D substructuring methods are considered. Using their ideas it is possible to extend the method to 3D.

Finally, the local edge based subspaces are defined as follows. For each subdomain edge $\varGamma _{k l}$, which is the interface between $\varOmega _k$ and $\varOmega _l$, we let $V_{k l}\subset W$ be the local edge based subspace consisting of functions which may be nonzero inside $\varGamma _{k l}$, but zero on the rest of the interface $\varGamma$, and discrete harmonic in the subdomains. It is not difficult to see that the support of $V_{k l}$ is contained in $\overline{\varOmega }_k \cup \overline{\varOmega }_l$.

We have the following decomposition of the finite element spaces W and $V_h$. Both the symmetric and the nonsymmetric variant of the preconditioner use the same decomposition:

$$\begin{aligned} \begin{aligned} W=&V_0+\sum _{\varGamma _{k l}\subset \varGamma } V_{k l}, \\ V_h=&W+ \sum _{k=1}^N V_k =V_0+\sum _{\varGamma _{k l}\subset \varGamma } V_{k l} + \sum _{k=1}^N V_k. \end{aligned} \end{aligned}$$

(4.1)

Note that the subspaces of W, i.e. $V_0$ and $V_{k l}$, $\varGamma _{k l}\subset \varGamma$, are orthogonal to the subspaces $V_k$, $k=1,\ldots ,N$, with respect to the bilinear form $a(\cdot ,\cdot )$.

Remark 4.1

If A(x) is the identity matrix, and $\{\varOmega _j\}_{1\le j\le N}$ form a coarse triangulation of the domain $\varOmega$, then the coarse space $V_0$ will consist of functions that are continuous and piecewise linear over the coarse triangulation, cf. [32, §5.4.1].

In the following, we describe the two preconditioners: the symmetric and the nonsymmetric preconditioner. We will see later in the numerical experiments section that the two are very similar in their performance. It is not difficult to see that they also have similar computational complexities.

4.1 Symmetric preconditioner

For the symmetric variant of the preconditioner, we define the coarse space operator and the local subspace operators, $T_k:V_h\rightarrow V_k$, $k=0,1,\ldots ,N$, as

$$\begin{aligned} a(T_ku,v)=a_h(u,v) \qquad \forall v\in V_k, \end{aligned}$$

and the local edge based subspace operators $T_{k l}:V_h\rightarrow V_{k l}$, $\varGamma _{k l} \subset \varGamma$, as

$$\begin{aligned} a(T_{k l}u,v)=a_h(u,v) \qquad \forall v\in V_{k l}. \end{aligned}$$

Note that the bilinear form used to calculate each of the operations above, that is on the left hand side of the equation, is the symmetric bilinear form $a(\cdot ,\cdot )$. Now, defining our additive Schwarz operator T as the sum of the operators, that is

$$\begin{aligned} T=T_0 + \sum _{k=1}^N T_k + \sum _{\varGamma _{k l}\subset \varGamma } T_{k l}, \end{aligned}$$

we can replace the discrete problem (3.2) by the following equivalent preconditioned system of equations, in the operator form, cf. [30, Chapter 5]:

$$\begin{aligned} T u_h=g, \end{aligned}$$

(4.2)

where $g=g_0 + \sum _{k=1}^N g_k + \sum _{\varGamma _{k l}\subset \varGamma } g_{k l}$, $g_0=T_0u_h$, $g_k=T_ku_h$, $k=1,\ldots ,N$, and $g_{k l} = T_{k l}u_h$, $\varGamma _{k l}\subset \varGamma$, are the right hand sides with $u_h$ being the exact solution. Note that the right hand sides can be calculated without knowing the exact solution, cf. [30].

The GMRES iteration is used to solve the preconditioned system (4.2). The convergence rate is given by the standard GMRES convergence (Theorem 5.1) with estimates of its two parameters using Theorem 4.1.

Theorem 4.1

There exists $h_1$ such that, if $h\le h_1$, then for any $u\in V_h$

$$\begin{aligned} a(Tu,Tu)\lesssim a(u,u), \qquad a(Tu,u)\gtrsim \left( 1+\log \left( \frac{H}{h}\right) \right) ^{-2} a(u,u), \end{aligned}$$

where $H=\max _k(H_k)$ and $H_k=\mathrm {diam}(\varOmega _k)$.

The theorem is proved using the abstract framework given in Sect. 5, i.e. by using Theorem 5.2, and the three propositions in Sect. 6, Propositions 6.1, 6.2, and 6.3, verifying the three assumptions required by the framework.

4.2 Nonsymmetric preconditioner

Analogously, for the nonsymmetric variant of the preconditioner, the coarse space operator and the local subspace operators, $S_k:V_h\rightarrow V_k$, $k=0,1,\ldots ,N$, are defined as

$$\begin{aligned} a_h(S_ku,v)=a_h(u,v) \qquad \forall v\in V_k, \end{aligned}$$

and the local edge based subspace operators, $S_{k l}:V_h\rightarrow V_{k l}$, $\varGamma _{k l} \subset \varGamma$, as

$$\begin{aligned} a_h(S_{k l}u,v)=a_h(u,v) \qquad \forall v\in V_{k l}. \end{aligned}$$

The bilinear form used to calculate each of the operations above is the nonsymmetric bilinear form $a_h(\cdot ,\cdot )$. Again, denoting the additive Schwarz operator by S, where

$$\begin{aligned} S=S_0 + \sum _{k=1}^N S_k + \sum _{\varGamma _{k l}\subset \varGamma } S_{k l}, \end{aligned}$$

the discrete problem (3.2) can be replaced by the equivalent preconditioned system of equations, in the operator form:

$$\begin{aligned} S u_h=\hat{g}, \end{aligned}$$

(4.3)

where $\hat{g}=\hat{g}_0 + \sum _{k=1}^N \hat{g}_k + \sum _{\varGamma _{k l}\subset \varGamma } \hat{g}_{k l}$, $\hat{g}_k=S_ku_h$, $k=0,1,\ldots ,N$, and $\hat{g}_{k l} = S_{k l}u_h$, $\varGamma _{k l}\subset \varGamma$, are the right hand sides with $u_h$ being the exact solution. As in the symmetric case, the right hand sides can be calculated without knowing the exact solution.

Again, the GMRES iteration is used to solve the preconditioned system (4.3), whose convergence rate is given by the standard GMRES convergence (Theorem 5.1) with estimates of its two parameters using Theorem 4.2.

Theorem 4.2

There exists an $h_1$ such that, if $h\le h_1$, then for any $u\in V_h$

$$\begin{aligned} a(Su,Su)\lesssim a(u,u), \quad a(Su,u)\gtrsim \left( 1+\log \left( \frac{H}{h}\right) \right) ^{-2} a(u,u), \end{aligned}$$

where $H=\max _k(H_k)$ and $H_k=\mathrm {diam}(\varOmega _k)$.

The theorem is again proved using the abstract framework of Sect. 5, i.e. by using Theorem 5.3, and the three propositions in Sect. 6, Propositions 6.1, 6.2, and 6.3, verifying the three assumptions required by the framework.

5 The abstract framework

In this section, we formulate an abstract framework for the convergence analysis of additive Schwarz methods for a class of finite volume elements, using the methods as preconditioners in the GMRES iteration. The framework is based on three key assumptions which need to be verified every time a convergence analysis is to be performed. Once the assumptions are verified, the framework can be used to derive estimates for the convergence of the method under consideration. For two very recent applications of the framework, where the Crouzeix–Raviart finite volume element has been considered, we refer to [24, 25].

We consider a family of finite dimensional subspaces $V_h$ indexed by the parameter h, an inner product $a(\cdot ,\cdot )$ and its induced norm $\Vert \cdot \Vert _a:=\sqrt{a(\cdot ,\cdot )}$, and a family of discrete problems: Find $u_h\in V_h$

$$\begin{aligned} a_h(u_h,v)=f(v) \quad \forall v \in V_h, \end{aligned}$$

where $a_h(u,v)$ is a nonsymmetric bilinear form.

We start by stating the convergence result of the GMRES iteration (cf. [28]) for solving a system of equations, in the operator form,

$$\begin{aligned}P u = b,\end{aligned}$$

where the pair P and b can be either the pair T and g or the pair S and $\hat{g}$, in our case. The theorem was originally developed using the $l_2$ norm, cf. e.g. [15], it however extends to any Hilbert norm, cf. [9, 29]. The convergence rate is based on the two parameters: the smallest eigenvalue of the symmetric part of the operator and the norm of the operator, respectively

$$\begin{aligned} \beta _1=\inf _{u\not =0} \frac{a(Pu,u)}{\Vert u\Vert _a^2} \quad \text{ and } \quad \beta _2=\sup _{u\not =0} \frac{\Vert P u\Vert _a}{\Vert u\Vert _a }. \end{aligned}$$

(5.1)

A standard convergence rate of the GMRES iteration, in the $\Vert \cdot \Vert _a$ norm, is given in the following theorem.

Theorem 5.1

(Eisenstat et al. [15]) If $\beta _1>0$, then the GMRES method for solving the linear system (5.9) converges for any starting value $u_0\in V_h$ with the following estimate:

$$\begin{aligned} \Vert g-P u_m\Vert _a\le \left( 1-\frac{\beta _1^2}{\beta _2^2}\right) ^{m/2}\Vert g-Pu_0\Vert _a, \end{aligned}$$

where $u_m$ is the m-th iterate of the GMRES method.

The abstract framework is based on three assumptions leading to the two main results of the framework, namely Theorems 5.2 and 5.3 respectively for the symmetric and the nonsymmetric case.

In the first assumption, we assume that the nonsymmetric bilinear form $a_h(\cdot ,\cdot )$ is a small perturbation of the symmetric bilinear form $a(\cdot ,\cdot )$.

Assumption

(1) For all $h < h_0$, where $h_0$ is a constant,

$$\begin{aligned} E_h(u,v):=a_h(u,v)-a(u,v) \end{aligned}$$

converges to zero as h tends to zero satisfying the following uniform bound.

$$\begin{aligned} \exists \; C_E >0: \; \forall h<h_0\quad \text{ and } \quad \forall u, v \in V_h, \quad |E_h(u,v)|\le C_Eh\Vert u\Vert _a\Vert v\Vert _a, \end{aligned}$$

(5.2)

where $C_E$ is a constant independent of h.

The above assumption is important, also because, it leads to the continuity and the coerciveness of the bilinear form $a_h(\cdot ,\cdot )$, as shown in the following lemmas.

Lemma 5.1

For any $M\in (1,2)$ there exists $h_1\le h_0$ such that if $h < h_1$ then the bilinear form $a_h(u,v)$ is uniformly bounded in the $\Vert \cdot \Vert _a$-norm, i.e.

$$\begin{aligned} \forall u, v \in V_h \quad |a_h(u,v)|\le M\Vert u\Vert _a\Vert v\Vert _a. \end{aligned}$$

(5.3)

Proof

It follows from (5.2) [Assumption (5)] that

$$\begin{aligned} a_h(u,v)= & {} a(u,v) + E_h(u,v) \le (1+C_Eh)\Vert u\Vert _a\Vert v\Vert _a \le (1+C_Eh_1)\Vert u\Vert _a\Vert v\Vert _a. \end{aligned}$$

Taking $h_1=\min ((M-1)/C_E,h_0)$ ends the proof.

Lemma 5.2

For any $\alpha \in (0,1)$, there exists $h_1\le h_0$ such that if $h<h_1$ then the bilinear form $a_h(u,v)$ is uniformly $V_h$-elliptic in the $\parallel \cdot \parallel _a$-norm, i.e.

$$\begin{aligned} \forall u\in V_h \quad a_h(u,u)\ge \alpha \Vert u\Vert _a^2. \end{aligned}$$

(5.4)

Proof

By assumption (5.2) [Assumption (1)], we have

$$\begin{aligned} a(u,u)\le a_h(u,u) +|E_h(u,u)|\le a_h(u,u)+C_Eha(u,u). \end{aligned}$$

If $h<h_1\le h_0$ and $C_Eh_1\le 1-\alpha$, then

$$\begin{aligned} a_h(u,u)\ge (1-C_Eh_1\,)a(u,u)\ge \, \alpha a(u,u), \end{aligned}$$

and the proof follows.

The following two assumptions are associated with the domain decomposition, where the function space $V_h$ is decomposed into its subspaces as follows,

$$\begin{aligned} V_h=Z_0 + \sum _{k=1}^N Z_k, \end{aligned}$$

where $Z_k \subset V_h$ for $k=0,1,\ldots ,N$, with $Z_0$ being the coarse space. These are the same assumptions used in the abstract Schwarz framework for symmetric positive definite systems, cf. [30, 32], the first one ensuring a stable splitting of the function space, while the second one ensuring a strengthened Cauchy–Schwarz inequality between the subspaces excluding the coarse space.

Assumption

(2) For any $u \in V_h$, there are functions $u_k\in Z_k$, $k=0,1,\ldots ,N$, such that the following holds. There exists a positive constant $C_0$ (which may depend on the mesh parameters) such that

$$\begin{aligned} u = u_0 + \sum _{k=1}^N u_k \end{aligned}$$

(5.5)

and

$$\begin{aligned} \sum _{k=0}^N a(u_k,u_k) \le C_0^2 a(u,u). \end{aligned}$$

(5.6)

Assumption

(3) For any $k,l=1,\ldots ,N$, let $\epsilon _{k l}$ be the minimal nonnegative constants such that

$$\begin{aligned} a(u_k,u_l)\le \epsilon _{k l}\Vert u_k\Vert _a \Vert u_l\Vert _a \qquad u_k\in Z_k, u_l\in Z_l. \end{aligned}$$

(5.7)

Let $\rho (\mathscr {E})$ be the spectral radius of the $N \times N$ symmetric matrix $\mathscr {E}=(\epsilon _{k l})_{k,l=1}^N$.

5.1 Symmetric preconditioner

For $k=0,1,\ldots ,N$, we define the projection operator $T_k:V_h\rightarrow Z_k$ as

$$\begin{aligned} a(T_k u,v)=a_h(u,v) \qquad \forall v \in Z_k. \end{aligned}$$

(5.8)

Note that the bilinear form a(u, v) is an inner product in $V_h$, hence $T_k$ is a well defined linear operator. Let the additive Schwarz preconditioned operator $T: V_h\rightarrow V_h$ be given as $T=T_0+\sum _{k=1}^N T_k,$ and the original problem be replaced by the preconditioned one:

$$\begin{aligned} Tu_h=g, \end{aligned}$$

(5.9)

where $g=g_0+\sum _{k=1}^N g_k$ with $g_k=T_k u_h$ for $k=0,1,\ldots ,N$. Note that $T_k$ and T are in general nonsymmetric.

The following lemma is needed for the two main theorems of the framework, namely Theorems 5.2 and 5.3.

Lemma 5.3

Let $u_k\in Z_k$ for $k=0,1,\ldots ,N$. Then

$$\begin{aligned} \left\| \sum _{k=0}^N u_k\right\| _a^2\le 2(1+\rho (\mathscr {E}))\sum _{k=0}^N\Vert u_k\Vert _a^2, \end{aligned}$$

where $\rho (\mathscr {E})$ is the spectral radius of the matrix $\mathscr {E}=(\epsilon _{k l})_{k,l=1}^N$.

Proof

We see that

$$\begin{aligned} \left\| \sum _{k=0}^N u_k\right\| _a^2\le & {} 2\Vert u_0\Vert _a^2+2\left\| \sum _{k=1}^N u_k\right\| _a^2. \end{aligned}$$

Using (5.7) and a Schwarz inequality in the $l_2$-norm we get

$$\begin{aligned} \left\| \sum _{k=1}^N u_k\right\| _a^2 = \sum _{k,l=1}^Na( u_k,u_l)\le & {} \sum _{k,l=1}^N \epsilon _{k l}\Vert u_k\Vert _a\Vert u_l\Vert _a \\\le & {} \rho (\mathscr {E})\sqrt{ \sum _{k=1}^N \Vert u_k\Vert _a^2} \sqrt{ \sum _{l=1}^N \Vert u_l\Vert _a^2} = \rho (\mathscr {E}) \sum _{k=1}^N \Vert u_k\Vert _a^2, \end{aligned}$$

and the proof follows.

The first main theorem of the framework giving estimates of the two parameters of the GMRES convergence, cf. Theorem 5.1, for the symmetric preconditioner, is stated in the following.

Theorem 5.2

There exists $h_1\le h_0$ such that if $h < h_1$ then

$$\begin{aligned} a(Tu,Tu)\le & {} \beta _2^2 a(u,u), \end{aligned}$$

(5.10)

$$\begin{aligned} a(Tu,u)\ge & {} \beta _1 a(u,u), \end{aligned}$$

(5.11)

where $\beta _2=2M(1+\rho (\mathscr {E}))$ and $\beta _1=\alpha ^2C_0^{-2} -\beta _2 C_E h$.

Proof

It follows from Lemma 5.3 that

$$\begin{aligned} a(Tu,Tu) = \left\| \sum _{k=0}^N T_k u\right\| _a^2 \le 2(1+\rho (\mathscr {E}))\sum _{k=0}^N\Vert T_ku\Vert _a^2. \end{aligned}$$

By (5.3) and (5.8), we get

$$\begin{aligned} \sum _{k=0}^N\Vert T_ku\Vert _a^2 = \sum _{k=0}^N a(T_k u,T_k u)= & {} \sum _{k=0}^N a_h(u,T_ku) = a_h(u,T u) \le M \Vert u\Vert _a\Vert T u\Vert _a. \qquad \nonumber \\ \end{aligned}$$

(5.12)

The upper bound (5.10) then follows with $\beta _2=2M(1+\rho (\mathscr {E}))$.

To prove the lower bound, cf. (5.11), we start with the splitting of $u\in V_h$, cf. (5.5), such that (5.6) holds. Then using (5.4), (5.8), a Schwarz inequality, and (5.6), we get

$$\begin{aligned} \alpha a(u,u)\le & {} a_h(u,u) = \sum _{k=0}^N a_h(u,u_k) =\sum _{k=0}^N a(T_k u,u_k)\\\le & {} \sum _{k=0}^N \Vert T_k u\Vert _a \Vert u_k\Vert _a \le \sqrt{\sum _{k=0}^N \Vert T_k u\Vert _a^2} \; \sqrt{\sum _{k=0}^N\Vert u_k\Vert _a^2} \le C_0 \sqrt{\sum _{k=0}^N \Vert T_k u\Vert _a^2} \; \Vert u\Vert _a. \end{aligned}$$

This and (5.12), then yield

$$\begin{aligned} \alpha ^2 a(u,u)\le & {} C_0^2 \sum _{k=0}^N\Vert T_k u\Vert _a^2= C_0^2a_h(u,Tu). \end{aligned}$$

Finally, from the assumption (5.2) [Assumption (1)] and the upper bound (5.10), we get

$$\begin{aligned} a_h(u,Tu) = a(u,Tu)+E_h(u,Tu)\le & {} a(u,Tu) + C_E h\Vert u\Vert _a\Vert Tu\Vert _a \\\le & {} a(u,Tu) +\beta _2 C_E h\Vert u\Vert _a^2. \end{aligned}$$

Hence,

$$\begin{aligned} a(Tu,u) \ge (\alpha ^2C_0^{-2} -\beta _2 C_E h)a(u,u). \end{aligned}$$

Taking $\beta _1=(\alpha ^2C_0^{-2} -\beta _2 C_E h)$ we get the lower bound in (5.11).

Remark 5.2

In some cases the constant $C_0$ in (5.6) may depend on h ($C_0=C_0(h))$ then $C_0(h)$ cannot grow too fast with decreasing h, otherwise $\beta _1$ may become negative and our theory would not work, e.g. if $\rho (\mathscr {E})$ is independent of h which is usually the case in ASM methods, then it would be sufficient if $\lim _{h\rightarrow 0} C_0^2(h)h =0,$ because then there exists an $h_1\le h_0$ such that $\beta _1$ is positive for any $h < h_1$.

5.2 Nonsymmetric preconditioner

For $k=0,1,\ldots ,N$, we define the projection operators $S_k: V_h\rightarrow Z_k$ as

$$\begin{aligned} a_h(S_k u,v)=a_h(u,v) \qquad \forall v \in Z_k. \end{aligned}$$

(5.13)

Note that the bilinear form $a_h(u,v)$ is $Z_k$-elliptic, cf. (5.4), so $S_k$ is a well defined linear operator. Now, introducing the additive Schwarz operator $S: V_h\rightarrow V_h$ as $S=S_0+\sum _{k=1}^N S_k,$ we replace the original problem with

$$\begin{aligned} Su_h=\hat{g}, \end{aligned}$$

where $\hat{g}=\hat{g}_0+\sum _{k=1}^N \hat{g}_k$ with $\hat{g}_k=S_k u_h$ for $k=0,1,\ldots ,N$.

The second main theorem of the framework giving estimates of the two parameters of the GMRES convergence, for the nonsymmetric preconditioner, is stated in the following.

Theorem 5.3

There exists $h_1\le h_0$ such that for any $h<h_1$, the following bounds hold.

$$\begin{aligned} a(Su,Su)\le & {} \beta _2^2 a(u,u),\\ a(Su,u)\ge & {} \beta _1 a(u,u) \end{aligned}$$

where $\beta _2=\frac{2M}{\alpha }(1+\rho (\mathscr {E}))$ and $\beta _1= \frac{\alpha ^3}{M^2 C_0^2} - \beta _2C_E h$, and, as before, $\rho (\mathscr {E})$ is the spectral radius of the matrix $\mathscr {E}=(\epsilon _{k l})_{k,l=1}^N$.

Proof

We follow the lines of proof of Theorem 5.2. For the upper bound, we use Lemma 5.3 to see that

$$\begin{aligned} a(Su,Su) \le 2(1+\rho (\mathscr {E}))\sum _{k=0}^N \Vert S_ku\Vert _a^2. \end{aligned}$$

Using (5.3), (5.4), and (5.13), we get

$$\begin{aligned} \alpha \sum _{k=0}^N a(S_k u,S_k u) \le \sum _{k=0}^N a_h(S_k u,S_k u)= & {} \sum _{k=0}^N a_h(u,S_ku) \nonumber \\= & {} a_h(u,Su) \le M \Vert u\Vert _a\Vert S u\Vert _a. \end{aligned}$$

(5.14)

The upper bound then follows with $\beta _2=\frac{2M}{\alpha }(1+\rho (\mathscr {E}))$.

For the lower bound, again, we use the splitting (5.5) of $u\in V_h$ such that (5.6) holds. Next (5.3), (5.4), (5.5), (5.13), a Schwarz inequality, and (5.6) yield that

$$\begin{aligned} \alpha a(u,u)\le & {} a_h(u,u) = \sum _{k=0}^N a_h(u,u_k) = \sum _{k=0}^N a_h(S_k u,u_k) \le M\sum _{k=0}^N \Vert S_k u\Vert _a \Vert u_k\Vert _a \nonumber \\\le & {} M\sqrt{\sum _{k=0}^N\Vert S_k u\Vert _a^2} \; \sqrt{\sum _{k=0}^N\Vert u_k\Vert _a^2} \le M \, C_0 \sqrt{\sum _{k=0}^N\Vert S_k u\Vert _a^2} \; \Vert u\Vert _a . \end{aligned}$$

Combining the estimate above with (5.14), we get

$$\begin{aligned} \alpha ^2 a(u,u)\le & {} M^2C_0^2 \sum _{k=0}^N \Vert S_k u\Vert _a^2\le \frac{M^2\,C_0^2}{\alpha }a_h(u,Su). \end{aligned}$$

Finally, using similar arguments as in the proof of Theorem 5.2, we can conclude that

$$\begin{aligned} a(u,S u)\ge \left( \frac{\alpha ^3}{M^2 C_0^2} - \beta _2C_E h\right) a(u,u), \end{aligned}$$

and the lower bound follows with $\beta _1=\frac{\alpha ^3}{M^2 C_0^2} - \beta _2C_E h$.

6 Technical tools

In this section, we present the technical results necessary for the proof of Theorems 4.1 and 4.2. We use the abstract framework developed in the previous section, based on which, we first show (5.2) [verifying Assumption (1)], then show that $\rho (\mathcal{E})$ is bounded by a constant [verifying Assumption (3)], and finally give an estimate of $C_0^2$ such that (5.5)–(5.6) hold [verifying Assumption (2)], all of these being formulated below as Propositions 6.1, 6.2, and 6.3, respectively.

We start with the proposition which shows that (5.2) holds true for the two bilinear forms $a(\cdot ,\cdot )$ and $a_h(\cdot ,\cdot )$ of (2.3) and (3.1), respectively.

Proposition 6.1

It holds that

$$\begin{aligned} \exists \; C_E >0: \; \forall h<h_0 \quad \text{ and } \quad u, v \in V_h, \quad |a_h(u,v)-a(u,v)|\le C_Eh\Vert u\Vert _a\Vert v\Vert _a, \end{aligned}$$

where $C_E$ is a constant independent of h and the jumps of the coefficients across $\partial D_j$s, but may depend on $C_\varOmega$ in (2.1).

The statement of this proposition is formulated in [17, §3] without proof. However, as stated in the paper, it can be proved by following the lines of the proof of Lemma 3.1 in [16].

The next two lemmas are well known, and are given here without proofs. The first lemma is the extension theorem for discrete harmonic functions, cf. e.g. [5, Lemma 5.1]. The second lemma gives an estimate of the $H^{1/2}_{00}(\varGamma _{kl})$ norm of a finite element function which is zero on $\partial \varOmega _k{\setminus }\varGamma _{kl}$ by its $H^{1/2}$ seminorm and $L^\infty$ norm, cf. e.g. [22, Lemma 4.1]. Let $\varGamma _{k l,h}$ be the set of nodal points that are on the open edge $\varGamma _{k l}$ common to $\varOmega _k$ and $\varOmega _l$.

Lemma 6.1

(Discrete extension theorem) Let $u\in W_k$, then

$$\begin{aligned} |u|_{H^1(\varOmega _k)} \lesssim |u|_{H^{1/2}(\partial \varOmega _k)}. \end{aligned}$$

Lemma 6.2

Let $u,u_1\in W_k$ be such that $u_1(x)=u(x)$ for $x \in \varGamma _{k l,h}$ and $u_{1|\partial \varOmega _k {\setminus } \varGamma _{k l}}=0$, then

$$\begin{aligned} \Vert u_1\Vert _{H^{1/2}_{00}(\varGamma _{k l})}^2\lesssim |u|_{H^{1/2}(\varGamma _{k l})}^2 + \left( 1+ \log \left( \frac{H_k}{h}\right) \right) \Vert u\Vert _{L^\infty (\varGamma _{k l})}^2 \end{aligned}$$

In the following we present additional set of technical lemmas, they are given here with proofs. The first one is a simple result which will be used to estimate the $H^1$ seminorm of functions from the coarse space $V_0$.

Lemma 6.3

For $u\in V_0$ and C being an arbitrary constant, the following holds, i.e.

$$\begin{aligned} |u|_{H^1(\varOmega _k)}^2\lesssim \sum _{x\in \mathscr {V}_k} |u(x)-C|^2, \end{aligned}$$

where $\mathscr {V}_k$ is the set of all vertices of $\varOmega _k$ which are not on $\partial \varOmega$.

Proof

Note that $u_{|\varOmega _k}=\sum _{x\in \mathscr {V}_k}u(x){\phi _x}_{|\varOmega _k}$, where $\phi _x$ is a discrete harmonic function which is equal to one at x, zero at $\mathscr {V}_k{\setminus }\{x\}$, and linear along the edges $\varGamma _{kl} \subset \partial \varOmega _k$ . Thus, for any constant C, we have

$$\begin{aligned} |u|_{H^1(\varOmega _k)}^2=|u-C|_{H^1(\varOmega _k)}^2\lesssim \sum _{x\in \mathscr {V}_k}|u(x)-C|^2|\phi _x|_{H^1(\varOmega _k)}^2\lesssim \sum _{x\in \mathscr {V}_k}|u(x)-C|^2. \end{aligned}$$

The last inequality follows from using the fact that a discrete harmonic function has the minimal energy of all functions taking the same values on the boundary, and then by applying the standard estimate of $H^1$-seminorm of the coarse nodal basis function.

Definition 6.1

Let $I_H:V_h\rightarrow V_0$ be a coarse interpolant defined using function values at the vertices $\mathscr {V}$ as follows. For $u\in V_h$, $I_H u \in V_0$ implies that

$$\begin{aligned} I_H u(x)=u(x) \quad x\in \mathscr {V}. \end{aligned}$$

Lemma 6.4

For any $u\in V_h$, the following holds, i.e.

$$\begin{aligned} |I_H u|_{H^1(\varOmega _k)}^2\lesssim \left( 1+ \log \left( \frac{H_k}{h}\right) \right) |u|_{H^1(\varOmega _k)}^2. \end{aligned}$$

Proof

From Lemmas 6.3 and the discrete Sobolev like inequality, cf. e.g. Lemma 7 in [30] or Lemma 4.15 in [32], we get

$$\begin{aligned} |I_H u|_{H^1(\varOmega _k)}^2\lesssim \left( 1+ \log \left( \frac{H_k}{h}\right) \right) \left( H_k^{-2}\Vert u-C\Vert _{L^2(\varOmega _k)}^2+ |u-C|_{H^1(\varOmega _k)}^2\right) , \end{aligned}$$

for any constant C. A scaling argument and a quotient space argument complete the proof.

Lemma 6.5

Let $\varGamma _{k l}\subset \partial \varOmega _k$ be an edge, and $u_{k l}\in W_k$ and $u \in V_h$ be functions such that $u_{k l}(x)=u(x)-I_Hu(x)$ for $x\in \varGamma _{k l,h}$, and $u_{k l}$ is zero on $\partial \varOmega _k{\setminus }\varGamma _{k l}$. Then, we have

$$\begin{aligned} |u_{k l}|_{H^{1/2}_{00}(\varGamma _{k l})}^2\lesssim \left( 1+ \log \left( \frac{H_k}{h}\right) \right) ^2 |u|_{H^1(\varOmega _k)}^2 \end{aligned}$$

(6.1)

Proof

Note that $u_{k l}$ equals to $u-I_H u$ on $\varGamma _{k l}$ and is zero on $\partial \varOmega _k {\setminus } \varGamma _{k l}$, and hence by Lemma 6.2, we get

$$\begin{aligned} \Vert u_{k l}\Vert _{H^{1/2}_{00}(\varGamma _{k l})}^2\lesssim |u-I_H u|_{H^{1/2}(\varGamma _{k l})}^2 + \left( 1+ \log \left( \frac{H_k}{h}\right) \right) \Vert u-I_H u\Vert _{L^\infty (\varGamma _{k l})}^2. \end{aligned}$$

(6.2)

The first term can be estimated using the standard trace theorem, a triangle inequality and Lemma 6.4 as follows,

$$\begin{aligned} |u-I_H u|_{H^{1/2}(\varGamma _{k l})}^2\lesssim |u|_{H^1(\varOmega _k)}^2 + |I_Hu|_{H^1(\varOmega _k)}^2 \lesssim \left( 1+ \log \left( \frac{H_k}{h}\right) \right) |u|_{H^1(\varOmega _k)}^2. \end{aligned}$$

(6.3)

For any constant C, we note that $u-I_Hu=u-C -I_H(u-C)$ on $\varGamma _{k l}$, and since $I_H u$ is a linear function along $\varGamma _{k l}$, $\Vert I_H u\Vert _{L^\infty (\varGamma _{k l})}\le \Vert u\Vert _{L^\infty (\varGamma _{k l})}$. Hence the $L^\infty$ norm of $u-I_H u$ in (6.2) can be estimated as follows,

$$\begin{aligned} \Vert u-I_H u\Vert _{L^\infty (\varGamma _{k l})}^2\lesssim & {} \Vert u-C\Vert _{L^\infty (\varGamma _{k l})}^2 + \Vert I_H (u-C)\Vert _{L^\infty (\varGamma _{k l})}^2 \lesssim \Vert u-C\Vert _{L^\infty (\varGamma _{k l})}^2\\\lesssim & {} \left( 1+ \log \left( \frac{H_k}{h}\right) \right) \left( H_k^{-2}\Vert u-C\Vert _{L^2(\varOmega _k)}^2+ |u-C|_{H^1(\varOmega _k)}^2\right) , \end{aligned}$$

where C is an arbitrary constant. The last inequality is due to the discrete Sobolev like inequality, cf. Lemma 7 in [30] or Lemma 4.15 in [32]. Finally, a scaling argument and a quotient space argument yield

$$\begin{aligned} \Vert u-I_H u\Vert _{L^\infty (\varGamma _{k l})}^2\lesssim \left( 1+ \log \left( \frac{H_k}{h}\right) \right) |u|_{H^1(\varOmega _k)}^2. \end{aligned}$$

The above estimate together with the estimates (6.3) and (6.2), complete the proof.

A standard coloring argument bounds the spectral radius, and is given here in our second proposition.

Proposition 6.2

Let $\mathscr {E}$ be the symmetric matrix of Cauchy–Schwarz coefficients, cf. (5.7), for the subspaces $V_k$, $V_l$, and $V_{k l}$, $k,l=1,\ldots ,N$, of the decomposition (4.1). Then,

$$\begin{aligned} \rho (\mathscr {E}) \le C, \end{aligned}$$

where C is a positive constant independent of the coefficients and mesh parameters.

The third and final proposition gives an estimate of the $C_0^2$ such that (5.5)–(5.6) hold for any $u\in V_h$.

Proposition 6.3

For any $u\in V_h$ there exists $u_k\in V_k$ $k=0,1,\ldots ,N$ and $u_{k l}\in V_{k l}$ such that $u = u_0 + \sum _{k=1}^N u_k + \sum _{\varGamma _{k l}\subset \varGamma }u_{k l}\;$ and

$$\begin{aligned} a(u_0,u_0)+ \sum _{k=1}^N a(u_k,u_k) + \sum _{\varGamma _{k l}\subset \varGamma }a(u_{k l},u_{k l})\lesssim & {} \left( 1+ \log \left( \frac{H}{h}\right) \right) ^2 a(u,u), \end{aligned}$$

where $H=\max _{k=1}^N H_k$ with $H_k=\mathrm {diam}(\varOmega _k)$.

Proof

We first set $u_0=I_H u\in V_0$, cf. Definition 6.1. Next, let $u_k\in V_k$ for $k=1,\ldots ,N$, be defined as $\mathscr {P}_k u_{|\overline{\varOmega }_k}$ on $\varOmega _k$, be extended by zero to the rest of $\varOmega$.

Now define $w = u-u_0-\sum _k u_k$. Note that w is discrete harmonic inside each subdomain $\varOmega _k$, since $u_0$ is discrete harmonic in the same way, and the sum

$$\begin{aligned} (w+u_0)_{|\overline{\varOmega }_k}= u_{|\overline{\varOmega }_k} - \mathscr {P}_k u_{|\overline{\varOmega }_k} = \mathscr {H}_k u_{|\overline{\varOmega }_k} \end{aligned}$$

is in fact a function of $W_k$. Moreover,

$$\begin{aligned} w(x) = u(x)-I_Hu(x)=0 \quad x\in \mathscr {V}. \end{aligned}$$

Consequently, w can be decomposed as follows,

$$\begin{aligned} w=\sum _{\varGamma _{k l}\subset \varGamma } u_{k l}, \end{aligned}$$

where $u_{k l}\in V_{k l}$, with $u_{|\varGamma _{k l}} = w_{|\varGamma _{k l}}$.

We now prove the inequality by considering each term at a time. For the first term, by Lemma 6.4, we see that

$$\begin{aligned} a(u_0,u_0)\lesssim & {} \sum _{k=1}^N \Lambda _k |u_0|_{H^1(\varOmega _k)}^2 = \sum _{k=1}^N \Lambda _k |I_H u|_{H^1(\varOmega _k)}^2 \nonumber \\\lesssim & {} \left( 1+\log \left( \frac{H}{h}\right) \right) \sum _{k=1}^N a_k(u,u)= \left( 1+\log \left( \frac{H}{h}\right) \right) a(u,u). \end{aligned}$$

(6.4)

For the second term, since $\mathscr {P}_k$ is the orthogonal projection in $a_k(u,v)$, we get

$$\begin{aligned} \sum _{k=1}^N a(u_k,u_k)=\sum _{k=1}^N a_k(\mathscr {P}_k u_{|\overline{\varOmega }_k},\mathscr {P}_k u_{|\overline{\varOmega }_k})\le \sum _{k=1}^N a_k(u_{|\overline{\varOmega }_k},u_{|\overline{\varOmega }_k})=a(u,u). \end{aligned}$$

(6.5)

And, for the last term, let $\varGamma _{k l}\subset \varGamma$ be the edge which is common to both $\varOmega _k$ and $\varOmega _l$. Note that $u_{k l} \in V_{k l}$ has support both in $\overline{\varOmega }_k\cup \overline{\varOmega }_l$. By Lemma 6.1, we note that

$$\begin{aligned} a(u_{k l},u_{k l}) = \sum _{s=k,l} a_s(u_{k l},u_{k l})\lesssim \sum _{s=k,l} \Lambda _s |u_{k l}|_{H^1(\varOmega _s)}^2 \lesssim \left( \sum _{s=k,l} \Lambda _s\right) |u_{k l}|_{H^{1/2}_{00}(\varGamma _{k l})}^2. \end{aligned}$$

Utilizing Lemma 6.5 for $s=k$ if $\Lambda _k\ge \Lambda _l$ (otherwise we take $s=l$), and (2.2), we get

$$\begin{aligned} \left( \sum _{s=k,l} \Lambda _s\right) |u_{k l}|_{H^{1/2}_{00}(\varGamma _{k l})}^2\lesssim & {} \left( 1+ \log \left( \frac{H}{h}\right) \right) ^2 \Lambda _k|u|_{H^1(\varOmega _k)}^2 \\\lesssim & {} \left( 1+ \log \left( \frac{H}{h}\right) \right) ^2 a_k(u,u). \end{aligned}$$

Combining the last two estimates, we get

$$\begin{aligned} \sum _{\varGamma _{k l}\subset \varGamma }a(u_{k l},u_{k l})\lesssim & {} \sum _{\varGamma _{k l}\subset \varGamma } \sum _{s=k,l} \left( 1+ \log \left( \frac{H}{h}\right) \right) ^2 a_s(u,u) \nonumber \\\lesssim & {} \left( 1+ \log \left( \frac{H}{h}\right) \right) ^2 a(u,u). \end{aligned}$$

(6.6)

The proof then follows by summing (6.4), (6.5), and (6.6) together.

7 Numerical experiments

In this section, we present some numerical experiments showing the performance of the proposed methods. We consider our model problem to be defined on the domain $\varOmega =[0,1]\times [0,1]$ with the right hand side f equal to 1, and apply the finite volume element discretization and the proposed additive Schwarz preconditioners for the solution. The domain is divided into $\frac{1}{H}\times \frac{1}{H}$ equally sized square subdomains of size $H\times H$, allowing equal number of subdomains in each direction, each of which is then further divided into $\frac{H}{h}\times \frac{H}{h}$ small equally sized squares of size $h\times h$, again with equal number of small squares in each direction. We get the primal mesh by slicing each small square into two triangles in a regular fashion, as shown in the figures.

All our numerical results have been obtained in Matlab, employing the preconditioned GMRES algorithm based on the $\Vert \cdot \Vert _a$-norm minimization, which is obtained by replacing the standard $l_2$ inner product with the $a(\cdot ,\cdot )$ inner product in the original algorithm, see for instance [29]. For the stopping criteria, on the other hand, for simplicity, we only look at the $l_2$-norm of the residual. We let the algorithm to run until the $l_2$ norm of the initial residual is reduced by a factor of $10^{6}$ in each test, i.e., until $\Vert r_i\Vert _2/\Vert r_0\Vert _2\le 10^{-6}$ where $r_0$ and $r_i$ respectively are the initial and the i-th residual vector.

The number of iterations to converge, and an estimate of the smallest eigenvalue of the symmetric part of the preconditioned operator P, that is the smallest eigenvalue of $\frac{1}{2}\left( P^t+P\right)$, which is also the most critical parameter of the two describing the GMRES convergence, are presented in the tables below. Our experiments have shown that the second parameter, which is the norm of the operator, is a constant independent of the mesh parameters H and h, and the coefficient A, which is in agreement with our analysis.

For the first numerical experiment we test the dependency of the iteration count and the smallest eigenvalue on the mesh parameters h and H, where the coefficient A is equal to $2+\sin (\pi x)\sin (\pi y)$. The results are reported in Table 1 for the symmetric preconditioner. We observe a mild decrease in the value of the smallest eigenvalue, with a slow increase in the iteration count, as the subdomain problem size $\frac{H}{h}$ increases, suggesting a poly-logarithmic dependence as predicted in our theory.

Table 1 Iteration numbers and estimates of the smallest eigenvalue (in parentheses) for the symmetric preconditioner for different values of h and H

In the second numerical experiment we perform similar tests, however, with a slightly faster varying A, namely $A = 2+\sin (10\pi x)\sin (10\pi y)$. The results are reported in Tables 2 and 3 respectively for the symmetric and the nonsymmetric variant of the preconditioner. In both cases, we observe convergence behavior which are similar to the one in the first experiment. We also note that the performances of the two variants of the preconditioner are almost identical.

Table 2 Iteration numbers and estimates of the smallest eigenvalue (in parentheses) for the symmetric preconditioner for different values of h and H

Table 3 Iteration numbers and estimates of the smallest eigenvalue (in parentheses) for the nonsymmetric preconditioner for different values of h and H

Each diagonal (subdiagonal) in the Tables 1, 2 and 3, corresponds to a fixed subdomain problem size $\frac{H}{h}$. As we can see from the entries along each such diagonal (subdiagonal), that both the eigenvalue estimates and the iteration counts remain almost unchanged suggesting that both preconditioners are algorithmically scalable, in the sense that, for a fixed subdomain size $\frac{H}{h}$, the number of GMRES iterations is (asymptotically) independent of the number of subdomains (processors).

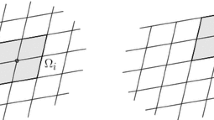
In the third numerical experiment, we consider an example where A is discontinuous across subdomains, which is given by $A=\alpha _1(2+\sin (10\pi x)\sin (10\pi y))$ with $\alpha _1$ being a constant in each subdomain. The mesh parameters are $H=1/8$ and $h=1/64$. We assign the parameter $\alpha _1$ in the coefficient A, the value 1 (white subdomain) or the value $\hat{\alpha }_1$ (red or shaded subdomain) in a checkerboard fashion as depicted in Fig. 2. Number of iterations and an estimates of the smallest eigenvalues for different values of $\hat{\alpha }_1$ (varying jumps) are reported in Table 4 showing that the convergence is independent of the jumps in the coefficient supporting our analysis. Again, we see an identical performance of the two variants of the algorithm.

Fig. 2

Checkerboard distribution of A, with $A=\alpha _1(2+\sin (10\pi x)\sin (10\pi y))$, where $\alpha _1 = \hat{\alpha }_1$ in the red (shaded) subdomains and 1 otherwise (color figure online)

Table 4 Corresponding to Fig. 2: iteration numbers and estimates of the smallest eigenvalue for different values of $\hat{\alpha }_1$, with fixed mesh sizes $h=1/64$ and $H=1/8$

Fig. 3

Distribution of A with channels and inclusions in the interior of subdomains. $A = \alpha _1(2+\sin (10\pi x)\sin (10\pi y))$, where $\alpha _1 = \hat{\alpha }_1$ in the red (shaded) regions and 1 elsewhere (color figure online)

In our fourth numerical experiment, we examine two different cases, where in the first the coefficients have jumps inside subdomains as depicted in Fig. 3, and in the second the jumps are along subdomain boundaries as depicted in Fig. 4. Their results are presented in Tables 5 and 6, respectively. As we can see from the table entries, both preconditioners are robust with respect to inclusions and channels inside subdomains, but not if the channels cross subdomain boundaries. This is not unexpected, as our coarse space include only functions that are linear along subdomain boundaries. Therefore any variations that are along the subdomain boundaries, the coarse problem cannot capture them that easy. For problems with inclusions and channels both inside and across subdomains, it may be enough to replace the coarse space with the so called multiscale coarse space, cf. [18, 19, 27], or in extreme cases to enrich it with eigenfunctions corresponding to bad eigen modes of some local eigenvalue problems, cf. [14, 21, 31]. These are subjects for future investigation.

Fig. 4

Distribution of A with jumps along the subdomain boundaries. $A = \alpha _1(2+\sin (10\pi x)\sin (10\pi y))$, where $\alpha _1 = \hat{\alpha }_1$ in the red (shaded) regions and 1 elsewhere (color figure online)

Table 5 Corresponding to Fig. 3: iteration numbers and estimates of the smallest eigenvalue for different values of $\hat{\alpha }_1$, with fixed mesh sizes $h=1/64$ and $H=1/8$

Table 6 Corresponding to Fig. 4: iteration numbers and estimates of the smallest eigenvalue for different values of $\hat{\alpha }_1$, with fixed mesh sizes $h=1/64$ and $H=1/8$