Abstract
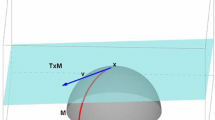
The goal of dimensionality reduction or manifold learning for a given set of high-dimensional data points, is to find a low-dimensional parametrization for them. Usually it is easy to carry out this parametrization process within a small region to produce a collection of local coordinate systems. Alignment is the process to stitch those local systems together to produce a global coordinate system and is done through the computation of a partial eigendecomposition of a so-called alignment matrix. In this paper, we present an analysis of the alignment process, giving conditions under which the null space of the alignment matrix recovers the global coordinate system up to an affine transformation. We also propose a post-processing step that can determine the global coordinate system up to a rigid motion. This in turn shows that Local Tangent Space Alignment method (LTSA) can recover a locally isometric embedding up to a rigid motion.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Z. Bai, J. Demmel, J. Dongarra, A. Ruhe, and H. van der Vorst, eds., Templates for the Solution of Algebraic Eigenvalue Problems: A Practical Guide, SIAM, Philadelphia, 2000.
M. Brand, Charting a manifold, in Advances in Neural Information Processing Systems, vol. 15, MIT Press, 2003.
J. Demmel, Applied Numerical Linear Algebra, SIAM, Philadelphia, 1997.
D. Donoho and C. Grimes, Hessian eigenmaps: new tools for nonlinear dimensionality reduction, in Proceedings of National Academy of Science, pp. 5591–5596, 2003.
Q. Du and X. Wang, Tessellation and clustering by mixture models and their parallel implementations, in Proceedings of the fourth SIAM international conference on Data Mining, pp. 257–268, 2004.
G. H. Golub and C. F. van Loan, Matrix Computations, 3rd edn., Johns Hopkins University Press, Baltimore, Maryland, 1996.
T. Hastie, R. Tibshirani, and J. H. Friedman, The Elements of Statistical Learning, Springer, Berlin, 2001.
A. K. Jain, M. N. Murty, and P. J. Flynn, Data clustering: a review, ACM Comput. Surv., 31 (1999), pp. 264–323.
R. Lehoucq, D. Sorensen, and C. Yang, ARPACK Users’ Guides, Solution of Large Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Method, SIAM, Philadelphia, 1998.
J. Money and Q. Ye, Algorithm 845: EIGIFP: a matlab program for solving large symmetric generalized eigenvalue problems, ACM Trans. Math. Softw., 31 (2005), pp. 270–279.
S. T. Roweis and L. K. Saul, Nonlinear dimensionality reduction by locally linear embedding, Science, 290 (2000), pp. 2323–2326.
J. B. Tenenbaum, V. de Silva, and J. C. Langford, A global geometric framework for nonlinear dimensionality reduction, Science, 290 (2000), pp. 2319–2323.
Y. Teh and S. Roweis, Automatic alignment of hidden representations, in Advances in Neural Information Processing Systems, vol. 15, MIT Press, 2003.
Z. Zhang and H. Zha, Principal manifolds and nonlinear dimension reduction via local tangent space alignment, SIAM J. Sci. Comput., 26 (2004), pp. 313–338.
Author information
Authors and Affiliations
Corresponding author
Additional information
AMS subject classification (2000)
65F15, 62H30, 15A18
Rights and permissions
About this article
Cite this article
Ye, Q., Zha, H. & Li, RC. Analysis of an alignment algorithm for nonlinear dimensionality reduction . Bit Numer Math 47, 873–885 (2007). https://doi.org/10.1007/s10543-007-0144-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10543-007-0144-x