Introduction

Shelf seas and carbon

Continental shelf seas play a disproportionately important part in the global cycling of carbon. They are estimated to provide 10–30% of the global oceanic primary production and 80% of organic carbon burial, while accounting for only 7% of the ocean surface area (Bauer et al. 2013). The shelf seas represent a substantial sink for atmospheric CO2 (8.5%) (Diesing et al. 2017). There is, however, a lack of understanding regarding how the rates of shelf sea biogeochemical processes vary across sediment types, or how they change over the annual cycle (Thompson et al. 2017). For large parts of the shelves it is unclear if the sediments are a source or sink for carbon (Thompson et al. 2017). Shelf seas can vary over short temporal and spatial scales, therefore long term and spatially broad averages do not well represent their dynamics. These knowledge gaps hinder our ability to design numerical models that can correctly reproduce the carbon dynamics of these regions, which limits their predictive potential (Aldridge et al. 2017; Diesing et al. 2017; Solan et al. 2020).

Oxygen

The oceans have lost approximately 2% of their oxygen over the last 50 years (Howes et al. 2015; Schmidtko et al. 2017). This loss is driven by rising global temperatures decreasing oxygen solubility in water, increasing oxygen consumption via respiration and increased stratification (Breitburg et al. 2018). The relative contribution of these processes is poorly known however (Breitburg et al. 2018). Predicting the magnitude and spatial distribution of future oxygen loss is hampered by insufficient data and the lack of mechanistic understanding of oxygen dynamics at a variety of scales (Breitburg et al. 2018; Aldridge et al. 2017). This oxygen loss can lead to bottom-water hypoxia (Holte 1920) which has a variety of implications including: loss of marine life and reduced biodiversity (Breitburg et al. 2018), altering the balance of nitrogen cycling (Neubacher et al. 2013) and increased production of the potent green-house gas nitrous oxide (Kitidis et al. 2017; Breitburg et al. 2018). These interactions can form complex and poorly understood feedback systems.

Oxygen and carbon are linked stoichiometrically (Anderson and Sarmiento 1994), with oxygen often being substantially easier to observe (Riser and Johnson 2008; Hull et al. 2016). Thus in environments devoid of primary production, the total oxygen uptake rate is a useful proxy to quantify carbon remineralisation (Larsen et al. 2013; Glud et al. 2016; Hicks et al. 2017). The majority of the shelf sea sediment is well below the photic zone, with the distribution and consumption of oxygen controlled by sediment type and the supply of organic matter from surface waters (Queste et al. 2016; Thompson et al. 2017). Quantifying total oxygen uptake rates provides us with critical information for understanding both deoxygenation and carbon cycling.

Retrieving intact seabed sediment samples for incubation to determine biogeochemical rates has some disadvantages. Sample recovery is often accompanied by physical changes, notably a reduction in pressure, differing temperature and the introduction of light, which can make it difficult to obtain representative data (Tengberg et al. 2006). Furthermore, for permeable sediments it is extremely difficult to maintain sediment advection under any realistic regime, which can result in anaerobic mineralization to be overestimated due to the reduction in sediment ventilation (Larsen et al. 2013).

It is similarly challenging to integrate over wide spatial and temporal scales as the short term changes or local processes seen in shelf seas may be missed with discrete sampling (Thompson et al. 2017). Mesoscale studies can capture these shorter scale dynamics which both discrete sampling and more coarse modeling approaches can miss. Improved management and conservation of coastal systems requires predictions of the effects of deoxygenation at the spatial and temporal scales most relevant to the ecosystem services provided (Breitburg et al. 2018).

The Celtic Sea

The Celtic Sea is a semi-enclosed seasonally stratified shelf sea on the north-western European shelf (Fig. 1), with open exchange with the North Atlantic at its south-west boundary. The southern Celtic Sea is thought to be a net sink for atmospheric CO2 over an annual cycle (Marrec et al. 2015), with the fate of this carbon being exported back to the open ocean (Humphreys et al. 2018) or sequestered in shelf sea sediments (Diesing et al. 2017).

Tides in this region are semidiurnal with the M2 constituent representing 75% and S2 a further 15% of the total tidal kinetic energy of the currents (Brown et al. 2003). There is considerable variability in tidal stream amplitude over the region with typical spring currents varying between 0.3 and in excess of 1 m s−1 depending on location (Carrillo et al. 2005). These tides are the primary driver of current variability, but play little role in long-term residual flow which is predominately controlled by wind forcing and density changes (Carrillo et al. 2005).

The water column is fully mixed during winter, transitioning into a two-layer stratified system with a transitional thermocline during early spring. We refer to these layers as the surface mixed layer (SML) and bottom mixed layer (BML). The onset of stratification is driven by increasing heat inputs overcoming tidal and wind mixing (Pingree et al. 1976; Wihsgott et al. 2016). Thus the thermocline is first established in areas of weak tides (Pingree et al. 1976).

Coincident with the formation of the thermocline is the initiation of a spring phytoplankton bloom, typically dominated by diatoms (Joint et al. 1986). This is followed by a persistent subsurface chlorophyll maximum (Hickman et al. 2009) and subsequent autumn bloom (Wihsgott et al. 2019). Production at the thermocline is thought to contribute half of the summer shelf production (Williams et al. 2013). In winter the loss of heat to the atmosphere triggers the breakdown of stratification (Thompson et al. 2017; Wihsgott et al. 2019). Stratification is thus temperature driven with little influence from salinity (Wihsgott et al. 2019).

In the Celtic Sea a bottom mixed layer (BML) forms where tidal mixing is strong enough to homogenise near bed density gradients (Wihsgott et al. 2019). Disconnected from direct gas exchange with the atmospheric and below the photic zone (> 50 m, Platt et al. 1993), the BML oxygen concentrations are controlled by oxygen consumption processes within the water column, at the sediment-water interface and indirect ventilation across the thermocline (Greenwood et al. 2010; Große et al. 2016; Queste et al. 2016). These sediment and water column processes comprising primarily of respiration and nitrification will consume oxygen and are fueled by the available organic matter. While mixing across the thermocline is a positive flux into the BML, the majority of the oxygen available for respiration during the stratified period is set at the onset of stratification. The magnitude of this flux can vary substantially. Short term changes in SML oxygen concentration, such as during the spring or autumn blooms, can rapidly change the vertical oxygen gradients. Vertical mixing rates have been shown to be highly dynamic, with wind-tide interactions increasing rates over two orders of magnitude (Palmer et al. 2008; Williams et al. 2013; Wihsgott et al. 2019).

This initial oxygen concentration is thus controlled primarily though the water column temperature just prior to the formation of the thermocline (Queste et al. 2016). With a near-fixed oxygen inventory and enhanced rates of respiration driven by sinking organic material, the bottom mixed layer experiences oxygen depletion during the summer months (Greenwood et al. 2010; Breitburg et al. 2018).

Different sediment types have been shown to exhibit variable consumption rates and responses to changes in the overlying water (Klar et al. 2017). This variation is thought to be due to the composition of the sediment, cohesive properties and permeability, together with the presence and activity of the benthic fauna (Silburn et al. 2017). The Celtic Sea has a diverse range of sediment types, spanning mud to gravel, with variable rates of oxygen consumption (Hicks et al. 2017).

This study

In this study we explore the temporal variability in bottom mixed layer oxygen consumption at two contrasting sites in the Celtic Sea during 2014 as part of the NERC-DEFRA Shelf Sea Biogeochemistry (SSB) project (Thompson et al. 2017). Although vertical mixing is typically described as the primary source of ventilation for the stratified shelf sea bottom mixed layer, in the Baltic sea horizontal (water-column) advection has been shown to be an additional important control on local oxygen concentrations (Bendtsen et al. 2009; Holtermann et al. 2019).

Recent modeling studies have highlighted the importance of these processes for predicting deoxygenation (Bahl et al. 2019). We implement two novel oxygen mass-balance methods to separate out local consumption processes from the horizontal advection. This integrated measure incorporates processes occurring within the bottom mixed layer and also at the sediment-water interface.

Method

Landers and sensors

Cefas benthic landers were placed at four sites during the SSB program (Thompson et al. 2017, Tables 1, 2, Fig. 1), two of which are included in this study: EHF, a benthic lander situated east of Haig Fras (Hull et al. 2017a), a 45 km long submarine rocky outcrop and NB, a lander on the Nymph Bank, West of Celtic Deep (Hull et al. 2017b). The East of Celtic Deep (ECD) site, was damaged by fishing activities during the first 10 days of deployment and is not used in this study. In addition, Fig. 1 shows the central Celtic Sea (CCS) study site (García-Martín et al. 2017a) and CD, the long term Celtic Deep site which included a surface mooring (Hull et al. 2017c) and a thermistor chain (Wihsgott et al. 2016). A lander was also deployed at CD in October 2014 (Table 2). Two nearby study sites, G and H, were used for sediment core incubation studies during SSB and are also shown in Fig. 1.

The landers were fitted with Aanderaa 3835 oxygen optodes (Aanderaa data instruments, Norway), Seapoint SCF chlorophyll-α fluorometers and Seapoint STM optical backscatter turbidity meters (Seapoint Sensors Inc, USA). The optode and Seapoint sensors were fitted with an anti-fouling wiper (Zebra-Tech inc. NZ). RDI Workhorse 600 acoustic Doppler current profilers (ADCP) were configured to observe the bottom 40 m of the water column, with the ADCP first bin at 1.9 m. The biogeochemical observations were recorded via Cefas ESM2 dataloggers (Hull et al. 2016) set for 5 minute burst sampling every 30 minutes synchronised with the hourly ADCP samples. The sensors were all mounted at 0.5 m above the seabed.

The optodes were two-point calibrated prior to deployment (Bittig et al. 2018). A linear offset correction was applied, determined from post-deployment and pre-recovery in situ Winkler samples. No detectable drift was observed; the difference between the post-deployed and pre-recovery offsets is smaller than the standard deviation for each (< 5 mmol m−3). This lack of drift is likely due to the relatively short duration of the deployment and the care taken in keeping the optodes wet and in the dark prior to use. These optodes have also had extensive use prior to this study, and thus the luminophore foils were thoroughly “burnt in” (Bittig et al. 2018; Tengberg et al. 2006).

Table 1 Study site sediment characteristics for for Nymph Bank (NB), East of Haig Fras (EHF) and Celtic Deep Lander (CD), sediment composition predicted using the parametrisation of Diesing et al. (2017)
Full size table
Fig. 1
figure 1

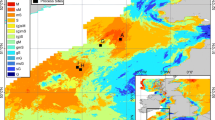
The Celtic Sea study sites. Red circle indicate tidal ellipses at each lander site (NB, EHF and CD). G, H are sample sites for benthic incubations, J2, A and CCS are sample sites for pelagic incubations. CCS and CD are also the locations for two Cefas SmartBuoy moorings. Bathymetry from GEBCO 2019, 15 arc-second grid. (Color figure online)

Full size image
Table 2 Study site current characteristics for Nymph Bank (NB) deployment 1, East of Haig Fras (EHF) deployents 1 to 3 and Celtic Deep Lander (CD) deployment 1
Full size table

Oxygen mass balance

We describe the bottom layer oxygen mass balance as follows.

$$h_\mathrm {b}\frac{dC_\mathrm {b}}{dt} = M_z - A_u - A_v - R$$
(1)

where \(C_{{\text{b}}}\) is the bottom mixed layer oxygen concentration, \(M_z\) is diapycnal eddy diffusion and \(A_u + A_v\) is horizontal advection. \(R\) is oxygen uptake, though bottom mixed layer processes, primarily respiration. \(h_{{\text{b}}}\) is the bottom mixed layer thickness.

$$M_z = K_z \frac{C_\text{s} - C_\text{b}}{h_\text{TC}}$$
(2)

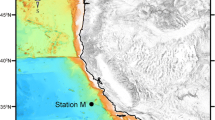
where \((C_{{\text{s}}} - C_{{\text{b}}})\) is the difference between the SML (\(C_{{\text{s}}}\)) and BML oxygen concentration (\(C_{{\text{b}}}\)). \(h_{{{\text{TC}}}}\) corresponds to the thickness of the thermocline. \(K_z\) is the vertical (diapycnal) eddy diffusion coefficient estimated to be in the region of 4.5 × 10−5 m2 s−1 (Palmer et al. 2008). \(M_z\) is constrained as a purely positive flux as SML oxygen concentrations at these sites are always greater than those in the BML (\(C_s > C_b\)). as indicated by long term mooring data (Hull et al. 2017c) and CTD casts (fig. 2).

$$A_{u} = u\beta _{u} h_{{\text{b}}}$$
(3)

where \(A_u\) is the advection in the east–west direction, \(u\) is the horizontal velocity in the east–west direction. \(\beta _u\) is the east–west gradient defined as.

$$\beta _{u} = \frac{dC}{dx}$$
(4)

where \(dx\) is the gradient length scale and \(dC\) is the horizontal oxygen concentration differential. The same formulation applies for the \(v\) north-south velocity.

Similar oxygen modeling studies such as (Emerson et al. 2008) and (Bushinsky and Emerson 2015) include a vertical entrainment term. However, in this study we have very little evidence for such processes, our estimate of the bottom mixed layer thickness does not feature any large scale changes with any associated increase in oxygen or temperature. We determine it is thus not appropriate to include an entrainment term, and all vertical mixed processes are encapsulated in our \(M_z\) term.

Constraining the depth of the bottom mixed layer (\(h_{{\text{b}}}\)) and the thickness of the thermocline (\(h_{{{\text{TC}}}}\)) is vital to enable good estimates of \(R\). As Eq. 1 indicates, uncertainty in \(h_{{\text{b}}}\) has a multiplicative effect on \(R\). The depth of the seasonal thermocline is typically shallower than the range of the bottom mounted ADCP, making direct observation impossible. Water column temperatures were thus taken from the UK Met Office FOAM Atlantic Margin Model 7 km reanalysis (AMM7) (O’Dea et al. 2017). Further details of the AMM7 processing and validation with our thermistor string observations is found in the “Supplementary material”.

Fig. 2
figure 2

Temperature and oxygen saturation profiles from CTD rosette casts at the East of Haig Fras and Nymph Bank sites. Colours indicate date of cast. (Color figure online)

Full size image

Probabilistic mass balance model

Oxygen based metabolic balance estimates can have multiple large uncertainties (Hull et al. 2016). By adopting a Bayesian approach we leverage the explicit use of probability for quantifying uncertainty in inferences (Grace et al. 2015; Holtgrieve et al. 2010). To this end, we define a probabilistic relationship between our observations, our prior knowledge of unobserved processes, such as the acceptable range of possible values for the diapycnal eddy diffusion coefficient and unknown parameters such as the respiration rate. In short, this Monte–Carlo method allows us to simultaneously estimate \(R\), \(h_{TC}\), \(K_w\), \(\beta _u\), \(\beta _v\) and \(h_{{\text{b}}}\) as parameters, and provide probable intervals for each. Full details of the model equations, prior distributions, implementation and validation are found in the “Supplementary material”.

Regressive matched-water method

In this dynamic environment with known horizontal gradients, some approach must be taken to separate out spatial and temporal variability. The observation sites, and in particular Nymph Bank (Fig. 4a), have periods of highly circular flow. Given the assumption that currents measured by the lander ADCP are reasonably representative of the surrounding area, we can observe multiple points where the cumulative vector intersects with itself. That is to say the previously observed patch of water has been observed again. We define a pair of observations as being within the same water mass when the cumulative vector intersection is within 150 m spatially and more than one one full tidal cycle away temporally. That is to say we only compare points where the water mass horizontal position is within 150 m of where it was previously, and more than 6 hours have passed since the last observation. Fitting a linear model to the change in oxygen observed between each spatially-temporally matched pair over time provides an estimate for the oxygen consumption rate in the BML without the influence of horizontal advection. This method can only be used where the tidal flow is reasonably circular and residual currents are either small or periodic. We use this method as a further validation of the probability model.

Results

In 2014 the central Celtic Sea began to stratify in late March, as confirmed by a thermistor array at the CD site. The analysis is thus restricted to the stratified period from the 5th of April (Fig. 3a). All sites show a decline in oxygen concentration after the onset of stratification. Throughout this section ± will be used to express 2 σ uncertainties where values are normally distributed and 95% quantile range [2.5%, 97.5%] if they are not.

Nymph Bank

Fig. 3
figure 3

Nymph Bank Time-series (NB), a AMM7 water column temperature with the upper and lower bound of the thermocline highlighted in green. b Bottom mixed layer oxygen concentration measured by the benthic lander. c Cumulative horizontal advection as measured from lander ADCP in the east (red) and north (blue) directions. (Color figure online)

Full size image
Fig. 4
figure 4

a and c Cumulative vector diagrams for Nymph Bank (a) and East Haig Fras deployment 1 (c), black diamond indicates start of the time-series, while black square represents the end. b and d linear model fits of matched water observations for Nymph Bank (b) and East Haig Fras deployment 1 (d). Each point represents a spatial paired observation, slope indicates average bottom mixed layer oxygen consumption without the influence of horizontal advection. Coloured markers indicate selected spatially paired points and their location in the linear model. (Color figure online)

Full size image

The tidally averaged (25 h) observations from Nymph Bank indicate a reduction in oxygen from 290 to 245 mmol m−3 over this 73 day period, equating to 0.62 mmol m−3 d−1 (Fig. 3b). Tidal current flow is in a NE-SW direction (Fig. 1). Residual flow is variable, with water moving first to the west, before returning east (Figs. 4a, and 3c). The semi-diurnal cycle shown in Fig. 3b suggests that the bottom oxygen concentration is influenced by tidal advection. This indicates a horizontal oxygen gradient within the BML. The \(u\) (east-west, zonal) vector inversely correlates with oxygen; positive \(u\) (current moving water to the east) is reducing the apparent local oxygen concentration and implies a negative \(\beta _u\) (\(\beta _u = \frac{dC}{dx}\)). Thus lower oxygen water is being advected from the west. AMM7 predicts the bottom mixed layer to be (59 ± 2) m and the thermocline is estimated to be between 5 and 15 m thick (Fig. 3a).

Linear regression using the matched water approach indicates a slope 0.65 mmol m−3 d−1 (Standard error = 0.005, Adjusted \(\text {R}^{2} = 0.981\), n = 451) (Fig. 4b). This slope represents the average bottom mixed layer oxygen consumption without the influence of horizontal advection. The linear model has a reasonable fit; we have the impression of variable slopes for some clusters indicating a variable relationship with oxygen consumption and time, i.e. variable respiration rates. However, the residuals appear normally distributed and there is fairly equal variance. This volumetric oxygen consumption rate can then be integrated over the BML (\(h_{{\text{b}}}\) = (59 ± 10) m), giving (38 ± 6) mmol m−2 d−1. Diapycnal mixing of oxygen using the thermocline thickness and Gaussian kernel smoothed (bandwidth = 1 week) surface oxygen concentrations observed from the Celtic Deep buoy, provides a mean flux of oxygen across the thermocline of 3.8 mmol [0.2, 11.1] m−2 d−1. Adding this to the integrated rate gives a total local bottom mixed layer oxygen consumption of (42 ± 8) mmol m−2 d−1, equating to (0.72 ± 0.09) mmol m−3 d−1.

Fig. 5
figure 5

Statistical model parameter estimates for Nymph Bank (NB). Solid lines represent mean posterior estimate, with 95% quantiles of the posteior shown with shaded region. Red line shows mean value over deployment. a Horizontal oxygen gradients, u = east-west, v = north-south. b Bottom mixed layer respiration, in depth integrated units, with bottom mixed layer chlorophyll fluorometery in green. c Estimated Diapycnal mixing rates, with horizontal current speed in orange. d Bottom mixed layer respiration, in volumetic units, with bottom mixed layer turbidity in blue. (Color figure online)

Full size image

We fit these same data using the probabilistic mass balance model. The residual random noise term \(\sigma\) is small and normally distributed (Fig. 14), (0.30 ± 0.004) mmol m−3, indicating the model fits well to the observations. Mean oxygen consumption (\(R\)) over this 73 day period is estimate as (0.63 [0.01, 1.62]) mmol m−3 d−1, but demonstrates short term variability as shown in Fig. 5 B and D. Peak consumption occurs around 2014-05-22 with an estimated rate of (100 ± 25) mmol m−2 d−1 (Fig. 5b). Lowest \(R\) is seen prior to the increase in BML chlorophyll associated with the spring bloom in around the 2014-04-08, here \(R\) is indistinguishable from zero. Similarly low BML oxygen consumption is seen between 2014-05-10 and 2014-05-15.

Peak chlorophyll is seen at the Celtic Deep Buoy on 2014-04-14 as shown in Fig. 5b. We surmise this BML chlorophyll signal is associated with falling phytoplankton material produced in the SML. Increases in turbidity are seen following the increase in chlorophyll. The chlorophyll signal returns to pre-bloom levels around the 2014-05-02. A second increase in turbidity is observed in mid May with a much reduced associated chlorophyll signal. This is associated first with a very low oxygen consumption rate, indistinguishable from zero by the model. Subsequently there is then a sharp spike in turbidity followed by another increase in consumption (Fig. 5d).

Horizontal gradients are are also estimated (Fig. 5a). We observe a persistent eastward gradient of (− 0.19 ± 0.12) μmol m−4 and a northward gradient of (0.53 ± 0.26) μmol m−4. This indicates lower oxygen water to the west and higher concentration to the south. Given the observed residual flow (Fig. 3c) this equates to a cumulative horizontal flux of (11.9 ± 0.8) mmol m−2 for this period.

Inspection of the \(K_z\) and \(h_{TC}\) parameters comprising the modeled \(M_z\) (Fig. 5c) indicates this model and these data are most compatible with slightly increased diapycnal mixing rates compared to our prior ( \(5.4 \times 10^{{ - 5}} {\text{ m s}}^{{ - 1}}\)). Wihsgott et al. (2019) demonstrated that \(K_z\) rates show short term variability and can vary over several orders of magnitude in shelf seas. Our model however is configured to estimate an average \(K_z\) over the entire deployment. Therefore, short term pulses in mixing rates will increase the uncertainty and move the average estimate (the posterior distribution for \(K_z\)) towards higher values.

Figure 5b shows a period between 2014-05-08 and 2014-05-15 where respiration is determined to be very low. This coincides with a deepening of the surface mixed layer and a thinning of the thermocline (20 m to 5 m) (Fig. 3a). Assuming the surface observations from the nearby buoy are reasonably representative of the oxygen concentration above the thermocline, the resulting cross-thermocline oxygen gradient is in the order of 3 μmol m−4 (Fig. 5c), with a temperature gradient of 0.63 °C m−1. We would thus expect to see a increase in temperature in BML in the region of 0.26 °C m−1. However, the observed temperature does not show this degree of warming. We conclude that the cross-thermocline flux is overestimated due to an overestimate of the vertical gradient, as such the respiration for this short period is likely underestimated.

East of Haig Fras 1

The AMM7 data indicates that the East Haig Fras region stratified later than Nymph Bank, on 2014-04-08 (Fig. 6a). Our analysis is thus restricted to a period of 52 days from 2014-04-09 onwards. The BML is between 43 and 73 m (mean = 64 m), with a thermocline thickness between 5 and 30 m (mean = 17 m). Tidally averaged total oxygen change in the BML is from 285.6 to 262.9 mmol m−3 (0.4 mmol m−3 d−1). The oxygen observations appear generally more noisy than the NB time-series (Fig. 6b). However, the oxygen optode performed normally during testing after recovery, so we have no reason to suspect bad data. A much weaker semi-diurnal signal is seen, indicating a much smaller horizontal oxygen gradient than that at NB. The tidal currents at EHF are much less circular (Fig. 1) and residual flow is also less variable than NB with flow first to the west and then to the north (Fig. 4c). This pattern in residual flow matches that seen by Pingree et al. (1976) (Site 014) in October 1975.

Fig. 6
figure 6

East Of Haig Fras #1 (EHF1) time-series, a AMM7 water column temperature with the upper and lower bound of the thermocline highlighted in green. b Bottom mixed layer oxygen concentration measured by the benthic lander. c Cumulative horizontal advection as measured from lander ADCP in the east (red) and north (blue) directions. (Color figure online)

Full size image

For the April EHF deployment the matched water approach provides an integrated consumption rate of 0.51 m−3 d−1 (Standard error = 0.003, Adjusted \(\text {R}^{2} = 0.972\), n = 618) (Fig. 4d). Mean diapycnal mixing rate is calculated to be (8.3 [1.8, 25.7]) mmol m−2 d−1. This equates to BML respiration rates of (41 ± 12) mmol m−2 d−1 ((0.64 ± 0.09) mmol m−3 d−1), following the same procedure as for Nymph Bank.

The statistical model oxygen consumption rates demonstrate a near 14 day cyclic pattern which closely matches the spring-neap tidal cycle (Fig. 7a, b). Rates vary between 13 and 58 mmol m−2 d−1 (0.20 and 0.91 mmol m−3 d−1). Increased rates are observed during, or shortly after, the periods of strongest tidal current flow (Fig. 7c). The mean rate is (36 ± 7) mmol m−2 d−1 ((0.57 ± 0.10) mmol m−3 d−1). There are three periods of enhanced vertical flux (\(M_z\), Fig. 7c) which are driven by a reduction in thermocline thickness. A horizontal oxygen gradient (Fig. 7a) is only detectable during a brief period towards the end of May. Here a negative east-west gradient of − 0.09 to − 0.02 μmol m−4 is seen for approximately one week, indicating a lower oxygen concentration to the east.

Fig. 7
figure 7

Statistical model parameter estimates for East of Haig Fras 1 (EHF1). Solid lines represent mean posterior estimate, with 95% quantiles of the posteior shown with shaded region. Red line shows mean value over deployment. a Horizontal oxygen gradients, u = east–west, v = north–south. b Bottom mixed layer respiration, in depth integrated units, with bottom mixed layer chlorophyll fluorometery in green. c Estimated Diapycnal mixing rates, with horizontal current speed in orange. d Bottom mixed layer respiration, in volumetic units, with bottom mixed layer turbidity in blue. (Color figure online)

Full size image
Fig. 8
figure 8

East Of Haig Fras #2 (EHF2) time-series, a AMM7 water column temperature with the upper and lower bound of the thermocline highlighted in green. b Bottom mixed layer oxygen concentration measured by the benthic lander. c Cumulative advection as measured from lander ADCP in the east (red) and north (blue) directions. (Color figure online)

Full size image

East of Haig Fras 2: Summer

Observations continued at the East of Haig Fras site with a replacement lander and second time-series between the 16th June and the 19th August 2014. The oxygen concentration in the BML decreased from 257.2 to 234.1 mmol m−3 over the 64 days (0. 32 mmol m−3 d−1). The water matching method provided a less than ideal fit and resulted in a low number of observations (R2 = 0.71, n = 422). This highlights a limitation of this method; that the number of matched points is dependent on the residual flow pattern.

As with the previous deployments the output from the statistical model is shown in Fig. 9. The average and peak rates from the statistical the vertical and horizontal fluxes together with oxygen consumption are summarised in Table 3. There are three periods (25th to 27th June, 9th to 19th July and 8th to 12th August) which show a persistent increase in oxygen concentration (Fig. 8b). These periods are not associated with a horizontal advective flux or increased mixing through thinning of the thermocline or movement (entrainment) of the BML boundary (Fig. 8a). We discuss these periods in more detail in Section 3.3.

Towards the end of the deployment the east-west horizontal oxygen gradient is particularly strong, approaching − 1 mmol m−4 (Fig. 9a). This coincides with a change in the residual flow moving from west to east (Fig. 8c) resulting in a large negative horizontal advective flux of (20 ± 2) mmol m−2 d−1) We can also see a thinning of the thermocline (panel A), and an associated increase in the estimated (positive) vertical flux (Fig. 9c). The horizontal flux while large does not fully explain the observed reduction in oxygen concentration and thus the model determines very high rates of consumption (Fig. 9b).

Fig. 9
figure 9

Statistical model parameter estimates for East of Haig Fras #2 (EHF2). Solid lines represent mean posterior estimate, with 95% quantiles of the posteior shown with shaded region. Red line shows mean value over deployment. a Horizontal oxygen gradients, u = east–west, v = north–south. b Bottom mixed layer respiration, in depth integrated units, with bottom mixed layer chlorophyll fluorometery in green. c Estimated Diapycnal mixing rates, with horizontal current speed in orange. d Bottom mixed layer respiration, in volumetic units, with bottom mixed layer turbidity in blue. (Color figure online)

Full size image

East of Haig Fras 3: Autumn

A third lander was deployed at the East of Haig Fras site between 20th of August and the 2nd of October 2014. During this period the thermocline is thin ((7 ± 3) m) and stable, with a BML thickness of (77 ± 1.7 m) (Fig. 10a). BML oxygen concentration decreased from 234.0 to 227.9 mmol m−3 over the 43 days (0.14 mmol m−3 d−1) (Fig. 10b). The matched water method is not viable with this deployment, with too few matched points to provide an adequate fit. Horizontal advection is predominantly to the south-west (Fig. 10c)

The statistical model reveals the strong horizontal gradients seen at the end of the previous deployment persist until the first week of September (Fig. 11a). However the residual flow is reduced (Fig. 10c), resulting in a reduced horizontal advective flux. The spring-neap cycle of oxygen consumption seen in the spring is now absent despite measurable increases in turbidity and thus presumably sediment resuspension (Fig. 11d). Mean consumption is estimated as 46 ± 13 mmol m−2 d−1 (0.59 ± 0.18 mmol m−3 d−1).

Fig. 10
figure 10

East Of Haig Fras #3 (EHF3) time-series, a AMM7 water column temperature with the upper and lower bound of the thermocline highlighted in green. b Bottom mixed layer oxygen concentration measured by the benthic lander. c Cumulative advection as measured from lander ADCP in the east (red) and north (blue) directions. (Color figure online)

Full size image
Fig. 11
figure 11

Statistical model parameter estimates for East of Haig Fras #3 (EHF3). Solid lines represent mean posterior estimate, with 95% quantiles of the posteior shown with shaded region. Red line shows mean value over deployment. a Horizontal oxygen gradients, u = east–west, v = north–south. b Bottom mixed layer respiration, in depth integrated units, with bottom mixed layer chlorophyll fluorometery in green. c Estimated Diapycnal mixing rates, with horizontal current speed in orange. d Bottom mixed layer respiration, in volumetic units, with bottom mixed layer turbidity in blue. (Color figure online)

Full size image

Discussion

Temporal variability

The EHF data demonstrates a convincing, approximately 14-day cycle in oxygen consumption, consistent with a spring-neap tidal cycle (Fig. 7). Increased respiration rates are correlated with the stronger spring currents. This is indicative of the tidal resuspension of bed material (e.g. sediment or benthic fluff, and the organic carbon contained within) which is then aerobically respired. Tidal resuspension is understood to be frequent in the Celtic Sea, with year round reworking of the sediments (Thompson et al. 2017). This is particularly true for EHF which has a higher fine sediment concentration (Table 1). This follows that the sandier NB site would experience less tidal resuspension than EHF. Flow dependent benthic oxygen consumption has also been ascribed to increased ventilation of the sediment with increasing currents (Glud et al. 2016). Hicks et al. (2017) supplied fully saturated overlying water to their incubations. This could partially mitigate the reduction ventilation from vertical water movement by increasing the diffusive concentration gradient between the overlying water and the sediment. This however does not represent the in-situ conditions.

NB by contrast does not demonstrate such a clear cycle. Highest rates are seen after the peak in BML chlorophyll. Higher rates are also observed immediately after brief large increase in turbidity toward the end of May (Fig. 5d). These very short term increases in turbidity increases could be due to resuspension from fishing activities, as these periods do not correlate with tidal currents or with chlorophyll. Indicating it’s not caused by frictional resuspension or falling phytoplankton material. The Celtic deep experiences the greatest fishing pressure within the Celtic Sea (Sharples et al. 2013; Thompson et al. 2017), additionally the loss of the second NB deployment is attributed to trawling activity.

Queste et al. (2016) calculated BML oxygen consumption rates from the central North Sea in summer 2011 of (2.8 ± 0.3) mmol m−3 d−1 using a short-term Seaglider deployment. They noted the apparent high consumption rates and questioned how representative these rates could be over longer timescales. We observe similarly high rates for short periods at NB.

In the Celtic Sea we see the BML oxygen concentration reducing from an atmospheric equilibrium concentration of approximately 285 mmol m−3 to 180 just prior to remixing in winter, as observed by NB in March and Celtic Deep lander in December. This equates to a average consumption rate over the stratified period of 0.42 mmol m−3 d−1. We see declining BML oxygen consumption rates post-bloom at EHF over the year, which is in agreement with Kitidis et al. (2017), Hicks et al. (2017) and García-Martín et al. (2017b) for 2015.

Advective dynamics

At NB the statistical model output shows a persistent positive north-west gradient. This indicates that more oxygenated waters lie to the south-east. Stratification in the Celtic Sea is generally reduced as you move towards the south-east from NB due to increased tidal forcing in shallower water (Brown et al. 2003).

For EHF the pattern is of typically negligible horizontal gradients for much of the year, with a very strong positive north-west gradient observed first in August which persists until mid September (Figs. 7, 9 and 11a). The absence of horizontal gradients suggest similar rates of processes occurring within the local area, with ‘local’ being the extent of tidal excursion. The brief occurrence of the strong gradient suggests a localised area of oxygenated water to the south east, perhaps from a summer phytoplankton bloom (e.g. as shown by Williams et al. (2013)). However subsurface blooms are not typically observable from remote sensing, and no direct observations are available from this region at this time to confirm this hypothesis.

Evidence for enhanced persistent vertical mixing

At EHF between 9th and 19th of July we observe 0.4 °C of warming in the BML. This can be explained by the observed cross-thermocline temperature gradient of 7 °C, the estimated 15 m thick thermocline and a moderately enhanced \(K_z\) of 7.5 × 10−5 m−2 s−1 which would provide a temperature change of 0.04 °C d−1. We also measured a 9 mmol m−3 increase in oxygen over the same period. Large oxygen gradients of up to 45 mmol m−3 over 5 m (9 mmol m−4) were observed in CTD casts from August 2014 (Fig. 2). Assuming oxygen consumption remains a constant 0.4 mmol m−3 d−1, this increase could be explained by a diapycnal oxygen flux of 111 mmol m−2 d−1. Using the same mixing parameters as inferred from the temperature changes this would indicate a cross-thermocline oxygen concentration gradient of at least 15 mmol m−4. However, the bulk of the oxygen is being produced at the subsurface chlorophyll maximum at the base of the thermocline resulting in a much stronger gradient. The preceding period with declining oxygen concentrations also showed similar warming. However, this can be shown to be controlled by northward advection, that is warmer water moving from the south. The shorter periods of increasing BML oxygen do not correlate with increasing BML temperatures. The main limitation of this dataset is thus highlighted; we lack observations to quantify the cross-thermocline concentration gradient. However, our approach does allow us to incorporate our available knowledge regarding the reasonable bounds for the surface oxygen concentration to improve the estimates.

Rovelli et al. (2016) used a combination of turbulence measurements and fast galvanic oxygen sensors to calculate vertical oxygen fluxes and a BML mass budget over a 3 day period in the North Sea. They calculated a \(M_z\) flux ranging between 9 and 134 mmol m−2 d−1 (average 54 mmol m−2 d−1). We summarise our calculated fluxes and compare those to Rovelli et al. (2016) in Table 3 Our results show similarly substantial vertical fluxes of oxygen.

Queste et al. (2016) demonstrated occasional short term mixing (~ 6 h) events, which supply oxygenated water to the BML in the North Sea at rates of 2 mmol m−3 d−1. Williams et al. (2013) similarly describe frequent wind-driven inertial oscillations which increased vertical mixing rates by up to a factor of 17. These events are estimated to occur every 2 weeks during the summer. However, both of these studies describe events with large fluxes but much shorter durations than the persistent ventilation over several days we observe.

Table 3 Mean (and peak) mass-balance fluxes for each of the study sites compared to the 52 h North Sea study of Rovelli et al. (2016)
Full size table

Oxygen uptake rates compared

Benthic processes studies were conducted in parallel with the seabed lander deployments which can further contextualise the observed rates of oxygen consumption. The estimates are integrated over the BML and thus combined processes occurring in the water column and at the seabed interface. For comparison with the SSB processes studies, in terms of both sediment type and location, Nymph Bank (NB) and the Celtic Deep (CD) (Table 1) are best represented by the “sand” process site G (Thompson et al. 2017). East of Haig fras (EHF) is most similar to and nearest the “muddy sand” site H. These processes study sites are within 10 km of the lander positions.

Hicks et al. (2017) calculated total benthic oxygen uptake rates from sediment core incubations in March 2014, March 2015, May 2015 and August 2015. The March observations occurred prior to the onset of stratification and are thus not directly comparable with this study.

Site G showed low total benthic oxygen uptake rates (1.5–2.5 mmol m−2 d−1) in March, with increased rates in May and Aug (5–6 mmol m−2 d−1). Site H rates had little seasonal variability with values 7–8 mmol m−2 d−1 for all observations. Hicks et al. (2017) derived further rates from a set of incubations designed to simulate resuspension. These produced larger rates of approximately 8–9 mmol m−2 d−1 for site G and 13 mmol m−2 d−1 for site H.

Kitidis et al. (2017) provide additional total oxygen consumption rates from an alternative core incubation experiment in 2015. Site H showed more variability between pre and post bloom compared to those of Hicks et al. (2017). Pre bloom (March) rates were estimated at 2.4 mmol m−2 d−1 with post bloom (May and August) rates of 6.1 and 6.6 mmol m−2 d−1. Site G had pre-bloom rates of 4.5, increasing to 6.3 mmol m−2 d−1 in May. August rates were much lower than those seen by Hicks et al. (2017) (1.7 mmol m−2 d−1).

Klar et al. (2017) calculated a late spring seasonal average oxygen consumption 15.4 mmol m−2 d−1 at site A. Site A consists of sandy mud and thus has a larger organic carbon content and higher rates of oxygen consumption. Their study suggests a very small contribution to oxygen consumption from Fe(II) oxidation; in the order of 30 μmol m−2 d−1 for spring and 5 μmol m−2 d−1 for summer. The contribution to oxygen consumption from Fe(II) oxidation at sits H or G is likely to be smaller.

The above studies show large differences in observed rates despite the similar sampling methods and with near identical spatio-temporal parameters. This is possibly due to very small scale spatial differences, or the presence or absence of fauna. Hicks et al. (2017) estimated the fauna mediated benthic oxygen uptake to be between 5 and 6 mmol m−2 d−1 for site H. Estimates are not available for site G.

García-Martín et al. (2017b) performed incubations of the BML plankton community respiration in November 2014, April, 2015 and July 2015. These observations were made at the CCS site, which is 163 km to the south west (Fig. 1). The incubation derived rates were calculated as between 0.1 and 1.1 mmol m−3 d−1 in April, and between undetectable and 0.5 mmol m−3 d−1 in July. Further BML incubations were also performed using water from site A and J2 (Fig. 1) in late April 2015 although these measurements were not included in their paper (Garcia-Martin per. comms.). Site A is to the north-east of NB, while J2 sits between NB and EHF. These provide rates of (0.96 ± 0.3) mmol m−3 d−1 for site A and (0.42 ± 0.18) mmol m−3 d−1 for J2. Bacterial respiration contributed 21–38% of the plankton community respiration (García-Martín et al. 2017b). The incubation derived rates are summarised, scaled to the observed BML depth and compared with the matched water and statistical model rates from this study in Table 4.

Table 4 BML integrated and combined mean incubation rates compared to the statistical model for spring and co-located regression from this study
Full size table

Both the statistical model and co-located regression provide estimates within the error bounds of the combined benthic and pelagic incubation derived oxygen consumption rates. It should be noted that these incubation were from the following year. We observe very similar mean rates from the statistical model for both NB and EHF sites between March and May.

The winter of 2013–2014 had atypically extreme wave conditions (Thompson et al. 2017) which may affect the validity of using the 2015 water column rates as a comparison. However, given the similar April benthic uptake rates seen by Hicks et al. (2017) we do not believe this to be the case. Larsen et al. (2013) determined sediment total oxygen consumption rates of (5.8–9.0) mmol m−2 d−1 for July 2008 at several muddy-sand sites near CCS (Jones bank) from sediment core oxygen microprofiles. These are very similar to those observed by Hicks et al. (2017) suggesting little interannual variability in sediment rates within this region.

These benthic rates suggest that the largest proportion (60–80%) of the BML oxygen consumption takes place in the water column not the sediment. Rovelli et al. (2016) similarly determined for the North Sea that 86% of the respiration was in the water column. This contrasts with the model study of Große et al. (2016) who determined that for the central North Sea benthic remineralisation processes are responsible for more than 50% of oxygen consumption, which corresponded to 3.9–6.5 mmol m−2 d−1. This disparity could be due to differences in remineralisation rates between the two shelf seas, or the choice of parametrisations and forcing data for the model.

Carbon

Ultimately it is the balance between carbon fixation by autotrophic production and remineralisation rate of the benthic organic carbon which determines if organic carbon is sequestered into the sediment (Diesing et al. 2017). All sites showed an increase in organic carbon deposition after the bloom in 2015 (Silburn et al. 2017). The typical benthic respiratory quotient, inferred from dissolved inorganic carbon and O2 exchange rates, can be considered close to unity (1.03 ± 0.11) (Glud et al. 2016). Kitidis et al. (2017) determined that ammonium-oxidation accounted for 10–16% of total oxygen consumption at H and 35–56% at G, that is to say, 10–50% of the oxygen consumption in the sediment is not due to carbon mineralization. Larsen et al. (2013) estimated that sulfate reduction, which does not consume oxygen, contributed (12–28%) of total benthic carbon mineralization. Microbial denitrification has a very small influence of < 2% (Larsen et al. 2013). Thus each mole of oxygen consumed can be thought of as approximately equivalent to one mole of carbon mineralisation, with the opposing effects of ammonium-oxidation and sulfate reduction potentially balancing out.

Conclusion

In this study we provide two alternative approaches to quantifying BML oxygen consumption using single point oxygen time-series. Our regression method accounts for horizontal advection, but is dependent on favourable patterns in BML residual flow at the study site. By contrast, our statistical method can resolve the short-scale dynamics observed in BML oxygen and horizontal advection, and is more suitable for use in situations with less circular BML residual flow patterns. While we were able to incorporate our limited knowledge of the cross thermocline oxygen gradient into our estimates, one of our sites benefited from co-located surface oxygen observations which helped constrain our vertical flux estimation. The vertical flux could be more directly observed using sheer probes coupled with a fast response optode (e.g. Holtermann et al. 2019). Concurrent in-situ vertical flux observations would likely reduce the uncertainty associated with our incomplete knowledge of both the diapycnal eddy diffusion coefficient and the cross-thermocline oxygen gradient. This would also provide an opportunity to further validate the limited observation approach described in this paper. We show that, in general, our methods agree with the upper range of estimates from the incubation studies. However, we observe significant short term variability in oxygen consumption rates, which is missed with the cruise-based observations.

Numerical models are known to only predict half the observed global oxygen decline (Breitburg et al. 2018). Modeled rates, informed from incubations, are typically too low or do not capture the temporal dynamics. In general our understanding of the contributions of offshore benthic communities to carbon sequestration and storage is lacking (Solan et al. 2020). The estimates we have provided, together with the methodology we have outlined, can capture the temporal variability and may help to close this knowledge gap.

Supplementary material

Probability model

We define the probabilistic relationship between the observed and predicted oxygen concentration (mmol m−3) in Eq. 5.

$$\begin{aligned} \hat{C} \sim \mathcal {N}(C,\sigma ) \end{aligned}$$
(5)

That is to say, the observed oxygen value \(\hat{C}\) is from a normal distribution with the mean \(C\) (our prediction of the true concentration) and standard deviation σ.

The time evolution of \(C\) is discretized as follows:

$$C_{t} = C_{{t - \Delta t}} - u~\Delta t~\beta _{u} - v~\Delta t~\beta _{v} + \Delta t~\frac{{M_{{\text{z}}} - R}}{{h_{{\text{b}}} }}$$
(6)

where \(\Delta t\) is our our time-step in seconds derived from our 30 min observations. \(\beta _u\) and \(\beta _v\) are the horizontal oxygen gradients (mmol m−4) in the east and north directions.

These parameters are modelled in a multi-level approach (Eq. 7) as such the estimates for each \(\beta\) are partially pooled (\(\bar{\beta }\)), so that each estimate contains information which is optimally used to improve all other estimates (Gelman et al. 2017). Specifically this approach primarily improves estimates during neap tides when currents are weak.

$$\begin{aligned}&\beta _u \sim \mathcal {N}(\bar{\beta _u},\tau _u) \end{aligned}$$
(7)
$$\begin{aligned}&\beta _v \sim \mathcal {N}(\bar{\beta _v},\tau _v) \end{aligned}$$
(8)

The model is run with the following priors:

$$\sigma \sim {\text{Cauchy}}(0,1)$$
(9)
$$\begin{aligned}&R \sim \mathcal {N}(0,1) \end{aligned}$$
(10)
$$\begin{aligned}&\bar{\beta _u} \sim \mathcal {N}(0,5) \end{aligned}$$
(11)
$$\begin{aligned}&\bar{\beta _v} \sim \mathcal {N}(0,5) \end{aligned}$$
(12)
$$\tau _{u} \sim {\text{Cauchy}}(0,1)$$
(13)
$$\tau _{v} \sim {\text{Cauchy}}(0,1)$$
(14)

Varying these priors over two orders of magnitude has a minimal effect on parameter estimation. They are weakly regularising and are chosen primarily for improved model convergence. A half-Cauchy distribution is used for the standard deviation (\(\sigma\)) as a weakly regularising prior as per Polson and Scott (2012).

The initial conditions are initialised as the first observation plus normally distributed zero mean noise (\(\varepsilon\)) (Eq. 15).

$$C_{0} = \hat{C}_{0} + \varepsilon$$
(15)

and the following prior:

$$\begin{aligned} \varepsilon \sim \mathcal {N}(0, 1) \end{aligned}$$
(16)

To capture our uncertainty regarding the AMM7 model outputs we apply the following further parameterisations (Eqs. 17, 18). Where \(\widehat{{h_{{\text{b}}} }}\) and \(\widehat{{h_{{{\text{TC}}}} }}\) are the bottom mixed layer thickness and thermocline thickness observations respectively. Uncertainty in the value of \(K_z\) is additionally incorporated into the estimates for the thermocline mixing and bottom mixed layer depth parameters (Eq. 19). For computational reasons we do not model the vertical diffusion coefficient (\(K_z\)) as a time varying parameter, we estimate a average value for each deployment.

$$\begin{aligned} \hat{h_\mathrm {b}}= & {} \mathcal {N}(h_\mathrm {b}, \sigma _\mathrm {b}) \end{aligned}$$
(17)
$$\begin{aligned} \hat{h_\mathrm {TC}}= & {} \mathcal {N}(h_\mathrm {TC}, \sigma_\mathrm {TC}) \end{aligned}$$
(18)
$$\begin{aligned} k_z= & {} \mathcal {N}(4.5 \mathrm {\times}10^{-5}, \sigma _{k_z}) \end{aligned}$$
(19)
$$\begin{aligned} C_s\sim & {} \mathcal {N}(\hat{C}_s, \sigma _{C_s}) \end{aligned}$$
(20)

where \(\sigma _{{\text{b}}}\), \(\sigma _{{{\text{TC}}}}\), \(\sigma _{K_z}\) and \(\sigma _{C_s}\) are standard deviations adjustable to our best estimate for each parameter. For this study \(\sigma _{{k_{z} }} = 0.5 \times 10^{{ - 5}}\) mmol m−2 s−1.

The above probability model was implemented using the probabilistic programming language Stan (Carpenter et al. 2017). Stan and its use of dynamic Hamiltonian Markov-Chain Monte Carlo (MCMC) is an extremely powerful tool for specifying and then fitting complex Bayesian models.

MCMC facilitates the simultaneous estimation of both β parameters, thus the horizontal adjective flux, and also \(R\). This is based on the assumption that changes in \(\beta\) and \(R\) are on relatively long timescales compared to the tidal signal, and that \(R\) can not be negative. This is done while indicating the quality of the model fit in the form of \(\sigma\), which also accounts for unknown processes not modelled directly, such as instrument noise. \(\sigma\) is thus analogous to the standard deviation of the residuals of a standard linear regression. The model is run several times with varying window sizes, (starting with a single value \(R\) and daily \(\beta\)) to determine window sizes which can resolve change in \(R\) and \(\beta\). We have opted for 3 days \(R\) varying window and a 12.5 h varying \(\beta\). These window sizes provide good fits with the observed data and reproduce well smoothly varying changes in \(\beta\) and \(R\) with our synthetic data. With shorter windows the model struggles to distinguish sampling error from varying \(\beta\) and fails to converge. With longer windows the model tends to underestimates the dynamics and excessively smooth the signal. Within the range of window sizes where the model can converge varying window size does not influence the average (integrated) estimates for these parameters i.e. The mean \(R\) estimate is within the same uncertainty bounds regardless of window size.

Unlike other MCMC algorithms, when Hamiltonian MCMC fails, it fails spectacularly and problems are easy to identify (Carpenter et al. 2017). The presence of a large number of divergent transitions (> 1% of total samples) is an indication that the model fit has failed. The potential scale reduction factor is another MCMC specific metric which when < 1.1 indicates that all sampling chains have reached a stable posterior distribution, that is to say, the model fit is complete (Carpenter et al. 2017). No divergent transitions are observed and the potential scale factors for each run are all < 1.1 The model fit is further assessed based on \(\sigma\) being a suitably low value close to the expected precision of the oxygen observations (<1 mmol m−3). A graphical posterior predictive check (Carpenter et al. 2017) is used to further assess the model fit where the modeled state for \(C\) is compared to the observations (Fig. 13d.).

Our implementation was tested against synthetic data using the same data generating processes as the model. That is to say we run the model with known parameters (Fig. 12), we then check the model can correctly re-estimate these parameters (Fig. 13). The diagnostic variables for each of the model runs are summarised in Fig. 14.

Fig. 12
figure 12

An example of the synthetic data used for validating the probabilistic model. (Color figure online)

Full size image
Fig. 13
figure 13

Validation of statistical model against synthetic data. True values shown in red, true + random noise in blue, mean model estimate in black and 95% credible intervals shown in grey. (Color figure online)

Full size image
Fig. 14
figure 14

Validation of statistical model for each run. Left panels show histogram for the σ model fit parameter, units are mmol m−3. Right panels show difference between BML oxygen concentration observations (\({\hat{C}}\)) and the modeled state (\(C\)). (Color figure online)

Full size image

AMM7

AMM7 reanalysis water column temperatures were extracted from the UK Met Office JASMIN archive. These temperatures are provided for 50 depth bins scaled over the local bathymetry (O’Dea et al. 2017). These bins are closer together near the surface, equating to depth intervals not exceeding 5 m and typically 1 m for the top 60 m. From these data the top of thermocline was defined by a 0.2 °C temperature threshold with a 10 m reference depth (Kara et al. 2000). The base of the thermocline was defined by the same threshold, with the reference depth being the depth of the lander.

These data were compared to the buoy and thermistor string observations at Celtic Deep (Wihsgott et al. 2016), The model does not correctly resolve the stratifying period in March, during which there are short lived transient periods of stratification (See Fig. 15). However after the 1st of April the seasonal thermocline has fully formed and persists though until late December (Thompson et al. 2017). We thus restrict our analysis to where the modelled mixed layer depth more closely agrees with the Celtic Deep observations.

Fig. 15
figure 15

Bottom mixed layer depth calculated with 0.2 °C threshold for AMM7 (green) and from the Celtic Deep thermistor chain (blue). (Color figure online)

Full size image

Glossary

  • \(C_{{\text{b}}}\) bottom mixed layer oxygen concentration (mmol m−3).

  • \(C_{{\text{s}}}\) surface mixed layer oxygen concentration (mmol m−3).

  • \(M_z\) is the diapycnal (cross-thermocline) flux (mmol m−2 s−1).

  • \(A_u\) horizontal advection in the east–west (\(u\)) direction (mmol m−2 s−1).

  • \(A_v\) horizontal advection in north−south (u) direction (mmol m−2 s−1).

  • \(\beta _u\) horizontal oxygen gradient in the east–west (u) direction (mmol m−4).

  • \(\beta _v\) horizontal oxygen gradient in the north–south (\(v\)) direction (mmol m−4).

  • \(R\) is oxygen consumption, though bottom mixed layer processes, primarily respiration (mmol m−2 s−1 if BML integrated, or mmol m−3 s−1 if volumetic).

  • \(h_{{\text{b}}}\) is the bottom mixed layer thickness (m).

  • \(K_z\) is the vertical (diapycnal) eddy diffusion coefficient (m2 s−1 ).

  • \(h_{{{\text{TC}}}}\) thickness of the thermocline (m).