Abstract
The conservation of animal populations often requires the estimation of population size. Low density and secretive behaviour usually determine scarce data sources and hampers precise abundance estimations of carnivore populations. However, joint analysis of independent scarce data sources in a common modeling framework allows unbiased and precise estimates of population parameters. We aimed to estimate the density of the European wildcat (Felis silvestris) in a protected area of Spain, by combining independent datasets in a spatially-explicit capture-recapture (SCR) framework. Data from live-capture with individual identification, camera-trapping without individual identification and radio-tracking concurrently obtained were integrated in a joint SCR and count data model. Ten live captures of five wildcats were obtained with an effort of 2034 trap-days, whereas seven wildcat independent events were recorded in camera traps with 3628 camera-days. Two wildcats were radio-tagged and telemetry information on their movements was obtained. The integration of the different data sources improved the precision obtained by the standard SCR model. The mean (± SD) density estimated with the integrated model (0.038 ± 0.017 wildcats/km2, 95% highest posterior density 0.013–0.082) is among the lowest values ever reported for this species, despite corresponding to a highly protected area. Among the likely causes of such low density, low prey availability could have triggered an extinction vortex process. We postulate that the estimated low density could represent a common situation of wildcat populations in the southern Iberia, highlighting the need for further studies and urgent conservation actions in the furthermost southwestern range of this species in Europe.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Accurate estimation of population size is often required to take decisions for the conservation of wildlife populations (Carbone et al. 2001). However, estimating population size of mammalian carnivore species is often difficult due to their expansive use of space, secretive nature and typical low population densities (Sollmann et al. 2014; Brassine and Parker 2015). Effective monitoring techniques for estimating population size of rare or low-density carnivore species are limited (Belbachir et al. 2015). Furthermore, when estimates are possible with scarce data, these are often biased or have low precision (Linkie et al. 2008). Consequently, scarce datasets are often discarded, and population estimates are not attained, with the loss of valuable information required for taking conservation measures. Conversely, recent advances in analytical approaches have opened doors to jointly analyze several sources of scarce data in a common modeling framework, allowing for the estimation of population parameters and adequately informing conservation measures (Anile et al. 2014; Velli et al. 2015; Murphy et al. 2018).
Camera-trapping is the current gold standard for monitoring rare and cryptic mammals, as it is relatively affordable and non-invasive (Meek et al. 2014; Burton et al. 2015). It has become particularly useful for monitoring populations of individually identifiable carnivores by unique markings such as spot or stripe patterns (Soisalo and Cavalcanti 2006). Recently, Kéry and Royle (2020) combined multiple datasets in a single integrated model with a joint likelihood, which is the product of the likelihoods of each individual dataset, e.g. using individual spatially-explicit capture-recapture (SCR) histories from camera traps (Brassine and Parker 2015; Weingarth et al. 2015) or genetically identified biological samples (Kéry et al. 2011; Sabino-Marques et al. 2018), and counts or occupancy data from unmarked individuals (e.g. Jiménez et al. 2021; Ruprecht et al. 2021). When these data are combined with telemetry-based movement data (Sollmann et al. 2013; Jiménez et al. 2019), this approach can further improve the precision of the standard SCR model (Kéry and Royle 2020).
The European wildcat (Felis silvestris Schreber, 1777) is a small felid, considered until recently the same species as wildcats from Africa and Asia (Nowell and Jackson 1996; Yamaguchi et al. 2015). However, European wildcats are currently recognised as a separate species according to the most recent revised taxonomy of Felidae (Kitchener et al. 2017). Although globally classified as a Least Concern species due to its wide distribution (Nowell and Jackson 1996; Yamaguchi et al. 2015), the recent split of European wildcats as a separate species emphasized the need for the ongoing revision of the wildcat’s conservation status, considering also the different metapopulations due to the fragmentation of the species range across Europe (Kitchener et al. 2017). This fragmentation is due to human-mediated habitat disturbance and large-scale persecution which led to severe local declines and even extinctions (Stahl and Artois 1991). As a result, the European wildcat became strictly protected and was included in “Annex IV” of the European Habitats Directive (92/43/EEC) and in “Annex II” of the Bern Convention. Accordingly, European wildcat populations need to be monitored regularly.
The recovery of some wildcat populations has been recently reported in central Europe, where the species range is currently expanding in countries such as France (Say et al. 2012) or Germany (Steyer et al. 2016). However, the wildcat still faces several threats throughout its range, namely in the southern range of its distribution, like the Iberian Peninsula (Yamaguchi et al. 2015; Breitenmoser et al. 2019).
The trends of the wildcat Iberian populations are uncertain due to the absence of monitoring, nonetheless several studies point to recent decreases both at local and regional scales (Sobrino et al. 2009; Soto and Palomares 2014; Gil-Sánchez et al. 2020). As consequence, it is classified as Near Threatened in Spain (López-Martín et al. 2007) and as Vulnerable in Portugal (Cabral et al. 2005). The main threats for the Iberian wildcat populations include hybridization with domestic cats (e.g. Oliveira et al. 2008; Tiesmeyer et al. 2020), mortality due to non-selective methods of predator control, habitat loss and fragmentation (López-Martín et al. 2007). Diseases may also pose a threat, although their relative importance is currently unknown. A recent study based on 222 radio-tracked European wildcats from all over Europe indicates that mortalities were mainly human-caused, namely by roadkills and poaching (Bastianelli et al. 2021).
In central Europe the wildcat is traditionally described as a species bound to forests (Klar et al. 2008), although wildcats can use open, agriculture-dominated landscapes (Jerosch et al. 2017). Human infrastructures, such as roads or villages, are also usually avoided by wildcats up to a certain distance (Klar et al. 2008). In Mediterranean areas, wildcats preferentially establish home ranges close to broadleaf forests and far from human-modified areas. Within their home ranges, they typically select areas dominated by scrublands and broadleaf forests (Oliveira et al. 2018).
Over most of Europe, wildcats mainly consume small mammals (Lozano et al. 2006) but in Mediterranean areas their diet is mostly based on European rabbits (Oryctyolagus cuniculus; Gil-Sánchez et al. 1999; Lozano et al. 2006). However, strong decreases of the European rabbit abundance across the Iberian Peninsula over the last decades (Villafuerte and Delibes-Mateos 2019) arises as an additional threat for wildcat populations in these areas. Information on wildcat population size in the Iberian Peninsula is very scarce (see Gil-Sánchez et al. 2020).
Therefore, our aim was twofold: (i) to estimate European wildcat population density in a Mediterranean protected area of central Spain; and (ii) to assess whether the integration of independent and scarce datasets, obtained with different methodologies, provided improved precision of wildcat density estimates when compared with those obtained from regular SCR models built from single-source datasets.
Study area
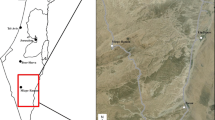
The study was carried out in Cabañeros National Park (hereafter, CNP; 39° 24′ N 4° 29′ W), central Spain (Fig. 1). CNP has a total surface of 409 km2 characterized by moderately elevated mountain systems (620–1500 m above sea level), and Mediterranean climate with hot dry summers, mild winters and moderately rainy springs and autumns (annual rainfall 450–750 mm). Vegetation is dominated by scrublands of Cistus sp., Phyllirea angustifolia, strawberry trees (Arbutus unedo) and Erica spp., and the tree layer is dominated by cork (Quercus suber) and holm oaks (Quercus rotundifolia). The central area of CNP is occupied by ‘dehesas’, a pastureland with savanna-like open tree layer of cork and holm oaks.
Wild ungulates, mainly red deer (Cervus elaphus) and wild boar (Sus scrofa), occur at high density. Main potential prey for wildcats are scarce in the Park. The European rabbit population declined over the last decades and has not recovered (Delibes-Mateos et al. 2008), and small mammals—mainly Apodemus sylvaticus and Mus spretus—are not abundant (< 5 ind ha; Ferreras et al. 2016) mainly due to the high density of wild ungulates (Muñoz et al. 2009).
The carnivore community is dominated by the red fox (Vulpes vulpes), although other carnivore species such as the stone marten (Martes foina), the common genet (Genetta genetta), the European badger (Meles meles), the Egyptian mongoose (Herpestes ichneumon) and the least weasel (Mustela nivalis) are also present (Ferreras et al. 2016, 2017).
Material and methods
Live capture and tagging
Wildcats were captured with box-traps, including Tomahawk (Model 208, Tomahawk Live Trap, WI, USA) and three models of metal mesh traps from local dealers, with the required animal care permits for live captures (approved code PR-2013-05-04 from the Ethical Committee on Animal Testing of Castilla-La Mancha University). As lure we used live house pigeons (Columba sp.) and red-legged partridges (Alectoris rufa), placed in an independent chamber unreachable to captured carnivores. These baits were provided with food and water ad libitum and covered with branches to protect them from inclement weather, following EU recommendations regarding animal welfare. We deployed 52 box-traps (Fig. 1) in three trapping campaigns between March and December 2014 (Table S1 and Fig. S1 in Supplementary Material 1). Box-traps were placed within a surface of 36.39 km2 (rectangular area encompassing all the traps) in locations potentially suitable for wildcats such as dense shrub and woodland areas close to ephemeral water courses. Because of the mainly crepuscular and nocturnal activity of wildcats (Monterroso et al. 2014), box-traps were checked daily after sunrise to minimize animal stress.
Captured wildcats were immobilized with a combination of medetomidine hydrochloride (Medetor, Virbac, Spain) and ketamine hydrochloride (Imalgene 1000, Merial, Spain) with average dosages of 0.1 mg/kg and 5 mg/kg, respectively. We used atipamezole (Antisedan, Pfizer, Spain) in dose of 0.5 mg/kg to reverse the effects of medetomidine and facilitate a faster recovery (Gunkel and Lafortune 2007). All the captured wildcats were tagged with a microtransponder (ID-100A, Trovan) injected subcutaneously in the neck side for identification in subsequent recaptures. Two wildcats (see results) were also equipped with VHF-GPS radio-collars (88 g, model TGB-318, Telenax, Mexico).
Wildcats were released where captured once fully recovered from anesthesia, always within three hours after capture. Fixes for the radio-tagged wildcats were attempted daily through triangulation of the VHF signal and retrieved from the GPS units. Home range sizes were estimated through the minimum convex polygon including 95% of the fixes and by 90% kernel isopleths (Oliveira et al. 2018).
Camera-trapping
We deployed 40 camera-trap stations (one camera per station) between January 15 and April 22, 2014 (Fig. 1; Fig. S2 in Supplementary Material 1). Spatial distribution of stations followed a grid-sampling scheme (average ± SD: 1.268 ± 0.045 km to nearest camera), covering a total area of approximately 84.9 km2 (rectangular area encompassing all the cameras). This design was aimed at characterizing the mesocarnivore community (Ferreras et al. 2017) and studying their ecological interactions (Monterroso et al. 2014; 2020). The camera-trapping grid partially overlapped the live-trapping grid (Fig. 1), covering the same habitats types, but not co-located with live-traps avoiding data dependence (Clare et al. 2017).
We used two low-glow infrared camera-trap models, namely ScoutGuard SG550 and SG570 (HCO Outdoor Products, Norcross, GA, USA), with similar performing features (e.g. 1.2–1.3 s trigger speed). Cameras were secured inside metal boxes, locked with a cable lock and attached to a tree approximately 50 cm above ground. As attractant, we placed Iberian lynx (Lynx pardinus) urine and valerian extract in separate vials, a combination proved effective for wildcats (Monterroso et al. 2011; Ferreras et al. 2018), at a distance of 2–3 m from the camera traps. We programmed cameras to shoot a burst of three photos when triggered, with medium sensitivity and minimal delay time (0 s). Camera-traps remained active between 52 and 98 days (Fig. S2 in Supplementary Material 1).
Differentiation of wildcats from domestic cats was based on physical appearance and on the pelage patterns (Ragni and Possenti 1996; Kitchener et al. 2005). Consecutive photographs of wildcats in a given camera within a 30-min interval were considered as the same event, unless individuals could be unambiguously identified as different (O’Brien et al. 2003). Pictures taken > 30 min apart were considered as independent events.
Modeling
We used a spatially-explicit capture-recapture approach to estimate wildcat density (Efford 2004; Royle and Young 2008). The individual identification of wildcats from pictures from low-glow infrared camera-trapping is subject to high levels of uncertainty, since differences between individuals (coat patterns) are often difficultly perceived, particularly when using only one camera per station. Consequently, analyses based on such reduced number of capture events can be seriously affected by misidentification errors (Yoshizaki et al. 2009; Johansson et al. 2020). For this reason, camera-trapping data were transformed to wildcat detection count histories, without considering individual information. We used only unequivocal identifications from live-trapped wildcats, thanks to microtransponders attached to each individual in its first capture, to build individual detection histories.
Furthermore, radio-tracking data indicated particularly large home range sizes in the study area (Oliveira et al. 2018), which would require an overlapping sampling grid for standard spatial capture-recapture analysis with dimensions that entail unbearable sampling costs (Sollmann et al. 2012). We therefore used a static version of Chandler and Clark’s (2014) approach, originally developed for a spatial (open) integrated model. This model, described by Kéry and Royle (2020), integrates SCR histories in detectors deployed in a core area, and count data in a set of detectors located in a surrounding zone, based on the latent point process (Chandler et al. 2018). In our study, we integrated live-trap and camera-trap data, and both grids were partially overlapped.
In our first dataset (live captures), with individual attributions, the model assumes that the activity centers (\({s}_{i}\)) of the N individuals i are uniformly distributed in a region (state space, S): \({s}_{i}\sim Uniform(S)\). In the sampling process, we used J trap locations \({x}_{j}\) along K occasions. To describe the population state we used data augmentation (DA); \({z}_{i}\sim Bernoulli(\psi )\), where: \(\psi\) is the data augmentation parameter, \(\psi =E(N)/M\), and \(M\) is the size of the augmented dataset. Under DA:
The SCR encounter model \({y}_{i,j,k}\) (using the notation i: individual, j: trap, and k: sampling occasion) follows a Poisson process \({y}_{i,j,k}\sim Poisson(K {\lambda }_{i,j})\), such that:
where \({\lambda }_{0}\) is the baseline detection rate, \(\Vert {x}_{j}-{s}_{i}\Vert\) is the Euclidean distance between the trap \({x}_{j}\) and activity center \({s}_{i}\) and \(\sigma\) is the scale parameter of the half-normal distribution, related with the individuals’ movement (Royle et al. 2014).
The second dataset (counts in camera traps), without individual attribution, are the total counts in each detector and occasion dataset (count data). In the conditional formulation (Chandler and Royle 2013):
In this formulation \({y}_{i,j,k}\) are the latent (unobservable) spatial encounter histories, which were modeled by the marginal formulation, considering a Poisson distribution for the counts \({n}_{j,k}\) such that:
Both datasets share the Poisson point process function, the latent activity centers’ (\({s}_{i}\)) location and \(\psi\) (the parameter of DA). The model was implemented in a BUGS code developed by Kéry and Royle (2020) using the R (R Core Team 2020) package NIMBLE (De Valpine et al. 2017; NIMBLE Development Team 2019).
Because we used different detectors (live-traps and camera-traps), we conducted a model with two different basal rates, one for live captures and another for camera-trapping counts. We also used telemetry data (see Table S2 Supplementary Material 1) to improve the parameter calculations as described in Sollmann et al. (2013). A graphical depiction of the integration of the different data sources in the SCR-Counts model is shown in Fig. 2.
Graphical depiction of the joint analysis of SCR and count data, showing the different data sources (represented by orange rectangles) to contribute to shared inference on N population size (in green). Blue nodes represent: data augmented (M) and observed quantities in three observation processes: (1) SCR data (\({y}_{ij}^{ID}\)) capture-recapture encounter histories in box-traps (marked and identified by transponders); (2) Count data (n) independent events of non-identified individuals in camera traps, and (3) Telemetry data (\({C}_{xy}\)) coordinates data of telemetry-tagged individuals. White nodes represent unknown quantities (latent variables and model parameters). \({\lambda }_{ij}\): detection rate; \({y}_{ij}^{real}\): total of real encounters; ψ: data augmentation parameter; \({s}_{i}\): individuals activity centers; \({z}_{i}\): latent binary indicator variable that describes the membership of individual i in the population; σ: scale parameter from the half-normal detection function, that describes the animal movement, and \({\lambda }_{0}\): basal detection rate. Arrows demonstrate the dependences between nodes
To evaluate the improvement of using SCR integration including both partially overlapped grids of different detectors over standard SCR, we conducted a simulation study comparing both approaches. We evaluated the precision improvement by adding the count data, considering the same live-trap and camera-trap grids deployments as in our datasets, under four simulated population size scenarios: 10 individuals (density ca. 0.02 individuals/km2); 15 (0.03); 20 (0.04) and 25 (0.05). We simulated 100 datasets (Supplementary Material 2) for each scenario (Gardner 2017) and fitted the SCR and SCR-Counts integrated models in NIMBLE. Posterior probabilities were calculated using three independent MCMC chains, with 50,000 iterations each, and a burn-in of 5000 iterations. We confirmed model convergence by examining trace plots and ensuring that the potential scale reduction factor (R-hat) statistic for each parameter was < 1.1 (Gelman et al. 2013). We compared the posterior modes, medians and means for point estimate using the root-means-square error (RMSE) and relative bias in each pairwise, using the R package SimDesign (Chalmers 2020).
Results
Captures, radio-tracking and camera-trapping
With a live-trapping effort of 2034 trap-days we obtained ten capture events (including recaptures) of five adult wildcats (three males and two females; Table S2 Supplementary Material 1), yielding a capture rate of 0.49 captures per 100 trap-days. Capture frequency ranged from one to four captures per individual (1, 3, 1, 1, and 4 captures per individual, respectively; Table S2 Supplementary Material 1). No domestic cats were captured during the survey. Genetic analyses of four of the captured wildcats revealed that all were pure wildcats except one individual (FSC04), which was a first- or second-generation hybrid with domestic cat (Tiesmeyer et al. 2020).
One female and one male were radio-tagged and tracked during 72 and 259 days, respectively. Due to the poor performance of the collar-GPS units, we retrieved a small number of GPS fixes from the female when recaptured (6.8% fix success rate) and no GPS fixes were retrieved from the male since it was not recaptured. As a result, most of the positions were obtained by triangulation of the VHF signal (Table S2 Supplementary Material 1). Sample size allowed reaching an asymptote and home range sizes were estimated at 29.8 and 19.9 km2 for female and male, respectively, according to the 95% minimum convex polygon, and 59.8 and 43.0 km2 respectively according to the 90% kernel isopleths.
With a total effort of 3628 camera-days seven wildcat independent events were recorded, resulting in a capture rate of 0.19 detections per 100 camera-days. All cats photographed in the camera-traps during the study had the physical appearance and pelage patterns typical of wildcats.
Simulation study
Density estimates were statistically similar for the SCR and SCR-Counts integrated models, and the proportion of 95% highest posterior density intervals covering the population size simulated value were close to nominal coverages in both cases (Table 1). However, the estimate precision was optimized with the SCR-Counts integrated model (Fig. S3 in Supplementary Material 1). The RMSE for mode was lowest for density if N = 10 (d \(\approx\) 0.02 individuals/km2) but differences in RMSE for mode, median and mean were small at higher values of N (Table 1). Accordingly, we used the median as point estimate.
For all the range of densities simulated (\(d \epsilon \left\{0.02, 0.03, 0.04, 0.05\right\}\)), the SCR-Counts integrated model outperformed the standard SCR model. However, the improvement in precision obtained by integrating SCR with counts depended on population size. The largest improvements in precision were expected for population sizes around 10 individuals (d \(\approx\) 0.02 individuals/km2), but this improvement decreased with larger population sizes (N = 25; d \(\approx\) 0.05 individuals/km2, Table 1 and Figs. S3 and S4 in Supplementary Material 1). The estimated population size was unbiased in our simulations using SCR-Counts integrated models. According to the results of this simulation study, the SCR-Counts integrated model was the selected approach for estimating the wildcat population size of CNP.
Modeling results
The SCR-Counts integrated model provided an estimated mean density (± SD) of 0.038 ± 0.017 wildcats/km2 in CNP, with a 95% highest posterior density interval of 0.013–0.082 wildcats/km2 (Table 2, Fig. 3). An absolute population size of 15 wildcats (95% confidence interval: 5–34 individuals) was estimated for the whole National Park, assuming a uniform density.
Discussion
The results of our models highlight the advantages of incorporating diverse data sources for low density populations, whereby an integrated approach provides the means to improve precision in SCR density estimates by making use of available data that might otherwise be discarded (Velli et al. 2015; Murphy et al. 2018) with the recipe “same process, different observation model” (Kéry and Royle, 2020). Other studies (Jiménez et al. 2021) that use both known and unknown identity samples from a single observation model using a natural mechanistic dependence between samples, also found that density estimates improvement adding non-ID data is higher in low density populations.
Although dependence between the data to be integrated should be avoided, we found that if it occurred in our study, the effect on density estimates was negligible. We demonstrated that sample sizes as low as 10 captures of five individuals in live-traps, seven independent detections in camera-traps, and telemetry data from two individuals provided enough information to obtain reliable density estimates through integrated SC-SCR models.
Precision of estimates can be also improved by optimizing sampling design. For instance, using SCR models with camera-trap data, Kilshaw et al. (2015) found that the precision of density estimates could be increased by using bait, placing camera stations ≤ 1.5 km apart, using multiple cameras at each station, and by lengthening the survey period. In integrated SCR-Counts models, the precision is also related with the number and spatial setting of detectors used to obtain counts (Kéry and Royle 2020).
The estimated wildcat density (0.038 ± 0.017 wildcats/km2) is below the values reported in the literature and is one of the lowest densities ever reported for European wildcat in a protected area (Kéry et al. 2011; Anile et al. 2012; Anile et al. 2014; Kilshaw et al. 2015; Gil-Sánchez et al. 2020; see Table 3). Previous studies have reported depleted wildcat populations in other protected areas across the Iberian Peninsula. In Doñana National Park, Soto and Palomares (2014) reported a surprising low abundance of wildcats, despite legal protection of this space for over five decades. Sarmento et al. (2009) reported the drastic reduction of wildcats in Serra da Malcata Nature Reserve (Portugal) in the early XXI century and their replacement by free-ranging domestic cats. However, caution is warranted in inter-study comparisons since differences in density may be due to the unequal nature of data sources or analytical approaches. Using SCR models, Anile et al. (2014) estimated wildcat densities of 0.32 ± 0.10 ind/km2 vs. 1.36 ± 0.73 ind/km2 in Sicily (Italy) based on camera-trapping records and genetically-identified hairs, respectively; these figures are far above our estimates. On the other hand, diverging estimates could also be related to genetic identity (proportion of hybrid vs. pure wildcats) of the target population. Using SCR models on camera-trapping records, Kilshaw et al. (2015) estimated 0.68 wild-living cats/km2 in Scotland, but their estimate included both wildcats and hybrids. Despite the phenotypical compatibility of all our captured individuals with pure wildcats’, one out of four individuals was genetically identified as a hybrid (F1) with domestic cats (Tiesmeyer et al. 2020). Therefore, the true density of pure wildcats in our study area might be even lower than the nominal values estimated.
The causes for the low wildcat density estimated in CNP could be multifold, as suggested in other Mediterranean areas of the Iberian Peninsula (López-Martín et al. 2007; Soto and Palomares 2014; Gil-Sánchez et al. 2020). The most likely cause for the current low wildcat density within CNP should be low prey abundance (wild rabbit and small mammals), which hampers reproduction and forces felids to roam over large home ranges (Ferreras et al. 2011; Monterroso et al. 2016). Other causes that could have further contributed to the dampening of the European wildcat population at our study area could be hybridization with domestic cats and disease transmission between the two counterparts (López-Martín et al. 2007; Oliveira et al. 2008; Tiesmeyer et al. 2020). If this is the case, then the low-density wildcat population at CNP could have entered into an extinction vortex (Palomares et al. 2012), likely initiated by prey scarcity, and potentially leading to an accelerated hybridization with domestic cats and disease transmission (López et al. 2009; Meli et al. 2010).
The minimum recommended surveyed area for capture-recapture models is of at least four times the average home range of the target species (Otis et al. 1978), although more recent studies recommend areas just larger than a single average home range (Sollman et al. 2012; Sun et al. 2014). Given that our SCR surveyed area fits this requirement, we decided to combine the approach with telemetry data and integrate a SCR model for live trapping recapture histories and counts from camera trapping. Simulations showed that the integrated SCR model is more accurate than the SCR alone. The improvement was large (17.6 and 6.3% RMSE reduction for mean and median) under low densities (~ 0.02 individuals/km2) and is weaker (5.2 and 5.7%, respectively) at higher densities.
The spatial configuration of traps and cameras directly influences the improvement in accuracy of the integrated model. As Kéry and Royle (2020) pointed out, this integrated model provides no benefit when the sampling area producing both the encounter histories and the auxiliary count or binary data are the same.
Previous studies suggest 90 days as the maximum survey length required for the population closure assumption implied in capture-recapture models for large felids (Karanth and Nichols 2002). However, when studying species that occur at very low population densities, such as wildcats in our study area, this survey length may be insufficient due to the small sample size and low recapture rates (Brassine and Parker 2015). Our camera-trapping survey (three months) fitted the maximum length suggested. However, the length of our live-trapping survey (nine months) was beyond this maximum survey length recommended and would require careful consideration of the temporal closure assumption (Foster and Harmsen 2012). Nonetheless, increasing the length of the survey may be appropriate for some species with long life expectations, as it could be the case of the wildcat (O’Brien and Kinnaird 2011; Brassine and Parker 2015).
An accurate definition of required conservation actions, and even the red list assessment criteria, rely on estimates of population size across the species range. In most cases, due to logistic and budgetary constraints, the collection of data to estimate reliable population sizes and trends is limited. By combining several scarce data sources into a unified spatially-explicit capture-recapture model we were able to estimate, with increased precision compared with regular single-dataset SCR models, the European wildcat density in a protected area from central Iberian Peninsula. A major contribution of this paper is, therefore, to develop and make a proof-of-concept for a species in low density and large home ranges, where estimates using detection with identification and standard SCR methods would have been prohibitively expensive. Combining small datasets into this integrated SCR-Counts framework could provide the means to make better inferences about population size, and thus adequately inform conservation actions and status assessments.
Conservation implications
Our results support an extremely low density of European wildcats in a highly protected area, suggesting that this population is likely undergoing a process of extinction. Furthermore, the situation found in this national park likely mimics the broader scenario of wildcat populations in the most southwestern region of the European wildcat range in Europe. Therefore, integrating all possible data available into a single analytical approach that optimizes their usefulness could prove an invaluable tool to identify and monitor low-density populations. This is the most likely scenario of multiple populations of the Iberian wildcat metapopulation, which are undergoing demographic reductions and increasing isolation. It is urgent to identify the causes of decline, though these could be multiple.
We argue that, in situations such as the one we identified at this protected area, improving prey abundance (rabbits and small mammals) could foster population recovery through favoring smaller home ranges, increasing survival and boosting fecundity, ultimately leading to increased wildcat density and reduced contact with domestic cats in peripheral areas, limiting the risks of hybridization and of disease transmission by domestic cats. However, further studies on these causal relationships are urgently required to guide sound conservation strategies and reverse the decline of Mediterranean wildcat populations.
Data availability
The datasets analyzed during the study will be available from the corresponding author on reasonable request.
Code availability
Not applicable.
References
Anile S, Bizzarri L, Ragni B (2010) Estimation of European wildcat population size in Sicily (Italy) using camera trapping and capture–recapture analyses. Ital J Zool 77:241–246. https://doi.org/10.1080/11250000903419731
Anile S, Amico C, Ragni B (2012) Population density estimation of the European wildcat (Felis silvestris silvestris) in Sicily using camera trapping. Wildl Biol Pract 8:1–12
Anile S, Ragni B, Randi E, Mattucci F, Rovero F (2014) Wildcat population density on the Etna volcano, Italy: a comparison of density estimation methods. J Zool 293:252–261. https://doi.org/10.1111/jzo.12141
Bastianelli ML, Premier J, Herrmann M, Anile S, Monterroso P, Kuemmerle T, Dormann CF, Streif S, Jerosch S, Götz M, Simon O, Moleón M, Gil-Sánchez JM, Biró J, Dekker J, Severon A, Krannich A, Hupe K, Germain E, Pontier D, Janssen R, Ferreras P, Díaz-Ruiz F, López-Martín JM, Urra F, Bizzarri L, Bertos-Martín E, Dietz M, Trinzen M, Ballesteros-Duperón E, Barea-Azcón JM, Sforzi A, Poulle ML, Heurich M (2021) Survival and cause-specific mortality of European wildcat (Felis silvestris) across Europe. Biol Conserv 261:239
Belbachir F, Pettorelli N, Wacher T, Belbachir-Bazi A, Durant SM (2015) Monitoring rarity: the critically endangered Saharan cheetah as a flagship species for a threatened ecosystem. PLoS ONE. https://doi.org/10.1371/journal.pone.0115136
Brassine E, Parker D (2015) Trapping elusive cats: using intensive camera trapping to estimate the density of a rare African felid. PLoS ONE. https://doi.org/10.1371/journal.pone.0142508
Breitenmoser U, Lanz T, Breitenmoser-Würsten C (2019) Conservation of the wildcat (Felis silvestris) in Scotland: Review of the conservation status and assessment of conservation activities. IUCN SSC Cat Specialist Group, commissioned by the Scottish Wildcat Conservation Action Plan Steering Group
Burton AC, Neilson E, Moreira D, Ladle A, Steenweg R, Fisher JT, Bayne E, Boutin S (2015) Wildlife camera trapping: a review and recommendations for linking surveys to ecological processes. J Appl Ecol 52:675–685. https://doi.org/10.1111/1365-2664.12432
Cabral MJ, Almeida J, Almeida PR, Dellinger T, Ferrand de Almeida N, Oliveira ME, Palmeirim JM, Queiroz AI, Rogado L, Santos-Reis M (2005) Livro Vermelho dos Vertebrados de Portugal. Instituto da Conservação da Natureza, Lisboa
Can OE, Kandemir I, Togan I (2011) The wildcat Felis silvestris in northern Turkey: assessment of status using camera trapping. Oryx 45:112–118. https://doi.org/10.1017/s0030605310001328
Carbone C et al (2001) The use of photographic rates to estimate densities of tigers and other cryptic mammals. Anim Conserv 4:75–79. https://doi.org/10.1017/s1367943001001081
Chalmers P (2020) SimDesign: structure for organizing Monte Carlo simulation designs. R Package Version 2:1
Chandler RB, Clark JD (2014) Spatially explicit integrated population models. Meth Ecol Evol 5:1351–1360. https://doi.org/10.1111/2041-210x.12153
Chandler RB, Royle JA (2013) Spatially-explicit models for inference about density in unmarked or partially marked populations. Ann Appl Stat 7:936–954
Chandler RB, Hepinstall-Cymerman J, Merker S, Abernathy-Conners H, Cooper RJ (2018) Characterizing spatio-temporal variation in survival and recruitment with integrated population models. Auk 135:409–426. https://doi.org/10.1642/auk-17-181.1
Clare J, McKinney ST, DePue JE, Loftin CS (2017) Pairing field methods to improve inference in wildlife surveys while accommodating detection covariance. Ecol Appl 27:2031–2047. https://doi.org/10.1002/eap.1587/full
Corbett LK (1979) Feeding ecology and social organization of wild cats (Felis silvestris) and domestic cats (Felis catus) in Scotland. PhD thesis, University of Aberdeen
de Valpine P, Turek D, Paciorek CJ, Anderson-Bergman C, Lang DT, Bodik R (2017) Programming with models: writing statistical algorithms for general model structures with NIMBLE. J Comput Graph Stat 26:403–413. https://doi.org/10.1080/10618600.2016.1172487
Delibes-Mateos M, Ferreras P, Villafuerte R (2008) Rabbit populations and game management: the situation after 15 years of rabbit haemorrhagic disease in central-southern Spain. Biodiv Conserv 17:559–574. https://doi.org/10.1007/s10531-007-9272-5
Dimitrijevic S (1980) Ecomorphological characteristics of the wildcat (Felis silvestris Schreber, 1777) on the territory of Voijvodina. Arhiv Biol Nauka Beograd 58:219–282
Efford M (2004) Density estimation in live-trapping studies. Oikos 106:598–610. https://doi.org/10.1111/j.0030-1299.2004.13043.x
Ferreras P, Travaini A, Zapata SC, Delibes M (2011) Short-term responses of mammalian carnivores to a sudden collapse of rabbits in Mediterranean Spain. Basic Appl Ecol 12:116–124. https://doi.org/10.1016/j.baae.2011.01.005
Ferreras P, Díaz-Ruiz F, Alves PC, Monterroso P (2016) Factores de la coexistencia de mesocarnívoros en parques nacionales de ambiente mediterráneo. In: Amengual P (ed) Proyectos de Investigación en Parques Nacionales 2011–2014. Organismo Autónomo Parques Nacionales, MAGRAMA, Madrid, pp 321–339
Ferreras P, Diaz-Ruiz F, Alves PC, Monterroso P (2017) Optimizing camera-trapping protocols for characterizing mesocarnivore communities in south-western Europe. J Zool 301:23–31. https://doi.org/10.1111/jzo.12386
Ferreras P, Diaz-Ruiz F, Monterroso P (2018) Improving mesocarnivore detectability with lures in camera-trapping studies. Wildl Res 45:505–517. https://doi.org/10.1071/WR18037
Foster RJ, Harmsen BJ (2012) A critique of density estimation from camera-trap data. J Wildl Manage 76:224–236
Gardner B (2017) Integrating spatial capture recapture with occupancy or count data. In: Paper presented at the EURING 2017 Analytical Meeting and workshop. Estimation and modeling of vertebrate populations with emphasis on marked individuals, Barcelona, 2–7 July 2017
Gelman A, Carlin JB, Stern HS, Dunson DB, Vehtari A, Rubin DB (2013) Bayesian Data Analysis, 3rd edn. Chapman & Hall/CRC, New York
Gil-Sánchez JM, Valenzuela G, Sánchez JF (1999) Iberian wild cat Felis silvestris tartessia predation on rabbit Oryctolagus cuniculus: functional response and age selection. Acta Theriol 44:421–428
Gil-Sánchez JM, Barea-Azcón JM, Jaramillo J, Herrera-Sánchez FJ, Jiménez J, Virgós E (2020) Fragmentation and low density as major conservation challenges for the southernmost populations of the European wildcat. PLoS ONE 15:e0227708. https://doi.org/10.1371/journal.pone.0227708
Gunkel C, Lafortune M (2007) Felids. In: West G, Heard D, Caulkett N (eds) Zoo Animal and Wildlife Immobilization and anesthesia, 1st edn. Blackwell, Ames, pp 443–459
Heller M (1992) Status and conservation of the wildcat (Felis silvestris) in the region Baden-Wurttemberg, Southwest Germany. In: Seminary on the biology and conservation of the wildcat (Felis silvestris). In: Proceedings of the Convention on the Conservation of the European Wildlife and Natural Habitats, vol 16. Environmental encounters. Council of Europe Nature and Environment, Strasbourg, pp 42–45
Heltai M, Biro Z, Szemethy L (2006) The changes of distribution and population density of wildcats Felis silvestris Schreber, 1775 in Hungary between 1987–2001. Nat Conserv 62:37–42
Jerosch S, Götz M, Roth M (2017) Spatial organisation of European wildcats (Felis silvestris silvestris) in an agriculturally dominated landscape in Central Europe. Mammal Biol 82:8–16. https://doi.org/10.1016/j.mambio.2016.10.003
Jiménez J, Nuñez-Arjona JC, Mougeot F, Ferreras P, González LM, García-Domínguez F, Muñoz-Igualada J, Palacios MJ, Pla S, Rueda C, Villaespesa F, Nájera F, Palomares F, López-Bao JV (2019) Restoring apex predators can reduce mesopredator abundances. Biol Conserv 238:108234. https://doi.org/10.1016/j.biocon.2019.108234
Jiménez J, Augustine BC, Linden DW, Chandler RB, Royle JA (2021) Spatial capture–recapture with random thinning for unidentified encounters. Ecol Evol 11:1187–1198. https://doi.org/10.1002/ece3.7091
Johansson Ö, Samelius G, Wikberg E, Chapron G, Mishra C, Low M (2020) Identification errors in camera-trap studies result in systematic population overestimation. Sci Rep 10:6393. https://doi.org/10.1038/s41598-020-63367-z
Karanth KU, Nichols JD (2002) Monitoring tigers and their prey: a manual for researchers, managers and conservationists in tropical Asia. Center for Wildlife Studies, Bangalore
Kéry M, Royle A (2020) Applied hierarchical modeling in ecology: analysis of distribution, abundance and species richness in R and BUGS. Volume 2: dynamic and advanced models, 1st edn. Academic Press, London
Kéry M, Gardner B, Stoeckle T, Weber D, Royle JA (2011) Use of spatial capture–recapture modeling and DNA data to estimate densities of elusive animals. Conserv Biol 25:356–364. https://doi.org/10.1111/j.1523-1739.2010.01616.x
Kilshaw K, Johnson PJ, Kitchener AC, Macdonald DW (2015) Detecting the elusive Scottish wildcat Felis silvestris silvestris using camera trapping. Oryx 49:207–215. https://doi.org/10.1017/S0030605313001154
Kitchener AC, Yamaguchi N, Ward JM, Macdonald DW (2005) A diagnosis for the Scottish wildcat (Felis silvestris): a tool for conservation action for a critically-endangered felid. Anim Conserv 8:223–237
Kitchener AC et al. (2017) A revised taxonomy of the Felidae. The final report of the Cat Classification Task Force of the IUCN/SSC Cat Specialist Group. Cat News Special Issue 11:80 pp
Klar N, Fernandez N, Kramer-Schadt S, Herrmann M, Trinzen M, Buttner I, Niemitz C (2008) Habitat selection models for European wildcat conservation. Biol Conserv 141:308–319
Linkie M, Haidir IA, Nugroho A, Dinata Y (2008) Conserving tigers Panthera tigris in selectively logged Sumatran forests. Biol Conserv 141:2410–2415. https://doi.org/10.1016/j.biocon.2008.07.002
López G, López-Parra M, Fernández L, Martínez-Granados C, Martínez F, Meli ML, Gil-Sánchez JM, Viqueira N, Díaz-Portero MA, Cadenas R, Lutz H, Vargas A, Simón MA (2009) Management measures to control a feline leukemia virus outbreak in the endangered Iberian lynx. Anim Conserv 12:173–182. https://doi.org/10.1111/j.1469-1795.2009.00241.x
López-Martín JM, García FJ, Duch A, Virgós E, Lozano J, Duarte J, España AJ (2007) Felis silvestris Schreber, 1777. In: Palomo LJ, Gisbert J, Blanco JC (eds) Atlas y libro rojo de los mamíferos de España. Dirección General para la Biodiversidad-SECEM -SECEMU, Madrid, pp 336–338
Lozano J, Moleon M, Virgos E (2006) Biogeographical patterns in the diet of the wildcat, Felis silvestris Schreber, in Eurasia: factors affecting the trophic diversity. J Biogeogr 33:1076–1085. https://doi.org/10.1111/j.1365-2699.2006.01474.x
Meek P, Fleming P, Ballard G, Banks P, Claridge A, Sanderson J, Swann D (2014) Camera trapping: wildlife management and research. CSIRO Publishing, Clayton
Meli ML, Cattori V, Martinez F, Lopez G, Vargas A, Palomares F, Lopez-Bao JV, Hofmann-Lehmann R, Lutz H (2010) Feline leukemia virus infection: a threat for the survival of the critically endangered Iberian lynx (Lynx pardinus). Vet Immunol Immunopathol 134:61–67. https://doi.org/10.1016/j.vetimm.2009.10.010
Monterroso P, Alves PC, Ferreras P (2011) Evaluation of attractants for non-invasive studies of Iberian carnivore communities. Wildl Res 38:446–454. https://doi.org/10.1071/wr11060
Monterroso P, Alves PC, Ferreras P (2014) Plasticity in circadian activity patterns of mesocarnivores in Southwestern Europe: implications for species coexistence. Behav Ecol Sociobiol 68:1403–1417. https://doi.org/10.1007/s00265-014-1748-1
Monterroso P et al (2016) Disease-mediated bottom-up regulation: an emergent virus affects a keystone prey, and alters the dynamics of trophic webs. Sci Rep 6:36072. https://doi.org/10.1038/srep36072
Monterroso P, Díaz-Ruiz F, Lukacs PM, Alves PC, Ferreras P (2020) Ecological traits and the spatial structure of competitive coexistence among carnivores. Ecology 101:e03059. https://doi.org/10.1002/ecy.3059
Muñoz A, Bonal R, Diaz M (2009) Ungulates, rodents, shrubs: interactions in a diverse Mediterranean ecosystem. Basic Appl Ecol 10:151–160
Murphy A, Gerber BD, Farris ZJ, Karpanty S, Ratelolahy F, Kelly MJ (2018) Making the most of sparse data to estimate density of a rare and threatened species: a case study with the fosa, a little-studied Malagasy carnivore. Anim Conserv 21:496–504. https://doi.org/10.1111/acv.12420
NIMBLE Development Team (2019) NIMBLE: MCMC, particle filtering, and programmable hierarchical modeling
Nowell K, Jackson P (1996) Wild cats: status survey and conservation action plan. IUCN, Gland
O’Brien TG, Kinnaird MF (2011) Density estimation of sympatric carnivores using spatially explicit capture–recapture methods and standard trapping grid. Ecol Appl 21:2908–2916. https://doi.org/10.1890/10-2284.1
O’Brien TG, Kinnaird MF, Wibisono HT (2003) Crouching tigers, hidden prey: Sumatran tiger and prey populations in a tropical forest landscape. Anim Conserv 6:131–139. https://doi.org/10.1017/S1367943003003172
Okarma H, Sniezko S, Olszanska A (2002) The occurrence of wildcat in the Polish Carpathian Mountains. Acta Theriol 47:499–504. https://doi.org/10.1007/bf03192474
Oliveira R, Godinho R, Randi E, Alves PC (2008) Hybridization versus conservation: are domestic cats threatening the genetic integrity of wildcats (Felis silvestris silvestris) in Iberian Peninsula? Phil Trans R Soc B-Biol Sci 363:2953–2961
Oliveira T, Urra F, López-Martín JM, Ballesteros-Duperón E, Barea-Azcón JM, Moléon M, Gil-Sánchez JM, Alves PC, Díaz-Ruíz F, Ferreras P, Monterroso P (2018) Females know better: Sex-biased habitat selection by the European wildcat. Ecol Evol 8:9464–9477. https://doi.org/10.1002/ece3.4442
Otis DL, Burnham KP, White GC, Anderson DR (1978) Statistical-inference from capture data on closed animal populations. Wildl Monogr 62:1–135
Palomares F, Godoy JA, López-Bao JV, Rodríguez A, Roques S, Casas-Marce M, Revilla E, Delibes M (2012) Possible extinction vortex for a population of Iberian lynx on the verge of extirpation. Conserv Biol 26:689–697
R Core Team (2020) R: a language and environment for statistical computing. R Found. Stat. Comput, Vienna
Ragni B (2006) Il gatto selvatico. [The wildcat]. In: Perdisa A (ed) Salvati dall’arca. [Saved by the ark]. WWF Italia, Bologna, pp 35–36
Ragni B, Possenti M (1996) Variability of coat-colour and markings system in Felis silvestris. It J Zool 63:285–292
Royle JA, Young KV (2008) A hierarchical model for spatial capture–recapture data. Ecology 89:2281–2289. https://doi.org/10.1890/07-0601.1
Royle JA, Chandler RB, Sollmann R, Gardner B (2014) Spatial capture–recapture. Elsevier Inc., Waltham, Oxford, Amsterdam
Ruprecht JS, Eriksson CE, Forrester TD, Clark DA, Wisdom MJ, Rowland MM, Johnson BK, Levi T (2021) Evaluating and integrating spatial capture–recapture models with data of variable individual identifiability. Ecol Appl. https://doi.org/10.1002/eap.2405
Sabino-Marques H, Ferreira CM, Paupério J, Costa P, Barbosa S, Encarnação C, Alpizar-Jara R, Alves PC, Searle JB, Mira A, Beja P, Pita R (2018) Combining genetic non-invasive sampling with spatially explicit capture–recapture models for density estimation of a patchily distributed small mammal. Eur J Wild Res 64:44. https://doi.org/10.1007/s10344-018-1206-x
Sarmento P, Cruz J, Eira C, Fonseca C (2009) Spatial colonization by feral domestic cats Felis catus of former wildcat Felis silvestris silvestris home ranges. Acta Theriol 54:31–38. https://doi.org/10.1007/BF03193135
Say L, Devillard S, Léger F, Pontier D, Ruette S (2012) Distribution and spatial genetic structure of European wildcat in France. Anim Conserv 15:18–27
Scott R, Easterbee N, Jefferies D (1993) A radio-tracking study of wildcats in western Scotland. Council of Europe Environmental Encounters Series 16:94–97
Sobrino R, Acevedo P, Escudero MA, Marco J, Gortazar C (2009) Carnivore population trends in Spanish agrosystems after the reduction in food availability due to rabbit decline by rabbit haemorrhagic disease and improved waste management. Eur J Wild Res 55:161–165
Soisalo MK, Cavalcanti SMC (2006) Estimating the density of a jaguar population in the Brazilian Pantanal using camera-traps and capture–recapture sampling in combination with GPS radio-telemetry. Biol Conserv 129:487
Sollmann R, Gardner B, Belant JL (2012) How does spatial study design influence density estimates from spatial capture–recapture models? PLoS ONE 7:e34575
Sollmann R, Gardner B, Parsons AW, Stocking JJ, McClintock BT, Simons TR, Pollock KH, O’Connell AF (2013) A spatial mark-resight model augmented with telemetry data. Ecology 94:553–559
Sollmann R, Linkie M, Haidir IA, Macdonald DW (2014) Bringing clarity to the clouded leopard Neofelis diardi: first density estimates from Sumatra. Oryx 48:536–539. https://doi.org/10.1017/S003060531400043X
Soto CA, Palomares F (2014) Surprising low abundance of European wildcats in a Mediterranean protected area of southwestern Spain. Mammalia 78:57–65. https://doi.org/10.1515/mammalia-2013-0054
Stahl P, Artois M (1991) Status and Conservation of the wild Cat (Felis silvestris) in Europe and around the Mediterranean rim. In: Convention on wildlife and natural habitat conservancy in Europe, Strasbourg, 1991. Council of Europe, p 61
Steyer K et al (2016) Large-scale genetic census of an elusive carnivore, the European wildcat (Felis s. silvestris). Conserv Genet 17:1183–1199. https://doi.org/10.1007/s10592-016-0853-2
Sun CC, Fuller AK, Royle JA (2014) Trap Configuration and spacing influences parameter estimates in spatial capture–recapture models. PLoS ONE. https://doi.org/10.1371/journal.pone.0088025
Tiesmeyer A et al (2020) Range-wide patterns of human-mediated hybridisation in European wildcats. Conserv Genet 21:247–260. https://doi.org/10.1007/s10592-019-01247-4
Velli E, Bologna MA, Silvia C, Ragni B, Randi E (2015) Non-invasive monitoring of the European wildcat (Felis silvestris silvestris Schreber, 1777): comparative analysis of three different monitoring techniques and evaluation of their integration. Eur J Wild Res 61:657–668. https://doi.org/10.1007/s10344-015-0936-2
Villafuerte R, Delibes-Mateos M (2019) Oryctolagus cuniculus. The IUCN Red List of Threatened Species 2019
Weber D, Ginter H-P, Hefti-Gautschi B (2008) Die aktuelle Verbreitung der Wildkatze (Felis silvestris silvestris Schreber 1777) in Kanton Basel-Landschaft (NW-Scheiz) und angrenzenden Gebieten [The Occurrence of the Wildcat (Felis silvestris silvestris Schreber 1777) in the canton Basel-Landschaft and adjacent Areas. Mitt Naturf Ges Beider Basel 11:177–185
Weingarth K, Zeppenfeld T, Heibl C, Heurich M, Bufka L, Daniszová K, Müller J (2015) Hide and seek: extended camera-trap session lengths and autumn provide best parameters for estimating lynx densities in mountainous areas. Biodiv Conserv 24:2935–2952. https://doi.org/10.1007/s10531-015-0986-5
Yamaguchi N, Kitchener A, Driscoll C, Nussberger B (2015) Felis silvestris. The IUCN Red List of Threatened Species 2015. https://doi.org/10.2305/IUCN.UK.2015
Yoshizaki J, Pollock KH, Brownie C, Webster RA (2009) Modeling misidentification errors in capture–recapture studies using photographic identification of evolving marks. Ecology 90:3–9. https://doi.org/10.1890/08-0304.1
Acknowledgements
Funding was provided by Organismo Autónomo Parques Nacionales, Project OAPN 352/2011. We are grateful for the support received during this study from the staff of Cabañeros National Park. We also thank the assistance received during the fieldwork from T. Oliveira, I. Vaz and J.C. Zarca, and during data processing from A. Fragoso. F. Díaz-Ruiz was supported by a Juan de la Cierva postdoctoral contract (FJCI-2015-24,949) and is currently supported by a postdoctoral contract from the University of Málaga (I Plan Propio de Investigación y Transferencia, call 2020). P. Monterroso was supported by UID/BIA/50027/2019 with funding from FCT/MCTES through national funds.
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.
Author information
Authors and Affiliations
Contributions
All authors contributed to the study conception and design; PF, FDR and JT collected the field data; JJ and PF designed the analysis of data; JJ performed the integrated SCR models; the first draft of the manuscript was written by PF and JJ and all authors commented on previous versions of the manuscript, read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Ethical approval
All the procedures followed national and international regulations for animal welfare and were approved by the Ethical Committee on Animal Testing of Castilla-La Mancha University (Permission Number: PR-2013-05-04).
Consent to participate
All the authors declare their consent to participate.
Consent for publication
All the authors declare their consent for publications.
Additional information
Communicated by Karen E. Hodges.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ferreras, P., Jiménez, J., Díaz-Ruiz, F. et al. Integrating multiple datasets into spatially-explicit capture-recapture models to estimate the abundance of a locally scarce felid. Biodivers Conserv 30, 4317–4335 (2021). https://doi.org/10.1007/s10531-021-02309-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10531-021-02309-1