Introduction

Non-physical or behavioral deterrents technologies, such as electricity, carbon dioxide (CO2), underwater acoustic deterrent systems (uADS), BioAcoustic Fish Fences (BAFF) and others, offer managers options that may help control migratory pathways and limit the range expansion of invasive fishes (Cupp et al. 2021a, b). The use of behavioral barriers has consistent benefits over physical barriers including not impeding the river flow or navigation and having possible species selectivity (Noatch and Suski 2012; Cupp et al. 2021a, b). Because behavioral deterrents can be turned on and off, they may be employed to disrupt specific life history events in invasive species or to target invasive species during times of migration (e.g., spawning). However, a high degree of uncertainty exists surrounding the effectiveness of different behavioral deterrents in field applications.

The effectiveness of behavioral deterrents can vary widely among type, species, and deployment and environmental conditions (e.g., barrier angle, substrate type; Noatch and Suski 2012). Most research on movement deterrents is also conducted using lab and mesocosm experiments, which adds to uncertainty about how they may function in the field. However, lab and mesocosm trials indicate that deterrents may be 50–97% effective in reducing movement depending on deterrent type, design, and species tested (Pegg and Chick 2004; Zielinski and Sorenson 2016; Dennis et al. 2019; Cupp et al. 2021b). Limited field trials of behavioral deterrents are underway but have not been fully evaluated (Cupp et al. 2021a). Because of this uncertainty in the field-effectiveness of deterrents, managers are left weighing the possible benefits of using deterrents against the costs of their implementation. Although decision analysis has been used to identify priority deterrent types and locations to limit range expansion in invasive species (Cupp et al. 2021a; Post van der Burg et al. 2021), data and modeling can also be used to assess possible management options (Samson et al. 2017; Day et al. 2018) such as the use and placement of deterrents.

Additional uncertainty is introduced into decision making when managers must evaluate multiple locations where they could deploy movement deterrents. While there has been steady accumulation of information about the effect of deterrents on individual behavior, the potential effects of deterrents on population and spatial dynamics in the context of multi-pooled river systems have not been rigorously examined. For example, does the placement in the river affect the population dynamics at the invasion front? If so, does the effectiveness of the placement vary across species? Do deterrents affect the river-scale growth rate of the population, or simply affect the spatial distribution in the river?

The Illinois River is one example where the use of movement deterrents is being considered. However, managers face a challenge in deciding where deterrents may be the most effective due to the complex nature of the river which is divided by locks and dams for navigation. Invasive silver carp (Hypophthalmichthys molitrix) and bighead carp (H. nobilis), collectively known as bigheaded carps (H. spp.), are abundant in the lower Illinois River (Sass et al. 2010; Coulter et al. 2018a) but decline in abundance in more upstream navigation pools approaching Lake Michigan. Interagency collaborative management in this river has the ultimate goal of reducing invasive carp abundances at the invasion front (most upstream pool) and limiting risk of individuals reaching the Great Lakes (Conover et al. 2007) where predicted ecological and economic costs are high (Currie et al. 2012; Whittman et al. 2014; Ivan et al. 2020; Rutherford et al. 2021). Although divided by a series of locks and dams that limit movement (Coulter et al. 2018b), individuals from high-density areas can move towards the invasion front and the Great Lakes. Commercial fishing in high-density areas and contracted removal in upstream navigation pools near the invasion front is ongoing and remove large numbers of invasive carps from the Illinois River. However, incorporating behavioral deterrents with ongoing removal efforts could further reduce the risk of upstream migration (Post van der Burg et al. 2021). The combination of population suppression through removal along with inhibiting movement with deterrents align with Integrated Pest Management (IPM) plans where multiple strategies are employed to control a nuisance species (Gaikowski and Kočovský 2021; Cupp et al. 2021a). As part of IPM plan development, data and models may be used to describe potential outcomes and inform resource management decisions.

In the Illinois River, movement deterrents could be deployed at any of five locks and dams, which represent the pool boundaries, within the current range of invasive bigheaded carp. In this study, we combined a metapopulation model of the Illinois River with monthly movement data among the pools for silver and bighead carp (Coulter et al. 2018b; Schoolmaster et al. 2022) to estimate best placement of deterrents with respect to the effect on the annual per capita growth rate of both bigheaded carp species at the invasion front (Dresden Island). In addition, we incorporate uncertainty in the movement parameter estimates to examine the benefits and risks of deterrents placed at different pool boundaries. Finally, we examine the predicted effect of deterrents on the per capita growth rate and transient (i.e., short-term, temporary) spatial dynamics of each species at the scale of the whole river. The effects of interventions at this larger scale is important because it represents a potential second-order effect of deterrents. For example, if fish are concentrated in the areas that are best for recruitment the resulting increase in the river-scale growth rates could overwhelm any pool-level reduction in growth rate. This modeling effort can assist managers with decision-making (Maguire 2004) regarding deterrent placement as well as what possible deterrent effectiveness they might require to achieve a desired outcome (Cupp et al. 2021a).

Methods

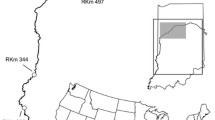
The Illinois River is approximately 273 km long and flows from Lake Michigan via the Chicago Area Waterway System (CAWS) to the Mississippi River with the confluence near Grafton, Illinois (Fig. 1). A series of 8 locks and dams are located throughout the river and partition the river into distinct pools. Locks and dams are operated by the U.S. Army Corps of Engineers for water level management and to support navigation. Invasive carps, a group comprised of silver, bighead, grass (Ctenopharyngodon idella), and black (Mylopharyngodon piceus) carps, are found throughout much of the middle and lower pools. Here, we focus on the 5 lock and dam structures below the Brandon Road Lock and Dam. Silver and bighead carps dominate much of the invasive fish biomass and comprise > 70% of all fish biomass in some locations (Coulter et al. 2018a). The invasive carp population front is in the Dresden Pool with the population intensely monitored by state and federal resource agencies. Fish can move among navigation pools in either direction throughout the river by transiting the lock and/or dam structures. However, the permeability of each dam varies (Coulter et al. 2018b). Two wicket-style dams (i.e., La Grange and Peoria) in the lower Illinois River allow free movement of fish during times of high discharge. Three gated dams (i.e., Starved Rock, Marseilles, and Dresden Island) in the upper Illinois River allow some passage through dams, especially during open water, but are believed to be less permeable to fish movement than the wicket-style dams. Passage through lock chambers can occur at any of these lock and dams, however, each represents a pinch-point where a deterrent could be deployed to potentially reduce upstream passage of bigheaded carps (Fig. 1). For model development, we followed the usual convention of using a numeric index for pools ordered by position in the river such that \(k=1\) indicates most upstream pool and \(k=6\) indicates the most downstream pool. This results in the assignments: Dresden Island (k = 1), Marseilles (k = 2), Starved Rock (k = 3), Peoria (k = 4), La Grange (k = 5) and Alton (k = 6).

Fig. 1
figure 1

Map of Illinois River with location of the locks and dams (L & D) that define the pools. Inset map highlighting the position of the State of Illinois. Upper pools (Dresden Island through Starved Rock pools) tend to be shorter and higher gradient than downstream pools (Peoria through Alton pools): Dresden Island (pool 1) 23 km; Marseilles (pool 2) 39 km; Starved Rock (pool 3) 26 km; Peoria (pool 4) 118 km; La Grange (pool 5) 125 km; Alton (pool 6) 129 km

Full size image

We applied the model used in Schoolmaster et al. (2022), which incorporates movement probabilities from Coulter et al. (2018b) and data available from Coulter et al. (2022). The movement estimates from Coulter et al. (2022) consist of 30,000 draws of the posterior distribution from an open mark-recapture multistate model (White and Burnham 1999) used to fit the observed movement data (described in Coulter et al. 2018b). The estimates included,\({\psi }_{i,h}\) which are the probability of a fish observed in pool h in month t being observed in pool i in month t + 1. Thus, based on movement among pools only,

$$ n_{h}^{t + \Delta t} = s_{h} \left( {1 - \mathop \sum \limits_{i \ne h} \psi_{i,h} } \right)n_{h}^{t} + \mathop \sum \limits_{j \ne h} \psi_{h,j} n_{j}^{t} , $$
(1)

where the \({n}_{h}^{t}\) is the population of fish in pool \(h\) at time \(t\) and \({s}_{h}\) is the probability of survivorship in pool \(h\). Note that superscript \(t\) indicates time step (as opposed to an exponent). We used the estimates of \({\psi }_{i,h}\) to estimate the posterior distributions of of the probability of adjacent upstream,\({\phi }_{h,h+1},h\in \{1,\dots ,5\}\), and downstream, \({\phi }_{j-1,j},j\in \{2,\dots ,6\}\), movement where

$$ \psi_{i,h} = \mathop \prod \limits_{j = h}^{j - 1 = i} \phi_{j - 1,j} $$
(2)

for \(h>i\) and

$$ \psi_{i,h} = \mathop \prod \limits_{j = h}^{j + 1 = i} \phi_{j + 1,j} $$
(3)

for \(h<i\). To estimate the parameters \(\phi \), we expressed the set of equations in Eq. 1 in matrix form, \({n}^{t+\Delta t}={A}^{t}{n}^{t}\) where the element \({a}_{j,h}\) represents the per capita contribution of individual from pool \(h\) to pool \(j\) in time \(t+\Delta t\). We created the matrix \({A}_{obs}\) by substituting values of \(\psi \) from the posterior distribution of estimates provided by Coulter et al. (2022). We created a matrix of the parameters \(\phi \) by substituting relationships shown in Eqs. 2 and 3 into \(A\) resulting in \({A}_{\phi }\). Finally, we expressed each parameter \({\phi }_{j,h}\) as \({\phi }_{j,h}=\frac{1}{1+{e}^{-{\alpha }_{j,h}}}\) resulting in matrix \({A}_{\alpha }\). We created the loss function \(L\left(\alpha \right)={\text{vec}}\left({A}_{obs}-{A}_{\alpha }\right)^{\prime}{\text{vec}}\left({A}_{obs}-{A}_{\alpha }\right)\), where \({\text{vec}}\left(x\right)\) represents the column vector composed of the columns of the matrix \(x\). The loss function is equivalent to the sum of the squared differences of each element of the matrices \({A}_{obs}\) and \({A}_{\alpha }\). Numerical minimization was used to find the best fitting values the parameters \({\alpha }_{0}\). The standard error of the estimates was calculated from the Hessian matrix of the loss functions evaluated at \({\alpha }_{0}\).

The set of distributions for \({\alpha }_{0}\) was calculated from 1000 random draws from the set of 30,000 samples of the posterior distribution of \(\psi \). The distributions of \(\alpha \) incorporate uncertainty from the estimation of \(\psi \) and the uncertainty from the estimation of \({\alpha }_{0}\). The parameters of the distribution for each estimated using the inverse of the squared standard error of the individual estimates as the weights. The resulting probability distribution function for the estimates of \(\phi \) are,

$$ f\left( x \right) = \frac{{e^{{ - \frac{{\left( {log\left( {\frac{1}{1 - x}} \right) + log\left( x \right) - \mu } \right)^{2} }}{{2\sigma^{2} }}}} \left( {\frac{1}{1 - x} + \frac{1}{x}} \right)}}{{\sqrt {2\pi } \sigma }},\quad \{ x|0 < x < 1\} $$
(4)

where \(\mu \) and \({\sigma }^{2}\) are the mean and variance estimates of \(\alpha \) described above.

As stated above, the time step (\(\Delta t\)) of the movement observations and the parameter t in Eq. 1 is one month. To add recruitment to the model and bring it in line with the time step of stock estimates, we scaled the time step up from a month to a year. We start with the matrix expression of Eq. 1,

$$ n^{t + \Delta t} = A^{t} n^{t} , $$
(5)

where \({n}^{t}\) is the 6 × 1 vector of population values at time \(t\) and \({A}^{t}\) is the 6 × 6 matrix of transition probabilities at time \(t\). With this formulation, the matrix element \({a}_{k,h}\) is the per capita contribution of individuals from pool \(h\) to pool \(k\) at time \(t\).

From Eq. 5, the expression for \({n}^{t}\) can be written as,

$$ n^{t} = A^{t - \Delta t} n^{t - \Delta t} . $$
(6)

Substituting Eq. 6 into Eq. 5 gives the expression for \({n}^{t+\Delta t}\) over the \(2\Delta t\) interval,

$$ n^{t + \Delta t} = A^{t} A^{t - \Delta t} n^{t - \Delta t} . $$
(7)

In Eq. 7, the product \({A}^{t}{A}^{t-\Delta t}\) is a 6 × 6 matrix \({A}^{\prime}\), of which the (\(k,{h}_{th})\) element of is,

$$ a_{k,h}^{\prime} = \mathop \sum \limits_{i = 1}^{6} a_{k,i}^{t} a_{i,h}^{t - \Delta t} . $$
(8)

The recursive substitution of \({n}^{t-i\Delta t}\) by \({n}^{t-(i+1)\Delta t}\) can be continued until for \(i=(0,...,T)\) to give an overall time-step of \(T+1\).

For general development of this model, we use annual time steps but allow demographic parameters to vary seasonally and assumed subpopulation censuses were done in March of every year. Thus, we defined four seasonal transition matrices as \({A}^{w}={A}^{2}{A}^{1}{A}^{12}\), \({A}^{f}={A}^{11}{A}^{10}{A}^{9}\), \({A}^{su}={A}^{8}{A}^{7}{A}^{6}\), and \({A}^{sp}={A}^{5}{A}^{4}{A}^{3}\), where the notation \(\{w,f,su,sp\}\) refers to season {winter, fall, summer, spring} and the number refers to the month (e.g., January = 1, February = 2). Finally, we assume that recruitment into the size class detectable by surveys occurs during summer and varies by pool. Putting these elements together gives,

$$ n^{T + 1} = A^{w} A^{f} \left( {A^{su} + B} \right)A^{sp} n^{T} , $$
(9)

where \(n\) is a vector of population densities for each pool, \(T\) is the year, \(B\) is a diagonal matrix such that \({b}_{kh}=0\) for all \(k\ne h\). Thus, \({b}_{11}\) is the per capita recruitment in pool 1. From here on, when referring to b, we drop one of the indices, (e.g., bkk = bk). The resulting entries in the matrix \({A}^{\prime}={A}^{w}{A}^{f}\left({A}^{su}+B\right){A}^{sp}\) are combinations of the month-based parameters \({\phi }_{kh}\) and the seasonal parameters \({b}_{k}\) that reflect the mixing of the populations among the pools at the shorter time scales. It contains information about both local and metapopulation scale dynamics. For example, at the local scale, \({a^{\prime}}_{kh}\) gives the per capita contribution of an individual in pool h to the population growth rate in pool k the following spring. At the metapopulation scale, the dominant eigenvalue of \(A^{\prime}\) gives the long-term per capita growth rate of the metapopulation and the dominant eigenvector, the stable population distribution across pools (Runge et al. 2006). The elements of \(A^{\prime}\) are too large to present in print, but the code for them are available at https://github.com/schoolmasterd/sigma-matrix.

For each potential location of a deterrent, we estimated four quantities representing the long-term population outcomes and short-term transient effects of the deterrent placement. Transient dynamics are the states that as system moves through as it returns to a stable state after perturbation. Examples of measures of transient behavior include the time it takes the system to settle back to a stable state, and the changes in the distribution of the population among pools during the transient period. We included the effects of transient behavior to account for potential risk from the short-term fluctuations in the spatial distribution of the population among the pools after deterrent placement and before the new, post-deterrent stable distribution is reached. The effects we estimated were: (1) percent change in per capita growth rate at the invasion front (Dresden Island pool), (2) percent change in the metapopulation (river-scale) growth rate, (3) duration of the transient period, and (4) maximum proportion of the river-scale population present at the invasion front during the transient period. Each of these metrics is described in detail below and estimated for silver carp and bighead carp separately.

Effect of movement deterrent on Dresden Island population. Given the model described in Eq. 9 above, the population dynamics of Dresden Island (indicated as pool \(k=1\)) has the form

$$ n_{1}^{T + 1} = \mathop \sum \limits_{h = 1}^{6} a^{\prime}_{1,h} n_{h}^{T} . $$
(10)

Each element, \({a^{\prime}}_{1,h}\) is a mixture of movement rates to adjacent pool \({\phi }_{h,h\pm 1}\) and the unknown recruitment terms \(b=\{{b}_{1},\dots ,{b}_{6}\}\). Equation 10 can be simplified by substituting \({p}_{k}={n}_{k}\text{/}N\), where \(N\) is the total population across all pools. Making this substitution in Eq. 10 gives

$$ n_{1}^{T + 1} = N^{T} \mathop \sum \limits_{h = 1}^{6} a^{\prime}_{1h} p_{h}^{T} = N^{T} {\Lambda }\left( {{\text{p}}^{{\text{T}}} } \right). $$
(11)

The function \(\Lambda \left({x}^{T}\right)\) in Eq. 11 takes in the vector of relative population density at time \(T\) and returns the weighted sum of the per capita contribution of each pool on the growth rate of the Dresden Island population at time \(T\). This form captures both local and river-scale effects of potential deterrent placement, since the \(p\) are also comprised of the elements \(\phi \) and \(b\), and reflect the spatial distribution of the river’s population across pools. The synthesis of local and river-scale information becomes clear if we assume the system has reached its stable spatial distribution, (i.e., \({p}^{T+1}={p}^{T}={p}^{\infty })\) in which case, by construction, \(\Lambda \left({p}^{\infty }\right)={\lambda ^{\prime}}_{1}{p}_{1}^{\infty }\), where \({\lambda ^{\prime}}_{1}\) is the dominant eigenvalue of \(A^{\prime}\), which gives the asymptotic metapopulation growth rate and \({p}_{1}^{\infty }\) is the element of the dominant eigenvector of \(A^{\prime}\) corresponding to the Dresden Island pool (\(k=1\)).

To estimate the asymptotic effect of a deterrent between pools \(h\) and \(h-1\), on the per capita growth rate of Dresden Island, the term \({\phi }_{h,h-1}\) in the pre-deterrent placement matrix \(A^{\prime}\) was replaced by the product \({\alpha \phi }_{h,h-1}\) to create the post-deterrent matrix \(\widetilde{A}\) where \(0\le 1-\alpha \le 1\) is the proportional reduction in movement between pools due to the deterrent. The effect of deterrent placement at each pool boundary was calculated as the percent change in the per capita growth rate at the invasion front: \(\%\mathrm{\Delta \Lambda }=\widetilde{\Lambda }\left({\widetilde{p}}^{\infty }\right)/\Lambda \left({p}^{\infty }\right)-1\), where the tilde indicates the alterations resulting from deterrent placement. Uncertainty in the percent change metric was estimated by resampling from the fitted distributions for the movement parameters. In Online Resource S1 we provide example of the effect of a deterrent at each location on the numerical values in the matrix \(\widetilde{A}\) and the resultant vectors of stable spatial distribution of the population.

As measure of risk, we estimated the local transient effect of the placement of each deterrent. We calculated the spatial distribution of the first 20 years after placement of the deterrent as, \({\widetilde{n}}^{t}={\left(\widetilde{A}\right)}^{t}{n}^{\prime}\) where \(n^{\prime}\) is the normalized dominant eigenvector of the pre-deterrent matrix \(A^{\prime}\), i.e., \(n^{\prime}={w}_{1}/\sum {w}_{1}\) for dominant eigenvector \({w}_{1}\), and the parentheses around \(\widetilde{A}\) are used to indicate that the superscript \(t\) represents an exponent. Deterrent placements that cause an increased, even if transient, proportion of the river-scale population in the Dresden Island pool, represent an increased risk of invasion into the Great Lakes. To capture this risk, we rescaled each vector to sum to one as \({\widehat{n}}^{t}={\widetilde{n}}^{t}/\sum {\widetilde{n}}^{t}\), and recorded the maximum value across all time points (years) corresponding to the proportion of the population in the Dresden Island pool. Finally, we represented this value as the percent change from the corresponding proportion of the stable spatial distribution of the matrix representing the pre-deterrent dynamics, i.e., \({{\%}\Delta {\text{max}} \, \widehat{n}}_{t}={\text{max}}{\left(\widehat{n}\right)}_{t}/{{n}^{\prime}}_{1}-1\), where the \({\text{max}}{\left(x\right)}_{y}\) indicates the maximum values over all values of the index \(y\).

Metapopulation (river-scale) effect of movement deterrents. To estimate the river-scale effect of deterrent placement, we calculated the effect of deterrent placement on the metapopulation growth rate, and the change in the spatial distribution of the population across pools and the length of time for the system to settle into the altered spatial distribution, i.e., the transient period. The effect of deterrent placement on the metapopulation growth rate was calculated as the percent difference in the dominant eigenvalue of the pre-deterrent matrix \(A^{\prime}\) and the post-deterrent matrix \(\widetilde{A},\) i.e., \({\%}\Delta {\widetilde{\lambda }}_{1}={\widetilde{\lambda }}_{1}/{{\lambda }^{\prime}}_{1}-1\). The timescale of the transient period was estimated as \(1/log\left(\uprho \right)\), where \(\uprho \) the “damping ratio” (Caswell 2001) calculated as the ratio of the largest eigenvalues of the post-deterrent matrix to the magnitude of the second largest eigenvalue, \(\rho ={\widetilde{\lambda }}_{1}/\left|{\widetilde{\lambda }}_{2}\right| .\) Our assumption is that shorter transient timescales represent less risk than longer timescales because there is less opportunity for the transient fluctuations to interact with elements of environmental heterogeneity to produce unpredicted dynamics.

We simulated the results of adding a deterrent at a single location that reduced upstream movement rates across the pool boundary for both bighead and silver carp by 50%, while leaving downstream movement rates unaffected. Because the recruitment rates in the pools are unknown, we estimated the effect of the deterrent over a range of recruitment rates, while assuming that the recruitment rate of the three lower pools (Alton, La Grange and Peoria) is equal, i.e. \({b}_{6}={b}_{5}={b}_{4}={b}_{0}\), and the recruitment rate of the tree upper pools is zero, \({b}_{3}={b}_{2}={b}_{1}=0\). In addition to the 50% reduction rate, we simulated other rates to check for non-linearities associated with reduction rate. However, alternative reductions in movement rates did not influence conclusions related to barrier placement (Online Resource S2).

Results

Long-term effect on Dresden Island per capita growth rate. Among the five possible locations evaluated for deterrent deployment, deterrents placed between Marseilles (pool 2) and Dresden Island (pool 1) have the smallest effect on the per capita growth rate of the Dresden Island population. This result is similar for both species, but with slightly more uncertainty in the outcome for silver carp (Fig. 2a). Deterrents placed at any of the boundaries between La Grange and Peoria (\({\phi }_{\mathrm{5,4}}\)); Peoria and Starved Rock (\({\phi }_{\mathrm{4,3}}\)); or Starved Rock and Marseilles (\({\phi }_{\mathrm{3,2}}\)) were the most effective for reducing the growth rate in Dresden Island pool and had similar effects on both species (Fig. 2b–d). Of the three most effective locations, a deterrent between La Grange and Peoria (\({\phi }_{\mathrm{5,4}}\)) showed the least uncertainty in its effect on per capita population growth (Fig. 2d). Deterrents placed between Alton and La Grange (\({\phi }_{\mathrm{6,5}}\)) had little effect on the per capita growth rate of bighead carp in the Dresden Island population but had a similar effect on the per capita growth rate of silver to more upstream deterrents (Fig. 2e). Plotting the effectiveness of deterrents as a function of the (undeterred) movement probability among pools shows that, for both bigheaded carps, deterrents placed where movement probabilities are the lowest are the most effective (Fig. 3).

Fig. 2
figure 2

Percent change in per capita growth rate in the Dresden Island population given a deterrent barrier that reduces the movement probability indicated by the plot label 50%. Results are shown for bighead carp (solid line) and silver carp (dashed line). The grey areas are the 95% confidence interval estimated by resampling. The plot labels present the movement probability that was modified by the deterrent barrier. For example, the plot labeled \({\phi }_{\mathrm{2,1}}\) shows the results of reducing the movement probability from Marseilles (pool 2) to Dresden Island (pool 1) by 50%

Full size image
Fig. 3
figure 3

Average percent change in per capita growth rate in the Dresden Island population as a function of the average per-deterrent placement movement probability for bighead carp (black points and text) and silver carp (gray points and text). Points are labeled with the movement probability

Full size image

Long-term effect on metapopulation (river-scale) growth rate. Overall, deterrents caused a small but positive increase in the per capita growth rate of the population at river-scale (Fig. 4). The effect tends to be larger and more variable for the bighead carp population (Fig. 4, solid lines) than the silver carp population (Fig. 4, dashed lines). Both species show a positive correlation between the percent reduction a deterrent caused to the Dresden Island growth rate and the increase to the metapopulation growth rate. This is because recruitment only occurs in the lower pools. Therefore, deterrents that most effectively prevent upstream movement also concentrate a greater proportion of river-wide population in the pools where recruitment occurs. The deterrent location that presented the best tradeoff of these effects was a deployment between Starved Rock and Marseilles, which caused reduced growth rate in Dresden Island by around 40–45% (Fig. 2b), while only increasing metapopulation by around 0.002% for bighead carp and 0.001% for silver carp (Fig. 4b).

Fig. 4
figure 4

Percent change in river-scale (metapopulation) per capita growth rate given a deterrent barrier that reduces the movement probability indicated by the plot label 50%. Results are shown for bighead carp (solid line) and silver carp (dashed line). The grey areas are the 95% confidence intervals estimated by resampling. The plot labels present the movement probability that was modified by the deterrent barrier. For example, the plot labeled \({\phi }_{\mathrm{2,1}}\) shows the results of reducing the movement probability from Marseilles (pool 2) to Dresden Island (pool 1) by 50%

Full size image

Transient effect of movement deterrent placement. The model predicts that the transient effect of deterrents are short-lived and unlikely to lead to additional risk of invasion into the Great Lakes. While at very low recruitment rates the timescale of transient dynamics could be quite long, especially for silver carp, the timescales shrink quickly with increasing recruitment to level out at about 1.4 years for both species and all deterrent locations (Fig. 5).

Fig. 5
figure 5

Time, in years, for the spatial distribution of the river -scale population to settle into the new stable spatial distribution following deterrent barrier placement that reduces the movement probability indicated by the plot label for bighead carp (solid line) and silver carp (dashed line). The grey areas is the 95% confidence intervals estimated by resampling

Full size image

During the transient period, the maximum proportion of the river-wide population in the Dresden Island pool was less than that of the pre-deterrent conditions for both species, for all potential deterrent locations, and for all recruitment rates (Fig. 6). The magnitude of this effect decreased with the distance downstream that the deterrents were placed.

Fig. 6
figure 6

Percent change of maximum proportion of river-scale population of bighead carp (solid line) and silver carp (dashed line) present in the Dresden Island pool (pool 1) during the transient period following the placement of a deterrent barrier that reduces the movement probability indicated by the plot label. The grey areas is the 95% confidence intervals estimated by resampling

Full size image

Discussion

Placement of a movement deterrent along a river interacts with the species’ demography to cause different consequences on invasion front and population growth rates. The most effective placements resulted in reductions in per capita growth rate at the invasion front of similar magnitude to the local effectiveness of the deterrent at reducing movement (i.e., 50% in this case), while placement at other locations had little effect. Interestingly, the effectiveness at reducing per capita growth rate at Dresden Island, the invasion front, was not directly related to the deterrent’s proximity to the invasion front. A deterrent placed directly below the invasion front was among the least effective at reducing the invasion front per capita growth rate for both bighead and silver carp. In fact, for both bigheaded carps, deterrents placed where movement probabilities are already lowest are, by far, the most effective (Fig. 3). These results could be consequential as behavioral deterrent are not considered to be complete barriers to upstream movement. However, when considered at locations where movements are already low, they may help drive fish passage towards zero, which could have outcomes similar to physical barriers where no fish are able to pass upstream.

One of the potential challenges of the management of this system is that there are multiple invasive species with slightly different movement patterns across the pools. It may have been the case, for example, that the locations of the most effective deterrents differed among species. However, this was not the case. We found that, while the population growth consequences were not identical across all potential deterrent locations, the locations that were most effective for both species coincided (Fig. 2). This result suggests that single management actions, for example the construction and maintenance of a single deterrent, can be highly effective for control of multiple invasive species populations.

Previous work on this system (Coulter et al. 2018b; Erickson et al. 2021) has shown that deterrents could reduce the abundance of bigheaded carp at the invasion front. In theory, this effect could be caused by either a decrease in the river-scale population (metapopulation) or a decrease in the growth rate in that pool (a local effect). These two mechanisms have potential management implications for the rest of the Illinois River. In this work, we have shown that the mechanism for decreased abundance at the invasion front is a decrease in the per capita growth rate of the population. Further, we show that the beneficial local effect at the invasion front from one deterrent location comes with the drawback of a potential increase in the river-scale population. The placement of deterrents should be determined to balance these effects. As mentioned above, this relationship is due to the observed spatial variation in recruitment for these carp species in the Illinois River. To date, recruitment has only been recorded in the three most downstream pools. Thus, any deterrent that effectively reduces upstream movement will result in a larger proportion of the population in the pools where reproduction is possible. However, it is important to note that this effect may be partially or fully mitigated by the concurrent increases in negative density dependence, which is not included in this model.

In addition to the main effects of deterrent placement, we also wanted to quantify any potential risks of each potential deterrent placement location. We did this in three ways, (1) by resampling the estimated variation in movement rates to place an uncertainty envelope around the asymptotic effects, (2) examining model behavior over a range of unknown demographic parameters (i.e., recruitment rates), and (3) examining the transient behavior of the populations in response to deterrent placement. None of these metrics indicate significant risks. However, there are other potential drivers of additional risk that we did not assess, including effects on native species (Snyder et al. 2022), uncertainty in demographic parameters other than movement, spatial variation in recruitment, and variation in demographic parameters across age or size classes (Erickson et al. 2021). While it will likely be worthwhile to incorporate these and other sources into models as data become available, the current analysis suggests that there is likely little risk regarding carp demographics from placement of deterrents in the Illinois River.

The analysis presented here shows results only for a deterrent that reduces cross-boundary movement by 50%. We have conducted analyses with a number of different effectiveness rates and found that, while the results differed quantitatively, the ranked order of population outcomes did not change (Online Resource S2). Thus, the conclusions presented here should be robust for any set of deterrents that reduce local movement equally regardless of placement. However, since the assumptions of purely asymmetric effects on movement and equal effectiveness across space are unlikely to be met, specific estimates of the local effectiveness of deterrents are required to allow an analysis based on this model to support management planning. However, the results of this, and similar modeling efforts, can help managers make difficult decisions regarding invasive species management. Given the limited state of research surrounding deterrents (i.e., mostly mesocosm studies), managers may be especially uncertain about both the benefits of a deterrent as well as the potential costs. The incorporation of modeling results can help reduce uncertainty in decision making and allow for data-driven decision making.