Introduction

Non-native invasive plant species are major threats to ecosystem structure and function (Asner et al. 2008; Hejda et al. 2009; Vitousek et al. 1987; Wilcove et al. 1998). Patterns of invasion result from a combination of species’ traits, propagule pressure and variation in the local environment and surrounding landscape (Eschtruth and Battles 2011; Kumar et al. 2006; Lonsdale 1999). A common research finding is that invasive plant species abundance increases with human-related disturbance and movement of propagules along roads, trails and water ways (Hodkinson and Thompson 1997; Pollnac et al. 2012; Von der Lippe and Kowarik 2007). Establishment rates are lower in intact natural areas (Lonsdale 1999) where disturbance and invasive propagule pressure are generally low (Eschtruth and Battles 2009b), but shade-tolerant invasives can threaten protected natural areas and have detrimental long-term impacts on intact forests (Martin et al. 2009). Understanding the spatial patterns of such invasions is critical for anticipating future changes in forest understory composition. Furthermore, models that predict vulnerability of intact forest can help target locations where control is likely to be warranted and effective.

Species distribution modelling is a common tool for examining species’ responses to environmental conditions (Austin and Meyers 1996; Matthiopoulos et al. 2004; Midgley et al. 2002), but applying it to patterns of invasive species can be challenging. In its most simple form, a distribution model assumes that a species is distributed according to environmental conditions, and that individuals in a population have equal chance of arriving at all locations in a specified study area. However, invasive species are often not in equilibrium with their environment, making species-habitat relationships difficult to detect. The species may be absent from favourable areas because the species has not yet arrived in those locations. Conversely, the species may be present in less favourable areas if they are proximal to an established population and subject to high propagule pressure. Habitat relationships in such ‘pioneer’ regions may differ substantially from regions in which the invasive is already widespread (Albright et al. 2009).

If an invasive species is not well-established across a landscape, there may be residual spatial structure (i.e., autocorrelation in model residuals) in its distribution that is not explained by environmental variables (Henebry 1995; Wagner and Fortin 2005). Residual spatial structure is often considered problematic because it can lead to inflated type I error rates (Cliff and Ord 1981; Lichstein et al. 2002) or erroneous inference on model parameters (Kühn 2007). However, if the spatial environment is sufficiently represented by explanatory variables and the spatial covariance error structure is modelled appropriately to remove spatial autocorrelation from the residuals, inference on model parameters should be correct (Bannerjee et al. 2004; Wagner and Fortin 2005). Importantly, the spatial covariance error structure can also provide insight into biological process (Legendre 1993; Palma et al. 1999). Spatial covariance error structure in an invasive-plant-species model should indicate a lack of equilibrium in species’ distribution in the landscape (e.g. not present in suitable areas) and identify the spatial scale of establishment around a focal source of propagules.

Detecting occurrence is another challenge for distribution modelling of an invasive species early in the invasion process. Sparse occurrences may make field sampling and robust modelling difficult. Existing vegetation survey data (often collected for other purposes) can provide a valuable resource for detecting invasions (Sagarin and Pauchard 2010). The use of existing data sources is becoming more feasible because new statistical methods can test predicted relationships among variables and quantify residual spatial structure even when sampled occurrences are sparse within a large data set (Ibañez et al. 2009; Latimer et al. 2009). In this study, we analyzed vegetation data that were collected in natural plant communities over 7 years across a 16,000-km2 mountainous region to characterize undisturbed plant communities, but in which the presence of a non-native shade-tolerant invasive herb also was recorded. We modeled the species occurrence in these relatively undisturbed plant communities to identify plot- and landscape-level covariates that influence its distribution and to quantify the spatial covariance error structure to make inference on the invasion process.

Our focal species was Microstegium vimineum (Trin.) A. Camus (Japanese stilt grass), a C4 annual grass native to Asia (Barden 1987). It was first recorded in the eastern United States in 1917 (Fairbrothers and Gray 1972) and is now widely distributed (Redman 2008). M. vimineum is highly shade tolerant (Winter et al. 1982) but can establish in both sunny and shady areas (Cheplick 2010) and both disturbed and undisturbed habitats (Huebner 2010a; Martin et al. 2009). Once established, it can become the dominant herbaceous species in invaded areas (Barden 1987; Cole and Weltzin 2005; Redman 2008), altering community composition (Barden 1987; Fairbrothers and Gray 1972), suppressing forest succession (Flory and Clay 2006, 2010), and changing ecosystem processes (Ehrenfeld et al. 2001; Fraterrigo et al. 2011; Kourtev et al. 1998; Strickland et al. 2011). M. vimineum is a prolific seeder (Cheplick and Fox 2011), but seed production is reduced in deep shade relative to high-light environments (Huebner 2010a). Little is known about the dispersal modes of M. vimineum (Warren et al. 2011b), and despite its wide distribution, empirical evidence suggests that it is a poor local disperser (Cheplick 2010; Warren et al. 2011b). At fine spatial scales, it forms dense, discrete patches, and evidence suggests that this pattern is influenced by mid-story canopy cover and soil pH (Cole and Weltzin 2004, 2005). Roadside surveys found M. vimineum to be more common in lower-elevation watersheds with less forest cover and located closer to an urban center (Kuhman et al. 2010), but the extent to which it has penetrated the extensive closed-canopy forests of the region is not known. Given the extensive research results available on environmental factors that influence the establishment and reproduction of M. vimineum, our objectives were: (1) to develop a region-wide explanatory model that included important broad- and fine-scale factors; (2) to quantify the spatial covariance error structure in M. vimineum occurrence that was not accounted for by the environmental variables; and (3) to synthesize our results with previous findings to make inference on the spatial attributes of the invasion process.

The establishment of M. vimineum should be influenced by propagule pressure and suitability of growing conditions for herbaceous species with similar requirements (Eschtruth and Battles 2011). Consequently, we anticipated that the probability of presence would increase with increasing proximity to human vectors for propagules (roads and development) and decrease with increasing intact forest cover. At the scale of this study, we expected invasives to do well in environments where many species of native herbs do well (Lonsdale 1999; Sandel and Corbin 2010; Stohlgren et al. 1999); therefore, we expected a positive relationship between native herbaceous species richness and the probability of presence of M. vimineum (Flory et al. 2011). In particular, increasing soil pH and cation concentrations should facilitate establishment of M. vimineum (Adams and Engelhardt 2009; Peet et al. 1998, 2003). Shading by trees and shrubs is not expected to inhibit the shade-tolerant M. vimineum; however, an increasing local abundance of acidophilic Ericaceae shrubs and associated decreasing pH and soil N availability, and recalcitrant leaf litter (Bloom and Mallik 2006; Clinton and Vose 1996; Horton et al. 2009; Nordin et al. 2001) should correspond with a decreasing probability of presence. Finally, we expected the occurrence of M. vimineum would not be at equilibrium with the environment (e.g. not present in many areas predicted to be suitable), because of its limited dispersal. However, because it is wide spread in the region (Redman 2008), we anticipated a hierarchical invasion process in which infrequent long-distance dispersal to nascent sub-populations was followed by spread via intermediate- and short-distance dispersal (Auld and Coote 1980).

Methods

Study site and data acquisition

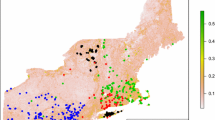
Data for this analysis were collected in the Southern Blue Ridge Province of the southern Appalachian Mountains in western North Carolina, USA (Fig. 1). The region is largely forested and characterized by high topographic variation (250 m–2,037 m asl). We extracted data from the database of the Carolina Vegetation Survey (CVS), which collects comprehensive data to characterise the natural vegetation of the region (Peet et al. 1998, 2005). Sampling plots of the CVS were located in areas that were deemed to represent natural forest cover. At each plot a standardized CVS sampling protocol was conducted in a single plot in which vegetation data were collected from adjacent 10 × 10-m quadrats (Peet et al. 1998). The number of quadrats varied across plots, but most commonly 10 quadrats (1,000 m2) were recorded as a 2 × 5 array. In the data analysis (see below), we accounted for un-equal sampling effort across plots. The presence or absence of M. vimineum was often only recorded at the plot level, and therefore the plot was the experimental unit in this study. We extracted data collected from 1995 to 2001 during which there were 26 occurrences of M. vimineum out of 434 plots that were sampled one time only.

Fig. 1
figure 1

Location of study in western North Carolina in the eastern part of the USA. Vegetation plots are indicated with black dots

Full size image

Plot covariates

Plot covariates were those that were collected by the CVS. At each plot the CVS quantified the native herbaceous species richness, basal area of woody species, and soil conditions. We calculated the mean herb species richness as the mean number of herb species per quadrat. Shrub and tree basal area was the basal area of woody vegetation with a diameter at breast height (dbh) of <5 and ≥5 cm, respectively, divided by the area sampled. The basal area of ericaceous shrubs (Rhododendron spp. and Kalmia spp.) was also extracted separately from the CVS data base and divided by area sampled. Soil pH, and concentrations (parts per million) of calcium, magnesium and manganese were measured in samples collected from the top 10 cm of mineral soil from each sampling quadrat (after removal of litter layer; Peet et al. 1998, 2003). Mean values for each soil chemistry attribute across all quadrats in plot were used in the analysis. While soil chemistry can vary at multiple spatial scales (Ettema and Wardle 2002) we were interested in the relationship between broad-scale patterns in soils and the presence of M. vimineum.

Landscape covariates

Landscape covariates (Table 1) were those derived from GIS data at 30-m pixel resolution and were spatially associated with the CVS data. Elevation, slope and aspect were created from a digital elevation map obtained from the National Elevation Database (Gesch et al. 2002). Aspect was transformed to “southwestness” (sw):

$$ {\text{sw}} = 1/2\,{ \cos }( 20 2- \alpha ) + 1 $$

where α is aspect. This index represents the directional deviation from the sun at the warmest time of the day (Beers et al. 1996). We calculated an insolation index (s):

$$ s = 2\,{ \sin }((\beta / 90) \times 1 80) \times {\text{sw}} - 1 $$

which incorporates slope (β) and the transformed southwestness variable (sw; Gustafson et al. 2003). We created a relative-slope-position index, which was a continuous measure of the height of a pixel relative to its neighbors in a 7 × 7 pixel neighborhood (4.41 ha; Homer et al. 2004). This index varies from 100 if a pixel was on a summit or ridge (higher than all neighbouring pixels), to 0 if it was the lowest in the neighbourhood, such as in a valley.

Table 1 Data elements used in analysis and the minimum, median and maximum non-transformed values
Full size table

We used raster data with a 30-m pixel resolution from the National Land Cover Database (NLCD; Homer et al. 2004) to create variables describing forest cover and human development within 7 × 7 pixel neighbourhood surrounding each plot. We calculated the percentage of pixels with forest cover, impervious surface and human development, and Fragstats (McGarigal and Marks 1995) was used to calculate forest-edge density. Lastly, we used GIS data on roads obtained from the Coweeta Long Term Ecological Research website (http://coweeta.ecology.uga.edu) to quantify road density in m/ha and to calculate distance to nearest road.

Modelling approach

At the core of our statistical analysis was logistic regression, which incorporated overdispersion by including a random error term that allowed for spatial autocorrelation. This was a non-standard approach; therefore we employed a hierarchical Bayesian framework to make inference on a complex dataset in which observations of presence were sparse (Clark 2005). Hierarchical Bayes decomposes complex models into simpler data, process, and parameter sub-models, whose parameters are iteratively estimated conditioned on each other. Inference is exact because it avoids the asymptotic theory of classical statistics, which cannot incorporate complex relationships within a single-level model (see Carlin et al. 2006). This approach allowed us to model robustly the two process models that were the focus of our research questions: probability of M. vimineum presence; and the residual error structure (details below). Bayesian logic incorporates external knowledge or expert opinion of parameter distributions (priors), which are subsequently updated using new data, producing posterior estimates. It is generally not possible to compute the posteriors of hierarchical models analytically, therefore we used Markov chain Monte Carlo (MCMC) to fit the models numerically (Clark 2007, Chap. 7). The MCMC simulation is used to generate random walks (“chains”) through the multivariate target-parameter distributions. Samples are drawn sequentially from sampling distributions, and parameter estimates are conditional on the values of all other parameters. After convergence, the parameter estimates from the MCMC iterations form the posterior parameter distributions, on which we make inference by evaluating summary statistics.

Because of the high number of landscape and plot-level covariates and the inherent multicollinearity, we used principal component analysis (PCA) to reduce the variables to orthogonal axes. The PCA was conducted separately for landscape and plot variables so as to facilitate the differentiation of local and landscape effects on M. vimineum. All plot and landscape covariates were included in the respective PCA analyses. We then explored a set of 11 a priori models to test the effects of landscape (human impacts) and plot (local conditions) variables on M. vimineum presence. The first 10 were composed of all combinations of the first two landscape- and plot-principal-component axes. The eleventh model was an intercept-only model and was included to provide a baseline with which to compare the explanatory strength of the preceding covariate models.

Data analysis

We analyzed the data with a spatial logistic regression. The presence/absence data (y ij ) across plots (i) and years (j) were modelled as a Bernouilli process:

$$ y_{ij} = {\text{Bernouilli(}}\theta_{ij} ) $$
(1)
$$ \theta_{ij} = 1 - (1 - \lambda_{ij} )^{{n_{i} }} $$
(2)
$$ {\text{logit}}(\lambda_{ij} ) = X_{i}^{\prime } \beta + \alpha_{j} + \varepsilon_{i} $$
(3)

where θ ij was the probability of a presence in plot i within one or more sampled quadrats, λ ij was the probability of presence in a single quadrat in plot i, n i was the number of quadrats sampled in plot i, X i β was the product of the environmental covariates and the associated coefficients, α j was a random year effect, and ε i were the spatially structured prediction errors (see below). This modelling approach accounted for differing sampling effort among plots and data obtained from multiple years. Environmental covariates were scaled to have a mean 0 and standard deviation 1, which facilitates comparisons among coefficients estimated in the model. The logit transform was used to constrain the Bernouilli-distributed probability to the range 0–1.

The probability of presence of M. vimineum at any given location was expected to be influenced by the presence or absence of M. vimineum at neighbouring locations (spatial autocorrelation; Ibañez et al. 2009; Latimer et al. 2009; Lichstein et al. 2002). Including ε i in the modelling removes the spatial autocorrelation from the residuals and allows for appropriate inference on the parameters (Bannerjee et al. 2004; Wagner and Fortin 2005). The spatial autocorrelation between pairs of ε i points was expected to decay with distance. We included a standard exponential spatial covariance error structure (C s) to account for spatial autocorrelation not explained by the environmental covariates:

$$ \varepsilon_{i} \sim {\text{MultiVariateNormal(}}0,C_{\text{s}} ) $$
(4)
$$ C_{s} = \sigma^{2} e^{{ - \left( {\varphi d} \right)}} $$
(5)

where σ 2 was the variance, φ was a correlation-distance parameter, and d was the distance between plots (Cressie 1993).

We used weakly informative Cauchy priors with center 0 and scale 2.5 for covariates, and scale 10 for the intercept and year-effect parameters (Gelman et al. 2008). Slightly informative lognormal priors were used for the covariance parameters to obtain proper posteriors (Clark 2007, pp. 410–412): σ 2 ~ logN(3,1); and φ ~ logN(1,1). All parameters were updated with a Metropolis rejection algorithm following Clark (2007, pp. 175–177). Within-chain serial autocorrelation was assessed to determine the appropriate thinning rate. Convergence on the posterior target distribution was confirmed with a scale reduction factor \( (\hat{R}) < 1. 2 \) calculated on 4 parallel chains (Gelman et al. 2004; Gelman and Rubin 1992). Convergence for all models was achieved with 50,000 iterations, and posterior summaries were taken from 4 chains containing 30,000 samples with a thinning rate of 10 (i.e., 12,000 samples). To compare the 11 competing models described above, we used the Deviance Information Criterion (DIC; Spiegelhalter et al. 2002), where low values indicate better model fit than high values. The DIC is a generalisation of the more familiar Akaike Information Criterion (AIC; Akaike 1973; Burnham and Anderson 2002) and is commonly used in Bayesian analysis.

Results

The first 3 axes of the principal components analysis of the landscape variables accounted for 30.8, 19.2 and 12.5 % respectively of the variance (Table 2; Fig. 2a). The first axis largely described the environmental gradient from areas with high human development (buildings, roads, impervious surfaces, and forest edge) to areas with high forest cover and high terrain indices. Axis 2 was dominated by the gradient from high to low southwest aspects and solar indices. Road density was retained in place of distance to nearest road in the PCA as it resulted in a higher proportion of variance explained.

Table 2 Results of principal components analysis of landscape variables, including relative importance of the first 3 axes and the loading values for each variable within the 3 axes
Full size table
Fig. 2
figure 2

First and second axes of the principal components analysis for landscape (a) and plot-level (b) variables

Full size image

The first 3 axes of the principal components analysis of plot variables accounted for 61, 26 and 12 % respectively of the variance (Table 3; Fig. 2b). The PCA performed on the plot-level variables captured the environmental variability resulting from the interactions among soils, herbs and woody vegetation. We found that the PCA model that resulted in the highest proportion of variance explained in the first axes included the variables for mean species richness, Ericaceae shrub basal area, and soil pH. The exclusion of the cation variables was further justified by exploratory data analysis that showed that these variables had no effect on the probability of presence of M. vimineum. Axes 1 and 2 quantified orthogonal gradients from low soil pH with associated high basal area of Ericaceae shrubs to relatively high pH and high mean species richness.

Table 3 Results of principal components analysis of plot variables, including relative importance of the first 3 axes and the loading values for each variable within the 3 axes
Full size table

A preliminary analysis showed that models that included year effects had high DIC values and the 95 % credible intervals (the probability that the true value occurs within the bounds) for random year effects all overlapped zero, indicating a lack of an important contribution. We subsequently removed the year effects from all models. The best model as measured by DIC included the first landscape and plot PCA axes (Model 6; Table 4). The ΔDIC value of the next best model was 16, indicating strong evidence for Model 6 being the best model. The models with the second and third lowest DIC values were uni-variable models that included LandscapePCA1 and PlotPCA1 (Models 2 and 3). The intercept-only model (Model 1) had a ΔDIC value of 243.

Table 4 Models and associated explanatory variables
Full size table

The positive regression parameter for LandscapePCA1 in Model 6 indicates that as forest cover increases (conditions associated with higher elevation, low edge density, low development, etc.), the probability of M. vimineum presence decreases (Table 5). The positive regression parameter for PlotPCA1 indicates that the probability of M. vimineum presence increased with decreasing basal area of Ericaceae shrubs, and increasing soil pH and mean species richness of native species. Model 6 may have the most explanatory power because it captures more completely the influence of both landscape and plot-level environmental factors.

Table 5 Posterior distribution summaries for parameters included in the most explanatory model as assessed by DIC (Model 6)
Full size table

Models 2 and 3 examined separately the effects of landscape and plot-level factors on M. vimineum. The DIC value for the LandscapePCA1 model was lower than that of the PlotPCA1 model, which provides some evidence that landscape factors may be more important in determining the distribution and invasion patterns of M. vimineum throughout the study region. In addition, the LandscapePCA1 parameter estimate was slightly higher than PlotPCA1 in model 6 (Table 5), which indicates greater explanatory strength because the variables were transformed so as to be directly comparable. There was, however, substantial overlap in the credible intervals.

The distance-correlation parameter (φ) provides strong evidence for spatial structure in the data that is not attributable to the environmental covariates (i.e. autocorrelation in prediction errors, ε i ). The inter-plot distances in this study were relatively well distributed across a range from approximately 0.1 to 250 km (Fig. 3a). Inspection of an exponential variogram generated from the posterior distributions of σ 2 and φ indicate that the probability of M. vimineum occurrence was correlated up to a distance of 3 km (Fig. 3b) after accounting for effects of environmental covariates.

Fig. 3
figure 3

a Histogram of inter-plot distances, and b a variogram of residuals of model 3. Median is shown with solid line and 95 % credible intervals are dashed lines

Full size image

Discussion

This study generated insights about the distribution and spread of a non-native invasive grass in natural plant communities of the southern Blue Ridge Mountains and demonstrated a modelling approach that could be useful for other regions and datasets. Microstegium vimineum was infrequent in the CVS data, which were collected as part of a state-wide effort to characterize natural vegetation. Despite the sparse occurrences, we were able to model the species’ distribution and quantify the spatial covariance error structure by using Bayesian techniques. Our analysis revealed that probability of presence was related both to local biotic and abiotic conditions and to landscape context, and the relationships we detected were consistent with those reported in other regions (Honu et al. 2009; Huebner 2010a). The model prediction errors (ε i ; Eq. 3), or the additional variation in the presence/absence data not explained by the covariates, were spatially autocorrelated, which indicates that M. vimineum is not yet at equilibrium in the landscape. Combining our finding that prediction errors were spatial autocorrelated up to 3 km with results from other studies, evidence is emerging that M. vimineum is invading the landscape by a hierarchical process. Long-distance dispersal, primarily along roads (Fig. 4; I), results in new nascent populations that then spread via intermediate- and short-distance dispersal (Auld and Coote 1980; Fig. 4; II and III).

Fig. 4
figure 4

A conceptual model of a hierarchical invasion process. Dots represent established fine-scale clusters of M. vimineum (e.g. 10 m2), and bold lines are roads. Long-distance dispersal events (I) occur infrequently and result in the establishment of nascent populations. Intermediate-distance dispersal events (II) result in sub-populations with an average spatial-aggregation scale of 3 km. Local spread (III) via gravity-dispersed seeds occurs at a slow rate and is not illustrated with an arrow

Full size image

Understanding the results of the spatial modelling of the prediction errors allows inference on the broad-scale invasion process of M. vimineum. All models are imperfect, and this was reflected in this study as incorrect predictions of a presence or absence. We explicitly quantified the prediction error using the ε i term (Eq. 3), which accounts for overdispersion in Bernouilli data and would be independently and normally distributed in a standard non-spatial logistic regression. The absence of M. vimineum from a location predicted by covariates to be highly suitable, and hence a poor model prediction, could be due to various stochastic factors (lack of dispersal to the plot, competition, disturbance, etc.). By estimating ε i for each data point, we effectively quantified the probability of occurrence of unknown and unobserved random events. If the occurrence of random events was independent across all plots, then the prediction error (variation not explained by the covariates) would be due to a non-spatial process (random lack of dispersal, competition, disturbance, etc.) that influences presence or absence. Completely independent prediction errors would indicate that the species has had reasonable opportunity to become established in all sampled locations, as expected for a species at equilibrium in the landscape. However, our estimated value of φ (correlation-distance parameter; Eq. 5) demonstrated spatial dependence in prediction-error values, such that over- and under-predictions respectively were found in close proximity to each other (Fig. 3b). The probability of M. vimineum presence was elevated, above and beyond the influence of landscape and plot covariates, near previously invaded areas and decreased exponentially up to a distance of 3 km. Similarly, the predicted probability of presence was low in very suitable locations if M. vimineum was not established nearby.

Microstegium vimineum has been in the eastern United States since 1917 (Fairbrothers and Gray 1972), and Kuhman et al. (2010) documented this species in 100 % of 25 Southern Appalachian watersheds surveyed and in 84 % of roadside plots. Long-distance dispersal must occur because this species could not otherwise have become so widely distributed, given the slow dispersal rates reported in fine-scale studies (Huebner 2010b; Mortensen et al. 2009; Rauschert et al. 2010). The long-distance dispersal must primarily occur along roads or be associated with human activity (Fig. 4; I) as these are known movement corridors, were important factors in our modelling, and have been ubiquitous in other studies (Cheplick 2010; Christen and Matlack 2009; Cole and Weltzin 2004; Flory and Clay 2006, 2009; Mortensen et al. 2009; Rauschert et al. 2010). The exact mechanism and dispersal kernel for long movements remain unknown (Warren et al. 2011b), and our data were insufficient to shed any light on this process (i.e., we cannot identify likely sources of nascent populations). However, these events must be infrequent and stochastic because efforts to quantify dispersal along roads have demonstrated very slow spread (Huebner 2010b; Mortensen et al. 2009; Rauschert et al. 2010; Warren et al. 2011a).

Following a long-distance dispersal event and subsequent establishment, intermediate-distance dispersal events must also occur to generate the 3-km spatial aggregation pattern suggested by the spatial covariance error structure in our modelling (Fig. 4; II). The mechanism for this dispersal also remains unknown (Warren et al. 2011b) but must be secondary dispersal as M. vimineum seeds generally fall very close to the maternal plant (Huebner 2010b; Rauschert et al. 2010; Warren et al. 2011a). Human activity is likely responsible for intermediate-distance dispersal along roads and trails (Cole and Weltzin 2004; Rauschert et al. 2010). Flooding and water flow paths that intersect a source population also have the potential to move propagules (Mehrhoff 2000; Miller and Matlack 2010; Warren et al. 2011a). While increased deer density accelerates M. vimineum invasion by enhancing local site conditions through herbivory and litter disturbance (Eschtruth and Battles 2009a; Warren et al. 2011a), strong evidence of animal dispersal does not exist (Mehrhoff 2000). The 3-km scale represents the average size of sub-populations and is likely to change over time as the invasive finds its way via intermediate-distance dispersal events to available and suitable locations.

At a local level, slow spread from maternal plants (Fig. 4; III) results in M. vimineum mats under a variety of conditions from roadsides to closed-canopy forests (Cheplick 2010; Cole and Weltzin 2005; Flory et al. 2011; Huebner 2010a). Fine-scale niche limiting factors are likely to constrain the establishment and spread rates (Marshall and Buckley 2008; Warren et al. 2011a, b). In addition, our analyses highlighted the complex and interacting factors operating at the plot level to influence the probability of M. vimineum presence. Similar to many native species, M. vimineum favours more fertile sites (Peet et al. 2003), which are associated with high pH and low basal area of acidophilic Ericaceae shrubs. While evidence exists for an inhibitory shading effect on M. vimineum (Cheplick 2010; Cole and Weltzin 2005), our results suggest that the apparent influence of woody vegetation, which is dominated by Ericaceous shrubs, on the probability of presence is most likely a reflection of the response of M. vimineum to the soil-fertility gradient (see gradient in Fig. 2b).

Our results also indicated that where native richness is high, the probability of M. vimineum presence was greater (see Adams and Engelhardt 2009). High herbaceous species diversity is predicted where growing conditions are favourable and there exists high heterogeneity in essential resources (niche partitioning; Chesson 2000; MacArthur 1970). At very fine scales (generally <1 m), native herbaceous species richness may offer some resistance to the spread of invasives into intact plant communities via competitive interactions for limited resources (Brown and Peet 2003; Sandel and Corbin 2010; Tilman 2004). At broader scales, such as examined in this study (plots ≥100 m2), the high levels of resource heterogeneity due to topography, vegetation, light, and edaphic conditions should be conducive for a shade-tolerant invasive (Stohlgren et al. 2006). Indeed, when M. vimineum invades and is able to achieve dominance, it may reduce native richness (Adams and Engelhardt 2009; Flory and Clay 2010; Hejda et al. 2009), and alter soil chemistry and arthropod communities (Fraterrigo et al. 2011; McGrath and Binkley 2009; Simao et al. 2010). Consequently, some high diversity plant communities in this region could be jeopardized by detrimental impacts of M. vimineum invasions (Barden 1987; Brewer 2011; Cole and Weltzin 2004; Ehrenfeld et al. 2001).

In conclusion, we developed Bayesian models of the distribution of M. vimineum that incorporated landscape- and plot-level factors, and results were consistent with previous studies (among others; Cole and Weltzin 2004, 2005; Honu et al. 2009; Huebner 2010a). This approach allowed us to take advantage of an existing large data set with sparse occurrences, and to model the spatial covariance error structure explicitly. At broad scales, the probability of M. vimineum was elevated in locations surrounded by high levels of human activity with reduced forest cover. At fine scales, presence of M. vimineum was reduced in low soil-fertility sites with dense Ericaceae shrub cover. Because our multi-scale models likely explained most of the variation in M. vimineum presence due to environmental factors, the remaining spatial variance not explained by the covariates allowed for inference on the spatial attributes of the invasion process. Explicit analysis of the spatial covariance error structure suggested that M. vimineum is invading the landscape by a hierarchical process resulting in 3-km spatial autocorrelation of sub-populations (Fig. 4). If a population is detected, extirpation efforts might best be focused within a 3-km radius. However, to manage the invasion of M. vimineum, a better understanding is required of the long- and intermediate-distance dispersal mechanisms and attributes (i.e. dispersal-kernel form; Warren et al. 2011a). Previous research has provided detailed information on fine-scale factors that limit establishment and reproductive capacity (among others; Cheplick 2010; Huebner 2010a; Marshall and Buckley 2008; Warren et al. 2011a, 2012). However, containment or minimisation of its impact on native plant communities will be contingent on understanding how M. vimineum can be prevented from colonizing new suitable habitats. The hierarchical invasion process proposed here provides a framework to organise and focus research and management efforts. Further, the present 3-km scale of aggregation, which is likely to expand if the invasion is not impeded (Welk 2004), provides a bench mark against which efforts to control the invasion can be assessed.