Fitting Procedures for Novel Gene-by-Measured Environment Interaction Models in Behavior Genetic Designs

Abstract

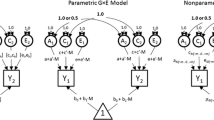
For quantitative behavior genetic (e.g., twin) studies, Purcell proposed a novel model for testing gene-by-measured environment (GxM) interactions while accounting for gene-by-environment correlation. Rathouz et al. expanded this model into a broader class of non-linear biometric models for quantifying and testing such interactions. In this work, we propose a novel factorization of the likelihood for this class of models, and adopt numerical integration techniques to achieve model estimation, especially for those without close-form likelihood. The validity of our procedures is established through numerical simulation studies. The new procedures are illustrated in a twin study analysis of the moderating effect of birth weight on the genetic influences on childhood anxiety. A second example is given in an online appendix. Both the extant GxM models and the new non-linear models critically assume normality of all structural components, which implies continuous, but not normal, manifest response variables.

Appendices

Appendix 1: Likelihood calculation through numerical integration

Adaptive Gauss–Hermite quadrature

In the calculation of a definite integral, even when the formula for the integrand is known, it may be difficult to find an antiderivative which has a closed-form expression. In such circumstances, numerical integration methods are often applied to obtain approximate results. The Gaussian quadrature rule is one of the most widely used numerical integration techniques to approximate the integral of a function $g(x)$ over a specified domain ${\mathcal {D}}$ with a known weighting kernel $\phi (x)$. If the integrand $g(x)$ can be well approximated by a polynomial of order $2k-1$ or less, then a quadrature with $k$ nodes suffices for a good estimate of the integral,

$$\int _{{\mathcal {D}}} g(x)\phi (x)dx \approx \sum _{i=1}^{k} w_i g(x_i).$$

The nodes $x_i$ and weights $w_i$, $i=1,\ldots ,k$, are uniquely determined by the domain ${\mathcal {D}}$ and the weighting kernel $\phi (x)$ (Stroud and Secrest 1966). In the case wherein the integration domain is the real line and the integration kernel is $\phi (x)=e^{-x^2}$, the resulting quadrature rule is known as Gauss–Hermite quadrature (GHQ).

Because of its close relationship to the normal distribution, GHQ is widely used in statistics. Adaptive GHQ (AGHQ) (Liu and Pierce 1994; Naylor and Smith 1982) arises by shifting and scaling the kernel for greater numerical accuracy, strategically placing the nodes $x_i$ to emphasize the areas of greatest mass in the integrand function. The advantages of AGHQ over traditional GHQ are shown in the estimation of latent models with nonlinear random effects by Pinheiro and Bates (1995) and Rabe-Hesketh et al. (2005). In this work, we relocate the nodes according to the easily obtainable location and scale of the normal density. Specifically, if $Y\sim {\mathcal {N}}(m, \sigma ^2)$ and $g$ is a known but complicated function, the expectation of $g(Y)$ can be calculated approximately as

$$\begin{aligned} {\mathbf{E}}(g(Y))&= \int _{-\infty }^{+\infty } g(y) \frac{1}{\sqrt{2\pi }\, \sigma } \exp \left\{ -\frac{(y-m)^2}{2\sigma ^2}\right\} dy \\&= \int _{-\infty }^{+\infty } \frac{g(m+\sqrt{2}\,\sigma x)}{\sqrt{\pi }} e^{-x^2} dx\; \approx \; \sum _{i=1}^k \frac{ w_i \, g(m+\sqrt{2}\,\sigma x_i)}{\sqrt{\pi }}\; , \end{aligned}$$

(10)

using $x=(y-m)/\sqrt{2}\sigma$. Whereas this is not “adaptive” in the strictest sense of Liu and Pierce (1994), we still use AGHQ to represent this technique because of the application of the relocation of nodes.

With regard to numerical evaluation of a multiple integral, a natural way forward is to decompose it into a sequence of nested one-dimensional quadratures and to repeatedly apply (10). Taking integration over domain ${R^p}$, we could use $k_j$ points in the $j$th dimension, $j=1,\ldots ,p$, and obtain a multi-dimensional version of AGHQ. Specifically, if ${\varvec{Y}}$ is a $p$-dimensional random vector which follows a multivariate normal distribution with mean vector $\mathbf{m}$ and covariance matrix $\Sigma$, the expectation of $g({\varvec{Y}})$, where $g(\cdot )$ is now a multivariate function, obtains approximately as

$$\begin{aligned} {\mathbf{E}}(g({\varvec{Y}}))&= \int _{R^p} g({\varvec{y}}) \; \frac{1}{(\sqrt{2\pi })^p \, |\Sigma |^{1/2}} \exp \left\{ -\frac{1}{2}({\varvec{y}}-{\mathbf{m}})^{T}\Sigma ^{-1}({\varvec{y}}-{\mathbf{m}})\right\} \; d{\varvec{y}} \\&= \int _{R^p} \frac{g({\mathbf{m}}+\sqrt{2} \, {\Sigma }^{1/2} \, {\varvec{x}})}{{\pi }^{p/2}} \exp \{-{\varvec{x}}^{T}{\varvec{x}}\} \; d{\varvec{x}} \qquad \quad \Big ( \text {with}\; {\varvec{x}} = \frac{1}{\sqrt{2}} \Sigma ^{-1/2} ({\varvec{y}}-{\mathbf{m}}) \Big ) \\&\approx \sum _{i_1=1}^{k_1} \cdots \sum _{i_p=1}^{k_p} w_{i_1} \cdots w_{i_p} \frac{g({\mathbf{m}}+\sqrt{2}\,{\Sigma }^{1/2}\,{\varvec{x_{(i)}}})}{{\pi }^{p/2}}, \end{aligned}$$

(11)

where ${\varvec{x_{(i)}}} = (x_{1i_1}, \ldots , x_{p\,i_p})^T$; $x_{j1},\ldots ,x_{jk_j}$ are the nodes for the $j$th dimension; and the product $w_{i_1} \cdots w_{i_p}$ is the corresponding weight for node ${\varvec{x_{(i)}}}$.

AGHQ in likelihood calculation

In the application of AGHQ to approximation of likelihood $f(P|M;\theta )$, we incorporate distribution functions from specific models into the integration. We denote ${\varvec{y}} = (A_M,C_M)^T$ to simplify the notation. Because $f(A_M,C_M|M)$ is a multivariate normal density function, we set ${\mathbf{m}}= \text {E}({\varvec{y}}|M;\theta _M)$ and $\Sigma = \text {Cov}({\varvec{y}}|M;\theta _M)$, so that the function specified by $f(P|{\varvec{y}},M)=f(P|A_m,C_M,M)$ plays the role of $g({\varvec{y}})$ in (11). Therefore, we have

$$\begin{aligned} f(P|M; \theta )&= \int _{R^3} \; f(P|{\varvec{x}},M; \theta ) \, \frac{1}{\pi ^{3/2} } \exp \{-{\varvec{x}}^T{\varvec{x}} \} \; d{\varvec{x}} \\&\approx \sum _{i_1=1}^{k_1} \sum _{i_2=1}^{k_2} \sum _{i_3=1}^{k_3} w_{i_1} w_{i_2} w_{i_3} \frac{f(P| {\varvec{x_{(i)}}},M;\theta )}{{\pi }^{3/2}} \ , \end{aligned}$$

where conditional distribution function $f(P|{\varvec{x_{(i)}}},M;\theta )$ is computable for all proposed models from Rathouz et al. (2008).

Appendix 2: Argument options in R package GxM

Model option

We consider both bivariate Cholesky models and bivariate correlated factors models, including Chol, CholGxM, NLMainGxM, CorrGxM, CholNonLin and CorrNonLin. The routines for fitting these models are provided in our ${\mathbf{R}}$ package, GxM. For models that do not admit a closed-form likelihood, we apply numerical integration techniques; for models that have closed-form likelihood, both fitting with closed formula and numerical techniques are provided. All models exploit derivative-free optimization.

Zero set option

This option provides for constraining some parameters to zero, greatly expanding the number of nested sub-models that are available, and allowing testing of specific parameters via likelihood ratio tests or by comparing BIC values. As explained in the Model section, GxM can be detected by testing statistical hypothesis under which certain parameters are zero. We supply an option named “zeroset” to enable users to fit models with chosen parameter(s) constrained to zero.

Initialization and priority option

For optimization problem with high dimensional parameters and non-concave surfaces, it is important to have reasonable and multiple starting points. By setting the non-linear latent terms to zero, all of our proposed models except Model (4) reduce to a common trivial model, and direct parameter estimation such as a method of moment estimator can be applied. This set of estimates serves as a desirable starting point. For Model (4), we use polynomial regression technique to eliminate the main effect of $M$ on $P$. After replacing the original $P$ with regression residuals, the modified model can also be viewed as a case of the common trivial model. For non-linear models, we further add an intermediate update using a small number ($k$ = 3) of AGHQ nodes. Lastly, we provide for the option of leaving the initialization to potential users. With priority level equal to 1, the user-specified initialization would be updated in the intermediate stage. By increasing priority level from 1 to 2, the manually specified initialization would ignore the intermediate update.

AGHQ nodes number option

We provide this option to allow a tradeoff between accuracy and computational intensity. As one may expect, a larger number of AGHQ nodes produces more accurate likelihood values. On the other hand, because the integration is 3-dimensional, the computation cost increases fast.

Parallel computing option

As an interpreted language, the performance of ${\mathbf{R}}$ in terms of computational speed is not as satisfactory as that for compiled languages. This issue is of concern when using computationally intensive numerical integration and derivative-free optimization techniques. Therefore, we embed parallel processing technique in response to the challenge.

Parallel computing with ${\mathbf{R}}$ is directly supported beginning with release 2.14.0. The package parallel provides convenient functions to perform parallel computing in both explicit and implicit modes. For instance, in the calculation of log-likelihood for GxM models, because of the summation over individual observations as $l(\theta ) = \log L(\theta ) = \sum _{i} \log f(M_i,P_i;\theta )$, the global log-likelihood computation can be performed in a parallel manner. Users are provided the option to use parallel computation, and if so the number of CPU cores to allocate the computations.

Appendix 3: Configurations for 23 scenarios

The configurations of simulation settings for 23 scenarios in numerical analysis is shown in Table 6.

Table 6 Configurations of model settings and data generation for 23 scenarios in numerical analysis