Vertical spanning wall elastically restrained at the top: validation and parametric dynamic analysis

Abstract

In unreinforced masonry structures, among the most dangerous events that can occur during earthquakes are the out-of-plane mechanisms. This type of response significantly changes if the wall is restrained by a horizontal element. The collapse, in this case, could take place for slipping/failure of the diaphragm connection or for overturning of the wall, following the formation of a crack at an intermediate height between the base and the top. A specific analytical model is used to capture the complex dynamic behavior of the wall, formed by two stacked rigid bodies (free to rock) with the top one connected to a flexible diaphragm. The model is calibrated using experimental data available in the literature and it is then used to carry out a dynamic parametric analysis. The variation range of relevant parameters refers to the building features surveyed in Emilia-Romagna region, Italy, and their effect on the global response of the system is investigated. Further, the influence of ground motion is considered, using different ground accelerations. The results of the analysis highlight that, for the considered area and return period, the maximum rotations of the system are significant only for large slenderness values. Further, the investigation shows that the diaphragm plays a crucial role in the dynamic response of the system. The stiffness of the diaphragm can significantly reduce the rotations and consequently the risk of overturning. Additionally, the study on the effect of the wall size pointed out how a top spring causes a reverse scale effect.

1 Introduction

Paulay and Priestley (1992) stated that out-of-plane failure for unreinforced masonry (URM) structures is “one of the most complex and ill-understood areas of seismic analysis”. URM structures are particularly vulnerable to out-of-plane mechanisms during earthquakes (Fig. 1) if the connections are inadequate (Andreotti et al. 2015; Lourenço et al. 2011; Al Shawa et al. 2012; Sorrentino et al. 2014), provided that no masonry disintegration takes place (de Felice et al. 2022). However, if the walls are supported by horizontal elements like floors, roofs or tie rods, the response to seismic ground motion can be very different. In these cases, collapse may occur as a result of slipping or failure of the connection to the diaphragm, or due to the overturning of the wall following the formation of a crack at an intermediate height between the base and the top (Bruneau 1994; Moon et al. 2014; Penna et al. 2014). While rigid floors are usually beneficial (Sisti et al. 2019; Sorrentino and Tocci 2008) for the earthquake performance of URM constructions, assuming a rigid top support when assessing the response of out-of-plane mechanisms may not be accurate, particularly in the case of timber diaphragms/roofs or small diameter and large length tie rods (AlShawa et al. 2019; Derakhshan et al. 2023; Ortega et al. 2017, 2018). The height, at which the wall breaks, depends on the ratio between the weight due to the diaphragm and that of the wall. The larger the weight acting at the top, compared to that of the wall, the more the crack moves downwards (Giuffrè 1996).

Fig. 1

Example of out-of-plane failure of URM wall connected to timber diaphragm during the 2012 Emilia, Italy earthquake

Various modelling approaches are employed to capture the out-of-plane response of masonry elements during earthquakes. These include the distinct element method (AlShawa et al. 2017; Chen et al. 2023; Damiani et al. 2023), the finite element method (Vlachakis et al. 2019), simplified static analysis (Casapulla et al. 2019; Sorrentino et al. 2017) and rocking dynamics (Coccia et al. 2023; Giresini et al. 2018a), which is used in this paper. For the case of the vertical spanning wall, when the horizontal diaphragm is not rigid enough, an elastic top restraint must be introduced (Casapulla et al. 2017). This boundary condition delivers a system with two degrees of freedom (DOFs), similar to the one observed in a stack of two bodies that are free at the top, as studied by Psycharis (1990) and Spanos et al. (2001). Therefore, the complexity of the problem increases as four patterns (or rocking modes) are possible. Single-story and two-story one-way spanning walls that are connected to flexible diaphragms were studied by Derakhshan et al. (2013a), who formulated a model disregarding the thickness of the façade. This assumption was also made by Gabellieri et al. (2013) in their study of a single-story URM wall. Derakhshan et al. (2015) developed a three DOFs model to consider both the wall thickness and the deformation of the base diaphragm, emphasizing the strong influence of diaphragm stiffness on the response of the wall.

Moreover, a variety of experimental tests have been conducted to investigate the out of plane behavior of masonry walls during earthquakes (Derakhshan et al. 2013b; Graziotti et al. 2019). Regarding the vertical spanning wall, experimental tests were conducted by Baggio and Masiani (1991) and Doherty et al. (2002) assuming a rigid top restraint and developing analytical models accordingly. Recently, Penner and Elwood (2016) conducted full-scale shaking table tests on five masonry wall specimens connected to a steel frame by elastic springs. The inertia forces on the wall and spring reactions initiate the rocking motion as two rigid bodies, causing a crack to form at a height intermediate between base and top. Hence, multi-rocking-body dynamic (MRBD) models are a reasonable choice to investigate the out-of-plane response of a vertical spanning wall. Previous works highlighted the highly non-linear behavior of MRBD models (Destro Bisol et al. 2023; Prajapati et al. 2022; Psycharis 1990; Spanos et al. 2001), which are formed of stacked rigid blocks, as the vertical spanning wall. The complexity of the model lies in the different patterns that the system can assume during the motion, and in the transition between one and another. For these reasons the MRBD model proposed in Prajapati et al. (2022) required a validation with experimental data, as well as calibration of energy dissipation; the experimental program performed by Penner and Elwood (2016) is used to this purpose. After providing a brief overview of the aforementioned tests, the MRBD model is updated to accurately reproduce the relevant experiments. The main uncertainties of the MRBD model lie in the description of the impacts, hence in the definition of the coefficients of restitution (CORs) for the different types of impact. Here, using a specific optimization algorithm, the analytical post-impact velocities are calibrated in order to reproduce the experimental results using the MRBD model. In this paper, the optimization algorithm procedure is explained as well, and the results of the calibration are presented.

For slender walls connected to a flexible diaphragm, the flexural out-of-plane mechanism is recurrent. These walls can be found mostly as façades in the Emilia-Romagna region of Italy, wherein brickwork is used allowing a smaller wall thickness compared to stonework prevalent in most Italian regions. For this reason, a building portfolio in Emilia is analyzed to derive mean and standard deviation of log-normal distributions of geometrical parameters. Based on these data, the dynamic behavior of a family of vertical spanning strip walls, connected to a flexible diaphragm at the top, is examined. The variation of relevant parameters is investigated, in order to evaluate their effect on the global response of the system. Further, the influence of ground motion is accounted for, using seven natural ground accelerograms compatible with the code site spectrum.

2 Description of the model

The MRBD model proposed in Prajapati et al. (2022) is used as a starting point for the following study. The wall is assumed as an assembly of two rigid bodies and, consequently, the system has two DOFs. The MRBD model explicitly considers the effect of thickness, thus accounting for geometric nonlinearities, allowing the blocks to rock around their lower corners. In the case of two stacked rigid blocks, the system can assume four different configurations or patterns, considering all possible scenarios in which the blocks rotate about different corners (Prajapati et al. 2022; Spanos et al. 2001). The extremely non-linear behavior of the system formed by two rigid rocking bodies requires a comparison with experimental results obtained for similar configurations. In this section, a relevant experimental program is briefly summarized then the MRBD model, updated to account for the test apparatus, is described.

2.1 Description of the experimental program by Penner and Elwood 2016

Penner and Elwood (2016) have performed full scale shaking table tests on five solid clay brick wall specimens, with the aim to simulate the out-of-plane response of unreinforced masonry walls restrained by flexible diaphragms at the bottom and the top. The specimens were connected to a steel frame by coil springs, which could have both equal and different stiffnesses. The inertia forces on the wall and the reactions of the springs initiate the rocking motion of the wall separating it into two rigid bodies, due to a crack at intermediate height. In this experimental program, using a specific test apparatus (Fig. 2), different combinations of boundary conditions were studied. In the case at the hand, only the configuration with a rigid restraint at the base (which allows rotations but not horizontal displacements) and a flexible restraint at the top is considered for the calibration.

Fig. 2

Test apparatus of the experimental program (adapted from Penner and Elwood (2016))

The total height of the tested wall is named ${h}_{tot}$, the length is $L$, the height of the intermediate crack ${h}_{1}$, and the thickness of the wall is $b$. The density of the specimen is denoted by $\rho$, and its total mass is named $m$. The nature of the test required the use of a carriage to connect the springs (whose total stiffness is named ${k}_{d}$) to a steel cap anchored to the top of the wall, which allows the top of the wall to rotate and whose mass is ${m}_{d}$ (Figs. 2, 4). The mass of the carriage, ${m}_{d,p}$ (about 18% of the wall total mass) contributes only as regards the horizontal translation. This element strongly influences the dynamic response of the system and must be considered for the validation of the model. Besides calibration, the addition of the translational carriage to the system allows to capture the response of a configuration where the diaphragm is not resting on the wall and is acting solely as a seismic mass. In practice, this scenario occurs when the diaphragm is parallel to the façade, and only a small portion of the weight is transmitted to the wall as vertical load, while a larger part is transmitted as horizontal load during earthquakes. The geometric and mechanical properties, of the specimen used in the experimental program, are summarized in Table 1.

Table 1 Geometric and mechanical properties of the wall tested by Penner and Elwood (2016)

The specimen was tested using two accelerograms as seismic input: one recorded during the 18 October 1989 earthquake in Loma Prieta, California (USA), at the Gavilan College in Gilroy (NGA0763), and one recorded during the 22 February 2011 earthquake in Christchurch, New Zealand at the Christchurch Hospital (CHHCN01). The test was conducted considering only horizontal acceleration. Although the MRBD model can capture the response to both vertical and horizontal ground motions simultaneously, only the latter was utilized in this study, consistently with the experimental setup. The specimen was subjected to the first record in order to obtain a longitudinal crack between the top and the bottom of the wall, so that two distinct blocks were formed. The tests were then conducted using this configuration, scaling the second accelerogram by 70%, 80%, 90%, 100% (Fig. 3), 110%, and 120% of the natural amplitude, until the wall collapsed. For the purposes of this study, only the tests where the crack in the wall was already present are considered.

Fig. 3

CHHCN01 accelerogram used in the tests by Penner and Elwood (2016)

2.2 Formulation of the updated model

As previously mentioned, the test required the use of a heavy carriage to connect the springs to the top of the wall. The MRBD model developed by Prajapati et al. (2022) does not account for this translational mass ${m}_{d,p}$, hence it must be modified in order to consider this additional element (Fig. 4). Accordingly, the kinetic energy T assumes the form:

$$T = { }\mathop \sum \limits_{i = 1}^{2} \left[ {\frac{1}{2}\left( {m_{i} \left| {{\mathbf{v}}_{Gi} } \right|^{2} + I_{Gi} \dot{\theta }_{i}^{2} } \right)} \right] + { }\frac{1}{2}m_{d} \left| {{\mathbf{v}}_{C} } \right|^{2} + { }\frac{1}{2}m_{d,p} v_{C,x}^{2} \quad {\text{where}}\;\left| {\mathbf{v}} \right| = \sqrt {v_{x}^{2} + v_{y}^{2} }$$

(1)

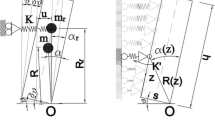
where ${m}_{i}$ is the mass of the i-th body, with $i$ = 1 or 2 makes reference to the lower or the upper body respectively, ${I}_{Gi}$ is the polar inertia moment of the i-th body about its center of mass ${G}_{i}$, ${\mathbf{v}}_{Gi}$ and ${\mathbf{v}}_{C}$ are respectively the velocity vectors of the i-th center of mass and of point $C$ where the diaphragm mass is applied (Fig. 4), ${\dot{\theta }}_{i}$ is the angular velocity. Additionally, if the system is moving in pattern 3 (Fig. 4), the center of mass is determined by considering the system as monolithic (with the lower and upper bodies joined) and is denoted as $G$.

Fig. 4

Model of the vertical spanning wall elastically restrained at the top with a top translational mass, and possible negative motion patterns. Patterns 1a, 2a, 3a, and 4a (not shown) are reversed in relation to their counterparts (1b, 2b, 3b, 4b), meaning that the blocks have opposite rotations around the opposite corners

The carriage mass acts only in the horizontal direction; hence, the potential energy is not updated and remains in the same form proposed by Prajapati et al. (2022). Differently, the non-conservative forces must consider the additional mass ${m}_{d,p}$; to this purpose the virtual work $W$ assumes the form:

$$W = - \ddot{x}_{g} \left( {\left( {m_{d} + m_{d,p} } \right)s_{C,x} + \mathop \sum \limits_{i = 1}^{2} m_{i} s_{{G_{i} ,x}} } \right) - \ddot{y}_{g} \left( {m_{d} s_{C,y} + \mathop \sum \limits_{i = 1}^{2} m_{i} s_{{G_{i} ,y}} } \right)$$

(2)

where ${s}_{C}$ is the displacement vector of point C, ${s}_{{G}_{i}}$ is the displacement vector of the i-th center of mass, ${\ddot{x}}_{g}$ and ${\ddot{y}}_{g}$ are the horizontal and vertical components of the seismic ground acceleration, respectively. Scalar components of vectors make reference to $x$, $y$ axes in Fig. 4.

As mentioned, during the motion of the system a pattern change can occur for two reasons: (a) sudden accelerations; (b) impacts. In the first case the carriage translational mass has a strong influence, hence the detection of this pattern change must be properly updated. To detect this type of pattern change, it is necessary to determine a threshold acceleration. To this purpose, it is necessary to compare the internal moment ${M}_{I}$, which typically stabilizes the bodies, with the external moment ${M}_{E}$, which tends to overturn the bodies. Also in this case, the procedure to determine the threshold acceleration follows that proposed by Prajapati et al. (2022), although some modifications are necessary. The external moment formulated to consider the top carriage mass assumes the form:

$${M}_{E}=\sum_{i=1}^{2}{m}_{i}\left({\mathbf{p}}_{{G}_{i}O}\times {\mathbf{a}}_{{\text{E}}}\right)+ {m}_{d}\left({\mathbf{p}}_{CO}\times {\mathbf{a}}_{E}\right)+ {m}_{d,p}\left({\mathbf{p}}_{CO}\times {\mathbf{a}}_{E,tc}\right)+{\mathbf{p}}_{CO}\times {\mathbf{f}}_{E}$$

(3)

where $\times$ is the vector product operator, ${\mathbf{p}}_{{G}_{i}O}$ and ${\mathbf{p}}_{CO}$ are the position vectors of the center of mass of the i-th body and of point C (with respect to the generic center of rotation O) respectively, ${\mathbf{a}}_{E}$ and ${\mathbf{f}}_{E}$ are the external acceleration vector and the external forces vector respectively (Prajapati et al. 2022), and ${\mathbf{a}}_{E,tc}$ is the updated external acceleration vector relative to the carriage mass:

$${\mathbf{a}}_{E,tc}=\left\{-{\ddot{x}}_{g} , 0, 0 \right\}$$

(4)

The internal moments are also calculated using the same procedure as in Prajapati et al. (2022), computing the normal and tangential acceleration vectors (for each mass), but introducing the effect of the carriage mass. To this end the acceleration vector ${\mathbf{a}}_{CR,tc}$ relative to the top carriage mass is calculated by summing the $x$ components of the normal and tangential acceleration vectors (relative to the point $C$, where the mass is located) and neglecting the $y$ components of these vectors:

$$\begin{array}{c}{\mathbf{a}}_{CR,tc}=\left\{{a}_{CR,n,x}+{a}_{CR,t,x} , 0, 0 \right\}\end{array}$$

(5)

The internal moment that considers the top carriage mass is computed as follows:

$${M}_{I}={I}_{{G}_{2}}{\ddot{\theta }}_{2}+{m}_{i}\left({\mathbf{p}}_{{G}_{2}O}\times {\mathbf{a}}_{{G}_{2}R,n}+{\mathbf{p}}_{{G}_{2}O}\times {\mathbf{a}}_{{G}_{2}R,{\text{t}}}\right)+ {m}_{d}\left({\mathbf{p}}_{CO}\times {\mathbf{a}}_{CR,n}+{\mathbf{p}}_{CO}\times {\mathbf{a}}_{CR,t}\right) + {m}_{d,p}\left({\mathbf{p}}_{CO}\times {{\varvec{a}}}_{CR,tc}\right)$$

(6)

where ${\ddot{\theta }}_{2}$ is the angular acceleration of the upper body, ${\mathbf{a}}_{{G}_{2}R,n}$ (${\mathbf{a}}_{CR,n}$) and ${\mathbf{a}}_{{G}_{2}R,t}$ (${\mathbf{a}}_{CR,t}$) are respectively the normal and the tangent acceleration vectors of point ${G}_{2}$ ($C$) that rotates about the generic point $R$.

Once the governing equations are modified in order to take into account the carriage mass used during the tests, the updated MRBD model can be calibrated using the results of the experimental program by Penner and Elwood (2016).

3 Calibration

Impacts of rigid bodies are a complex phenomenon that involves intricate relations between energy dissipation, momentum transfer, elastic and plastic deformation, impact velocity and body geometry (Meriam and Kraige 2001). For these reasons, the greater uncertainties in the MRBD analytical model relate mainly to the dissipation of energy following an impact (ElGawady et al. 2011; Sorrentino et al. 2011). This loss of energy is expressed as a loss of angular velocities of the blocks after the impact. The analytical post-impact velocities, ${\dot{\theta }}_{i,an}^{+}$, are those calculated in Prajapati et al. (2022). Here, with the aim to improve the agreement between the experimental results and the response of the MRBD model, these analytical velocities are calibrated. Using additional scalar coefficients ${C}_{l}$ (for the $l$-th pattern change), the calibrated angular velocity, ${\dot{\theta }}_{i,cal}^{+}$, can be obtained as follows:

$${\dot{\theta }}_{i,cal}^{+}={C}_{l } {\dot{\theta }}_{i,an}^{+}$$

(7)

The two bodies moves together in the Penner and Elwood (2016) low-amplitude tests, although in some circumstances differences between the rotations of the two blocks are observed. This behavior does not allow to estimate all the ${C}_{I}$ coefficients, because not all the pattern changes occurred during the available tests. Further, another parameter that influences the experimental response, and on which there are some uncertainties, is the position of the hinges at the base of each body. Because the compressive strength of the masonry specimen is finite, during the rocking motion the corner of the wall tends to crush reducing the i-th base width from $b$ to ${b}_{i}$. Regarding the lower body, the width reduction was equal to 20 mm as available within the published documentation (Penner and Elwood 2016), hence delivering ${b}_{1}$ = 291 − 20 = 271 mm. Concerning the upper body this information was not available, however, given the crack position ${h}_{1}$ and the presence of the mass ${m}_{d}$ at the top, half of the previous value can reasonably be assumed, hence delivering ${b}_{2}$ =291 − 10 = 281 mm. The calibrated coefficients ${C}_{l}$ reported in the following were applied to a model having a base reduction equal to 50 and 150% of the previous values obtaining again a very good match of the experimental time histories.

3.1 Differential evolution algorithm for calibration

Calibration proved to be challenging. The first reason lies in the complexity of the test apparatus, the second in the several ${C}_{l}$ coefficients to be estimated in order to calibrate the analytical model with experimental data. The use of a specific optimization algorithm was necessary. To this scope, a differential evolution algorithm proved to be effective (Carboni et al. 2015, 2018; Worden and Manson 2012). This algorithm is part of the evolutionary optimization procedures family: a population of possible solutions (in this case the vector of coefficients ${C}_{l}$) is iterated in such a way that succeeding generations of the population contain better solutions to the problem, in accordance with the Darwinian principle of ‘survival of the fittest’. The problem was framed here as a minimization of the weighted mean error (WME) between the measured data and that predicted results (in terms of rotation over time):

$${\text{WME}}\left({C}_{1},{C}_{2},{C}_{3},{C}_{4},{C}_{5},{C}_{6},{C}_{7},{C}_{8}\right)=\sum_{i=1}^{2}\frac{{\int }_{0}^{t}\left|{\theta }_{i,exp}-{\theta }_{i,num}\left({C}_{1},{C}_{2},{C}_{3},{C}_{4},{C}_{5},{C}_{6},{C}_{7},{C}_{8}\right)\right|}{\underset{0}{\overset{t}{\int }}\left|{\theta }_{i,exp}\right|}$$

(8)

where ${\theta }_{i,exp}$ and ${\theta }_{i,num}$ are the rotations (for the lower and upper block) obtained from the experiment and from the MRBD model respectively, and $t$ is the time.

To improve the efficiency of the algorithm a range of values, in which the coefficients ${C}_{l}$ can vary (Eq. 9), must be defined. Based on a first trial parametric study, a range of values is defined for each coefficient (Table 2). The upper bound of this range has been found to be greater than one for the pattern change from 1 to 2 and from 2 to 1. This assumption is considered acceptable because such a value does not necessarily indicate a calibrated post-impact velocity larger than the pre-impact velocity, whereas it just implies a calibrated post-impact velocity that exceeds the analytically determined value. Moreover, contrary to what Housner (1963) observed for a single rigid block, for two stacked blocks Psycharis (1990) and Destro Bisol et al. (2023) reported a post-impact velocity larger than the pre-impact velocity for a part of the system. In this study, post-impact velocities larger than pre-impact velocities were more frequently observed for impacts between the two blocks (middle impacts).

$$\begin{array}{c}{C}_{l}\in \left\{{\beta }_{0,l} ; {\beta }_{f,l}\right\}\end{array}$$

(9)

where ${\beta }_{0,l}$ and ${\beta }_{f,l}$ are the lower bound and the upper bound of the range, respectively.

Table 2 ${C}_{l}$ parameters for pattern change: range and best-fit values

The procedure of the differential evolution algorithm (Fig. 5) can be summarized as follows: (a) the first-generation matrix ($r$ rows, $c$ columns) is built; in this case, each row (r = 8) corresponds to a specific ${C}_{l}$ coefficient representing a pattern change, while each column (c = 21) corresponds to a distinct value that the ${C}_{l}$ coefficients can assume. These values are linearly spaced within the range of $\left\{{\beta }_{0,l} ; {\beta }_{f,l}\right\}$, and subsequently, their order is randomly permutated (without repetitions); (b) the target vector ${\mathbf{T}}_{AV}$ is selected; (c) the vectors $\mathbf{A}$, $\mathbf{B}$ and $\mathbf{C}$ are picked randomly (without repetitions); (d) the mutation operation is performed to obtain the mutation vector ${\mathbf{M}}_{V}$ = $\mathbf{C}$  + $F$($\mathbf{A}$ − $\mathbf{B}$), in which the constant $F$ is assumed equal to 0.9 (Carboni et al. 2015). It is important to notice that during the calculation of the mutation vector, the boundaries ${\beta }_{0,l}$ and ${\beta }_{f,l}$ (Table 2) can be exceeded: in this case the value is set equal to the closest boundary (Carboni et al. 2021); (e) the crossover operation is performed by selecting the parameter ${R}_{CR}$ randomly between 0 and 1; (f) based on the parameter ${R}_{CR}$ one component between the target vector and the mutation vector is selected (operations (d) and (e) are iterated for $r$ times to assemble the trial vector${\mathbf{T}}_{RV}$); (g) the vector characterized by the lowest cost (lowest WME in this case) between the trial vector ${\mathbf{T}}_{RV}$ and the target vector ${\mathbf{T}}_{AV}$ is selected to build the j-th column of the last generation matrix (operations b, c, d, e, f and g are iterated for $j =1, 2, \dots , c$ to complete the last generation matrix). The entire procedure can be iterated (updating the initial matrix with the last generation one) until the results are converged.

Fig. 5

Flowchart of the differential evolution algorithm procedure

This algorithm is used to calibrate the model for each time history separately, and the convergence of the numerical solution with the experimental data is obtained for each record. The convergence is estimated by comparing the sum of the WME (Eq. 8) obtained for each vector in the last generation matrix with that obtained using the first generation matrix. The last generation matrix is then treated as the 'first' and the differential evolution algorithm is applied once more. This process is repeated iteratively until the sum of the WME converges (Fig. 6).

Fig. 6

Convergence of the differential evolution algorithm for different CHHCN01 scaled records

Once convergence is obtained for all the scaled records separately, the vectors must be compared to find the optimal solution. To this purpose the cosine similarity is used (Dinani et al. 2021):

$$\begin{array}{*{20}c} {sim\left( {h,k} \right) = \frac{{h_{n}^{T} k_{n} }}{{| {h_{n} } |\space | {k_{n} |} }}} \\ \end{array}$$

(10)

where ${h}_{n}$ and ${k}_{n}$ are the two generic vectors for which the level of similarity is estimated.

All the vectors contained in the last generation matrices (for which the differential evolution algorithm converged) are compared using Eq. (10) to find the optimal solution for all input signals. Each vector undergoes a comparison with all the others, resulting in a vector that contains the “best fit” ${C}_{l}$ coefficients (Table 2). This vector is identified as the one with the highest sim values across all six scaled records. Further, this vector contains the coefficients (to be applied to the analytical post-impact velocities) for every possible pattern change that was possible to detect in the experiments.

After deriving the optimal coefficients ${C}_{l}$ for each scaled signal separately, a single set of these coefficients (Table 2), which are valid for every accelerogram, is derived using the cosine similarity. The response of the updated MRBD model, with the post-impact velocities opportunely calibrated using the best-fit coefficients in Table 2, is compared with the outcomes of the experimental program (Figs. 7, 8). These best-fit coefficients are also used for the parametric study in the subsequent section. The results obtained with the calibrated MRBD model are first compared with the experimental data related to accelerograms scaled at 70% (Fig. 7a) and at 80% (Fig. 7b) of natural amplitude. The comparison highlights the agreement between experimental and numerical data, in tests wherein the wall moves mostly monolithically. Similar considerations to the previous case can be made for the accelerogram scaled at 110% (Fig. 8a): also in this instance the wall tends to move monolithically and the numerical results have good agreement with the experimental data. In the last test performed by Penner and Elwood (2016) the wall was subjected to the accelerogram scaled at 120% until overturning occurred (Fig. 8b). In the final phase of the test the intermediate crack opened, and the two portions of the wall started to move with different rotations: also in this stage the calibrated MRBD model was able to capture the failure mechanism obtained in the test (Fig. 8b).

Fig. 7

Comparison between the experimental data by Penner and Elwood (2016) and the predicted results obtained using the updated MRBD model: a record scaled at 70%; b record scaled at 80% of natural amplitude

Fig. 8

Comparison between the experimental data by Penner and Elwood (2016) and the predicted results obtained using the updated MRBD model: a record scaled at 110%; b record scaled at 120% of natural amplitude

Model update and calibration proved to be challenging, but this necessity is demonstrated comparing the numerical results obtained using the validated MRBD model with the response of two different configurations (Fig. 9): (a) MRBD model updated but not-calibrated, hence calculating the post-impact velocities analytically (${C}_{l}$ = 1); (b) MRBD model not-calibrated (${C}_{l}$ = 1) and not-updated, hence the mass of the carriage m_d,p is lumped and included in m_d. The responses of the different models are compared using the scaled time histories (Penner and Elwood 2016) employed for the validation study in Figs. 7 and 8. The response to the accelerograms scaled at 70 and 80% (Fig. 9a and b, respectively) pointed out that using the analytical post-impact velocities the dissipation of the system decreases, and rotations generally increases especially when the system is moving monolithically (Pattern 3). It is also noticeable that in configuration b, where the total mass acts in both vertical and horizontal directions, the middle crack is less prone to open (Fig. 9b). Indeed, the mass contributing also to the vertical direction provides a stabilizing effect, while if the mass acts only in the horizontal direction, the crack is more prone to open (consequently the two blocks move differently, hence in Patterns 1 and 2).

Fig. 9

Comparison between the numerical results obtained using the updated calibrated model, the updated not-calibrated model, and the not-updated not-calibrated model; record scaled at: a 70%; b 80%; c 110%; d 120% of natural amplitude

Similar observations can be made for the ground motions scaled at 110 and 120% (Fig. 9c, d). In this case, as well, the motion starts in Pattern 3 for all configurations. As the amplitude increases, the crack tends to first open in the updated not-calibrated model (configuration a), followed by the not-updated not-calibrated model (configuration b). Similarly, this trend is observed for collapse, with overturning occurring first in configuration a and subsequently in configuration b. The updated calibrated model, in comparison to the previous configurations, generally exhibits smaller rotations. Indeed, collapse occurs only under the signal scaled at 120% (Fig. 9d) and only after the systems in configurations a and b have already overturned. In conclusion, it can be stated that the calibrated post-impact velocities substantially increase the damping of the system during impact, particularly when the system is moving monolithically (pattern change from 3a to 3b). Further, an effect of model update is observed: the translational mass strongly influences the response, as the vertical stabilizing effect of the mass vanishes.

In this study, the analytical post-impact velocities (Prajapati et al. 2022) can be assumed as multiplied by ${C}_{l}=1$, while the calibrated post-impact velocities are equal to the analytical velocities multiplied by ${C}_{l}\ne 1$ (Eq. 7). These coefficients are usually smaller than 1 (Table 2), indicating that the real system generally dissipates more energy than the analytical one. The only exception is ${C}_{2}$ which is larger than 1 for the reasons previously illustrated. These observations align with the previous comparisons (Fig. 9), where the not-calibrated configurations exhibited larger rotations and smaller dissipation. This behavior was particularly evident when the system was moving monolithically, hence for the pattern change from 3a to 3b (or vice versa), where in the calibration process the analytical post-impact velocity is reduced by a factor ${C}_{6}$ = 0.76. In general, it can be noted that the analytical post-impact velocities are substantially larger than the calibrated values for pattern changes resulting from impacts between the lower block and the ground. However, the calibrated post-impact velocities are closer to the analytical values for impacts between the two blocks at the crack interface.

4 Parametric study

In this section, the calibrated MRBD model is used to explore the response of a vertical spanning wall elastically restrained at the top when subject to earthquakes. The mechanical and geometrical characteristics used in the following analysis are derived from existing buildings in order to investigate the response of “real life” façades.

4.1 Input data for the analysis

For a slender façade connected to a diaphragm, the flexural out-of-plane mechanism is recurrent. These façades are more common in Emilia-Romagna compared to other regions of Italy, because in the former brickwork is used due to the prevalence of alluvium soil and the lack of natural stone. A building portfolio located in Emilia (52 façades) is analyzed to derive mean and standard deviation of a log-normal distribution of geometrical parameters (thickness, $b$, and slenderness, ${h}_{tot}/b$) as well as floor-to-total (floor + wall), ${m}_{tot}$, mass ratio (Table 3).

Table 3 Relevant parameters values corresponding to lognormal mean, μ, and standard deviation, σ

Two façade configurations are possible (Fig. 10): (1) the floor is perpendicular to the façade, the beams rest on the façade, and therefore 50% of the mass of the floor acts both as a gravity mass and a seismic mass; (2) the floor is parallel to the façade, and therefore only a conventional 10% of its mass develops a vertical force on the façade, while 50% will act as a seismic mass (i.e. it will only be able to translate in the horizontal direction). This latter percentage assumes that half of the seismic mass is loading the transverse walls, while the other half loads unilaterally the façade under investigation. It is worth mentioning that Derakhshan et al. (2015), based on the analytical modeling of the diaphragm as a single degree of freedom system whose stiffness is determined by the in-plane shear behavior of the floor (Giongo et al. 2014), suggest an 8/15 $\approx$ 53% value, reasonably close to the one assumed here.

Fig. 10

Floor configurations: perpendicular to the façade (left); parallel to the façade (right)

Floor orientation substantially influences the stiffness as well. The literature collection in Giresini et al. (2018b), accounting for 15 stiffness values of the two floor orientations, was used to compute the mean and standard deviation values in Table 3. The model already assumes the crack position at ${h}_{1}$, therefore the model cannot be used to predict the first onset of damage. An equation to predict the crack position as a function of superimposed load and tensile strength of the masonry, but assuming a rigid diaphragm, was proposed by Sorrentino et al. (2008). Here existing literature (ABK 1981; Dazio 2008; Derakhshan et al. 2013b; Meisl et al. 2007; Penner and Elwood 2016; Simsir et al. 2004), accounting also for flexible diaphragms, was used to derive a log-normal distribution of ${h}_{1}/{h}_{tot}$ and hence the three values in Table 3. Given the assumed location, unreinforced masonry is made of fired clay bricks and lime mortar. The corresponding compressive strength $f$ is derived from the commentary to the Italian building code (2019). Data from Ferretti et al. (2019) on units and mortar implemented in the Eurocode 6 (2005) formula. The compressive strength determines the position of the corner about which the block will rock, because masonry crushing moves the hinge inwards. To estimate the indentation of this hinge, a rectangular stress distribution is assumed in the following, with amplitude equal to 85% of compressive strength.

As input, seven natural accelerograms (Table 4) compatible (in the range of periods between 0.15 and 2.00 s) with the Italian building code spectrum (NTC 2018) for a return period of 475 years and a soil type C located in the municipality of Mirandola are used (Fig. 11). The code REXEL was used for record selection (Iervolino et al. 2010). Observing Table 4 it is possible to notice that records 1 and 2 belong to the same event, as well as records 3 and 4 belong to another event. Additional analyses, not shown here for the sake of conciseness, computed assuming two other accelerograms recorded during different events have shown similar results with a slightly reduced record-to-record variability.

Table 4 Suite of accelerograms compatible with the seismicity of Mirandola (Emilia-Romagna, Italy)

Fig. 11

Elastic response spectra compatible with the code spectrum of Mirandola (Emilia-Romagna, Italy), return period of 475 years and soil type C

4.2 Description of the parametric analysis

A parametric analysis was carried out with the goal of determining the impact of each system parameter on the dynamic response. The parametric analysis is carried out by defining a reference façade for both configurations (perpendicular floor and parallel floor), whose geometric and mechanical characteristics are obtained from the mean values of Table 3. Then, for each parameter, the response of the reference façade is evaluated for three cases: (1) Reference façade with the parameter of interest equal to the mean value minus the standard deviation; (2) Reference façade with the parameter of interest equal to the mean value 3) Reference façade with the parameter of interest equal to the mean value plus standard deviation. For each case, the response of the façade is evaluated as the slenderness (${h}_{tot}/b$) varies. As will be shown in the following, slenderness mildly affects the results unless it becomes rather large. To evaluate the effect of the different input record, the response of each case is studied for the seven accelerograms mentioned above and the median maximum normalized rotation is assumed as the final value reported in the plots of the parametric analysis. Hence, for each reference case, 189 dynamic analyses are performed. Because of the four possible patterns (Fig. 4), the rotations are normalized with respect to the slenderness angle of the corresponding body (${\alpha }_{1}$, ${\alpha }_{2}$) or with slenderness angle of the uncracked wall ($\alpha$).

4.3 Effect of the geometrical and mechanical characteristics of the façade

The parametric study on the thickness $b$ of the façade (Fig. 12), pointed out that, especially for slender walls, the contribute of the flexible diaphragm produces a reverse scale effect (Fig. 13): the bigger the wall the less relevant the role of the diaphragm because the inertia forces increase while the elastic top force remains constant. In the configuration where the floor is parallel to the façade, this phenomenon is amplified. Moreover, the floor parallel to the façade configuration involves much larger rotations, a trend that will be observed systematically, sometimes more markedly, also while investigating other parameters and that is related both to the lack of a stabilizing mass and of a lower stiffness of the floor (Table 3). Further, it is important to notice that, for the considered area and return period, the maximum rotations of the system are significant ($\uptheta /\alpha$ > 0.05) only for large slenderness values.

Fig. 12

Median, over seven accelerograms, of the maximum absolute non-dimensional rotations for bottom and upper bodies, varying floor orientation with respect to façade, slenderness, façade size (Fig. 13)

Fig. 13

Schematic representation of the reverse scale effect

Further, the façade is assumed to be cracked, and the effect of the height of this crack is investigated. The parametric analysis highlighted that (Fig. 14): (1) the rotations are larger when the height of the crack is larger; (2) the rotations of the upper body are usually smaller than the rotations of the lower body. This behavior reverses itself when increasing the slenderness and it is particularly evident in the configuration of floor parallel to façade. Rotations of façades are about five times larger when the floor is parallel to the façade.

Fig. 14

Median, over seven accelerograms, of the maximum absolute non-dimensional rotations for bottom and upper bodies, varying floor orientation with respect to façade, slenderness, intermediate hinge position

The crushing of the masonry in the corners of the façade, during the rocking motion, depends on the compressive strength of the material. The parametric analysis on this parameter (Fig. 15) pointed out that lower compressive strength is generally associated with higher rotations. However, it must be underlined that the influence of this parameter is rather negligible.

Fig. 15

Median, over seven accelerograms, of the maximum absolute non-dimensional rotations for bottom and upper bodies, varying floor orientation with respect to façade, slenderness, masonry compressive strength

4.4 Effect of the diaphragm characteristics

The effect of the diaphragm stiffness is also investigated. For the configuration where the floor is assumed perpendicular to the façade, the parametric analysis (Fig. 16) highlighted that to an increase in stiffness is associated a decrease in terms of rotations. This trend is usually true also for the configuration where the floor is assumed parallel to the façade, although for extremely slender façades the benefic effect of this contribution is true only for very stiff diaphragms.

Fig. 16

Median, over seven accelerograms, of the maximum absolute non-dimensional rotations for bottom and upper bodies, varying floor orientation with respect to façade, slenderness, floor stiffness

The façade is subjected to vertical and horizontal forces, the former is related to all the masses that are directly supported by the façade, the latter are due to all the masses that act in the horizontal direction (active only during seismic motion, either because supported in the vertical direction or because transferring earthquake inertia forces to the façade). When the floor is assumed to be perpendicular to the façade, the parametric study aims to evaluate the influence of the mass directly supported by the façade (Fig. 17 left). In this case, an increase in maximum rotations is generally observed with an increase in mass. This behavior is attributed to the normal masses acting in both horizontal and vertical directions. However, as the slenderness increases, this behavior reverses itself and the top mass becomes stabilizing. If the floor is parallel to the façade, the parametric study is aimed at evaluating the influence of the mass acting as seismic mass only (Fig. 17 right). The parametric analysis on the parallel masses reveals that as this parameter is increased, the rotations of both the upper and lower bodies increase. This effect is amplified for large slenderness.

Fig. 17

Median, over seven accelerograms, of the maximum absolute non-dimensional rotations for bottom and upper bodies, varying floor orientation with respect to façade, slenderness, floor mass

4.5 Sensitivity to the input signal and to the coefficients of restitution

In this section, the sensitivity of the system to the input signal and to the ${C}_{l}$ coefficients for the analytical post-impact velocities is investigated. In order to study the influence of the input signal, the mean wall (Table 3) is subjected to a suite of accelerograms, while varying the slenderness of the wall, and evaluating the maximum normalized rotations for the lower and upper body (Figs. 18, 19). The analysis of the system’s sensitivity to the input signal for both the lower (Fig. 18) and upper body (Fig. 19) reveals a significant influence of the floor orientation on record-to-record variability. When the floor is assumed to be perpendicular to the façade, the sensitivity to the input signal is relatively small, and it becomes more marked for very slender walls. On the other hand, when the floor is assumed to be parallel to the façade, the record-to-record variability becomes particularly noticeable for squatter walls compared to the previous case. Notably, slender walls connected to a parallel floor (as shown in Figs. 18 and 19) are extremely sensitive to the input signal. Finally, lower and upper bodies confirm present similar trends.

Fig. 18

Maximum absolute non-dimensional rotation for the lower body, varying floor orientation with respect to façade, slenderness, and input records (Table 4)

Fig. 19

Maximum absolute non-dimensional rotation for the upper body, varying floor orientation with respect to façade, slenderness, and input records (Table 4)

The influence of the ${C}_{l}$ coefficients on the response of the system is investigated. The study follows the same methodology used for the previous parametric analyses, with the values derived from Table 2. The response of the reference façade is evaluated for three cases (Fig. 20): (1) Reference façade with each coefficient ${C}_{l}$ set to the lower bound of its relevant range (${\beta }_{0,l}$) in Table 2; (2) Reference façade with the coefficients ${C}_{l}$ set to the best-fit values obtained from the calibration (Table 2); (3) Reference façade with each coefficient ${C}_{l}$ set to the upper bound of its corresponding range (${\beta }_{f,l}$) in Table 2. For each case, the maximum response of the façade is evaluated as the slenderness (${h}_{tot}$ /$b$) varies.

Fig. 20

Median, over seven accelerograms, of the maximum absolute non-dimensional rotations for bottom and upper bodies, varying floor orientation with respect to façade, slenderness, coefficients ${C}_{l}$ in Table 2

For the configuration where the floor is assumed to be perpendicular to the façade, the parametric analysis (Fig. 20) indicates that the influence of the ${C}_{l}$ coefficients on the maximum response of the system is small, and it becomes slightly more pronounced for slender walls. This trend is similarly observed for the configuration where the floor is assumed parallel to the façade. However, for slender walls, the use of the ${C}_{l}$ coefficients for calculating the post-impact velocities has larger effect on the response. The less evident influence of the ${C}_{l}$ coefficients in Fig. 20 compared to the DE algorithm calibration in Fig. 6 can be explained considering that in Sect. 3.1 the metric is based on the complete time history, while in this section only the maximum value is considered.

Most of the previous plots show small rotation amplitudes because of the only moderate seismic hazard of Mirandola. To consider a stronger excitation the accelerogram recorded in the municipality of Mirandola on May 29, 2012 (event ID: HLN.D.IT-2012–0011, ${M}_{w}$ = 6.0, station ID: MIRH, epicentral distance = 4.5 km) is used with its natural amplitude (PGA = 0.26 g, PGV = 0.55 m/s) was selected. For a vertical spanning wall connected to a flexible restraint at the top, the stiffness of the diaphragm can be seen as one of the most crucial parameters. Therefore, the varying stiffness condition, for the floor perpendicular and parallel configurations, is investigated to evaluate the maximum normalized rotations while varying the slenderness. In Fig. 21 the response to this stronger record confirms the effect of the diaphragm stiffness already observed Fig. 16: increasing the stiffness, maximum rotations generally decrease.

Fig. 21

Maximum absolute non-dimensional rotations (For the unscaled Mirandola earthquake), varying slenderness for the configuration of floor parallel to the façade and varying diaphragm stiffness

5 Conclusions

The out-of-plane response of an unreinforced masonry strip wall elastically supported at the top was studied in this paper. To this purpose the multi rocking body dynamic (MRBD) model formed by two stacked rigid bodies elastically restrained at the top is used. The highly non-linear behavior of the system required a validation of the model with experimental data, to this end the tests performed by Penner and Elwood (2016) are used. To replicate the experimental data, the MRBD model proposed in Prajapati et al. (2022) is updated to reproduce the horizontal carriage of the test apparatus. This update proves to be useful, because it allows to evaluate the response of two different configurations of the diaphragm: (a) perpendicular to the façade; (b) parallel to the façade. Then, using the genetic differential evolution optimization algorithm, the model is validated modifying the analytical post-impact velocities for each type of impact. The calibration procedure proves to be effective, and the predicted results obtained using the MRBD dynamic model show a reasonable agreement with the experimental data: the model is also able to capture the collapse mechanism characterized by impacts and different rotations of the two portions of the cracked wall.

Once the model is calibrated, a parametric analysis is carried out to understand the influence of the main geometrical and mechanical properties is evaluated with reference to the construction practice in the Emilia-Romagna region of Italy, for which lognormal distributions of relevant parameters are derived based on ad hoc survey. Summarizing:

• (1) Calibration proves to be challenging. The differential evolution algorithm demonstrates itself to be an essential tool for tuning the analytical post-impact velocities of the MRBD model.

• (2) For the region and return period considered in the parametric analysis, the vertical spanning wall (elastically restrained at the top) exhibits significant rotations ($\uptheta /\alpha$ > 0.05) only for large slenderness values. This phenomenon is more marked for the case of floor parallel to the wall, where the beneficial effect of the vertical mass is missing, and the stiffness is smaller.

• (3) The presence of the spring plays a crucial role in in the dynamic response of the system. The stiffness of the diaphragm can substantially reduce the rotations and consequently the overturning occurrence.

• (4) The top spring causes a reverse scale effect. Contrary to Housner (1963), increasing the size of the block, while keeping the slenderness and the diaphragm stiffness constant, decreases the resistance of the façade to overturning due to horizontal ground motion. This remarkable phenomenon happens because increasing the size of the block, inertia forces increase as well, while the elastic top force remains constant.

• (5) The diaphragm mass is not relevant if it acts in both vertical and horizontal directions. If it acts only as seismic mass, especially for slender walls, its effect must be considered.

• (6) For the considered area and return period, the sensitivity of the system to the input ground motion as well as to the coefficients for the analytical post-impact velocities is particularly evident for slender walls (${h}_{tot}/b$ > 14) only. This sensitivity is further amplified when the floor is parallel to the façade.

Additionally, future studies with a larger record dataset would allow the exploration of quartiles of the maximum normalized rotation and thus a more comprehensive understanding of the response of the vertical spanning wall elastically restrained at the top.