Abstract
An analysis of the interaction between reinforced concrete walls and slabs tested on the shaking table was performed. The tested structure consisted of four walls connected by three slabs without coupling beams. Although these walls would be typically considered cantilever walls, significant coupling was observed, resulting in considerably different response mechanisms than those observed for typical cantilever walls. As observed in past earthquakes, these unexpected response mechanisms can cause walls' brittle failure. Numerical analyses were performed to study the critical parameters causing the observed response. The response was primarily influenced by the considerable slabs' effective width (EW), significantly affecting the walls' and slabs' strength ratio. Owing to the large EW, the slabs' strength was threefold larger than the standard value typically considered in the design. The slabs provided considerable coupling (CL) of walls, significantly increasing the total stiffness and the total base shear (BS) of the structure compared to standard cantilever walls. Owing to the increased BS and redistribution of the demand between wall piers caused by large CL, the maximum shear forces in the piers were more than doubled than that observed in the cantilever walls. The compression axial forces in piers were also considerably increased, causing the buckling of the longitudinal reinforcement.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Reinforced concrete (RC) walls are among the most frequently used lateral load-resisting systems in buildings. They are generally connected using a floor system consisting of slabs, either with or without coupling beams, providing a certain coupling level (CL). When the coupling is weak, RC walls are typically considered cantilever walls. The essential features of their seismic response are presented in Fig. 1a. In this case, the flexural response of wall piers is the predominant response mechanism resisting the overturning moment induced by the seismic load. When the coupling is more significant, the response mechanism is significantly different, and the walls are considered coupled walls. The essential response features in such cases are presented in Fig. 1b. A considerable portion of the overturning moment is resisted by the frame action provided by the floor system, which induces the axial forces NE into the wall piers. The level of the frame action primarily depends on the ratios of the strengths and stiffnesses of the floor system and wall piers.
Standard Eurocode 8 (EC8) distinguishes cantilever walls from coupled walls by setting the CL limit of 25%, where CL is defined as the ratio of the moment resisted by the frame action and the overturning moment (CEN 2005). It is generally assumed that the coupling of wall piers connected only by the slabs is weak. Consequently, they are considered cantilever walls. Such a model results from a belief that the flexural stiffness and strength of slabs are negligible compared with those of the wall piers; thus, they can be neglected in the analysis. In other words, the slabs are assumed to only function as a rigid diaphragm (having large in-plane and negligible out-of-plane stiffness and strength) connecting the walls.
However, recent experiments presented in the literature (Panagiotou et al. 2011; Nagae et al. 2011; Fischinger et al. 2017) question these assumptions, demonstrating that even relatively thin slabs without coupling beams can provide relatively strong coupling, which can significantly change the response mechanism. The unexpected response mechanism can lead to unforeseen damage and failure of the wall piers. This was observed in previous earthquakes in Chile in 2010 and New Zealand in 2010 and 2011 (Boroschek et al. 2014; Massone 2013, Elwood 2014). The damage was particularly severe in taller buildings, where buckling and rupture of the longitudinal boundary reinforcement and shear damage of the piers were observed. One of the reasons for this unexpected damage is the inability of the elastic models used in design to account for the variable interaction between piers and floors.
In coupled walls, the seismic excitation can considerably change their axial forces, and these changes can influence the stiffness and strength of the piers. The stiffness and strength of piers subjected to tensile forces NE (axial forces in walls caused by the seismic excitation only—see Fig. 1b) can be significantly smaller than those subjected to compression NE. Because of the stiffness and strength changes, significant redistributions of the demand between piers can occur. Owing to the increased flexural capacity in piers subjected to compression NE, the corresponding shear demand can also be considerably increased. Reports (e.g. Alvarez et al. 2019; Santhakumar 1974) have demonstrated that the shear forces in piers subjected to compression NE can be double the value of those obtained in the elastic analysis. Namely, even the sophisticated elastic shell numerical models, which are being applied in practice, cannot accurately consider changes in stiffness and strength of individual piers owing to variable axial forces. Consequently, the maximum shear forces in piers can be considerably underestimated.
The interaction between wall piers and slabs without coupling beams has been examined experimentally using a large-scale shaking table (Isakovic et al. 2020, Isakovic et al. 2021). The experiment is summarised in Sect. 2 and presented in more detail in the abovementioned references. Considering the relatively strong interaction between slabs and walls, the response significantly differed from that of cantilever walls. In the present study, a detailed post-experimental numerical analysis of the tests was performed to determine the main reasons for a strong coupling and the main parameters affecting the interaction between the slabs and walls. The analysis is described in Sect. 3. First, the numerical model of the structure is presented in Sect. 3.1 and then verified in Sect. 3.2, comparing the analytical and experimental responses. Next, the CL observed in the experiment is analysed in Sect. 3.3. In Sect. 4, different parameters influencing the response mechanism and interaction of the wall piers and slabs and CL are analysed in more detail, employing the example of the tested structure.
2 Large-scale shaking table experiment
2.1 Description of the experiment
A shaking table test of the half-scale three-story specimen, subjected to a series of seismic excitations, was previously performed (Isakovic et al. 2020, Isakovic et al. 2021) to evaluate the RC slab-to-wall pier interactions (see Fig. 2). To obtain realistic information about this interaction, the maximum possible size of the specimen was employed, considering the limitations of the shake table with respect to the overturning moment (approximately 500 kNm).
The specimen consisted of four rectangular walls coupled with three slabs. The walls' height, lengths, and thicknesses were 4.50 m, 0.75 m, and 10 cm, respectively (see Figs. 3 and 4). The aspect ratio of the walls (the ratio between the height of the wall and its length) was 6. Thus, conditions typical of slender walls were created. The 0.5 m-wide openings (simulating door openings) were used between two inplane adjacent walls. The slabs' lengths, widths, and thicknesses were 3 m, 3 m, and 8 cm, respectively. These dimensions were defined considering typical tributary areas in RC wall buildings in central Europe.
The total mass of the specimen was 8.8 t. In scaled shaking table experiments, additional masses are often used to achieve realistic seismic demand in tested specimens. In the presented case, this was not an appropriate option since the additional masses on the slabs can significantly influence the properties of the slabs and change their interaction with the wall piers. Thus, the time and acceleration were scaled by factors 0.4 and 2.25, respectively, in order to obtain realistic seismic forces (Isakovic et al. 2021).
The similitude law was chosen, taking into account that the stresses in the prototype and the specimen are the same, allowing the use of conventional materials and reinforcement. The strength of concrete was 26 and 27.5 MPa for walls and slabs, respectively. The yield and ultimate strength of the longitudinal wall reinforcement were 330 and 420 MPa, respectively. The yield and ultimate strength of the walls' transverse reinforcement and the slabs' reinforcement were 560 and 650 MPa, respectively.
Each wall was reinforced using 12 longitudinal bars with diameters of 8 mm (Fig. 4). Stirrups with diameters of 6 mm were placed at distances of 7.5 cm along the whole wall. The slabs were reinforced using two welded meshes (one at the top and one at the bottom), providing 1.31 \({{\text{cm}}}^{2}/{\text{m}}\) of flexural reinforcement in both directions (Fig. 4).
The shake table was excited using an artificial accelerogram generated by modifying Petrovac N-S accelerogram, which was registered during the 1979 Montenegro earthquake (Isakovic et al. 2021). This accelerogram was changed to match the EC8 elastic acceleration spectrum corresponding to soil site type A and 2% damping. A series of uniaxial tests were performed by applying gradually increasing seismic intensity (i.e., 0.1–1.5 g) in the direction along the axis of the walls (i.e., N–S, see Fig. 3). The peak accelerations for the various tests are listed in Table 1. More data regarding the experimental specimen and tests are available in the previous reports (Isakovic et al. 2020, Isakovic et al. 2021).
2.2 The main observations of the experiment
The damage observed in the tested structure was limited up until test R120, corresponding to a peak acceleration of 1.2 g at the shaking table. After this test, the damage in the wall piers was spread approximately 100 cm from the foundation level (Fig. 5). Cracks were initially formed at the outer edges of the wall piers, and when the seismic intensity was increased, they gradually extended toward the inner edges (toward the opening). The crack pattern differed from the cross-shaped damage pattern that is typical for cantilever walls.
In the last two tests (R150(1) and R150(2)), in specific time steps, the differences in the responses of the two piers were visible to the naked eye (Fig. 6). Cracking of the considerable part of the wall pier subjected to the seismic tension forces NE was observed (see the orange areas circled in red in Fig. 6), whereas the wall pier subjected to compression NE cracked only owing to the maximum bending moment at the foundation level. In the last test, buckling of the longitudinal reinforcement at the outer edge of one of the piers was observed, indicating that this pier was subjected to relatively large compression stresses.
In the last three tests, the cracks in all slabs were spread over their entire width, between the two rows of the wall piers (Fig. 7). They were visible at both surfaces (top and bottom surface) of all slabs. Yielding of the reinforcement in the slabs was achieved. The slabs' effective widths (EW) were equal to their total widths. The frame action generated by the slabs was considerable (see the discussion in Sect. 3). More details concerning the observed response can be found in the previous reports (Isakovic et al. 2020, Isakovic et al. 2021).
3 Analysis of the tested specimen
3.1 Description of the numerical model
Herein, the tested specimen was analysed using a two-dimensional numerical model, as presented in Fig. 8a. Since the structure was symmetric (Figs. 2, 3 and 4), only half of it was modelled. The analysis was performed using the OpenSees (Mazzoni et al. 2006) platform.
Wall piers were modelled using the 2D UL FGG version of the multiple-vertical-line-element model (MVLEM) (Fischinger et al. 2004, Isakovic and Fischinger 2019). The slab was modelled using Giberson's (Giberson 1967) nonlinear model with lumped plasticity considering the Takeda hysteretic rules (Takeda et al. 1970). During the experiment, notable rotations of the foundations were observed, which were modelled using rotational springs at the level of the foundations.
The mesh of elements used to model the wall piers is presented in Fig. 8a and b. Shorter elements were employed within the areas of potential plastic hinges and considering the position of the measuring instrumentation. The cross-section of the wall piers was divided into six segments, each including two reinforcing bars, as shown in Fig. 8b, illustrating the mesh of segments on the first floor. Each segment was represented with one vertical spring in the MVLEM (see Fig. 8e). Note that vertical springs in MVLEM are connected with rigid links in order to take into account Bernoulli’s hypothesis. The numbers and locations of the vertical springs were the same in all elements representing the wall piers. More details about the used MVLEM can be found in Fischinger et al. 2004.
The hysteretic response of each vertical spring was described using the VertSpringType2 material model, defining an appropriate force–displacement relationship corresponding to the geometry of segments and the quality of materials, as reported in Sect. 2. As an example, representative properties of the outer springs in the bottom elements are presented in Fig. 9a. The default values of the element parameters defining the shape of the hysteretic loop, such as \(\mathrm{\alpha }=1.0\), \(\upbeta =1.5\), \(\upgamma =1.05\), and \(\updelta =0.5\) (proposed by Fischinger et al. 2004), were used. The typical response of one of the vertical springs is presented in Fig. 9b.
The model of the slabs is presented in Fig. 8a and 8c. The nonlinear response was simulated using two nonlinear springs considering Takeda's hysteretic rules. The EW of the slab that was considered to define the properties of these springs was as large as half of the total width of the slab (since half of the structure was analysed), according to the experimental observations. The elements used to model the slabs and walls were rigidly connected (see the thick horizontal elements in Fig. 8a). The response of the slabs is illustrated in Fig. 10.
Owing to the handling of the specimen and the calibration tests, the specimen was somewhat cracked before the sequence of main tests was conducted, and its initial stiffness was reduced. Subsequent analysis of the periods of vibrations in the tested specimen revealed that the initial stiffness was reduced threefold. This is typical for most experiments where the vertical elements are subjected to relatively low axial forces under the gravity load (Fischinger et al. 2017; Janevski et al. 2023). Upon the reduction of the initial stiffness, the analytical and experimental values for the initial fundamental period of vibration were consistent (T1 = 0.14 s in the specimen and the model; note that this period of vibration corresponds to the period of 0.3 s in the prototype). No shear damage to the piers or slabs was observed during the experiment, which was deliberately prevented by reinforcing the wall piers with considerable shear reinforcement. Consequently, only the elastic shear response was considered.
Notable rotations of the foundations were observed starting from test R060(1). As these rotations significantly influenced the response of the whole specimen, they were simulated using rotational springs at the bottom of the wall piers (Fig. 8a and d). Their response is presented in Fig. 11. When defining the properties of these springs, the results of optical measurements were taken into account. Rotations of the foundations were modelled using origin-oriented hysteretic rules. For this purpose, the Pinching4 model was used, as defined in OpenSees (Mazzoni et al. 2006).
The specimen's mass was lumped for each floor level at the intersections between the walls and slabs and at the bottom of the walls. Each mass included the tributary mass of the slab and wall (i.e., half of the wall's mass above and below the slab).
Lumped masses of 0.59, 0.73, and 0.15 t were considered for the top, two bottom floors, and the base of the wall, respectively. They were lumped at the intersections between the walls and rigid elements and at the base of the walls (Fig. 12a). The dead load was simulated by applying concentrated forces (i.e., 5.8, 7.2, and 1.4 kN at the top, two bottom floors, and the base of the wall, respectively) to each floor at the intersections between the walls and rigid elements, as well at the base of the walls (Fig. 12b). The specimen was subjected to a sequence of seismic excitations (Table 1), same as those applied in the experimental tests. Two percent mass-proportional viscous damping was considered.
3.2 The comparison of the analysis and the experiment
The global response in terms of the total base shear force (BS) versus top displacement is compared in Fig. 13. For clarity, only the results of four selected tests are presented, namely R030, R090, R120, and R150(1), which correspond to the elastic response, the yielding of the piers, the yielding of the slabs, and the nonlinear response, respectively. The results presented in this section correspond to half of the specimen (i.e., two walls).
The numerical model captured the gradually decreased stiffness of the specimen good. The maximum measured top displacement of 5.3 cm, corresponding to 1.2% drift, and the maximum BS of 88 kN, corresponding to 0.9% drift, were simulated with reasonable accuracy. The corresponsidng analytical values were 5.7 cm and 88 kN for the maximum top displacement and BS, respectively.
The measured and calculated maximum accelerations and displacements at different levels of the specimen (i.e., stories) are compared in Figs. 14 and 15. Solid and dashed lines represent analytical and experimental results, respectively.
The presented accelerations are the average accelerations measured at two stations for each slab (Isakovic et al. 2021). An acceleration of 3.0 g was registered at the top of the specimen in test R150(1), corresponding to the peak acceleration of 1.5 g at the shake table. Note, however, that seismic excitation of 1.5 g was applied only in one single time step (Isakovic et al. 2021). Most of the local maximums corresponded to the acceleration excitation of approximately 1 g (note that this acceleration matches the acceleration of 0.4 g in the prototype structure).
The shape of the horizontal displacement envelopes appeared to increase linearly with the applied seismic excitations, which is different from that typically observed for cantilever walls (where the displacement profile is nonlinear and its derivation increases toward the top), indicating that the coupling of the wall piers was significant.
Figures 16 and 17 demonstrate that the top displacement and acceleration response histories were also simulated with reasonable accuracy, showing the results corresponding to tests R030, R090, R120, and R150(1).
In Fig. 18, analytical values of the overturning moments are compared with those calculated based on the average accelerations measured at individual floors. The overturning moment increased proportionally to the seismic intensity until test R120, where the maximum value of 274 kNm was achieved (548 kNm in the whole specimen). The corresponding analytical value was 263 kNm. In the last two tests, the damage to the slabs and piers was more pronounced, and their strength was somewhat degraded, particularly in walls that were subjected to seismic compression forces. In the last test, R150(2), the overturning moment was 249 kNm (497 kNm in the whole specimen). The corresponding analytical value was 239 kNm.
In Fig. 19, analytical and experimental values of cumulative input energy all over the performed tests are compared. The input energy is calculated according to Uang and Bertero 1990 for multistorey buildings and presented in a manner used in Lamuela et al. (2021). The somewhat more notable discrepancy of input energy can be observed only in tests R080 and R090, corresponding to the transition from linear to nonlinear response range. In this region, relatively simple models (Giberson’s and MVLEM) are typically less accurate since the fast stiffness changes are modelled only approximately.
3.3 Analysis of coupling provided by the slabs and its effects
As noted in Sects. 2.2 and 3.2, several indications of strong coupling of the wall piers were observed in the experiment. The analysis confirmed the large CL, which is discussed below for the analysis of half of the tested structure (see the numerical model in Sect. 3.1) under the conditions of test R150(1), for which the nonlinear response of piers and slabs was observed. The discussion presented below corresponds to analytical values of moments, axial and shear forces.
The maximum overturning moment in test R150(1) was Mover = 246 kNm (492 kNm in the whole specimen). The maximum forces NE in the wall piers (compression or tensile axial forces caused by the seismic action, only—see Fig. 1) were NE = ± 88.8 kN, corresponding to the compression force in one wall pier and the tension force in the other. The axial force NE response history is presented in Fig. 20. The compression force due to gravity load (NG = 21.6 kN) should be added to the presented values to obtain the total axial forces in the piers.
The maximum moment corresponding to the frame action was MFA = NE xT = 88.8 · 1.25 = 111 kNm, where xT is the horizontal distance of vertical piers' axes, as shown in Figs. 1 and 8. The CL was defined as the ratio of the moment MFA and overturning moment Mover:
The rest of the overturning moment was resisted by the bending moments at the base of the wall piers, which were 43.2 and 91.3 kNm in the pier subjected to tensile and compression forces NE, respectively. The response of both piers was in the nonlinear range (their yielding was achieved) when the maximum overturning moment occurred.
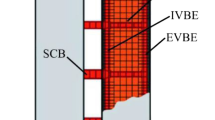
The maximum moment of the frame action MFA was limited by maximum forces NE, which depended on the flexural strength of the slabs. In the tested structure, the flexural strength of the slab was Ms = 7.4 kNm, which corresponded to the EW of 1.5 m, equal to half of the slab's total width (i.e., the total length of the cantilever part, 0.5 m, plus half of the slab span between walls, 1.0 m). The corresponding shear forces in the slabs were Qs = 2 · 7.4 kNm/0.5 m = 29.6 kN. The sum of the shear forces in the slabs was equal to forces NE in the wall piers (axial forces in piers caused by the seismic action) (Fig. 1b). The sum of the maximum shear forces in all slabs was 29.6 · 3 = 88.8 kN.
The CL was not the same in all tests. It gradually increased as long as the yielding of the slab was achieved, in the test R120 with a maximum seismic intensity of 1.2 g. In the first three tests, where the drift demand was small (less than 0.15%), the CL was approximately 25% (Fig. 21). This is the CL used in EC8 to distinguish cantilever walls from coupled walls. When the seismic intensity and the drift demand increased, the CL increased almost linearly as long as the drift demand of 1% was achieved (Fig. 21). In the last two tests with a seismic intensity of 1.5 g, corresponding to a drift of 1.27%, the CL was not significantly changed (i.e., from 42 to 45%).
Generally, the CL noticeably increased as long as the yielding of the slab was not achieved. The CL increased because the bending moments and shear forces in the slabs increased, simultaneously increasing forces NE in piers and amplifying the frame actions. After the slabs yielded, the CL level became almost invariant.
The strong CL and frame action influenced the plastic mechanism and the redistribution of bending moments and shear forces between piers subjected to tensile and compression NE forces. The piers subjected to tensile NE forces yielded before the slab in test R090 at 0.82% drift. In test R120 at 1% drift, the yielding of the piers subjected to compression forces NE and the yielding of the slabs were observed. In the last two tests with 1.27% drift, the strengths of the slabs and the strengths of the walls subjected to significant compression stresses (i.e., piers subjected to compression forces NE) degraded.
The maximum overturning moment of Mover = 263 kNm was reached in test R120. At the time step when it was achieved, the bending moments were 43.5 and 109.3 kNm in the piers subjected to tensile and compression forces NE, respectively. The corresponding shear demand was 24.6 and 62.9 kN in the piers subjected to tensile and compression NE forces, respectively. The bending and shear demand differed significantly from those in typical cantilever walls, where the values in both piers are usually the same. Notably, the increase of the shear forces in the pier subjected to compression forces NE, was as large as 72% of the total BS, which is larger than that observed in standard cantilever walls (i.e., 50% of the total BS). Further discussion and analysis regarding the increase of demand in piers subjected to compression forces NE are provided in the following sections.
4 Major parameters conditioning the response mechanism and influencing the interaction between wall piers and slabs
In the tested structure, the two most important parameters influencing its response mechanism and the CL were (a) the strength ratio of the piers and slabs and (b) the rotations of the foundations (i.e., base rotations). To evaluate their effects, additional analyses of the tested structure were performed, excluding the base rotations and reducing the slabs' EW, which affected the strength ratio of the piers and slabs. First, the EW was reduced from 150 cm to a standard value of 50 cm. Then, the bending strength of the slab was neglected entirely, considering that it connected the wall piers but only functioned as a rigid diaphragm. In this way, the analysis of pure cantilever walls was performed.
The main results of these additional studies (maximum overturning moments Mover, corresponding forces NE, maximum CL, maximum total BS, and maximum shear forces in the piers V, fundamental mode vibration period T, and maximum spectral accelerations Sa,max at last run) are summarised in Table 2. They are analysed in more detail in the following subsections.
The base rotations significantly affected the specimen's response, increasing the demand for slabs and enhancing the frame action. The influence of this parameter is analysed in Sect. 4.1.
The strength of the slabs crucially depended on their activated EWs. In the experiment, the EW gradually increased, and at the large seismic intensities/drifts, it was considerably larger than that typically considered in the design. Similar observations have been reported in the literature (Pantazopoulou and French 2001, Kabayesawa et al. 2017). The influence of EW on slabs is discussed in Sect. 4.2.
It has been demonstrated that the frame action may strongly affect the maximum shear forces in piers compared with that observed for standard cantilever walls. This redistribution is also discussed and analysed in Sect. 4.2.
4.1 The base rotations
To evaluate the effects of the base rotations, an additional analysis was performed using the same model (Fig. 8) as that for the experiment's simulation, but the base rotations were prevented. The global response is shown in Fig. 22, comparing the total BS vs. top displacement relationship with and without base rotations.
The base rotations somewhat increased the top displacements and flexibility of the structure. The maximum displacement was approximately 35% larger with rotations (5.7 cm) than that in the structure without base rotations (4.2 cm). The maximum total BS was 10% larger (87.5 kN) in the structure with base rotations than that without base rotations (79.6 kN). The rotations of the pier subjected to tensile forces NE were noticeably larger than those in the pier subjected to compression forces NE, particularly under stronger seismic excitation.
The piers subjected to tensile forces NE yielded somewhat earlier when the base rotations were excluded. The yielding was observed in the test R060(1) at the seismic intensity of 0.6 g and 0.3% drift. In the experiment, their yielding was observed in test R090 at the seismic intensity of 0.9 g and 0.82% drift. When no base rotations were considered, the degradation of the piers' strength subjected to tensile forces NE started at 0.5% drift in test R090.
The yielding of piers subjected to compression forces NE was somewhat postponed when the base rotations were excluded. Limited yielding was observed in the last test, R150(2), at the seismic intensity of 1.5 g, and the nonlinearity was minor. It should be noted that the corresponding drift of 0.92% was similar to that observed in the experiment, where these piers subjected to axial compression forces yielded at 1% drift. Since the nonlinear response was considerable only when piers were subjected to tensile forces NE, the failure occurred owing to the rupture of the longitudinal reinforcement rather than their buckling, as observed in the experiment.
In the structure without base rotations, the maximum overturning moment was 242 kNm, which was reached in the last test at 0.92% drift. At that moment, the shear forces were 20.3 and 59.3 kN in piers subjected to tensile and compression forces NE, respectively. The influence of CL on the distribution of shear forces is discussed later in Sect. 4.2.
Excluding the base rotations, the demand for the slabs was reduced. No yielding and strength degradation was observed. The bending moments were reduced from 7.4 to 6.5 kNm (Fig. 23). The reduction of the bending moments also caused the reduction of the shear forces in slabs and axial forces in the piers. The maximum force NE was reduced from ± 88.8 to ± 78.4 kN. The CL was also somewhat reduced, from 45 to 40% (Fig. 24). However, the maximum CL value was still significant, occurring at 0.92% drift in the structure without base rotations, whereas it occurred at 1.27% drift in the structure with base rotations. The other trends of CL without base rotations were similar to those observed in the structure with base rotations. The CL increased in the same manner, directly proportional to the drift, from an initial CL value of 15% to a maximum of 40%. However, the gradient in the case without base rotations was larger.
It can be concluded that in the tested structure, the base rotations increased the CL and consequently increased the demand in slabs and piers subjected to compression forces NE, inducing the buckling of their longitudinal reinforcement. In the structure without base rotations, the longitudinal bars in the walls ruptured when subjected to tensile forces NE before buckling owing to compression forces NE.
4.2 The ratio of piers' and slabs' strength, the effective width of slabs
It has been demonstrated that slabs in the tested structure were strong enough to provide considerable coupling of the piers, and the piers yielded before the slabs. One of the main reasons for this response was the large EWs of the slabs that were activated at relatively large drifts (i.e., 1% or more).
To evaluate the impact of the slab EW and illustrate its effects, additional analyses of the tested structure were performed. First, the EW of slabs was reduced from 150 to 50 cm, a standard value typically considered in the design. In this way, the strength of the slab was reduced by approximately three times. The yielding moment was reduced from 7.4 to 2.5 kNm.
Then additional studies were performed by completely neglecting the flexural strength of slabs. In other words, another extreme case was analysed by considering piers as perfect cantilever walls.
The global responses of all analysed structures with different effective slab widths in terms of the total BS vs. top displacement relationship are compared in Fig. 25. The response of the structure with a large EW of 150 cm, where base rotations were excluded, differs from the other two cases, exhibiting a larger stiffness, shorter period of vibrations, larger maximum accelerations and total BS (see Table 2). The responses of cantilever walls and the structure with a shorter slab EW are similar. This can be explained by comparing the CL, as shown in Fig. 26.
It has already been shown that the CL in the structure with a larger slab EW increased proportionally to the drift level from an initial value of 15% to a maximum of 40%, corresponding to 0.92% drift. On the contrary, the CL was almost invariant when the EW was reduced. The CL was in the range of 14–22%, which is below the level of 25%, the value used in standard EC8 to distinguish cantilever walls from coupled walls. This limit appears to be appropriate, at least in the analysed case, because the response of the structure with a shorter slab EW was similar to the response of cantilever walls (Fig. 25).
Along with the CL, the axial forces NE were also reduced. In both structures, the maximum values were achieved approximately at the same drift. The NE of ± 78.4 kN in the structure with a large slab EW and without base rotations was reduced to ± 29 kN when the slab EW was reduced. Consequently, the yielding moments in piers and their distributions along the structure were changed. When the piers were subjected to compression forces NE, the bending moments were reduced, whereas they increased when the tensile forces NE were applied, compared with the structure with a larger EW.
A change in the bending moments also affected the shear forces in the piers. In the structure with a large EW and large CL, the shear forces were much larger than in the cantilever walls. In the particular time step when the maximum overturning moment was achieved, the shear forces in the two piers were considerably different from each other since they were subjected to large forces NE (compression on one side and tension on the other). The shear force in the pier subjected to compression forces NE was 59.3 kN (74% of the total BS), whereas the opposite pier exhibited 20.3 kN (26% of the total BS).
In the structure with a shorter slab EW, smaller CL, and reduced forces NE, the difference between shear forces in two piers at a specific time step was smaller. When the maximum overturning moment was achieved, the shear forces were 22 and 38 kN (37% and 63% of the total BS) in the piers subjected to tensile and compression forces NE, respectively. In both cantilever walls, the shear forces were the same, 25 kN (50% of the total BS).
Overall, a considerable redistribution of the shear forces can be expected between strongly coupled wall piers. The shear force in a pier subjected to compression forces NE can be considerably larger than that observed in the cantilever walls. In this particular case, the shear force was more than doubled. It should be noted, however, that this increase is not only the consequence of the shear redistribution but, to a great extent, also the increase in the overall stiffness, resulting in larger total BS (i.e., 79.6 and 50 kN in strongly coupled and cantilever walls, respectively). Once more, the increase in the overall stiffness is the consequence of the strong coupling. In the tested structure, the base rotations further increased the maximum shear force in a single pier to 62.9 kN.
The tested structure was relatively flexible with a somewhat larger fundamental vibration period. When the base rotations were excluded, in the last run, the fundamental period of vibration was 0.3 s (0.75 s in the prototype). In the structure with shorter EW and in the cantilever walls, the fundamental periods of vibrations were longer—0.37 s and 0.38 s, respectively. All these periods match the constant velocity part of the acceleration spectrum (see Fig. 27). Consequently, larger accelerations correspond to shorter periods of vibrations, increasing the total BS.
In lower buildings with shorter fundamental periods of vibrations, which match the constant acceleration part of the spectrum, smaller shear force amplification can be expected, because the maximum accelerations do not depend on the periods of vibrations. In such cases, the total BS should be similar in cantilever and coupled walls regardless of the EW of slabs. However, the shear forces in single piers can still be increased when EW is large owing to their redistribution between piers subjected to compression and tension forces NE.
It should be noted that the tested structure was subjected to a specific accelerogram, which corresponds to a nonsmooth acceleration spectrum presented in red in Fig. 27, where the accelerations corresponding to periods of vibrations presented in Table 2 are marked.
The ratio of BS in structures with EW 150 cm and EW 50 cm with respect to cantilever walls would be somewhat smaller if the smooth acceleration spectrum (blue line in Fig. 27) was considered (this spectrum is defined considering the similitude low considered in the experiment—see Sect. 2.1). In this case, the maximum accelerations in all structures would be smaller: 2.7 g, 2.2 g and 2,1 g in EW150, EW50 and cantilever walls, respectively. However, the ratio of maximum acceleration in structure EW150 with respect to cantilever walls would still be significant and would amount to 1.3. Consequently, considering the redistribution between piers, the shear forces in piers would still be almost doubled with respect to cantilever walls.
To generalise the previous observations, an extensive parametric study of buildings with different configurations (e.g., different ratios of wall and slab strength, different wall aspect ratios subjected to different sets of accelerograms, different shapes of walls’ cross-sections, etc.) is ongoing. The preliminary studies reported by Janevski et al. 2022 already confirmed previously described findings.
5 Conclusions
During the recent earthquakes in Chile in 2010 and New Zealand in 2010 and 2011 (Boroschek et al. 2014; Massone 2013, Elwood 2014) several unforeseen types of failures were detected in RC structural walls. The buckling and the rupture of the longitudinal bars in the boundary regions of walls, as well as their shear failure, were identified, particularly in taller buildings and walls with larger aspect ratios. The present study explains some of the reasons for these responses.
The previous experiment, analysed in the current paper, confirmed several observations reported in the literature, showing that RC slabs without coupling beams can still induce strong coupling in RC walls. In this particular case, the CL, defined as the ratio of the moment resisted by the frame action and the overturning moment, was as large as 45%. Consequently, the response was significantly different from that observed for typical cantilever walls. The failure of the walls occurred because of the longitudinal bars buckling in the boundary regions of the walls, caused by the strong frame action effect (i.e., a high CL).
The CL and response mechanism of the tested specimen were influenced primarily by two basic parameters: (a) the strength ratio of the walls and slabs and (b) the base rotations. The ratio of the strengths crucially depended on the activated EW of the slabs, which was threefold larger than the standard value considered in the design according to standard EC2. Larger EWs increased the strength of the slabs, activating more frame action, which increased the CL. Consequently, the overall stiffness of the structure was increased, and considerable axial forces were induced in the walls, causing the buckling failure of the longitudinal bars in the boundary regions of the walls. When the standard EW was considered in the analysis, the response was similar to that of the cantilever walls.
It was also observed that the total BS was increased because of the large CL, and the maximum shear forces in wall piers were more than doubled compared with those in cantilever walls. This increase was affected by the larger overall stiffness of the coupled structure, as well as the redistribution of the seismic demand between piers subjected to tensile and compression axial forces NE owing to the seismic action. Despite the substantial increase in shear forces, the shear failure of the piers did not occur in the experiment because it was deliberately prevented by adequate shear reinforcement.
The base rotations of the walls also somewhat influenced the CL. When these rotations were excluded, the CL was reduced but remained high (40%). The base rotations increased the demand in the slabs and postponed the yielding in the piers subjected to tensile forces NE owing to the seismic action.
According to the properties of the analysed walls, it can be concluded that the observed seismic response and considerable CL can be expected primarily in taller buildings with fewer walls that are relatively close to each other and have larger aspect ratios. To generalise this and previous observations, an extensive parametric study of buildings with different configurations (e.g., different ratios of wall and slab strength, different wall aspect ratios subjected to different sets of accelerograms, etc.) is ongoing.
Data availability
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
References
Alvarez R, Restrepo JI, Panagiotou M, Santhakumar AR (2019) Nonlinear cyclic Truss Model for analysis of reinforced concrete coupled structural walls. Bull Earthq Eng 17:6419–6436. https://doi.org/10.1007/s10518-019-00639-8
Boroschek R, Bonelli P, Restrepo JI, Retamales R, Contreras V (2014) Lessons from the 2010 Chile earthquake for performance based design and code development. In: Fischinger M (ed) Performance-based seismic engineering: vision for an earthquake resilient society. Springer, Netherlands, pp 143–157
CEN/TC 250/SC 8 (2005) Eurocode 8: design of structures for earthquake resistance—Part 1: General rules, European Committee for Standardisation, Brussels
Elwood, K. J., Pampanin, S., Kam, W. Y., & Priestley, N. (2014). Performance-Based Issues from the 22 February 2011 Christchurch Earthquake. In Performance-Based Seismic Engineering: Vision for an Earthquake Resilient Society (pp. 159–175). https://doi.org/10.1007/978-94-017-8875-5_12
Fischinger M, Isakovic T, Kante P (2004) Implementation of a macro model to predict seismic response of RC structural walls. Comput Concr. https://doi.org/10.12989/cac.2004.1.2.211
Fischinger M, Kante P, Isakovic T (2017) Shake-table response of a coupled RC wall with thin T-shaped piers. J Struct Eng 143(5):04017004. https://doi.org/10.1061/(ASCE)ST.1943-541X.0001718
Gale-Lamuela D, Donaire-Avila J, Benavent-Climent A (2021) Energy dissipation capacity for waffle-flat-plate structures subjected to bi-directional seismic loadings. Eng Struct 248:113220. https://doi.org/10.1016/j.engstruct.2021.113220
Giberson M (1967) The response of nonlinear multi-story structures subjected to earthquake excitation. Dissertation (Ph.D.)
Isaković T, Fischinger M (2019) Assessment of a force–displacement based multiple-vertical-line element to simulate the nonlinear axial–shear–flexure interaction behaviour of reinforced concrete walls. Bull Earthq Eng 17(12):6369–6389. https://doi.org/10.1007/s10518-019-00680-7
Isaković T, Gams M, Janevski A, Rakićević Z, Bogdanović A, Jekić G, Kolozvari K, Wallace J, Fischinger M (2021) Shake table test of RC walls’ coupling provided by slabs. Građevinski Materijali i Konstrukcije : Časopis Za Istraživanja u Oblasti Materijala i Konstrukcija 64(4):225–234
Isaković T, Gams M, Janevski A, Rakićević Z, Bogdanović A, Jekić G, Kolozvari K, Wallace J, Fischinger M (2020) Large scale shake table test of slab-to-piers interaction in RC coupled walls. In: Proceedings of the 17th WCEE, September 13th to 18th 2020, Sendai, Japan
Janevski A, Kang JD, Isaković T (2023) Simulation of the E-Defense 2015 test on a 10-storey building using macro-models. Bull Earthq Eng. https://doi.org/10.1007/s10518-023-01734-7
Janevski A, Remec M, Isakovic T (2022) Parametric study of the seismic response of RC walls coupled by slabs. In: Proceedings of the Third European Conference on Earthquake Engineering and Seismology: 3ECEES: September 4 - September 9 2022, Bucharest, Romania. pp. 514–521
Kabeyasawa T, Kabeyasawa T, Fukuyama H (2017) Effects of floor slabs on the flexural strength of beams in reinforced concrete buildings. Bull N Z Soc Earthq Eng 50:517–526. https://doi.org/10.5459/bnzsee.50.4.517-526
Massone LM (2013) Fundamental principles of the reinforced concrete design code changes in chile following the Mw 8.8 earthquake in 2010. Eng Struct 56:1335–1345
Mazzoni S, McKenna F, Scott MH, Fenves GL (2006) OpenSees command language manual. University of California, Berkeley, http://opensees.berkeley.edu/manuals/usermanual
Nagae T, Tahara K, Matsumori T, Shiohara H, Kabeyasawa T, Kono S, Nishiyama M, Wallace J, Ghannoum W, Moehle J, Sause R, Keller W, Tuna Z (2011) Design and instrumentation of the 2010 e-defense four-story reinforced concrete and post-tensioned concrete buildings, PEER Report 2011/104
Panagiotou M, Restrepo JI, Conte JP (2011) Shake-table test of a full-scale 7-story building slice. Phase I: rectangular wall. J Struct Eng. 137:6
Pantazopoulou SJ, French CW (2001) Slab participation in practical earthquake design of reinforced concrete frames. ACI Struct J 2001:479–489
Santhakumar AR (1974) The ductility of coupled shear walls. Dissertation, University of Canterbury
Takeda T, Sozen MA, Nielsen NN (1970) Reinforced concrete response to simulated earthquakes. J Struct Div 96:2557–2573
Uang CM, Bertero VV (1990) Evaluation of seismic energy in structures. Earthquake Eng Struct Dynam 19:77–90
Acknowledgements
The experimental work was conducted within the SERA-TA project "Influence of the floor-to-wall interaction on the seismic response of coupled wall systems," a part of the EU Horizon 2020 research and innovation programme. The Slovenian National Research Agency supported the analytical research.
Funding
This work was funded the by European Union's Horizon 2020 research and innovation programme under grant agreement No 730900, and the Slovenian Research and Innovation Agency.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
All authors declare they have no financial interests.
Ethical approval
All authors read and approved the final manuscript.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Isakovic, T., Janevski, A. Analysis of interaction between reinforced concrete walls and slabs tested on a shaking table. Bull Earthquake Eng (2024). https://doi.org/10.1007/s10518-024-01862-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10518-024-01862-8