1 Introduction

Bridges are crucial elements of transportation networks and have considerably contributed to economic development and social communication (Guo et al. 2017). However, in recent years, several cases of severe damage and even collapse have been observed as a result of worldwide earthquakes that threatened the normal operations of intercity roadway systems and the safety of citizens. Highway administrators require a thorough understanding of the seismic response of bridges to make informed decisions to ensure users’ safety. Otherwise, the rescue or restoration efforts may be delayed (Baso¨z et al. 1999; Han et al. 2009). Typically, this is done by means of Rapid Visual Inspection and does not involve numerical analysis due to the challenges associated with nonlinear modelling of the pier response. However, the post-earthquake seismic performance of bridges could be rapidly and more accurately evaluated employing Knowledge-Enhanced Neural Networks for the Lumped Plasticity Modelling of RC Piers, so as to accelerate the timely relief efforts.

With the development of accelerometric networks, ground motion records can be retrieved in nearly real-time. Conventional methods used to predict seismic damage by correlating mapping ground motion intensity measures (IMs), such as peak ground acceleration (PGA) or spectral acceleration at the fundamental period of the structure (Sa(T1)), with engineering demand parameters, that is essentially, proxies of seismic demand either based on historical/empirical/test data (Billah and Alam 2015; Zentner et al. 2016; Buratti et al. 2017; Zhong et al. 2021) or numerical simulations (Abbasi et al. 2016; Jeon et al. 2019). These correlation mapping methods can be used to generate fragility curves, expressing the probability to exceed a specific limit state given an IM, before the earthquake event. The fragility curves can then be used to predict the damage state of bridge members and systems. In that process, the inevitable uncertainties in structural characteristics, material properties, and ground motions will affect the accuracy of the predicted bridge response (Lu et al. 2021). More detailed, bespoke (i.e., bridge-specific) nonlinear time-history analyses can provide a more reliable estimate of their seismic performance (Jeon et al. 2016). Nevertheless, such analyses require extensive modeling time and computation resources (Agalianos et al. 2017). This is particularly true when, in case of a strong earthquake event, the regional portfolio of bridges contains a large number of individual structures that need to be rapidly assessed in which case, the mechanical properties of all individual piers need to be identified separately, often by using external software (i.e., for fiber section analysis). As a result, a faster, yet reasonably accurate way for analysis-based rapid performance assessment of bridges is of paramount importance.

Another important matter is that numerical simulation methods heavily rely on the mechanical properties of components and the interactions among them. For simply-supported or continuous girder bridges, reinforced concrete (RC) pier columns are the main weight-bearing components, but are vulnerable to earthquakes (Yuan et al. 2020; Zhong et al. 2022). Due to the highly complicated mechanisms of concrete and steel materials, modeling RC columns is challenging (Fawaz and Murcia-Delso 2021). For example, the commonly used distributed plasticity models, such as those based on fiber elements and solid elements, may require substantial finite element division and time-intensive iterative computation processes (Lucchini et al. 2017; Li et al. 2021) that is prohibitive for post-earthquake conditions for the reasons outlined above. Furthermore, lumped plasticity (LP) models are inherently limited by the coarse and potentially inaccurate empirical methods used for the identification of hysteretic parameters (Verderame and Ricci 2018; Lee et al. 2021). Therefore, several existing methods for predicting LP model parameters of RC columns have been developed based on a limited number of tests and empirical assumptions and are thus ineffective in certain cases. Extensive research works have also demonstrated that test data-calibrated model parameters can improve numerical simulation methods. For example, Atamturktur et al., (2015) and Lee et al., (2021) developed an enhanced Ibarra–Medina–Krawinkler (I–M–K) model for RC columns based on a database of experimental results. Interestingly though, in a blind competition on numerical simulations, more than 60% of the models failed to precisely predict the well-documented test behavior of a 3-story frame even when all structural and material characteristics were provided (Lu et al. 2012). In addition to the contestant’s expertise in configurating and fine-tunning models, the simulation errors mainly result from the determination of model parameters, especially in the context of the LP model cases.

With the development of computation technologies, Machine Learning (ML) methods have shown great promise in solving classical problems in various fields including earthquake engineering (Xie et al. 2020), bridge engineering (Liu et al. 2022a), and hydrodynamics (Jin et al. 2018). Previous studies have accumulated a substantial amount of experimental and simulation data (Popa et al. 2014; Bechtoula et al. 2015) that can enable the development of ML alternatives for the mechanical property assessment of bridge components. Nevertheless, these methods depend highly on the quantity and quality of the training data, which are difficult to ensure in the tests of RC specimens. In fact, the test data of RC columns is usually small due to the high laboratory testing cost, and there are many inconsistencies observed in the specimen configurations by different researchers. Moreover, purely data-driven ML methods lack interpretability and as such, they are less generalizable. Thus, the use of ML methods in bridge engineering is still challenging (Liu and Li 2019).

To address these drawbacks, several knowledge enhanced neural network (KENN) or physics-informed neural network (PINN) methods have been developed. The essential concept involves utilizing neural networks as approximators of the desired solution and then guiding the training process based the domain-specific knowledge. KENN methods have exhibited strong potential for solving high-order partial differential equations (Chen et al. 2021) as well as forward and inverse problems (Raissi et al. 2019). Zhang et al., (2020) and Liu and Guo, (2021) also validated the feasibility of introducing physical laws into ML to overcome the limitations of current approaches for the seismic response analysis of bridges and numerical simulation of RC columns. Karniadakis et al., (2021) comprehensively reviewed their diverse applications, and concluded that KENN still needs to be well configured according to the specific problem.

Based on the above research needs and challenges, this study aims to (a) investigate the effects of the characteristics of RC columns on the critical model parameters as empirical laws in order to; (b) develop a KENN-calibrated LP model of RC columns; and (c) propose a parametric FEM for concrete bridges; finally (d) employ the KENN model to facilitate the development of FEMs of bridges, thereby enabling rapid yet accurate assessment of their post-earthquake seismic responses. Section 2 describes the fundamentals of the bridge model and the schematic to determine the LP model parameters followed by the description of the KENN methodology which is detailed in Sect. 3. The development and validation of the KENN model based on a collected test database are discussed in Sect. 4. Section 5 describes how the proposed model is applicable to the seismic assessment of bridges and finally, Sect. 6 illustrates the main conclusions and the practical usefulness of this study.

2 Framework overview

2.1 Seismic response assessment of regular concrete bridges

One of the primary objectives of numerical simulation for bridges is to capture their response under earthquakes, which can be used to determine the component damage state. For that purpose, several reasonable FEM assumptions are adopted (Jeon et al. 2019; Mangalathu and Jeon 2019): (1) the superstructure (i.e., bridge deck and girder) remains elastic under earthquake loading owing to its large stiffness compared to other components; (2) the plastic deformation of pier columns is predominantly concentrated at the ends where plastic hinges develop; (3) the geometric dimensions of other components (e.g., bearings, abutments, and foundations) can be neglected as they have little impact on the response of piers in the transverse direction.

As illustrated in Fig. 1, a classical three-dimensional regular concrete bridge FEM is established. The superstructure is simulated as a spine with a distributed mass system interconnected by elastic beam columns (Nielson and Desroches 2007b). For a simply supported bridge, the compression-only impact element proposed by Muthukumar and Desroches (2010) is added to account for potential pounding effects. Each pier column is modeled using an LP spring and an elastic element (Verderame and Ricci 2018). The geometric nonlinearities like P-Δ effects are included, while Rayleigh damping is introduced. The foundation is simulated using 6DOF linear translational and rotational springs (Ux, Uy, Uz, Rx, Ry, Rz) to account for soil–structure interaction. Abutments are modeled using zero-length elements with a hyperbolic model (Shamsabadi et al. 2010) and a hysteretic model (Mangalathu et al. 2018) in series, which represent the effects of passive soil pressure and pile, respectively. The commonly used elastomeric bearings are adopted in this study, which are simulated by the zerolength elastomericBearingPlasticity element (Nielson and Desroches 2007b) (Fig. 2).

Fig. 1
figure 1

Schematic of a typical regular bridge and the corresponding 3D FEM

Full size image
Fig. 2
figure 2

FEM configurations and corresponding elements of critical bridge components

Full size image

The above is quite a standard FEM refinement in the literature and is well established. The reliability of the FEM, however, for a specific bridge, depends on the accuracy of component model parameters. Given that pier columns are susceptible to structural damage, and wield strong influence on bridge performance, serviceability, and safety, their LP model parameters deserve meticulous calibration. The model parameters of other components, such as the superstructure and bearings can be derived from structural and site documentation.

2.2 KENN methodology for lumped plasticity model of RC columns

The LP model parameters for RC columns are typically determined using (1) empirical or semi-empirical knowledge as well as (2) data retrieved by structural laboratory testing. The challenge here is that most empirical or semi-empirical formulas have been developed based on a limited sample of test data and subjective assumptions. On the other hand, the increasingly popular ML methods, being purely data-driven, may lack generalizability when the training data are limited or have a high scatter. Since many specimens are designed and tested under specific conditions, the test data from different resources contains many uncertainties, limiting the consistency of the data-driven model with empirical knowledge.

To overcome the abovementioned limitations, we explored empirical knowledge to enhance the data-driven neural network and to realize more effective alternatives to capture the complex relationship between RC column properties and LP model parameters. As illustrated in Fig. 3, the proposed KENN methodology involves four steps: (1) a set of appropriate parameters, representing the characteristics of RC columns (geometries, material properties, reinforcement arrangements, etc.), are considered as the input vector X, and the critical LP model parameters are represented as the output vector Y; (2) a test database of abundant RC columns with well-distributed X and Y is collected and normalized; (3) the empirical knowledge about the effects of inputs X on the outputs Y is summarized and formulated as the physical laws \({\mathbf{P}}_{phy}\); (4) both the test data from step (2) and empirical knowledge from step (3) are used to develop the KENN surrogate model for mapping the relationships among the elements of X and Y, that is, \(f_{{{\text{KENN}}}} :[{\mathbf{X}},{\mathbf{P}}_{phy} (\partial {\mathbf{Y}}/\partial {\mathbf{X}})] \to {\mathbf{Y}}\). Finally, the KENN model can be used to develop the LP model of RC columns. The KENN-calibrated LP model is expected to improve the accuracy and efficiency of numerical simulation of bridges by providing more reliable model parameters.

Fig. 3
figure 3

Framework of the KENN-calibrated lumped plasticity model of the RC column

Full size image

3 Descriptions of the KENN methodology

3.1 Schematic of the KENN

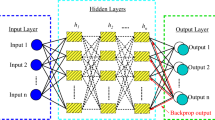
Motivated by biological neural systems, artificial neural network (ANN) has become one of the most well-known and extensively used ML paradigms. As illustrated in Fig. 4, a multilayer perceptron (MLP) neural network, comprising of an input layer, one or more hidden layers, and an output layer, was adopted in this study. Each layer contains multiple processing elements (i.e., neurons), which are connected with the neurons of adjacent layers. The key characteristics and LP model parameters of RC columns were assigned to the input layer and output layer, respectively. The neurons in the hidden layers performed nonlinear transformations of the inputs to the outputs through the activation function.

Fig. 4
figure 4

Detailed configurations of the KENN method for the I–M–K model for RC columns

Full size image

To develop the KENN, a set of well-distributed specimens was first introduced in the database; each specimen was represented by {X, Y}. Furthermore, empirical knowledge about the qualitive effects of the inputs on outputs was be formulated as \({\mathbf{P}}_{phy} (\partial {\mathbf{Y}}/\partial {\mathbf{X}})\). Thereafter, the data were randomly divided into the training set and test set. Both the training data and empirical knowledge were embedded into the neural network to supervise the training process, during which the inputs were transmitted forward to the output layer through connections among neurons in different layers. Then, the predicted outputs \({\hat{\mathbf{Y}}}\) and the trend \({\mathbf{P}}_{phy} (\partial {\hat{\mathbf{Y}}}/\partial {\mathbf{X}})\) were determined. Actually, there may be several potential candidate models (PCMs) yielding similar prediction results. Their predicted trend \({\mathbf{P}}_{phy} (\partial {\hat{\mathbf{Y}}}/\partial {\mathbf{X}})\) will be compared with the empirical knowledge-based trend \({\mathbf{P}}_{phy} (\partial {\mathbf{Y}}/\partial {\mathbf{X}})\), based on which the inconsistent PCMs were rejected. Furthermore, the \(Loss_{{{tot}}} (\hat{y}_{k} ,y_{k} )\) errors of the remaining PCMs were used to update the weights from the output layer backward to the input layer. The feedforward and backpropagation processes iteratively adjusted the weights until \(Loss_{{{tot}}} (\hat{y}_{k} ,y_{k} )\) converged. The abovementioned steps were repeated for all KENN models with potential configurations. Consequently, all the PCMs were consistent with the empirical knowledge, and thus the optimal KENN model for LP model parameters was selected as the one with minimum error.

To further guarantee the generalizability of the KENN model, K-cross validation was employed. The training set was arbitrarily split into K subsets, each of which acts as the validation set in turn for verifying the model trained by the other K-1 subsets. According to the mean performance of the K trained models, the efficiency of the trained model was evaluated. The root mean squared error (RMSE) and the coefficient of determination (R2) were employed, as follows:

$$RMSE = \sqrt {\frac{1}{{m_{y} n_{y} }}\sum\limits_{j = 1}^{{m_{y} }} {\sum\limits_{i = 1}^{{n_{y} }} {\left( {\frac{{y_{ij} - \hat{y}_{ij} }}{{y_{ij} }}} \right)^{2} } } } ,\;R^{2} = 1 - \frac{{\sum\limits_{j = 1}^{{m_{y} }} {\sum\limits_{i = 1}^{{n_{y} }} {(y_{ij} - \hat{y}_{ij} )^{2} } } }}{{\sum\limits_{j = 1}^{{m_{y} }} {\sum\limits_{i = 1}^{{n_{y} }} {(y_{ij} - \overline{y}_{j} )^{2} } } }}$$
(1)

where \(y_{ij}\) and \(\hat{y}_{ij}\) denote the j-th observed and predicted normalized model parameter of the i-th specimen, respectively, \(\overline{y}_{j}\) is the corresponding mean value vector, \(m_{y}\) is the number of specimens, and \(n_{y}\) is the dimensions of the outputs (\(n_{y}\) = 7 herein).

3.2 Determination of inputs and outputs

Several studies have investigated the seismic response of RC columns with rectangular or square sections (Haselton et al. 2016; Liu and Li 2019); however, the results may not be directly applicable to RC columns with circular sections (Mangalathu et al. 2017; Liu and Guo 2021). Therefore, this study simulated the nonlinear load-deformation response of circular and octagonal RC columns using a KENN-calibrated I–M–K model.

The schematic of a typical circular RC column is illustrated in Fig. 5a. As discussed in the aforementioned sections, the key influencing factors should be first identified as the input vector X. Currently, a large number of parameters have been proposed for the seismic assessment of RC columns and several parameters of different semi-empirical formulas are employed in plastic hinge length assessment. In this study, a selection of key parameters was made based on previous studies (Poljanšek et al. 2010; Ou et al. 2013; Popa et al. 2014; Bechtoula et al. 2015; Li et al. 2016), focusing on the effects of geometry size, material properties, reinforcement configurations, and testing/loading protocols using the following input parameters:

$${\mathbf{X}} = \{ X_{j} \} = \{ D_{c} ,D_{e} /D_{c} ,\lambda ,n_{c} ,f_{c}^{{^{\prime } }} ,\rho_{l} ,f_{yl} ,\rho_{sv} f_{yt} ,s/D_{c} ,h_{T} \}$$
(2)

where \(D_{c}\) and \(D_{e}\) denotes the gross and effective cross-section diameters, respectively; \(\lambda\) denotes the span-to-depth ratio (the ratio of the length of the equivalent cantilever to the section diameter); nc represents the axial compression ratio; \(f_{c}^{\prime}\), \(f_{yl}\), \(f_{yt}\) are the measured compressive strength of concrete, longitudinal steel and hoop steel tensile strength, respectively; \(\rho_{l}\) and \(\rho_{sv}\) denote the longitudinal steel ratio and hoop volumetric ratio; s stands for the hoop spacing; \(h_{T}\) denotes the hoop type of the RC column (\(h_{T}\) = 1 and \(h_{T}\) = 2 represent circular and spiral hoops, respectively).

Fig. 5
figure 5

Schematic of a circular RC column and corresponding hysteretic curve

Full size image

The key parameters of the I–M–K LP model should be included in the output vector Y. It has been demonstrated that the I–M–K model with suitable model parameter values is reasonably accurate for RC columns (Haselton et al. 2008; Liu and Li 2019). As illustrated in Fig. 5b, the I–M–K model is described in terms of the base moment (M) versus the chord rotation (\(\theta\)). It comprises an envelope with four branches (i.e., elastic, hardening, post-capping softening, and residual) as well as hysteretic rules. The envelope can be reasonably simplified as a trilinear one. Bending moment M is linearly proportional to the chord rotation \(\theta\) up to the yielding point (\(M_{y}\), \(\theta_{y}\)), then linearly increases to the capping point (\(M_{c}\), \(\theta_{c}\)) at a lower slope \(\alpha_{s} K_{e}\) (\(K_{e}\) denotes the elastic stiffness; \(\alpha_{s} \in [0,1]\) denotes the hardening ratio), and linearly drops to 30% of the maximum resistance (\(M_{r} = 0.3M_{c}\)) at a slope of \(\alpha_{c} K_{e}\) in the post-capping phase (\(\alpha_{c}\) denotes the softening ratio) (Lignos and Krawinkler 2011). Because most quasi-static tests are terminated when the resistance decreases to 80% or 85% of the maximum resistance to ensure safety (Gardoni et al. 2002; Liu and Guo 2021), \(\alpha_{c}\) can be calculated as \(0.2M_{c} /(\theta_{t} - \theta_{c} )/K_{e}\) (\(\theta_{t}\) denotes the chord rotation corresponding to 80% of the maximum resistance in the post-capping phase). Therefore, the backbone curve is characterized by five parameters, namely yielding moment \(M_{y}\) yielding rotation \(\theta_{y}\), capping moment \(M_{c}\) and rotation \(\theta_{c}\), as well as ultimate termination rotation \(\theta_{t}\). Therefore, the parameters defining the critical hysteretic properties are determined as the output vector:

$${\mathbf{Y}} = \{ Y_{k} \} = \{ M_{y} ,\theta_{y} ,M_{c} ,\theta_{c} ,\theta_{t} ,\Lambda \}$$
(3)

where \(\Lambda\) denotes the cyclic damage parameter for properly simulating the degrading load-deformation response. The envelope is extracted from the first cycle of the load deformation hysteretic curve; the mean of the curve in the positive and negative directions is determined using the observed model parameter value.

3.3 Empirical knowledge formulation

Empirical knowledge (or physical laws) is implemented to supervise the training process to reject any unqualified candidate PCMs. It should be mathematically formulated before implementing into the KENN training process. However, most empirical knowledge regarding the effects of RC column characteristics on mechanical properties are qualitative. For example, increased reinforcement strength corresponds to enhanced lateral strength. Thus, traditional methods incorporate assumptions regarding such relationships based on the subjective opinions of experts. To overcome this limitation, \(P_{phy} (\partial \hat{y}_{k} /\partial x_{j} )\) is defined to measure whether the trained model violates the known empirical knowledge laws, as follows:

$$P_{{phy}} (x_{j} ,\hat{y}_{k} ) = \left\{ {\begin{array}{*{20}c} {{\text{Accept,}}} & {\partial \hat{y}_{k} /\partial x_{j} \times \partial y_{k} /\partial x_{j} \ge 0} \\ {{\text{Reject,}}} & {\partial \hat{y}_{k} /\partial x_{j} \times \partial y_{k} /\partial x_{j} < 0} \\ \end{array} } \right.$$
(4)

where \(\partial \hat{y}_{k} /\partial x_{j}\) and \(\partial y_{k} /\partial x_{j}\) denote the partial differentials of the trained model and empirical knowledge law, respectively. If the trained model is consistent with empirical knowledge, i.e., all \(\partial \hat{y}_{k} /\partial x_{j} \times \partial y_{k} /\partial x_{j} \ge 0\), the trained model is accepted; otherwise, it is rejected. For example, the deformability of a specimen tends to increase with more reinforcement arrangements, such that \(\partial y_{k} /\partial x_{j} > 0\); if the trained model predicts a decrease to some extent, such that \(\partial \hat{y}_{k} /\partial x_{j} < 0\), then \(\partial y_{k} /\partial x_{j} \times \partial \hat{y}_{k} /\partial x_{j} < 0\) and will be rejected.

For simplification, the effects of the key characteristics on the I–M–K model parameters are divided into three categories: (1) positive, letting \(\partial y_{k} /\partial x_{j} = 1\); (2) negative, letting \(\partial y_{k} /\partial x_{j} = - 1\); (3) unsignificant or unclear, letting \(\partial y_{k} /\partial x_{j} = 0\). Based on previous studies (Iztok et al. 2006; Bae and Bayrak 2009; Acun and Sucuoglu 2010; Popa et al. 2014; Jin et al. 2019; Monserrat López et al. 2021), several qualitative trends regarding the mechanisms of RC columns are summarized as follows:

  1. 1.

    \(M_{y}\): positive factors are \(D_{c}\), \(D_{e} /D_{c}\), \(f_{c}^{{^{\prime } }}\), \(\rho_{l}\), \(f_{yl}\), and \(\rho_{sv} f_{yt}\), while a negative factor is \(\lambda\);

  2. 2.

    \(\theta_{y}\): positive factors are \(\lambda\), \(f_{c}^{{^{\prime } }}\) and \(f_{yl}\), while negative factors are \(D_{c}\) and \(s/D_{c}\);

  3. 3.

    \(M_{c}\): positive factors are \(D_{c}\), \(D_{e} /D_{c}\), \(\rho_{l}\), \(f_{c}^{{^{\prime } }}\), and \(f_{yl}\), while a negative factor is \(\lambda\);

  4. 4.

    \(\theta_{c}\): positive factors are \(\lambda\) and \(\rho_{sv} f_{yt}\), negative factors are \(n_{c}\), \(s/D_{c}\);

  5. 5.

    \(\theta_{t}\): positive factors are \(\lambda\) and \(\rho_{sv} f_{yt}\), negative factors are \(n_{c}\), \(f_{c}^{\prime}\), \(s/D_{c}\).

Other effects are assumed to be insignificant, nonmonotonic or unclear. For example, the resistance increases with increasing axial load ratio \(n_{c}\) when \(n_{c}\) is small, but decreases when \(n_{c}\) is large. Although the effects of \(n_{c}\) on \(M_{y}\) and \(M_{c}\) may be significant, they are neglected in this study.

Finally, the knowledge regarding the effects of the inputs on the outputs can be formulated into an empirical law matrix \({\mathbf{P}}_{phy} \left( {{\mathbf{X}},{\mathbf{Y}}} \right)\)

(5)

:

4 KENN-calibrated model for RC column

4.1 Test database

A test database with well-distributed inputs and outputs is required to develop a KENN model. The configurations and techniques of RC column tests may be different, and thus the specimens should be first standardized. Each specimen was transformed into its equivalent cantilever counterpart to obtain X and Y. In addition, only circular section specimens composed of concrete and steel bars (without any additives) and under both lateral cyclic loading and constant axial loading, were considered. For the outputs, the test hysteretic curve was carefully and consistently calibrated. For example, the yield point was determined according to a commonly used procedure (Sezen and Moehle 2004), and the point at which the resistance dropped to 20% maximum resistance was considered the termination point (Verderame and Ricci 2018; Liu and Li 2019).

A series of well-distributed specimens, i.e., those with characteristics across a diverse range, should be first collected into a test database \(\{ {\mathbf{X}}_{i} ,{\mathbf{Y}}_{i} \}\). For each specimen, the inputs \({\mathbf{X}}_{i}\) were determined according to basic test configurations and detailed descriptions in the original literature. The outputs \({\mathbf{Y}}_{i}\) were extracted from the corresponding tested hysteretic curves, wherein the envelope parameters were first calibrated to a monotonic resistance-deformation response, and the cyclic damage parameters were then determined according to the hysteretic curve. Based on the abovementioned criteria, a total of 276 specimens were collected from open literature (Goodnight 2015) and databases (Berry et al. 2004). Because of space limitation, the details of the specimens are not included herein but have been uploaded on GitHub for transparency purposes (https://github.com/liuzhenliang08/Circular-Column-Test- Database-for-KENN-model).

Figure 6a, the inputs and outputs of the specimens expand within a relatively wide engineering range. For example, the longitudinal reinforcement ratio was varied from 0.5 to 6.0%. In addition, the yielding moment varied from as low as 15–16,000 kN m. Admittedly, the distributions of these parameters are uneven. In particular, a majority of the specimens were tested at reduced scales, with 90% of them having diameters less than 0.7 m and only six specimens having diameters in the range of 0.7–1.5 m. Only 12 specimens had a span-to-depth ratio of 7–10, whereas 64 specimens featured a span-to-depth ratio of 4–5.

Fig. 6
figure 6

Characteristics of the test specimens’ input and output properties in the database

Full size image

Figure 6b depicts the correlation coefficients of inputs and outputs. It can be seen that the effects of section dimension on My and Mc are most obvious. However, the small correlation coefficients of several inputs do not necessarily represent minor effects. For example, the effect of \(f_{c}^{\prime}\) on Mc cannot be neglected despite their low coefficient of 0.10. This is due to the non-uniform distribution of the experimental database, where the presence of samples with extreme distributions disturbs the statistical results. Therefore, the database may not be able to objectively reflect the effects of inputs on the outputs across all intervals. This underscores the necessity of implementing empirical knowledge to enhance the capacity of neural networks.

4.2 KENN model training and testing

Training a KENN model not only minimizes the prediction errors but also satisfies the known empirical knowledge, which is a key factor for the reliability of the predictor. As illustrated in the flowchart of Fig. 4, for training the KENN model, 80% and 20% of the specimens in the test database were randomly divided into the training set and test set, respectively. The units and value ranges of the characteristics and model parameters were different and might result in non-objective evaluation of their relationships. To address this limitation, the characteristics and model parameters were scaled into the range of [− 1, 1]:

$$x_{j} = 2 \times \frac{{X_{j} - \min ({\mathbf{X}}_{j} )}}{{\max ({\mathbf{X}}_{j} ) - \min ({\mathbf{X}}_{j} )}} - 1,\;y_{k} = 2 \times \frac{{Y_{k} - \min ({\mathbf{Y}}_{k} )}}{{\max ({\mathbf{Y}}_{k} ) - \min ({\mathbf{Y}}_{k} )}} - 1$$
(6)

where \(x_{j}\) denotes the j-th normalized input characteristic; \({\mathbf{X}}_{j}\) denotes the j-th characteristic vector of the training set; \(y_{k}\) denotes the k-th normalized output parameter; \({\mathbf{Y}}_{k}\) is the k-th property vector of the training set.

Since there are no explicit available methods to determine optimal KENN architecture configurations (Morfidis and Kostinakis 2018; Liu et al. 2022b), several potential optimal candidates with 10–37 hidden neurons were selected, each of which was trained for PCMs. The optimal KENN was determined by comparing the PCMs. Other parameters were also adopted: (1) sigmoid function as the activation function; (2) gradient descent method in the backpropagation process; (3) termination condition when either error tolerance reaches 10−3 or the number of iterations reaches 104 times, (4) learning parameter, momentum parameter, and noise set to 0.15, 0.05, and 0.01. The quality of the model was measured using the following cost (loss) function:

$$Loss_{{{tot}}} (\hat{y}_{k} ,y_{k} ) = Loss_{{{obs}}} (\hat{y}_{k} ,y_{k} ) + Loss_{{{com}}} ({\mathbf{w}})$$
(7)

where \(Loss_{{{obs}}} (\hat{y}_{k} ,y_{k} )\) (\(\hat{y}_{k}\) and \(y_{k}\) were the predicted and observational outputs, respectively), and \(Loss_{{{com}}} ({\mathbf{w}})\) (\({\mathbf{w}}\) is the connection weight matrix) denotes the network complexity-related loss.

The KENN PCMs with different configurations were developed through the abovementioned procedure. Figure 7 depicts the comparison of the performance indices of the PCMs. The number of hidden neurons was crucial for developing the KENN model. Most developed PCMs could provide relatively reliable I–M–K model parameters, with RMSE ranging from 0.098 to 0.2506, and R2 ranging from 0.658 to 0.899 for the training and test sets. The optimal KENN is expected to have the minimum RMSE and the maximum R2 for both the training and test sets. The comparison indicated that the optimum KENN had 15 hidden neurons, yielding RMSEtrain = 0.098, \(R_{{{train}}}^{2}\) = 0.887 and RMSEtest = 0.101, and \(R_{{{test}}}^{2}\) = 0.893 for the training and test sets, respectively.

Fig. 7
figure 7

Comparison of the KENN PCMs with different configurations

Full size image

4.3 Comparison with purely data-driven model

The effectiveness and accuracy of the developed KENN model were further validated by comparing it with several commonly used purely data-driven backpropagation neural network (BPNN) methods. A BPNN model with similar configurations was developed using the test database through commonly used procedures (Liu et al. 2022c). For comparison purposes, the relative error of each specimen in the test set was calculated as follows:

$$\varepsilon {(}y_{k} {)} = \frac{{\hat{y}_{k} - y_{k} }}{{y_{k} }}$$
(8)

The figures in Fig. 8 provide the relative error distributions of the KENN and BPNN models. Notably, the BPNN model with RMSE and R2 in the ranges of [0.018, 0.142] and [0.871, 0.974], respectively, outperformed the KENN model to some extent, with to [0.027, 0.209] and [0.732, 0.941], respectively. However, most of the predicted errors for the moment resistance were less than 15%. For example, the RMSE and R2 of Mc by the KENN model were 0.018 and 0.941, respectively, whereas they are 0.018 and 0.974 of the BPNN model, respectively. This is because that there are less uncertainties (and discrepancies) in the observed resistances than in the rotation, both of the two models could accurately predict the resistance values. For example, the RMSE and R2 of \(\theta_{c}\) by the KENN model were 0.209 and 0.732, respectively, compared to 0.142 and 0.871 of the BPNN model.

Fig. 8
figure 8

Comparison of the I–M–K model parameters predicted by the developed KENN and purely data-driven BPNN model

Full size image

It is also noted that the test database did not cover the entire engineering range of RC column characteristics. Thus, it was hard to conclude that the BPNN model was actually better, although it performed well in both the training and test sets. Figure 9 illustrates the effects axial compression ratio \(n_{c}\) and hoop reinforcement factor \(\rho_{sv} f_{yt}\) on Mc and \(\theta_{t}\). As discussed in Sect. 3.3, the effects of these factors should not be neglected; the increasing \(n_{c}\) leads to a decreasing \(\theta_{t}\), and a larger \(\rho_{sv} f_{yt}\) corresponds to a smaller Mc and \(\theta_{t}\). As illustrated in Fig. 9a, the BPNN model predicted that \(\rho_{sv} f_{yt}\) had negligible effect on \(\theta_{t}\), and Fig. 9b illustrates the prediction by the BPNN model that Mc decreases with the increase of \(\rho_{sv} f_{yt}\) when \(\rho_{sv} f_{yt} > 18\). These trends are not consistent with empirical knowledge. By contrast, the effects predicted by the KENN model are more consistent with empirical knowledge.

Fig. 9
figure 9

Effects of several inputs on the outputs by the KENN and purely data-driven BPNN

Full size image

Therefore, the KENN methodology holds the potential to achieve better generalization performance, and obtain reliable I–M–K model parameters. Nevertheless, in contrast to purely data-driven methods that are efficient when equipped with large and fully representative training datasets (Yang et al. 2023), the KENN requires a thorough understanding of the domain-specific knowledge and may involve more intricate implementation process.

5 Model validation and application

5.1 Comparison using hysteretic curves

The KENN-calibrated model was further validated by comparing the obtained hysteretic curves for RC columns with observed results. For brevity, only two typical specimens from the PEER database (Berry et al. 2004) were selected. It should be noted that those specimens were not included in the KENN training set. Their hysteretic curves were obtained from quasi-static tests. Each of them was simulated in the OpenSees platform (Mazzoni et al. 2006) by integrating an elastic element and a rotational LP spring at the base, as illustrated in Sect. 2.1. The LP model parameters were calibrated by the developed KENN model. After imposing cyclic horizontal displacements on to the top of the specimen, the resistance can be recorded, and the predicted hysteretic curves were obtained.

The simulated hysteretic responses obtained using the KENN-calibrated LP model were compared with the quasi-static test data of the specimens. As can be seen in Fig. 10, the proposed KENN-calibrated method was able to capture the overall load-deformation response, especially the backbone, with reasonable accuracy. For example, the predicted onsets of stiffness hardening, and strength softening were consistent with the obtained results. However, some discrepancies were observed in the unloading and reloading phases of the specimens, as the example shown in Fig. 10b. This is because the hysteretic rules depended on the loading process. Moreover, there were some uncertainties inherent in RC column characteristics, calling more efforts to investigate the effects of hysteretic rules and uncertainties in future. Despite these drawbacks, the developed KENN model is still expected to improve the reliability and effectiveness of LP models of RC columns.

Fig. 10
figure 10

Numerical simulations of RC columns based on the KENN-calibrated I–M–K model

Full size image

5.2 Seismic response analysis of bridges

As illustrated in Sect. 2, the developed KENN model can also be used to assess the seismic response of bridges with the aim to facilitate fast and accurate post-earthquake numerical analysis. A three-span simply-supported bridge prototype, with three identical columns per pier, was analyzed as an illustrative example herein, as shown in Fig. 11. The prototype represents a typical bridge in seismic regions such as Western US and Japan, and has been used to represent a class of bridges (Nielson and DesRoches 2007a). For seismic response assessment, the horizonal ground motions will be split into orthogonal excitations. The vertical component of ground motions is not considered herein on the assumption that their effects are not significant at a distance from the near-field (Zhong et al. 2023).

Fig. 11
figure 11

Configuration and detail illustration of the bridge prototype used for validation

Full size image

To compare the efficiency and accuracy of the proposed parametric FEM, two bridge models, based on the fiber-based distributed plasticity model (commonly used model) and the KENN-calibrated LP model for pier columns, respectively, were established for nonlinear seismic response assessment using the OpenSees platform (Mazzoni et al. 2006). However, each column had two potential plastic hinge zones in the transverse direction because of the restraint of the capping beam and had one potential plastic hinge zone in the longitudinal direction. Therefore, two LP springs were assigned to the top and bottom of the pier column in the transverse direction. According to the detailed configurations, the KENN input parameters \(\{ D_{c} ,D_{e} /D_{c} ,\lambda ,n_{c} ,f_{c}^{{^{\prime } }} ,\rho_{l} ,f_{yl} ,\rho_{sv} f_{yt} ,s/D_{c} ,h_{T} \}\) of the two transverse LP springs were \(\{ 0.92,\;0.935,\;2.5,\;0.05,\;20.7\;{MPa},\;1.19\% ,\;414\;{MPa},\;83.8,\;0.33,1\}\). Accordingly, the LP model parameters calibrated using the developed KENN model in the above section were \(\{ 1439.9\;{kN}\;{m},0.51\% ,1692.8\;{kN}\;{m},1.77\% ,\;3.82\% \}\). Additionally, only one LP spring is assigned to the bottom of the pier columns in the longitudinal direction, with inputs \(\{ 0.92,\;0.935,\;5.0,\;0.05,\;20.7\;{MPa},1.19\% ,\;414\;{MPa},\;83.8,\;0.33,\;1\}\). The KENN-calibrated LP model parameters were \(\{ 1474.6\;{kN}\;{m},\;0.61\% ,\;1734.9\;{kN}\;{m},\;2.12\% ,\;5.40\% \}\). It is assumed that the soil type is B, with the horizonal stiffness of \(4.{13} \times {10}^{5} \;{\text{kN/m}}\) and rotational stiffness of \(3.{41} \times {10}^{{6}} \;{\text{kN}}\;{\text{m/rad}}\) for the horizonal and rotational springs, respectively.

Both KENN-calibrated FEM and common FEM were first used to conduct time response-history analyses under a selected ground motion (San Fernando earthquake, 1971, Lake Hughes #4 station, moment magnitude Mw = 6.61, duration 29.5 s, PGA scaled to 1.0 g) on a PC (Intel Core i5 2.50 GHz CPU 8 GB RAM). During that process, (1) convergence test with a tolerance of 10−8 and a max number of iterations of 20, and (2) Newton–Raphson solution algorithm are employed. It took 506 s for the common FEM with distributed plasticity model for pier columns, compared to 483 s for the KENN-calibrated FEM with LP model for pier columns. The FEM calculation duration was highly dependent on the number of iterations in the nonlinear phase, thus the calculation efficiencies of the two models are similar. If the bridge remains in the elastic range, the KENN-calibrated FEM will be more efficient.

Figure 12 depicts the time history response of the piers. As can be seen, the drift response histories obtained using the KENN-calibrated FEM (red solid line) matches well with those using the common FEM (blue dash line) based on fiber-based distributed plasticity model of pier columns. It should be noted that the KENN-calibrated FEM may underestimate the residual drift, especially in the longitudinal direction. This results from the discrepancies in the two models in terms of damage accumulation effects. However, it can be still be concluded that the responses from the two models were consistent with each other in both longitudinal and transverse directions. For example, the peak drifts using the common FEM and KENN-calibrated FEM were 1.31% and 1.28% in the longitudinal direction, respectively, and 0.63% and 0.59% in the transverse direction, respectively.

Fig. 12
figure 12

Comparisons of the pier time-history responses by different pier models of the bridge

Full size image

Further, for comparing the peak seismic demand in terms of drift of the examined pier columns, 160 real ground motions selected by Baker et al. (2011) were used as seismic excitations. Figure 13a shows several sample ground motion records, and Fig. 13b provides their individual and mean response spectra. As can be seen, they cover a wide range of frequencies, thus can comprehensively reflect the effects of earthquakes on bridges (Ramanathan 2012). Employing incremental dynamic analysis (IDA), each ground motion record is scaled to PGA of 0.1 g, 0.5 g, and 1.0 g, yielding 480 suites of seismic excitations.

Fig. 13
figure 13

Illustration of ground motion records and spectra of the 160 ground motions

Full size image

All of the ground motions are used to carry out time history analysis with the aim to identify the seismic demand. The results from the two FEM models are compared in Fig. 14a, b, with computation time of 420 h for the common fiber-based FEM compared to 321 h of the KENN-calibrated FEM. Similarly, it can be seen that the discrepancies between the two models increase with the seismic demands. This is because the LP model may be unable to capture the mechanical properties deeply within the nonlinear regime. Overall, the KENN-calibrated LP model is able to help provide reliable seismic response estimates for bridges at reduced computation costs.

Fig. 14
figure 14

Comparisons of the seismic demands of the bridge based on the two FEMs

Full size image

Comparing to traditional seismic demand assessment methods (Choi et al. 2004), while the calculation efficiency improvement from the KENN-calibrated LP model may not be highly pronounced, the utilization of parametric FEM reduces the fiber-based FEM complexity. Moreover, to account for the uncertainties inherent in structural characteristics and ground motions, traditional fragility analysis methods require rigorous FEM modeling and a large number of time history analyses, especially for the bridge portfolios assessed at a regional scale. In such scenarios, the KENN-calibrated FEM can serve as a more fitting alternative.

6 Conclusions

This study explored the possibility of using a parametric FEM for rapid seismic analysis of regular concrete bridges. This model was composed of several nonlinear springs and elements to numerically simulate the seismic behaviour of critical components. Its effectiveness and accuracy was demonstrated by comparing it with commonly used fiber models for the case of a well-studied bridge. For the LP model parameters of RC pier columns, this study explored a KENN methodology, which integrated both empirical knowledge and test data. The developed KENN model not only addresses the limitations of purely data-driven methods, but also reduced the requirements for extensive and high-quality training data. Therefore, the KENN method is more effective in seismic response analysis, and additionally, it can further reflect the physical laws of the mechanisms of RC columns.

However, the developed methodology presented some limitations that warrant future investigation, particularly in terms of (a) the fact that the LP model does not account for the varying axial load, (b) the KENN-calibrated model is not yet suitable for columns with non-circular sections, and (c) the integration of physical knowledge complicates the training process, requiring more efficient training algorithms.