1 Introduction

Barcelona is the second largest city in Spain and is located towards the Northeast of the Iberian Peninsula, on the Mediterranean Coast, between the Llobregat and Besòs Rivers and bounded to the West by the Serra de Collserola Mountain range. The city is divided into ten Districts and within the urban area it has approximately 1.6 million inhabitants (IDESCAT, 2022), and over 66,000 buildings (SEC 2021).

Although Barcelona has mostly been perceived as a city of low seismicity because of the lack of recent earthquakes, the historical perspective of the region spells a different story. A seismic crisis began in Catalonia at the end of February 1427 lasting until August 1428 (Perea 2009) which was one of the most destructive seismic episodes that has happened in the North-eastern Iberian Peninsula (Cadiot et al. 1979; Banda and Correig 1984; Olivera et al. 2006). More recently, lower intensity earthquakes that did not cause any damage to the infrastructure, nor fatalities, have occurred in the surroundings of Barcelona such as the MW 4.6 earthquake on 15th May 1995, and Ml 4.0 earthquake on 21st September 2004, with focal distances of 73.4 and 104.5 km, respectively with nearby faults that can trigger much larger magnitudes.

The earthquake risk of Barcelona has been recently reassessed with a probabilistic approach in the framework of PI-PLATES,Footnote 1 a local project to generate data for prospective disaster risk management and territorial planning (Salgado-Gálvez et al. 2022). For this task, an updated earthquake hazard model based on the SHARE dataset (Woessner et al. 2015) was developed, including the city’s microzonation (Cid et al. 2001), yielding an event-set with multiple ruptures characterized by their location, depth, orientation, and occurrence frequency. Also, a high-resolution and building-by-building exposure database has been developed for the city based on official and updated cadastral information (Ajuntament de Barcelona 2021). The detailed exposure model allowed the definition of all relevant attributes such as height (in terms of number of stories), year of construction, construction material, and structural system. Finally, an economic appraisal was carried out to estimate the replacement cost of each building making use of official information from the cadastral office of the city, disaggregated at census section (SC), which corresponds to the smallest administrative level of the city.

Different specific earthquake studies have been developed in the past for Barcelona over the past 20 years. Most of those have been vulnerability analyses focused on the development of fragility curves (Barbat et al. 2006, 2008, 2010; Pujades et al. 2012; Vargas et al. 2013, 2020; Gonzales-Drigo et al. 2015; Moreno-González and Bairán, 2015), although there have been other studies that have quantified earthquake risk in monetary terms (Lantada et al. 2009, 2018; Marulanda et al. 2013; Vargas et al. 2020; Aguilar-Meléndez et al. 2019, 2022). Although these studies have provided valuable information regarding earthquake vulnerability and risk in Barcelona, a major limitation is that the city has not been struck by any major earthquake for over hundreds of years, so little if any validation or calibration procedures have been performed to assess the validity of the results, particularly for the vulnerability models.

This paper aims to present an objective and quantitative comparison of earthquake risk results in Barcelona after using different sets of vulnerability functions for masonry and reinforced concrete (RC) units, while using common hazard and exposure datasets and risk assessment methodology. Although the vulnerability functions used for the comparisons included in this paper are representative for masonry and RC buildings only, it must be noted that these two building classes account for more than 97% of the building stock in the urban area of the city (Barbat et al. 2008). For the comparisons, three cases have been analysed (namely, Comparison 1, Comparison 2, and Comparison 3), where a total of 32 vulnerability functions have been utilised. Out of the 32 vulnerability functions used in the comparisons in this research, 11 were obtained from fragility curves published in previous studies for the city using the consequences’ functions (i.e., loss ratios) proposed by Dolce et al. (2006).

In Comparison 1, three different vulnerability sets are considered: (i) one derived from the fragility curves after Barbat et al. (2006; 2008) for masonry and RC buildings of Barcelona; (ii) one from a previous earthquake risk assessment in Barcelona (Marulanda et al. 2013), and (iii) the vulnerability functions set assigned to Spain in the framework of the UNDRR’s Global Assessment Report on Disaster Risk Reduction—GAR13 (CIMNE et al. 2013; Cardona et al. 2014).

Comparison 2 is a typology and building class-specific assessment for reinforced concrete high-rise (RCH) buildings, for which vulnerability functions developed after the fragility curves by Vargas et al. (2013) were included. For Comparison 2, the exposure model was filtered to only include the RCH buildings.

Finally, Comparison 3 is a typology, building class and District specific assessment for masonry high-rise (MH) buildings, for which vulnerability functions were developed after the fragility curves by Gonzales-Drigo et al. (2015) and Moreno-González and Bairán (2015). All risk assessments were carried out using the R-CAPRA software (ERN 2022), which implements the event-based risk assessment framework by Ordaz, (2000), which details are available in English at Salgado-Gálvez et al. (2014a) and that can be applied at different resolution levels (see for instance Ordaz et al. 2014; Cardona et al. 2014; Salgado-Gálvez et al. 2014a, b; 2016; Ordaz et al. 2019). The earthquake loss comparisons have been made in terms of the average annual losses (AAL) and the 500-year return period losses. Figure 1 shows a summary of the analysed cases.

Fig. 1
figure 1

Summary of the three comparisons

Full size image

2 Probabilistic seismic hazard analysis

For this study, a probabilistic seismic hazard analysis (PSHA) was developed considering seismogenic sources in Spain, France, and North Africa. Seismicity data and models were adapted from the SHARE project datasets (Woessner et al. 2015) and implemented in the well-known PSHA program R-CRISIS (Ordaz et al. 2021, 2022). A seismic microzonation is available for Barcelona (Cid et al. 2001), and site-effects have been included in this study to obtain a more comprehensive representation of the earthquake hazard and risk levels at urban level. There are different approaches to include site-effects in event-based PSHA and risk assessments, such as the ones described in (Ordaz et al. 2022). For this case and considering the soil zones defined by (Cid 1998; Cid et al. 2001), spectral transfer functions were obtained and used to estimate the ground motion intensities at the surface level. Figure 2 shows the amplification functions assigned to each zone of the city. For areas with rock condition (Zone 0), the amplification factor is equal to 1.0.

Fig. 2
figure 2

Spectral transfer functions for the different soil zones in Barcelona

Full size image

Although more recent microzonation studies have been published for Barcelona (Cadet et al. 2011; Pinzón et al. 2019), in this study we have preferred the approach by Cid et al. (2001) which is based on numerical modelling of 70 soil columns with the 1D equivalent linear method, that allowed defining transfer functions, indexed to PGA, for each of the soil zones, instead of horizontal-over-vertical ratio on noise, or predominant soil periods only.

Figure 3 shows the earthquake hazard maps for 475-year return period in terms of peak ground acceleration (PGA) and spectral acceleration (Sa) at T = 0.5 s for Barcelona including the site-effects. From these two maps, which are depicted for surface conditions and the same return period, the differences in the hazard level because of the soil amplification are clear and therefore, the relevance of its consideration when carrying out a high-resolution earthquake risk assessment, such as the one presented in this study, becomes evident.

Fig. 3
figure 3

Earthquake hazard maps for 475-year return period, a for PGA and b Sa at T = 0.5 s on soil (in cm/s.2)

Full size image

The main outcome of this PSHA is a stochastic event-set, which constitutes a collectively exhaustive and mutually exclusive list of earthquake ruptures with different locations, depths, magnitudes, shapes, areas, orientations, and occurrence frequencies. Figure 4 shows the epicentres and MMax values of all the synthetic earthquakes included in the event-set and that have been used to estimate, in a probabilistic manner, the future earthquake losses in the study area.

Fig. 4
figure 4

Epicenters and Mmax values from the stochastic event-set

Full size image

3 Development of the exposure model

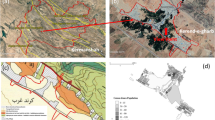
A high-resolution and building-by-building exposure model was developed for the building stock of Barcelona in the framework of the PI-PLATES project, as shown in Fig. 5 for the buildings within a specific district in the city.

Fig. 5
figure 5

Spatial distribution of buildings classes at Eixample District

Full size image

The exposure model includes all urban buildings present in the cadastral database, excluding monuments, stadiums, and other special purpose buildings. Buildings have been classified into six categories based on their primary use (i.e., residential, agricultural, industrial, office, commercial, and public buildings). Figure 6 shows the number of buildings belonging to each of these main use categories, by District. Even if most of the buildings are classified as residential, it is common to find offices and/or commercial activities in them, especially at the ground floors.

Fig. 6
figure 6

Number of buildings by primary usage in each District

Full size image

According to the Risk-UE project (Milutinovic and Trendafiloski 2003) the most common building type in Barcelona is unreinforced masonry with different types of floor systems: timber (32%), masonry vaults (18%), steel or timber beams with masonry vaults (26%) and RC beams and masonry vaults (1%). According to (Moreno-González and Bairán, 2015) most of these masonry buildings have an average age of 80 years and were designed and built without considering any earthquake resistant criteria. In summary, masonry is the most representative type of building in the central area of Barcelona, where the Eixample District is located, and whose large number influences the overall earthquake vulnerability and risk of the city. These buildings were designed mostly only for vertical static loads, without considering seismic design criteria (Dimovska et al. 2021). RC buildings, which are considerably fewer, are prevalent in the newer districts of the city (e.g., Nou Barris, Sant Andreu, and Sant Marti).

3.1 Definition of the building typologies

In the exposure model the typologies were attributed to the buildings using the Risk-UE classification, and based on the construction year. The sub-classifications of the typologies in the exposure model are the following: simple masonry with wooden slab -M31- (Low-rise (L), Mid-rise (M), and High-rise (H)), simple masonry with vaults -M32- (L, M, H), simple masonry with composite slab -M33- (L, M, H), simple masonry with reinforced concrete slab -M34- (L, M, H), and reinforced concrete frames -RC32- (L, M, H).

To adapt the full exposure model with all buildings within the urban area of Barcelona for the purpose of this study, two procedures were carried out. Firstly, it was filtered such that only masonry and RC buildings were included; and secondly, the typologies were simplified and broadly categorized into groups such as masonry low-rise (ML), masonry mid-rise (MM), masonry high-rise (MH), RC low-rise (RCL), RC mid-rise (RCM) and RC high-rise (RCH) as shown in Table 1. For each building class, a representative fundamental period was assigned based on the estimations by Milutinovic and Trendafiloski (2003).

Table 1 Building typologies, classes, and fundamental periods
Full size table

3.2 Economic appraisal

An economic appraisal in terms of replacement cost for the exposed assets has been carried out by making use of updated data from the cadastral office of the city of Barcelona (Ajuntament de Barcelona 2021). The replacement cost was taken as the mean cadastral value, in €/m2 for each of the over 1000 census section (SC) of the city, allowing to capture the differences at the most detailed administrative level. Table 2 shows the minimum and maximum values per square metre of the corresponding SC at each District.

Table 2 Minimum and maximum mean cadastral value (€/m2) by SC
Full size table

The total number of buildings included in this study is 66,378 with an estimated replacement cost of €134.1 billion, which is approximately 4.25 higher than the value estimated by Marulanda et al. (2013), which is a study that adopted a much more simplified procedure for estimating the value at risk and that did not reflect variations in the replacement costs as a function of the building typologies. Figure 7 shows the replacement costs by District in the study area.

Fig. 7
figure 7

Exposed value (replacement cost) for the ten Districts of Barcelona

Full size image

3.3 Exposure model statistics

The number of masonry buildings is considerably higher than the number of RC buildings, as shown in Fig. 8, whereas the two building classes with the highest value at risk are RCH and MH, comprising of 44% and 32% to the total exposed value, respectively, as shown in Fig. 9. The Eixample District has the highest exposed value, whereas Nou Barris District the lowest. The highest number of buildings are present in Horta-Guinardo, although with a much lower total exposed value.

Fig. 8
figure 8

Total number of buildings per District and building class

Full size image
Fig. 9
figure 9

Replacement cost by building typology and District

Full size image

4 Available vulnerability models

Over the past two decades, various authors have developed vulnerability models for Barcelona that have been used in previous earthquake studies (Bonett et al. 2006; Moreno 2007; Barbat et al. 2008; Pujades et al. 2012, 2015; Vargas-Alzate et al. 2013; Gonzalez-Drigo et al. 2015; Moreno-González and Bairán 2015). Many of those studies have used the fragility curves by (Barbat et al. 2008) to carry out local risk assessments, or to provide recommendations for large scale ones (Lantada et al. 2009; 2018; CIMNE et al. 2013; Marulanda et al. 2013; Cardona et al. 2014).

Within the event-based risk assessment framework proposed by (Ordaz 2000) earthquake vulnerability must be represented in a continuous, qualitative, and probabilistic manner, the reason why vulnerability functions are needed. Vulnerability functions can be derived from other representations, such as fragility curves and probability matrices (Ordaz 2008). A summary of the available vulnerability models for Barcelona by different authors is presented next, where also a description of the procedure to convert from fragility curves to vulnerability functions, if applicable, is included.

4.1 Barbat et al. (2006)

The fragility curves by (Barbat et al. 2006; 2008) were developed after collecting and assessing an extensive database of current buildings falling under the two main types of buildings: unreinforced masonry and RC. Thereafter, a set of buildings from various building classes were computationally modelled using the computer program TREMURI (Lagomarsino et al. 2013) for masonry buildings, and RUAUMOKO (Carr 2007) for RC ones. The seismic performance of each building was characterized through the capacity spectrum method, obtained using a bilinear pushover analysis. Fragility curves were reproduced using the values in Table 3 and using Eq. 1.

Table 3 Fragility parameters after Barbat et al., (2006)
Full size table

The subsequent vulnerability functions can be generated by following the procedure described by Eqs. 1 and 2, where the lognormal fragility is described by the following equation as per Barbat et al., (2008).

$$Probability of exceedance=\Phi \left(\frac{1}{\beta }\bullet \left(ln\left(\frac{x}{IM}\right)\right)\right)$$
(1)

where, \(\Phi \) is the lognormal distribution, \(x\) the mean, \(IM\) the intensity measure, and β the standard deviation.

$$Sa= {\left(\frac{2\pi }{T}\right)}^{2}\times Sd$$
(2)

where, Sa is the Spectral acceleration (in g), Sd is the spectral displacement (in cm), and T(s) is the period of the building (in seconds).

4.1.1 Consequence model

Once the fragility curve is computed, the next step is to convert it into a vulnerability function. For this purpose, a consequence model (or damage-to-loss model) is required, and this study made use of the one by Dolce et al. (2006) which values are shown in Table 4. The damage states (DS) of the fragility curves were matched with the corresponding values proposed by Dolce et al., (2006). Figure 10 schematically depicts the conversion from fragility curves to vulnerability functions. The derived vulnerability curves after the fragility curves of Barbat et al., (2006) are shown in Fig. 13a–f.

Table 4 Loss ratios after Dolce et al. (2006)
Full size table
Fig. 10
figure 10

Development of a vulnerability function from fragility curves. a Fragility curves for four DS, b conversion from fragility curves to vulnerability curves, c vulnerability function

Full size image

The statistical moments required to calculate loss are computed using Eqs. 3 and 4 (Ordaz 2008).

$$E\left(L|S\right)= \sum_{i=0}^{n}{L}_{i}\mathrm{ Pr}(DS=d{s}_{i}|S)$$
(3)
$${SD}^{2}= \sum_{i=0}^{n}{({L}_{i}-E(L|S)}^{2}\mathrm{ Pr}(DS=d{s}_{i}|S)$$
(4)

where E(L|S) represents the expected value of the loss, L, given a seismic demand S, DS the damage state, and SD the standard deviation.

4.2 Marulanda et al. (2013)

In the work by Marulanda et al. (2013) the vulnerability functions were defined by relating the mean loss ratio (MLR) to the ground motion intensity in terms of Sa. Thus, for a given building type, the MLR was calculated using the parameters provided by Miranda (1999) and Ordaz (2000). The vulnerability functions for several building classes were chosen from the CAPRA Platform library, which were originally intended and developed for Central America, and are shown in Fig. 13a–f. Since this vulnerability representation is suitable for the comparisons of this paper, no changes were made. Different studies have been published regarding the selection and use of existing vulnerability functions in other locations different from where they were developed for (Rossetto et al. 2014, 2015; Meslem et al. 2015; Stone et al. 2017) clearly indicating the shortcomings and limitations. About this specific vulnerability dataset, it is worth noting that the buildings for which the vulnerability functions were developed are quite different to the ones found in Barcelona, as well as the earthquake resistant code levels and enforcement.

4.3 GAR13

The vulnerability functions from GAR13 were derived following the HAZUS methodological approach (FEMA 2003; CIMNE et al. 2013). In this method, fragility curves were derived first, and then subsequently each vulnerability function was modified to use spectral acceleration as a seismic intensity measure. To do so, the methodology proposed by Miranda (1999) was employed. The vulnerability functions assigned in the GAR13 model for the building stock of Spain were used directly to carry out the risk assessments and are shown in Fig. 13a–f.

4.4 Vargas-Alzate et al. (2013)

Vargas-Alzate et al. (2013) modelled an eight-storey RC structure with a waffle slab using two approaches: a simplified non-linear static method, and a non-linear dynamic analysis method. By doing so, it was possible to evaluate the influence of uncertainties due to the seismic action and then, develop the fragility curves. The fragility curves used in this comparison are based on the deterministic values for which the parameters are shown in Table 5. The derived vulnerability function is shown in Fig. 13f.

Table 5 Fragility parameters after Vargas-Alzate et al., (2013)
Full size table

4.5 Gonzalez-Drigo et al. (2015)

This set of vulnerability functions was derived after the fragility curves developed by Gonzalez-Drigo et al. (2015). During the development of the Eixample District, buildings were typically built in the form of blocks. In these blocks there are buildings located at the central and corner positions, as shown in Fig. 11. The fragility curves by Gonzalez-Drigo et al. (2015) consider the relative location of the building within each block and thus, the exposure model for the MH analyses was further sub-classified into central buildings (MH-M01 and MH-M02), and corner buildings (MH-M03), so that the vulnerability models could be assigned appropriately.

Fig. 11
figure 11

Classification of MH buildings as per their location in the building blocks at Eixample District after Gonzales-Drigo et al. (2015)

Full size image

These fragility curves were derived for the X and Y directions, although for the purpose of this analysis, we only utilized the ones that produced the worst-case scenario to develop the vulnerability functions shown in Fig. 13c with the parameters shown in Table 6. It is beyond the scope of this paper to consider the directionality effects within the earthquake hazard and risk assessment.

Table 6 Fragility parameters after Gonzales-Drigo et al., (2015)
Full size table

4.6 Moreno-González and Bairán (2015)

Fragility curves for seven-story buildings were derived after Moreno-González and Bairán (2015). The buildings were further sub-classified based on the dimensions of the central buildings as shown in Fig. 12. The construction technique used for these buildings did not leave any gap between (i.e., buildings share sidewalls without any clearance), forming aggregate building blocks that interact under lateral loads. The fragility curves were derived for the X and Y direction, although for the purpose of this analysis, only the fragility curves that produced the worst-case scenario were used to derive the vulnerability functions shown in Fig. 13c with the parameters shown in Table 7.

Fig. 12
figure 12

Classification of MH buildings as per their location in the building blocks at Eixample District after Moreno-González and Bairán, (2015)

Full size image
Fig. 13
figure 13

Comparison vulnerability functions. a Masonry low-rise. b Masonry mid-rise. c Masonry high-rise. d RC low-rise. e RC mid-rise. f RC high-rise

Full size image
Table 7 Fragility parameters after Moreno-González and Bairán (2015)
Full size table

From the comparisons shown in Fig. 13a–f, clear differences and similarities can be observed between the vulnerability functions used in this paper. The most evident one has to do with the definition of no-damage threshold (i.e., the Sa up to where no losses are expected). In general, those vulnerability functions of GAR13 have a higher no-damage threshold which is reflected in considerably lower AALs (since the occurrence frequency of small earthquakes is higher in the stochastic event-set, if compared to moderate and large events). Another clear difference has to do with the steepness of the function (i.e., how smooth, or abrupt is the transition between small and large losses), for which again, the GAR13 dataset in general shows lower values.

Qualitatively there are many differences in the compared models, arising from the fact that the vulnerability modelling for each case has followed different strategies. For instance, Barbat et al. (2006) was developed as a result of local knowledge that pertains to the buildings at the Eixample District in Barcelona and making use of local building surveys, structural systems, etc. This is certainly much better than the generalized vulnerability models such as Marulanda et al. (2013), and GAR13. As will be shown in the following section, despite the quantitative differences between the vulnerability datasets, they produce results that are consistent across the districts.

5 Results

The results and comparisons of the risk assessments carried out are discussed in detail next. These comparisons were all made in terms of: (1) the loss exceedance curves (LEC) that provide a relationship between the loss values and their annual exceedance frequencies; (2) the average annual loss (AAL), which is a robust indicator to represent risk at various resolutions and the overall risk participation of low and frequent events as well as high and infrequent events, calculated as the area under the LEC, and, (3) the 500-year return period losses.

5.1 Comparison 1

Figure 14 shows the LEC for each of the vulnerability datasets, whereas Fig. 15 and Table 8 show the loss results in terms of both relative and absolute AAL and the 500-year return period loss. The comparison of the results is bounded by the low AAL’s after using the GAR13 vulnerability dataset, and the very large AAL’s after using the functions by Marulanda et al., (2013).

Fig. 14
figure 14

LECs for Comparison 1

Full size image
Fig. 15
figure 15

Absolute and relative AAL for Comparison 1

Full size image
Table 8 Relative and absolute AAL and 500-year return period losses for Comparison 1
Full size table

Earthquake losses for Comparison 1 have been aggregated at District level for each of the three vulnerability datasets. Figure 16 shows the relative AAL by District from where considerable differences in the results are found depending on the vulnerability functions used, being systematic across all districts. Except for Les Corts District, the vulnerability dataset by Marulanda et al. (2013) yields the highest earthquake risk results, followed by the one by Barbat et al. (2006). As previously explained, this difference can be because of the use of vulnerability functions developed for a very different seismotectonic environment, and for a region where earthquake resistant design highly differs from that one in Spain.

Fig. 16
figure 16

Relative AAL by District for Comparison 1

Full size image

In all districts, the vulnerability dataset after GAR13 yields the lowest earthquake risk results by factors of up to 10, which can be explained by the assumption in that model of updated and high enforcement levels of building codes in Europe, which is not necessarily the case for Spain. Also, the vulnerability dataset after Marulanda et al. (2013) yields the highest risk results in all districts except for Les Corts, which can be explained by two reasons: first, it is a vulnerability dataset that was developed for a very different region than Spain and that was used without any modifications, and second, that the share of RC buildings at that district is considerably higher than in the others, and as will be shown later in Comparison 2, the vulnerability datasets after Barbat et al. (2006) yield larger earthquake risk estimates for that type of buildings.

Comparison 1 results have also been disaggregated by typology and their respective building classes, as shown in Fig. 17, allowing the identification of the common building classes with the highest AALs.

Fig. 17
figure 17

Disaggregation of the results produced from each vulnerability dataset per building class for Comparison 1

Full size image

MH buildings show high AAL in all the three cases, which can be explained by the large number of unreinforced buildings built during the pre- to low-code period, although in recent times many RC buildings with waffle slabs have substituted the demolished unreinforced masonry buildings. For the case of RCH, the functions after Barbat et al. (2006) show higher AAL as compared to the other two datasets, which can be explained by the existence of buildings with waffle slabs, that fall within the high vulnerability part of the European Macroseismic Scale, EMS-98 (Grünthal, 1998). Apart from the Eixample District, such buildings can be found in a significant number in Districts with a more recent development, such as Sarria-Sant Gervasi, and Sant Marti.

Table 9 summarizes the common building classes identified with potentially higher AALs for each of the vulnerability datasets.

Table 9 Building classes with the highest relative and absolute AAL
Full size table

5.2 Comparison 2

Comparison 2 was carried out to further investigate the modelled losses for the RCH buildings. From Comparison 1, it was observed that the losses estimated by the Barbat et al. (2006), dataset, particularly for the RCH class of buildings are higher than with the other two vulnerability datasets.

For this comparative analysis, a filtered database that only included the RCH buildings of Barcelona was used. The filtered exposure model includes 11,965 buildings for which their replacement cost is approximately €60 billion, which is equivalent to 44% of the total exposed value of Barcelona, while only accounting for 18% of the buildings.

Figure 18 shows the LECs for each of the vulnerability datasets in this comparison, whereas Fig. 19 and Table 10 show loss results in terms of both relative and absolute AAL and 500-year return period loss. As shown in Fig. 20, a significant reduction in losses arising from RCH exists when vulnerability functions by Vargas-Alzate et al., (2013) are used, since those buildings show a higher seismic resistance capacity if compared to the vulnerability dataset by Barbat et al. (2006) for the same type of buildings.

Fig. 18
figure 18

LECs for Comparison 2

Full size image
Fig. 19
figure 19

Absolute and relative AAL for Comparison 2

Full size image
Table 10 Relative and absolute AAL and 500-year return period losses for Comparison 2
Full size table
Fig. 20
figure 20

Relative AAL by District for Comparison 2

Full size image

An interesting finding of Comparison 2 is that the ranking of the earthquake risk results by vulnerability dataset is consistent along all Districts. In all cases, the RC vulnerability functions by Barbat et al. (2006) yield the highest risk levels by factors larger than 10, followed by the vulnerability models of Marulanda et al. (2013), GAR13, and Vargas-Alzate et al. (2013). The considerable differences in the non-damage thresholds and steepness of the vulnerability functions in each case, explain these findings.

5.3 Comparison 3

Comparison 3 further investigates MH buildings at the Eixample District, where unreinforced brick masonry buildings constitute approximately 70% of the building stock (Lantada 2007), with many of these structures built over 100 years ago and representing an integral part of the architectural heritage of the city.

For this comparative analysis, a second filtered exposure model was used, including only the MH buildings within the Eixample District. These buildings were further sub-classified into MH-M01, MH-M02 and MH-M03 after Gonzales-Drigo et al., (2015) and into MH-NB, MH-WB, and MH-CB after Moreno-González and Bairán, (2015), as previously explained.

Figure 21 shows the LEC for each of the vulnerability datasets in this comparison, whereas Fig. 22 and Table 11 show the results in terms of both relative and absolute AALs, and the 500-year return period loss.

Fig. 21
figure 21

LECs for Comparison 3

Full size image
Fig. 22
figure 22

Absolute and relative AAL for Comparison 3

Full size image
Table 11 Relative (‰) and absolute (ABS) AAL and 500-year return period absolute and relative (%) losses for Comparison 3
Full size table

6 Conclusions and discussion

In this paper we carried out a comparative, quantitative, and probabilistic earthquake risk assessment for Barcelona. For this purpose, we utilized a high-resolution exposure model for public and private buildings in Barcelona, which made use of the latest census data available and reflects an updated economic appraisal in terms of replacement cost. Making use of existing vulnerability models for representative buildings of Barcelona, and with a quantitative and probabilistic risk assessment this study compared the earthquake losses through probabilistic risk metrics, finding large differences, some of them systematic across the analysed districts.

The earthquake hazard and exposure data were kept constant for the three comparisons. Thus, there is no variability that arises from these components of the modelling scheme. Also, the same consequence model (Dolce et al. 2006) was used in the derivation of vulnerability functions from fragility curves. Therefore, it can be concluded that all differences arise from the fact that most of the fragility and vulnerability studies have only considered certain specific buildings, different structural modelling strategies and levels of detail.

In the absence of historical earthquake losses, it is not possible to objectively conclude which of the earthquake vulnerability models used in the three comparisons shown in this paper reflects the characteristics of the buildings in Barcelona in a better manner. However, the results can guide the selection of the vulnerability models to be used; by comparing the results of this paper to those of other locations with better historical earthquake loss data. For instance, the results by Marulanda et al., (2013) for Barcelona, are within the order of magnitude of earthquake losses obtained at locations of high-seismicity and with high vulnerability such as in Peru, Mexico, and Colombia (Salgado-Gálvez et al. 2014a, b, 2017; Ordaz et al. 2019), indicating a possible overestimation of earthquake losses in Barcelona with that model.

Most of the previous research about earthquake vulnerability in Barcelona has been focused on mainly buildings at Eixample District. However, there are other districts that despite not having an equivalent architectural and heritage value, are home to most of the population of the city and have not been studied in detail (i.e., adopting refined structural modelling strategies, considering architectural building-to-building variations, suitable ground motion selection and subjecting the models to bi-directional components of the ground motion) and that should be considered in future earthquake vulnerability and risk assessments to better understand their particularities and differences, allowing the development of specific models that can be used in future earthquake risk assessments.