1 Introduction

As demonstrated by the recent earthquakes occurred in different areas of the Italian territory, industrial structures represent a structural typology at high seismic risk (Buratti et al. 2017). In particular, steel structures usually exhibit a better response to seismic action than precast concrete ones (Formisano et al. 2015), as damages produced by Emilia earthquake in 2012 have highlighted (Savoia et al. 2017). However, if designed without any seismic criteria, even steel structures can undergo severe damages and collapses under seismic actions (Formisano et al. 2017). For this reason, recent works are focusing on developing strategies for estimating the seismic vulnerability of steel structures in both residential (Annan et al. 2009; Silva et al. 2020; Nazri et al. 2017) and industrial areas (Formisano et al. 2019, 2022).

Within the framework of urban scale seismic vulnerability estimate, empirical methods, based on input data obtained through observed damages after past earthquakes, are usually adopted (Zuccaro et al. 2020; Li and Chen 2023; Li 2023). Empirical methods provide the probability of occurrence of a certain damage state for varying seismic intensity as discrete damage probability matrices or continuous fragility functions. Usually, this information is given for vulnerability classes, easily recognised to within a building stock. Many empirical methods are available, related to the most frequent structural typologies, as reinforced concrete (Rosti et al. 2021a; Li and Formisano 2023) or masonry (Perelli et al. 2019; Rosti et al. 2021b; Li and Gardoni 2023) buildings.

However, the statistically low number of post-earthquake damage data and the high variability of the typological features of industrial steel structures prevent empirical methods to be used. An alternative is provided by mechanical-based methods (Polese et al. 2008; Rota et al. 2010). As opposite to the empirical ones, these approaches consist in defining numerical models of the structures under consideration which are then analysed to obtain the damage level (D’Ayala and Speranza 2003; Lagomarsino and Giovinazzi 2006; Frankie et al. 2013; Asteris et al. 2014; Simões et al. 2015; Furtado et al. 2016). Uncertainties, that are intrinsically present in empirical methods, need to be explicitly considered and propagated in mechanical models. In fact, random and epistemic uncertainties affect the geometry, the mechanical properties, the seismic action, the damage grades identification and many other aspects involved in the construction of mechanical-based fragility functions (Baker and Cornell 2008). The uncertainties propagation increases the computational cost of the fragility analysis with respect to the analysis of a single building, since numerical simulations need to be repeated many times (Cosenza et al. 2005; Polese et al. 2012). For this reason, the availability of efficient numerical models that allow to reduce the computational cost is of great importance.

The construction of the numerical models can be performed in different ways. One option is to select some index buildings, namely actual buildings taken as representative of a class. In such a case, the advantage is that the analysis is conducted on real buildings, but on the other hand, the proper selection of the index buildings is not an easy task and can significantly influence the results of the vulnerability analysis. Alternatively, it is possible to refer to the so called archetype buildings, ideal representation of the building stock (Leggieri et al. 2021; Ruggieri et al. 2022). In this case, parametric models are constructed and the relevant parameters are changed within properly tuned ranges of variations to cover the possible configurations of the real structures. Other approaches for large scale vulnerability analyses are worth mentioning, as the hybrid methods that combine empirical observation and mechanical analyses (Kappos et al. 2006), or vulnerability analyses using machine learning techniques (Ruggieri et al. 2021).

One of the main advantages provided by mechanical-based approaches over the empirical ones is represented by the possibility of considering structural typologies for which little post-earthquake real damages are available. This is the case of industrial steel structures, for which mechanical-based fragility curves have been recently proposed by Formisano et al. (2019, 2022).

A relevant aspect to be considered in vulnerability analyses conducted on relatively large areas is represented by the data required for their application. In Italy a recent project carried out by Italian Civil Protection and many Italian universities are being devoted to collecting typological data using the Cartis form (Zuccaro et al. 2015; Zuccaro et al. 2023). In its database (Cartis 2024), many relevant information on building typologies are available regarding both large areas, called compartments, and single structures. Thanks to its features, Cartis form has been recently used in medium-large territorial scale vulnerability analyses (Olivito et al. 2021; Formisano et al. 2021; Sandoli et al. 2022; Chieffo et al. 2021). Interestingly, Cartis database also includes information on industrial structures by the Cartis long-span (GL) form. The effort in collecting data using Cartis GL form remarks the interest of civil protection departments on the vulnerability of these structural typologies and provides many information of reliable vulnerability assessment strategies.

Among the long-span industrial structures, a quite widespread typology is represented by steel structures designed without any seismic criteria and characterised by the total absence of bracings, but with masonry infill along the entire perimeter. As it is well known, infill provide a certain resistance to horizontal actions (Di Sarno et al. 2021) and therefore likely represent the main seismic resistant structural component for this typology. In fact, secondary elements, can play a significant role on the fragility of civil (Uva et al. 2012) and industrial (Babič and Dolšek 2016) buildings. However, to the best of the authors’ knowledge, no specific study is available in the literature to assess their seismic vulnerability.

Starting from the premises discussed above, this work focuses on the seismic vulnerability of industrial steel structures with masonry infills. Since no sufficient empirical data are available for this structural typology, a mechanical-based approach is adopted. The starting point is the exposure analysis conducted by using the CARTIS-GL form (Formisano et al. 2022). Then, Finite Element (FE) models are constructed, considering both geometrical and material nonlinearities. Geometrical nonlinear phenomena can be relevant in the seismic behaviour of many structural typologies characterised by high slenderness ratios, as pallet racks (Ungureanu et al. 2016; Tsarpalis et al. 2022) or silos (Khalil et al. 2023). In fact, slender structures under the seismic forces can exhibit stability loss and collapses due to buckling phenomena, as it can be observed from pictures of post-earthquake damages in Clifton et al. (2011), Formisano et al. (2017), Faggiano et al. (2009).

Parametric analyses are conducted to recognise the influence of geometrical and mechanical features on the seismic behaviour. Finally, mechanical-based fragility curves are constructed and the role played by masonry infills is highlighted. Fragility curves are evaluated using a full-blown Monte Carlo method, considering the variability of the structural features observed in the studied area (Liguori et al. 2023). Finally, the approach is tested on the steel structures in the industrial area of Spezzano Albanese, in Southern Italy, where this structural typology has been found extensively.

The work is organised as follows. The numerical model for the analysis of nonlinear beams is presented in Sect. 2. The mechanical-based approach for the evaluation of the fragility curves is described in Sect. 3. The application of the procedure to the industrial area of Spezzano Albanese is shown in Sect. 4. Finally, conclusions are drawn in Sect. 5

2 Numerical model

The structure is modelled using plane beam FE. In particular, a shear deformable mixed assumed stress FE (Garcea et al. 2012) is used in which displacements and generalised stresses are considered as primary variables. The assumed stress interpolation satisfies equilibrium equations for zero bulk loads (Liguori and Madeo 2021). An elastic-perfectly plastic behaviour is assumed for steel members and the yield surface is represented by an ellipsoid to efficiently consider axial-flexural interaction. The accuracy of the representation of the yield surface can be readily improved by adopting techniques based on the Minkowsky sum of ellipsoids (Magisano et al. 2018). Plasticity is checked at 3 Gauss-Lobatto points on each FE and the integration of the constitutive equation is performed at the element level in order to preserve the assumed stress interpolation (Magisano and Garcea 2020; Liguori et al. 2022).

Masonry infills are modelled by adopting a simple single equivalent strut behaviour, even if more complex model can be used to improve accuracy (Yekrangnia and Mohammadi 2017; Gentile et al. 2019). A backbone uniaxial response is adopted (Cavaleri et al. 2014; Cavaleri and Di Trapani 2014).

Columns are supposed to be fully clamped on foundations. The model has been validated by comparing the results of simple benchmark with those obtained using the commercial FE software SAP 2000 (Computer and Structures 2010) and Abaqus (Hibbit and Sorenson 2007) which are not reported here for brevity. Because of the peculiar structural typology characterised by a symmetric geometry, the assumed planar behaviour with no torsional effect can be certainly accepted. However, in the general case of more complex stiffness and mass distributions, the proposed model ought to be enhanced by considering a three dimensional behaviour.

2.1 Static nonlinear analysis

The equilibrium condition of a structure subject to gravitational loads \(\varvec{p}_0\) and seismic forces \(\varvec{p}\), is expressed as

$$\begin{aligned} \varvec{s}[{\textbf{d}}] - \varvec{p}_0 - \lambda \varvec{p}= \textbf{0} \end{aligned}$$
(1)

where \(\lambda\) is a load multiplier and \(\varvec{s}[{\textbf{d}}]\) is the internal force vector.

Equation (1) is usually solved by means of a continuation method which gives a sequence of equilibrium points, with coordinates \(\varvec{z}= \{ {\textbf{d}}, \lambda \}\), forming the so-called equilibrium path or capacity curve. While a deeper discussion can be found elsewhere (Magisano and Garcea 2020; Liguori et al. 2022), only a little background is given herein.

Starting from a known equilibrium point \(\varvec{z}_0 \equiv \varvec{z}^{(n)}\), a new state \(\varvec{z}^{(n+1)}\) is obtained by solving, through a Newton iteration, the following system representing the equilibrium equations plus the arc-length constraint for an assigned value of \(\Delta \xi\)

$$\begin{aligned} \left\{ \begin{aligned} \varvec{r}[{\textbf{d}},\,\lambda ]&\equiv \varvec{s}[{\textbf{d}}]- \lambda \varvec{p}= \textbf{0} \\ r_\lambda [{\textbf{d}},\,\lambda ]&\equiv \varvec{n}_z^T \varvec{M}_z (\varvec{z}-\varvec{z}_0) - \Delta \xi = 0 \\ \end{aligned}\right. \quad \text {with} \quad \Delta \xi \equiv \varvec{n}_z^T \varvec{M}_z (\varvec{z}_1- \varvec{z}_0). \end{aligned}$$
(2)

where \(\varvec{z}_1\) is the first predictor. The most used and effective arc-length equation is a moving hyperplane having normal vector \(\varvec{n}_z= \{ \varvec{n}, n_\lambda \}\) and metric matrix \(\varvec{M}_z =\text {diag}[\varvec{M}, \mu ]\). Letting

$$\begin{aligned} \varvec{K}= \frac{\partial \varvec{s}[{\textbf{d}}]}{\partial {\textbf{d}}} \end{aligned}$$
(3)

evaluated as assemblage of element matrices \(\varvec{K}_{e}\), Newton iterations are applied to the extended nonlinear system of Eq. (2), giving a sequence of estimates

$$\begin{aligned} \Delta \varvec{z}_{j+1} = \Delta \varvec{z}_{j} + \dot{\varvec{z}}_{j} \quad \text {and} \quad \varvec{z}_{j+1} = \varvec{z}_0 + \Delta \varvec{z}_{j} \end{aligned}$$

where \(\Delta = (\cdot )^{(n+1)} - (\cdot )^{(n)}\) represents the difference between quantities at step \(n+1\) and n and the correction \(\dot{\varvec{z}}_j\) is evaluated as

$$\begin{aligned} \left\{ \begin{aligned}&\varvec{K}_j \dot{{\textbf{d}}} - \dot{\lambda } \varvec{p}= -\varvec{r}_j\\&\varvec{n}^T \varvec{M}\dot{{\textbf{d}}} + \mu n_\lambda \dot{\lambda } = -r_{\lambda j}\\ \end{aligned}\right. \quad \Rightarrow \quad \left\{ \begin{aligned}&\dot{{\textbf{d}}} = - \varvec{K}_j^{-1}\left( \varvec{r}_j - \dot{\lambda }_j \varvec{p}\right) \\&\dot{\lambda } = \frac{r_{\lambda j} - \varvec{n}^T \varvec{M}\varvec{K}^{-1} \varvec{r}_j}{\varvec{n}^T \varvec{M}\varvec{K}_j^{-1} \hat{\varvec{s}}_j - \mu n_\lambda } \\ \end{aligned} \right. \end{aligned}$$

The internal force vector at each iteration, \(\varvec{s}^j\), is evaluated by assembling the contribution of each element \(\varvec{s}_e\). The solution of Eq.(2) is carried out with a global scheme in only displacement variables, while the stresses are maintained at the element level only and evaluated using a return mapping scheme.

2.2 Beam finite element

The steel members are modelled using a beam FE with constitutive and geometrical nonlinearities. We adopt the 2D beam model (Pignataro et al. 1982; Salerno and Lanzo 1997; Garcea et al. 1999) based on the following spatial strain measure

$$\begin{aligned} \varvec{e}= \begin{bmatrix} \varepsilon \\ \gamma \\ \chi \end{bmatrix}, \quad \left\{ \begin{aligned} \varepsilon&= 1 + u_{,s} - \cos \varphi \\ \gamma&= w_{,s} - \sin \varphi \\ \chi&= \varphi _{,s}\\ \end{aligned}\right. \end{aligned}$$
(4)

where u, w and \(\varphi\) represent the axial displacement, the transversal displacement and the rotation, respectively, s is an abscissa along the beam axis and a comma indicates derivative. The displacement fields are interpolated using 3 nodes, located at FE ends and at midspan as

$$\begin{aligned} {\textbf{d}}[s] = \begin{bmatrix} u \\ w\\ \varphi \end{bmatrix} =\varvec{N}_d[s] {\textbf{d}}_e, \end{aligned}$$
(5)

where \({\textbf{d}}_e = [u_i, w_i, \varphi _i, u_j, w_j, \varphi _j, \varphi _k]^T\) are the nodal displacements, being i and j the end nodes. For the node k located at midspan only the rotation is considered as degree of freedom. The assumed displacement interpolation is linear for the translations u and w and quadratic for the rotations. Then, the interpolation matrix \(\varvec{D}[s]\) becomes

$$\begin{aligned} \varvec{N}_d[s] =\begin{bmatrix} \dfrac{l-s}{l} &{} 0 &{} 0 &{} \dfrac{s}{l} &{} 0 &{} 0 &{} 0\\ 0 &{} \dfrac{1-s}{l} &{} 0 &{} 0 &{} \dfrac{s}{l} &{} 0 &{} 0\\ 0 &{} 0 &{} \dfrac{(l-s)(l-2s)}{l^2} &{} 0 &{} 0 &{} \dfrac{-s(l-2s)}{l^2} &{} \dfrac{4s(l-s)}{l^2} \end{bmatrix} \end{aligned}$$
(6)

where l is the beam’s length.

The first variation of the geometrically nonlinear strains \(\varvec{e}= \varvec{e}[{\textbf{d}}_e]\) can we expressed as

$$\begin{aligned} \delta \varvec{e}[{\textbf{d}}_e] = \varvec{B}_e[{\textbf{d}}_e] \delta {\textbf{d}}_e, \end{aligned}$$
(7)

where \(\varvec{B}_e[{\textbf{d}}_e]\) is a compatibility operator.

A mixed assumed-stress interpolation is adopted, namely stresses are also assumed as primary variables. Then, the generalised stresses, work-conjugate to \(\varvec{e}\), are interpolated as

$$\begin{aligned} \varvec{t}_s = \begin{bmatrix} H\\ V\\ M \end{bmatrix} =\varvec{N}_\beta {\varvec{\beta }}\end{aligned}$$
(8)

where H, V and M represent the horizontal resultant, the vertical resultant and the flexural moment, respectively, \(\varvec{N}_\beta\) is the stress interpolation matrix and \({\varvec{\beta }}\) are stress parameters. The material stress resultant \(\varvec{t}\) are related to the material ones as

$$\begin{aligned} \varvec{t}= \begin{bmatrix} N\\ T\\ M \end{bmatrix} = \varvec{R}^T \varvec{t}_s \end{aligned}$$
(9)

where N and T are normal and shear force, respectively, while \(\varvec{R}\) is a suitable rotation matrix. According to the displacement interpolation, H and V are assumed to be constant, while the flexural moment is linear, namely

$$\begin{aligned} \varvec{N}_\beta =\begin{bmatrix} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} s \\ \end{bmatrix}. \end{aligned}$$
(10)

The elastic constitutive law is expressed in terms of generalised quantities as

$$\begin{aligned} \varvec{e}[s] = {\mathbb {F}} \varvec{t}_s [s], \end{aligned}$$
(11)

where \({\mathbb {F}}=diag(EA,EA,EJ)\), where E, A, and J are normal modulus, cross section area and inertia, respectively (Pignataro et al. 1982; Salerno and Lanzo 1997; Garcea et al. 1999).

2.2.1 Linear response

For the linear elastic problem, using a Hellinger-Reissner approach and the assumed displacement and generalised stresses interpolation one obtains

$$\begin{aligned} \int _{s=0}^l \varvec{t}_s[s]^T \varvec{e}[s] ds - \frac{1}{2} \int _{s=0}^l \varvec{t}_s[s]^T {\mathbb {F}} \varvec{t}_s[s] ds - {\mathcal {L}}_{ext}\equiv {\varvec{\beta }}_e^T\varvec{Q}_e{\textbf{d}}_e -\frac{1}{2}{\varvec{\beta }}_e^T \varvec{H}_e {\varvec{\beta }}_e - {\textbf{d}}_e^T \varvec{p}_e \end{aligned}$$
(12)

where \({\mathcal {L}}_{ext}\) is the work of the element external loads \(\varvec{p}_e\) and \(\varvec{H}_e\) and \(\varvec{Q}_e\) are the element compliance and the compatibility/equilibrium matrices.

From the stationary condition of Eq. (12) one obtains the equilibrium equations and the constitutive laws of the element in discrete generalised format as

$$\begin{aligned} \left\{ \begin{aligned}&\varvec{H}_e {\varvec{\beta }}_e - \varvec{Q}_e {\textbf{d}}_e = {\textbf{0}}\quad \forall e\\&\varvec{Q}_e^T {\varvec{\beta }}_e -\varvec{p}_e = {\textbf{0}}\\ \end{aligned} \right. \end{aligned}$$
(13)

The stresses can be obtained from the first of Eq. (13) at the FE level and then substituted into the equilibrium equation to obtain a pseudo-displacement format

$$\begin{aligned} \varvec{K}_{e0} {\textbf{d}}_e = \varvec{p}_e , \end{aligned}$$
(14)

where \(\varvec{K}_{e0}\) is the element stiffness matrix. It is worth noting that the equilibrium condition in Eq. (14) has the same format than in usual displacement-based formulations and the stress parameters are evaluated only at the element level.

2.2.2 Constitutive nonlinear law

An elastic perfectly-plastic behaviour is adopted for the steel beam. Plastic admissibility is checked at some Integration Points (IG), located at the midspan and at the two ends at coordinates \(s_g\). The yield function \(f[\varvec{t}[s_g]]\) is adopted, defined in the space of the axial force N and bending moment M, while an elastic behaviour of shear force is assumed. The yield surface is described by a Minkowski sum of ellipsoids, as proposed in a general 3D case elsewhere (Magisano et al. 2018). For the purposes of constructing vulnerability curves, when many analyses needs to be executed, the use of only one ellipsoid provides a good compromise between accuracy and efficiency. In such a case, the plastic admissibility condition on the cross section \(s_g\) becomes

$$\begin{aligned} f[\varvec{t}_g] = \varvec{t}_g^T \varvec{C}_g \varvec{t}_g - 1 \le 0 \end{aligned}$$
(15)

where for simplicity \(\varvec{t}_g=\varvec{t}[s_g]\) and

$$\begin{aligned} \varvec{C}_g = \begin{bmatrix} 1/N_y^2 &{} 0 &{} 0\\ 0&{} 0 &{} 0\\ 0 &{} 0 &{} 1/M_y^2 \end{bmatrix} \end{aligned}$$
(16)

in which \(N_y\) and \(M_y\) are axial force and flexural moment at yielding. If one wants to increase the accuracy in the evaluation of the yield surface, it is possible to adopt more ellipsoids (Magisano et al. 2018).

On the basis of a strain-driven formulation, the stress update is obtained by using a backward Euler scheme for integrating the constitutive law, where the stresses become an implicit function of the assigned strain (displacement) increment. For a mixed FE, the weak form of the finite step constitutive relations over the element becomes

$$\begin{aligned} \left\{ \begin{aligned}&\varvec{H}_e ({\varvec{\beta }}_e - {\varvec{\beta }}_e^{(n)}) + \sum _{g} \mu _g \frac{\partial f_g}{\partial {\varvec{\beta }}_e} = \Delta \varvec{\epsilon }_e \\&\mu _g \ge 0 \quad f_g \le 0 \quad \mu _g f_g = 0 \end{aligned}\right. \end{aligned}$$
(17)

where we assume to test the plastic admissibility conditions in a discrete number of IP identified by the subscript g, \(\Delta =(\cdot )^{(n+1)} - (\cdot )^{(n)}\) represents the difference between quantities at step \(n+1\) and n, f is the yield function, and \(\mu _g\) are the positive plastic multipliers. The quantity \(\varvec{\epsilon }_e\) is work-conjugate to \({\varvec{\beta }}_e\) and can be obtained as

$$\begin{aligned} \varvec{\epsilon }_e = \sum _g \varvec{N}_{t g}^T \Delta \varvec{e}_g w_g, \end{aligned}$$
(18)

where g is the numerical integration weight. The superscript \((n+1)\) is omitted to simplify the notation.

This problem, is solved by adopting the dual decomposition approach presented elsewhere (Magisano and Garcea 2020; Liguori et al. 2022) which is based on the solution of two sub-problems. The first regards only IP variables and consist in obtaining \(\varvec{t}_g = \varvec{t}_g[\varvec{t}_g^{(n)}, \Delta \varvec{e}_g]\) for assigned \(\Delta \varvec{e}_g\), by solving the following equations

$$\begin{aligned} \left\{ \begin{aligned}&{\mathbb {F}}_g (\varvec{t}_g -\varvec{t}_g^{(n)}) + \mu _g \frac{\partial f_g[\varvec{t}_g]}{\partial \varvec{t}_g} - \Delta \varvec{e}_g = {\textbf{0}}\\&\mu _g f_g[\varvec{t}_g] = 0 \quad \mu _g \ge 0 \quad f_g[\varvec{t}_g] \le 0\\ \end{aligned}\right. \quad \forall g, \end{aligned}$$
(19)

which represent a well-known scheme solved in displacement-based formulations.

The second problem, referred to as element state determination, consists in obtaining \({\varvec{\beta }}_e = {\varvec{\beta }}_e[{\varvec{\beta }}_e^{(n)}, \Delta {\textbf{d}}_e]\) for assigned \(\Delta {\textbf{d}}_e\) by solving the following equations regarding elemental variables

$$\begin{aligned} \left\{ \begin{aligned} \varvec{r}_{g} = &\varvec{t}_{sg} - \varvec{N}_{t g} {\varvec{\beta }}_e = {\textbf{0}}\quad \forall g \\ \varvec{r}_{e} = &\Delta {\varvec{\epsilon }}_e - \sum _g \varvec{N}_{t g}^T \Delta \varvec{e}_g w_g = {\textbf{0}}\\ \end{aligned}\right. \end{aligned}$$
(20)

where the unknowns are \({\varvec{\beta }}_e\) and \(\Delta {\varvec{\epsilon }}_e\) and \(\varvec{t}_{sg} = \varvec{t}_s[s_g]\).

Finally, it is possible to obtain the element force vector as

$$\begin{aligned} \varvec{s}_e = \varvec{Q}_{te}[{\textbf{d}}_e]^T{\varvec{\beta }}_e, \end{aligned}$$
(21)

where the tangent compatibility operator \(\varvec{Q}[{\textbf{d}}_e]\) can be obtained as

$$\begin{aligned} \varvec{Q}_{te}[{\textbf{d}}_e] = \frac{\partial {\varvec{\epsilon }}[{\textbf{d}}_e]}{\partial {\textbf{d}}_e} = \sum _g \varvec{N}_{tg}^T \varvec{B}_g[{\textbf{d}}_e] w_g \end{aligned}$$
(22)

By adopting well-known procedures, it is possible to evaluate the element stiffness matrix \(\varvec{K}_e\).

2.2.3 Masonry infill

The masonry infill is modelled using an equivalent strut model. Therefore, only axial deformation in small displacements is considered, namely

$$\begin{aligned} \varvec{e}= \begin{bmatrix} \varepsilon \\ 0\\ 0 \end{bmatrix}, \quad \varepsilon =u_{,s}. \end{aligned}$$
(23)

Accordingly, the axial force N is the only generalised force. The equivalent strut has width \(w_m\) evaluated through the expression proposed by Papia et al. (2003)

$$\begin{aligned} w_m = d k \frac{c}{z} \frac{1}{(\lambda ^\star )^\beta } \end{aligned}$$
(24)

where \(k = l/h\), while c and \(\beta\) depend on Poisson’s ratio \(\nu _d\) along the diagonal direction (Cavaleri et al. 2014)

$$\begin{aligned} c&= 0.249 - 0.0116 \nu _d + 0.569 \nu _d^2\nonumber \\ \beta&= 0.146 - 0.0073 \nu _d + 0.126 \nu _d^2. \end{aligned}$$
(25)

The parameter \(\lambda ^\star\) is obtained as

$$\begin{aligned} \lambda ^\star = \frac{E_m}{E} \frac{t_m h'}{A_c} \left( \frac{h'^2}{l'^2} + \frac{A_c l'}{4 A_b h'}\right) \end{aligned}$$
(26)

where \(E_m\) and E are masonry and steel Young modulus, respectively, \(A_c\) and \(A_b\) are the area of columns and beam, respectively, \(t_m\) is the thickness while \(h'\), \(l'\) are frame height and length.

A backbone curve is used to describe the infill nonlinear behaviour, as indicated in Fig. 1, providing the axial force as a function of the stress, namely \(N= N[\varepsilon [{\textbf{d}}_e]]\). The characteristic points having strain \(\varepsilon _1\), \(\varepsilon _2\) and \(\varepsilon _3\) and axial force \(N_1\), \(N_2\) and \(N_3\) are evaluated according to (Cavaleri and Di Trapani 2014).

Fig. 1
figure 1

Backbone curve describing the infill nonlinear behaviour

Full size image

2.3 Damage levels

Nonlinear static analyses are performed on the FE model to simulate the seismic response. An arc-length algorithm is employed to trace the equilibrium path (Liguori et al. 2022).

Figure 9 shows the capacity curves obtained both for the infilled structure and the bare one. It is possible to observe that the presence of the masonry infill increases the initial stiffness and the peak shear force (T). After peak, a strong degradation is observed and the infills contribution vanishes, so that the structural behaviour coincides with that of the bare frame (De Luca et al. 2013).

Three damage levels are considered, namely immediate occupancy (IO), Life Safety (LS) and Near Collapse (NC) (Agency 2013; Formisano et al. 2017, 2022). The damage state is defined in terms of inter-storey drift, on the basis of the FEMA (Agency 2013) legislative provisions, which refers to the following limits: 0.0075 for IO, 0.025 for LS and 0.05 for NC.

Furthermore, a NC limit state is reached when the shear force reaches a limit value \(T_y=\dfrac{f_y}{\sqrt{3}} A_s\), being \(A_s\) the shear area, depending of the cross section shape.

3 Mechanical based fragility curves

In this Section, the procedure for constructing the fragility curves using a mechanical-based approach is presented. Its essential steps are summarised in the flowchart in Fig. 2, whose details are given in the following.

Fig. 2
figure 2

Flowchart showing the main steps of the mechanical based fragility curves construction method

Full size image

3.1 Exposure analysis and data collection

The first step of the proposed approach consists in the data collection of the industrial buildings in the area under consideration. Data can be obtained by exploiting different sources, as the information contained in available database. In the Italian territory, a relevant source is represented by the CARTIS GL form, specifically developed to collect data on large span industrial structures. In particular, the CARTIS GL provides information on material, geometrical features, as height, plan dimensions, number of frames and distance, presence and type of bracing and constraints. In addition, other specific details are provided, as the presence of infill, their typology and regularity. The information are available at two different scales: a wider area containing homogeneous structures and which are called compartments, and a specific one at the level of the single structures. In this work, the compartment CARTIS GL form is adopted to identify the area under consideration, while the CARTIS GL at the structural level is used for obtaining the detailed information used in the construction of the fragility curves. It is worth noting that usually not all the structures on a compartment are surveyed, then specific data are available only for a sample of the industrial buildings. The collected parameters and the possible source are summarised in Table 1. In the last two rows, the geometry of the roof and its structure are inserted. In this case, specific surveys are required to identify in detail this information.

Table 1 Parameters collected in the data collection and the possible source
Full size table

However, other data are difficult to estimate, even if detailed surveys are conducted, as the mechanical parameters of the material. In this case, if no specific information can be obtained from original drawings or material tests, material properties are treated as epistemic uncertainties and a wide range of variations are adopted, according to the usual values for the period of construction of the examined structures.

3.2 Parametric models generation

On the basis of the collected data on the industrial buildings under consideration, parametric models are constructed. These models are devised in order to represent the essential features of the family of structures under consideration, even if no actual building is specifically modelled. In the field of seismic vulnerability, these are usually referred to as archetype models Ruggieri et al. (2023). The archetypes are constructed by combining the parameters given in Table 1, which represent the variation of geometrical and mechanical features among the structural typology under consideration. Then, for each archetype a FE model is constructed, as shown in Sect. 2.

The combination of the structural parameters, which define the archetypes, is done using a Monte Carlo technique. A large number of structures is generated by randomly assigning a value to each structural parameter to within observed ranges of variation. If the number of available CARTIS GL forms is statistically relevant, information on the occurrence frequency can be used in the random generation and if not, a uniform variation is assumed. The dimension of the Monte Carlo population needs to be checked by performing a convergence study on the fragility curves, whose construction is described in the following Sections.

3.3 Vulnerability model

Each FE model representing an archetype building is subject to static-nonlinear analysis, in order to identify the performance point for the damage levels introduced in Sect. 2.3. The seismic action is represented by the idealised spectra of Newmark–Hall type defined by Italian seismic code (Ministerial Decree 2008). In order to obtain the displacement demand, we make use of the inelastic spectra method. In particular, the modified N2 method (Dolšek and Fajfar 2004, 2005, 2008), specifically devised to be used in presence of masonry infills, is adopted. The analysis is repeated along the two main directions of the structure.

3.4 Fragility curves

Fragility curves are constructed for the structural typology under consideration. As usual (Rota et al. 2010; Liguori et al. 2023; Formisano et al. 2022), fragility curves are expressed by means of cumulative lognormal probability functions of the ground acceleration \(a_g\) taken as intensity measure

$$\begin{aligned} p(d \ge d_i) = \Phi \left( \dfrac{log \left( \frac{\lambda _i}{a_g}\right) }{\beta _i} \right) , \quad i=1,\dots ,3, \end{aligned}$$
(27)

where d is the structural damage (IO, LS, NC), \(\Phi\) is a normal cumulative probability function, while \(\lambda _i\) and \(\beta _i\) are the mean value and the logarithmic standard deviation of the \(a_g\) values that cause the \(d_i\) damage grade, respectively. For each damage grade \(d_i\), the definition of a fragility curve requires the evaluation of the two parameters \(\lambda _i\) and \(\beta _i\) on the basis of the results of the analyses conducted.

4 Fragility curves for the industrial area of Spezzano Albanese

In this Section, the mechanical based approach for the evaluation of the seismic fragility curves for infilled industrial steel structures is applied to a case-study concerning the industrial area of Spezzano Albanese.

4.1 Exposure analysis

The area under consideration, indicated in Fig. 3, is located in the municipality of Spezzano Albanese, in Calabria region, southern Italy. It is an industrial area built before 1980 and mainly devoted to agricultural purpose which is the principal economic activity of the zone. The total number of industrial buildings is 48, of which 14 made of steel. The structural data for 11 structures is collected using Cartis-GL form and some of them are given in Table 2.

Fig. 3
figure 3

Localisation of the studied area

Full size image
Table 2 Some data collected through the Cartis form for the surveyed industrial structures
Full size table

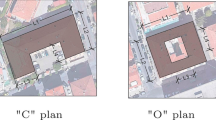
The structures are composed by a sequence of parallel frames, realised by steel columns and a truss arch. A typical plan view of the industrial structure is shown in Fig. 4. Figure 5 shows some pictures of the industrial steel structures. It is possible to observe how masonry walls are present along the perimeter of the structures. In particular, two configurations are recognised, depending on the walls height, as shown in Fig. 6.

Along y directions, the structures are characterised by a curved truss, as it can be observed in Fig. 5.

Each surveyed structure is characterised by the group of data listed in Table 3 in which their ranges of variations are also given. Based on these parameters, it is possible to construct the archetype models of the industrial structures. Regarding the x direction, a representation is given in Fig. 7. Columns are considered to be fully clamped at the base, while rotation is allowed in the connection between column and beams. Figure 8 shows the model of the archetype industrial building along y direction. Also along this direction columns are clamped at the base, while the other trusses are hinged to each other. The geometrical parameters vary to within the ranges given in Table 3. Column and beam sections are indicated through an index, as shown in Tables 4 and 5.

The considered variation allows to cover all the possible configurations obtained from the Cartis GL form. Unfortunately, no information is available with respect to some other parameters, as the steel yield stress, and, therefore, their variation has been assumed to within the reasonable values given in Table 6. The elastic modula are kept constant during the FE simulation. For the steel elements, we consider \(E=210000\) MPa, while for the masonry infill \(E_m=7540\) MPa and \(\nu _d=0.25\).

Finally, the seismic action is described by a Newmark-type response spectrum, evaluated according to Italian building code (Ministerial Decree 2008) for a soil of class C and a topography type T1, as expected in the municipality of Spezzano Albanese.

Fig. 4
figure 4

Plan of an industrial steel structure under consideration

Full size image
Fig. 5
figure 5

Some pictures of the industrial structures in the area under consideration. It is possible to observe the geometry of the curved roof truss (a, c, e), the connection between truss and columns (b, f) and a view from the outside (d)

Full size image
Fig. 6
figure 6

Full height (a) and windowed (b) infills configurations along x direction

Full size image
Table 3 Variability of geometrical and mechanical parameters of the recognised industrial buildings
Full size table
Fig. 7
figure 7

Geometric and FE parametric model of an infilled frame along x direction

Full size image
Fig. 8
figure 8

FE parametric model along y direction

Full size image
Table 4 Section types used for columns
Full size table
Table 5 Section types used for beams
Full size table
Table 6 Variability of additional parameters
Full size table

4.2 Parametric analyses

In this Section, a parametric analysis is presented, with the aim of identifying the influence that each structural parameter has on the seismic capacity of inspected structures. To this aim, a reference structure, characterised by the parameter values given in Table 7, is considered. Starting from these values, sensitivity curves are constructed by varying each parameter and obtaining the seismic intensity, expressed in terms of peak ground acceleration \(a_g\), which produces the damage levels.

Figure 9 shows the capacity curve of the reference building for seismic action along x direction, in both cases of bare frame and infilled type A. The bare frame gives an elastic-perfectly plastic response, with a low softening branch due to the p-delta effect. As expected, the infill increases the initial stiffness and the maximum force with respect to the bare frame case. However, the behaviour is more fragile, with a pronounced softening branch after attainment of the peak the force. For large displacements, when the infill contribution is strongly reduced, the capacity curves of the infilled frame coincides with that of the bare one.

Fig. 9
figure 9

Capacity curves for bare and infilled type A frames, x direction

Full size image

Figure 10 shows, instead, the capacity curve for seismic force along y direction. In particular, two cases are analysed, namely a first one in which geometrical nonlinearities are considered and a second one in which their effect is neglected. Results show that in the first case the structure reaches a peak force with a short plastic range, followed by a softening branch. This is due to the instability phenomenon produced by the local buckling of a compressed truss located near the left column, as it can be observed from the deformed configuration at equilibrium point B in Fig. 10. Conversely, if geometrical nonlinearities are not considered, the model is not capable of capturing this phenomenon, and no softening is observed.

Fig. 10
figure 10

Capacity curves for seismic action along y direction (a) and deformed configurations at the last evaluated equilibrium point when neglecting (b) and considering (c) geometrical nonlinearities (GNL)

Full size image
Fig. 11
figure 11

Deformed configuration and heatmap of the yield function for the reference structure at IO (a), LS (b) and NC (c) limit states, y direction

Full size image

For the reference structure, Fig. 11 shows the deformed configuration for a seismic action along the y direction and a heatmap of the yield function for the three limit states. It is worth noting that at IO yielding occurs at one column base only, while one truss element is near yielding. Then, at LS, both columns base sections are yielded and a local buckling is observed at one truss, while the stresses increase on many elements on the truss structure. Finally, at the most severe limit state, NC, many truss elements reach the yield stress. Similar considerations can be done for a seismic action along the x direction. Figure 12 shows how the yield stress evolves with the limit states in the bare frame case. The collapse mechanism in this case is very simple and involves the base section of the columns. Figures 13 and 14 for the type A and B infills, respectively, show that at IO only the infill is damaged, while the steel members behave elastically. For the more severe limit states, the stress level increases at the columns base sections that reach the yield stress at NC. Interestingly, no relevant difference is observed in the nonlinear structural behaviour between infill types A and B.

Fig. 12
figure 12

Deformed configuration and heatmap of the yield function for the reference structure at the IO (a), LS (b) and NC (c) limit states, x direction (bare frame)

Full size image
Fig. 13
figure 13

Deformed configuration and heatmap of the yield function for the reference structure at IO (a), LS (b) and NC (c) limit states, x direction (type A infill)

Full size image
Fig. 14
figure 14

Deformed configuration and heatmap of the yield function for the reference structure at IO (a), LS (b) and NC (c) limit states, x direction (type B infill)

Full size image

Figure 15 shows the sensitivity curves for the case of bare frames. It is possible to observe that high significance is given by the column type, which influence both the elastic and plastic response. Additionally, the permanent load has a high relevance, especially on the damage levels LS and NC, since it influence the total mass of the dynamic system.

Figures 16 and 17 show the sensitivity curves for the infilled frames for the infill types A and B, respectively. In general, one can observe how the \(a_g\) values that produce each damage level significantly increase with respect to the bare frame case.

Finally, Fig. 18 shows the results of the parametric study for seismic force along y direction. Again, permanent load and column type turn put to be the most relevant parameters, capable of influencing the seismic response significantly.

Table 7 Parameters of the reference structure
Full size table
Fig. 15
figure 15

Sensitivity analysis for some geometrical (a, b, d, f) and mechanical (c, e) attributes, bare frame

Full size image
Fig. 16
figure 16

Sensitivity analysis for some geometrical (a, b, d, f) and mechanical (c, e, g) attributes, type A infills, X direction

Full size image
Fig. 17
figure 17

Sensitivity analysis for some geometrical (a, b, d, f, h) and mechanical (c, e, g) attributes, type B infills, X direction

Full size image
Fig. 18
figure 18

Sensitivity analysis for some geometrical (a, b, c, d, e, h) and mechanical (f, h) attributes, y direction

Full size image

4.3 Fragility curves

Fragility curves are obtained by applying the procedure proposed in Sect. 3, based on a Monte Carlo generation of a virtual population of industrial structures. The parameters considered in the variations discussed above are assumed to be equally probable, since no information about more detailed statistics are available. Then, a population of buildings is generated for all the considered infills and seismic directions. The population is increased until a converged value is obtained for logarithmic mean and standard deviation \(\lambda\) and \(\beta\). Figure 19 show how these parameters change for increasing population sizes. It is possible to observe how, after a population of about 1000 structures, the values do not change significantly.

Fig. 19
figure 19

Variation of the parameters \(\lambda\) and \(\beta\) for the fragility curves normalised for the values \(\lambda ^\star\) and \(\beta ^\star\) obtained for 10000 buildings, damage level NC, direction x and bare frame

Full size image
Fig. 20
figure 20

Fragility curves obtained using the proposed mechanical-based procedure for the industrial steel structures in Spezzano Albanese for seismic action along the x direction in the case of bare frame (a), type A infills (b) and type B infills (c) and for seismic action along the y direction (d)

Full size image

Fragility curves are given in Fig. 20. In particular, Fig. 20a shows the fragility curves for bare frame and x direction. In this case, IO damage level is reached for very low intensities of the seismic action. Also the other damage levels are reached for low intensities, thereby highlighting the high vulnerability of steel industrial structures if braces or infills are not present. A completely different behaviour is observed in the infilled case. In fact, as it can be observed in Fig. 20b and c for infill type A and B, respectively, the fragility functions are characterised by high intensity values, with high damage grades having low probability of occurrence even for very high intensities. Then, the presence of the infill drastically modifies the structural behaviour by reducing the seismic vulnerability. Then, it is possible to state that for this type of structure modelling the infill is of crucial importance and suggests that it does not play a secondary structural role, but it behaves as the main seismic-resistant component. However, no relevant difference is observed between the fragility curves for infill type A and B.

Finally, Fig. 20d gives the fragility curves obtained for seismic action along the y direction. In this case, the structures result vulnerable especially to damage grade IO, because for low intensity it has a high probability of occurrence.

For all the analysed cases, the parameters of the lognormal fragility curves are given in Table 8.

Table 8 Parameters of the fragility curves
Full size table

5 Concluding remarks

In this work, the problem of the seismic vulnerability of steel industrial structures designed without anti-seismic criteria and with masonry infills was addressed. An exposure analysis of an industrial area in the municipality of Spezzano Albanese (Italy) was conducted using Cartis GL form. A numerical model, based on beam finite elements having geometrical and mechanical nonlinearities was constructed to analyse the industrial structures. On the basis of the surveyed data, sensitivity analysis has been conducted to identify the most relevant parameters. Results have shown that the mass of the construction has a remarkable influence on the seismic vulnerability, thereby suggesting to reduce the weight of the roof to alleviate the seismic risk. By comparing fragility curves for bare and infilled frames, it was noticed that the presence of masonry infills has a positive influence on the seismic vulnerability of the analysed structures.

Further developments of the study will foresee additional nonlinear dynamic analysis on the examined structures to validate and refine the achieved results.