The generalized E-DVA method: a new approach for multi-modal pushover analysis under multi-component earthquakes with local variables maximization

Abstract

Pushover analysis is a common nonlinear static procedure, performed to evaluate seismic response of civil structures. This approach allows considering the structural nonlinear behavior under earthquake loading in a simplified yet effective way; however, in its classic formulation, it is limited by restrictive and unrealistic assumptions. Thus, the basic method is inadequate for the accurate analysis of buildings without a vertical plane of symmetry and/or for multi-component earthquakes, where torsion effects cannot be neglected. Furthermore, standard pushover analysis only comprises one dominant mode of vibration; higher modes, and therefore their effects, are not accounted for. For all these reasons, the standard technique is generally not considered suitable for the assessment of buildings at high risk of natural-technological (NaTech) events, such as nuclear facilities in areas of high seismic activity. To overcome these limitations, a multi-modal pushover analysis procedure is here tested and validated on the data from a non-symmetric structure (the SMART case study) under multi-component earthquakes. In detail, the procedure applies a linear combination of modal load patterns, defined according to the well-established Direct Vectorial Addition (DVA) method. With respect to other existing multi-modal pushover analysis techniques, elliptical response envelopes are employed to calculate the corresponding combination factors. Innovatively, the identification of the dominant modes for the load pattern is not limited to the classic maximization of the forces at the basis of a structure but rather generalized to shear and displacement maximization at different heights and locations throughout the whole structural frame.

1 Introduction

Strategic structures require highly accurate assessment procedures. This is particularly true for industrial plants operating with hazardous materials (such as chemical and process plants (Caputo et al. 2020; Ricci et al. 2021), storage steel tanks (Brunesi et al. 2014; Ozsarac et al. 2021), or nuclear facilities) in dangerous environments, e.g. earthquake-prone areas. This falls in the broader context of technological accidents triggered by natural events, referred to as natural-technological (NaTech) events (Krausmann and Baranzini 2012; Krausmann and Necci 2021).

A well-known and recent example is the case of Tepco’s Fukushima Daiichi plant event during the 2011 Tohoku-Taiheiyou-Oki earthquake, where three reactors suffered considerable earthquake-induced direct damage, exacerbated by the following tsunami hit (World Nuclear Association 2022). This event caused radioactive releases in the atmosphere; the removal of contaminated water, fuel rod assemblies, and fuel debris are still undergoing as of 2022 (Tokyo Electric Power Company Holdings Inc 2021).

For these reasons, most developed countries require plant-specific reviews of seismic safety (European Parliament 2012; United States Nuclear Regulatory Commission 2018). These safety requirements are vital to avoid the leakage of radioactive fuel into the surrounding environment. Apart from the direct effects, with all their long-term consequences, the structural integrity of the plant is also a necessary (but not sufficient) condition for its operability. In the mid and short term, this guarantees the resilience of the energy production infrastructure, which is even more necessary during emergencies such as after major seismic events.

Given this context, the pushover analysis is widely used for the seismic structural assessment of existing structures—see e.g. (Capanna et al. 2021)—and the performance-based seismic design (PBSD) of new ones, alongside other alternatives such as incremental dynamic analysis or fragility estimation (Baker 2015; Aloisio et al. 2021, 2022).

In brief, the procedure consists of an incremental iterative solution of the static equilibrium equations corresponding to a nonlinear structural model subjected to a monotonically increasing lateral load pattern. While nonlinear, this approach is static, hence more practical—from a professional use perspective—than the nonlinear response time history analysis method, which is the conventional alternative but requires a dynamic analysis. However, despite more than 50 years of development, the traditional pushover methods (including the ones prescribed by the current seismic design codes) are still affected by many relevant issues (Krawinkler and Seneviratna 1998).

Nevertheless, further improving the current practices is not an easy task, as the key aim of any novel variant of pushover analysis is to further improve the reliability of the analysis while maintaining its core simplicity. This is the aim and motivation of the methodology described here, which departs from the current best practices and recent previous works from the Authors.

1.1 The state of the art and the limits of the current practice

In any pushover analysis, the structural resistance of a target structure is evaluated at each increment of an external forcing function, defined according to an arbitrary global load pattern, up to convergence. The iterative process is stopped when a predefined performance limit state or structural collapse is reached (or if the program fails to converge). For earthquake engineering purposes, this allows defining an envelope of the response parameters that would otherwise be obtained through many (computationally demanding) dynamic analyses, corresponding to different intensity levels.

This general framework for pushover analysis was first proposed in the mid-70 s (Freeman et al. 1975; Freeman 1978), specifically in the form of the well-known Capacity Spectrum Method (CSM). The CSM became the adopted methodology in the ATC 40 guidelines (Comartin et al. 1996), arguably the first all-encompassing technical guidelines for PBSD. Another classic approach—namely, the Displacement Coefficient Method (DCM)—was also introduced in ATC 40 but then better detailed in the Federal Emergency Management Agency (FEMA) 356 report (Federal Emergency Management Agency (FEMA) 2000), finally becoming the standard proposed by ATC-55, better known as FEMA 440 (Federal Emergency Management Agency (FEMA) 2005). These reports represent the most classic guidelines on pushover analysis; the scientific consensus of the literature published in the following years seems to identify a widespread preference for DCM over CSM (Bertero 1995; Fajfar 1999; Chopra and Goel 1999).

Other well-established methods include the N2-method (Fajfar and Fischinger 1988), which established the concepts for the definition of the load pattern under a single-component earthquake; these were then incorporated into the Eurocode 8 (Annex B, (CEN 2004)).

However, all these approaches assume a single earthquake component, which needs to be both horizontal and perfectly parallel to a vertical plane of symmetry of the structure, such that the structural displacements lie in this plane. These hypotheses lead to many drawbacks. Mainly, they are unrealistic in general seismic conditions and do not account for torsional displacements (De Llera and Chopra 1995; Penelis and Kappos 2002). Even for single-component earthquakes and symmetric structures, they do not include the effects of higher modes, focusing only on the first one. This limitation reduces the viability of pushover analysis to the first mode-dominated structures, which is not the case for buildings with complex shapes (such as industrial or power plants) or high-rise, tall structures (Poursha and Amini 2015; Liu and Kuang 2017). Hence, further improvements and/or new methodologies were still required.

At the beginning of the third millennium, Fajfar et al. extended their N2-method to account for torsion in nonsymmetric buildings (Fajfar et al. 2008) via correction factors; the efficiency of this correction was assessed in (Bhatt and Bento 2011). The same corrective approach was later applied to compensate for higher modes as well in (Kreslin and Fajfar 2012). A more principled approach to deal with both non-symmetric structures and multi-modal analysis was put forward in (Chopra and Goel 2002) and (Chopra and Goel 2004), suggesting using a combination of single-mode pushover analyses (one per each important mode of the given structure). This also implicitly allows for its extension to multi-component earthquakes, as reported in (Reyes and Chopra 2011), even if requiring multiple runs of the code, which is highly inefficient. Even more importantly, the underlying concept of the linear combination of modes was valid in theory, however, the specific combination formulas proposed (Square-Root-of-Sum-of-Squares or Complete Quadratic Combination) caused loss of both sign and equilibrium at the final stage (Lopez-Menjivar 2004).

This finally led to the introduction of the notion of the global pushover load pattern assumed as a linear combination of several modal load patterns, proposed by Kunnath (2004). In this context, the linearity assumption is motivated by the orthogonality of vibration modes and allows preserving the equilibrium and the signs of the seismic responses. However, (Kunnath 2004) still considered a single-mode response to a single-component earthquake, while also assuming arbitrary values for the combination factors, without a procedure for the definition of such weighting coefficients. This approach, hereinafter referred to as Direct Vectorial Addition (DVA) (Lopez-Menjivar 2004), represents the departing point for the proposal discussed here and will therefore be better detailed on its own in the following subsection.

Figure 1 provides a visual interpretation of the timeline of the major progressions that led to the current state of the methodology proposed here.

Fig. 1

Timeline of the main developments in pushover analysis that led to the current approach reported here. Official guidelines are reported as well in the upper side, indicated in lighter grey, at the time of their first publication

It must be said that other recent developments in the field of pushover analysis did not follow the path described here, focusing on other aspects instead. For instance, (Aydinoǧlu 2003) and other authors experimented with incremental response spectrum analysis and time-adaptive pushover, by updating the load pattern at each analysis step. However, while such methodologies return a better agreement between static and dynamic analysis, this is achieved at the cost of greatly increasing the complexity of the analysis, reducing the competitive advantage of (static) pushover analysis over dynamic ones (Papanikolaou and Elnashai 2008; Papanikolaou et al. 2008). It should also be added that the experimental identification of nonlinear and hysteretic behaviour under seismic loading is still an open problem (Bursi et al. 2012; Ceravolo et al. 2013; Miraglia et al. 2020). Other recent works in the field of multimodal pushover analysis worth mentioning include (Ferraioli et al. 2018; Porco et al. 2018; Ruggieri and Uva 2020), and the very recent incremental modal pushover analysis procedure IMPAβ (Bergami et al. 2020), specifically intended for applications to bridges.

1.2 Comparison of the proposal to closely-related works

This article is a direct continuation of Erlicher et al. (2020) and falls into the research field initiated by Erlicher and Huguet (2016) and (Lherminier et al. 2018). These works introduced the Enhanced Direct Vectorial Addition (E-DVA) method. The E-DVA approach relies on an operational definition of the combination factors, named α-factors, defined for each vibration mode and each earthquake component. This extended the DVA concept of Lopez-Menjivar (2004) and Kunnath (2004) to multi-modal and multi-component pushover analyses in a physically principled manner, without resorting to tailor-made weighting coefficients. Indeed, as these weights are directly linked to the relevance calculated for each mode and component with respect to a specific quantity of interest, the E-DVA also naturally provides for a hierarchy of vibration modes. In turn, this allows selecting only the most relevant (dominant) modes for the considered quantity of interest, discarding the remaining ones. This results in a good trade-off between accuracy and simplicity.

The novelty and main contributions of this paper is to simplify the equations for the application of the method (Sect. 2.2), to consider any quantity of interest in the definition of the load pattern (Sect. 2.3) and to minimize the number of necessary pushover analysis when analyzing many different quantities of interest (Sect. 2.4). In particular, it is worth highlighting that the main novelty is that the procedure can now be applied to analyse local structural behaviour, for exemple the shear in one beam, while the analysis presented in Erlicher et al. (2020) was based on the resultant of the inertial forces at the building basis (global structural behaviour analysis).

These improvements with respect to the previous E-DVA formulation are intended to comply with the recently released Norme Tecniche per le Construzioni (NTC 2018, Chapter 7 (Ministero delle Infrastrutture e dei Trasporti 2018)), which—following the guidelines expressed in the Eurocode 8 (CEN 2004)—state the need to consider alternative control nodes, such as the corner points of the last story, especially when the structural system presents a significant coupling among translations and rotations. This also aligns the proposed method with the most recent developments in the field of pushover analysis, e.g. (Ruggieri and Uva 2020).

The remainder of this paper is structured as follows. In Sect. 2, after recalling what was retrieved from the previous E-DVA formulation (Sect. 2.1), the proposed novelties are presented. Section 3 reports the case study of interest, the so-called SMART building (Richard et al. 2016). Finally, the Conclusions (Sect. 4) end this paper.

2 Generalized E-DVA formulation

This section lists the major steps of the generalized E-DVA procedure and its important equations. First, the basics of the previous formulation of the E-DVA algorithm will be briefly recalled; please refer to Erlicher et al. (2020) for further details.

2.1 Recalls on E-DVA

As mentioned in the introduction, the central point of the method is its multi-modal multi-directional load pattern $\underline{Q}$ applied to the $N$ degrees of freedom of the considered structure, defined as a linear combination of modal load patterns:

$$\underline{Q}=\sum_{k=1}^{{n}_{ec}}\sum_{i=1}^{{n}_{m}}{\alpha }_{i,k}{\underline{Q}}_{i,k}$$

(1)

with ${n}_{m}$ being the number of considered modes and ${n}_{ec}$ the number of earthquake components. Considering the x- and y-axes as two orthogonal directions on the horizontal plane and the z-axis as the vertical one, ${n}_{ec}$ can assume any value between 1 and 3. ${\underline{Q}}_{i,k}$ represents the modal load pattern for the i-th mode and the k-th earthquake direction and ${\alpha }_{i,k}$ the corresponding coefficient of the linear combination. As reported in Erlicher et al. (2020), the main novelty of the E-DVA procedure is the rigorous definition of each ${\alpha }_{i,k}$ factor.

The method breaks down in five consecutive steps. The first two steps return the modal load patterns ${\underline{Q}}_{i,k}$. The third step concerns the definition of the corresponding linear combination coefficients ${\alpha }_{i,k}$. Finally, the last two steps are conceptually identical to the classical pushover analysis, with some modifications to account for multi-directional earthquakes. For more details, please refer to Erlicher et al. (2020).

In more detail, these five steps can be defined as follows.

• Step 1: Modal analysis of the structure, in order to get for each i-th mode its natural frequency ${f}_{i}$, mode shape ${\underline{\varPhi }}_{i}$, damping ratio ${\xi }_{i}$, participation factor ${\gamma }_{i,k}$ (for each k-th direction), participating mass ${M}_{i,k}$ and matrix of the modal correlation coefficients $\underline{\underline{H}}$. For this specific case, the CQC coefficients are used to define $\underline{\underline{H}}$, according to previous works (Erlicher et al. 2020).

  The matrix $\underline{\underline{\widetilde{H}}}$ is also computed, defined as a block-diagonal matrix with one $\underline{\underline{H}}$ block per earthquake component.

  This modal analysis is conducted for all the modes below a given upper boundary frequency, generally referred to as the frequency Zero Period Acceleration ${f}_{zpa}$ (Erlicher et al. 2020). The basic assumption is that for modes with a frequency higher than ${f}_{zpa}$, there is no dynamic amplification of the modal seismic responses, thus, they can be considered in a simplified manner, like in a static (zero-period) condition. In the case study reported here this upper limit was assumed at 35 Hz. Modes with a frequency above this threshold can then be considered in a simplified manner through an additional (residual) rigid response at the Peak Ground Acceleration (PGA).

• Step 2: Response spectrum analysis, to evaluate the maximum pseudo-acceleration vector ${\underline{A}}_{\mathrm{max},i,k}$:

  $${\underline{A}}_{\mathrm{max},i,k}={S}_{\alpha ,k}\left({f}_{i},{\xi }_{i}\right){\gamma }_{i,k}{\underline{\varPhi }}_{i}$$

  (2)

  where ${S}_{\alpha ,k}\left({f}_{i},{\xi }_{i}\right)$ is the pseudo-acceleration spectrum for a natural frequency ${f}_{i}$ and a damping ratio ${\xi }_{i}$.

  As mentioned in step (1), in practice, one would only consider a limited number of modes of the structure of interest; according to the classic modal truncation framework, this can be achieved by considering only the modes up to a certain frequency and then approximate the effects of out-of-bounds modes—see e.g. (Civera et al. 2021a, b)—as a residual rigid response. In this case (Gupta and Chen 1984),

  $$\underline {A}_{{\max ,n_{m} + 1,k}} = \underline {A}_{R,k} = S_{\alpha ,k,\max } \left( {\underline {{\Delta }}_{k} - \mathop \sum \limits_{i = 1}^{{n_{m} }} \gamma_{i,k} \underline {\Phi }_{i} } \right): = S_{\alpha ,k,\max } \underline {\Phi }_{R,k}$$

  (3)

  with ${n}_{m}$ being, in this case, the number of modes below the given threshold and ${\underline{\Delta }}_{k}$ the so-called influence vector, i.e. a vector of size $N$ filled with ones for the k-th direction and with zeroes elsewhere. ${S}_{\alpha ,k,\mathrm{max}}$ indicates the highest spectral acceleration in the interval between the highest target frequency, ${f}_{{n}_{m}}$, and ${f}_{zpa}=35$ Hz.

  The i-th modal load pattern for the earthquake direction $k$ can be then defined as an ensemble of inertial forces, i.e.

  $${\underline{Q}}_{i,k}=\underline{\underline{M}}\cdot {\underline{A}}_{\mathrm{max},i,k}$$

  (4)

  with $\underline{\underline{M}}$ being the mass matrix of the structure

• Step 3: Definition of the α-factors and evaluation of the pushover load pattern $\underline{Q}$:

• (1) Choice of a set of ${n}_{r}$ scalar seismic response quantities $[{F}_{1},{F}_{2},...,{F}_{{n}_{r}}]$ of interest, to be grouped in the response vector $\underline{f}$.

• (2) Calculation of the modal response matrix ${\underline{\underline{R}}}_{f}$ and of the response matrix $\underline{\underline{{X}_{f}}}$, both associated with $\underline{f}$

  Note that the $j$-th column of ${\underline{\underline{R}}}_{f}$ is the modal response of the quantity ${F}_{j}$, while each line corresponds to one considered mode and earthquake direction. ${\underline{\underline{R}}}_{f}$ is then of size $\left({n}_{ec}{n}_{m}\right)\times {n}_{r}$ or ${n}_{ec}\left({n}_{m}+1\right)\times {n}_{r}$ if including the residual rigid motion. The response matrix ${\underline{\underline{X}}}_{f}$ reads:

  $${\underline{\underline{X}}}_{f}={\underline{\underline{R}}}_{f}^{T}\cdot \underline{\underline{\widetilde{H}}}\cdot {\underline{\underline{R}}}_{f}$$

  (5)

  The diagonal coefficients of Eq. (5) are then equal to the square of the directional CQC combinations (Erlicher et al. 2020). Moreover, in (Erlicher et al. 2020) it is showed that ${\underline{\underline{X}}}_{f}$ is symmetric positive-definite, which allows defining a response ellipsoid, implicitly characterized by:

  $${\underline{f}}^{T}\cdot {\underline{\underline{X}}}_{f}^{-1}\cdot \underline{f}\le 1$$

  (6)

• (3) Choice of an engineering meaningful feature scalar quantity $F= {\underline{f}}^{T}\cdot \underline{b}$ to be maximized, constructed as a linear combination of scalar quantities $[{F}_{1},{F}_{2},\dots ,{F}_{{n}_{r}}]$ with the ${n}_{r}$ weighting coefficients given by the components of $\underline{b}$. The vector $\underline{f}$ that lies on the ellipsoid given by $\underline{\underline{{X}_{f}}}$ and that maximizes $F$. $\underline{f}$ is then the solution of:

  $$\mathrm{argmax}\left[{\underline{f}}^{T}\cdot \underline{b}+\frac{\lambda }{2}\left({\underline{f}}^{T}\cdot {\underline{\underline{X}}}_{f}^{-1}\cdot \underline{f}-1\right)\right]$$

  (7)

  where $\lambda$ is the Lagrange multiplier associated with the constraint ${\underline{f}}^{T}\cdot {\underline{\underline{X}}}_{f}^{-1}\cdot \underline{f}=1.$

• (4) Calculation of the vector of modal combination coefficients $\underline{\alpha }$ as (Erlicher et al. 2014):

  $$\underline{\alpha }=\underline{\underline{\widetilde{H}}}\cdot {\underline{\underline{R}}}_{f}\cdot {\underline{\underline{X}}}_{f}^{-1}\cdot \underline{f}$$

  (8)

• (5) Calculation of the final load pattern $\underline{Q}$ as (recalling Eq. (1) and Eq. (4)):

  $$\underline {Q} = \mathop \sum \limits_{k = 1}^{{n_{ec} }} \mathop \sum \limits_{i = 1}^{{n_{m} }} \alpha_{i,k} \underline {Q}_{i,k} = \mathop \sum \limits_{k = 1}^{{n_{ec} }} \mathop \sum \limits_{i = 1}^{{n_{m} }} \alpha_{i,k} \underline{{\underline {M} }} \cdot \underline {A}_{\max ,i,k} : = \underline{{\underline {M} }} \cdot \underline {A}$$

  (9)

  As mentioned, the last two steps (reported hereinafter) are conceptually identical to the classical pushover analysis, with some modifications to account for multi-directional earthquakes. More details can be found in (Erlicher et al. 2020).

• Step 4: Choice of a control node and execution of the non-linear static analysis, with the load pattern $\underline{Q}$. Recording of the forces at the basis of the structure and of the displacements of the control node.

• Step 5: Normalization of the response spectrum and of the force–displacement curve in the ADRS (Acceleration-Displacement Response Spectrum) formalism. Search for the target point at the intersection of the two curves. Calculation of the physical responses associated with the target point.

Finally, if several load patterns are to be calculated, related to several seismic response quantities of interest, the steps (3) to (5) must be repeated for each one. Since this is inconvenient from a practical perspective, Sect. 2.4 of this paper proposes a strategy for minimizing the number of runs when considering several quantities of interest.

These concludes the recall on the previous E-DVA formulation.

2.2 The novel simplified approach for the calculation of α-factors

In this paper, we propose a simplified operational method for the calculation of the α-factors and the evaluation of the pushover load pattern $\underline{Q}$ of step (3), when the load pattern is defined to maximize a given scalar quantity of interest $F$.

The developments are based on the analytical solution given by Tokoro and Menun (2004) for the nonlinear problem of Eq. (7):

$$\underline{f}=\frac{{\underline{\underline{X}}}_{f}\cdot \underline{b}}{\sqrt[2]{{\underline{b}}^{T}\cdot {\underline{\underline{X}}}_{f}\cdot \underline{b}}}$$

(10)

The demonstration of this expression is given in Appendix 1. Then, we calculate the α-factors by inserting Eq. (10) in the calculation of $\underline{\alpha }$ given by Eq. (8) and we use the definition of the response matrix ${\underline{\underline{X}}}_{f}$ given by Eq. (5):

$$\underline{\alpha }=\frac{\underline{\underline{\widetilde{H}}}\cdot {\underline{\underline{R}}}_{f}\cdot \underline{b}}{\sqrt[2]{{\underline{b}}^{T}\cdot {\underline{\underline{X}}}_{f}\cdot \underline{b}}}$$

(11)

This solution is valid for any dimension of the vector $\underline{f}$, and in particular for the case of a vector with only one scalar value $\underline{f}=F$ whose associated linear combination vector is $\underline{b}=$ 1. For this case:

• The modal response matrix ${\underline{\underline{R}}}_{f}$ becomes a modal response vector ${\underline{R}}_{F}$ which contains the spectral responses of the quantity $F$ for each mode and earthquake direction. ${\underline{R}}_{F}$ is then of size ${n}_{ec}{n}_{m}$ or ${n}_{ec}\left({n}_{m}+1\right)$ if including the residual rigid motion.

• The response matrix ${\underline{\underline{X}}}_{f}$ given by Eq. (5) becomes a scalar value ${\underline{R}}_{F}^{T}\cdot \underline{\underline{\widetilde{H}}}\cdot {\underline{R}}_{F}$, which is the square of the definition of the direction combination of the $F$ variable; for the chosen assumptions for the construction of $\underline{\underline{\widetilde{H}}}$ in step (1), that corresponds to a CQC mode combination and a SRSS direction combination.

Inserting these results in:

• Eq. (10), we obtain the maximized value of the scalar quantity of interest $F$:

  $$F=\sqrt[2]{{\underline{R}}_{F}^{T}\cdot \underline{\underline{\widetilde{H}}}\cdot {\underline{R}}_{F}}$$

  (12)

• Eq. (11), we obtain the α-factors:

  $$\underline{\alpha }=\frac{\underline{\underline{\widetilde{H}}}\cdot {\underline{R}}_{F}}{\sqrt[2]{{\underline{R}}_{F}^{T}\cdot \underline{\underline{\widetilde{H}}}\cdot {\underline{R}}_{F}}}$$

  (13)

We can identify that the obtained result for:

• $F=\sqrt[2]{{\underline{R}}_{F}^{T}\cdot \underline{\underline{\widetilde{H}}}\cdot {\underline{R}}_{F}}$ is the mode and direction combination of the quantity of interest $F$

• $\underline{\alpha }$ is the vector (with the minimum norm with respect to $\underline{\underline{\widetilde{H}}}$ from (Erlicher et al. 2020)) whose scalar product with the response vector ${\underline{R}}_{F}$ gives $F=\sqrt[2]{{\underline{R}}_{F}^{T}\cdot \underline{\underline{\widetilde{H}}}\cdot {\underline{R}}_{F}}$, so the α-factors define the mode and direction linear combination maximizing the value of the quantity of interest $F$.

Therefore, we propose the following simplified step (3) for each quantity of interest $F$.

• Step 3: Definition of the α-factors and evaluation of the pushover load pattern $\underline{Q}$:

  • (1) Choice of the seismic response scalar quantity of interest $F$

  • (2) Calculation of the response vector ${\underline{R}}_{F}$ containing the modal responses of $F$ for each earthquake direction (see Sect. 2.3 for calculation examples)

  • (3) Calculation of the vector of linear combination coefficients $\underline{\alpha }$ with Eq. (13)

  • (4) Calculation of the load pattern $\underline{Q}$ using Eq. (1) together with Eqs. (4) and (13).

2.3 Choice of the scalar quantity of interest $F$ and calculation of the associated response vector ${\underline{R}}_{F}$

In previous publications, the E-DVA method was applied to maximize the inertial forces (induced by the seismic acceleration) at the basis of the structure (Huguet et al. 2018; Erlicher et al. 2019, 2020). However, the method can be generalized, allowing both:

• Selection of locations different from the structure’s basis;

• Maximization of local variables, for example proportional to displacements, velocities or accelerations in the linear case.

The only possible difficulty when choosing the quantity of interest $F$ is to define the associated response vector ${\underline{R}}_{F}$. Three different cases are presented hereinafter:

• (1) If $F$ is a direct result of the structural analysis, one can obtain ${\underline{R}}_{F}$ directly from the response spectrum analysis

• (2) If $F$ is not a direct result of the structural analysis but can be calculated as a linear combination $F= {\underline{f}}^{T}\cdot \underline{b}$ of direct results $\underline{f}$ of the structural analysis, one can calculate ${\underline{R}}_{F}={\underline{\underline{R}}}_{f}\cdot \underline{b}$

• (3) For other cases, it is necessary to calculate the spectral response ${F}_{i,k}$ of the interest variable $F$ for each mode $i$ and earthquake direction $k$

2.4 Simplified methodology when considering different quantities of interest $F$

The E-DVA method allows defining a load pattern which maximizes a variable of interest $F$, which may be necessary to verify a design criterion. Thus, if one is interested in a set of ${N}_{q}$ quantities of interest (to evaluate the worst-case scenario for each criterion), ${N}_{q}$ pushover analyses would be necessary, which could be long and impractical if ${N}_{q}$ is large. It will even go against the main advantage of the pushover method, which is to be faster than the equivalent non-linear time-history analysis.

Another possibility, discussed here in this subsection, is to use correction coefficients to conduct a limited number of pushover analysis—for example, by maximizing the basis forces in some directions—and then to modify the obtained results for other quantities of interest (displacements, shear forces, …) to obtain an approximation of their maximal values without going through other full pushover analyses. The proposed methodology is the following:

• (1) Perform a pushover analysis maximizing a first quantity of interest $F$ (for example, a force at the basis of the structure). At the target point, we obtain the results ${F}^{*}$ for the quantity that has been maximized and the vector ${\underline{v}}^{*}$ containing the obtained results for all the concomitant quantities of interest.

• (2) The vector ${\underline{v}}^{*}$ obtained during the maximization of ${F}^{*}$ is in general different than the value that would have been obtained by performing a pushover analysis with a load profile defined to maximize the components of $\underline{v}$. If an elliptical response of concomitant values of $\underline{v}$ have to be defined from the results of the pushover analyses maximizing other quantities of interest, we propose, for each available pushover analysis result ${\underline{v}}^{*}$, to retain the vector $\widetilde{\underline{v}}$ which (i) is proportional to ${\underline{v}}^{*}$ and (ii) has an unitary norm with respect to the corresponding seismic response matrix ${\underline{\underline{X}}}_{v}^{-1}$ (so the vector $\widetilde{\underline{v}}$ lies on the response ellipsoid):

  $$\widetilde{\underline{v}}={\underline{v}}^{*}\frac{1}{\sqrt[2]{{\underline{v}}^{*T}\cdot {\underline{\underline{X}}}_{v}^{-1}\cdot {\underline{v}}^{*}}}$$

  (14)

where the demonstration ${\widetilde{\underline{v}}}^{T}\cdot {\underline{\underline{X}}}_{v}^{-1}\cdot \widetilde{\underline{v}}=1$ is trivial.

This concludes the presentation of the methodology.

3 Results

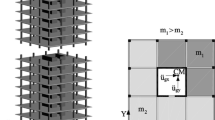
The two methodologies described in the previous section have been applied to the case study of the SMART (Seismic design and best-estimate Methods Assessment for Reinforced concrete buildings subjected to Torsion and nonlinear effect) building. This structure (shown in Fig. 2) was assembled as part of an experimental program of the Electricité De France (EDF) company and the French Atomic Energy Commission (Commissariat à l’Energie Atomique, CEA), supported by the International Atomic Energy Agency (IEAE) (Richard et al. 2016). The program aimed at testing this 1:4 scale mock-up building on a shaking table. The structure was then monitored under several seismic inputs (Richard et al. 2016). The declared intent was to investigate the seismic response of a large structure characterized by a strong asymmetry in its mass and stiffness distribution as a cautionary measure for buildings with large Reinforced Concrete (RC) shear walls, such as nuclear power plants (Richard et al. 2016).

Fig. 2

SMART building: a Experimental model (picture retrieved from (Richard et al. 2016)). b FE Model: mesh, global reference system, and selected nodes

The experimental results were then used by EDF in several test-cases of its Finite Element (FE) software Code Aster (EDF 2023) and the geometrical data as well as the mesh were made available. In this study, this calibrated FE model used for validation. According to its original formulation (Richard et al. 2016), the column, beams, and foundations were considered as linear elastic, while the walls and slabs were modeled with GLRC_HEGIS global nonlinear constitutive model for shell elements (refer to (Huguet et al. 2017) for further details). To summarize, the model is formulated using an innovative analytical multi-scale analysis (without any computational-costly numerical homogenization) using an RC strut between two constitutive cracks as the Representative Volume Element (RVE), which allows a formulation in the thermodynamics of irreversible processes framework at the global RC scale for various local nonlinear phenomena: concrete isotropic diffuse damage evolving in compression; concrete smeared cracking in tension; tension stiffening effect from concrete-reinforcement relative slip and stress; yielding of steel reinforcement bars.

The colored circles and squares in Fig. 2b indicate the nodes selected for the maximization of the local variables; these will be better detailed in the following subsections.

For the seismic input, three couples of accelerograms, named here “1004”,“1032” and 1052”, are considered. They are selected as to have both the same PGA (around $2.5 \mathrm{m}/{\mathrm{s}}^{2}$) and very similar spectra. For all the three cases, the acceleration time histories are applied in the X and Y directions. The first pair (1004) is shown in Fig. 3 by way of example.

Fig. 3

a An example of input acceleration time series (1004), defined along the X and Y directions. b the spectra corresponding to 1004 and to the other two time series, plus the average spectrum (indicated as 'moy.' in the legend) with the additional $+\sigma$ amplitude, along the X direction. The same approach was applied for the Y direction as well

The response spectrum considered for the pushover analysis is the average of the accelerogram spectra. However, the averaging procedure has the side effect of smoothing the resulting function. This might lead to the unintentional removal of the maximum accelerations and thus potentially to an underestimation of the final results. Hence, to stay as conservative as possible, it is decided to increase the resulting accelerations by one standard deviation, resulting in the graph shown by the thick black line in Fig. 3b.

In the next subsections, the results are reported and discussed mirroring the five procedural steps introduced in Sect. 2.2 for describing the novel local variable maximization approach.

3.1 First variable maximization

Two local variables are studied: the shear forces inside the central column of the SMART building and the displacements of several nodes. At this stage, it is then possible to follow the procedure presented in (Erlicher et al. 2020) to reach the final results. These will be discussed hereinafter.

3.1.1 Results of Step 1 : Modal analysis of the structure

The results of the first step are identical for both shear force maximization and displacement maximization. These are summarized in Table 1. The following intermediate steps (2 to 6) will be addressed separately for the two cases considered here.

Table 1 The modal values ${\underline{v}}_{modal,i}$ of the quantity of interest for shear forces maximization and displacement maximization

3.1.2 Shear forces maximization

For shear forces maximization, two nodes, located in the central column and indicated by the red circles at the mid-height between the floors 1–2 and 2–3, are selected.

The intermediate results can be briefly summarized as follows:

3.1.2.1 Results of Step 2 for the maximization of shear forces between the floors 2–3

Table 2 Response spectrum analysis obtained for the shear forces $\text{V} \text{x}\, \text{and} \, \text{V} \text{y}$ due to the seismic action in the directions X et Y

We consider ${V}_{x}$ and ${V}_{y}$ the horizontal components of the shear force (according to the global reference frame reported in Fig. 2b) at these nodes. The shear force $F= {V}_{x}\mathrm{cos}(\theta )+{V}_{y}\mathrm{sin}(\theta )$ is maximized for a total of eight cases, obtained considering $\theta = n\cdot 45^\circ$, with $\theta$ oriented as depicted in Fig. 2 and $n \in [\mathrm{0,7}]$ increasing in unit step, thus resulting in $\theta =$ 0°, 45°, 90°, 135°, 180°, 225°, 270°, and 315°. The corresponding eight load patterns $\underline{Q}$ given by the E-DVA method are applied to the structure in a non-linear static calculation run on Code Aster (EDF 2023). The response spectrum analysis of the shear forces in the different floor level is summarized in Table 2. The used spectrum if the average spectrum (indicated as ‘moy’ in the legend) of Fig 3.

3.1.2.2 Results of Step 3 for the maximization of shear forces between the floors 2–3

The analytical solution for the maximization is given in Table 3 and the linear ellipsoid is compared to the CQC rectangle in Fig 4. The α-factors are given in Table 4.

Fig. 4

Ellipsoid given by ${\underline{\underline{X}}}_{f}$ in black, projection in green, CQC rectangle in blue and maximized shear forces in red (units in N)

Table 3 Analytical solution $\underline{f}=({V}_{x},{V}_{y})$ given by Eq. (10) (Tokoro and Menun 2004)

One can notice that, for two different maximizations whose direction is separated by an angle of 180 degrees, the results are equal but with a different sign. For this reason and for the sake of brevity, only the results for the directions along 0°, 45°, 90° and 135° are shown.

Table 4 Vector of modal combination coefficients $\underline{\alpha }$ with Eq. (13)

3.1.2.3 Results of Step 4 for the maximization of shear forces between the floors 2–3

The chosen control node is the center of mass of each corresponding upper floor: when maximizing shear between the 1st–2nd floor, the control node is the center of mass of the 2nd floor and when maximizing shear between the 2nd–3rd floor, the control node is the center of mass of the 3rd floor.

3.1.2.4 Results of Step 5 for the maximization of shear forces between the floors 2–3

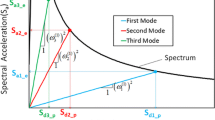
The identification of the target point of each pushover is performed considering the intersection of the capacity spectrum with the ADRS spectrum, accordingly to the previous studies outlined in (Erlicher et al. 2020), Sec. 7.4, and following the suggestions reported in (Bergami et al. 2015). That leads to the evaluation of the target shear forces, which can be plotted in a $({V}_{x},{V}_{y})$ diagram to form an 8-sided polygon (one side per case) (Figs. 5).

Fig. 5

Normalization of the response spectrum and of the force–displacement curve in the ADRS for 0°, 45°, 90° and 135°

Table 5 Target shear force responses used to create the polygonal envelopes

3.1.2.5 Results of Step 6 for the maximization of shear forces between the floors 2–3

Figure 6 compares this polygon to non-linear time-history analyses of the same shear forces, calculated with the three chosen accelerograms. The fitting ellipse is obtained by Least Mean Square fitting.¹ The use of an elliptical envelope is justified by the E-DVA method: the load patterns are obtained by the maximization of the quantity $F$ under the constraint that $\underline{f}=\left({V}_{x} ,{V}_{y}\right)$ lies on the ellipse characterized by the matrix ${\underline{\underline{X}}}_{f}$ (Erlicher et al. 2014). The target shear force responses are presented in Table 5.

Fig. 6

Shear forces maximization: a Node between the floors 2 and 3 b Node between the floors 1 and 2

As it can be seen, the polygonal and elliptical envelopes captured the transient results in a satisfying manner, in magnitude as well as in orientation, as $> 99.9\%$ of the dynamic states $({V}_{x},{V}_{y})$ are included inside these two envelopes.

3.1.3 Displacement maximization

For displacement maximization, three nodes are selected at the center of mass of each of the three floors. These are depicted as green squares in Fig. 2b. As for the previous case, the intermediate results are here discussed before commenting on the final ones. The intermediate results can be briefly summarized as follows:

3.1.3.1 Results of Step 2 for the maximization of displacements of the 3rd floor

Table 6 Response spectrum analysis obtained for the displacement Ux, Uy due to the seismic action in the directions X et Y

We consider ${U}_{x}$ and ${U}_{y}$ the horizontal components of the displacement, for each node. The quantity maximized was then $F = {U}_{x}\mathrm{cos}(\theta )+{U}_{y}\mathrm{sin}(\theta )$, again considering $\theta = n\cdot 45^\circ$ and $n \in [\mathrm{0,7}]$, i.e. for the eight orientations mentioned above. As before, the eight load patterns are then applied to the SMART structure and compared to transient results. The same accelerograms and response spectra for the previous case are applied (Figs. 7, 8). The response spectrum analysis of the displacements in the different floor levels is summarized in Table 6. The used spectrum if the average spectrum (indicated as ‘moy’ in the legend) of Fig 3.

3.1.3.2 Results of Step 3 for the maximization of displacements of the 3rd floor

The analytical solution for the maximization is given in Table 7 and the linear ellipsoid is compared to the CQC rectangle in Fig 7. The α-factors are given in Table 8.

Fig. 7

ellipsoid given by ${\underline{\underline{X}}}_{f}$ in black, projection in green, CQC rectangle in blue and maximized displacements in red (units in m)

Table 7 Analytical solution $\underline{f}$ = (${U}_{x}$,${U}_{y}$) given by (Tokoro and Menun 2004)

Table 8 Vector of modal combination coefficients $\underline{\alpha }$ with Eq. (13)

3.1.3.3 Results of Step 4 for the maximization of displacements of the 3rd floor

The chosen control node is the center of mass of each corresponding floor: when maximizing displacement of the 1st floor, the control node is the center of mass of the 1st floor, when maximizing displacement of the 2nd floor, the control node is the center of mass of the 2nd floor and when maximizing displacement of the 3rd floor, the control node is the center of mass of the 3rd floor.

3.1.3.4 Results of Step 5 for the maximization of displacements of the 3rd floor

The same method as for shear force maximization is applied to compute the displacement maximization in the ARDS format, see Fig. 8. The results obtained by the target displacement responses are presented in Table 9

Fig. 8

Normalization of the response spectrum and of the force–displacement curve in the ADRS for 0°, 45°, 90° and 135°

Table 9 Target displacement responses used to create the polygonal envelopes

3.1.3.5 Results of Step 6 for the maximization of displacements of the 3rd floor

As before, at this stage, the rest of the procedure returns the final outcomes of this analysis.

As for the case of shear forces maximization, the E-DVA method led to a satisfying envelope of the non-linear time-history analyses, in magnitude as well as in orientation; again, $> 99.9\%$ of the transient states — $({U}_{x},{U}_{y})$ fall inside their borders, see Displ X and Displ Y in Fig. 9 .

Fig. 9

Displacement maximization: a Floor 1; b Floor 2; c Floor 3

3.2 Correction for indirect variables maximization

The proposed methodology with correction coefficients for indirect variables maximization is applied to the shear forces studied in 3.1.1 and to the displacements seen in the first case of 3.1.2. Figure 10 shows what happens when this correction is applied analytically on the previous results, without the need of re-running the FE analyses.

Fig. 10

Correction factors on analytical results: a Displacement at the center of mass of the top floor b Shear force between the floors 2 and 3

The green ellipse is characterized by the matrix ${\underline{\underline{X}}}_{v}$ (where $\underline{v}$ gathers displacements or shear forces). The pink polygon consists of the displacements (resp. shear forces) simultaneous to the maximized basis forces, calculated via Eq. (13). The correction factors are applied to this pink polygon, giving the black one.

Please keep in mind that the maximized basis forces are used here by way of example only; as mentioned in 2.3, any maximized variable can be corrected. As expected, the pink polygon is stretched so that its vertices now lie on the green ellipse of the maximized local quantities.

Figure 11 shows the correction factors applied to the pushover results.

Fig. 11

Correction factors on non-linear results: a Displacement at the center of mass of the top floor b Shear force between the floors 2 and 3

As it can be seen in Fig. 11a, the ratio-modified pushover $maxF$ (which maximizes the basis forces) matches well $maxU$ (which maximizes the displacements at the selected nodes), while instead the two differed noticeably before correction. In order to do so, the corresponding displacements of the third floor are stretched from a minimum of 2% to a maximum of 3.5%, depending on the direction (for the eight values of θ considered). The same considerations apply to Fig. 11b: after the (linear) correction, the modified $maxF$ closely resemble $maxV$, which maximizes the shear forces at the three nodes of interest on the central column. In this case, this is achieved by correcting the shear forces in the column by 3–7%.

These results prove how this proposed approach, based on linear correction coefficients, allows to perform a quick estimation of the local quantities maxima without the need of conducting a full pushover analysis for each quantity of interest.

4 Conclusions

This paper presents a generalization of the E-DVA method, recently proposed for the multi-modal pushover analysis of (symmetric or non-symmetric) buildings subjected to multi-component earthquakes.

With respect to other closely-related methodologies, the selection of the multi-modal load pattern is not limited to the classic maximization of the inertial forces acting at the structure basis. Instead, the procedure is pioneeringly extended to encompass other variables, such as shear force and displacement, maximized at different heights and locations throughout the whole structural frame in full compliance with the current requirements from EC 8 and NTC 2018.

Another novelty proposed in this paper is a procedure to extend the results of the pushover analysis performed for the maximization of a particular (local) variable, to obtain any other variable of interest. This is intended to keep the proposed generalized E-DVA as a limited-run method, thus not requiring multiple pushover analyses.

These two proposed methodologies have been tested on the calibrated Finite Element Model of the SMART building, a well-known case study realized by the French Atomic Energy Commission specifically for the seismic assessment of nuclear power plants. The results show that:

• (1) Regarding the first part, the proposed generalized E-DVA method can be applied to the maximization and evaluation of every local quantity, providing a good assessment of the maximum responses under seismic actions. These quantities are not necessarily limited to displacements and shear forces as taken here by way of example.

• (2) Regarding the second part, the proposed correcting factors allow evaluating in a simpler manner the maxima of the simultaneous responses.

Crucially, thanks to this correction method, it is possible to indirectly obtain the results related to the maximization of any variable at any point directly from the results of the classic case, i.e. the maximization of the basis forces.

Both these contributions represent a further step ahead in making the E-DVA as flexible and useful as possible. The result is a fast and reliable pushover analysis, which retains the simplicity of the standard quasi-static procedure while being more accurate and generalized to multiple dominant modes, multi-component earthquakes, non-symmetric buildings, and different quantities of interest, taken at any node of interest in the structure’s frame.

Appendix 1: solution from Tokoro and Menun to the maximisation of \(\underline{{\varvec{f}}}\)

In this Appendix, we discuss the adaptation of an expression given by Tokoro and Menun (2004) to deal with the maximisation of the response vector $\underline{f}$.

Recalling Eq. (7), the problem is to find the argument of:

$$\mathrm{max}\left[{\underline{f}}^{T}\cdot \underline{b}+\frac{\lambda }{2}\left({\underline{f}}^{T}\cdot {\underline{\underline{{X}_{f}}}}^{-1}\cdot \underline{f}-1\right)\right]$$

(15)

Differentiating with respect to $\underline{f}$ and $\lambda$ in order to find the stationary point gives:

$$\left\{\begin{array}{l}\underline{b}+\lambda {\underline{\underline{{X}_{f}}}}^{-1}\cdot \underline{f}=0\\ {\underline{f}}^{T}\cdot {\underline{\underline{{X}_{f}}}}^{-1}\cdot \underline{f}-1=0\end{array}\right.$$

(16)

By combining the two equations of Eq. (16):

$$\lambda =-{\underline{f}}^{T}\cdot \underline{b}$$

(17)

By substituting Eq. (17) in the first equation of Eq. (16):

$$\underline{b}-\left({\underline{f}}^{T}\cdot \underline{b}\right)\left({\underline{\underline{{X}_{f}}}}^{-1}\cdot \underline{f}\right)=0$$

(18)

The expression adapted from (Tokoro and Menun 2004) (indicated here by the subscript _TM) is:

$${\underline{f}}_{\mathrm{TM}}=\frac{\underline{\underline{{X}_{f}}}\cdot \underline{b}}{\sqrt[2]{{\underline{b}}^{T}\cdot \underline{\underline{{X}_{f}}}\cdot \underline{b}}}$$

(19)

Inserting (20) in (19), given that ${\underline{\underline{X}}}_{f}\cdot {\underline{\underline{X}}}_{f}^{-1}={\underline{\underline{I}}}_{d}$ and using transposition rules:

$$\underline{b}-\frac{{\left(\underline{\underline{{X}_{f}}}\cdot \underline{b}\right)}^{T}\cdot \underline{b}}{\sqrt[2]{{\underline{b}}^{T}\cdot \underline{\underline{{X}_{f}}}\cdot \underline{b}}}\cdot \frac{\underline{b}}{\sqrt[2]{{\underline{b}}^{T}\cdot \underline{\underline{{X}_{f}}}\cdot \underline{b}}}=\underline{b}-\frac{{\underline{b}}^{T}\cdot \underline{\underline{{X}_{f}}}\cdot \underline{b}}{{\underline{b}}^{T}\cdot \underline{\underline{{X}_{f}}}\cdot \underline{b}}\cdot \underline{b}=0$$

(20)

Which proves that ${\underline{f}}_{\mathrm{TM}}$ is a solution to (15); hence, finally we can write:

$$\underline{f}={\underline{f}}_{\mathrm{TM}}=\frac{\underline{\underline{{X}_{f}}}\cdot \underline{b}}{\sqrt[2]{{\underline{b}}^{T}\cdot \underline{\underline{{X}_{f}}}\cdot \underline{b}}}$$

(21)