Seismic risk-informed prioritisation of multi-span RC girder bridges considering knowledge-based uncertainty

Abstract

In earthquake-prone countries, transport network managers need to perform extensive seismic risk assessments coping with a considerable number of bridges characterised by an unsatisfying knowledge level and designed in the past without anti-seismic requirements. This study proposes a framework for efficient risk assessment of multi-span girder bridges considering knowledge-based uncertainties. The framework is intended to be applied to risk-informed prioritisation of bridge portfolios. It is based on subsequent modules that involve the input of knowledge data, the simulation of knowledge-based uncertainties, simplified seismic analysis, fragility and loss assessment. The seismic vulnerability of a given bridge is represented by loss ratio percentiles related to a given seismic intensity measure which can be used to quantify the expected annual losses and the corresponding variability due to the influence of knowledge-based uncertainty. A case-study section demonstrates the framework for the widespread category of simply supported girder-reinforced concrete bridges. It addresses issues such as the use of optimal intensity measures, the required number of model realisations and discrepancies with respect to accurate nonlinear time-history analysis. Finally, an illustrative example of the proposed framework for eight case-study bridges in Southern Italy demonstrates its applicability for seismic risk-informed prioritisation of critical bridges and for directing in-depth knowledge data collections where needed.

1 Introduction and motivation

Transport network managers need to ensure the safety or resilience of roadway and railway networks considering service loads (Sangiorgio et al. 2021; Miluccio et al. 2021), and the effects induced by natural hazards (Borzi et al. 2015; Anisha et al. 2022; Nettis et al. 2023). In the aftermath of strong earthquakes, the serviceability of entire transport networks can be affected by the inadequate seismic response of bridges which may lead to relevant direct and indirect losses for entire populated contexts. In developed countries, such as Italy, most of the existing bridges require a seismic safety evaluation since these were built in the’60–70 decades without appropriate anti-seismic requirements (Borzi et al. 2015). Currently, transport network managers are lacking sufficient financial resources and manpower to perform extensive and accurate seismic assessments, to address appropriate risk mitigation strategies. In this context, simplified procedures for seismic risk-informed prioritisation to be applied on large bridge portfolios are currently strongly required.

In earthquake engineering, risk-informed prioritisation is commonly performed by using efficient and fast methods that estimate synthetic risk ratings involving a reasonable degree of approximation. Based on such ratings, structures needing further refined assessment are selected and analysed in detail. For example, the Italian guidelines on the risk management and safety assessment of existing bridges (Ministero delle Infrastrutture e dei Trasporti 2020), recently adopted by the Ministry of Transportation, foresee calculating preliminary risk classes aimed at addressing accurate code-based assessment for high-risk bridges. Additionally, indirect typological approaches, already consolidated for regional-scale assessment of buildings, can be used for a fast risk assessment of bridges. In this case, bridge classes should be preliminarily defined, depending on structural typical characteristics within a given geographical area. For each class, a set of class fragility models should be defined. These models (e.g. the well-known HAZUS model in the United States) can be adopted for approximate risk assessment of existing bridges without resorting to structure-specific analysis. Although research developments of the last decade demonstrate the interest in typological fragility models for several geographical contexts (e.g. Moschonas et al. 2009; Tavares et al. 2012; Nielson and DesRoches 2007), several weaknesses correspond to such approaches. Indeed, the accuracy of these methods is influenced by the complexity of the adopted classification scheme, usually based on key structural and geometric characteristics that could be not directly related to the expected seismic behaviour (Stefanidou and Kappos 2019). Additionally, class fragility curves are commonly calculated based on the analysis of archetype structures extracted from a given geographical context. This determines that the representativeness of class fragility models may decrease for contexts other than those in which they are developed.

To avoid these shortcomings, several research studies focus on using simplified structure-specific mechanics-based seismic assessment approaches for portfolio-scale risk predictions. In these cases, simplified analytical models and equivalent elastic or nonlinear static analysis approaches (e.g. Şadan et al. 2013; Gentile et al. 2020; Cademartori et al. 2020; Nettis et al. 2022; Cardone 2014) are used to achieve fragility curves. For example, Stefanidou and Kappos (2017) present a hybrid methodology for bridge-specific fragility analysis to be used for portfolio assessment, using simplified response spectrum analysis. Cardone et al. (2011) propose a methodology based on the use of the inverse capacity spectrum method to derive bridge fragility curves. Simplified modelling and analysis approaches may involve a lower accuracy with respect to advanced methodologies based on complex bridge finite-element models and nonlinear time-history analysis (NLTHA). However, this disadvantage is balanced by a low computational burden for analysts justifying the potential of analysing several structures in a short time. For these reasons, such simplified approaches should not be directly applied for refined structure-specific risk assessment but represent an ideal solution for portfolio-scale risk-informed prioritisation with the scope to identify critical high-risk structures deserving further in-depth analysis.

To ensure efficiency, the process of risk-informed prioritisation can not rely on a complete knowledge level of the analysed structures. Indeed, since on-site surveys and tests aimed to characterise structural details or material mechanical properties are time-consuming and expensive, risk-informed prioritisation should generally be based on data already included in the transport authority’s databases or to be quickly collected onsite. However, authorities’ databases are lacking design documents, material certificates and blueprints which may be lost by operators or stored in inaccessible archives in paper form (Borzi et al. 2015; Calvi et al. 2019). Therefore, the influence of knowledge-based uncertainty, also called epistemic uncertainty, should be necessarily considered for preliminary risk assessment.

Effective risk-informed prioritisation methodologies should be based on risk metrics being easily understandable and transparent to decision-makers. Recent research developments analyse direct losses such as repair cost (e.g. Perdomo et al. 2022; Kameshwar and Padgett 2017) which is of main interest to transportation authorities in charge of managing the structural maintenance cost of a given network. In addition, other studies focus on procedures for estimating indirect losses (e.g. Dong and Frangopol 2015; Zhang and Wang 2016) impacting the network resilience and deriving from the reduction of functionality of a given bridge and redistribution of traffic flows. Considering economic losses in terms of repair cost, the most advanced approach for direct loss assessment is proposed by the FEMA (2018) P-58 framework and detailed for buildings (so-called component-level approach). This latter requires significant computational efforts resulting hardly applicable within a risk prioritisation framework considering a relevant number of structures. Conversely, simplified loss assessment approaches for bridges are proposed in the literature (Perdomo et al. 2022; Miano et al. 2016) and suggested by the well-known HAZUS methodology (FEMA 2012). These do not consider component-level contributions, but calculate economic losses based on a structure-level probability of damage and represent a valid solution to be used within risk-informed prioritisation frameworks.

In summary, common challenges associated with the structural safety management of bridges are related to the high number of structures requiring assessment; incomplete knowledge information and the need for transparent risk metrics (e.g. economic losses) to identify critical bridges. To face the abovementioned issues, this study presents an efficient framework involving a bridge-specific fragility analysis and structure-level direct loss assessment accounting for knowledge-based uncertainties, suitable for risk-informed prioritisation. The framework involves a data collection based on pre-defined spreadsheets which can be filled in through fast onsite inspections. Knowledge-based uncertainties are considered by using statistical sampling to generate a set of bridge model realisations. Seismic analyses are carried out by using simplified modelling and displacement-based assessment methods, which can be performed through simple programming routines. For the investigated bridge, percentiles of the damage probability and loss ratio for a given seismic intensity measure are computed. These are used to quantify expected annual losses (considering the repair cost) and the corresponding variation interval due to epistemic uncertainty.

The outputs of the framework applied for a given bridge portfolio can be used to 1) define risk-informed prioritisation plans based on the current knowledge state on the analysed bridges; 2) identify cases in which the risk evaluation is significantly affected by the knowledge-based uncertainty and address accurate surveys and testing to refine the ranking. Being based on a structure-specific analysis, the procedure is considered to outperform typological approaches affected by the above-mentioned limitations. In addition, an advantage of the proposed procedure with respect to previously developed simplified risk assessment approaches is related to the potential of explicitly modelling the influence of knowledge-based uncertainty on risk. This latter, indeed, may have a significant role in the risk-based prioritisation of bridges affected by non-uniform completeness of initial knowledge data. Other existing approaches do not consider a bridge-tailored knowledge-based uncertainty which is simply modelled as a variable increase of dispersion in fragility estimations based on judgemental assumptions.

The methodology is developed with reference to multi-span reinforced concrete (RC) bridges with simply supported (i.e. isostatic) or continuous superstructure, which are the most spread bridge typologies in Europe. A refined description of the framework is reported in Sect. 2. Section 3 addresses the application for simply supported girder bridges by investigating the use of optimal seismic intensity measures, the definition of appropriate sampling size and an evaluation of the discrepancies with respect to more accurate numerical models and NLTHA. In Sect. 4, an illustrative application is provided in which the framework is applied to eight existing simply supported RC bridges belonging to the national road network of the Basilicata region in Italy.

2 Description of the methodology

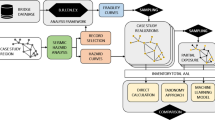
The framework to perform the simplified loss assessment of multi-span RC girder bridges considering knowledge-based uncertainty is described in this section. The different steps are resumed in Fig. 1 and discussed in the following sub-sections.

Fig. 1

Flowchart of the proposed framework

2.1 Data collection and modelling uncertainties

The initial data collection is aimed at achieving necessary deterministic and probabilistic knowledge data for the analysed bridges. An appropriate spreadsheet is developed, composed of several data forms, suitable to allocate general data and knowledge parameters related to the superstructure, piers, abutments, materials, and constructive details. Appendix includes a complete list of the required input data. The required knowledge data can be retrieved from design documents and blueprints stored in the archives of transport network managers. If design documents are lacking, the data collection may require a fast survey. The spreadsheets are designed to be analysed by programming routines, which import the necessary knowledge data and perform automatically the calculations. Note that a specific routine for performing a simulated design procedure in case of the absence of blueprints is also included. It is aimed to compute a minimum amount of steel reinforcements for piers according to the old reference codes (currently only old Italian codes are implemented).

Generally, simplified approaches for risk assessment include an implicit consideration of the uncertainty of knowledge parameters and seismic actions (i.e. record-to-record variability) which is modelled by using pre-defined typology-based values of dispersion in probabilistic relationships representing fragility curves. Conversely, as mentioned in Sect. 1, the probabilistic seismic assessment carried out in the proposed framework explicitly considers aleatory and epistemic uncertainties. According to Bradley (Bradley 2010) the distinction between the two types depends on whether these can be reduced or not by the analyst. Aleatory uncertainties concern inherently random processes and, generally, include record-to-record variability. Two strategies can be adopted to model record-to-record variability. The first is based on the selection of groups of ground motions scaled to be compatible with conditional spectra representing the expected hazard conditions at given intensity levels for the selected structure (Skoulidou and Romão 2019; Baker 2011). In this case, a multi-stripe approach is used for fragility analysis. Instead, the second strategy foresees the use of a large suite of natural unscaled ground motions spanning from low to high seismic intensity and the fragility analysis is based on the so-called cloud approach. While the first approach is the most accurate and suitable for single-structure refined risk assessment, the second requires minor analysis effort and, therefore, is preferable for risk-informed prioritisation purposes. Therefore, the cloud approach is used in the proposed framework, and the record-to-record variability is modelled by a single suite of natural unscaled ground motions reflecting the hazard conditions (in terms of soil type, source distance and magnitude) of the analysed bridges.

Conversely, epistemic uncertainties are knowledge-based, i.e. derive from imperfect initial knowledge, and usually can be reduced by the analyst, via e.g. appropriate surveys and destructive or non-destructive testing, involving inevitably additional effort in the assessment process. In the presented framework, geometry parameters, mechanical properties of the materials, structural details and other data, which can not be reasonably assumed “deterministic”, are considered knowledge-based uncertainties. These are represented by random variables characterised by appropriate statistical distributions which can be judgementally assumed or derived from literature studies (e.g. Tavares et al. 2012; Nielson and DesRoches 2007; Zelaschi et al. 2016). Knowledge-based uncertainties are accounted for through the random generation of a population of bridge model realisations characterised by sets of variables sampled from the corresponding statistical distributions. The Latin Hypercube Sampling (LHS) (Iman and Conover 1982) is used to perform the random sampling according to other past literature studies dealing with bridge structural assessment (e.g. Tavares et al. 2012; Du and Padgett 2020; Monteiro 2016). The LHS, thanks to the stratification of the input probabilistic distributions, generates statistical samples composed of a lower number of realisations with respect to the standard Monte Carlo technique, reducing the computational effort needed for further seismic analyses. In this study, for the sake of efficiency of the methodology, the random variables are considered uncorrelated, while perfect (i.e. full) correlation of the random parameters within the single bridge model realisation is assumed. However, these assumptions may be easily relaxed accounting for appropriate correlation coefficients (Tubaldi et al. 2012).

2.2 Simplified modelling strategy

In this sub-section, the simplified methodology to model the seismic response of bridges is described. This is directly applied to analyse each bridge model realisation. The methodology is described in detail with reference to multi-span RC bridges with adjacent independent bearing-supported girders (i.e. commonly referred to as simply supported girder bridges) and for continuous-superstructure bridges.

2.2.1 Definition of subassembly capacity curves

The seismic behaviour of each bridge model realisation is represented by means of capacity curves related to an equivalent single-degree-of-freedom (SDoF) system and a given analysis direction. The adopted approach to calculate equivalent SDoF capacity curves of the investigated bridge realisation considers the following assumptions. First, only the nonlinear response of the piers and the superstructure-substructure connection systems is considered, while the superstructure is supposed to respond as an elastic frame during the seismic excitation. Additionally, the nonlinear response of the foundation system is not considered. This assumption is justified by the study by Calvi et al. (2013) stating that, in past bridge design practice, foundations were generally conservatively designed. However, appropriate recommendations to include to model soil-structure interaction within this simplified approach are provided by Ni et al. (2014).

The first step foresees the analysis of the seismic response of each superstructure-substructure subassembly, including a substructure component (pier or abutment) and the corresponding connection system with the superstructure (composed of e.g. bearing devices, shear keys) to derive an equivalent SDoF bilinear subassembly capacity curve (i.e. a force–displacement relationship). This latter can be achieved by the combination of the force–displacement laws of the connection system and the pier or abutment acting as a series system.

The force–displacement relationship of single-column piers can be computed as proposed by Priestley et al. (2007) based on sectional bilinear moment–curvature analyses (Montejo and Kowalsky 2007). In the case of multi-column piers, the pier force–displacement relationship can be computed by simplified analytical methods based on mechanism analysis (Gentile et al. 2019), by using nonlinear pushover analyses, or by simply aggregating the force–displacement laws of the columns working in parallel and double-bending condition. If the deformation of the bearings is negligible (i.e. steel hinges, pin bearings or, generally, fixed bearings) these can be assumed rigid and only the nonlinear behaviour of the pier or abutment is considered in the subassembly. However, in most of the non-seismically designed existing simply supported bridges, an inadequate response of the bearing devices can determine the reaching of relevant damage states such as shear failure of old fixed bearings or slipping of old neoprene pads, leading to unseating of the girders. In these cases, the cumulative constitutive law of the superstructure-substructure connection system can be attained as the sum of the force–displacement relationships of the bearing devices acting in parallel. If present, the contribution of shear keys should be also included. Multi-linear force–displacement relationships for bearing devices and shear keys are reported in Cardone (2014).

The force–displacement relationship for abutments should consider the abutment type (e.g. gravity, spill-through or pile bent types) and the presence of back walls and wing walls. A rigid behaviour of gravity-type abutment walls can be assumed for the seismic response in the transverse direction, while the response in the longitudinal direction should consider the interaction with the soil backfill and the gap size. Guidelines for the modelling of the abutment-backfill interaction are reported by Shamsabadi et al. (2007) and Xie et al. (2019).

For piers, once the force–displacement relationships of the substructure components and their connection systems are achieved for a given analysis direction, the capacity curve of the equivalent SDoF representative of each subassembly can be calculated analytically as shown in Fig. 2.

Fig. 2

Calculation of the equivalent SDoF force–displacement relationship of a subassembly (${V}_{sub}-{\Delta }_{sub}$) based on the force–displacement relationships of a single-column pier (${V}_{p}-{\Delta }_{p}$) and of a generic connection system (${V}_{c}-{\Delta }_{c}$)

The equivalent viscous damping of the pier and the bearing system is also calculated through the ductility-based formulation proposed by Priestley et al. (2007) reported in Eq. (1). The coefficient ${C}_{evd}$ is equal to 0.444 for piers. ${C}_{evd}$ can be assumed equal to 0.565 for neoprene bearings (Cardone 2014). The equivalent viscous damping of the subassembly for a given ${\Delta }_{sub}$ is computed through Eq. (2). For increasing values of base shear, the effective displacement and the equivalent viscous damping of the subassembly are calculated, until one of the members reaches its ultimate displacement capacity. In addition, a value of the SDoF effective mass of the subassembly (${m}_{sub}$) is also computed (Pinto and Franchin 2010). The same approach can be similarly adopted for the equivalent SDoF force–displacement characterisation of superstructure-abutment subassemblies.

$$\xi _{{eq}} = 0.05 + C_{{evd}} \left( {{\raise0.7ex\hbox{${\mu - 1}$} \!\mathord{\left/ {\vphantom {{\mu - 1} {\pi \mu }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\pi \mu }$}}} \right)$$

(1)

$${\xi }_{eq,sub}=\frac{{\Delta }_{p}{\xi }_{eq,p}+{\Delta }_{c}{\xi }_{eq,c}}{{\Delta }_{sub}}$$

(2)

2.2.2 Seismic analysis of simply supported girder bridges

The modelling and analysis strategy to characterise the global bridge seismic response differs depending on the structural scheme. For multi-span simply supported girder bridges, the individual pier model proposed by Pinto and Franchin (2010) and suggested by the Italian code (Ministero delle Infrastrutture e dei Trasporti 2018) can be applied for the seismic response in the transverse direction. Each superstructure-substructure subassembly can be analysed separately, assuming that relative rotations between adjacent independent decks are allowed. Within this approach, the seismic demand under a given earthquake-induced shaking is calculated for each subassembly and the “weakest” component (i.e. the first experiencing a given damage) determines the reaching of a global damage state. Generally, this approach is effective for first-mode-dominated structures (Cardone 2014). This condition is, generally, met if the ratio of the periods of adjacent independent subassemblies is contained into the range [0.50–2.00] guaranteeing weak interaction between independent decks.

In the longitudinal direction, the individual pier model can be also used if subassemblies do not transfer seismic forces to each other. This occurs in case the width of the expansion joint gap between adjacent decks allows each subassembly responding independently until a damage state is reached. It is worth mentioning that non-seismically designed bridges usually exhibit low joint width, designed considering thermal deformations only. In this case, premature closure of the gaps fosters the onset of a parallel system, in which the subassemblies resist the total bridge seismic inertia force depending on the proper stiffness. Similarly, this occurs if shock transmitters are present to ensure a hyperstatic longitudinal seismic response during the seismic excitation. In this case, a capacity curve of the equivalent SDoF of the bridge can be calculated by aggregating the force–displacement laws of each subassembly, assuming that these are subjected to an equal superstructure longitudinal displacement ${\Delta }_{i}$. For each value of ${\Delta }_{i}$, the equivalent SDoF base shear is given by the sum of the shear forces absorbed by all the resisting subassemblies (${V}_{su{b}_{j}}$). Additionally, for each ${\Delta }_{i}$, the equivalent viscous damping of the equivalent SDoF system is calculated via Eq. (3). It is worth mentioning that such simplified analysis approaches are suggested by codes and, therefore, can be conveniently used by practitioners for loss assessment according to the proposed framework.

$${\xi }_{eff}=\frac{{\sum }_{j=1}^{N}{\xi }_{eq,su{b}_{j}}{V}_{su{b}_{j}}}{{\sum }_{j=1}^{N}{V}_{su{b}_{j}}}$$

(3)

2.2.3 Seismic analysis of continuous-superstructure bridges

The seismic behaviour of hyperstatic continuous-superstructure bridges in the transverse direction is characterized by the coexistence of two load paths since the seismic inertia forces are absorbed by the superstructure-abutments system or resisted by the substructure components (Tubaldi et al. 2012). To calculate the equivalent SDoF capacity curve of such bridge typology, the displacement-based pseudo-pushover proposed by Gentile et al. (2020) can be adopted. The procedure involves a series of progressive iterative linear (modal or static) analyses performed for incremental control node displacement. A simple equivalent elastic model is assumed in which the superstructure is modelled by an elastic beam and the substructure components are represented through elastic springs equipped with effective stiffness in the target displacement condition. The stiffness of the supports is updated step-by-step according to the increasing ductility demand. For the sake of brevity, the procedure is not described in detail in this study and the interested readers are referred to the study by Gentile et al. (2020). It is worth mentioning that several modifications to this displacement-based assessment algorithm for bridges governed by higher modes are also proposed by Nettis et al. (2022).

In the longitudinal direction, the equivalent SDoF capacity curve of the bridge is calculated in two ways. In existing continuous-superstructure bridges, a common design strategy was based on the definition of a “fixed” substructure component designed to respond to the seismic actions, whereas the others were released by the superstructure through roller or slider bearings. In this case, the equivalent SDoF capacity curve of the bridge coincides with the force–displacement relationship of the “fixed” subassembly. On the contrary, if more subassemblies are designed to resist seismic action, the force–displacement laws of these subassemblies should be aggregated as a parallel system (as anticipated for simply supported girder bridges).

2.3 Seismic performance analysis through CSM

Generally, NLTHA is used for the calculation of the seismic performance under a given excitation within a probabilistic analysis considering record-to-record variability. However, to foster the efficiency of the methodology, in the proposed framework, the NLTHA is replaced by the Cloud-CSM algorithm (referred to as CCSM in this study) described by Nettis et al. (2021a). It is a modified version of the capacity spectrum method (CSM) (Freeman 1998) which adopts real (un-smoothed) response spectra. The algorithm allows for the identification of the record-specific displacement demand given an input equivalent SDoF force–displacement capacity curve and elastic response spectrum. This algorithm computes the displacement demand by deriving the graphical intersection between the so-called capacity spectrum of the structure and the “variable-damping spectrum” in the acceleration-displacement format. The former is achieved by converting the equivalent SDoF capacity curve in the acceleration-displacement format. Conversely, the variable-damping spectrum collects the acceleration-displacement pairs of the overdamped demand calculated for each value of the secant period and equivalent viscous damping associated with increasing displacement demand for the analysed structure.

For further clarification, the reader is directly referred to the study by Nettis et al. (2021a). Note that if the variable-damping spectrum does not intersect the capacity curve (or the displacement demand exceeds a given pre-defined collapse displacement), the algorithm leads to a collapse case (Nettis et al. 2021a).

2.4 Damage states and damage-to-loss ratios

In the proposed methodology, the fragility of a bridge is characterised with reference to pre-defined damage states (DS). Four DSs are considered, defined according to the HAZUS methodology (FEMA 2012). The DS1 is related to light damages (e.g. minor cracking and spalling) that may require minor repairs with no service interruption. DS2 corresponds to moderate damages (i.e. moderate shear cracks of columns, moderate movement of the connection systems) requiring repairs and short service interruption. The DS3 is attained for severe damages (shear failure or strength degradation for columns without collapse, significant residual movements at the connections) that require expensive interventions and traffic interruption. The DS4 is related to a near-collapse condition characterised by unrepairable damages leading to necessary bridge replacement. The displacement-based DS thresholds reported in Table 1 are used. These are computed for each bridge realisation based on the force–displacement relationship of the components and are used for the fragility analysis described in the following section.

Table 1 Considered damage state (DS) thresholds for different bridge components and damage-to-loss ratios (DLRs)

The loss assessment requires the quantification of the repair cost associated with a given DS through appropriate consequence models. In this framework, the damage-to-loss ratios (DLR) provided by HAZUS (FEMA 2012) are implemented (Table 1). These express the loss ratio with respect to the total replacement cost (${C}_{REPL}$) for a given DS. It is worth mentioning that the DLRs provided by HAZUS are developed with specific reference to the United States and, therefore, their applicability for the European context requires validation. DLRs for bridges calibrated for the European contexts should be developed in future studies and integrated into the presented framework. However, to increase the accuracy of the loss assessment, transport authority’s analysts can estimate the repair cost associated with a given DS for a given bridge or bridge portfolio through market surveys specific to the considered geographical context.

2.5 Fragility analysis

Fragility analysis for a given DS is aimed at the calculation of the probability of reaching or exceeding the considered DS thresholds for a given seismic intensity measure (IM). This process requires the consideration of different components which can be susceptible to damage. Generally, fragility curves for bridges are calculated by aggregating the component-specific fragility curves assuming appropriate correlation (Tavares et al. 2012; Stefanidou and Kappos 2017; Choi et al. 2004) or via a simplified approach in which the “weakest” member determines the global DS of the bridge (Borzi et al. 2015). In this study, to reduce the analysis effort in applying this methodology for large bridge portfolios, the second approach (also defined as series system assumption) is used. This approximation is consistent with the goal of seismic risk-informed prioritisation considering that further refined analysis should be directed to bridges characterised by a significant value of risk metrics. The performance of each i-th bridge component (e.g. pier, bearing, abutment) under the j-th ground motion, with respect to a given DS, is expressed by a demand-capacity ratio (DCR) calculated with Eq. (4) where ${\Delta }_{i}^{DS}$ is the appropriate displacement-based DS threshold (Table 1).

$${DCR}_{ij}^{\mathrm{DS}}=\frac{{\Delta }_{ij}}{{\Delta }_{i}^{\mathrm{DS}}}$$

(4)

The system-level bridge DCR is the maximum of the DCRs of the different components for the considered ground-motion excitation. In other words, the fragility functions express the probability that one of the components of the bridge reaches a unitary $DC{R}^{DS}$ for a determined IM. As anticipated in subsection 2.1, fragility curves are calculated through a regression-based probabilistic seismic demand model according to the cloud analysis approach (Jalayer et al. 2017). First, the results of the seismic performance analyses are organized in pairs of $[{IM}_{j},{DCR}_{j}^{DS}]$. It is assumed that a power-law model expresses the relationship between the structural demands and ground-motion seismic intensity. The parameters [$a,b$] of the power model are estimated by fitting a linear model to the cloud data transformed in the natural logarithmic scale, as in Eq. (5), using the least square regression method. The dispersion of the demand around the median estimated with the regression model is assumed constant and is given by Eq. (6) where M is the number of ground motions. The fragility function is represented by the normal cumulative distribution function $\upphi (\bullet )$ in Eq. (7).

$$\mathrm{ln}{\alpha }_{{DCR}^{DS}|IM}=\mathrm{ln}\left(a\right)+b\mathrm{ln}(IM)$$

(5)

$${\beta }_{{DCR}^{DS}|IM}=\sqrt{\frac{{\sum }_{j=1}^{M}(\mathrm{ln}{DCR}_{j}^{DS}-\mathrm{ln}{a({IM}_{j})}^{b})}{M-2}}$$

(6)

$$P\left({DCR}^{DS}\ge 1|IM\right)=1-\phi \left(\frac{-\mathrm{ln}{\alpha }_{{DCR}^{DS}|IM}}{{\beta }_{{DCR}^{DS}|IM}}\right)=\phi \left(\frac{\mathrm{ln}{\alpha }_{{DCR}^{DS}|IM}}{{\beta }_{{DCR}^{DS}|IM}}\right)$$

(7)

To consider collapse cases included in the cloud data, the approach adopted by Jalayer et al. (2017) should be adopted. In this case, the probability of reaching a given DS for a given IM should be computed by aggregating, through the total probability theorem, the result of Eq. (7), applied for non-collapse cases only, and the probability of collapse. The probability of collapse given IM value can be computed by fitting a logistic regression model suitable to binary (collapse-no collapse) variables (Nettis et al. 2021a).

Note that the abovementioned fragility analysis approach involves some strict assumptions (related to the use of a power model relationships between demand and IM and lognormality of the fragility functions) which may be inaccurate for certain existing case-study bridges and if knowledge-based uncertainties are considered (Romão et al. 2013; Karamlou and Bocchini 2015; Mangalathu and Jeon 2019; Mohamed et al. 2023).

In the proposed methodology, the fragility analysis is repeated for the entire dataset of bridge model realisations. Therefore, the global bridge fragility may be expressed by the achieved population of fragility curves (Fig. 1).

Each fragility curve, related to a given bridge model realisation, expresses the probability of reaching a given DS conditioned to a given value of IM and a given bridge knowledge scenario. The population of fragility curves is synthetically represented by extracting the 16th, 50th and 84th percentiles of the probability of reaching a DS for variable IM values. The curves collecting the percentiles of the damage probability are defined as fragility percentiles and inform the analyst of the uncertainty in fragility estimations (e.g. Bradley 2010; Celik and Ellingwood 2010) derived by the lack of complete initial knowledge information. The 50th fragility percentile is used to derive a synthetic single bridge fragility curve which includes the uncertainty in terms of record-to-record variability and knowledge-based uncertainty. Moreover, the 16th and 84th percentiles can be assumed as fragility curves conditioned to “good quality” and a “poor quality” construction scenarios and display a fragility area summarising the fragility variability that accounts for the influence of the knowledge-based uncertainty. The wider the area, the wider the uncertainty of further risk estimations.

2.6 Risk assessment and risk-informed prioritisation

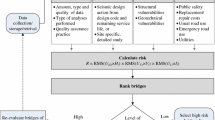
The seismic risk is quantified through the direct economic losses associated with the repairing/replacement of the damaged bridge. Indirect losses related to disruption time, variation of traffic flows within the network and increasing travelling time for users are not considered. This is because, currently, modelling indirect losses requires advanced traffic simulations and statistical data on bridge repair/replacement which are not currently available (Abarca et al. 2022).

In the proposed framework, the computation of direct losses is based on the simplified structure-level approach (FEMA 2012). For this purpose, hazard curves $H(IM)$, representing the mean annual frequency of exceeding seismic intensity, should be collected with specific reference to the location of bridge by means of a probabilistic seismic hazard analysis. The probability of the structure being in a given DS for a given IM value (${{P}_{DS}}_{(k)}$(IM)) can be calculated via Eq. (8) in which ${N}_{DS}$ is the number of considered DS thresholds. Loss ratio curves $LR(IM)$ relating the expected loss ratio to IM values (referred to also as vulnerability curves in literature) are calculated by Eq. (9).

$${P}_{D{S}_{k}}\left(IM\right)=\left\{\begin{array}{l}P\left(DC{R}_{DS(k)}\ge 1|IM\right)-P\left(DC{R}_{DS(k+1)}\ge 1|IM\right), k=1,\dots ,{\mathrm{N}}_{DS}-1\\ P\left(DC{R}_{DS(k)}\ge 1|IM\right), k={\mathrm{N}}_{\mathrm{DS}}\end{array}\right.$$

(8)

$$LR(IM)=\sum_{k=1}^{{N}_{DS}}DL{R}_{k}{P}_{D{S}_{k} }\left(IM\right)$$

(9)

Finally, the expected annual losses (EAL) can be computed by solving the integration in Eq. (10), where $L(IM)$ is the expected loss function computed by multiplying $LR(IM)$ for ${C}_{REPL}$.

$$EAL=\int L(IM)\left|\frac{dH\left(IM\right)}{dIM}\right|dIM$$

(10)

Similar to the fragility analysis (sub-Sect. 2.5), a loss ratio curve and a value of EAL can be computed for each of the bridge model realisations. The population of loss ratio curves and EAL can be summarized by using 16th, 50th and 84th percentiles. These outputs can be useful for transport authorities’ operators in defining optimal risk-mitigation plans for bridge portfolios:

• $EA{L}^{50th}$ can be directly used for a risk-based ranking and for defining a priority scheme for mitigation strategies. The priority scheme based on $EA{L}^{50th}$ reflects the current knowledge state of the investigated bridge portfolios.

• The range $[EA{L}^{84th}; EA{L}^{16th}]$ quantifies the variability of direct losses involved by the knowledge-based uncertainty. It can be used to identify bridges for which the highest influence of knowledge-based uncertainty is registered. These should be subjected to appropriate surveys and testing campaigns aimed at reducing such uncertainty. After these in-depth investigations, the $[EA{L}^{84th}; EA{L}^{16th}]$ and $EA{L}^{50th}$ should be recalculated and the priority scheme should be updated.

3 Case-study application

This case-study analysis investigates the application of the framework for multi-span simply supported RC bridges. It is the most spread existing bridge typology in Italy and Europe. In addition to illustrating an application example for interested readers, the analysis is aimed at investigating some issues affecting the use of the framework related to optimal IMs for fragility assessment, an appropriate sampling size in LHS, and the evaluation of sources of discrepancy of the simplified modelling and analysis strategy compared to NLTHA.

3.1 Description of the case-study bridge and modelling uncertainty

The case-study bridge exhibits an isostatic structural scheme with five 30 m-long spans as shown in Fig. 3. The superstructure is composed of simply supported independent decks consisting of three I-shaped prestressed RC girders. The bridge was built between 1980–1984 and designed according to old Italian reference codes (DM 1975 and DM 1980 for seismic and traffic loads, respectively). The geometric data are retrived through a 3D point-cloud model defined via a drone-based survey and photogrammetric elaborations  (Nettis et al. 2020). Two versions of the case-study bridge are analysed. The first (B1a) exhibits unbolted neoprene bearing devices which are observed on site. In the second case study (B1b), the superstructure-substructure connections are composed of fixed bearings (simulating steel hinges or pin bearings) and sliders (Fig. 3). In this case, two conditions are assumed: 1) the deformability and shear failure of fixed bearings are excluded and 2) the bearing arrangement allows for relative rotations between the piers and the superstructures along the vertical axis of the pier. The case-study bridge exhibits non-seismically designed joints (the gap is equal to 20 mm) between the adjacent decks and between the decks and the abutments. According to the presented procedure in Sect. 2.2.2, this condition implies that the bridge seismically behaves as a parallel system in the longitudinal direction. The knowledge data are inserted into the spreadsheet reported in Appendix. The calculation procedures included in the proposed framework are run via MATLAB (MATLAB 2018) programming routines which are developed to perform the statistical sampling for modelling the epistemic uncertainties, the simulated design of columns, if needed, and the seismic risk assessment procedure.

Fig. 3

Geometric and constructive characterization of the case-study bridge (dimensions in meters)

Table 2 lists the statistical distribution associated with the knowledge-based uncertainties derived from literature studies (Tavares et al. 2012; Nielson and DesRoches 2007; Cardone et al. 2011; Zelaschi et al. 2016; Monteiro 2016). If statistical distributions related to some uncertain data are not available, a uniform distribution (representing the maximum uncertainty according to Celik et al.(2010) is assigned. As shown in Table 2, variability in the design class of the materials (${f}_{ck}$ and${f}_{yk}$) is assumed. The mean strength values (${f}_{cm}$ and${f}_{ym}$) are calculated depending on the corresponding design characteristic values (Borzi et al. 2008) assuming a coefficient of variation of 0.09 and 0.18 for steel and concrete, respectively (Monteiro 2016). The longitudinal reinforcement in bridge piers is calculated through a simulated design procedure considering the old design reference codes. The procedure automatically neglects the couples of design concrete and steel classes leading to an incompatible design with respect to the old reference code. Furthermore, it is recognized that, in the’70-’90 decades, the design of transverse reinforcements of bridge columns was dictated by constructive needs rather than mechanical ones because of the low seismic design actions. Consequently, the volumetric ratio of the transverse reinforcement (${\rho }_{t})$ is modelled with a uniform distribution and not calculated via a simulated design. A discrete uniform distribution is assumed since the simulated values of ${\rho }_{t}$ are converted in a “real” configuration of transverse reinforcements. Finally, in absence of core drilling to measure the real width of the layers composing the road surface, an average value of the non-structural load (${W}_{NS}$) is judgementally estimated, equal to 3.60 kN/m² and modelled through a uniform distribution considering a ± 20% uncertainty.

Table 2 Simulation of knowledge-based uncertainties

For the record-to-record variability, a suite of natural ground motions is selected from the SIMBAD database (Smerzini et al. 2014) consistently with the characteristic of soil type, magnitude and distance of expected earthquakes in the bridge location. The magnitude and distance de-aggregation is achieved using the software Rexel (Iervolino et al. 2010). The ground motions compatible with these requirements are selected (176 ground motions) in the SIMBAD database. Then, the 100 records with the highest peak ground acceleration (PGA) are selected to perform the fragility analysis. The PGA of the selected records varies between 1.77 g and 0.16 g.

The moment–curvature laws of the piers are calculated using CUMBIA (Montejo and Kowalsky 2007). The mechanical behaviour of neoprene bearings is modelled through an elastic-perfectly plastic relationship assuming a slipping failure between the rubber and the concrete surfaces (which well represents the seismic behaviour of low-thickness neoprene bearings according to Cardone 2014). Finally, the nonlinear abutment-backfill interaction accounting for soil passive resistance is calculated as proposed by Nielson (2005).

3.2 Optimal IM analysis

The first issue concerning the applicability of the presented framework is related to the choice of optimal IM parameters to be used within fragility analysis. In cloud analysis, a robust computation of regression-based fragility curves is fostered by a high number of records, selected based on the modal periods and nonlinear response of the investigated structure, and the so-called efficiency of the adopted IM. The efficiency of a given IM represents the correlation of the IM to a given engineering demand parameter representative of the seismic damage. Since this framework does not foresee a structure-specific record selection, it is essential to use efficient IM so that the fragility analysis is accurate for bridges having different modal and nonlinear behaviour. Padgett et al. (2008) indicate PGA as a good compromise for fragility analysis of bridge portfolios given the corresponding advantages in terms of hazard computability. Furthermore, O’Reilly (2021) investigates optimal IM for risk assessment of continuous-deck multi-span RC bridges and proves the efficiency of the geometric average of spectral accelerations ($AvgSa$) provided that an appropriate period range is defined. The advantages of $AvgSa$ are induced by the possibility to synthesize the intensity of the ground motion in a period interval representative of the inelastic structural response. To the authors’ best knowledge, no recommendations exist in literature on selecting efficient IMs for fragility analysis of simply supported-girder bridges. Therefore, a preliminary optimal IM analysis is necessary to suggest efficient IMs to be adopted within the presented methodology.

The optimal IM analysis carried out in this study considers spectral shape-dependent candidate IMs which can be used within CCSM. Note that, since the presented simplified methodology considers separately the analysis in the longitudinal and transverse directions, two different optimal IM analyses are performed using different candidate IMs. First, the PGA and the peak ground velocity (PGV) are selected as conventional structure-independent candidate IMs for both the analysis directions. The spectral acceleration, $Sa(T)$, calculated at the first fundamental period (corresponding to the vibration mode exciting the highest percentage of participating mass) is commonly adopted for fragility analysis of structures. For simply supported-girder bridges, according to the abovementioned assumption, each superstructure-substructure subassembly responds isostatically in the transverse direction, preventing the identification of a fundamental vibration mode. Therefore, in this study, the spectral acceleration calculated at ${T}_{T,min}$, ${T}_{T,max}$, and ${T}_{T,avg}$, are selected as candidate IMs, where ${T}_{T,min}$, ${T}_{T,max}$, and ${T}_{T,avg}$ are the minimum, maximum and average values of the elastic (secant-to-yielding) periods of the subassemblies of the bridges. Finally, three versions of $AvgSa$ are used, calculated within different ranges of periods: (1) $AvgSa({T}_{T,min}-1.5{T}_{T,min})$ ; (2) $AvgSa({T}_{T,min}-2{T}_{T,min})$; (3) $AvgSa({T}_{T,avg}-1.5{T}_{T,avg})$. For the optimal IM analysis in the longitudinal direction, the fundamental period ${T}_{L}$ of the bridge (modelled as a parallel system) is extracted and used to define structure-dependent candidate IMs: 1) the spectral acceleration at ${T}_{L}$, $Sa({T}_{L})$, $AvgSa({T}_{L}-1.5{T}_{L}$) and $AvgSa({T}_{L}-2{T}_{L}$).

The optimal IM analysis is performed for the case-study bridges B1a and B1b. According to previous studies (e.g. Nettis et al. 2021a), the fragility dispersion (Eq. 6) is used to evaluate the efficiency of the candidate IMs. In this case, since a higher fragility dispersion is associated with DS4 with respect to the other considered DSs, ${\beta }_{{DCR}^{DS4}|IM}$ is adopted: the lower ${\beta }_{{DCR}^{DS4}|IM}$, the higher the efficiency of a given candidate IM. It is worth mentioning that the optimal IM analysis is repeated considering other DSs leading to similar results (not presented for brevity). The efficiency is evaluated considering a single bridge model realisation (filled bars in Fig. 4), and the entire bridge model population (empty bars in Fig. 4). In this case, the average of ${\beta }_{{DCR}^{DS4}|IM}$ for 100 bridge model realisations is calculated. The bar charts in Fig. 4 show that, consistently with the results by O’Reilly (2021), structure-independent IM, i.e. PGA and PGV, exhibit a low efficiency. Generally, the investigated structure-dependent IMs offer a satisfying efficiency with a dispersion lower than 0.40. Minor differences are observed for B1a and B1b. In the transverse direction, $AvgSa$ is the most efficient IM provided that the ${T}_{T,min}$ is used as a lower limit of the period range. Additionally, the low discrepancies between $AvgSa({T}_{T,min}-1.5{T}_{T,min}$) and $AvgSa({T}_{T,min}-2{T}_{T,min}$) prove that the upper limit of the period range has a low influence on the efficiency of $AvgSa$. Concerning the seismic response in longitudinal direction, $Sa({T}_{L})$ and $AvgSa({T}_{L}-1.5{T}_{L}$) represent optimal choices for both B1a and B1b, providing a dispersion lower than 0.25. According to these results, in the following sub-sections, $AvgSa({T}_{T,min}-1.5{T}_{T,min}$) and $AvgSa({T}_{L}-1.5{T}_{L}$) are used as IM for the fragility analysis.

Fig. 4

Results of the optimal intensity measure analysis

3.3 Sampling size

The number of bridge model realisations adopted in statistical sampling (subsection 2.1) affects the outputs (i.e. percentiles of fragility, loss ratios and expected annual losses) of the framework. This subsection shows the results of a preliminary analysis aimed at investigating the sampling size, representing a compromise between computational effort and stability (i.e. convergence in results compared to an exact solution). The convergence analysis investigates fragility estimations and is carried out as follows.

The exact solution is represented by a benchmark sampling size of 10,000 bridge model realisations (Silva et al. 2014). First, the population of fragility curves is derived and the vector of IM corresponding to the 50% damage probability for DS4 is extracted. Subsequently, the 50th, 16th and 84th percentiles are calculated (${\alpha }_{DS4}^{50th}$, ${\alpha }_{DS4}^{16th}$, ${\alpha }_{DS4}^{84th}$, respectively) and taken as benchmark solutions. This process is repeated for reduced (tentative) values of sampling size (from 10 to 2500, as shown in the abscissas of Fig. 5). For each reduction, ten sampling repetitions are carried out. The relative errors on ${\alpha }_{DS4}^{50th}$, ${\alpha }_{DS4}^{16th}$, ${\alpha }_{DS4}^{84th}$ with respect to the benchmark values are evaluated for each tentative value of sampling size. The convergence is checked for both B1a and B1b. The errors are shown in Fig. 5. It observed that the use of 100 bridge model realisations limit the discrepancies with respect to the exact solutions under a 10% tolerance. As shown in Fig. 5a, if 50 realisations are generated, the errors rise up to 20%. Conversely, to limit errors under a 5% tolerance, a number of realisations higher than 250 should be adopted.

Fig. 5

Relative errors (tentative sampling size vs. benchmark sampling size) on the 16th, 50th and 84th percentiles of ${\alpha }_{DS4}$

3.4 Comparisons to NLTHA

As mentioned in Sect. 1, the seismic analysis simplifications pay an inevitable loss of accuracy compared to refined NLTHA which is commonly adopted for loss assessment. This sub-section is aimed to identify sources of discrepancies introduced by the simplified analysis strategy (i.e. simply identified as CCSM as follows) compared to NLTHA taken as a benchmark. First, CCSM-vs-NLTHA comparisons concerning fragility estimations are presented. Subsequently, loss results are compared.

Numerical models for both the case-study bridges are generated by using Opensees (McKenna 2011). The piers are modelled through BeamWithHinges elements composed of an internal elastic part and a nonlinear hinge at the base. The hysteretic material is used to model the nonlinear cyclic behaviour of the plastic hinges. The superstructure and the pier caps are modelled through elastic beam elements. TwoNodesLink elements are used to simulate the nonlinear response (Fig. 3) of the bearing devices and the abutment-backfill system. As suggested by Nielson (2005), neoprene bearings are modelled via an elastic-perfectly plastic relationship, while an elastic-perfectly plastic gap element is used for the longitudinal response of the abutment-backfill system. A tangent stiffness proportional damping is defined as suggested by Priestley et al. (2007). Moreover, a 5% Rayleigh damping model is assigned. Further information on the modelling strategy is reported by Nettis et al. (2021b).

3.4.1 Differences in fragility estimations

Probabilistic seismic demand models are first compared for a random bridge model realisation related to each case-study bridge in Fig. 6 and Fig. 7. Figure 6 shows examples of the linear probabilistic seismic demand models in logarithmic scale (only DS2 is chosen, for brevity). Figure 7 illustrates the power-law relationships for all the considered DSs. For the selected bridge model realisation, CCSM and NLTHA lead to similar values of ${\alpha }_{DS1}$ and ${\alpha }_{DS2}$. A slight overestimation of the CCSM with respect to NLTHA is generally observed with reference to ${\alpha }_{DS3}$ and ${\alpha }_{DS4}$ (relative errors lower than 20% are observed). For B1a analysed in the transverse direction, variability on the most critical damage condition is observed, ranging between damage for flexure of one of the piers and slipping of neoprene bearings. For B1b, the most critical component varies between the abutment-backfill system and a pier (damage for flexure) for the longitudinal direction. This observation leads to the consideration that the variability in seismic action may induce different damage types for a given bridge, enhancing the need for multi-component seismic assessment approaches. As a consequence, typological fragility models that neglect bridge-specific components may be inaccurate.

Fig. 6

Probabilistic seismic demand models in logarithmic scale for DS2 related to a single bridge model realisation

Fig. 7

Probabilistic seismic demand models (power-law models) related to random bridge model realisations

Fig. 8

Fragility percentiles calculated via CCSM and NLTHA for (a) B1a-transverse direction; (b) B1a-longitudinal direction; (c) B1b-transverse direction; (d) B1b-longitudinal direction

Fragility estimations are compared in Fig. 8. The 50th percentile of the whole fragility curve population is plotted as a continuous line. Additionally, the variation in fragility estimations associated with the influence of the knowledge-based uncertainty is quantified by the area bounded by the dotted curves corresponding to the 16th and 84th fragility percentiles. Figure 8 further emphasizes how the CCSM overestimations (observed in Fig. 7 for a single realisation) propagate on fragility predictions. For B1a (Fig. 8a, b), the CCSM-vs-NLTHA discrepancies are very reduced for DS1 and DS2 for both transverse and longitudinal directions. The highest relative errors between the two strategies on ${\alpha }_{DS}$ of the 50th fragility percentile (computed as $({\alpha }_{DS}^{CCSM}-{\alpha }_{DS}^{NLTHA})/{\alpha }_{DS}^{NLTHA}$) are equal to − 13.0% and − 16.0% and corresponds to DS4 in transverse and longitudinal direction, respectively. For B1b (Fig. 8c, d), the highest discrepancies are, again, observed for DS4, where the simplified approach leads to relative errors of the ${\alpha }_{DS}$ equal to approximately -10%. As reported for the 50th percentile, a qualitative observation of Fig. 8 leads to notice that the discrepancies on 16th and 84th fragility percentiles given by the influence of knowledge-based uncertainty increase as the nonlinear demand increases for both B1a and B1b. The errors for B1a are higher than B1b. The highest CCSM-vs-NLTHA error is equal to -23.1%, registered for the 16th fragility percentiles at DS4 in the longitudinal direction.

The overestimation of the fragility estimates induced by the CCSM with respect to NLTHA may be determined by several factors. A first source of overestimation may derive from the adopted equivalent viscous damping formulations which, as demonstrated by Nettis et al. (2021a), involve an overestimation of seismic displacement demand with respect to NLTHA. For B1b, the inaccuracies are slightly amplified with respect to bridge B1a since additional equivalent viscous damping formulations are adopted to simulate the nonlinear demand for the neoprene bearings. Equivalent viscous damping formulations for elastic-perfectly plastic kinematic hardening are proven to overestimate NLTHA results by Priestley et al. (2007). Additionally, considering the transverse direction only, the simplified modelling methodology is deemed to predict higher displacement demand on the critical subassembly by neglecting the transfer of seismic forces among the different subassemblies. However, the accuracy of the CCSM with respect to NLTHA is judged to be satisfying considering the reduction in the computational effort involved by the simplified approach. Indeed, the relevant number of required analyses in the presented framework to explicitly simulate the uncertainty for each analysed bridge ($100 \, realisations \, \times \, 100 \, records = 10000 \, analyses$) prevents the extensive use of numerical models tailored for specific bridges within a portfolio, analysed via NLTHA. It is worth mentioning that, as evidenced by Pertuzzelli and lervolino (2021), a systematic overestimation of seismic risk is preferable over underestimations when approximate approaches are adopted. Indeed, once the most critical cases have been identified on the basis of risk-informed prioritisation, further analysis should be carried out to resolve such risk overestimations. To conclude, it is worth reminding that the abovementioned discussion is constrained to some assumptions of the adopted cloud approach (see sub-Sect. 2.5). Additional future analyses should be aimed at assessing the influence of such assumptions while evaluating the CCSM accuracy for of other case-study bridges and the CCSM accuracy if other fragility analysis algorithms are employed.

3.4.2 Differences in loss estimations

The second CCSM-vs-NLTHA comparison discusses the influence of the abovementioned fragility-based discrepancies on seismic losses. Hazard curves related to the city of Cosenza, located in Southern Italy and subjected to high-severity seismic hazard, are computed using the REASSESS platform developed by Chioccarelli et al. (2019), by applying the source model by Meletti et al. (2008). Loss ratio curves for CCSM and NLTHA and hazard curves are compared in Fig. 9.

Fig. 9

Loss ratio fractiles and hazard curves

By observing Eq. (9), it can be assumed that the discrepancies between CCSM and NLTHA on loss ratio curves depend on the accuracy of fragility estimations related to different DSs. In addition, considering the DLRs in Table 1, it can be easily deduced that, for each IM value, errors on fragility for DS3 and DS4 (DLRs equal to 0.25 and 1.00) have a greater influence on discrepancies in loss ratio estimation, rather than DS1 and DS2 (DLRs less than 0.08). For these reasons, since the accuracy on the fragility of the CCSM is high for slight DSs and decreases for more severe DSs, good accuracy is expected in loss predictions conditioned to IM values where the fragility for DS1 and DS2 prevail with respect to DS3 and DS4. Conversely, a loss of accuracy should be registered for IM values associated with relevant damage probability for DS3 and DS4. This is demonstrated by the loss ratio results in Fig. 9b. For example, considering the 50th loss ratio percentile, for B1a analysed in the longitudinal direction (Fig. 9b), a satisfying accuracy of the CCSM with respect to NLTHA for IM values lower than 1.00 g is observed. This is because in this case DS1 and DS2 are reached prematurely with respect to other case studies. Conversely, the errors in loss calculation increase for increasing IM values, where the contribution of the fragility related to DS3 and DS4 raises. An opposite trend is observed for B1a analysed in the transverse direction. Indeed, Fig. 9a shows greater CCSM discrepancies on the 50th loss ratio percentiles for IM values lower than 1.00 g, since the contributions of fragility errors (Fig. 8a) of DS3 and DS4 is relevant.

Expected annual losses in terms of percentage of total replacement cost are computed by integrating the loss ratio curves and the hazard ones. Table 3 illustrates that, for both the case-study bridges, the highest EAL value is related to the response in the longitudinal direction, which is associated with higher IM frequencies of exceedance with respect to the transverse direction.

Table 3 Expected annual loss ratios [% of replacement cost] and associated variation interval involved by knowledge-based uncertainty

Considering Eq. (10), fragility/loss ratios related to low IM values (associated with a significant frequency of exceedance) induce a higher contribution on seismic risk/losses with respect to fragility/loss ratios related to less frequent, but more severe, IM values. Therefore, it can be expected that the more accurate is the CCSM in predicting loss ratios for IM values characterised by the significant frequency of exceedance, the more accurate are CCSM-based EAL estimates. In fact, by considering the 50th EAL percentiles results in Table 3, the minimum CCSM-vs-NLTHA relative error on EAL is equal to -9.1% and is related to B1a analysed in the longitudinal direction where accurate CCSM loss predictions are observed for IM lower than 1.00 g. Conversely, the maximum relative error is related to B1a analysed in the transverse direction. It is equal to -24.5% and is caused by large discrepancies in loss estimates conditioned to IM values lower than 1.00 g.

In conclusion, it can be stated that the accuracy of the proposed simplified risk assessment approach increases in case the slight DSs govern the computation of the expected annual loss. Conversely, its accuracy decreases for cases in which the severe and collapse DSs induce the highest contribution to seismic risk. These considerations should be kept in mind by transport authority operators interested in applying this simplified methodology and considered for future developments of the presented framework.

4 Example of a portfolio application

4.1 Description of the bridges and fragilty analysis

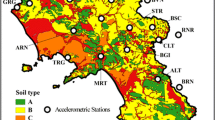
This final section illustrates an application example of the proposed framework for efficient seismic risk assessment. The case-study bridge portfolio includes eight RC girder bridges (presented in Fig. 10) which are part of the Basilicata national road network in Southern Italy. The bridges present a different number of spans, an isostatic structural scheme and single-column piers. Fast onsite surveys aimed to determine geometric and structural characteristics are carried out to accomplish the initial data collection. The B1a bridge analysed in the previous section is included in this portfolio-scale analysis and simply identified as B1. Although a real application would require a bridge-specific characterisation of knowledge-based uncertainties, given the illustrative purpose of this exercise, the same input knowledge-based uncertainties are assigned for all the bridges. These are listed in Table 2 (Sect. 3.1). The girder-pier connection of B2 to B6 is composed of neoprene bearings equipped with shear keys. In these cases, the nonlinear response of shear keys is neglected and, given the low thickness of the girder-shear key gap size, a fixed connection is assumed. The deck-deck and deck-abutment gaps measure 20 to 25 mm for B1 to B7 and 70 mm for B8. Figure 10 includes significant geometric and structural parameters, together with the old Italian design code and the soil classification according to the current Italian code (Ministero delle Infrastrutture e dei Trasporti 2018). A probabilistic seismic hazard analysis is carried out for each of the case-study bridges to retrieve bridge-specific hazard curves considering $AvgSa$ for significant ranges of periods.

Fig. 10

Geometric and structural parameters of the case-study bridges

Preliminary fragility curves for the case-study bridges are calculated and compared with other fragility curves proposed in the literature for similar bridge taxonomies in Fig. 11. Fragility curves representing the most critical response between the two analysis directions are calculated for the case-study bridges (identified as “single” in the figure) and, subsequently, a class fragility curve is computed by averaging the damage probability varying the IM values (identified as “typology” in the figure). Figure 11a shows fragility comparisons with reference to the study by Borzi et al. (2015), proposing a synthetic set of fragility curves derived from 485 RC bridges in Italy, and the study within the SYNER-G project, presenting fragility curves for regular RC bridges with bearing-supported superstructures (Crowley et al. 2011). Figure 11b shows fragility comparisons with respect to the class fragility functions proposed in the INFRANAT project (INFRANAT 2018) related to simply supported-girder RC bridges in Southern Italy having: 1) from two to four spans and multi-column piers (RC-2/4-MC); 2) more than five spans and single-column piers (RC- + 5-SC). Apart from emphasising the differences between the class fragility curves (caused by the taxonomy definition and modelling/analysis approaches), Fig. 11 presents the significant differences observed between bridge-specific fragility curves and typological ones which highlight the inadequacy of typology-based approaches for risk-informed prioritisation.

Fig. 11

Comparisons between fragility curves computed by means of CCSM and literature studies: (a) Borzi et al. (Borzi et al. 2015) and SYNER-G project (Crowley et al. 2011); (b) INFRA-NAT project (INFRANAT 2018)

4.2 Risk-informed prioritisation

In this exercise, the proposed framework aims to reach a satisfying knowledge level of the case-study portfolio to address an appropriate risk-informed retrofit prioritisation scheme. For this purpose, this exercise is developed in two steps. The first step (1) foresees a preliminary calculation of the seismic risk and the corresponding uncertainty considering an initial basic knowledge level. It is aimed to identify bridges which should be subjected to a refined knowledge process for increasing the accuracy of portfolio-scale risk estimations. The second step (2) updates the initial assessment and evaluates the beneficial reduction of uncertainty after reaching a more refined knowledge level for the bridges selected in the previous step (1).

4.2.1 Preliminary risk-informed prioritisation

For step (1), the methodology for seismic loss assessment is applied. The loss ratio (i.e. vulnerability) curves calculated in phase (1) are shown in Fig. 12 by means of grey curves. Figure 12 also includes blue dotted curves representing the hazard curves and the total replacement cost for each bridge computed according to Zanini et al. (2016). The loss ratio curves allow for discussing the vulnerability (and the corresponding uncertainty) of the investigated bridges. Considering the response in the transverse direction, the 50th loss ratio percentiles show that the most “vulnerable” bridges are B1, B2 and B3, reaching a 50% loss ratio for IMs equal to 0.90g, 0.93g and 0.89g, respectively. Similar values of uncertainty can be qualitatively observed for all the investigated bridges, with the exception of B2 and B7 which exhibit a reduced area between the 16th and 84th loss ratio percentiles compared to the other cases. For example, for B6 and B2 respectively, the variability of the 50% loss ratio related to the knowledge-based uncertainty ranges between [-25; + 25]% and [-9; + 14]% with respect to 50th percentile estimates. For the seismic action in the longitudinal direction, the cases B2, B3, B5 and B7 reach a 100% loss ratio for IM values higher than 1.50 g typically associated with an IM frequency of exceedance ${\lambda }_{IM}$ lower than ${10}^{-5}$. In these cases, a negligible vulnerability uncertainty with respect to other cases, such as B1 and B8, is registered. This effect is caused by the low variability in terms of fragility percentiles (not shown for brevity) calculated for DS4 which, according to the adopted DLRs (sub-Sect. 2.4), governs the calculation of loss ratio curves.

Fig. 12

Loss ratio curves and corresponding uncertainty for the case-study bridges

To perform the risk-informed prioritisation considering EAL as a risk metric, the vulnerability information should be convoluted with the hazard and weighted by the total replacement cost associated with each bridge. Figure 13 illustrates the 50th EAL percentile values together with the corresponding error bars reflecting the variation between $EA{L}^{16th}$ and $EA{L}^{84th}$. B1 is associated with a low value of EAL given its low hazard severity with respect to other cases. While the knowledge-based uncertainty is relevant for vulnerability estimations of B1, it results negligible with respect to risk-prioritisation purposes. Considering all the cases, the maximum value of the 50th EAL percentile is equal to 741 € and corresponds to B5 for the seismic response in the longitudinal direction which is associated with a severe hazard intensity. A high value of EAL is, also, registered for B2 (731 and 676 € for longitudinal and transverse directions, respectively) given the corresponding significant replacement cost and hazard level. For B2, significant uncertainty is associated with EAL estimations, ranging from 421 to 1001 €, considering the transverse direction. Conversely, as can be expected by observing the vulnerability estimations (Fig. 12), the knowledge-based uncertainty influence strongly decreases considering the longitudinal direction. Low EAL values and low uncertainty are assigned to B1, B6 and B7 based on the associated loss and hazard levels.

Fig. 13

Expected annual losses for the case-study bridges and RUI values

After step (1), a preliminary risk-informed prioritisation can be accomplished by using $EA{L}^{50th}$. The highest value of $EA{L}^{50th}$ computed considering the two analysis directions for each bridge may be used for this goal.

4.2.2 Updated risk-informed prioritisation

The first risk estimation can be used to select the bridges which should be subjected to a more thorough data collection (phase (2) of this exercise) to further refine the risk-based ranking. Judgemental criteria may be adopted by transport authority analysts depending on their needs and available budgets. In this exercise, a synthetic risk uncertainty index (RUI) is introduced to numerically quantify the influence of knowledge-based uncertainty on the risk prioritisation plan. To compute the RUI the following approach is used. First, the maximum value of $EA{L}^{50th}$ calculated on the entire bridge portfolio is extracted considering the response in both directions and identified as a loss reference value ${EAL}_{ref}$. The RUI for a given bridge is calculated by using Eq. (11) which multiplies the ratios of the amplitude of [$EA{L}^{84th}$- $EA{L}^{16th}$] risk range and of the $EA{L}^{50th}$ to ${EAL}_{ref}$ for a given analysis direction.

$$RUI=\underset{\mathrm{d}=\{\mathrm{transv},\mathrm{ long}\}}{\mathrm{max}}\left[\left(EA{L}_{d}^{16th}-EA{L}_{d}^{84th}\right){\mathrm{EAL}}_{\mathrm{d}}^{50\mathrm{th}}/{{(\mathrm{EAL}}_{\mathrm{ref}})}^{2} \right]$$

(11)

The calculated RUI values are reported in Fig. 13. The higher the RUI is, the greater the uncertainty of the risk estimates for a given bridge compared to the other cases included in the analysed portfolio. Considering the highest RUI values, bridges B2, B4, B5 are selected for further in-depth data collection.

In phase (2) of this exercise, additional knowledge data is assigned to B2, B4, B5 and reported in Table 4. These concerns material design parameters, constructive details and the backfill soil type. The resulting loss ratio curves and $EAL$ are reported in red and superimposed to the results corresponding to the initial knowledge level in Figs. 12 and 13. The recalculated values of $EAL$ show reductions in the risk-based uncertainty for these cases, allowing for a more accurate risk-informed prioritisation. It is evident that the $EA{L}^{50th}$ is increased for B2 reaching 797 € and 783 € for the transverse and longitudinal directions, respectively. B2 should be ranked first considering its high EAL values, followed by B4 and B5. In these latter, the $EA{L}^{50th}$ decreases with respect to the preliminary risk assessment. For example, the re-calculated $EA{L}^{50th}$ value associated with the longitudinal direction, are equal to 622 € and 680 €, respectively.

Table 4 Additional data collected for B2, B4, B5 associated with the refined knowledge level

5 Conclusion

This study presents an efficient framework for bridge-specific risk assessment explicitly accounting for knowledge-based uncertainties. The framework is intended for risk-informed prioritisation of bridge portfolios. It is based on subsequent modules involving the collection of input of knowledge data, the simulation of knowledge-based uncertainties, simplified seismic analysis, and fragility and loss assessment. The efficiency of the approach is fostered by the use of a simplified modelling approach and capacity spectrum-based method to carry out fragility and loss assessment. Relationships relating percentiles of fragility and loss ratios for a given value of seismic intensity measure are computed. These are subsequently used to quantify the expected annual losses which are used as a metric for seismic risk prioritisation. The outputs of the framework applied for a given bridge portfolio can be used to (1) define risk-informed prioritisation plans based on the current knowledge state on the analysed bridges; (2) identify cases in which the risk evaluation is significantly affected by the knowledge-based uncertainty and address accurate surveys and testing to refine the ranking.

The study presents a single case-study application to solve some practical issues in implementing the framework for simply supported girder multi-span RC bridges. The first issue is related to the proposal of optimal intensity measures to be applied within the fragility analysis. This analysis suggests that the geometric average of spectral accelerations calculated within an appropriate period range allows for satisfying efficiency in fragility assessment. This outcome may be used for other studies dealing with fragility analysis of existing simply supported girder bridges. Additionally, a convergence analysis is carried out to prove that an appropriate sampling size from 100 to 250 realisations should ensure robust fragility estimations. Finally, the discrepancies of the simplified modelling and analysis approach are evaluated compared to nonlinear time history analysis. The simplified seismic analysis strategy provides errors lower than 20% in terms of median fragility for the analysed case study. In addition, the accuracy of risk assessment is particularly sensitive to fragility errors for severe damage states, while it increases in case the slight damage states govern the computation of the expected annual loss.

The second case study section presents an example application for the risk-informed prioritisation of bridge portfolios. The methodology is applied for a preliminary risk assessment based on a first knowledge level of eight case-study simply supported girder RC multi-span bridges. The framework allows for the definition of a preliminary risk-based ranking and identification of the cases which should be conveniently subjected to thorough knowledge characterisations.

Further advances in the framework may be focused on proposing practical recommendations for addressing testing and surveys on parameters which are deemed to involve significant uncertainty on risk estimation depending on the investigated bridge typology. In addition, further evaluations on the risk-based inaccuracies involved by the simplified analysis approach are needed, considering the variability of bridge structural characteristics, which can be found in practice, and by relaxing some assumptions of the employed fragility analysis method. Finally, appropriate developments may be aimed at extending the framework to compute indirect losses which may be of strong interest for effective risk-informed prioritisation.

Appendix

In this Appendix, a complete list of the input data (Tables from A1, A2, A3, A4, A5) which should be collected and included in the spreadsheet to run the proposed framework is provided. The knowledge data corresponding to the B1a bridge (Sect. 3) are reported, as an example. Different forms are used to arrange the input data: (A) General; (B) Superstructure; (C) Substructure—Piers; (D) Substructure—Abutments; (E) Materials and reinforcement details. For each substructure component, a data form (labelled as C or D) should be filled in. Each parameter affected by knowledge-based uncertainty can be characterised by appropriate probability distributions defined through the code [P + “Type of distribution” + “distribution parameters (e.g. mean-dispersion)”].

Table A1 List of the general knowledge data (data form A) included in the 1 input spreadsheet

Table A2 List of the input data concerning the superstructure components (data form B)

Table A3 List of the input data concerning the piers and the connection systems (data form C)

Table A4 List of the input data concerning the abutments and the connection systems 7 (data form D)

Table A5 List of the input data concerning the materials and reinforcement details (data form E)