A site amplification model for Switzerland based on site-condition indicators and incorporating local response as measured at seismic stations

Abstract

The spatial estimation of the soil response is one of the key ingredients for the modelling of earthquake risk. We present a ground motion amplification model for Switzerland, developed as part of a national-scale earthquake risk model. The amplification model is based on local estimates of soil response derived for about 240 instrumented sites in Switzerland using regional seismicity data by means of empirical spectral modelling techniques. These local measures are then correlated to continuous layers of topographic and geological soil condition indicators (multi-scale topographic slopes, a lithological classification of the soil, a national geological model of bedrock depth) and finally mapped at the national scale resorting to regression kriging as geostatistical interpolation technique. The obtained model includes amplification maps for PGV (peak ground velocity), PSA (pseudo-spectral acceleration) at periods of 1.0, 0.6 and 0.3 s; the modelled amplification represents the linear soil response, relative to a reference rock profile with V_S30 (time-averaged shear-wave velocity in the uppermost 30 m of soil column) = 1105 m/s. Each of these amplification maps is accompanied by two layers quantifying its site-to-site and single-site, within event variabilities, respectively (epistemic and aleatory uncertainties). The PGV, PSA(1.0 s) and PSA(0.3 s) maps are additionally translated to macroseismic intensity aggravation layers. The national-scale amplification model is validated by comparing it with empirical measurements of soil response at stations not included in the calibration dataset, with existing city-scale amplification models and with macroseismic intensity observations from historical earthquakes. The model is also included in the Swiss ShakeMap workflow.

1 Introduction

Mapping the site response of strong ground motion is one of the key steps for earthquake risk assessment studies, due to the marked spatial variability and wide range of variation of soil amplification factors (Cultrera et al. 2011; Assimaki et al. 2012; Mayoral et al. 2019; Crowley et al. 2021). Local, accurate site amplification models are generally obtained in the framework of microzonation studies (e.g. Lachet et al. 1996; Michel et al. 2017; Panzera et al. 2019; Hailemikael et al. 2020), using different approaches and data (Lacave et al. 1999; Pitilakis 2004; Foti et al. 2019). Many microzonation studies resort to the acquisition and interpretation of ambient vibrations for mapping site response (e.g. Duval et al. 1995; Bard 1999; Salameh et al. 2017; Martorana et al. 2018; Perron et al. 2018; Mase et al. 2021), others to numerical simulations of 1D soil columns (e.g. Field & Jacob 1993; Assimaki et al. 2008; Stewart et al. 2014; Mahajan et al. 2007; Panzera et al. 2010) or of 2D/3D geophysical models (e.g. Fäh and Suhadolc 1994; Lanzo et al 2011; Smerzini et al. 2011; Pitilakis et al. 2011); furthermore, direct measures of earthquake local response may also be used (e.g. Lermo and Chavez-Garcia 1993; Lachet et al. 1996; Laurenzano et al. 2017). On the other hand, for larger-scale (e.g. national scale) site response layers, the approach is generally more approximate, and can consist in mapping proxies for site amplification (e.g. V_S30 or ground types), using topographical and/or geological indicators (e.g., Allen and Wald 2007; Yong et al. 2012; Vilanova et al. 2018; Karimzadeh et al. 2019; Mori et al. 2020; Li et al. 2022; Crespo et al. 2022; Weatherill et al. 2022). More recently, a number of studies have sought to directly map the ground-motion amplification at large scales, resorting to approaches drawn from microzonation studies (e.g. numerical simulations of 1D soil columns, Falcone et al. 2021, or combined microtremor and ground-motion data, e.g. van Ginkel et al. 2022); besides, Crowley et al. (2019) and Weatherill et al. (2020a) illustrated the possibility of inferring the soil response at a regional scale using indirect site condition parameters. Pursuing this line of research (i.e. direct mapping of soil amplification over wide spatial extents), in this study we derive a national soil response model for Switzerland, integrated as one of its key elements in the Earthquake Risk Model Switzerland, the first publicly accessible seismic risk model for the country (Roth et al. 2018; Papadopoulos et al. 2023; Dallo et al. 2024); our soil amplification model is also embedded in the latest implementation of the Swiss ShakeMap (Cauzzi et al. 2022). The amplification model is based on a joint dataset of site amplification factors measured at Swiss seismic stations from regional seismicity and of continuous layers of soil condition proxies (topographic and geological information), which have proven to display a robust correlation with local amplification (Bergamo et al. 2019, 2021a; Sect. 2). The empirical amplification factors at instrumented sites are then mapped over the whole Switzerland using a geostatistical interpolation technique (regression kriging, Hengl et al. 2007), which allows to consistently combine regressions between target (soil amplification) and predictor variables (site proxies) with local samplings of measured soil response at instrumented sites (Sect. 3). The obtained model (illustrated in Sect. 4) consists in four maps representing the local ground-motion amplification for each of the following intensity measures: PGV, PSA(1.0 s), PSA(0.6 s) and PSA(0.3 s). These parameters were chosen considering the typical resonance periods of the Swiss building stock (Lestuzzi et al. 2016; Khodaverdian and Lestuzzi 2022); also, Panzera et al. (2016, 2021a) showed that PGV and spectral acceleration at 0.3 s are instrumental quantities that well correlate with macroseismic intensity and hence, by extension, with possible damage. The four amplification maps are accompanied by layers mapping their associated epistemic (site-to-site variability) and aleatory uncertainties (single-site, within event variability; Sect. 5). It should be noted that the implemented interpolation method (regression kriging) allows to locally modulate the epistemic uncertainty consistently with the availability of points of measured amplification in the area. The PGV, PSA(1.0 s) and PSA(0.3 s) soil response layers are additionally translated to macroseismic intensity aggravation maps thanks to established conversion relationships (Faenza and Michelini 2010, 2011; Sect. 6). The presented amplification model is validated through the comparison with empirical measurements of soil response at stations not included in the calibration dataset, with existing city-scale amplification models and with macroseismic intensity observations from historical earthquakes (Sect. 7). We finally present the use of the produced soil-response model in the Swiss ShakeMap application (Cauzzi et al. 2022; Sect. 8).

2 Compiled datasets

Our amplification model is based on a joint dataset of ground-motion amplification factors measured at seismic stations and layers of site condition information.

2.1 Amplification response at seismic stations

The local earthquake response was estimated at Swiss instrumented sites by means of the empirical spectral modelling technique (ESM, Edwards et al. 2013). ESM combines physical modelling and statistical approach for the interpretation of the acceleration spectra recorded by seismic stations after each event; the interpretation is based on the separation of source, path and site terms, modelled according to Edwards and Fäh (2013). The method is routinely applied at the Swiss Seismological Service since more than a decade for the determination of the events’ spectral moment magnitude as well as for the reconstruction of local effects at instrumented sites. The Fourier spectra of earthquake recordings by Swiss stations are fitted with those expected from a Brune (1970, 1971) ω² source model, accounting for geometrical decay and path attenuation. The spectral matching allows the determination of magnitude and stress drop (Edwards et al. 2010), and the fitting residuals at each station are then interpreted as the local Fourier amplification function, relative to the Swiss standard rock model (having V_S30 = 1105 m/s; Poggi et al. 2011). This model is a standard velocity profile of outcropping rock, used as national reference soil condition for the ground motion model of Edwards and Fäh (2013) and Cauzzi et al. (2015) as well as for the Swiss seismic hazard (Wiemer et al. 2016). Its adoption in the ESM allows to consistently define local amplification as relative to that produced by the reference rock profile. In the ESM approach, the local inelastic site response at station j (relative to the Swiss standard rock model) is modelled as ${A}_{j}{a}_{j}\left(f\right){e}^{-\pi f({\kappa }_{0,j}-{\kappa }_{0,ref})}$, where A_j (average amplification over all frequencies) and a_j(f) (frequency-dependent site amplification functions) are retrieved by inverting the residuals of the modelled versus empirical Fourier spectra; the site attenuation κ_0,j is obtained regressing the measured high-frequency decays κ_r against the respective epicentral distances (Ktenidou et al. 2015) and κ_0,ref is the local attenuation of the reference site (= 0.016 s according to Poggi et al. 2011). The amplification function representative of a specific instrumented site is therefore obtained averaging its site-term estimates from several events. Specific quality control criteria are implemented, requiring the signal-to-noise ratio to be > 3 over a frequency band at least one log₁₀ unit wide in each employed record; these conditions must be verified at ≥ 3 stations (on both horizontal components) for an event to be considered for processing (Edwards et al. 2013; Bergamo et al. 2020). The reliability of ESM-derived local response functions has been assessed by means of comparison with site-to-reference spectral ratios (Edwards et al. 2013), with SH-transfer functions from measured V_S profiles (Michel et al. 2014; Hobiger et al. 2021; Bergamo et al. 2022a), with empirical amplification functions estimated with alternative approaches (Bindi et al. 2022), as well as by collating them with measured site-condition parameters (Bergamo et al. 2020). For further details about the ESM technique and its implementation, the reader is referred to Edwards et al. (2013).

We processed with ESM all recorded local and regional earthquakes from the period 2001–2021 with local magnitude ≥ 2.0 (~ 2000 events with max. local magnitude = 5.0 and epicentral distance between 5 and 250 km, producing ~ 60,000 records). We focused on free-field and urban free-field installations, which total to 387 available stations belonging to either permanent (SED 1983; Cauzzi and Clinton 2013; Diehl et al. 2014; Michel et al. 2014; Hobiger et al. 2021) or temporary Swiss networks (see https://networks.seismo.ethz.ch/en/networks/ch/). We then retained only the stations whose inelastic Fourier amplification function is constrained by at least 5 events in the band 0.5–10 Hz (243 instrumented sites, Fig. 1a–d), Given the magnitude range of the processed events, the obtained amplification functions are to be considered as representative of the local soil response in its linear domain. Finally, for consistency with the common approach of earthquake engineering to use response spectra to define the seismic demand, the Fourier amplification functions were translated to 5% damped pseudo-spectral acceleration (PSA) and peak ground velocity (PGV) amplifications, resorting to random vibration theory (RVT, Boore 2003; Poggi and Fäh, 2015; Weatherill et al. 2020b; see Fig. 2a, b). For the selection of the earthquake scenario for the RVT conversion, we relied on the results of the disaggregation (Bergamo et al. 2022b) of the hazard model for Switzerland with return period 475 years (Wiemer et al. 2016). At intermediate periods (disaggregation available for SA(1.0 s)), the most common dominant scenario to exceedance is magnitude (M_W) = 5.8 and Joyner-Boore distance (R_JB) = 15 km. This combination has the highest contribution to a SA(1.0 s) exceedance in 55% of the Swiss territory (Bergamo et al. 2022b). Sensitivity analyses carried out varying magnitude and distance show a small dependence of the obtained PGV, PSA amplification on the selected scenario, largely comprised within the within-event variability of local response observed at the stations (in agreement with the findings of Poggi and Fäh, 2015 and Michel et al. 2017). Finally, consistently with the choice of the ground motion intensity measures to be mapped (see Introduction), the PGV, PSA(0.3 s), PSA(0.6 s) and PSA(1.0 s) amplification factors and their standard deviations were extracted at all considered stations and stored in a spatially-referenced dataset. It is worth mentioning that such amplification factors span a wide range, from less than 0.5 to more than 8 (Fig. 2b), highlighting the marked variability of soil response and hence its relevance for an overall risk estimation.

Fig. 1

a Map of Switzerland displaying the location of the stations selected for this study. b Example of Fourier amplification function retrieved by means of empirical spectral modelling for a sample station (SHER, Hérémence, SW Switzerland). c Dataset of average empirical amplification functions retrieved for all the stations in a; in d we display the corresponding number of events contributing at each station to the mean amplification curve. In c and d the colour assigned to each amplification function refers to the lithogroup where the corresponding station is installed (see Table 1 and Sect. 2.2)

Table 1 List of lithological groups defined for this study and number of hosted seismic stations from the calibration dataset

Fig. 2.

a Conversion of the Fourier amplification function of station SHER (Fig. 1b) to PSA and PGV amplification by means of random vibration theory (RVT). b Fourier amplification functions of Fig. 1c translated to PSA and PGV amplification; the colour legend is the same of Fig. 1c.

2.2 Layers of site-condition indicators

For the extrapolation of the high-quality (but local) information provided by the empirical amplification functions from instrumented sites, we resorted to site condition proxies (SCPs) as predictor variables. In fact, several studies have evidenced the correlation between topographical or geological indicators and geophysical parameters related to site response (e.g. V_S30, see for instance Wald and Allen 2007; Ahdi et al. 2017) as well as site amplification itself (Crowley et al. 2019). Based on existing literature and our own studies dedicated to Switzerland (Bergamo et al. 2019, 2021a), we selected the following SCPs, which are described below: lithological classification of soil, topographic slope and estimated depth-to-bedrock.

• Lithological classification of Switzerland, based on the 1:500,000 Geological Map of Switzerland (Swisstopo 2005, see Data Availability). We defined 9 lithogroups (5 dedicated to unconsolidated sediments, 4 to consolidated rocks), identified following the lithological and rock genesis information of the Geological Map of Switzerland (Fig. 3a, Table 1). For the classification we relied on expert judgement as well as on previous works grouping the numerous geological units into wider categories (e.g. Zappone and Kissling 2021); at the same time, we ensured that each lithogroup is represented by a sufficient number of seismic stations (all lithogroups host at least 11 instrumented sites, see Table 1). The significance of the adopted lithological classification in terms of site response was assessed by (1) collating the distribution of measured site condition parameters (e.g. V_S30) among the various lithotypes (see Fig. 3 in Panzera et al. 2021b) and (2) observing the resulting classification of empirical amplification functions estimated at seismic stations; for example, in Figs. 1c, 2b the amplification functions from stations installed on unconsolidated sediments (colors from pink to dark brown) generally display higher amplification factors when compared to instruments located on consolidated rocks (colors from yellow to blue). Besides this categorization developed from the Geological Map of Switzerland (Swisstopo 2005), we explored the possibility of preparing a lithological classification with finer spatial resolution based on the 1:25,000 Geological Atlas (Swisstopo 2017), covering Switzerland with 222 different sheets. However, this option had to be dropped due to inconsistencies between neighbouring sheets.

• Multi-scale maps of topographic slope (θ). Several studies (Burjánek et al. 2014a; Maufroy et al. 2015; Bergamo et al. 2021a) have highlighted that the correspondence between local response and topographic parameters is scale-dependent. Topographic parameters representative for a wider spatial extent correlate more robustly with lower-frequency site response, which involve longer wavelengths; vice versa, higher-resolution topographic parameters display a better correspondence with site effects at higher frequencies, which involve shorter wavelengths. Consistently with these studies, we computed a set of maps of topographic slope evaluated at seven spatial extents from 75 to 3600 m (e.g. Fig. 3b). For the computation of θ we employed the digital height model DHM25 (Swisstopo 2004, covering Switzerland with a regular grid of 25 × 25 m cells; see Data Availability), integrated with the bathymetries available for the main Swiss lakes (Swisstopo 2021; see Data Availability). A subsequent sensitivity analysis correlating the local amplification factors at seismic stations with their topographical slopes identified θ at 275 m scale as the one achieving the highest correspondence with PGV and PSA(0.3 s) amplification (r² = 0.47 and 0.38), and θ at 600 m scale as the one best correlating with PSA(1.0 s) and PSA(0.6 s) amplification (r² = 0.44 and 0.43, respectively).

• Estimated depth-to-bedrock, as derived from the bedrock elevation model by Swisstopo (2019, see Data Availability), which covers most of Switzerland (Fig. 3c) with a spatial resolution of 25 m. The significance of this dataset in terms of correspondence with site condition parameters was assessed by comparing it with 140 V_S profiles from site characterization surveys performed across its extent (source: Site Characterization Database for Seismic Stations in Switzerland, SED 2015, see Data Availability). Figure 3d displays the collation between the depth to engineering bedrock (H800, depth to the shallowest layer with V_S ≥ 800 m/s, Derras et al. 2017), computed from each of the measured velocity profiles, and the estimated depth-to-bedrock extracted from the geological model at the same locations. We observe a reasonable correspondence for predicted bedrock-depth values larger than few meters; however, at small values of estimated depth-to-bedrock (< 3 m) the measured H800 is—in the majority of cases—significantly deeper. We therefore consider the areas where the estimated bedrock depth is ≥ 3 m as reliable and consequently useful for our study; the portions with a predicted depth-to-bedrock < 3 m (~ 60% of the area covered by the bedrock-depth model) were not taken into consideration (see Fig. 3c).

Fig. 3

a Lithological classification of Switzerland used in this study (see Table 1 for the description of the various lithogroups. b Multi-scale topographic slope: examples at scales of 75 (left) and 600 m (right); note the smoother distribution of slope angle in the latter when compared to the former. c Geological model of the depth to bedrock (Swisstopo 2019). d Comparison between the depths to engineering bedrock (H800) derived from 140 measured V_S profiles and the bedrock depth estimated by the geological model in c at the same locations

3 Mapping of soil amplification

The joint datasets of measured soil amplification factors and layers of local condition parameters (Sect. 2) were combined for the mapping of PGV, PSA(1.0 s), PSA(0.6 s) and PSA(0.3 s) amplification across all Switzerland. As anticipated in the Introduction, the method we employed for the areal prediction of soil response is the regression kriging algorithm (RK, Hengl et al. 2007; Ge et al. 2011). RK is a geostatistical interpolation technique combining a regression analysis of the target variable versus mapped predictors with simple kriging of the regression residuals. RK was selected as it allows to consistently integrate local measures of soil amplification in a mapping scheme based on empirical relationships between soil response and layers of SCPs; indeed, after analysing the spatial autocorrelation of the residuals of such regressions, it is possible to locally constrain the prediction to observed values in its neighbourhood and to modulate accordingly the prediction uncertainty. For details about the RK algorithm and its implementation in our study, we refer the reader to the “Appendix”. In brief, for each ground motion parameter, the mapping workflow involves the following four steps, which are also schematized in the flowchart of Fig. 4:

• First, amplification-vs-slope and amplification-vs-bedrock depth relationships are estimated for each lithogroup (see Fig. 5a, b as example for LG3); in these correlations, both dependent and independent variables are represented in logarithmic scale, following—among others—Perron et al. (2022a, amplification), Wald and Allen (2007, slope) and Zhu et al. (2020, depth to bedrock). As the bedrock-depth geological model does not span the entire Switzerland and we exclude its areas with predicted depth < 3 m (Fig. 3c), some lithogroups are not “covered” by the minimum number of stations (10) we require to define the regression, hence for these classes only the amplification-vs-slope correlation is available. Only for lithogroup LG2, hosting the highest number of stations (58), a multivariate correlation between amplification and both slope and bedrock depth could be reliably constrained (e.g. Fig. 5c).

• Secondly, the spatial autocorrelation of the residuals of the amplification-vs-proxy relationships is assessed, by means of semivariograms. These display a decrease of the semi-variance γ with decreasing separation distance h, after the onset of the decrement at a range R of few kilometres (e.g. Fig. 5d, e). After testing various models (Gaussian, spherical), the experimental semivariograms were finally fitted with an exponential model with null nugget (i.e. γ = 0 for h = 0, see Sect. 5 and “Appendix”; Chilès and Delphiner 2012). The plateau of the fitted semivariogram for separation distances h > R, termed sill (S), corresponds to the variance of residuals of uncorrelated stations. It is worth noticing that the semivariogram range generally decreases with decreasing period, in agreement with the scaling of the corresponding wavelengths (see Figs. 5d, e, 14b in the “Appendix”).

• Consistently with the spatial resolution of the raster predictor layers (digital elevation model and bedrock-depth model, that is 25 m), the Swiss territory is mapped as a grid of 25 × 25 m cells. At each cell, the local values of proxies (topographic slope and bedrock depth) are retrieved and used to enter the amplification-vs-proxy regressions for the relevant lithogroup, thus yielding an estimate for local amplification as well as the variance of uncorrelated residuals of the corresponding regression (assumed as RK prediction uncertainty, σ_RK² = S, see “Appendix”). If two concurring amplification estimates are available (from the amplification-vs-slope and -vs-bedrock depth relationships) the one issued by the regression with higher r² is preferred.

• If the considered cell is < R far from the nearest seismic station(s) on the same lithogroup, a local correction based on the linear combination of the regression residuals is computed and added to the amplification prediction from the previous step. Simultaneously, the RK prediction uncertainty (σ_RK²) is corrected by subtracting a linear combination of the covariances of residuals at the target cell (see “Appendix”).

Fig. 4

Workflow of the methodology implemented for the mapping of ground motion amplification and its prediction uncertainty

Fig. 5

a, b PSA(1.0 s) amplification-vs-topographic slope (a) and vs-bedrock depth (b) relationships for lithogroup LG3. c PSA(1.0 s) amplification vs slope and bedrock depth relationship for lithogroup LG2. All the amplification-vs-proxy relations are displayed in the Online Resources 1, Figs. OR1.1–OR1.8. d, e Semivariograms of the residuals of the PSA amplification-vs-slope relationships, for T = 1.0 s (d) and T = 0.3 s (e). The experimental semivariograms (one for each lithogroup) display the distance-dependent semi-variance normalized by the overall variance of the residuals for the corresponding lithotype (square of σ in a, b). The exponential model is fitted on the whole set of normalized semivariograms for all lithotypes (see “Appendix”). All the semivariograms (for all ground motion measure types and amplification-vs-proxy relations) are displayed in the Online Resource 1, Figs. OR1.9–OR 1.12)

4 Obtained ground motion amplification model

Following the algorithm presented in Sect. 3, for each of the considered ground motion parameters a joint map of the predicted soil amplification (Fig. 6) and of the associated prediction uncertainty (examples in Fig. 7a, b) is obtained. The predicted local response is to be intended as relative to the Swiss reference rock condition (Vs₃₀ = 1105 m/s, Poggi et al. 2011), consistently with the input measured amplification data (see paragraph 2.1); this condition makes it readily compatible with the national hazard model of Wiemer et al. (2016) and with the Swiss ground motion model of Cauzzi et al. (2015). The maps intend to primarily capture the stratigraphic amplification; topographic effects (e.g. Massa et al. 2014) are not explicitly modelled, although they are inevitably embedded in part of the measured amplification functions used in input (Burjánek et al. 2014b). Furthermore, given the data and procedure used to estimate such local response factors (paragraph 2.1), the mapped amplification corresponds to the soil response in the linear domain, i.e. the progressive increase of damping ratio and concurrent decrease of shear modulus in the near-surface at high levels of strain (Darendeli 2001), is not accounted for. This approximation (modelling of linear soil amplification only) has been considered acceptable given the applications for which the soil response maps were developed (assessment of seismic risk and mapping of ground shaking at the Swiss national scale, Cauzzi et al. 2022; Papadopoulos et al. 2023) and considering the level of seismic hazard estimated for Switzerland for a return period of 475 years (Wiemer et al. 2016; Bergamo et al. 2022b).

Fig. 6

Obtained soil amplification maps for PGV (a), PSA(1.0 s) (b), PSA(0.6 s) (c) and PSA(0.3 s) (d)

Fig. 7

a, b Maps of RK prediction uncertainty (σ_RK) for PSA(1.0 s) (a) and PSA(0.3 s) amplification (b). The color scale is the same as in d. The σ_RK maps corresponding to PGV and PSA(0.6 s) are displayed in Online Resource 2, Fig. OR2.1. c Close-up of the PSA(1.0 s) amplification map for the area of Basel, with the position of the seismic stations (circles) and their measured local amplifications (inner colour of circles). d Close-up of the PSA(1.0 s) amplification prediction uncertainty (σ_RK) map for the area of Basel, with the position of the seismic stations (circles)

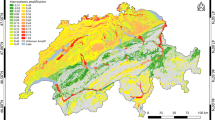
Overall, the maps predict in general a soil amplification < 1 (i.e. lower than the one expected for the Swiss standard rock profile) for the mountainous areas of the Alps (mostly covered by lithogroup LG9, Fig. 3a). The expected local response is slightly higher (around 1) for the Jura massif and the Swiss Prealps (LG7, LG8) and little above 1 (1–1.5) for the Molasse of the Swiss Plateau (lithogroup LG6). Relatively stiff unconsolidated sediments like moraines and gravel terraces (LG3 and LG4, mainly present across the Swiss Plateau and at its northern border) display amplifications mostly between 1.2 and 2.4. The valley beds of the alpine valleys and the alluvial areas north of the Alps (LG2) generally bear amplification factors of 1.4–3.5, however, not rarely reaching also 6–7; for even finer and softer sediments (LG1), the amplification is in the range 1.7–6, but at times up to 10.

In terms of variation across the various ground motion parameters, consolidated-rock lithogroups (LG6–LG9) show little variability. As for unconsolidated sediments, it is worth noting that LG1 and LG2 generally display higher PSA amplification at T = 0.6 s, possibly because these soft formations usually have fundamental periods of resonance (T₀) between 0.5 and 1 s; in fact, by cross-referencing the dataset of fundamental periods from microtremor horizontal-to-vertical spectral ratios (source: Site Characterization Database for Seismic Stations in Switzerland, see Data Availability) with the lithological classification map (Fig. 3a), the average T₀ from measurements performed on LG1 and LG2 is 0.68 s. Vice versa, the coarser sediments of LG5 show an increase of amplification with decreasing period, as it is likely that the resonance period is in this case generally closer to 0.3 s (average T₀ from microtremor horizontal-to-vertical spectral ratio measurements on LG5 is 0.41 s).

To illustrate the local constraining of predicted amplification to nearby measures at seismic stations, we display in Fig. 7c, d a close-up of the PSA(1.0 s) amplification and prediction uncertainty maps for the city of Basel (Northern Switzerland), where several permanent and temporary seismic stations have been deployed (Michel et al. 2017; Imtiaz et al. 2022). Thanks to the RK method, in the neighbourhood of seismic stations the prediction is conditioned by the measured amplification at the instrumented sites, converging towards the observed value at the station location (Fig. 7c); simultaneously, the prediction error decreases nearby the stations tending to 0 at the installation site (Fig. 7d). Indeed, the RK prediction constraint affects only a small portion of the Swiss territory; however, the advantage (in terms of more accurate amplification estimate and lower uncertainty) is quite relevant, as many of the stations employed in this study have been installed in urban areas (Diehl et al. 2014; Michel et al. 2014; Hobiger et al. 2021), thus covering zones which are significant from the risk point of view, and the range R of spatial correlation is of the order of few kilometres (between 1.3 and 9.8 km).

5 Treatment of uncertainties

The uncertainties related to the predicted soil amplification layers were comprehensively assessed and mapped in the spatial domain. We adopted the common partition, in ground motion modelling, of the variability related to soil response into site-to-site variability (φ_S2S, accounting for epistemic uncertainty) and single-site, within event variability (φ_SS, accounting for aleatory uncertainty; see e.g. Atkinson 2006; Atik et al. 2010; Edwards and Fäh, 2013; Cauzzi and Faccioli 2018; Kotha et al. 2020).

As far as the site-to-site variability φ_S2S is concerned, this was equated with the RK prediction uncertainty σ_RK (Sects. 3, 4). In fact, at locations with distance > R (range of the spatial correlation of residuals) from the closest observation, σ_RK coincides with the standard deviation of the amplification residuals—with respect to the relevant amplification-vs-proxy relationship—of spatially uncorrelated sites belonging to the corresponding lithogroup. σ_RK is therefore the overall site-to-site variability of local response within the corresponding lithogroup. Furthermore, consistently with the equation φ_S2S = σ_RK, in the neighbourhood of a measured local amplification (distance < R), σ_RK decrements with decreasing distance from the sampled location, tending to 0 at the instrumented site (in other words, understandably, the site-to-site variability is null at a sampled location; note that the variogram model we suitably selected is an exponential one with null nugget, i.e. the semivariance γ(h) tends to 0 as the distance h tends to 0, Fig. 5d, e). Since σ_RK is mapped jointly with the predicted amplification (Sect. 3), a spatial representation of φ_S2S is obtained for each treated ground motion parameter (e.g. Fig. 7a, b). The site-to-site variability beyond the range of spatial correlation varies significantly among lithogroups (between 0.05 and 0.3 log₁₀ units) and, on average, it slightly increases with decreasing period (Fig. 8a). It should be noted that the site-condition proxies we use (Sect. 2.2) overall display—at least at the considered periods—an explanatory “power” (expressed by the level of φ_S2S) that is comparable with or slightly better than that of a more direct indicator such as V_S30, as per the study of Kotha et al. (2020; Fig. 8a). The reason could be twofold: (1) the higher homogeneity of the ground motion data we used (only Swiss stations versus the European database of Kotha et al. 2020); (2) V_S30 actually displays its highest level of correlation with site response at shorter periods (Bergamo et al. 2020).

Fig. 8

a Site-to-site variabilities (φ_S2S) for the various lithogroups, at distance h > R (range of spatial correlation of regression residuals) from the nearest station; these are compared with the φ_S2S from Kotha et al. (2020), adopting different proxies as site condition indicators. b Single-site, within-event variability (φ_SS) for PGV amplification at the stations considered in this study, classified by lithogroup. Lithogroups are sorted from the softest to the stiffest, following an increasing average value of V_S30 (V_S30 data from the Site Characterization Database for Seismic Stations in Switzerland SED, 2015; see Data Availability). c Average φ_SS for the various lithogroups from this study and φ_SS from the ground motion models of Edwards and Fäh (2013) and Rodriguez-Marek et al. (2011). d, e Maps of φ_SS for PSA(1.0 s) (d) and PSA(0.3 s) (e) amplification. The φ_SS maps corresponding to PGV and PSA(0.6 s) are displayed in Online Resource 2, Fig. OR2.2.

As for the single-site, within-event variability (φ_SS), similarly to Zhu et al. (2022) we associated it with the variability observed within the population of single-event response functions measured at the same seismic station, quantified by their period-dependent standard deviation (Fig. 2a). For the interpolation of the observed φ_SS at instrumented sites in a map format, we considered only the single-site, within-event variabilities from stations covered by at least 10 events in the band 0.5–3.33 Hz (198 out of 243 sites), so to ensure a reasonably robust estimate of such variability term. We did not recognize any significant correlation between φ_SS and the continuous-variable proxies employed in this study (topographic slope and inferred bedrock depth); however, we observed a mild correspondence with the lithological classification, with sites on softer lithogroups generally displaying higher φ_SS than stations on stiffer classes (e.g. Fig. 8b). A possible explanation is that softer lithogroups, in Switzerland, often cover elongated valley beds or sedimentary basins (Fig. 3a), where directionality effects are likely to occur, thus determining a higher variability of ground motion response (Matsushima et al. 2017; Wirth et al. 2019). Furthermore, softer soils may display some level of temporal variability of geophysical properties (Bergamo et al. 2016; Miao et al. 2018; Roumelioti et al. 2020). In comparison to φ_S2S, the values of φ_SS determined for the various lithological units show a narrower variability (overall, the mean values by lithogroup lie in the range 0.1–0.2 log₁₀ units, see Fig. 8c); φ_SS distinctly increments as period decreases. The obtained φ_SS values are similar to those produced by other studies (e.g. Rodriguez-Marek et al. 2011; Edwards and Fäh, 2013); in the comparison with the latter work, dedicated to Switzerland as well, our slightly lower φ_SS might be determined by the higher number-of-events threshold (10 instead of 5) we set for the evaluation of the single-site, within-event variability at each station. To spatially map φ_SS we attributed to each lithogroup the average standard deviation of the empirical amplification functions of the stations falling on that lithogroup (e.g. Fig. 8b); this average value is then corrected locally with ordinary kriging (Webster and Oliver 2007) so that in the neighbourhood of seismic stations φ_SS gradually converges to the standard deviation observed at that instrumented site. Thus, a national map of φ_SS was obtained for each ground motion measure (e.g. Fig. 8d, e).

6 Conversion to macroseismic intensity aggravation

The soil response maps for PGV, PSA(0.3 s) and PSA(1.0 s) (Fig. 6) were additionally translated to macroseismic intensity aggravation (∆I) layers. The rationale is twofold: (1) enabling the use of the produced amplification model in intensity-based applications (in the macroseismic intensity-based branch of the Earthquake Risk Model Switzerland, Papadopoulos et al. 2023, and in the Swiss ShakeMaps, Cauzzi et al. 2022, see Sect. 8); (2) allowing the comparison between the amplification model and a database of macroseismic intensity observations from historical earthquakes (Fäh et al. 2011; see Sect. 7). The conversion is based on the relations between macroseismic intensity and ground motion measures of Faenza and Michelini (2010, 2011; these authors do not provide a relation for T = 0.6 s). The amplification in macroseismic intensity units ∆I (i.e. aggravation at the target site with respect to a reference I_ref) was obtained following Michel et al. (2017) and Panzera et al. (2021a):

$$\Delta I=I-{I}_{ref}=[a+b{\mathrm{log}}_{10}(PSA\left(T\right))]-[a+b{\mathrm{log}}_{10}({PSA}_{ref}\left(T\right))]=b{\mathrm{log}}_{10}(A\left(T\right))$$

(1)

where a,b are the coefficients of the relations by Faenza and Michelini (2010, 2011), and A(T) is the PSA amplification at period T or the PGV amplification. Using Eq. 1, the maps of PGV, PSA(1.0 s) and PSA(0.3 s) amplification were translated to ∆I layers. Eventually, these were brought from the reference rock condition of ground motion amplification (V_S30 = 1105 m/s; Poggi et al. 2011) to that of the intensity prediction equation (IPE) developed for Switzerland by Fäh et al. (2011), identified by Panzera et al. (2021a) as a softer soil reference (V_S30 ≈ 600 m/s). Panzera et al. (2021a) also provide the range of the correction to be applied to the ∆I maps to shift their reference soil condition from V_S30 = 1105 m/s to the reference of the IPE of Fäh et al. (2011); the correction values were determined from the comparison between empirical ground motion amplification measured at seismic stations and converted to amplification in intensity with the values of the macroseismic amplification map of Fäh et al. (2011) at the same instrumented sites. According to Panzera et al. (2021a), for ∆I = f(PGV ampl.) the correction factor lies between −0.42 and −0.37 macroseismic intensity units; for ∆I = f(PSA(1.0 s) ampl.) between −0.27 and −0.17; for ∆I = f(PSA(0.3 s) ampl.) between −0.32 and −0.31; we used the central values from these intervals. The obtained macroseismic intensity amplification maps, referred to the soil condition of V_S30 ≈ 600 m/s, are represented in Fig. 9a–c.

Fig. 9

a–c Macroseismic intensity aggravation (∆I) maps derived—by means of Eq. 1—from PGV amplification (a), PSA(1.0 s) amplification (b) and PSA(0.3 s) amplification (c). The maps are here referred to the reference soil condition of Fäh et al. (2011; V_S30 ≈ 600 m/s). d Comparison between the distributions of the absolute coefficient of variations (CV) evaluated, cell-by-cell, across the three ∆I maps of a–c and the three corresponding ground motion (GM) amplification maps (Fig. 6a, b, d). CV is computed at every raster cell as the ratio between the sample standard deviation and mean of the amplification values of the three overlapped maps

In each ∆I map, the variation of amplification across the various lithogroups and geographical areas obviously follows the same pattern observed for the ground motion amplification layers (see Sect. 4 and Fig. 6). Furthermore, among the three ∆I maps we observe a slightly higher degree of reciprocal consistency, when compared to the corresponding ground motion amplification layers. This is shown by the distribution of the coefficient of variations (CV, ratio between standard deviation and mean of the amplification predictions at the same cell) computed cell-by-cell across the two sets of layers (Fig. 9d). The distribution of the absolute CVs from the ∆I layers appears more skewed towards lower values. In fact, the overall difference between the cumulative distributions of the absolute CVs from the ∆I layers and from the ground motion amplification maps is positive (+ 74%). A higher similarity among the macroseismic amplification maps is obviously desirable as they all portray the same ∆I factor, while each of the ground motion amplification layers refers to a different parameter (local soil response for PGV and PSA at various periods).

As far as the ∆I uncertainty is concerned, following Eq. 1 the variability terms φ_SS and φ_S2S, quantified for the ground motion soil amplification (Sect. 5), would indeed propagate into ∆I. However, it should be considered that the intensity prediction equation yielding I_ref in Eq. 1 (Fäh et al. 2011) does carry its own uncertainty term, which comprises epistemic and aleatory variabilities, including the uncertainties related to site response (see also Bindi et al. 2011; Baumont et al. 2018). It is not straightforward to disentangle such uncertainties from other sources of variability (path- and source-related); indeed, most IPEs currently available in the literature do not explicitly model local site amplification (e.g. Teng et al. 2021). Consequently, to avoid a double-counting of uncertainties, no uncertainty layer was associated to the ∆I maps of Fig. 9a–c.

7 Validation of the amplification model

The produced amplification model was validated by collating it with three comparison datasets: (1) site amplifications measured at a validation ensemble of stations, (2) soil response as predicted by several local models at city scale, and (3) a dataset of macroseismic intensity observations from historical earthquakes.

The first benchmark is represented by the soil amplification empirically measured at a set of seismic stations not included in the calibration ensemble (paragraph 2.1). This validation dataset consists of 50 sites whose measured amplification functions did not meet the criterion of the minimum number of event of coverage (Sect. 2.1) at the time of selection of calibration stations (December 2021); the minimum number of contributing earthquakes (5) was successively reached thanks to newly recorded ground motions (January–September 2022) or by processing older events (1999–2000). The benchmark set includes stations both within and outside the area covered by the spatial correlation of amplification residuals of the calibration ensemble (average distance from the closest calibration station is 3.3 km; see Fig. 10a). At each validation site, the soil amplification factors for PGV, PSA(1.0 s), PSA(0.6 s), PSA(0.3 s) and their corresponding single-site, within event variabilities (φ_SS) were derived consistently with the procedure illustrated in paragraph 2.1; these observed values were then collated with the predicted amplification and variability at the same locations (Fig. 10b–e, Table 2). As shown in Fig. 10b–e, the validation set includes both stiff and soft sites (measured amplification values span the range 0.4–10); the correspondence with the measured amplification values is reasonably fair. As displayed in Table 2, the average prediction error is close to 0 in log₁₀ scale, suggesting no systematic under- or over-prediction bias in the produced maps. The mean absolute error, measured in terms of root-mean-squared error (RMSE), is lower for PGV than for PSAs (Table 2); this can be ascribed to the better correlation of PGV with seismically-induced strains in the shallower subsurface and hence, by extension, with the local geology (Panzera et al. 2016, 2021a), since the lithological classification is in fact one of the key predictors in the amplification model of this study. When collated with the predicted total variability φ ($=\sqrt{{\varphi }_{S2S}^{2}+{\varphi }_{SS}^{2}}$), the difference measured minus predicted amplification results to be comparable with the former (the RMSE normalized by φ is slightly higher than 1, see Table 2). It should be additionally noted that the prediction error tends to increase slightly for measured higher values of amplification; the probable reason is that the softest lithogroup LG1 (“fine-grained sediments”), hosting sites with the highest soil amplification, is represented in the calibration dataset by the lowest number of stations (11, see Table 1), hence it is possibly less robustly constrained than other lithologies. Finally, we also observe a reasonable agreement between predicted and measured single-site, within-event variability (φ_SS; compare vertical and horizontal error bars in Fig. 10b–e; see also Table 2).

Fig. 10

Comparison between predictions from the ground motion soil amplification model and measured site response at 50 validation stations. a Location of calibration and validation stations. b–e Comparison predicted versus measured amplification and predicted versus measured φ_SS (single-site, within-event variability) at the set of validation stations for PGV (b), PSA(1.0 s) (c), PSA(0.6 s) (d) and PSA(0.3 s) soil response

Table 2 Summary statistics for the comparison measured versus predicted amplification and single-site, within-event variability (φ_SS) at the validation stations

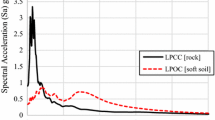
The second validation comparison was performed with local (city-scale) ground motion amplification models, available for the Swiss cities of Basel (Michel et al. 2017), Lucerne (Janusz et al. 2022a), Sion (Perron et al. 2022b) and Visp (Panzera et al. 2022). We focus here on the juxtaposition with the Basel model, which represents the soil response in terms of PSA, hence it is directly comparable with our Swiss national amplification model On the other hand, the soil response layers for Lucerne, Sion and Visp represent the amplification in the Fourier domain, so the quantitative comparison is inevitably less rigorous, and it is described in the Online Resource 3.

The Basel site amplification layer (Michel et al. 2017) was obtained by cross-referencing ESM (Edwards et al. 2013) amplification functions at local seismic stations, validated with site-to-reference spectral ratio method (Borcherdt 1970), with a set of geophysical surveys of the subsurface and about 2200 single-station microtremor measurements processed in terms of horizontal-to-vertical spectral ratio (Nakamura 1989). The Basel model is therefore based on extensive, locally acquired geophysical datasets and it is therefore considered more reliable than the global national model issued by this study; besides, it generally achieves a higher spatial resolution.

We quantitatively compared the PSA(1.0 s) and PSA(0.3 s) amplification maps from Michel et al. (2017; Fig. 12 therein) with the corresponding national amplification layers from this study. As an example, Fig. 11a, b juxtapose the national and city-scale model, respectively; the difference between the two (Fig. 11c) is generally moderate along the Rhine valley bed (South-East of Basel) and on the Rhine Graben area (North and West of Basel). Zones of higher discrepancy are met on (1) the hilly ridges south-west of Basel, where, however, Michel et al. (2017) had to extrapolate an amplification prediction as the area was not covered by field measurements; and (2) at the interface between the Rhine plain and the surrounding hills, which coincides with borders between different lithogroups (the plain being covered by unconsolidated sediment lithogroups, while the elevations mostly belong to consolidated sedimentary rock classes, see Fig. 11d). Such disagreements at the interfaces between lithogroups are to be ascribed to the relatively large scale of the lithological classification we employ (based on the 1:500,000 Swiss National Geological Map, lacking a homogeneous geological description of Switzerland at finer scale at the time of our study, see paragraph 2.2). Globally, as shown in Table 3, the mean cell-by-cell difference (in log₁₀ scale) local minus national model is close to 0 for both periods of comparison, suggesting that no systematic bias exists between the two datasets. The general agreement is measured by the square root of the mean of the squared cell-by-cell differences (RMSD) between amplification models; the RMSD is 0.173 and 0.235 log₁₀ units for T = 1.0 and 0.3 s, respectively (Table 3). For comparison, the RMSDs computed for the local models of Visp, Sion and Lucerne and for periods of T = 1.0, 0.6 and 0.3 s range between 0.198 and 0.345 log₁₀ units, with a median of 0.271 (see Table OR3.1 in Online Resource 3); the slightly larger difference values are to be mainly ascribed to the inconsistency in the representation of amplification (in Fourier for the local models, in PSA in our national model; see Online Resource 3). It should be noted that, particularly for Basel, the RMSDs of the local versus national amplification models are of the same order of magnitude of the variabilities (φ_SS and φ_S2S) estimated for the latter (see Sect. 5 and Fig. 8a, c in particular); in fact, when the difference is collated with the overall variability φ of the national model (φ = $\sqrt{{\varphi }_{S2S}^{2}+{\varphi }_{SS}^{2}}$), the majority of the overlap area falls in the range ± φ (e.g. Fig. 11e), and the RMSD normalized by φ is close to 1 (Table 3; see also the similar results for Lucerne, Visp and Sion in Online Resource 3).

Fig. 11

a, b Comparison between the PSA(1.0 s) amplification predicted for the area of Basel by the national model (a, this study) and by the local model by Michel et al. (2017) (b). c Difference (in log₁₀ scale) between the PSA(1.0 s) amplification model in b and the model in a. d Close-up for the area of Basel of the lithological map employed in this study. d Same difference as in c, normalized by the predicated overall variability (φ) from the national model

Table 3 Summary statistics for the comparison between the city-scale amplification model for Basel and the national model from this study

The third validation set of data collated with the amplification model from this study is a catalogue of macroseismic intensity observations compiled by Fäh et al. (2011) and based on data from historical earthquakes. Specifically, for the comparison we used the average residuals computed by Fäh et al. (2011) for 146 Swiss settlements between reported macroseismic intensity observations and the predicted intensities from the intensity prediction equation (IPE) they developed based on the same data (Fig. 12a); the reference soil condition (i.e. V_S30 ≈ 600 m/s) is therefore the same of the macroseismic intensity aggravation layers of this work (Sect. 6). The mean ΔIs of Fäh et al. (2011; see Data Availability) are derived from at least 10 intensity data points geographically assigned to the same relevant postcode; these values were cross-referenced with the average prediction extracted from the ΔI maps from our study (Sect. 6) in an area of 500 m radius around the coordinates of the corresponding postcode (Kästli 2020, personal communication). Quite positively, for the majority of the settlements the differences observed vs estimated local aggravations are comprised between − 0.5 and  + 0.5 units (see Fig. 12b); secondly, as reported in Table 4, the mean difference over the 146 sites is close to 0 for all three ΔI maps of this study, suggesting that no systematic bias is present between the two datasets; finally, the overall root-mean-squared errors observed-estimated local amplifications (0.41 for all three maps of this study) are close to the RMSE (0.40) similarly computed for the ΔI map of Fäh et al. (2011; see Data Availability), which was, however, calibrated on the very same dataset.

Fig. 12

a Average ∆Is (in macrosesimic intensity units) derived by Fäh et al. (2011) for 146 Swiss settlements. b Boxplots of the difference (in macroseismic intensity units) between the measured ∆Is from Fäh et al. (2011) and the predictions from the three concurring ∆I layers from this study.

Table 4 Summary statistics for the comparison between average ∆I amplification factors obtained by Fäh et al. (2011) for 146 Swiss settlements (Fig. 12a) and the predicted ∆I from the maps of this study, as well as the Fäh et al. (2011) macroseismic intensity amplification map

8 Integration of the amplification model in the Swiss ShakeMap

The amplification model from this study is integrated as “generic amplification factors” (Worden et al. 2020) in the Swiss ShakeMap workflow described in Cauzzi et al. (2015, 2022); the workflow maps the ground motion for vibration periods equal to 0.3 s, 0.6 s, 1.0 s, 2.0 s, along with PGA, PGV and macroseismic intensity. The aggravation factors for macroseismic intensity, for log₁₀PGA and for log₁₀PSA(2.0 s) were derived from those for log₁₀PGV estimated in this study using the conversion equations of Faenza and Michelini (2010, 2011). The other components of the Swiss ShakeMap workflow are: (1) the ground motion models of Edwards and Fäh (2013) parameterized by Cauzzi et al. (2015) and available in OpenQuake (Pagani et al. 2014); (2) the conversion equations of Faenza and Michelini (2010, 2011); (3) the peak motions recorded by the seismic stations monitored by the Swiss Seismological Service (mainly from the permanent seismic network “CH”, Swiss Seismological Service 1983) and automatically computed by using the software module “scwfparam” (Cauzzi et al. 2016). An example of the improvements yielded by the use of the new amplification models in Swiss ShakeMap is shown in Fig. 13 for an earthquake with moment magnitude ~ 4.3 occurred in region of Urnerboden / Linthal, central Switzerland, in 2017 (Diehl et al. 2021). Figure 13a shows the authoritative Swiss instrumental ShakeMap for this event, constrained by recorded peak ground motions: the instrumental macroseismic intensity exceeded V in the epicentral area, and especially along the alluvium-filled Linthal valley, where station SLTM2 recorded a PGA ~ 85 cm/s² and a PGV ~ 2 cm/s. Figure 13b shows the predictive ShakeMap for the same event, i.e., not constrained by peak-motion records, using the new amplification model presented in this study. Figure 13c is also a predictive ShakeMap for this earthquake, yet using the former amplification models of Fäh et al. (2011, its Appendix D) as implemented by Cauzzi et al. (2015). The macroseismic intensity field of the predictive ShakeMap in Fig. 13b shows a remarkable consistency with that of the instrumental ShakeMap, confirming the reliability and soundness of the new amplification models. In particular, the use of the new amplification model can effectively limit the spatial extent and the severity of the predicted shaking levels, avoiding the overprediction apparent in Fig. 13c both in the epicentral area and in the far-field, especially in Western Switzerland in this case. This is crucial for earthquake planning scenarios as well as for real earthquakes occurring in areas of lower seismic network density, e.g., close to the Swiss national borders.

Fig. 13

a Instrumental ShakeMaps for the Urnerboden / Linthal Mw ~ 4.3 earthquake of 2017. b Predictive ShakeMaps for the same event using the amplification model presented in this work. c Predictive ShakeMaps for the same event using the previous amplification model of Swiss ShakeMaps (Fäh et al. 2011).

9 Conclusions

We present a soil amplification model for Switzerland, developed to represent the site response term for the purpose of assessing the seismic risk at the national scale; the model is also integrated in the procedure for the mapping of shaking scenarios in Switzerland (ShakeMaps). The model consists of four layers mapping the soil response for the following ground motion parameters: PGV, PSA(1.0 s), PSA(0.6 s) and PSA(0.3 s), considered as significant given the range of resonance periods of the Swiss building stock. Each map is accompanied by two layers portraying the corresponding epistemic (site-to-site variability φ_S2S) and aleatory (single-site, within event variability φ_SS) uncertainties. Three amplification maps (for PGV, PSA(1.0 s) and PSA(0.3 s)) were additionally translated into macroseismic intensity aggravation (∆I) layers.

The national amplification model is based on two companion datasets: one of site amplification factors retrieved for more than 240 seismic stations using empirical spectral modelling techniques, and one of geological and topographic site condition proxies (lithological classification of Swiss territory, multi-scale topographic slopes, bedrock depth inferred from a national geological model). The two datasets were first correlated and then the local empirical measures of site amplification factors were interpolated using regression kriging as geostatistical mapping scheme. Regression kriging combines a spatial prediction based on correlations between the target variable and continuous layers of predictors and the interpolation of the regression residuals at sampled locations, after the assessment of spatial autocorrelation of the residuals (here in the order of few kilometres). Regression kriging ensures full consistency between predicted soil response and local measures of site amplification at and around stations’ locations; furthermore, in the neighbourhood of the latter the epistemic uncertainty (site-to-site variability) is concurrently reduced. The national soil amplification model was validated by comparing it with ground motion amplification factors from 50 stations not included in the calibration dataset, with four city-scale amplification models from microzonation studies and with a dataset of average macroseismic intensity aggravation factors computed for about 150 Swiss settlements and based on historical earthquakes data. Furthermore, the integration of the produced model in the Swiss ShakeMaps application is also illustrated.

The presented model intends to primarily capture the stratigraphic component of site amplification; topographic amplification, although embedded in part of the empirical amplification factors used in input, is not explicitly modelled. Furthermore, our model represents the soil response in the linear domain, that is, the strain-dependent decay of the stiffness of soil materials at high levels of strain is not accounted for. However, the most common scenarios with the highest contribution to hazard for the return period = 475 years (generally M_W ≤ 6.2, Bergamo et al. 2022b) and the tectonic regime of Switzerland (without subduction zones) suggest that such high strain levels may not occur over vast areas. Additionally, nonlinear behaviour affects loose sediments in a differentiated manner depending on their granulometry, composition and depositional conditions (Ciancimino et al. 2020). Furthermore, works based on ground motion empirical observations such as Løviknes et al. (2021) indicate that—in generalized studies at large scales—nonlinear soil response, although relevant for specific sites, is “diluted” in the dominant linear behaviour, and hence it does not emerge as globally significant. Indeed, the inclusion of nonlinearity may be a topic for the future improvement of the current soil amplification model, in the perspective of its use in combination with the seismic hazard for long return periods (≥ 975 years; Wiemer et al. 2016; Bergamo et al. 2021b). Given the current lack of significant instrumental evidence for nonlinearity in Switzerland, of particular relevance are undergoing studies combining numerical simulations and in situ geotechnical surveys for the prediction of the strain-dependent soil behaviour in areas of moderate seismicity (Janusz et al. 2022b).

Besides the addition of nonlinearity, further possibilities for improvement of the current model lie (1) in the increment of the calibration set of station, to improve the robustness of its prediction, particularly for some lithotypes (e.g. fine-grained sediments); in this context, an iterative update of the model as soon as new instrumented sites are available can be envisaged; (2) in the implementation of more advanced geospatial prediction techniques (e.g. random forest, Hengl et al. 2018), and (3) in the adoption of a finer-scale lithological description of soils, as soon as this is homogeneously available for Switzerland. The latter would also contribute to the reliability of the integration of nonlinear soil response in the amplification model, as an accurate mapping and classification of the various sediments’ typologies would be required.

Appendix: regression kriging

Regression kriging (RK, Hengl et al. 2007) is a geostatistical scheme for spatial mapping combining the prediction of a target variable based on regressions between the latter and spatially-continuous predictor variables and the kriging interpolation of the regression residuals; hence, RK allows to consistently integrate local samplings of the target variable in the output prediction layer. The technique is frequently used for the mapping of soil properties (e.g. Keskin and Grunwald 2018).

According to RK, the target variable z (in our case, the logarithm of soil amplification) at location s₀ is predicted as:

$$\widehat{z}\left({s}_{0}\right)=f\left(q\left({s}_{0}\right)\right)+ \sum_{i=1}^{n}{w}_{i}\left({s}_{0}\right)\cdot \left[z\left({s}_{i}\right)-f(q\left({s}_{i}\right))\right]$$

(2)

where f(q) is the regression function correlating the predictor variable(s) q to z, [z(s_i) − f(q(s_i))] is the regression residual at the ith measure of z (out of a total of n samples) and w_i is the corresponding kriging weight. In our implementation of RK, f(q) is obtained as a univariate or bivariate smoothing spline, correlating—for each lithogroup—the logarithm of observed amplification with the logarithm of topographic slope and/or the logarithm of the inferred bedrock depth (Fig. 5a–c).

The vector of kriging weights w in Eq. 2 is spatially dependent, that is, at the generic location s₀ is obtained as:

$$\left[\begin{array}{c}{\mathbf{w}}_{0}\\ \lambda \end{array}\right]={\left[\begin{array}{cc}\begin{array}{cc}C({s}_{1},{s}_{1})& \cdots \\ \vdots & C({s}_{i},{s}_{j})\end{array}& \begin{array}{cc}C({s}_{1},{s}_{n})& 1\\ \vdots & \vdots \end{array}\\ \begin{array}{cc}C({s}_{n},{s}_{1})& \cdots \\ 1& \cdots \end{array}& \begin{array}{cc}C({s}_{n},{s}_{n})& 1\\ 1& 0\end{array}\end{array}\right]}^{-1}\cdot \left[\begin{array}{c}{\mathbf{c}}_{0}\\ 1\end{array}\right]$$

(3)

where C(s_i,s_j) indicates the covariance between the residuals at sampled locations s_i and s_j, c₀ is the vector of the C(s₀,s_i) covariances between residuals at the unvisited and observation locations (on the same lithogroup) and λ is a Lagrange multiplier imposing the constraint $\sum_{i=1}^{n}{w}_{i}=1$(in other words, the local correction of the regression at the prediction location is a weighted average of the regression residuals at the sampling locations on the same lithogroup; note that this correction is significant only within the range of spatial autocorrelation of the residuals, see later in the text). The covariances C in Eq. 3 are obtained from a model expressing C as a function of the separation distance h; the model is in turn derived from the fitting of the experimental semivariance function of the regression residuals (γ(h) e.g. Fig. 5e, d). For the fitting we chose an exponential model with null nugget (Chilès and Delfiner 2012), as the variability at h = 0 is attributed to aleatory rather than epistemic uncertainty (see Sect. 5):

$$\gamma \left(h\right)=S\cdot \left[1-\mathrm{exp}\left(-3h/R\right)\right]$$

(4)

where S is the sill (the asymptote of γ(h) for h → ∞, i.e. the variance of spatially-uncorrelated residuals) and R is the range of spatial autocorrelation of regression residuals. To obtain a robust and consistent estimate of the modelled semivariogram across all lithogroups, and to compensate for the low number of samples of some of them, the exponential model is fitted over the entire set of experimental semivariograms (from all lithogroups) relevant to the regressions linking the same ground-motion parameter amplification with the same proxy (see example in Fig. 14 for the residuals of the PGV amplification vs topographic slope correlations). Before the fitting, the experimental semivariograms are each normalized by the corresponding variance of all residuals (correlated and uncorrelated; Fig. 14). In other words, we assume that the scaling of covariance with separation distance is similar for all lithogroups, once set aside the different levels of site-to-site variability in each lithogroup. The retrieved range of autocorrelation of residuals R and the ratio between the sill S and the variance of all residuals are therefore the same across all lithogroups (Fig. 14b).

Finally, consistently with the formalization of RK, the spatially-dependent kriging weights from Eq. 3 are also employed in the spatial modulation of the RK prediction uncertainty σ_RK:

$${\widehat{\sigma }}_{RK}^{2}\left({s}_{0}\right)=S- {\left[\begin{array}{c}{\mathbf{w}}_{0}\\ \lambda \end{array}\right]}^{\mathrm{T}}\cdot \left[\begin{array}{c}{\mathbf{c}}_{0}\\ 1\end{array}\right]$$

(5)

Fig. 14

a Experimental semivariograms for each individual lithogroup of the PGV amplification-vs-slope regressions. The variances of all residuals (correlated and uncorrelated) for each lithogroup are reported close to the ordinate axis. b Experimental semivariograms of a normalized by the corresponding variance of all residuals and fitted exponential model. The range R of spatial autocorrelation of the residuals is highlighted with a red segment. For the colour legend of the various lithogroups see Fig. 1

This local correction of RK prediction uncertainty is significant only for h ≤ R; beyond the range of spatial autocorrelation R, σ_RK coincides with S.