1 Introduction

Due to the high concentration of pollutants and humidity in coastal areas, steel structures continuously exposed to harsh environments are highly vulnerable to corrosion attacks over time. The corrosion-induced damage can substantially influence the efficiency of such systems and cause enormous costs for rehabilitation and repairing corroded elements. According to research conducted by the National Association of Corrosion Engineers (NACE) in 2016, the yearly global corrosion cost was estimated to be approximately US$2.5 trillion accounting for about 3.4% of the global gross domestic product (GDP) in 2013 (Koch et al. 2016 Mar). This cost can be broken down into direct costs (e.g., cost of maintenance and repairs), which are related to the owners or operators and indirect costs (e.g., cost of shutting down a factory or damage to people due to the ineffectiveness or failure of corroded elements), which are related to the users. Indirect costs are more significant than direct costs. As mentioned in the NACE study, nearly half of the global cost of corrosion damage is attributable to industry economics. For example, this cost is around 57% of the overall cost of corrosion in the European region, and in the United States, infrastructure corrosion accounts for about 17% of the overall cost of the industry sector.

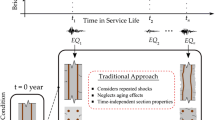
Severe corrosion damage over a long period can modify the response characteristics of the building, cause a loss of mass and increase the vulnerability of the structure subjected to severe loading conditions. Recent analytic and experimental studies (Xu et al. 2016, 2019; Wang et al. 2021; Wang et al. 2018) revealed that with the growth of corrosion level, the characteristics of steel structures, including mechanical properties (yield strength, ultimate strength, elongation, and module of elasticity) and energy dissipation capacity are affected. It is also mentioned that story drift ratio thresholds for global performance evaluations gradually decrease in an environment containing chloride (Zhang et al. 2020). The seismic performance will be affected due to these structural modifications.

In European codes (EN 2006, 2007), only general specifications and design control measures for the corrosion resistance of new structures were provided. The primary step to define the corrosion rate mathematically is by monitoring changes in the mass loss of the structure. As shown by Eq. (1), this rate is directly proportional to the corrosion thickness loss.

$$D=\frac{W}{\rho . A}$$
(1)

where D is the corrosion thickness loss (in millimetre or micrometre), W is the mass loss (g), \(\rho\) and A are the density of the material and exposed area, respectively.

As the corrosion loss over the lifetime of the structure is of the greatest concern to engineers, time-dependent corrosion thickness loss models have been developed based on experimental research data collected over exposure time (Rizzo et al. 2019; Landolfo et al. 2010). In such models, uniform thickness loss over the entire metal surface as the most common form of corrosion in the long run was considered as shown in Eq. (2)

$$d\left(t\right)=A.{t}^{B}$$
(2)

where A is the first-year corrosion rate, B is the long-term impact coefficient, and d(t) is the thickness loss of the corroded element over time (t). Environmental parameters, including the presence of pollutants such as sulphur dioxide (SO2), chloride ion (CL-), relative humidity (RH), and temperature, affect the value of the A and B coefficients (Benarie and Lipfert 1967; Feliu et al. 1993b). In practice, the B exponent denotes the rate of corrosion acceleration over time.

The International Organization for Standardization (ISO) has published several reports on the computation of corrosion related to exposure time considering various damage levels (ISO - 2012a, 2012b). ISO9223 (ISO - 2012b) divided the corrosivity level into six categories, ranging from C1 for the dry or cold zone, where there are virtually no pollutants with a low corrosion rate, to CX for the tropical and subtropical zone along the coast and offshore areas, where there are significant amounts of contaminants, mostly in contact with sea salt spray with a high rate of salinity. In addition, a model for calculating corrosion loss based on exposure length and environmental effects was proposed which assumes that the corrosion rate becomes linear after 20 years (ISO - 2012a). Several researchers suggested similar models utilising Eq. (1) to estimate the A and B values by analysing the interactions between multiple environmental attacks (Soares and Garbatov 1999; Kee Paik et al. 1998). It is assumed that corrosion process starts once the coating system (e.g. layers of paint) loses its effectiveness. In practice, corrosion attacks begin as pitting corrosion before the loss of all coating layers when the first scratch occurs. A few models addressed this aspect (Kere et al. 2019; Qin and Cui 2003). The influence of environmental parameters such as sulphur dioxide (SO2), chloride (Cl−), temperature, and time of wetness (TOW) was outlined in a base power function model (Klinesmith et al. 2007). Other studies present the use of probabilistic methods to determine corrosion loss attacks through statistical analysis (Kere et al. 2019; Klinesmith et al. 2007). Even though the constant corrosion thickness reduction model for the entire cross-section has been suggested in previous several works, Sarveswaran et al. (Sarveswaran et al. 1998) proposed a more realistic corrosion thickness reduction model that accounts for varied thickness decay. According to this model, stagnant water increases the likelihood that the bottom of the H-shaped cross sections may corrode.

The seismic risk assessment of industrial structures has been the subject of a number of research projects (Gabbianelli et al. 2022; Merino Vela et al. 2019; Ozdemir et al. 2010) However, few studies were conducted on the damage and loss assessment of steel infrastructure in a corrosive environment over long periods (Sarno et al. 2021). Evaluating the susceptibility of these structures following various corrosion-induced damage states is still a matter of discussion.

Figure 1 provides the research workflow adopted in this paper. After a brief review of the mechanism of corrosion in severe environmental conditions, the risk assessment of corroded structure during the life of the structure is addressed based on the following steps: (1) The corrosion effect was modelled using Finite Element (FE) numerical simulations of a steel petrochemical plant as a case study located in a high corrosivity level zone based on the available models in the literature. (2) The damage states were then determined based on the responses of the structure to the multiple time history analyses. (3) To determine the damage and consequences (repair costs) at various intensity measures, fragility and vulnerability functions were obtained. (4) For risk evaluation, fragility and vulnerability curves were combined with hazard characteristics for the case study structure.

Fig. 1
figure 1

Graphical illustration of the research methodology

Full size image

2 Research objectives and significance

This study employs seismic probabilistic risk assessment approaches to evaluate the influence of corrosion damage on the performance of steel industrial structures in a harsh atmospheric environment subjected to ground motion activities over the design lifetime. The probability of damage and expected maintenance and repair costs in light of corrosion attacks have been investigated. The current work is valuable for asset managers/decision makers to estimate the damage and related costs (repair costs) caused by corrosion attacks over a long period of time, particularly for insurance companies in estimating future losses and generating sufficient revenue for building owners to pay reasonable maintenance costs to ensure the safety of the building over its lifetime. This study also is also relevant for researchers investigating the seismic risk of structures affected by corrosion.

3 Corrosion mechanism

Atmospheric Corrosion rate is influenced by two key variables: humidity (vicinity to seawater) and air pollution (e.g. Sulphur dioxide and Chloride ion). As an example, construction in coastal areas with high salinity or chemical activity in a factory might accelerate corrosion loss over the lifetime of the structure. As a result, recognising corrosive environments based on environmental parameters might help assess the corrosion rate. On the other hand, using an effective corrosion control system can be advantageous.

3.1 Corrosive environment

According to the corrosion classification provided by International Organization Standardization (ISO) report (ISO - 2012b), C5 category, denoted as an area with a very high rate of corrosivity, is related to coastal and industrial buildings with a high rate of pollutants. Table 1. ISO report on pollutant and corrosion rates at C5 level for industrial outdoor environments (ISO - 2012b). shows the range of most significant environmental factors at this level that influences the rate of corrosion, where the source of particles (PM10) and Sulphur dioxide (SO2) are industrial plant emissions and chloride ions (\({\mathrm{Cl}}^{-}\)) derived from sources such as airborne sea spray. The time a metal surface remains wet during atmospheric exposure is commonly referred to as the time of wetness (TOW).

Table 1 ISO report on pollutant and corrosion rates at C5 level for industrial outdoor environments (ISO - 2012b)
Full size table

This study proposes a time-dependent corrosion model in which Eq. (1 \()\) is used for the first 20 years (t = 20) and the corrosion loss is assumed to be linear after this point because of the formation of corrosion products, as shown in Eq. (2).

$$d\left( t \right) = \left\{ {\begin{array}{*{20}l} {At^{B} ,t \le 20} \hfill & {} \hfill \\ {A\left[ {20^{B} + B\left( {20^{{B - 1}} } \right)*\left( {t - 20} \right)} \right],t} \hfill & {gt;20} \hfill \\ \end{array} } \right.$$
(2)

According to the above formulation, the highest B value for carbon steel can be assumed equal to 0.575 and the effect of corrosion protective systems (e.g. coating) in calculating the corrosion loss may be ignored.

3.2 Corrosion protection techniques

The cost of corrosion can be reduced by 15% to 35% by adopting effective corrosion management techniques and adequate design (Koch et al. 2016 Mar). Structures lacking an appropriate corrosion maintenance plan must be repaired in order to improve the performance of corroded elements. Traditional rehabilitation techniques, such as adding a plate to the damaged parts had numerous drawbacks, such as increasing the weight of the structure and the vast cost of rehabilitation. The first two prevention strategies are implemented during the design process to minimise situations that contribute to corrosion or by using corrosion-resistant materials such as stainless steel instead of regular-grade steel. Inhibitors can be used as a passivation layer to impede electrochemical reactions between metal and the environment. Cathodic protection protects the metal by converting the active (anode) parts of the metal surface to passive (cathode). Coating is the most common corrosion protection method which acts as a barrier system to protect the metal from environmental attacks. Figure 2 summarises the various corrosion protection strategies that are often used. The use of Carbon Fibre Reinforced Polymer (CFRP), a cost-effective, lightweight and easy-to-install material that can increase the resistance of damaged components, is another alternative by attaching to the damaged parts through the adhesive. Many studies on the evaluation of corroded elements have been conducted using CFRP products (Jagtap and Pore 2020; Yousefi et al. 2021; Elchalakani 2016; Jayasuriya et al. 2018). The results of the experiments illustrated that using the CFRP products can increase the endurance and strength of the damaged element significantly. The selection of an acceptable protective strategy depends on a variety of factors, including the initial investment budget, the size of the project, the accessibility, etc.

Fig. 2
figure 2

Common corrosion protection techniques

Full size image

Most of the available models do not account for the effect of corrosion protection methods on total corrosion loss. In reality, corrosion initiates when the first scratch of the coating layer occurs. As illustrated in Fig. 3a, pits begin to grow along with the breakdown of the coating layer (phase 2, t > ts) and eventually progress to general (uniform) corrosion (phase 3, t > ta) after the first few years. In this phase, the rate of corrosion increases with time. Along with the creation of a corrosion product layer (rust) on the metal surface, this accelerated process changes to decelerated (transition time) and the corrosion rate will be nearly zero over time (phase 4, t > tl). In the absence of a coating protective system, the deteriorated components must be repaired or replaced by the end of the design life of the sample structure (tl). For simplicity in the calculation, it is assumed that the coating life (tc) is equal to the initiation of uniform corrosion (ta) (Qin and Cui 2003).

Fig. 3
figure 3

Corrosion model: a general mechanism of corrosion with coating system b comparison of available corrosion wastage models

Full size image

Employing an adequate corrosion control system can significantly reduce the damage. Using a barrier coating system, for example, is often a good choice. Equation (3) was proposed to estimate the rate of corrosion over time while considering the interaction between metal corrosion and coating layer deterioration (Kere et al. 2019).

$$d\left(t\right)=\left\{\begin{array}{c}\frac{1}{{A}_{0}}{\int }_{0}^{t}d\left(t-\tau \right) . {{A}^{^{\prime}}}_{l}\left(\tau \right).d\tau ,\quad t<tc\\ \frac{1}{{A}_{0}}{\int }_{0}^{tc}d\left(t-\tau \right) . {{A}^{^{\prime}}}_{l}\left(\tau \right).d\tau , \quad t\ge tc\end{array}\right.$$
(3)

where A0 and A'l(t) represent the initial and rate of corrosion area loss, respectively (Kallias et al. 2017). In practice, there is a direct relationship between coating layer deterioration and metal corrosion loss before the loss of the entire surface coating layer (tc). After tc, all coating protection layer is removed and only the metal deteriorates.

A comprehensive corrosion protection system is essential for extending the life of the building and reducing the likelihood of damage. In the case of employing painting as a protection system, it is essential to know when to renew the damaged paintings. Predicting the service life of the coating layers can therefore provide a solid reason for establishing a more effective maintenance plan (Helsel and Lanterman 2022). The following stages might be considered for an appropriate maintenance plan according to the coating layers’ practical life (P), which is the time when 5 to 10% of the protective layer’s efficiency is lost: Touch-up at P (related to minor damage and small surface defects), maintenance repaint after 1.5*P (recoating of the damaged parts), and thorough painting after 2*P (removing existing coating and repaint). The efficiency of having a maintenance system in a corrosive environment (e.g. C5 level) can be seen in Fig. 3b which three scenarios have been compared during the long-term exposure: the structure without coating system (Eq. (2)), with the original painting and with maintenance plan (Eq. (3)). In this figure a three-layer Inorganic Zinc (IOZ) coating system (Inorganic Zinc as a primer and epoxy and polyurethane as top coats) with a 16-year practical life was chosen due to its widespread industrial application and high resistance to corrosion attacks in harsh atmospheric environments.

Figure 3b shows that by using an effective barrier protective system with the appropriate maintenance plan, the rate of damage (corrosion loss) can be reduced by 90% over the life of the structure. Similarly, 38% less damage can be caused when only initial painting is applied after construction.

4 Methodology of risk assessment

4.1 Case study

A 61-m-tall, irregular steel petrochemical plant structure in the Caribbean region equipped with a piping system that runs along the height of the structure was selected as a case study to examine the effect of corrosion on the seismic performance of the skeleton of the system. The lateral resistant system consists of ordinary braced frames in the X direction and ordinary moment frames in the Y direction. The structure is supported by horizontal members braced in the XY plane and by some vertical cross-bracings in the Y axis. Normal carbon steel material with a grade of A36 (expected yield and ultimate strength of 372.32 MPa and 439.89 MPa and elasticity module of 203 GPa) was employed. The petrochemical structure was founded in soil class D and 1.37 and 0.869 s for 0.2 and 1-s spectral response acceleration with a 5% of damping ratio. According to IBC 2018 (International Code Council 2018) the building was classified as risk category three. Based on reports from Environmental Management Authority (EMA) organisation, the building was close to the sea with a high level of humidity (International Code Council 2018).

4.2 Model description

A three-dimensional nonlinear Finite Element (FE) model was implemented in the structural design program CSI SAP2000 (SAP2000 CSI xxxx). For evaluating the behaviour of the structure in the nonlinear region, nonlinear hinges were assigned at both ends of the elements, including the axial load-bending P-M2-M3 hinges for obtaining the coupled axial and bending behaviour in columns and bending hinges (M3) for the bending behaviour of the beams according to ASCE41-13 (Seismic Evaluation and Retrofit of Existing Buildings 2014). Also, the axial hinges with a relative length-to-distance ratio of 0.5 were chosen to simulate the buckling behaviour of the bracing frames. The model is illustrated in Fig. 4. To consider the corrosion loss over the lifetime of the structure, the uniform cross-section thickness loss method was used for all cross-sections of the main building structure. As a worst-case scenario, the upper limit of the first-year corrosion rate at the C5 level based on the ISO 9224 model (ISO - 2012a), with A = 200 m/year and B = 0.575 was selected (see Table 1 and Eq. (3)).

Fig. 4
figure 4

The finite element modelling of the case study: a YZ view plan, b 3D view and c XZ view plan

Full size image

4.3 Probabilistic seismic assessment

To make a risk-management decision, the structure should be evaluated by determining the probability of damage and quantifying the consequences (loss) during earthquakes of varying intensity levels likely to occur. Incremental dynamic analysis (IDA) (Vamvatsikos and Allin 2002) is a powerful tool for analysing the behaviour of the structure in both linear and nonlinear regions. This technique uses a series of analyses to achieve varying performance and damage levels by gradually increasing the intensity of the ground motion. In this study, spectral acceleration at the dominant-mode period of the structure, Sa(Ts), was selected as a sensitive ground motion intensity measure (IM), and the maximum inter-story drift ratio (MIDR) as an engineering demand parameter (EDP) was chosen to reflect the extent of damage at each IM level.

Seismic fragility analysis is an effective method for evaluating the seismic performance of a structure based on the probability of failure as a function of IM in which failure is defined with respect to damage states (DS) (Muntasir Billah and Shahria 2014). Under the assumption of a lognormal distribution between EDP and IM, the fragility curve can be represented by the probability of reaching or exceeding the damage limit state (dsi) for a given level of seismic excitation (IM). The following distribution represents the fragility function.

$$P \left[DS\ge d{s}_{\mathrm{i}}|IM=x\right]= \Phi \left(\frac{\mathit{ln}\left(\mathrm{im}/\mathrm{\theta i}\right)}{\mathrm{\beta i}}\right)$$
(4)

where \(\Phi\) is the cumulative normal distribution function,\(\theta\) and β are referred to as the median and standard deviation of natural logarithmic of the capacity of the structure to resist damage state i.

The median value (\(\theta\)), 16th and 84th percentiles (\(\theta *{\mathrm{e}}^{\pm \beta }\)) were obtained and compared in this study for both damaged and undamaged cases.

Vulnerability function (loss or consequence function) predicts the probability distribution of consequence (not failure) as a function of IM. Consequences include, for instance, the cost of repairs, the number of injuries, the number of fatalities, and the amount of time needed to repair or replace the damaged components. Industrial structures engaged in chemical activities are especially vulnerable to catastrophic accidents that endanger workers, the environment, and surrounding communities. The general formulation of the vulnerability function can be found as follows:

$$P\left(C>c|IM=x\right)=1-F(c|IM=x)$$
(5)

where \(F(C|IM)\) is the cumulative distribution function (CDF) for the consequence C evaluated at c as a given IM. The repair cost at each level of IM was selected herein as the consequence variable and the probability of exceeding costs at each level of damage was determined.

4.3.1 Seismic damage states and performance levels

Damage states are correlated with performance objectives (Elnashai and Sarno 2015). Damage states are the circumstances under which a structure performs its intended function (e.g. exceeding a MIDR level). Performance levels can often be separated into three stages: serviceability, damage control, and collapse prevention which might be impeded by structural, non-structural damage or social losses. At the limit of serviceability, the structure has experienced only minor damage, the elements have not reached their significant yield point, and there is no permanent drift. This performance is linked to the initial yielding of the structure (first damage state) and is primarily affected by stiffness. At the damage-control state level, the structure is severely damaged, most elements have reached their yield strength, and a moderate residual drift can be observed. Buckling and stretching of braces, cracked welds and the creation of plastic hinges can be associated with this performance. This level is mostly determined by the system's strength. And at the collapse prevention level, the structure is severely damaged and has substantial permanent drifts. This behaviour is associated with the global collapse of the structure.

In this study, the structural response was measured to detect the damage states by tracking the formation of nonlinear hinges in structural components using multiple time history analyses corresponding to the dominant vibration mode. The assessment was carried out for both local and global rates of damage. For measuring the local damage levels, the intensity was increased until components reached their first yielding and ultimate capacities. The initial damage state was selected when the initial yielding point was observed. The global ultimate damage limit state (collapse prevention) is characterised by the tangent stiffness of the IDA curve equalling 20% of the initial stiffness (Vamvatsikos and Allin 2002). It is important to note that in seismic risk assessment of industrial buildings, the damage states of non-structural components such as tanks and pipes should also be considered (Nardin et al. 2022). However, the present study focuses on the effect of corrosion on the behaviour of the main structure.

4.3.2 Seismic hazard definition and input ground motions

The features of ground motion activities at the location of a structure can be described by hazard curves, which represent the frequency of earthquakes at each IM level in a specific geographical location. This information can be gathered from previous investigations in that area or by doing a probabilistic seismic hazard assessment at the same location, that considers all potential earthquakes. Vulnerability and fragility functions can be combined with the hazard curve to determine the annual failure rate at each damage state and the exceedance probability of various degrees of loss, which is then useful for the decision-making process. In this study, the hazard curve and the seismic hazard map for the site of the case study are shown in Fig. 5 (Karagiannakis et al. 2022; The UWI Seismic Research Centre xxxx).

Fig. 5
figure 5

Seismic hazard for the structural part: a seismic hazard map b active faults and c hazard curve

Full size image

Based on the Federal Emergency Management Agency report (FEMA P-695) (FEMA P695. 2009), 22 far-field and 28 near-field records were selected and applied to the structure as IM input. The response spectra of these records are shown in Fig. 6. The effective duration of the accelerogram that contains the main potential energy is the most important factor in determining which ground motion amplitude can cause structural damage. In this study, the significant duration, one of the most common methods for identifying the effective length was used (Kempton and Stewart 2006 Nov). This period of time is defined as during which the integral of the square of the ground acceleration is within a fixed range of its total value, often between 5 and 95%. More details about the selected ground motions can be found in Appendix.

Fig. 6
figure 6

The response spectra of two sets of ground motions: a far-field records and b near-field records

Full size image

4.3.3 Annual failure rate and loss exceedance curve

To assess the safety of the structure, the annual failure rate can be calculated for each damage state at various input IMs. In other words, this metric represents the annual average number of failures at a given IM. By combining the hazard curve and fragility function in a discrete format, the annual failure rate can be determined as follows:

$$\lambda (F)={\sum }_{\mathrm{i}=1}^{\mathrm{n}}P \left[DS\ge d{s}_{\mathrm{i}}|IM=x\right]*{\Delta \lambda }_{\mathrm{i}}$$
(6)

where λ(F) represents the annual failure rate, reaching a particular damage state, \(\mathrm{P }\left[\mathrm{DS}\ge {\mathrm{ds}}_{i}|\mathrm{IM}=\mathrm{x}\right]\) is the fragility function at each damage state (see Sect. 4.2.1) and Δλi is the difference between the hazard curve values at each discrete IM level.

Loss exceedance function defines the rate of exceedance of losses (e.g. repair cost) by combining the ground motion hazard curve with the vulnerability function (see Sect. 4.2.1) as follows:

$$\lambda (C>c)={\sum }_{\mathrm{i}=1}^{\mathrm{n}}\mathrm{P}\left(\mathrm{C}>\mathrm{c}|\mathrm{IM}={x}_{\mathrm{i}}\right)*{\Delta \lambda }_{\mathrm{i}}$$
(7)

where λ(C > c) is the annual rate of loss, P(C > c | IM = xi) is the vulnerability function at each IM level. This risk metric can be represented in a probabilistic time-dependent format to illustrate the probability of costs at each level of intensity during a period of time which can be shown through the Poisson distribution as follows:

$$P(C > c) = 1{-}\exp ( - \lambda (C > c) \, * \, t)$$
(8)

where P(C > c) represents the probability of exceedance loss over the period of time, t.

In this study, the repair cost estimation of the component was examined using FEMA P-58 report (FEMA P58-1. 2012). Table 2 displays the repair costs utilised in this study.

Table 2 Repair cost estimation based on FEMA P-58 (FEMA P58-1. 2012)
Full size table

4.4 Maintenance and retrofitting costs

Considering the costs of various protective and strengthening strategies to prevent damage in the future, can assist the users in selecting the optimal strategy for preserving the structure's durability over time. For example, the hot-dip galvanising coating technique is less expensive than the other coating systems over thirty years of exposure (Kowalski et al. 2017) because the practical life of the hot-dip galvanising coating system is about 72 years in a harsh industrial environment (level C5), essentially no maintenance costs are incurred (Helsel and Lanterman 2022). Utilising corrosion-resistant steel (e.g. stainless steel) is initially more expensive than painting, but is financially advantageous in the long run due to the material's high resistance and durability, as well as its lack of maintenance requirements. Without a corrosion control system, the structural system capacity should be increased by using retrofitting techniques.

Two distinct strategies have been compared in this paper in the event of corrosion at the C5 corrosivity level: Using a maintenance control plan for the initially painted structure or in the absence of a coating system, using rehabilitation techniques to repair corroded elements during the lifetime of the structure. Table 3 shows a methodology to estimate the maintenance costs over time (Helsel and Lanterman 2022) based on the original cost (OC) of the initial painting. The IOZ coating system was employed as a protective coating layer. It is assumed that the initial painting was applied in 2010 using the shop painting system after the completion of construction with a maintenance plan for the following 100 years, considering an annual inflation rate of 2%.

Table 3 The cost analysis for preventing corrosion damage through painting (Yousefi et al. 2021)
Full size table

As discussed in previous studies (Jagtap and Pore 2020; Yousefi et al. 2021; Elchalakani 2016; Jayasuriya et al. 2018), it is possible to effectively increase the capacity of corroded steel structural components with fibre-reinforced polymer (FRP) based materials. In the present analytical work, using the specifications found in Table 4 through market research (Sika UK | Sika Limited | Sika Group n.d 2022), a cost estimation to rehabilitate a corroded structure by using CFRP fabrics has been conducted at 50 years and has been compared with the case of using a maintenance system over time.

Table 4 CFRP laminate and adhesive specification
Full size table

For consistency in comparing the two methods, surface preparation and related costs (including labour costs, site facilities, etc.) were excluded from the calculations, and only the material costs were compared. For estimation of the rehabilitation cost of the corroded model per square metre, two layers of CFRP and 1.5 kg of resins (as an adhesive layer) are utilised (Jagtap and Pore 2020).

5 Results and discussion

5.1 Modal analysis

Table 5 displays the natural periods of the corroded (C) and uncorroded (UC) structures associated with the highest mass participation. For the uncorroded model, in the X direction, modes 4 and 32 and in the Y direction, modes number 3 and 31 were identified as the dominant modes. For the corroded case, in the X direction, modes 73 and 17 and in the Y direction modes 72 and 16 were identified as the dominant modes. It should be noted that mode number 32 and 73 in the X direction and modes 31 and 72 in the Y direction were related to the displacement of the pipes and vessels and mode shape numbers 3,4,16 and 17 were for the main structure. Figure 7 illustrates the graphical mode displays related for modes 3 and 4.Damage limit states.

Table 5 Natural period of two first dominant modes, keys
Full size table
Fig. 7
figure 7

The 3D and a plane view of modal displacement of the structure for a mode no. 4 and b mode no. 3. (A few items have been hidden to improve the quality of images)

Full size image

Table 6 shows the threshold of the local and global damage states according to the formation of nonlinear hinges at various damage stages, based on the response of the structure subjected to ground motion records (FEMA P695. 2009). At the initial loading stage (Sa(Ts) = 0.2 g), the yield strength of the first beam and brace was reached, which corresponds to the initial damage state (Serviceability). Minor damage, such as light buckles in the braces, can be depicted and is barely visible to the naked eye. As the intensity level increased (Sa(Ts) = 0.6 g), the yield capacity of the first column was reached and it was considered as the second damage state (Damage control-light). At this stage of deterioration, the damage can be detected by the buckling of the braces, the light damage to the beam, connections and the onset of cracks at the base plate. At Sa(Ts) = 1.4 g, the first column reached its maximum ultimate capacity, showing the beginning of the third damage stage (Damage control-extensive). At this stage, the major damage can be identified by buckled braces, local beam web and flanges buckling, and the major cracks at the base plate. At the point at which most nonlinear hinges reach their maximum capacity, the global ultimate damage limit state (collapse prevention) was estimated by the tangent stiffness of the IDA curve being equal to 20% of the initial stiffness (Vamvatsikos and Allin 2002). It should be noted that below the initial damage (DS1) state is considered an undamaged state.

Table 6 Structural damage limit states (DSs)
Full size table

As illustrated in the above table, the results are compared with the damage limit states in HAZUS standard code for an industrial building (Agency and (FEMA). Multi-Hazard Loss Estimation Methodology, Earthquake Model, Hazus-MH 2.1, Technical Manual. 2013). The results demonstrate that the HAZUS limit states were comparable to or slightly lower than the intended limit states, but they remain within an acceptable range.

5.2 Fragility curves

Figures 8 and 9 summarise the fragility curves for all corroded and uncorroded cases subjected to far and near-fault ground motion records, with solid lines representing the uncorroded model (UC) and dashed lines showing the corroded structure (C). Also, the median, 16th and 84th percentiles are plotted to illustrate the diversity of the results. As illustrated, the fragility curves flatten and the probability of exceedance increases gradually for all performance levels as IM (Sa(Ts)) rises, while the probability of damage decreases as the level of damage state goes up at the specific IM.

Fig. 8
figure 8

Fragility curves for a structure subjected to: a, c and e far-field and b, d and f near-field ground motion records for 16, median and 84 percentiles at different performance levels and g and f for the difference between corroded and uncorroded median fragility curves subjected to far and near-field records respectively

Full size image
Fig. 9
figure 9

Fragility curves for a structure subjected to all near and far-field records for a median, b 16th percentile and c 84th percentile values and d for the difference between corroded and uncorroded median values

Full size image

To further illustrate the effects of corrosion on the performance of the structure, the difference between the median fragility curve data is graphically displayed (Figs. 8g, h and 9d). Considering all records as input, this difference is approximately 40% on average (Fig. 9d). This discrepancy is greater for structures subjected to far-field records rather than near-field earthquakes (see Fig. 8g, h). As an example, in the case of low damage level (DS1), the effect of corrosion on the likelihood of structural damage is approximately 30% greater than in the case of near-field records.

Tables 7, 8 and 9 summarise the median (θ) and standard deviation (β) for each distribution of median fragility shown in figures Figs. 8 and 9. In the case of an undamaged model exposed to near-fault events, the medians of Sa(Ts) for various damage states from DS1 to DS4 were approximately 9.5%, 14.5%, 15.1%, and 14.7% greater than in the case of a corroded model. For far-fault records, this difference is 25%, 22%, 20%, and 18% in the same order, and when considering all records, it is nearly 25% and 22% for the first three damage states and DS4, respectively.

Table 7 The median (θ) and standard deviation (β) of the fragility curves in Fig. 8d
Full size table
Table 8 The median (θ) and standard deviation (β) of the fragility curves in Fig. 8c
Full size table
Table 9 The median (θ) and standard deviation (β) of the fragility curves in Fig. 9a
Full size table

5.3 Vulnerability curves

Figure 10a, b, and c illustrates the repair cost of corroded and uncorroded structures for varying intensities of ground motion (IM). The average value is plotted for both corroded and uncorroded conditions, and it gradually rises with increasing earthquake intensity. As an example, when considering all ground motion records, the average cost to repair a corroded case is 1.5 times that of a non-corroded case, at 0.6 g (Fig. 10c). This difference which can be denoted as the corrosion cost is approximately 1.7 and 1.3 at the same intensity level for far- and near-field records, respectively (Fig. 10a, b). The cost of corrosion increases significantly at higher earthquake levels. Considering far-field, near-field, and total records as input for ground motion, the corrosion cost at 0.6 g is 12, 4.5, and 8 times higher than at 0.2 g.

Fig. 10
figure 10

Repair cost estimation and vulnerability curves at different IM for a and d far-field records, b and e near-field records and c and f for all records

Full size image

As illustrated in Fig. 10d, e and f, vulnerability curves for the corroded and uncorroded cases at different intensity measures are plotted based on the distribution fitting curve at each IM using the Gamma- distribution approach. At the lower IM, the difference between the probability of reaching the cost of corroded and uncorroded cases (probability of corrosion cost) becomes more noticeable. For example, in all earthquake input scenarios, the maximum difference at IM = 0.2 g is approximately 2.8 times greater than at IM = 0.6 g. Similarly, this ratio at 0.4 g for far-field and total records is 1.7 and 1.3 times greater than at 0.2 g, respectively. In cases of near-field records, this ratio is equal to one.

5.4 Maintenance and retrofitting cost estimation

According to the graph in Fig. 11, the cost of rehabilitation using a CFRP product is around 640$ per square metre at the design life of the structure, which is approximately 43% higher than the cost of having a complete maintenance system over the lifetime of the structure (100 years). The figure does not include the price of facilities, labour, and other associated expenses. However, the cost of installation of the products depends on a variety of case-specific variables, such as access, work size, night/day shifts, amount of surface preparation required, site facilities, etc., which could alter these calculations. For retrofitting strategy, periodic inspections are required to identify damaged components which should be considered in cost estimation.

Fig. 11
figure 11

Results of discrete cost analysis for long-term corrosion exposure in harsh environment

Full size image

To compare the results, the construction cost of the structure was estimated, based on the material cost of the superstructure and foundation. The superstructure cost was estimated to be approximately 550$ per tonne, with the connection cost being about 15% of this cost and the foundation cost was projected to be around one-third of the total building cost. The results showed that the maintenance and rehabilitation costs were expected to be around between 50 and 70% of the initial construction cost over the structure's lifetime, respectively.

5.5 Annual failure rate

The annual failure rate, λ(F), is plotted in for each damage state level by combining the hazard characteristics into the fragility curve’s results (see Fig. 5, 9). The findings are plotted separately for each ground motion record group (far- and near-field records) and for the total number of records. The results show a slight difference in annual rate between cases with and without corrosion. For example, when considering all near- and far-field records, the annual failure rate of the corroded case was around 1.5 and 2.8 times greater than that of the uncorroded case in the first two damage states. In this case, the return period for the damaged model at DS1 and DS2 decreased by 240 and 10,557 years, respectively.

The results summarised in Figs. 12, 13 also show that at damage stage DS3, corresponding to the column ultimate capacity (see Table 6) there was a negligible effect on the uncorroded structure.

Fig. 12
figure 12

Annual failure rate ratio as a function of the damage states (DSs)

Full size image

5.6 Exceedance probability curve

Figure 13 reports the evaluation of the risk of exceeding various levels of loss (cost) based on the data from the hazard curve within a particular timeframe. The provided curves are obtained by combining the vulnerability function (Fig. 10) and the hazard curve (Fig. 5). As shown in Fig. 13b there is a difference between the probability of costs when corroded and uncorroded scenarios are considered. Corrosion of a structure can increase the likelihood of causing repair costs in the first year by up to 40 and 60 times after 50 and 100 years, respectively.

Fig. 13
figure 13

Cost estimation considering hazard curve data: a cost exceedance probability function, b cost difference

Full size image

The results pictorially displayed in Fig. 13 can be efficiently utilized for proactive maintenance of new and existing ageing petrochemical plants, thus extending their design life and enhancing their resilient seismic performance.

6 Conclusions and recommendations

High corrosion rates can lead to mass loss and compromise the performance and durability of steel infrastructures. This research evaluated the seismic risk of damage to a realistic case study of an ageing steel industrial infrastructure in a harsh environment and its likely consequences (repair costs). Comprehensive nonlinear dynamic response analyses were carried under different earthquake scenarios, considering both near- and far-field seismic records. The major outcomes and conclusions of the present analytical study can be summarised as follows:

  1. (1)

    According to the modal analysis of the model, corrosion-induced damage can shift the dominant mode of vibration to a higher frequency.

  2. (2)

    Corrosion can considerably increase the probability of damage at all severity levels. Fragility analyses indicated that the corrosion mass reduction can raise the probability of damage to the corroded structure by an average of 40% over the lifetime of the structure. This effect was greater for models subjected to far-field records, which were more significant for low-intensity measurements, with a maximum 49% difference compared to non-corroded cases (corrosion damage effect) in the first damage condition (DS1). In the case of near-field records, corrosion had little effect on the structural response at the same damage level and for the succeeding damage condition, the result was almost identical, which was approximately 33% more than the uncorroded instance.

  3. (3)

    The repair cost of the damaged structure was gradually increased for higher ground motion intensity measures and the difference in the probability of reaching or exceeding the specific repair cost between corroded and uncorroded cases (probability of the corrosion cost) was more significant at higher intensities (IM). For instance, the maximum corrosion cost at IM = 0.2 g was approximately 2.8 times that at IM = 0.6 g.

  4. (4)

    By comparing the annual failure rates at each level for both the corroded and uncorroded model, the results showed that the annual failure rate was increased in the range of 1.5 and 2.8 times for the first two damage states which represented 240 and 10,557 years decrease in return period of the earthquake respectively.

  5. (5)

    The probability of cost during the window of time denoted that long-term corrosion exposure can increase the corrosion cost between corroded and uncorroded structures. The probability of cost after 50 and 100 years was around 40 and 60 times more than the first-year probability cost value.

The above findings can be utilized as efficient and robust means for stakeholders and insurance companies to estimate repair costs and make more informed decisions on retrofitting or the deployment of corrosion protection systems for proactive maintenance especially of ageing petrochemical plants, thus extending their design life and enhancing their resilient seismic performance.