Abstract
This paper presents the seismic mitigation of typical storage tanks where extreme loading conditions are considered by safe shutdown earthquakes. To reproduce the main dynamic properties of the superstructure, a standard structural model was considered, where both the presence of the impulsive mode and of the convective mode were considered. Thus, to protect the tank from strong earthquakes, finite locally resonant multiple-degrees-of-freedom (MDoFs) metafoundations were designed and developed; and resonator parameters together with bistable columns were optimized by means of an improved time domain multiobjective optimization procedure. Also, the stochastic nature of the seismic input was taken into account. Therefore, it is proposed: (i) a linear metafoundation endowed with one/two layers and multiple cells, linear springs, and linear viscous dampers; and (ii) a relevant foundation equipped with columns operating in an elastic buckled state. With this arrangement, additional flexibility and dissipation against horizontal seismic loadings are activated. It was shown in both cases, how each metafoundation can be successfully optimized via a sensitivity-based parameter technique. Thus, the performance of the optimized metafoundations was assessed by means of time history analyses; and results were compared with a storage tank endowed with both rigid foundation solutions. Finally, single cells were analysed in the frequency domain while finite lattices and periodic metafoundations in the linear and bistable regime were characterized by means of dispersion relationships.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Background and motivations
To reveal the fascinating wave dynamics capabilities of nonlinear metamaterials, recent years have witnessed many investigations on the topic (Patil and Matlack 2022). Owing to nonlinearity, nonlinear metamaterials are sensitive to wave amplitudes; and an increased nonlinearity entails different wave phenomena such as amplitude-dependent dispersion properties (Hussein and Khajehtourian 2018; Narisetti et al. 2010; Ganesh and Gonella 2013), nonreciprocity (Nesterenko et al. 2005), solitons (Remoissenet 2013), and supratransmission (Geniet and Leon 2002; Leon 2003). Over the last few years, bistability has attracted great attention due to its intricate but advantageous dynamics. Herein, bistability refers to a system that exhibits two stable equilibrium states which can be observed in several systems. In mechanical systems, buckled columns or beams provide a neat example of bistable systems (Cazottes et al. 2009; Camescasse et al. 2013); thus, when a bistable system is excited, two types of motion are possible: the first one oscillates around one of the stable points, i.e. the intrawell motion; the second one, instead, oscillates between or around two stable points, the so-called interwell motion (Wang and Harne 2017). In the latter case, the fast dynamics from one stable point to the other one, i.e. the snap-through buckling, entails the so-called negative stiffness effect, where motion is not restricted but assisted. Thus, the advantages of the snap-through motion have been widely adopted in various fields, such as energy harvesters (Cohen and Bucher 2014; Li and Kong 2021), nonlinear energy sinks and MEMS (Qiu et al. 2018; Sulfridge et al. 2004). Additional key features related to the bistable mechanism are the harmonic energy diffusion which simply corresponds to the distribution of input energy to multiple harmonics (Wang and Harne 2017). Owing to the dispersed energy, the entire response amplitude reduces as the wave propagates prompting self-adaptivity. In particular, self-adaptivity is a feature that entails a different band structure for each cell (Liu et al. 2020; Liu et al. 2022).
One of the complex features of bistable systems is the stochastic resonance which happens due to snap-through dynamics caused by both low-level noise and low-level periodic excitations. Notwithstanding these motion features, they are very beneficial for energy harvesting systems (Zheng et al. 2014; Zhao et al. 2020). Conversely, both low-level noise and periodic excitation may individually be insufficient to trigger interwell dynamics which favours high speed and dissipation due to damping. Along these lines, also a chaotic response is characterized by wide and rich dynamics. In this respect, although earthquake records are characterized by significant randomness, the chaotic response of a system subjected to an earthquake is not a major concern; in fact, hysteretic damping readily cancels out chaotic phenomena.
Since periodic systems can be used as acoustic resonant metamaterials (AMs), due to their local resonance capabilities, they can exhibit subwavelength band gaps and negative material properties (Li et al. 2004; Carta et al. 2016). More precisely, the combination of periodicity and local resonances can generate low-frequency bandgaps and ultra-low band wave attenuations well below Bragg scattering bandgaps (Ma and Sheng 2016). In such instances, nonlinear acoustic metamaterials (NAMs) represent the necessary extension of the primary work on linear AMs. Based on the source of nonlinearity, NAMs can be divided into two classes: i) NAMs where nonlinearities are located in primary cells (Zhou et al. 2018; Zivieri et al. 2019); and ii) NAMs where nonlinearities are linked to resonators (Manimala and Sun 2016; Fang et al. 2017). These studies clearly show that nonlinearities affect band gap characteristics that, if properly designed, can be expanded. The bistability phenomenon was also utilized in metamaterials. In particular, some studies considered energy dissipation by means of snap-back motion (Sun et al. 2019) whilst Xia et. al. (2019) studied the band-gap behaviour of nonlinear metamaterial with bistable attachments. Their findings showed that bistable attachments considerably improve the vibration mitigation properties of systems.
The use of locally resonant AMs as seismic isolators, the so-called locally resonant metafoundations (LRMs), in structural media is a brand new topic, still under development. In particular, LRMs aim to attenuate low‐frequency seismic waves and protect superstructures by means of unit cells endowed with resonators much smaller than the seismic wavelengths present in earthquake-prone regions. A comprehensive review of metamaterials for seismic applications can be found in Mu et. al. (2020). Among other issues, one of the most pressing problems of LRMs is the excessive size of the metafoundation, needed to achieve an effective attenuation.
The pioneering works on LRMs devoted to the seismic protection of process plant components showed promising results (La Salandra et al. 2017; Cheng and Shi 2018; Basone et al. 2019). Both the antiresonance phenomena and damping in resonators prevented significant vibrations and related damages in storage tanks. Then, improved performances were achieved by the inclusion of negative stiffness elements to lower the resonant frequency of resonators (Wenzel et al. 2020). Another improvement relied on the utilization of resonator bearings with significant hysteresis, such as wire ropes, to achieve high dissipative capabilities (Bursi et al. 2021).
Along this main vein, novel LRMs that utilize bistable columns are proposed and investigated herein. Although bistability concepts were considered earlier for seismic isolation (Plaut et al. 2008; Jeffers et al. 2008), the protection focussed on the vertical component of seismic waves. In this respect, metafoundations have also been profitably proposed to mitigate the vertical motion of storage tanks and small modular reactors (Franchini et. al. 2020; Guner et al. 2022). Conversely, the concept of combining bistability with LRMs devoted to the seismic isolation of process components against the horizontal component of waves is largely unexplored.
Another issue to be considered is redundancy. In fact, and in agreement with NUREG/CR-7253 (U.S.NRC, 2019), a seismic isolation system is not redundant because it uniquely connects the superstructure to the foundation. Though no specific attention will be given to the issue of redundancy in metafoundations, it could be easily taken into account during columns design in X and Y directions. In particular, only half of the columns can be considered to resist earthquake lateral forces coming from one horizontal direction or the other. Therefore, if a failure occurs in a specific direction (X or Y), the columns that are devoted to the orthogonal direction are still available; though they cannot fully resist lateral forces in the direction of failed columns, they can still sustain the weight of the superstructure. Moreover, also the presence of the resonators could increase redundancy; in fact, their size and strength naturally represent a second barrier and can prevent the full collapse of the metafoundation under gravity loadings.
Finally, it must be underlined the actual limitation of the European standard on anti-seismic devices (EN15129 2018), that does not allow for a softening behaviour of their force–displacement relationships in the loading phase up to the maximum design displacement or force.
1.2 Scope and core contributions
In sum, the objective of the paper is to leverage the specific features of bistable systems such as harmonic energy diffusion and adaptive bandgaps with the isolation/dissipation properties of locally resonant metafoundations (LRMs). Along these veins, the main objectives are pursued herein: i) optimization of the proposed bistable LRM, simply called BM, in the time domain, and investigation of its performance by means of the dissipated energy of the LRM; ii) use of harmonic energy diffusion, snap-through motions and other phenomena to increase damping entailed by the primary cell; iii) determination of the effect of resonators on characteristics of bistable single cells, finite lattices and periodic systems.
Along these lines, the LRMs were designed to remain undamaged at an active seismic site at the safe shutdown earthquake (SSE) (ASCE/SEI 2016) located in Priolo Gargallo, Sicily, Italy. The optimization of the drift angle of the snap-through column buckling of the main cell, frequency and damping parameters of resonators was conducted in the time domain by means of nonlinear time-history analyses (THA) based on properly selected natural seismic records. The proposed LRMs were then optimized according to the dissipated energy of the LRM with respect to the dissipated energy of the whole structure. Both to consider uncertainty and to reduce the computational effort, a surrogate response model similar to the one proposed by Phan et. al. (2020) was used. More specifically, the central composite design (CCD) method was adopted in conjunction with the Kriging approximation to tune a quadratic low-fidelity response model of the coupled system. The variation of ground motions was also included by considering both design bases earthquakes (DBE) and safe shutdown earthquakes (SSE) in the optimization stage. Eventually, the optimized LRMs without and with bistable elements were investigated and compared in terms of seismic input energy transfer and dissipated energy.
Then, additional investigations on the bistable LRM cell were conducted on a single cell, a finite lattice and a periodic system. Initial disturbances and sinusoidal-driven boundary input conditions were supplied to the single cell and dynamical properties were investigated through energy flow and velocity response. The periodic system, instead, was investigated both numerically and analytically to define the dispersion relationships.
The paper is organized as follows. Initially, details about the seismic design and modeling of the components of the coupled foundation-tank system are provided in Sect. 2. The section also provides detailed information about seismic spectra and records. For the sake of comparison, also LRMs with linear columns, shortly named LMs were designed. Section 3 explains the optimization procedure adopted in the time domain. More precisely, the optimization parameters, the details of the low-fidelity model and the optimal design parameters are provided. Section 4, instead, presents time history analysis (THA) results for the proposed BM. The comparison between LMs and BMs, i.e. for one and two layers, is conducted in terms of energy transferred to the superstructure. Section 5 deals with the dynamics of a single, finite lattice and periodic system that consists of a BM unit cell. Subsection 5.1 investigates the characteristic of bistability with and without a resonator. Subsection 5.2 extends the work to finite and periodic systems and investigates both wave dispersion and energy propagation properties. Finally, conclusions and future developments are presented in Sect. 6.
2 Description of the coupled system and design of the bistable metafoundations
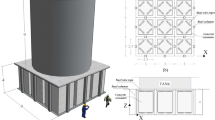
In total, 4 different LRMs were designed with single and double layer configurations as well as endowed with linear and bistable columns. For clarity, the single-layer and the double-layer LRMs are identified with the prefix 1L- and 2L-, respectively. Along this line, the structural details of the 2L-BM are depicted in Fig. 1. Each metafoundation cell consists of two parts: (i) the primary cell is composed of four flexible slender steel columns and two concrete slabs; (ii) the concrete resonator that is connected to the slab with steel wire ropes. The relevant design followed both Eurocode 1993 Part 1-1 (2005) and Eurocode 1998 Part 1 (2004). The construction site was selected in Priolo Gargallo in Sicily, Italy, and is characterized by soil type B with peak ground acceleration (PGA) equal to 0.56 g for a return period of 2475 years. Each layer has a height H = 1 m and contains 9 LRM unit cells in a 3 by 3 layout. The superstructure is a slender fuel unanchored storage tank that is a part of an existing plant (La Salandra et al. 2017; Carta et al. 2016). To simplify computations, the base uplift of the tank was not considered in the study. The resonators were assumed to be connected to the concrete slab by wire ropes which allow motion in all three main directions. Moreover, wire ropes can provide high and adjustable damping values as required by the optimization process.
In this study, due to the complex nature of the bistable mechanism, the connection between resonator and primary cell was modelled by means of a linear spring and a damper system, i.e. the wire rope was simulated to be in the linear range. In fact, favourable performances can also be achieved with a linearized model of wire ropes (Bursi et al. 2021; Basone et al. 2021).
2.1 Bistable column design
To introduce the bistability effect into the LRMs, pre-buckled steel columns were conceived. In particular, columns were designed to elastically buckle due to gravity loading along their weak axis. The weight of the tank was assumed to be constant at its maximum capacity for the safe life limit state. The foundation is symmetric in the x and y axes; as a result, half of the columns are designed to buckle on the x-axis while the rest buckle on the y-axis. One of the critical points of the buckled columns is that once the buckling load is reached, the stable region where the column stiffness in the lateral direction is positive is comparatively small and sensitive to axial loading. To overcome this issue, the strong axis of the buckled columns was used as a restraining mechanism for lateral displacements of buckled columns. However, it is not favourable to add the strong axis stiffness of columns to the stiffness of the snap-through region. Consequently, the column ends are designed such that they allow unrestrained motion in the strong axis up to an amount of allowed snap-through buckling distance. In other words, between two stable points of weak axis buckled columns, there is no additional stiffness induced from the columns in the strong axis. However, in the case of a significant demand, the strong axis of the columns contributes to the lateral resistance and prevents instability.
Due to the coupled mechanism of buckling where the lateral stiffness is bound with axial load, the design of the columns becomes a challenging problem. In the design process, two main points were considered. In the weak axis, the columns should be weak enough and slender, with a slenderness ratio \({\raise0.7ex\hbox{${L_{e} }$} \!\mathord{\left/ {\vphantom {{L_{e} } r}}\right.\kern-0pt} \!\lower0.7ex\hbox{$r$}} \ge 200,\) to elastically buckle due to the superstructure load; but they should exhibit a high moment capacity, in order to remain elastic after buckling. Furthermore, in the strong axis, they must resist lateral loads. The selection of the steel column section was governed by weak axis limitations. In this respect, two parameters are important: the section width b and the flange thickness \(t_{f}\); to minimize the buckling load, the weak axis moment of inertia must be reduced and depends on b3 and \(t_{f}\); to maximize the moment capacity, b2 and \(t_{f}\) should be increased. As the effect of b is more prominent on the buckling load, \(t_{f}\) should increase to improve the moment capacity. Therefore, \(t_{f}\) is maximized, and the favourable section is the rectangular one.
Preliminary analyses carried out with rectangular sections, it has been concluded that the allowed post-buckled drift angle \(\alpha_{s}\) of the column, significantly influences the system response. The \(\alpha_{s}\) value can be also defined as the drift angle of snap-through buckling range in both directions (\({ - }\alpha_{s}\), \(\alpha_{s}\)) or the drift angle that corresponds to half of the distance between stable points and reads,
where \(u^{pb}\) represents the post-buckled displacement and H defines the story height. This angle can be adjusted during the design stage by limiting the drift capability of the column using the strong axis allowance of the adjacent columns.
The upper boundary for \(\alpha_{s}\) is determined by the column elastic moment capacity. Therefore, it is advantageous to achieve maximum \(\alpha_{s}\) values that do not entail column plastic deformation. With the pre-buckling condition, the column design becomes an optimization problem where the objective reads \(\alpha_{S} = \alpha_{S}^{max}\) with the following constraints: i) the critical Euler buckling load Pb must be smaller than the superstructure load Pss; ii) the column must remain elastic after buckling. For a rectangular section, with Pss = Pb and the moment due to post-buckling deformation equal to the moment capacity, \(\alpha_{S}^{max}\) reads,
where L, fy, E represent, length, yield strength, and elastic modulus of the column, respectively. From Eq. (2), one can observe that the section height h is not present for the weak axis; conversely in the strong axis, h appears with a cubic power in the moment of inertia. Therefore, the height and width of the columns can be separately designed for the weak and strong axis directions. In sum, the columns can buckle in the weak direction under the superstructure load, but will not plastify under the ground motion design.
To present the benefits of the BM, as anticipated at the beginning of Sect. 2, also LMs were designed and analyzed. The corresponding columns were designed to remain elastic and undamaged for the considered seismic design level; therefore, the hollow square steel sections were considered with a S355 steel material. The dimensions of the designed cross sections are gathered in Table 1.
2.2 Seismic input
The optimization of the BM was conducted on the time domain using 16 natural seismic records selected from both Italian and European databases. These seismic records were selected and normalized according to the uniform hazard spectrum (UHS) relevant to Priolo Gargallo in Sicily, Italy, with 5% and 2% probability of exceedance in 50 years, corresponding to design bases earthquakes (DBE) and safe shutdown earthquakes (SSE), respectively (ASCE/SEI, 2016). The selection of seismic records was carried out as follows: let’s consider \({\varvec{s}}_{0}\) the target spectrum vector, i.e. the UHS; and let’s evaluate \({\mathbf{S}}\), i.e., the spectra matrix of the \({\varvec{n}}_{{\varvec{a}}}\) selected seismic records; a vector of \({\varvec{n}}_{{\varvec{a}}}\) selection coefficients, \({{\varvec{\upbeta}}}_{{\varvec{s}}}\), can be defined where each element can take a binary value of 1 or 0 and the sum of these elements must equal \({\varvec{n}}_{{\varvec{s}}}\), i.e. the predetermined number of seismic records to be selected. Therefore, the optimization problem reads: \({\text{min}}\left( {{\mathbf{S}}/{\varvec{n}}_{{\varvec{s}}} - {\varvec{s}}_{0}^{2} } \right)\), which can be solved for \({{\varvec{\upbeta}}}_{{\varvec{s}}}\). The selection was performed with all possible combinations of the \({\varvec{n}}_{{\varvec{s}}}\) accelerograms among a set of \({\varvec{n}}_{{\varvec{a}}}\) records; and the dispersion of the records around the mean spectrum was taken into account. Therefore, the selection followed the principle of minimizing the error between both the mean spectrum and the mean spectrum plus one standard deviation of the selected records \({\varvec{s}}_{0}\) in a least-square sense within the target period range. Furthermore, the analysis takes into account the uncertainties in location, magnitude and fault mechanism, while the record-to-record variability, expressed by the distribution of the spectral ordinates, is transferred to the fragility functions.
In sum, for each DBE and SSE limit state, eight seismic records were selected to assess the performance of the proposed LRMs, respectively. The selected seismic records are collected in Table 2 whilst the acceleration spectra, their mean, and mean plus one standard variation are plotted in Fig. 2. Further details about the selection of a seismic record sample size can be found in the work of Phan et al. (2020).
2.3 System modeling
To simplify the resonator optimization and dynamic analysis of the coupled system, a condensed mass system shown in Fig. 3a is considered. Since resonator masses and column stiffnesses are equal, the dynamic condensation is exact. Along the same vein, the simplified hydrodynamic response model suggested by Malhotra et al. (2000), that entails equivalent mechanical models for the correct base shear on the LRM due to impulsive and convective masses is implemented. It is worthwhile to underline that the effects of the very low-frequency motion of the convective mass, about 0.3 Hz, need to be reduced with other cheap/convenient means, e.g. baffles, etc. To reproduce internal friction and material level damping, 3% mass proportional damping ratio is considered. Thus, the mechanical properties of the superstructure are collected in Table 3, where {\(m_{i}\), \(c_{i}\) and \(k_{i}\)} and {\(m_{c}\), \(c_{c}\), \(k_{c}\)} represent mass, stiffness and damping coefficients of the impulsive and convective mass of the superstructure, respectively.
The dynamics of the BM can be described with the following system of equations of motion,
where M, C, and KL represent mass, damping, and linear stiffness matrices, respectively; KNL is the nonlinear stiffness component of the EOMs which is a nonlinear function of vector u(t). The vector u(t) indicates the displacement vector, where single and double dots represent single and double derivatives with respect to time, respectively. Additionally, \({\mathbf{F}}_{{\mathbf{E}}} \left( t \right)\) represents the external force vector.
To accurately analyse the bistable mechanism, the designed columns were modelled by the FE ABAQUS software (Smith 2009). Each column was modeled with shell elements and the static-Riks method was utilized to compute the post-buckling regime. Consequently, the force-deformation relationship for each column was determined as depicted in Fig. 4b.
The connection between columns and slabs was realized to be fixed. To visualize the bistable mechanism, the single DoF force-deformation relationship of each column can be represented by means of a Duffing equation,
where \(P_{1}\) and \(P_{3}\) define the first and third-order stiffness terms, respectively. According to the sign of these terms, the Duffing oscillator can simulate three different mechanisms: \(P_{1} > 0\), \(P_{3} > 0\) refers to a monostable hardening Duffing oscillator; \(P_{1} > 0\), \(P_{3} < 0\) refers to a monostable softening Duffing oscillator; and \(P_{1} < 0\), \(P_{3} > 0\) refers to a bistable Duffing oscillator. The force deformation relationship with stored potential energy on the displacement position for a representative Duffing oscillator is depicted in Fig. 4a. The shape of the potential relation is named double-well potential where the bottom of the wells represents stable points. Between the two stable points, the effective stiffness is negative and therefore, the system assists the motion of the mass rather than resisting to it.
To capture the main bistable phenomena, the 3rd order Duffing Eq. (4.b) was fit to the FE results as illustrated in Fig. 4b for the 1L-BM case of Table 1. Thus, for the single 360 × 16 mm HSS column, the Duffing’s model parameters read \(P_{1} = - 1.02{ }e + 4{ }kN/m\) and \(P_{3} = 5.08{ }e + 6{ }kN/m^{3}\), respectively. Hence both the stable points and the post-buckled drift angle αs read,
3 Linear and bistable metafoundation optimization
To achieve the best performance from each BM, an optimization process on some mechanical parameters is deemed necessary. As mentioned in Sect. 2, the connection of the resonators to the primary cell is realized by means of linear springs and dashpots can be subject to optimization of the LRMs. For each resonator mass, in view of efficiency, the largest mass compatible with the unit cell dimensions is taken (Reggio and De Angelis 2015; Basone et al 2019).
In addition to the resonator variables, the allowed snap-through buckling range [0,\( \alpha_{S}^{max}\)] is also considered as an optimization parameter, where \(\alpha_{S}^{max}\) is computed from the elastic limits of the column steel section. In fact, low \(\alpha_{s}\) values trigger more snap-through motions, and this behaviour entails wanted energy dissipation.
The performance index (PI) adopted in the optimization of the BM is the energy dissipation index (EDI, Basone et al. (2019),
In particular, the EDI is defined as the ratio of dissipated energy by the LRM with respect to the whole structure. Since all elements of the metastructure are elastic, and the bistable system exhibits no hysteretic dissipation, the energy can only be dissipated through viscous damping. Hence, the damping energy can be calculated as:
where \(c_{n}\) and \(v_{n}\) represent the damping coefficient and velocity of nth DoF, respectively. For the single-layer LRMs, after dynamic condensation four DoFs are involved: the primary cell, the resonator, the impulsive and the convective mass. Note that \(E_{d}^{con}\) is negligible wrt \(E_{d}^{imp}\).The dissipated energy by each DoF is computed for the whole seismic record duration. Hence, the optimal \(\alpha_{s}\) and optimum resonator variables, \(\zeta_{r}^{opt}\) and \(\omega_{r}^{opt}\), can be defined through the following relationship,
where X is the parameter vector of the optimization problem. The optimization procedure was also conducted for the LMs in which only 2 variables \(\zeta_{r}\) and \(\omega_{r}\) were involved; therefore,
3.1 Central composite design method
As mentioned above, the optimization variables \(\zeta_{r}\), \(\omega_{r}\) of the resonators and \(\alpha_{s}\) of columns subjected to seismic records with different PGA values, can be identified as random variables that can significantly influence the seismic vulnerability of unanchored tanks. Therefore, the CCD method was used to lower the computational cost associated with the initial parameter selection. It simulates an experimental design, based on the response surface methodology, where a second-order (quadratic) model for the response variable is built without needing to use a complete three-level factorial experiment (Gilmour and Trinca 2012). The CCD is composed of three types of design points: corner points or factorial points in the two-level designs (± 1); star points at \(\pm \alpha_{CCD}\) which are used for quadratic design; and center points. Since in pure numerical simulations we cannot achieve additional information on variance, only one center point was evaluated. The pictorial representation of the CCD points for the 2-factor CCD (\(\alpha_{CCD} = 1.414\)) relevant to the LMs and to the 3-factor CCD (\(\alpha_{CCD} = 1.682\)) employed for the BMs are given in Fig. 5. Other details of the procedure can be found in Phan et al. (2020).
Once the boundaries and means values of variables are defined with a uniform distribution, see Table 4, it is possible to associate both the values of coded and uncoded variables as collected in Table 5. The coded and uncoded variables are given in Table 6 for the LM.
3.2 The kriging model
Nonlinear time history analyses on the coupled LM and BM models depicted in Fig. 1 are carried out using the set of sixteen ground motion records of Table 2 for each sample indicated by the CCD. Then, the EDI value in agreement with Eq. (6), and its median were evaluated. The median values, indeed, represent the 50 percent probability of occurrence which is robust against outliers, especially in earthquake analyses. Thus, a low-fidelity model was fitted by means of a Kriging model,
where \(x_{ui}\) and β’s are the design variables and regression coefficients, respectively. The \(x_{ui} \) denotes the level of the ith factor (i = 1, 2, …, k) in the uth run (u = 1, 2, …, n) of the experiment. Basically, the Kriging method is an approximation method that can predict unknown values of a random process based on a covariance or variogram model derived from data (Van Beers and Kleijnen 2003). Given the variable vector \({\mathbf{x}}\), the Kriging model is divided into two parts: the global regression model and the stochastic process,
where \({\mathbf{Y}}\left( {\mathbf{x}} \right)\) is the function to be fitted, \(f\left( {\mathbf{x}} \right)\) is the polynomial of the input variables, β is the unknown regression coefficient vector, and Z(\({\varvec{x}}\)) is a zero-mean stationary Gaussian process with a covariance function,
where \(\sigma^{2}\) is the process variance. The spatial kernel function \(R\left( \cdot \right)\) controls the smoothness of the resulting Kriging model and the influence of nearby points; it describes the correlation between two sample points in the output conditioned by the hyperparameter θ. Since the behavior of the correlation in each dimension may differ, an anisotropic ellipsoidal correlation function \(R\left( \cdot \right)\) was utilized (Williams and Rasmussen 2006); it can be calculated as follows,
In this particular case, the commonly used Mat´ern kernel with a shape parameter equal to ν = 5/2 was used (Genton 2001). The relevant expression reads,
3.3 Optimization results
The performance of both the CCD and the Kriging metamodel were improved by means of an iterative procedure. Given the initial CCD points for each case of Table 1, Eq. (10) was used to locate the maximum of the median EDI (Eq. (6)). The corresponding sampling point was estimated and added to the CCD points; the Kriging metamodel was updated and the procedure was repeated until the optimum sampling did not vary more than the predetermined tolerance. The fitting of the Kriging metamodel was carried out with UQLab (Lataniotis et al. 2015) and the unknown hyperparameter vector θ was estimated using the K-Fold cross-validation method and optimized using a hybrid genetic algorithm.
The outcome of the optimization procedure is gathered in Table 7; and the attentive reader can appreciate for each case, the EDI median values provided by the metamodel and THAs; relative errors are limited to 1.2%. Moreover, one can observe that the optimized resonator parameters of bistable metafoundations differ with respect to the linear counterparts.
To appreciate the optimization surfaces, the outcomes of the Kriging for 2L LRMs are depicted in Fig. 6. For the BM case, the results correspond to \(\alpha_{s} = 2.7^\circ\) in agreement with Table 7. The results clearly show that the EDI values of the BM case easily exceed 90% and that the variance effect on the optimal values of \(\omega_{res}\) and \(\zeta_{res}\) was less marked with respect to the LM case.
4 Time history analyses
To validate the optimized solutions defined in Sect. 3, nonlinear THAs were carried out; therefore, Eqs. (3, 4.a, 4.b) were integrated in time by means of a standard semi-implicit Runge–Kutta method. For completeness, both the earthquakes listed in Table 2 associated with the DBE and the SSE events were considered; moreover, the resonators were characterized by the optimized mechanical parameters collected in Table 7. In view of completeness, in addition to the EDI defined in Eq. (6), we quantify the seismic input energy provided to the superstructure \(E_{SS}\). \(E_{SS}\) can be computed as follows,
where, \(m\) and \(v\left( t \right)\) define both mass and velocity while subscripts i and c identify impulsive and convective masses, respectively; \(a_{g} \left( t \right),\) instead, defines the ground acceleration at time t whilst τ defines the generic duration of each seismic record. Clearly, an efficient performance of the metafoundation limits the amount of \(E_{SS}\).
Figure 7 depicts the EDI values for each seismic record of Table 2 both for the 1L and 2L LRMs, respectively, with their median values. In both cases, the BM entails more than 10 per cent increased median EDI values whilst keeping EDI value above 70 per cent for all events. Clearly, there are a couple of SSE events where the 1L LM does not exhibit a favourable behaviour. Conversely, the 2L BM exhibit a favourable median EDI for both DBE and SSE events. Consequently, the bistable snap-through motions in the metafoundations cause an increased damping and prevent damage to the superstructure.
EDI results for each seismic record collected in Table 2, where the solid and dashed lines represent the median for SSE and DBE events, respectively: a 1L LRMs case; b 2L LRMs case
The advantages of the proposed bistable metastructures can be clearly appreciated through the estimate of \(E_{SS}\). The results are depicted in Fig. 8 for both DBE and SSE events, respectively. In the case of a single layer, see Fig. 8a and c, given the large amounts of \(E_{SS}\), the BM underperforms with respect to the LM in almost all cases. Though the 1L-BM is characterized by a favourable EDI, the energy dissipated in the BM is not enough. The 2L-BM instead, entails a different isolation effect due to the presence of 2 layers of bistable columns. More precisely, in the case of DBE events, the 2L-BM transfers only 6.1% of energy to the superstructure, in terms of median, compared to the 2L-LM case. With regard to the SSE events, see Fig. 8d, reductions of about 8.9% of \(E_{SS}\) in terms of median are achieved. Clearly, there are cases, the 1st and 3rd SSE event, where the 2L-BM underperformed with the high \(E_{SS}\). The seismic records and their frequency content causes the 2L-BM to work outside of the snap-through region delimited by \(\alpha_{s}\). Therefore, the strong axis of the columns significantly contributes to the response, with an increase in stiffness and high energy transfer \(E_{SS}\).
Plots of the energy \(E_{SS} \) transferred to the superstructure for the seismic records of Table 2. Continuous lines define median values: a DBE-1L case; b DBE-2L case; c SSE-1L case; d SSE-2L case
The main slabs time history displacement responses of the 2L-BM in terms of relative drift angle are depicted in Fig. 9 for the GM-1 and the GM-5 SSE seismic records -1992 Erzincan and 2009 L'Aquila events of Table 2-.The first event entails the worst case for the 2L-BM and 2L-LM performs better. In particular, from Fig. 9a, one can argue that the first layer switches from the starting position to the other stable point and then, both layers move in a synchronized manner. Therefore, both layers act together rather than creating asymmetric modes. In particular, the GM-1 record excites low-frequency modes where both layers move together and the energy transfer to the superstructure increases. The opposite behaviour can be observed in Fig. 9b, where both layers vibrate and even columns buckle from one stable point to the other one, simultaneously, in opposite directions. This type of motion shows that the movement of the first layer slab governs and, simultaneously, excites the connected resonators with significant energy dissipation.
5 Analysis of the uncoupled metafoundation
The performance of the finite optimized metafoundations depicted in Figs. 1 and 3 both with one and two layers, and endowed with nonlinear columns generally provided a favourable seismic performance of the coupled system discussed in Sect. 4. Therefore, given the potential vibration attenuation capabilities offered by periodic bistable metamaterials, it is worthy to examine both the dynamic properties of the single cell and the relevant uncoupled periodic metafoundation depicted in Fig. 3b and c. Therefore, the optimized 1L-BM cell is selected and analyzed; herein, the investigation is carried out both numerically and analytically, where the columns were modeled using the Duffing approximation of (4.b).
5.1 Single-cell dynamics
To investigate the effect of resonator on the response of a bistable system, an undamped BM unit cell with and without resonator was investigated through an initial displacement imposed to the main cell. Due to the bistable nonlinearity, the initial displacement amplitudes were chosen to be: \(A_{0} = 0.01 m\), \(A_{0} = 0.02 m\), and \(A_{0} = 0.05 m\) respectively, to entail intrawell, low amplitude interwell and high amplitude interwell motions. It must be noted that the input is given relative to the stable state and in the same direction. Successively, fast fourier transforms (FFT) were conducted on the free vibration responses.
The FFT results and the corresponding phase portraits are depicted in Fig. 10. The phase portrait of the first case, Fig. 10b, proves the intrawell motion, where the trajectory is kept around one of the wells. The frequency response function shows the harmonic energy diffusion property. The circular frequency of the main cell is at about \(\omega_{1} = 58 rad/s\) and resonance peaks can be observed at frequencies \(n\omega_{1}\), \(n = 1,2,3, \ldots\). When the resonator is considered, the diffusion effect also allocates the antiresonances due to the resonator at various frequencies. Differently from the case without resonator, resonant peaks do not occur at integer multiples. Moreover, a slight increase of the main cell frequency is observed, i.e. \(\omega_{1} = 60 rad/s\).
FFT results for the free vibrations of a bistable unit cell with and without resonator; a, b FFT and phase portrait for \(A_{0} = 0.01m\) (intrawell motions); c, d for \(A_{0} = 0.02m\) (low amplitude interwell motions); e, f for \(A_{0} = 0.05m\) (high amplitude interwell motions); g, h for \(A_{0} = - 0.05m\) (high amplitude intrawell motions)
In the case of the low amplitude interwell case, see Fig. 10c and d, the harmonic diffusion is observed at frequencies \(n\omega_{1} ,n = 1,3,5, \ldots\) with a significant stiffness reduction, i.e. \(\omega_{1} = 23 rad/s\). When the resonator is taken into account, the aperiodic motion is significant and the peak response is reduced. Moreover, the phase portrait indicates that the system response is chaotic in some regions and this can be verified through the evaluation of the maximum Lyapunov exponents.
When higher initial amplitude are considered, aperiodic motions disappear and an increase on the main cell stiffness is observed with \(\omega_{1} = 62 rad/s\). In contrast to the intrawell case, the addition of the resonators reduces the stiffness of the main cell. The phase portrait shows a motion similar to that of a linear system where the oscillation occur around stable points with an elliptical orbit. These results explain the performance loss observed in the SSE events, see Fig. 8d where the BM performance drastically decreases; in particular, the input seismic energy entailed high amplitude interwell motions and therefore, the whole stiffness of the system increased with a high energy transfer.
To investigate the interaction between input direction and bucked state, \(A_{0} = - 0.05 m\) was also considered, i.e. an input direction opposite to the buckled state and relevant results are depicted in both Fig. 10g and h. The results clearly show a different frequency content of the free vibration wrt to those depicted in Fig. 10e and f; moreover, the favourable dynamic effect of bistability is confirmed.
5.2 Finite Lattice and Periodic System Behaviour
To further analyse the energy attenuation properties of the bistable mechanism, both a finite lattice and a periodic system composed of BM cells endowed with resonators are considered; see, in this respect, Fig. 3b and c. In the first case, a sinusoidal driven boundary excitation with different frequencies and amplitude was applied to one end of the chain. To prevent any shock-correlated error due to a sudden change from zero velocity and displacement, the excitation was chosen to fit a smooth and slowly increasing profile. In particular, it reads,
where \(A_{0}\) and \(\omega_{0}\) define the input amplitude and frequency, respectively. \({\Lambda }\) is a modulating smooth multiplier defined as,
where \(t_{s}\) defines the smooth starting duration. The smooth starting profile which is very helpful in reaching a steady-state dynamics is depicted in Fig. 11.
Initially, the finite chain composed of 100 cells is excited at one end with a driven boundary input Eq. (16) with \(A_{0} = 0.01m\), for \(t_{d} = 1 sec\) and \(t_{d} = 20 sec\), respectively, with circular frequencies considered in the range 0—60 rad/sec. The energy \(E_{n}^{t}\) that is transferred to the next cell is calculated as follows,
where \(E_{n}^{s}\) and \(E_{n}^{d}\) represent the strain and damping energy flow from the (n-1)th cell to the (n)th cell. To perform computations, the resonator frequency and the damping values are assumed to be 11 rad/s and 25%, respectively, with the optimized 1L-BM.
For \(t_{d} = 1 sec\), the \(E_{n}^{T} /E_{1}^{T}\) ratio in per cent is plotted in Fig. 12a; for such a short \(t_{d} , \) less than 5 cells are sufficient to prevent the energy transfer in the whole frequency range examined. Figure 12b instead, depicts the case \(t_{d} = 20 sec\); more precisely, except for the 3—8 rad/s range, less than 10 cells are sufficient to attenuate the 90 per cent of \(E_{1}^{T}\). For the sake of clarity, these results are also compared with a finite lattice consisting of linear unit cells of 1L-LM; and the required number of cells to dissipate 90% of \(E_{1}^{T}\)- corresponding to the red lines of Fig. 12, are plotted in Fig. 13. The results prove the efficacy of the bistable finite chain against its linear counterpart at both low and high input time durations. In the case of short duration pulses with low frequencies, the bistable chain prevents the wave propagation by a limited number of cells. If the excitation continues, since the transients will decay, the energy slowly flows.
Energy flow \(E_{n}^{t}\) for a finite lattice bistable chain as a function of \(\omega_{0}\) and cell number: a time duration of Eq. (18) \(t_{d} = 1 sec\), b \(t_{d} = 20 sec\)
If one uses the same finite chain, the transferred energy to a unit cell in terms of time can also be investigated for \(\omega_{0} = 5 rad/s\). In this case, Fig. 13c shows how the energy reaches the 5th cell, i.e. \(E_{5}^{T}\) vs. time. Clearly, the bistable finite lattice carries less energy wrt the linear finite lattice.
To further characterize the dynamic properties of the periodic bistable chain, its wave propagation and dispersion features are explored by means of analytical and numerical tools. To evaluate the dispersion properties, the system of EOMs (3) with the condition (4.b) is solved using the harmonic balance linearization method (HBM) (Wenzel et al. 2020). Therefore, the HBM coupled to the Floquet-Block 1D boundary conditions, see Appendix 1, entails an approximate solution for the dispersion relationship which depends on the nonlinearity level. Analytical results are depicted in Fig. 14. The dispersion effects can be clearly appreciated from the amount of κimag depicted in Fig. 14a.
To verify the analytical results, a numerical approach was also considered. A periodic chain of bistable elements with 300 cells was exited using a driven boundary. The system was forced for a total of 60 s with \(t_{s} = 20 sec\) of smooth profile, where the first 40 s of response were neglected due to the transient response. To prevent reflection from the undriven end of the chain, perfect match layers (PMLs) were applied at both ends. Therefore, a total of 1000 cells were utilized (Zhou et al. 2018), de facto a system with an infinite number of unit cells. After the simulation of the system at any wavenumber, one can determine the 2D Fourier transform of data in both frequency and wavenumber domains; and the real part of the wavenumber κreal was extracted from the 2D FFT of the time-displacement results. Some points extracted from the procedure are shown in Fig. 14b. Nonetheless, both the self-adaptivity and the strong wave attenuation effects of the resonators prevent the extraction of points in all branches. For the sake of clarity, the 2D FFT decomposition for the intrawell motion is depicted in Fig. 15. The FFT amplitude peaks show the wave propagation. In the low-frequency range, strong long-wavelength wave propagation is observed. The cut-off frequency of the bandgap region can also be clearly noted. At higher frequencies, the wave propagation is weak.
6 Conclusions and future studies
With the aim of improving the performance of locally resonant metafoundations, bistability-based nonlinearities were introduced in the primary cells. The bistability was governed by elastically buckled steel columns, that can freely snap-through from one stable point to another. Along this vein, an optimization framework based on the Central Composite Design and Kriging is proposed and utilized to optimize both resonator linear spring and damper properties and allowed bistable column snap-through distance.
Time history analyses conducted on optimized bistable metafoundations (BMs) highlighted the favourable behaviour of these isolation systems in terms of reduction of the total seismic energy input transferred to the superstructure. Clearly, the nonlinearity that characterizes the bistable mechanism significantly reduces the total structure stiffness and result in more compact locally resonant metafoundations wrt the linear metafoundations.
To further explore the dynamics and investigate the underlying properties of the BM, the uncoupled single cell, the finite lattice and a periodic chain system of BM unit cells was investigated. Sinusoidal driven boundary inputs were applied to all systems and both time/frequency domain responses were obtained.
The single cell analysis clearly showed the harmonic diffusion property. In addition, the harmonic diffusion of the antiresonance features of the resonators was also observed. The possibility of aperiodic motions were also discovered.
Then, the energy transfer through finite chains was investigated by finite lattices. It has been shown that in both short and long input durations, the bistable finite lattices prevent energy transfer by snap-through motions with less than ten cells. Moreover, as the input duration increases, the energy transferred to the generic cell significantly differs between the bistable and linear finite lattices; and the bistable lattice outperforms.
In addition, the dispersion relations of the bistable periodic system have been computed using both analytical and numerical tools. The analytical results obtained through the harmonic balance method showed a very good agreement with the numerical approach based on the 2D FFT. Thus, the dispersion properties of the nonlinear system have been quantified.
Finally, the complex dynamics related to bistability and wire rope hysteresis deserve further studies. More specifically, the effects of varying gravitational loads, vertical seismic excitations together with the physical realization of wire ropes and a finite lattice with the control of parameters that accurately replicate bistable nonlinear components warrants further research.
Data availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author on a kind request.
References
ASCE/SEI (2016) Seismic analysis of safety-related nuclear structures. Standard 4–16
Basone F, Wenzel M, Bursi OS, Fossetti M (2019) Finite locally resonant metafoundations for the seismic protection of fuel storage tanks. Earthq Eng Struct Dynam 48(2):232–252
Basone F, Bursi OS, Aloschi F, Fischbach G (2021) Vibration mitigation of an MDoF system subjected to stochastic loading by means of hysteretic nonlinear locally resonant metamaterials. Sci Rep 11(1):1–15
Bursi OS, Basone F, Wenzel M (2021) Stochastic analysis of locally resonant linear and hysteretic metamaterials for seismic isolation of process equipment. J Sound Vib 510:116263
Camescasse B, Fernandes A, Pouget J (2013) Bistable buckled beam: elastica modeling and analysis of static actuation. Int J Solids Struct 50(19):2881–2893
Carta G, Movchan AB, Argani LP, Bursi OS (2016) Quasi-periodicity and multi-scale resonators for the reduction of seismic vibrations in fluid-solid systems. Int J Eng Sci 109:216–239
Cazottes P, Fernandes A, Pouget J, Hafez M (2009) Bistable buckled beam: modeling of actuating force and experimental validations. J Mech Des. https://doi.org/10.1115/1.3179003
Cheng ZB, Shi ZF (2018) Composite periodic foundation and its application for seismic isolation. EarthqEng Struct Dynam 47(4):925–944
Cohen N, Bucher I (2014) On the dynamics and optimization of a non-smooth bistable oscillator–application to energy harvesting. J Sound Vib 333(19):4653–4667
Eastham M (1973) The spectral theory of periodic differential equations. Scottish Academic Press, Chatto & Windus, London
BS EN 15129 (2018) European standard on anti-seismic devices. BSI Standard Publication
European Committee for Standardization (2004) Design of structures for earthquake resistance. - Part 1: General rules, seismic actions and rules for buildings. Eurocode 8–1, CEN/TC 250, Brussels
European Committee for Standardization (2005) Design of steel structures. Part 1–1: general rules and rules for buildings. Eurocode 3–1–1, CEN/TC 250, Brussels
Fang X, Wen J, Bonello B, Yin J, Yu D (2017) Ultra-low and ultra-broad-band nonlinear acoustic metamaterials. Nat Commun 8(1):1–11
Franchini A, Bursi OS, Basone F, Sun F (2020) Finite locally resonant metafoundations for the protection of slender storage tanks against vertical ground accelerations. Smart Mater Struct. https://doi.org/10.1088/1361-665X/ab7e1d,Vol.29,5
Ganesh R, Gonella S (2013) Spectro-spatial wave features as detectors and classifiers of nonlinearity in periodic chains. Wave Motion 50(4):821–835
Geniet F, Leon J (2002) Energy transmission in the forbidden band gap of a nonlinear chain. Phys Rev Lett 89(13):134102
Genton MG (2001) Classes of kernels for machine learning: a statistics perspective. J Mach Learn Res 2(Dec):299–312
Gilmour SG, Trinca LA (2012) Optimum design of experiments for statistical inference. J Roy Stat Soc: Ser C (appl Stat) 61(3):345–401
Guner T, Bursi OS, Erlicher S (2022) Optimization and performance of metafoundations for seismic isolation of small modular reactors. Comput-Aided Civil Infrastr Eng. https://doi.org/10.1111/mice.12902
Hussein MI, Khajehtourian R (2018) Nonlinear Bloch waves and balance between hardening and softening dispersion. Proc Royal Soc A: Math, Phys Eng Sci 474(2217):20180173
Jeffers AE, Plaut RH, Virgin LN (2008) Vibration isolation using buckled or pre-bent columns—Part 2: three-dimensional motions of horizontal rigid plate. J Sound Vib 310(1–2):421–432
La Salandra V, Wenzel M, Bursi OS, Carta G, Movchan AB (2017) Conception of a 3D metamaterial-based foundation for static and seismic protection of fuel storage tanks. Front Mater 4:30
Lataniotis C, Marelli S, Sudret B (2015) UQLab user manual–Kriging (Gaussian process modelling). Report UQLab-V0, pp 9–105
Leon J (2003) Nonlinear supratransmission as a fundamental instability. Phys Lett A 319(1–2):130–136
Li J, Chan CT (2004) Double-negative acoustic metamaterial. Phys Rev E 70(5):055602
Li H, Li A, Kong X (2021) Design criteria of bistable nonlinear energy sink in steady-state dynamics of beams and plates. Nonlinear Dyn 103(2):1475–1497
Liu E, Fang X, Wen J, Yu D (2020) 1/2 sub-harmonic resonance in bistable structure and its effect on vibration isolation characteristics. Acta Physica Sinica 69(6):064301
Liu E, Fang X, Wen J (2022) Harmonic and shock wave propagation in bistable periodic structure: regularity, randomness, and tunability. J Vib Control 28(21–22):3332–3343
Ma G, Sheng P (2016) Acoustic metamaterials: from local resonances to broad horizons. Sci Adv 2(2):e1501595
Malhotra PK, Wenk T, Wieland M (2000) Simple procedure for seismic analysis of liquid-storage tanks. Struct Eng Int 10(3):197–201
Manimala JM, Sun CT (2016) Numerical investigation of amplitude-dependent dynamic response in acoustic metamaterials with nonlinear oscillators. J Acousti Soc Am 139(6):3365–3372
Mu D, Shu H, Zhao L, An S (2020) A review of research on seismic metamaterials. Adv Eng Mater 22(4):1901148
Narisetti RK, Leamy MJ, Ruzzene M (2010) A perturbation approach for predicting wave propagation in one-dimensional nonlinear periodic structures. J Vib Acoust. https://doi.org/10.1115/1.4000775
Nesterenko VF, Daraio C, Herbold EB, Jin S (2005) Anomalous wave reflection at the interface of two strongly nonlinear granular media. Phys Rev Lett 95(15):158702
Patil GU, Matlack KH (2022) Review of exploiting nonlinearity in phononic materials to enable nonlinear wave responses. Acta Mech 233(1):1–46
Phan HN, Paolacci F, Di Filippo R, Bursi OS (2020) Seismic vulnerability of above-ground storage tanks with unanchored support conditions for Na-tech risks based on Gaussian process regression. Bull Earthq Eng 18(15):6883–6906
Plaut RH, Favor HM, Jeffers AE, Virgin LN (2008) Vibration isolation using buckled or pre-bent columns—Part 1: two-dimensional motions of horizontal rigid bar. J Sound Vib 310(1–2):409–420
Qiu D, Li T, Seguy S, Paredes M (2018) Efficient targeted energy transfer of bistable nonlinear energy sink: application to optimal design. Nonlinear Dyn 92(2):443–461
Reggio A, Angelis MD (2015) Optimal energy-based seismic design of non-conventional tuned mass damper (TMD) implemented via inter-story isolation. Earthq Eng Struct Dynam 44(10):1623–1642
Remoissenet M (2013) Waves called solitons: concepts and experiments. Springer Science & Business Media, Cham
Smith M (2009) ABAQUS/standard user's manual, Version 6.9
Sulfridge M, Saif T, Miller N, Meinhart M (2004) Nonlinear dynamic study of a bistable MEMS: model and experiment. J Microelectromech Syst 13(5):725–731
Sun S, An N, Wang G, Li M, Zhou J (2019) Snap-back induced hysteresis in an elastic mechanical metamaterial under tension. Appl Phys Lett 115(9):091901
United States Nuclear Safety Commission (U.S.NRC), 2019. Technical Considerations for Seismic Isolation of Nuclear Facilities; NUREG/CR-7253; U.S. NRC: Washington, DC, USA
Van Beers WC, Kleijnen JP (2003) Kriging for interpolation in random simulation. J Op Res Soc 54(3):255–262
Wang KW, Harne RL (2017) Harnessing bistable structural dynamics: for vibration control, energy harvesting and sensing. John Wiley & Sons, Hoboken
Wenzel M, Bursi OS, Antoniadis I (2020) Optimal finite locally resonant metafoundations enhanced with nonlinear negative stiffness elements for seismic protection of large storage tanks. J Sound Vib 483:115488
Williams CK, Rasmussen CE (2006) Gaussian processes for machine learning, vol 2. MIT press, Cambridge, MA, p 4
Xia Y, Ruzzene M, Erturk A (2019) Dramatic bandwidth enhancement in nonlinear metastructures via bistable attachments. Appl Phys Lett 114(9):093501
Zhao W, Wu Q, Zhao X, Nakano K, Zheng R (2020) Development of large-scale bistable motion system for energy harvesting by application of stochastic resonance. J Sound Vib 473:115213
Zheng R, Nakano K, Hu H, Su D, Cartmell MP (2014) An application of stochastic resonance for energy harvesting in a bistable vibrating system. J Sound Vib 333(12):2568–2587
Zhou WJ, Li XP, Wang YS, Chen WQ, Huang GL (2018) Spectro-spatial analysis of wave packet propagation in nonlinear acoustic metamaterials. J Sound Vib 413:250–269
Zivieri R, Garesci F, Azzerboni B, Chiappini M, Finocchio G (2019) Nonlinear dispersion relation in anharmonic periodic mass-spring and mass-in-mass systems. J Sound Vib 462:114929
Acknowledgements
The first author acknowledges the financial support of the Italian Ministry of Education, University and Research (MIUR) in the frame of the ‘Departments of Excellence’ (grant L 232/2016). The remaining authors acknowledge the Italian Ministry of Education, Universities and Research (MUR) in the framework of the project PNRR CN ICSC Spoke 9.
Funding
Open access funding provided by Università degli Studi di Trento within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Contributions
T.G and O.S.B developed the initial concepts and outlined the research. T.G performed theoretical calculations and conducted numerical simulations. O.S.B and M.B verified the results and contributed to their presentation. T.G prepared the relevant figures and drafted the manuscript. Finally, the authors jointly discussed the results and revised the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix 1
Appendix 1
The two-DoFs system associated with the uncoupled bistable periodic system can be represented as
where dots refers to differentiate wrt time. The application of the Floquet-Bloch theorem (Eastham 1973) and the formulation of the harmonic balance method (HBM) with the complex exponentials (Wenzel et al. 2020) entails,
where \(k = 1, 3, \ldots\) denote the kth harmonic and \(n = \left\{ { - 1, 0, 1} \right\}\) identifies the previous, center, and next cell; μ defines the propagation constant. Specifically, the unit cell length d is taken as d = 1 m and, therefore, the propagation constant reads μ = κd = κ. Since the objective is the definition of the dispersion properties of the chain around the linear natural frequency, the higher harmonics are disregarded, and the series is truncated to the 1st harmonic. For the specific case, the solution represents a plane wave with a fundamental wave mode supported by the nonlinear system. The application of the harmonic terms to (19a and 19b), and collecting frequency terms and equating the first-order terms to zero, the following functions are obtained,
where \(U_{n}\) and \(U_{r}\) are the amplitude of the primary cell and resonator, respectively. \(\tilde{U}_{n}\) corresponds to complex conjugate; and consequently, the amplitude can be rewritten as \(\left| U \right| = \sqrt {U_{n} *\tilde{U}_{n} } .\) The term N is the sum of high order κ terms and reads,
The substitution of (21.b) into (21.a), and the rearrangements of terms entails the dispersion relationships between \(\omega\) and κ and can be computed as:
Due to the high order κ terms, a direct solution of \(F\left( {\omega ,\kappa } \right)\) is not possible. Therefore, for each frequency ω, the κ is computed by the trust-region-dogleg algorithm. When the amplitude term, U is equal to 0, (23) corresponds to the dispersion relationship of a linear system (Wenzel et al. 2020).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Guner, T., Bursi, O.S. & Broccardo, M. Seismic vibration mitigation of steel storage tanks by metafoundations endowed with linear and bistable columns. Bull Earthquake Eng 22, 29–54 (2024). https://doi.org/10.1007/s10518-023-01692-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10518-023-01692-0