Damage modelling of a bridge pier subjected to multiple earthquakes: a comparative study

Abstract

This paper discusses and compares two recently developed methodologies for the prediction of damage accumulation in structures subjected to multiple earthquakes within their lifetime, one based on a regression model and one based on a Markov-chain based approach. A stochastic earthquake hazard model is considered for generating sample sequences of ground motion records that are then used to estimate the probabilistic distribution of the damage accumulated during the time interval of interest using the various methodologies. A simulation-based approach provides a reference solution against which the other methodologies are compared. Besides assessing the effectiveness and accuracy of the two methodologies, some improvements of the regression model are proposed and evaluated. The comparison between the methodologies is carried out by examining a reinforced concrete (RC) bridge pier model and using the Park–Ang damage index to describe the damage accumulation. The study results demonstrate the importance of considering the possibility of occurrence of multiple shocks in estimating the life-cycle performance of structures and highlight strengths and drawbacks of the investigated methodologies.

1 Introduction

A large percentage of the world’s infrastructure is located in earthquake-prone regions and is subjected to repeated seismic excitations during their design life. Multiple earthquakes occurring in the form of mainshock-aftershock sequences or multiple shocks can result in a progressive reduction in structural capacity over a long period of time and this can eventually lead to the collapse of the structure, with a devastating impact in terms of human lives and economic losses. As an example, the 1997 Umbria-Marche earthquake was characterized by a long sequence of earthquakes (i.e., six) of magnitude between 5 and 6 (Amato et al. 1998). In this case, although the main-shock event caused significant seismic damage in several structures, it was the subsequent events that led to structural collapse (Dolce and Larotonda 2001; Abdelnaby 2012).

In earthquake-prone regions, there is a high probability of observing more than one damaging earthquake during a structure’s service life. Thus, it is fundamental to take into consideration this aspect in the seismic assessment and design because it can significantly influence the structural reliability and the expected levels of seismic losses. Several studies have investigated the performance of structural systems under earthquake sequences, using models with different levels of complexity (see e.g. Fragiacomo et al. 2004; Di Sarno 2013; Hatzivassiliou and Hatzigeorgiou 2015; Aljawhari et al. 2021). Researches have also focused on the development of state-dependent fragility curves (Zhang et al. 2020; Aljawhari et al. 2021) which are essential tools for the life-cycle risk assessment.

Few studies have addressed the problem of damage accumulation during the structure’s lifecycle by accounting for the probabilistic nature of the hazard, i.e. the randomness inherent to the occurrence time and intensity of the earthquakes. Specifically, Kumar and Gardoni (2012) developed a probabilistic model for computing the degraded deformation capacity of flexural RC bridge columns under multiple damaging events as a function of cumulative low-cycle fatigue damage. They concluded that the fragilities of the piers for a given deformation demand rise with the increase in the value of fatigue damage and the fragilities of ductile piers increases faster than that of non-ductile piers. Ghosh et al. (2015) proposed an approach based on predictive regression model describing the probability of reaching a given damage level based on the intensity of the earthquake and previously accumulated damage. The model was used to predict the probability of damage exceedance conditioned on the number of earthquakes experienced by the structure. Time-dependent exceedance probabilities were computed using site-specific hazard curves for main shocks and aftershocks, characterized respectively by homogeneous and non-homogeneous Poisson process rates. Gusella (1998) proposed a method to estimate the reliability of masonry structures undergoing cumulative damage. In this methodology, the structural damage is represented by a finite number of discrete states and the evolution of damage is described as a homogeneous Markov discrete process, with a transition matrix that describes the probability of moving from a damage state to another given the occurrence of an earthquake. The occurrences of the earthquake events was modelled through a homogeneous Poisson process. Montes-Iturrizaga et al. (2003) implemented a Markovian model to describe the accumulation of damage under future multiple earthquakes and integrated it in an algorithm for optimal maintenance decisions for structures located in seismic regions. A Bayesian approach was employed for damage updating by incorporating information from sensors. Iervolino et al. (2015) evaluated alternative approaches for defining the state transition matrix within the Markovian framework for damage accumulation, and also proposed an extension of the framework to account for non-stationary earthquake occurrence rates typical of aftershock sequences and ageing.

The present study aims to review, evaluate and compare the effectiveness and accuracy of the abovementioned approaches for the prediction of damage accumulation in structures subjected to multiple earthquakes within their lifetime. In particular, the method of Ghosh et al. (2015) and the Markov-chain based approach of Gusella (1998), Montes-Iturrizaga et al. (2003) and Iervolino et al. (2015) are considered. In order to evaluate these methods, a simulation-based approach similar to the one followed in Scozzese et al. (2020) for evaluating multiple stripe analysis is employed. For this purpose, a stochastic earthquake hazard model is used to generate sample sequences of ground motion records that are then used to estimate the probabilistic distribution of the damage accumulated during the time interval of interest. This simulation-based approach provides a reference solution against which the other methods are evaluated. Besides assessing the effectiveness of each approach, some possible improvements of the cumulative demand model of Ghosh et al. (2015) are proposed and evaluated.

A reinforced concrete (RC) bridge pier model (Lehman and Moehle 2000) is considered to apply and compare the various approaches for damage assessment, and the Ang-Park damage index (Park and Ang 1985) is used to describe the damage accumulation. It is noteworthy that the action of continuous progressive degradation (i.e. ageing) and the impact of retrofit interventions (e.g. Bender et al. 2019) between subsequent shocks are not considered in this study, although they may play an important role in the life-cycle assessment. Moreover, while this study focuses on a single pier and a single damage indicator, a more comprehensive assessment of the seismic risk of bridges should consider the fragility of multiple components and their contribution to the system reliability (see e.g. Stefanidou and Kappos 2017, Stefanidou et al. 2017, Liu et al. 2022, Gkatzogias and Kappos 2022). The study results demonstrate the importance of considering the possibility of occurrence of multiple shocks in estimating the performance of structures, highlight strengths and drawbacks of the investigated methodologies, and provide indications on the optimal procedures to follow for applying them.

The rest of paper is organized as follows. Section 2 presents the probabilistic model for the accumulation of damage and the alternative methods employed to calculate it. Section 3 introduces the seismic hazard model and describes the details of the model of the reinforced concrete (RC) bridge pier adopted as case study. Finally, Sect. 4 shows the results of the comparison of the different methodologies. This is followed by a final section that presents the conclusions drawn from this work and a discussion on future developments.

2 Framework for damage accumulation

2.1 Damage index for seismic damage accumulation

The choice of a suitable parameter for describing the damage is an essential step at the base of the development of any methodology for evaluating the structural reliability under multiple earthquake shocks. A large number of damage indicators have been proposed in the scientific literature. These can be broadly categorized in two main classes: deformation-related and energy-related indices (Cosenza and Manfredi 2000). The first group comprises for example the maximum ductility demand (Aamir et al. 2022) or the maximum drift demand (Gentile and Galasso 2020; Bouazza et al. 2022). The second class of damage indices comprise parameters as the amount of energy dissipated through hysteretic response (Gentile and Galasso 2021). In addition, there are hybrid indices that capture the combined effects of deformation and energy dissipation in order to have a better assessment of the cyclic load effects. One of such parameters is the Park and Ang damage index (Park and Ang 1985; Park et al. 1985), defined as follows for a structural component under cyclic flexural loadings:

$$D=\frac{{d}_{max}}{{d}_{u}}+{\beta }_{D}\frac{{E}_{h}}{{F}_{y}{d}_{u}}$$

(1)

where ${d}_{max}$ is the maximum displacement of the structural member, ${d}_{u}$ represents the ultimate displacement under monotonic loading, ${E}_{h}$ denotes the dissipated hysteretic energy, ${F}_{y}$ is the yield strength and ${\beta }_{D}$ is a dimensionless empirical factor describing the contribution of hysteretic energy to damage compared to the displacement demand. Experimental values of ${\beta }_{D}$ are in the range of − 0.3 and 1.2 (Cosenza et al. 1993).

Park et al. (1985) proposed the relation reported in Table 1 between observed empirical damage and calculated damage index values. Values lower than 0.1 are associated with virtually no damage, while values higher than 1 are associated with a total loss of the load carrying capacity. The Park and Ang damage index has been employed in many studies on damage for RC columns under single shock scenarios (see e.g. Kappos 1997 and Kunnath et al. 1997).

Table 1 Park and Ang index classification

2.2 Overarching framework for seismic damage accumulation

The failure condition of a system under a seismic sequence within a time frame T is controlled by the probability of exceedance of different levels of the considered damage index. Denoting with D the damage index, the probability of D exceeding the value d during the time T can be expressed through the total probability theorem as follows:

$$P\left[D\ge d\right]=\sum_{1}^{\infty }P\left[D\ge d|n\right]*P[n,T]$$

(2)

where $P\left[D\ge d|n\right]$ is the probability that the damage D exceeds d, conditional on having the occurrence of n shocks, and $P\left[n,T\right]$ is the probability of having n shocks during T. It is noteworthy that in this study only mainshock events are considered, and that the hazard model is assumed as time-invariant. Thus, the probabilistic distribution of the earthquake characteristics is the same at each earthquake occurrence and the occurrence of the main shock events can be described by a time-invariant Poisson process with constant hazard rate $\overline{\nu }$. In view of this, the term $P\left[n,T\right]$ can be evaluated as follows:

$$P\left[n,T\right]=\frac{{(\overline{\nu }T)}^{n}}{n!}{e}^{-\overline{\nu }T}$$

(3)

where $\overline{\nu }$ denotes the mean annual frequency of occurrence of events of any intensity, and it is specific for the site of interest.

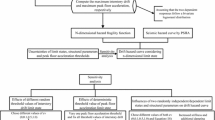
In the following, two different approaches for evaluating $P\left[D\ge d|n\right]$ are illustrated: (1) the approach put forward by Ghosh et al. (2015), referred herein as “Regression-based Method (RBM)”, and (2) the approach proposed by Gusella (1998), Montes-Iturrizaga et al. (2003) and Iervolino et al. (2015) denoted as “Markovian Method (MM)”. These approaches are evaluated against the classic frequentist approach, called hereafter “Simulation-based Method (SBM)”. The three approaches have in common that they require a set of ground motion sequences in order to evaluate $P\left[D\ge d|n\right].$ In this study, similarly to Scozzese et al. (2020), these sequences are generated with a Monte Carlo approach by sampling from a stochastic ground motion model. Figure 1 summarizes the overarching framework for the evaluation of $P\left[D\ge d\right]$ following the three approaches. It is noteworthy that for practical purposes, the sum in Eq. (2) is carried out up to a value of n equal to N, beyond which the probability of occurrence of the given number of events becomes negligible.

Fig. 1

Framework for seismic damage accumulation

2.3 Simulation-based method (SBM)

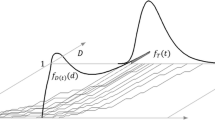
The Simulation-based Method (SBM) requires a stochastic representation of the earthquake hazard, as the one employed in Scozzese et al. (2020). It estimates directly $P\left[D\ge d|n\right]$ by a Monte-Carlo approach, which involves generating a series of N_s earthquake sequences from the hazard model and performing time history analyses of the finite element (FE) model of the structure to obtain samples of the damage index for different number of shocks (N = n). Figure 2 shows an example of earthquake sequence consisting of various shocks and the corresponding evolution of accumulated damage. Note that only the damage at the end of a shock is reported. For minor intensity earthquakes, the increase in damage is zero or not noticeable at the scale of the figure.

Fig. 2

a Sample earthquake sequence consisting of 7 shocks with time history a_g(t) and intensity IM, b damage level D accumulated under the various shocks

The damage exceedance probability is obtained by the following equation:

$$P\left[D\ge d|n\right]=\sum_{1}^{{N}_{s}}\frac{I\left[D\ge d|n\right]}{{N}_{s}}$$

(4)

where I is the indicator function, assuming the value of 1 if $D\ge d$ conditional to the occurrence of n earthquakes, and zero otherwise, and N_s is the number of sequences, i.e., of samples of the damage index for a given number of shocks. Obviously, a significant number of samples is required to achieve confident estimates of $P\left[D\ge d|n\right]$, particularly for high d values.

2.4 Regression-based method (RBM)

The approach proposed by Ghosh et al.(2015), denoted herein as RBM, is based on a probabilistic model that is a direct extension of the probabilistic seismic demand models (PSDMs) commonly used in Performance Based Earthquake Engineering (see e.g. Cornell et al. 2002 and Tubaldi et al. 2016). According to Cornell et al. (2002), for a single event, the relationship between the median value of a generic demand (in this case the damage index D) and the intensity measure of ground motions (IM) can be approximated by a power law:

$$\widehat{{D}_{1}}={a}_{1}{({IM}_{1})}^{{b}_{1}}$$

(5)

The linear regression model (LR) is better represented in the log–log space, with Eq. (5) rewritten as:

$$\mathrm{ln}\,{D}_{1}|{IM}_{1}={a}_{1}+{b}_{1}\mathrm{ln}{D}_{1}+{\varepsilon }_{1}$$

(6)

where a₁ and b₁ are the regression coefficients and ${\varepsilon }_{1}$ is the error variable relative to the regression, which has a normal distribution with zero mean and standard deviation β₁. The unknown coefficients and ${\varepsilon }_{1}$ can be evaluated through a least squares regression. In order to define the model for damage accumulation, Ghosh et al. (2015) introduced the Markovian assumption that the probabilistic distribution of the damage ${D}_{n}$ at the end of the n-th earthquake (with n >  = 2), depends only on the damage accumulated up to the time when the earthquake occurs, and not on the whole earthquake sequence and damage progression history. Obviously, the probabilistic distribution of ${D}_{n}$ must depend also on the intensity of the n-th earthquake, IM_n. This leads to the following multilinear regression model, developed by Ghosh et al. (2015) and denoted as RM1:

$$\mathrm{ln}\left.{D}_{n}\right|{IM}_{n},{D}_{n-1}={a}_{n}+{b}_{n}\mathrm{ln}{D}_{n-1}+{c}_{n}\mathrm{ln}{IM}_{n}+{d}_{n}\mathrm{ln}{D}_{n-1}\mathrm{ln}{IM}_{n}+{\varepsilon }_{n}$$

(7)

where a_n, b_n, c_n, d_n, are the regression coefficients and the term ${\varepsilon }_{n}$ is the error variable relative to the regression, which is normally distributed with zero mean and lognormal standard deviation ${\beta }_{n}$. This model can be seen as an extension of the model presented in Eq. (6) because the damage index of the structure after the n-th shock of a sequence depends on how “weak” the structure has become after being exposed to the previous n−1 shocks (quantified herein only by ${D}_{n-1}$) (Ghosh et al. 2015).

Alternative models are proposed hereinafter to improve further the model of Eq. (7), by introducing more terms in the regression, similar to what was done e.g. by Tubaldi et al. (2022) and Tubaldi et al. (2016).

The second regression model (RM2) considers a bilinear surface regression:

$$\mathrm{ln}\left.{D}_{n}\right|{IM}_{n},{D}_{n-1}=\left({e}_{n}+{f}_{n}\mathrm{ln}{D}_{n-1}\right){H}_{n}+\left({g}_{n}\mathrm{ln}{IM}_{n}+{h}_{n}\mathrm{ln}{IM}_{n}\mathrm{ln}{D}_{n-1}\right)\left(1-{H}_{n}\right)+{\varepsilon }_{n}$$

(8)

where H_n is a step function that is H_n = 1 for IM_n ≤ IM^* and H_n = 0 for IM_n > IM^*. The IM^* parameter can also be evaluated through a nonlinear least squares regression.

The third model (RM3) is an improvement of RM1, using the max function:

$${\text{ln}}\;D_{n} |IM_{n} ,D_{{n - 1}} = {\text{max}}\left\{ {\begin{array}{*{20}l} {i_{n} + l_{n} {\text{ln}}D_{{n - 1}} + m_{n} {\text{ln}}IM_{n} + n_{n} {\text{ln}}D_{{n - 1}} {\text{ln}}IM_{n} } \hfill \\ {D_{{n - 1}} } \hfill \\ \end{array} } \right. + \varepsilon _{n}$$

(9)

The previous models may return values of ${D}_{n}$ lower than ${D}_{n-1}$ due to the nature of the regression model and ${\varepsilon }_{n}$. One way to overcome this physical inconsistency (i.e., damage can only increase) is to postulate that ${D}_{n}$>${D}_{n-1}$. The fourth regression model (RM4) employs the max function to solve the issue:

$${\text{ln}}\;D_{n} |IM_{n} ,D_{{n - 1}} = {\text{max}}\left\{ {\begin{array}{*{20}l} {a_{n} + b_{n} {\text{ln}}D_{{n - 1}} + c_{n} {\text{ln}}IM_{n} + d_{n} {\text{ln}}D_{{n - 1}} {\text{ln}}IM_{n} + \varepsilon _{n} } \hfill \\ {D_{{n - 1}} } \hfill \\ \end{array} } \right.$$

(10)

In order to fit the regression models described above, the FE model of the structure must be analysed under N_s = 5000 sequences of ground motions consistent with the considered hazard model. The 5000 samples of the responses under the first shock are used to fit the model of Eq. (6). The fitting of the model for ${(D}_{n}|{IM}_{n},{D}_{n-1})$ is based on the samples of the damage indexes at the end of the n-th and of the (n-1)-th shocks, as well as of the samples of IM_n. In theory, different models should be considered for n = 2,…,N. However, assuming the regression model as homogeneous, the term n in the regression coefficient can be dropped, or in other words the regression coefficients (and thus the probability of moving from a state of damage to another) do not depend on the number n of the shock considered. Thus, the samples corresponding to different values of n can be considered jointly to fit the regression model. Once the regression model is fitted, the unconditional probability of exceeding the specified damage levels can be assessed with a Monte Carlo-based approach. For this purpose, N_s sequences of earthquake intensities can be generated by sampling from the stochastic model of the earthquakes for the site, and the regression equations with the associated uncertainties can be repeatedly applied to estimate the damage indices conditional to the number n of shocks. Finally, the probability exceeding a threshold damage level is estimated following a similar approach as the one used for the SBM method (i.e. Equation (4)).

2.5 Markovian method (MM)

The approach proposed by Gusella (1998), Montes-Iturrizaga et al. (2003) and Iervolino et al. (2015), denoted herein as MM, is applied to structures accumulating seismic damage and it is based on a Markovian representation of the degradation process (Serfozo 2009). The underlying hypothesis is the stationarity of the process meaning that the evolution of the damage after a given time depends probabilistically only on the state of the structure at that time. The vulnerability is then represented as a state-dependent phenomenon described by a homogeneous Markovian chain, modelled through the transition probability matrix (TPM) that completely characterizes the stochastic process. For this purpose, damage d is discretized into a finite number of states ${n}_{e}$ where the first state corresponds to the undamaged structure (d₁ = 0) and the last state corresponds to failure or collapse (d_ne = 1). Defining (k-1) and k, with k = 2,…, N, as two sequential seismic events, the transition probability between two damage states can be computed as:

$${\phi }_{ij}^{k}=P\left[j-th\,state\,at k|i-th\,state\,at\,(k-1)\right], \quad i,j=1,\dots , {n}_{e}$$

(11)

where ${\phi }_{ij}^{k}$ denotes the probability that at the end of the k-th earthquake the structure reaches damage state j, given that the initial state is i. The probabilities of transition ${\phi }_{ij}^{k}$ can be arranged in the TPM $\Phi \left( k \right)$ of dimensions (${n}_{e}$ x ${n}_{e}$):

$${\varvec{\Phi}}\left(k\right)=\{{\phi }_{ij}^{k}; i,j=1,\dots , {n}_{e}\}$$

(12)

The rows and columns of the TPM are labelled with the damage states of the structures arranged progressively from the top one corresponding to the as-new state to the bottom one that necessarily denotes the failure of the structure. The matrix is upper triangular because of the monotonous nature of the damage process. It may be used entering the row with the pre-event condition of the structure to get the probability to find it in any of the other states. It is noteworthy that ${\varvec{\Phi}}\left(k\right)$ is estimated via simulation, as no closed form expressions are available.

The damage probability vector ${\varvec{P}}\left(k\right)$ of dimensions (1x ${n}_{e}$), computed at the end of the k-th event, can be express as:

$${\varvec{P}}\left(k\right)={\varvec{P}}(k-1){\varvec{\Phi}}(k)$$

(13)

where ${\varvec{P}}(k-1)$ is the damage probability vector of dimensions (1x ${n}_{e}$) at the start of the k-th event. The j-th element ${P}_{j}^{k}$ of the vector ${\varvec{P}}\left(k\right)$, which expresses the probability of being in damage state j at the end of the k-th seismic event, is given by:

$${P}_{j}^{k}=\sum_{i=1}^{{n}_{e}}{P}_{i}^{k-1}{\phi }_{ij}^{k}$$

(14)

where ${P}_{i}^{k-1}$ represents the probability of being in damage state i at the start of the k-th seismic event.

Under the assumption of homogeneity already introduced for the RBM, the damage accumulation process can be described as a homogeneous Markov chain defined by a single TPM ${\varvec{\Phi}}$, and the probability mass function after the occurrence of the N-th earthquake can be written as:

$${\varvec{P}}\left(N\right)={\varvec{P}}(0){{\varvec{\Phi}}}^{{\varvec{N}}}$$

(15)

where ${\varvec{P}}(0)$ is a vector (1x ${n}_{e}$) that denotes the initial state of the structure. The probability that damage does not exceed a damage level ${d}_{j}$ conditional on the number of shocks n can be expressed by:

$$P\left[D<{d}_{j}|n\right]=\sum_{i=1}^{j}{\psi }_{ij}^{N}{p}_{i}^{0}=\sum_{i=1}^{j}\left(\sum_{l=1}^{j}{q}_{il}^{N}\right){p}_{i}^{0}$$

(16)

where ${q}_{il}^{N}$ is the element at row i and column l of the N-th product of matrix ${\varvec{Q}}=\{{\phi }_{il};i,l\le j\}$. This matrix is obtained by deleting from the matrix ${\varvec{\Phi}}$ the rows and columns whose index is higher than l. Then, the matrix Ψ^N $=\left\{{\psi }_{ij}^{N}\right\}=\{\sum_{l=1}^{j}{q}_{i,l}^{n}\}$ can be formed. Therefore, the conditional probability of exceeding a given damage state ${d}_{j}$ is:

$$P\left[D\ge {d}_{j}|n\right]=1-\sum_{i=1}^{j}{\psi }_{ij}^{N}{p}_{i}^{0}$$

(17)

3 Case study

3.1 Stochastic earthquake model

Similarly to previous studies (Dall'Asta et al. 2017; Altieri et al. 2018), the seismic scenario is described by a single source model, characterized by two main random seismological parameters, namely the moment magnitude M_m, and the epicentral distance R. Earthquakes of magnitude between M_min = 5.5 and M_max = 8 have the same likelihood of occurrence within a circular area of radius R_max = 25 km centred at the site where the structure is situated. The frequency of occurrence of the earthquakes is described by the Gutenberg-Richter recurrence law and the mean annual frequency of occurrence $\overline{\nu }$ of earthquakes of any intensities is 0.0997 per year. The attenuation from the source to the site of the structure is described by the Atkinson–Silva (Altieri et al. 2018) source-based ground motion model, combined with the stochastic point source simulation method of Boore (2003). The Spectral acceleration Sa(T_fund,ξ) at the fundamental period T_fund and the damping ratio ξ of the structure is chosen as intensity measure (IM). Figure 3a illustrates the probability mass function of the number n of shock occurrences during the lifetime of the structure (T = 50 years). It can be seen that the probability of having 15 or more shocks is negligible. Figure 3b the probability of exceedance of IM, conditional on the number of occurrences. The values of T_fund and ξ refer to the case-study pier illustrated in Sect. 3.2. A pool of N_s = 5000 ground motion records are generated by sampling from the probabilistic distributions of M_m and R and by using the Atkinson-Silva attenuation model (see Altieri et al. 2018 for further details). Since the model is homogeneous, N_s sequences of 20 consecutive ground motions are built by randomly extracting the sampled records from the pool of records. These ground motion sequences are then used as input for the time-history analyses required to estimate the evolution of damage.

Fig. 3

a Probability of n shocks in lifetime T = 50 years; b Probability of exceedance of IM in 50 years conditional to the number of shocks n

3.2 RC pier model

A RC bridge pier (Fig. 4) of height L = 4.9 m is selected as case study. It corresponds to specimen denoted as 815 in Lehman and Moehle (2000). The details of the considered bridge pier are summarised in Table 2. The pier is characterized by a circular cross-section with diameter D_m = 610 mm and it has a mass of 35.6 ton. The fundamental period of the pier is T_fund = 0.69 s and the damping ratio ξ is 0.05. Figure 4 represents an illustration of the chosen column.

Fig. 4

Schematic view of the bridge pier (Lehman and Moehle 2000) a longitudinal view b cross section

Table 2 Details of the structural model Lehman and Moehle (2000)

A detailed numerical model of the RC column was constructed in OpenSees (2011) with due account of geometric and material nonlinearities by means of the fibre-based section discretisation technique (Spacone et al. 1996a, b; Kashani et al. 2016, 2017). This includes an accurate representation of the influence of inelastic steel buckling and low cycle fatigue degradation. To this end, beam-column elements were employed to model the bridge pier and the cross-section of the element was discretized into a number of steel and concrete fibres at the selected integration points. This research follows the modelling approach described in Kashani et al. (2016) in which three Gauss–Lobatto integration points (Berry and Eberhard 2006) are specified for the first element, where most of the nonlinear response is concentrated, based on the recommendations provided by Coleman and Spacone (2001) and Pugh (2012). Similarly, a force-based element with five integration points is considered to model the top part of the column, in accordance with Berry and Eberhard (2006). A schematic view of the fibre model and fibre sections is shown in Fig. 5. The following material properties were assumed: a steel yield stress of f_y = 540 MPa, maximum deformations of confined and unconfined concrete under compression of ε_ccore = 0.035 (Van et al. 2003) and ε_ccover = 0.00428 (Karthik 2009), respectively, and a maximum longitudinal concrete tensile deformation of ε_t = 0.000125 (Mander et al. 1988), while a maximum deformation of the steel under compression of ε_cs = 0.08 was adopted.

Fig. 5

Schematization of fibre beam-column element (a) with the bar buckling and bar slip model (b)

The material nonlinearity was described through a uniaxial material relationship for steel (tension and compression) and concrete (confined and unconfined). In this study, the Concrete04 model available in OpenSees (2011) was used to model the unconfined concrete in the cover and the confined concrete in the core of the pier. This model is based on the Popovics (1988) curve in compression, and a linear-exponential decay curve in tension. The Karsan–Jirsa model (Karsan and Jirsa 1969) was used to account for the stiffness degradation and determine the unloading–reloading stiffness in compression while the secant stiffness was employed to define the unloading/reloading stiffness in tension. The confinement parameters (i.e., the maximum compressive stress of the concrete and the strain at the maximum compressive stress) were taken from Mander et al. (1988). The model developed by Scott et al. (1982) was used to define the confined concrete crushing strain in the confined concrete model. Besides, the phenomenological uniaxial model developed by Kashani et al. (2015) was used to describe the behaviour of steel reinforcement. For its implementation, the Hysteretic material model available in OpenSees (2011) was used. Moreover, the generic uniaxial fatigue material developed by Uriz (2005) was wrapped to the steel material in order to simulate the low cycle fatigue failure of vertical reinforcing bars. Further information about the model can be found in Kashani et al. (2016) and Kashani et al. (2017).

4 Results

4.1 Reference solution via SBM

The direct simulation (SBM) approach provides the reference solution for the comparison of the RBM and MM methods. Figure 6 shows the probability of damage exceedance, computed for an increasing number of earthquake sequences N_s from 200 to 5000. The total number of shocks N examined for each curve is 20, and 40 discrete damage levels between 0 and 1 were considered to calculate the probability of exceedance. The value of the coefficient ${\beta }_{D}$ considered in the calculation of the damage index using Eq. (1) is 0.05. It can be noted that by increasing N_s the exceedance curves tend toward the one calculated for N_s = 5000 and the curves obtained considering N_s ≥ 1000 are very close to each other. The maximum value of the coefficient of variation of the estimate of the exceedance probability for the highest damage level (D = 1) is of the order of 6.5%. Thus, quite accurate estimate of the probability is achieved with the maximum number of sequences N_s considered. Beyond N_s = 5000, there is no appreciable change in the estimated curve: the maximum relative difference in the probability of exceedance between the curves calculated with N_s = 4000 and N_s = 5000 is less than 2.5%. Thus, it can be assumed that the curves have reached convergence and for this reason, the solution obtained with N_s = 5000 is considered as reference solution for evaluating the accuracy of the other methods under analysis.

Fig. 6

Influence of the number of samples on the probability of exceedance of the damage D computed via SBM

A further study is conducted to assess the maximum number of earthquake occurrences N to be considered during the assumed design life (T = 50 years) of the structure in the summation of Eq. (2). Figure 7 shows the probability of failure for an increasing number of N and for a number of N_s equal to 5000. It can be seen that, for low values of N, by increasing the maximum number of occurrences, the probability of failure increases significantly, whereas for value of N higher than 10, there is no change in the risk estimate. The value of N in the subsequent analyses is set equal to 20.

Fig. 7

Exceedance probability of a limit threshold, evaluated via SBM for 5000 samples, for an increasing number N = n of shocks in 50 years

4.2 RBM fitting

This subsection describes the results of the application of the linear and multi-linear regression models obtained by employing a set of N_s = 5000xN = 20 samples. Figure 8 shows the sample values of the damage index ${D}_{1}$ versus ${IM}_{1}$ in the log–log plane, together with the median of the linear model of Eq. (6). It can be observed that log(${D}_{1}$) increases linearly with the log(${IM}_{1}$). The high value of the coefficient of determination (R²=0.964), and the low value of the mean square error or lognormal standard deviation (β₁ = 0.187), reported in Table 3, reveal a satisfactory fit of the model to the data. Figure 9 illustrates the response samples and the fitted median demand obtained by using the various multi-linear regression models of Eqs. (7)-(10). Each figure shows the logarithm of the samples of the damage index ${D}_{n}$ observed for the n-th event as a function of the logarithms of the intensity measure ${IM}_{n}$ and of the damage index ${D}_{n-1}$ observed for the (n-1)-th event. The surface plotted in the figures corresponds to the fitted median models (see Table 4 for the model parameters). The values of the ${\beta }_{n}$ and R² (Table 3) corresponding to the various models show that overall, the regression models are quite accurate, and RM3 is the one that performs best.

Fig. 8

Linear regression model for predicting damage after the first occurrence

Table 3 β_n and R² values of the linear and multi-linear regression models

Fig. 9

Models for damage accumulation: a RM1; b RM2; c RM3; d RM4

Table 4 Parameters of the linear and multi-linear regression models (LN, RM1, RM2, RM3, RM4)

4.3 Convergence analysis of the RBM

Figure 10 shows the estimates of the probability of damage exceedance obtained for each of the RBM models fitted in the previous sections and compares them to the reference solution. The curves are obtained considering N_s = 5000 sequences and N = 20 occurrences per sequence, and 40 discrete damage levels. It can be observed that the curves obtained with RM3 and RM4 are more stable and closer to the reference curve while the curves of RM1 and RM2 are more scattered for high values of D. The bias of the RM-based estimates is quantified numerically through the errors Δmax and Δmean, denoting respectively the maximum and the mean of the normalized distances between the curves obtained with each RM and the corresponding reference curve. The values of Δmax and Δmean are reported in Table 5. As already expected by observing Fig. 10, the lowest values of the errors are obtained for RM3 and RM4. In particular, RM3 presents the minimum values of Δmax and Δmean, thus it can be considered in general as the most accurate model. It is noteworthy that the β_n and R² values of Table 3 follow the same trend of the values of Δmax and Δmean in Table 5, i.e., the best performing demand models yield the most accurate risk evaluations.

Fig. 10

Estimate of the damage exceedance probability evaluated for the four regression models for N_s = 5000 and N = 20

Table 5 Max and mean values of the normalized distances between the probability curves computed for each RM and the reference solution (minimum values are in bold)

A further study has been conducted on RM3 in order to establish the minimum number of N_s and N to be considered for estimating the probability of failure without affecting significantly the accuracy of the results. For this purpose, different regression models are built by fitting RM3 to different samples sets, obtained for an increasing number of N_s between 200 and 5000, for N = 20. Figure 11 shows the probability of damage exceedance obtained considering the different sample sets. Figure 12 compares the corresponding values of the errors Δmax and Δmean. It can be observed that by increasing N_s, the errors tend to decrease as the exceedance curves become closer to the reference solution. The curves corresponding to values of N_s ≥ 500 are very close to each other, and thus N_s = 500 can be considered as a good number of sequences for estimating the damage exceedance curve.

Fig. 11

Influence of number of sequences N_s on the estimate of the damage exceedance probability for RM3 (N = 20)

Fig. 12

Plot of the normalized distances between the probability curves calculated for an increasing number of N_s and the reference solution a max values; b mean values

The influence of the number of shocks N to be considered for RM3 is also assessed. Figure 13 shows the probability of damage exceedance obtained with RM3 for N_s = 500 and for an increasing number of N. The deviation between each curve and the reference solution is measured by the errors reported in Fig. 14: the errors are very high for low values of N, whereas they decrease and stabilise for N ≥ 10. Thus, N = 10 is deemed sufficient to achieve accurate estimates of the curve.

Fig. 13

Influence of number of shocks N on the estimate of the damage exceedance probability for RM3 (N_s = 500)

Fig. 14

Plot of the max and mean values of the normalized distances between the probability curves calculated for an increasing number of N and the reference solution. a max values; b mean values

4.4 Convergence analysis of the MM

Following the same methodology of Sect. 4.3, this subsection investigates the accuracy of the MM and examines how the number of N_s and N affects the estimation of the curve expressing the probability of damage exceedance. For these purposes, the probability curves are built initially using the MM for an increasing number of N_s between 200 and 5000, 40 damage levels and N = 20. The obtained curves are compared against the reference solution in Fig. 15. As expected, for increasing values of N_s, the probability curves approach the reference solution. Figure 16 compares the error measures expressing the normalized distances between the probability curves and the reference solution. In general, the errors are low and decrease for increasing N_s values. For values of N_s increasing beyond 1000, the errors do not decrease significantly. Thus, N_s = 1000 is a good number of sequences to be considered for fitting MM.

Fig. 15

Influence of number of sequences N_s on the estimate of the damage exceedance probability evaluated with the MM (N = 20)

Fig. 16

Plot of the max and mean values of the normalized distances between the probability curves calculated for an increasing number of N_s and the reference solution a max values; b mean values

In order to evaluate the effect of the number of shocks N, the probability of damage exceedance is calculated for an increasing number of N, keeping fixed the number of sequences N_s = 1000. Figure 17 shows the probability of damage exceedance versus D for an increasing number of N. The curves tend to overlap with the reference curve for a high number of N. Figure 18 compares the error measures obtained for the different values of N. As expected, increasing the number of N improves the estimate of the exceeding probability as the values of the Δmax decrease. In this case, N = 20 must be considered as the error values decrease considerably up to N = 20.

Fig. 17

Influence of number of shocks N on the estimate of the damage exceedance probability

Fig. 18

Plot of the max and mean values of the normalized distances between the probability curves calculated for an increasing number of N and the reference solution a max values; b mean values

4.5 Comparison of the different methods

This subsection summarizes the results obtained and shown in the previous paragraphs. The analyses whose results are reported in Sects. 4.2 and 4.3 show that among the various RBMs, RM3 is the one that provides more accurate estimates of the probability of damage exceedance. It is sufficient to consider N_s = 500 and N = 10 to fit this model. With regards to the MM, based on the results reported in Sect. 4.4 it can be concluded that a slightly higher number of samples (N_s = 1000 and N = 20) is required to fit the model.

Figure 19 shows the curves of the probability of damage exceedance resulting from the application of the RM3 (N_s = 500 and N = 20) and of the MM (N_s = 1000 and N = 20). It is possible to observe that the MM provides results very close to the reference ones obtained with the SBM, since it introduces no simplification in the evaluation of the evolution of damage during consecutive events. The estimates of the probability of damage exceedance obtained with the RBM, on the other hand, present some divergences due to the assumption introduced through the regression model. However, despite the differences, all methods lead to similar results. MM needs a slightly larger number of samples (and thus of analyses) with respect to RBM: this is due to the fact that in order to estimate with accuracy all the terms of the transition matrix, a greater number of samples is required, particularly to fit the bottom right part (corresponding to high levels of damage). The RBM yields some savings in terms of computational cost but at the expense of some bias.

Fig. 19

Comparison between the different approaches for evaluating the damage exceedance probability

4.6 Results for T = 5 years

The methodologies investigated in this study assume that during the time T no interventions take place to return the structure to its undamaged state. This could be realistic only for small time frames. Thus, this subsection briefly illustrates some results obtained considering a shorter time interval T = 5 years for the evaluation of the unconditional damage exceedance probability. As shown in Fig. 20, the probability of having more than 5 shocks in T = 5 years is negligible. Nevertheless, the value of N = 20 has been considered in the application of the methods for computing the risk via Eq. (2).

Fig. 20

Probability of n shocks in lifetime T = 5 years

Figure 21a, b show the probability of damage exceedances built using RM3 and the MM respectively for an increasing number of N_s between 200 and 5000. Figure 22a shows the variation with N_s of the mean error measure, expressing the normalized distances between the probability curves of Fig. 21a and the reference solution. It can be seen that the error values decreases only slightly for increasing N_s values, since the method provides biased estimates of the risk. For values of N_s increasing beyond 1000, the reduction of the error can be considered not significant. Figure 22b compares the error measures for the curves obtained with the MM method, which are shown in Fig. 21b. For values of N_s increasing beyond 1000, the error does not decrease significantly.

Fig. 21

Influence of number of sequences N_s on the estimate of the damage exceedance probability computed for N = 20 and for a period T = 5 years, built with a RM3 b MM

Fig. 22

Plot of the mean values of the normalized distances between the probability curves calculated for an increasing number of N_s and the reference solution: a RM3, b MM

5 Conclusions

The work provides a critical evaluation of alternative approaches for evaluating the evolution of damage in structures subjected to multiple shocks during their design life. The first approach considered is based on an existing regression model (RBM) that has been improved introducing three alternative models. The second approach is based on a Markovian method (MM) that requires fitting a transition probability matrix. The estimates of the probability of damage exceedance obtained via the alternative approaches are compared against the estimates obtained using a simulation-based Monte Carlo (SBM) approach. The nonlinear numerical model of a bridge pier is considered for the comparison.

With regards to the first approach, it can be concluded that all the regression models exhibit similar performances but the RM3 model presents the lowest value of the lognormal standard deviation $\beta$ and highest value of R². As a result of this, the estimate of the damage exceedance probability curve obtained with the proposed RM3 model for a time frame of 50 years is the closest to the reference one. Both the number of sequences N_s and the number of events within a sequence N significantly affect the estimates of the probability curves. A number of N_s equal to 500 and a number of N equal to 10 are sufficient to achieve accurate estimates of the probability of damage exceedance in 50 years.

With regards to the MM, a good level of accuracy in the estimates of the probability of damage exceedance in 50 years can be obtained for N_s = 1000 and N = 20. The mean and maximum error in the risk estimate associated with this method are lower compared to the error values associated to the RBM.

The various methods have also been applied considering a reduced time frame of 5 years for the evaluation of the probability of damage exceedance, during which it is more realistic to assume that no retrofit interventions take place following earthquake occurrences. The results obtained confirm that the RM3 model provides a biased estimate of the damage exceedance curve, and thus increasing the number of samples to consider for fitting the regression model does not result in significant improvements in terms of accuracy. On the other hand, by applying the MM method, quite accurate estimates of the probability of damage exceedance can be obtained for N_s = 1000 and N = 20.

In conclusion, the RBM is computationally more efficient than the MM, since it is able to provide quite accurate damage estimates with a lower number of samples. However, it introduces some bias in the estimates of the probability of damage exceedance. Using the MM fitted considering a slightly higher number of samples, accurate and unbiased damage estimates can be achieved. In this study, no interventions were assumed to happen along the service life of the structure. This assumption could be realistic considering that retrofitting can often be impractical. This is the case when the level of damage following an earthquake event is visually irrelevant to motivate interventions or when economic restraints render retrofit actions infeasible after every earthquake. Moreover, the study does not consider the effect of material aging, as it is more advantageous to model it separately from the cumulative seismic damage. Despite the limitations, the analysis shows accurate results that can be used in practice.

The combination of earthquake damage and aging as well as the contribution of aftershocks in the damage accumulation process, not addressed in this study, will be object of future investigations, where real earthquakes ground-motion sequences could be considered instead of simulated ones. The methodologies investigated here could also be extended to account for the vulnerability of multiple critical components of bridges as well as for the possibility of including retrofit interventions between subsequent seismic events.