Fragility curves of masonry buildings in aggregate accounting for local mechanisms and site effects

Abstract

The seismic evaluation of masonry buildings in aggregate, largely diffused within the existing Italian and European building stock, represents a difficult and open task that has not been exhaustively investigated so far. The study proposes a procedure aimed at evaluating the potential impact of the combination of local mechanisms and site-amplification in terms of fragility curves on an existing unreinforced masonry (URM) aggregate which is made of five adjacent structural units mutually interacting with each other during seismic sequences. The case study is inspired by built heritage of the historic centre of Visso struck by the Central Italy 2016/2017 earthquakes. The in-plane (IP) response of URM buildings was simulated through nonlinear dynamic analyses performed on a 3D equivalent frame model of the structure, whereas out-of-plane (OOP) mechanisms were analysed by adopting the rigid-block assumption but assuming, as seismic input, the floor accelerations derived from the post-processing of data derived from the global 3D model. An innovative procedure considering the pounding effect to the global response of the building is also presented. Two soil conditions were assumed with (freefield) and without (bedrock) site amplification. The results showed that site effects strongly affected the seismic vulnerability of the aggregate, also altering the combination between IP and OOP mechanisms. In fact, for bedrock condition, especially for medium–high damage levels, local mechanisms were prevailing with respect to the IP response. Conversely, for freefield condition, IP mainly governed the overall behaviour for all the damage levels, consistently with the field evidence.

1 Introduction

The seismic risk of existing unreinforced masonry (URM) buildings is particularly emphasized when they belong to historical centres of small municipalities, as testified by damage and losses produced by many seismic events (e.g. Decanini et al. 2004; Augenti and Parisi 2010; D’Ayala and Paganoni 2011; Cattari et al. 2012; Carocci 2012; Penna et al. 2014; Sextos et al. 2018; Sorrentino et al. 2019). Such high seismic risk derives from a combined role of vulnerability and hazard. Vulnerability factors arise from the fact that small historical centres were often developed in a poor economic context and without following a specific urban development plan. Indeed, they are usually the result of a process of building growth across centuries, leading to buildings in aggregate with interacting units characterized by different materials, construction techniques, heights, state of preservation and, often, improvised renovations (e.g. Valluzzi et al. 2022). In addition, the geomorphologic context in which such historical centres are built often highlighted the important role on the seismic response of local amplification phenomena associated with topographic and soil stratigraphic effects (e.g Sextos et al. 2018; Stewart et al. 2018; Sorrentino et al. 2019; Brando et al. 2020; Chieffo and Formisano 2020). This potential risk factor was confirmed by microzonation studies performed in various Italian areas after the aforementioned earthquakes (e.g. Lanzo et al. 2011; Monaco et al. 2014; Pagliaroli et al. 2020).

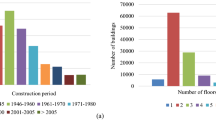
Buildings in aggregate may be founded in many countries worldwide (e.g. Russel and Ingham 2010, for New Zealand), but they are especially diffused within the existing Italian and European building stock (e.g. Moretic et al. 2022 for Croazia, Ferreira et al. 2013 for Portugal, just to mention a few).The large diffusion of URM buildings in aggregate in Italy is confirmed by Fig. 1a that depicts data available from the Da.Do. platform (Database of Observed Damage, Dolce et al. 2019), referring only to residential URM buildings and neglecting mixed structures (i.e. R.C.-masonry buildings). In particular, one can see that the number of buildings in aggregate is about 3 times (i.e. 35,261/12,624) higher than the individual buildings by considering all municipalities and even higher, namely 4 (i.e. 26,205/7045) focusing only on small municipalities (< 2000 residents). The ratio is even larger only focusing on historical centres (e.g. Sisti et al. 2019).

Fig. 1

Comparison in terms of diffusion (a) or damage level (b) of URM buildings in aggregate or individual URM buildings among the data collected in the Da.Do. platform and related to surveyed buildings struck by the L’Aquila earthquake in 2009

Figure 1b shows a comparison between the global damage level (DL) that occurred for individual URM buildings and URM buildings in aggregate. That information was taken from Da.Do. that associates a DL to each surveyed building according to the conversion criteria proposed in (Dolce et al. 2019) thanks to the availability of the respective AeDES forms (Baggio et al. 2007). The DL are graduated in five levels consistently with the Macroseismic European Scale (EMS98, Grünthal 1998). From that figure, one can see that the DL tends to be statistically higher for buildings in aggregate than for individual ones.

Obviously, the results are merely qualitative since they refer to buildings located in zones with different seismic hazards and soil conditions and only struck by the L’Aquila earthquake in 2009. However, this outcome is confirmed by the results of the empirical fragility curves derived from the Da.Do data by Penna et al. (2022a) or from Norcia’s survey data (Sista et al. 2019). However, it is worth noting that isolated buildings are usually characterized by structural typology and architectural configurations different from buildings belonging to aggregate, that in general turn out less vulnerable (e.g. isolated buildings are often in peripheric area and belong to modern ones). This is important to be specified in light of the so-called “aggregate-effect” discussed in this study, meant as the effect that boundary conditions provided by adjacent structural units may have on the seismic response of an individual building belonging to an aggregate. Indeed, a proper comparison to assess such an effect may be carried out only if the isolated and in-aggregate configurations are consistent one to each other (as examined in this study), circumstance that obviously is very difficult to be applied when referring to empirical observed data.

In recent years, some studies tried to overcome the issues related to the seismic vulnerability assessment of URM aggregates by adopting various approaches, i.e.: holistic approach (Cardinali et al. 2021); heuristic approach (e.g. Ferreira et al. 2013; Vicente et al. 2014; Brando et al. 2017; Sandoli et al. 2022; Moretic et al. 2022), analytical-mechanical approach (Cocco et al. 2019; Cima et al. 2021; Nale et al. 2021, Lagomarsino et al. 2015); analytical–numerical approach (Ramos and Lourenço 2004; Senaldi et al. 2010; Vicente et al. 2011; Fagundes et al. 2017; Formisano and Massimilla 2019; Bernardini et al. 2019; Degli Abbati et al. 2019; Valente et al. 2019; Greco et al. 2020; Grillanda et al. 2020; Angiolilli et al. 2021; Battaglia et al. 2021; Valluzzi et al. 2021; Bernardo et al. 2022); large-scale approaches based on empirical evaluations obtained from post-earthquake data (Del Gaudio et al. 2019; Penna et al. 2022a; Sisti et al. 2019); as well as hybrid methods (Kappos et al. 2006; Maio et al. 2015) combining the previous approaches through the individuation of representative building classes. Comparisons between different approaches for specific case studies are reported in Chieffo et al. 2019 and Chiumiento and Formisano 2019.

Despite the efforts already made in literature, the following limitations are still recognized. For the pure empirical approach, only the position of the unit is considered as additional vulnerability factors with respect to ordinary residential buildings; moreover, there is the intrinsic difficulty aforementioned to investigate the “aggregate effect”. For heuristic approaches, vulnerability factors specific for buildings in aggregate are based only on expert judgment.

Within different available methods for modelling masonry structures (e.g. D’Altri et al. 2019), several studies regarding analytical-mechanical or analytical–numerical approaches account only for the in plane (IP) response—without explicitly considering local mechanism effects associated to the out of plane (OOP) response of walls—while other are conversely mostly addressed to OOP. Moreover, in most of the studies based on analytical–numerical models, the aggregate is modelled as an entire structure without explicitly considering the interacting effect among adjacent units. However, when aggregates are investigated as entire structures, an unreliable shear redistribution among the structural units may result since the presence of discontinuities between the adjacent buildings is neglected. The interaction effect of adjacent structural units was recently investigated in Angiolilli et al. (2021) through an analytical–numerical approach, by considering different connection level assumptions and by assessing the seismic response in terms of fragility curves; the study highlighted that the effectiveness of the structural link may affect the interaction between IP and OOP mechanisms, especially at the collapse performance state. Please refer also to RELUIS (2010) and Lagomarsino et al. (2015) to consider, in a practice-oriented way, possible interaction effects when the accurate modelling of the entire aggregate is disregarded.

In addition to that, focusing on the role topographic and soil stratigraphic effects, few literature studies have specifically addressed the site-effect on URM study cases to provide clear evidence of the phenomenon and sufficient data accuracy for moving forward with numerical simulation and model validation (e.g. Ferrero et al. 2020, Brunelli et al. 2021a, Brunelli et al. 2022a, Cattari et al. 2022a). Actually, most fragility curves are derived without explicitly considering site effect, which is simplistically considered by using an amplified value of the intensity measure (e.g. Formisano et al. 2021). However, the amplification factor can be estimated too roughly through ground motion prediction equations (e.g. Sabetta and Pugliese 1996), roughly from studies at national scale (e.g. Falcone et al. 2021), and more accurately from seismic microzonation studies at city-scale (e.g. Pagliaroli et al. 2020). Thus, a rigorous approach would require site response analyses under numerous input motions.

Within this general context, the novelty of the present research regards the quantification of effects associated with the combined role of site amplification and the mutual interaction between adjacent structural units during seismic events in terms of fragility curves, explicitly accounting also for both out-of-plane and structural pounding. The case-study consists of five URM buildings inserted in an existing aggregate located in the historic centre of Visso (Italy) struck by the Central Italy 2016/2017 earthquakes (Sect. 2). A 3D Equivalent Frame (EF) model (fixed based assumption) was adopted to represent the IP behaviour of the structural units composing the aggregate (Sect. 3). Nonlinear dynamic analyses (NDAs), according to the Cloud Method approach (e.g. Jalayer et al. 2017), were performed by adopting sets of accelerograms considering either the bedrock and free-field conditions. The adopted EF approach has been selected among other possibilities (D’Altri et al. 2019, Cattari et al. 2022b) for its computational efficiency in performing a huge number of NDAs and for its suitability in the case of URM buildings characterized by quite regular openings, as those analysed. The reliability of such an approach in analogous contexts has been already proven in previous research, as documented in Sect. 3. Local mechanisms were evaluated separately, as usually done in the literature (see Simoes et al. 2014) but based on the storey accelerations derived from the NDAs performed on the 3D global model. That allows to implicitly consider the filtering effect provided by the nonlinear dynamic response of the structure, as proposed in Angiolilli et al. (2021) and further tested in Lagomarsino et al. (2022). The fragility curves derived for the IP global response and local mechanisms, in both the soil conditions, as well as their combinations are discussed in Sect. 4.

2 Key-features of the selected buildings in aggregate and adopted soil profiles

The case-study presented herein deals with an existing masonry aggregate located in the historical centre of Visso (see Fig. 2).

Fig. 2

The case study aggregate in the historical centre of Visso (Italy) with the indication of the five structural units in the façades facing the municipality’s square (U1 to U5 from right to left; picture bottom)

The municipality of Visso was struck by several earthquakes in 2016 causing casualties and widespread damage to the built environment. The three mainshocks (E1, E2 and E3), occurred on 24th August, 26th October and 30th October, were characterized by low epicentral-distance with respect to the investigated case study (i.e. 16 km, 3 km and 11 km for E1, E2 and E3, respectively) and significative moment magnitude MW (i.e. 5.4, 5.9 and 6.5, for E1, E2 and E3, respectively).

2.1 The investigated “row housing” aggregate

The type of the investigated aggregate is very widespread in Italian historical centres and is usually called "row housing" (consisting of a series of buildings aggregated in lines). In particular, the aggregate is composed of five-unit buildings dating back to different eras, each of them characterized by small and simple regular shapes. The openings are mostly on the main façades, and the number of floors varies from three to four. Figure 3a, b depicts the elevations view (a) and the architectural plan (b) of the aggregate.

Fig. 3

Front view facing the municipality’s square (a) and architectural plan (b) of the Visso’s aggregate

The geometric and structural details of the units were assumed on the basis of field survey and, in some cases, were also based on the characteristics of neighboring damaged buildings that showed almost clearly the type of the masonry, the diaphragm system, and the distribution of the internal space, as illustrated in Fig. 4. In particular, the load-bearing walls were characterized by two-leaf stone masonry, with rough stones sizing about 90–120 mm in height and 360–400 mm in length. Floor diaphragms were assumed to be composed of concrete slab (not reinforced) system 150 mm tick, whereas the foundation system was supposed to merely be a prolongation of the load-bearing walls, slightly embedded in the soil, as typically observed for existing URM buildings. The presence of sporadic tie-rods could be observed (see Fig. 4 and Table 1) making some of structural units possibly susceptible to the activation of OOP mechanisms, especially at the upper building floor. Table 1 describes the main geometric features and the structural details of the five structural units.

Fig. 4

Damage of different structural elements of the neighboring masonry buildings located in the historical centre of Visso, useful 178 also to understand structural details of the case study

Table 1 Geometric and structural features of the structural units composing the investigated aggregate. Note that the effective interstory heights were slightly changed in the simulation to avoid numerical issues (i.e. *2.8 m, **3.4 m, ***3.2 m, ****2.8 m

A detailed description of the five structural units is described in the following. The thickness of the external walls was 70 cm at the ground floor and 60 cm at the other levels. The only exceptions regard the thickness of the perimeter walls over the entire U1 height equal to 80 cm. The internal walls were supposed to be 5 cm lower in thickness than the perimeter walls of each specific floor.

In particular, U1 is a 4-story building located on one edge of the aggregate and is the smallest structural unit. For this unit, the ratio between the total resistant wall section and the total surface (defined as RA in the following) is about 14% and 21% along X and Y directions, respectively. U2 is a 3-story building with RA of about 10% in both the directions due to its almost squared plan. The U3 is a 4-story building with RA of about 6% and 18% in X and Y directions, respectively, due to its rectangular shape in plan. U4 is a 3-story building presumably built in an earlier era with respect to the other structural units, sharing the pre-existing walls of U3 and U5 (see the plan configuration of Fig. 3). Indeed, it is characterized by a different height with respect to U3 and presents a structural continuity with the U5 roof system. Actually, due to its structural configuration, U4 cannot be considered as a completely autonomous structural unit and, therefore, it was considered only for the analyses of the possible OOP mechanisms of the front façade because of the absence of tie rods and the scarce wall-to-wall connection with the adjacent structures. Finally, the U5 is located at the other end of the aggregate and is the biggest structural unit of the aggregate in terms of the total surface. For it, RA is about 6% and 17% in X and Y directions, respectively. Regarding the observed DL that occurred following the seismic events, according to EMS98 scale proposed by Grünthal (1998) (i.e. from DL0 to DL5) and on basis only of an external survey, U1 suffered DL3, both U3 and U4 suffered DL2, whereas U2 suffered a damage comprising between DL2 and DL3.

2.2 Topographic and soil stratigraphic features of Visso’s municipality

The municipality of Visso is in a valley characterized by two main soil profiles and represents an interesting case. A detailed study on the site and soil-foundation-structure interaction effects for the P.Capuzi school, very close to the investigated aggregate (see Fig. 2), was already investigated in Brunelli et al. (2021, 2022a,b,c).

In particular, a soil profile representative of the central valley area corresponds to that under the Visso’s school (see Fig. 2), already in-depth studied by Brunelli et al. (2021, 2022b). The other soil profile characterizing the historical center area (see Brunelli et al. 2022a) was classified through two boreholes and a HVSR (Horizontal to Vertical Spectral Ratio) test (MZS3 2018). This profile is made of clayey silt for the first 4 m, overlaying a 11 m thick sandy gravel layer. The lack of exhaustive information about the soil stiffness necessitated the use of correlation functions between SPT data (done for the Visso’s School) and the shear wave velocity (V_S) of each layer of soil profile (see Brunelli et al. 2021a, 2022b). In particular, V_S = 162 m/s was obtained for the clayey silt soil and V_S = 337 m/s for gravel layer. The consequent equivalent V_S up to the bedrock depth is V_Seq = 272 m/s. For the Visso’s school area, there is substantially no discrepancy between the punctual 1D subsoil model and the more detailed 2D analysis, while the valley-effect has resulted to be beneficial for the historical center area as shown in (Brunelli et al. 2022a). In the latter study, a validation of the numerical model adopted in this paper has been provided by comparing the actual damage with the simulated one. For the sake of simplicity, a 1D subsoil model was herein adopted for the studied aggregate since the main purpose of this study was not to obtain the most reliable numerical model reproducing the real overall damage level (as done in Brunelli et al. 2021a or Cattari et al. 2022a for another cases study). Therefore, the seismic inputs under freefield condition were based on the stratigraphic amplification effects simulated in 1D condition with the STRATA software (Kottke and Rathje 2008). In particular, the ground motions used in this paper were recorded at stations located on stiff rock outcrop (i.e. V_S30 > 700 m/s) and selected from the SIMBAD database (Iervolino et al. 2014). Definitively, freefield seismic signals were obtained by propagating the bedrock ones by considering soft soil profiles consistent with the real foundation subsoil of the aggregate. The complete list of used signals and their characteristics are illustrated in Brunelli et al. (2022b).

Note that 370 and 320 ground motions were adopted for bedrock and free-field soil conditions, respectively. In particular, for bedrock, it was necessary to use 50 additional seismic inputs to ensure a consistent derivation of the fragility curves also for high damage levels; these signals are characterized by a higher value of intensity measures and have been extracted from the selection made by (Manfredi et al. 2022). Figure 5 illustrates the response acceleration—response displacement spectra (Sa-Sd) of the ground motions adopted for the two soil conditions. In the same figure, lines proportional to the fundamental periods of the buildings associated with their two main directions (X and Y) are also represented.

Fig. 5

Displacement- and acceleration- response spectra (Sd-Sa) for bedrock and freefield with indication of the fundamental periods along the two directions (X and Y)

3 Modelling and analysis criteria

3.1 Global in-plane response

The structural model of the URM aggregate was developed according to the equivalent frame (EF) modelling approach implemented in the Tremuri software (Lagomarsino et al. 2013). Figure 6a-c illustrates the EF model constituted of piers (vertical elements), spandrels (horizontal elements) and rigid areas (nodes); the indication of the units investigated in detail during the NDAs is also reported.

Fig. 6

a, b 3D equivalent frame model of the aggregate: a front view, b back view; c detail on the EF mesh obtained for the external walls of U1, U2 and U3; d backbone and hysteretic response of masonry elements: piers under shear

More specifically, the piecewise-linear beam model (i.e. NLBEAM) has been assumed to describe the nonlinear response of URM panels (Cattari and Lagomarsino 2013; Cattari et al. 2018). The NLBEAM features a constitutive law describing the nonlinear response until very severe damage levels (DL, from 1 to 5), through the definition of a relation between the drift value δ_E,i and the corresponding fraction of the residual shear strength β_E,i at the attainment of the i-th DL differentiated for piers, spandrels, flexural and shear behaviour (see for example Fig. 6d).

The mechanical parameters adopted are listed in Table 2 and were based on those calibrated for the Visso’s school (Brunelli et al. 2021) through a very accurate numerical simulation of the actual response of this permanently monitored asset. The reliability of those values was also confirmed in Cattari and Angiolilli (2022) and Angiolilli et al. (2022). Some mechanical parameters were slightly modified with respect to those assumed for the Visso’s school based on expert judgment and some preliminary sensitivity analyses performed on the aggregate for the aim of the numerical simulation of actual response reported in Brunelli et al. (2022a). More specifically, the strength values (τ₀) are slightly higher than that used for the school (about 10%), but still consistent with the reference values proposed by MIT (2019) for analogous masonry type. Both the elastic properties (E,G) and the compressive strength (f_m) of spandrels were reduced by 0.7 with respect to that of piers, whereas tensile strength (τ₀) by 0.5, due to the anisotropic behaviour of masonry as well as the prevailing failure to vertical joints of spandrels.

Table 2 Mechanical parameters adopted in Tremuri

Instead, the hysteretic response is controlled by parameters (c1…c4), defining the slope of unloading and loading branches of the hysteresis loops. Parameter values adopted in this study were calibrated to be consistent with experimental campaigns (Morandi et al. 2018, for piers, and Beyer and Dazio 2012, for spandrels) and are listed in Table 3. Please refer to Cattari et al. (2018) and Angiolilli et al. (2021) for further details on the formulation of NLBEAM and its potential in executing NDA.

Table 3 Pier and spandrel parameters adopted for the model at the first and second rows, respectively

Diaphragms are modelled as orthotropic membrane elements. The moduli of elasticity describe the connection degree between diaphragms and vertical wall parallel to its reference direction, whereas the shear modulus represents the shear stiffness of the floor and the horizontal force transfer among the walls.

To explicitly account for the interaction effect between adjacent units, the procedure proposed in Angiolilli et al. (2021) has been implemented. Thus, the units were modelled separately to each other by introducing a finite-length gap and, then, connected by elastic truss elements (sectional area of 0.00164 m² and elastic modulus E of 210,000 MPa with null tensile behaviour) as well as fictitious floors (thickness of 0.05 m, E = 39,420 MPa, G = 13,112 MPa). The finite-length gap represents the semi-length of the shared mid-wall, while fictitious floors limit openings along transversal directions and allow openings between units mainly along their longitudinal directions. Indeed, in the transversal direction, the effect of the fictitious floors strongly reduced the openings between buildings, as usually one can observe in existing units built separately but in contact with the pre-existing ones. The aggregate-effect was first investigated by modal analyses on both the entire 3D EF model of the aggregate (i.e. from U1_A to U5_A) and the ones developed for the individual structural units (U1_I and U3_I) to obtain a preliminary insight into their dynamic behaviour. All the buildings in aggregate were characterized by the same T₁ (i.e. 0.172 s) along the X direction. On the other hand, in Y direction, U1_A and U2_A were characterized by T₁ = 0.144 s, whereas U3 and U5 (as well as U4) by T₁ = 0.117 s due to small “torsional” modes. Furthermore, T₁ associated with the individual buildings was higher (about 12% and 78% for U1_I and U3_I, respectively) than that of the buildings in aggregate (i.e. U1_A and U3_A) along the direction where the interaction takes place (i.e. X direction) due to the confinement among structural units. On the other hand, T₁ was almost similar along the other direction (variation of 5% and −2% for U1_I and U3_I with respect to U1_A and U3_A, respectively). Fundamental periods of the individual buildings in the two main directions are reported in Table 4.

Table 4 Fundamental periods (values expressed in seconds) of the individual buildings and the buildings in aggregate (indicated respectively with the subscript I and A)

Figure 7 shows the capacity curves of some structural units under both buildings in-aggregate and individual buildings cases. The curves are expressed in terms of base shear coefficient (i.e. base shear over weight) versus roof drift, and have been obtained through NSA by applying a uniform force distribution proportional to the mass in X and Y directions and both verses.

Fig. 7

Dimensionless pushover curves obtained for the buildings in aggregate (U1_A, U2_A, U3_A) or individual buildings (U1_I, U3_I) along the X (a) or Y directions (b). The weights of U1_A, U2_A, U3_A, U5_A are 5,528 kN, 5,375 kN, 4,154 kN, 10,371 kN, respectively. Note that the weight of U1_I coincides with that of U1_A, whereas the weight of U3_I is 5762kN (in U3_A, the mass associated with the walls in contact with the adjacent unit was halved)

In particular, regarding the structural response of the buildings in aggregate, in both X and Y directions, a similar behaviour can be observed along the positive and negative directions due to the almost symmetric plan configuration of each structural unit (apart for the U1 in the X negative direction, where connections with adjacent structures are limited). Furthermore, the higher vulnerability of the buildings in aggregate can be observed along the X direction (where the interaction between structural units takes place), especially in terms of base shear coefficient. In that direction, U3_A is characterized by the highest vulnerability, whereas U2_A by the higher seismic response. Note that, in the Y direction, the U3_A is instead characterized by the highest base shear coefficient although its response is very brittle (i.e. almost sudden drop in the shear strength), as compared to the others.

Regarding the aggregate-effect of U1, one can see that, along the X direction, drift capacity (both negative and positive directions) and base shear coefficient (positive direction) are negatively affected by about 5%. Instead, U1 is positively influenced by the aggregate-affect in both the shear strength (up to 10%) and drift capacity (up to 50%) along the Y direction (both negative and positive directions). On the other hand, the aggregate-effect positively affected the shear strength of the U3 in the X direction (about 65% and 55% in the positive and negative directions, respectively) and negatively affected that in the Y direction (about 5%). Moreover, for both X and Y directions, a clear reduction in the drift capacity can be observed for the U3_A with respect to U3_I. Definitively, by observing the capacity curves obtained by NSA, one cannot generalize whether the aggregate-effect positively or negatively affects the seismic behaviour of the individual buildings.

With the aim of deriving fragility curves, it is necessary to synthetically interpret the structural response data derived from each NDA. In particular, the multiscale approach originally proposed in Lagomarsino and Cattari (2015), and then further developed in Sivori et al. (2022) and Brunelli et al. (2022b), was adopted to assign a specific damage level to the building compatible with the EMS98 scale (i.e. from DL1 to DL5). Please refers also to Cattari and Angiolilli (2022) for the description of a more accurate criterion aimed at evaluating the EMS‑98 global damage grade. In particular, the adopted multiscale approach combines two heuristic criteria at wall and global scale. The first (i.e. associated to the “wall scale”) is based on the extension of the “minimum DL” that occurred to piers (DL_min,P), weighted on their shear stress contribution. The concept of the “minimum DL” was originally proposed in Marino et al. (2019) to replace the adoption of the interstorey drift thresholds at the wall scale, as previously adopted in Lagomarsino and Cattari (2015); in particular, such a proposal assigns a damage level to the wall based on the minimum damage level attained by all the elements of a certain floor. The second (i.e. associated to the “global scale”) is based on the top displacement associated with specific fractions of the overall base shear (V_b/V_b,max) of the building estimated on the pushover curves obtained through nonlinear static analyses (NSAs). The multicriteria adopted are summarized in Table 5. For each record, the worst criterion (i.e. the one that occurs at first) is then adopted to assign the final resulting global DL. According to this procedure, results of records can be properly grouped as those associated to the same DL.

Table 5 Multicriteria to define the global DL consistently with the EMS98 criteria (|= or)

3.2 Local mechanism associated with OOP response

Among possible OOP collapse mechanisms usually observed in URM structures after post-earthquake scenarios (e.g. D’Ayala and Speranza 2011; D’Ayala and Paganoni 2017), in this paper, the overturning of façades (i.e. the so-called one way cantilever mechanism) and that of tympanum (or gable) were considered.

The individuation of the walls susceptible to overturning was defined on the basis of building geometry, opening layout, constructive details and restraints given by the structure. In particular, it was reasonable to consider the OOP mechanisms involving the only upper level as well as the two upper levels of the façades facing the municipality’s square, as illustrated in Fig. 8, because of the wall slenderness and the amplification phenomena generally occur for the upper building levels (e.g. Degli Abbati et al. 2018). Those mechanisms were called one-floor cantilever mechanism (1FM) and two-floors cantilever mechanism (2FM), respectively. Note that those mechanisms were assumed only for the Y direction of the building (see Fig. 8a).

Fig. 8

a Individuation of the walls investigated for the OOP analyses; b TM assumed for a portion of a U3 wall, with the indication of the equivalent walls considered in the OOP analyses, c,d walls for which the 1FM a and 2FM b were considered

Furthermore, due to the different number of stories between U1 and U2, as well as between U3 and both U2 and U4, the tympanum (or gable) mechanism I of the wall portion taller than walls of the adjacent units was evaluated. Note that the TM-U3 regards OOP along the X direction of the building and both the positive and negative directions (i.e. TM-U3p and TM-U3n, respectively), whereas TM-U1 regards OOP only along the positive X direction.

Among possible criteria for numerically analyzing OOP mechanisms (Sorrentino et al. (2017), Abrams et al. (2017), Vaculik and Griffith (2018), Derakhshan et al. (2018), Degli Abbati et al. (2021), Galvez et al. (2021), Cattari et al. 2022b), the engineering practice-oriented model based on the classic idealization of single-degree-of-freedom (SDOF) rigid block was adopted in this study. The legitimacy of the rigid-block assumption was proven also by the actual response of the aggregate under examination. More in general, in presence of poor quality of masonry with consequent scarce cohesion of stone/clay units with mortar, disintegration phenomena of the external leaf may also occur (De Felice 2011); this circumstance must be carefully verified for filling units (like U4). In particular, the three-linear SDOF constitutive model proposed in Angiolilli et al. (2021) was adopted, In Fig. 9, it is depicted in terms of OOP displacement (d^*) and pseudo-acceleration (α^* = g x_G/z_G). The latter is computed accounting also for the possible interlocking contribution (α_i = g F 2 h/(3Wx_G)) provided by the internal orthogonal panels to the façade panels subjected to overturning.

Fig. 9

a idealization of the walls subject to OOP mechanisms; b SDOF model for the different units under the assumption of the mechanisms 1FM, 2FM and TM. For the sake of simplicity, in those curves are indicated the thresholds of the four limit states (A, AS, AU, CF) for the only U3 unit and 1FM

It is worth noting that the roof structure is placed perpendicular to the walls located along the X direction of the building (see also Fig. 4). However, because of the structural details of the roof system, it was assumed that 80% of the load was transferred to those walls, while the remaining part to the orthogonal walls placed along the Y direction (i.e. the ones for which TMs were considered). Differently from Simões et al. (2014), the possible restrain (i.e. stabilizing horizontal force) between the panels and the roof was neglected. Also the restrain between panels and diaphragms was neglected for the 2FMs. Table 6 lists all the geometric features and loads referred to walls belonging to U1, U2, U3 and U4 and to the mechanisms 1FM, 2FM and TM. Please see Fig. 9a for the meaning of those parameters. Note that for all the cases, heights and overlap lengths of the masonry units (h_b and l_b) were assumed 0.11 m and 0.19 m according to the typology of the masonry. Moreover, wall density and friction coefficient were assumed 2,100 kg/m³ and 0.577, respectively.

Table 6 Geometric features and loads needed for the definition of the OOP constitutive laws for the wall belonging to U1,U2,U3 and U4 regarding mechanisms 1FM, 2FM and TM

As known, the OOP behaviour is ruled by the loss of equilibrium (sudden overturning phase of the panel after the initial rocking within the pseudo-elastic phase) rather than the attainment of the material strength limits or crack-band lengths. Hence, the difficult definition of specific DL thresholds related to OOP mechanisms can be established only in a conventional manner. However, their definition should ensure, as much as possible, a physical meaning similar to that associable with the IP failure modes reported in the EMS98 and established in Table 5. To this aim, Table 7 defines four different phases of the OOP behaviour based on the maximum d* value computed during the NDAs, namely from the activation of the mechanism (A) to the activated mechanisms with high probability of stable or unstable response (AS or AU, respectively), to certain failure (CF). That classification regards individual OOP mechanisms.

Table 7 Definition of the damage levels for OOP mechanisms

Then, by considering the frequency and extension of the OOP mechanisms, it is possible to convert the four initial OOP phases in five OOP damage levels referred to the overall behaviour of the building and, therefore, ensure a comparison with the five DL defined for the IP behaviour. The “frequency and extension of OOP mechanisms” refer to the activation of all the potentially activable mechanisms for a specific wall or the activation of a single mechanism involving a portion associated to a significant building’s volume. In particular, from DL1 to DL3 it is considered the higher d* among all the considered mechanisms for a specific wall, whereas DL4 and DL5 take into account the occurrence of all the considered mechanisms for a specific wall.

3.3 Local mechanism associated with structural pounding

As described in detail in §1, most existing buildings in aggregate are either with no separation distance or with insufficient separation with respect to the adjacent buildings. Therefore, an earthquake-induced structural pounding may occur, resulting in substantial damage or even total destruction of colliding portions. Typically, the buildings at the end of the “row” aggregate suffer the most severe damage because of the momentum transfer from the internal buildings as well as because of the larger openings that occur for the one-side free buildings; that was also noticed in Shrestha and Hao (2018), where it was also observed that a building sandwiched between two relatively massive buildings could be susceptible to a global crushing effect (Cole et al. 2012). Depending on the dynamic characteristics of the buildings (e.g., fundamental period, mass, height, stiffness, orientation, geometry, etc.), during a seismic excitation, one can observe two phases: i) lateral displacements of adjacent buildings are synchronized (in-phase response) for which collision does not occur; ii) the adjacent buildings most likely develop different lateral responses (out-of-phase) due to the building-to-building variability, as such collisions between adjacent buildings with insufficient/null separation gap are inevitable. Hence, pounding could lead to more severe conditions in the case of adjacent buildings with very different dynamic characteristics because the out-of-phase response occurs more frequently. A schematic representation of the structural pounding between nearby buildings is depicted in Fig. 10 noting that impacts may occur also at the diaphragm levels.

Fig. 10

a Scheme of the possible responses of two adjacent buildings during seismic excitation; b impact phases within the out-of-phase response of two bodies schematized as spheres

Furthermore, in the past earthquakes, it was observed that, generally for cases of adjacent buildings with same height, pounding location mainly took place at the top floors of the pounded buildings except for cases with relatively small gap distance, where pounding tended to take place at the middle or bottom floors (e.g. Naserkhaki et al. 2013).

Structural pounding is a complex phenomenon involving plastic deformations, local crushing, fracturing, and friction at contact points. The process of energy transfer during impact is highly complicated, which makes the analytical/numerical analysis of this problem very difficult because of the high nonlinearity of the phenomenon that, in spite of its complexity, it has been intensively studied in the years, especially for RC buildings or bridges, by developing various models and using different models of collisions (e.g. Anagnostopoulos 1988; DesRoches and Muthukumar 2002; Lin and Weng 2001; Jankowski 2005, 2008; Maison and Kasai 1990; Naserkhaki et al 2013; Raheem 2006; Malomo and De Jong 2022 among the other).

Here, a very simplified procedure was introduced to account for the effect of the structural pounding on the fragility curves of the studied buildings in aggregate. In particular, that phenomenon was analysed in the post-processing of the data derived from the global 3D model, similarly to what also performed for the investigation of OOP mechanisms. The pounding (impulsive) force P_f in an infinitesimal time dt (i.e. between the instant i and i’) is equal to the momentum variation M dv (i.e. P_f dt = M dv, assuming a constant value for M). In finite terms become P_f Δt = M Δv, under the assumption that the P_f value remains constant during the impact. Furthermore, in this study, it was assumed that, at the collision instant, the final velocity was null (i.e. Vi’ = 0), so that ΔV = (Vi-Vi’) = Vi; this is a conservative assumption. Based on the aforementioned considerations, the formulation adopted in this study to compute the pounding force P_f is described as:

$${P}_{f,k}=\frac{{M}_{n} {|V}_{n,k}| }{\Delta {t}_{,k}}$$

(1)

where M_n is the total mass associated with the n-th node of the numerical model (representative of the building portion for which pounding was susceptible to occur), V_n,k is the velocity of the n-th node during the k-th time history, and represents the estimation of the deceleration-time during the k-th time history. In particular, Δt_,k is evaluated within the out-phase response (up to collision) and represents the time needed to pass from a certain value of axial force N_truss,k different to zero (for which pounding phase begin) to null axial force, for which opening between the adjacent units begins. Figure 11 illustrates an example of the evolution of both V_n,k and N_truss,k during the time of a specific NDA at the upper building level, between U2_A and U1_A. From that figure, one can see also the procedure adopted to evaluate Δt,k during the time of the NDA. Therefore, it is possible to compute the variable P_f,k (and its maximum value, P_f,max,k) for each k-th time history. It is important to observe that P_f,max,k does not occur at the same instant of the maximum value of N_truss,k needing the evaluation of P_f,k for all the duration of the k-th time history to correctly estimate P_f,max,k.

Fig. 11

Graphical procedure to depict the estimation of the pounding force during a certain time history

Among the possible pounding mechanisms between the investigated buildings, in this paper, that phenomenon was investigated between U2 and its adjacent units, namely U1 and U3. Furthermore, it was assumed that the effect generated by the pounding of U2 with respect to U1 and U3, was the same as that occurred from U1 to U2 as well as from U3 to U2 (i.e. by computing P_f, only by using Vn and Δt taken from U2). Obviously, this is a simplification because in real cases, pounding between buildings of different mass could result in more severe damage to the lighter building (Shrestha and Hao 2018). Finally, it is worth specifying that the study of the structural pounding is here proposed only to the main façade of the aggregate, where pounding damage that occurred in the real case. Table 8 lists the Mn values involving the structural pounding between U2-U1 and U2-U3 at the three building-levels.

Table 8 Values of the mass (Mn) involving the structural pounding between U2-U1 and U2-U3 at different building levels

Hence, one can compute the maximum P_f (i.e. P_fmax), evaluated during the entire duration of each time history (see Fig. 11c), for each building level. Then, it is possible to verify if that force overestimates the compressive strength of the walls f_m (see Table 2), namely if P_fmax/A_p ≥ f_m, where A_p is the pounding area. As depicted in Fig. 12, for the definition of A_p, it was assumed a 45° load diffusion (in both longitudinal and transversal directions) from a wall portion of U2 to that of U1 or U3. This assumption is consistent with the typical one adopted for the tie-rods design/verification. In particular, the impacting area of U2 depends on the height of the diaphragm (to which the higher mass is usually associated with respect to the other structural elements) as well as the thickness of the wall orthogonal to the façade where impact occurs (i.e. t_x,U2 in Fig. 12).

Fig. 12

Graphical definition of the pounding area

Then, assuming a 45° load diffusion and referring to the mid-plane of the wall belonging to the impacted building, one can compute the A_p. With a diaphragm thickness H_D of 0.15 m (for all the building levels) and wall thicknesses (t_x,U1, t_x,U2) equal to 0.70 m and 0.65 m, at the first and the two upper building levels, respectively, one can calculate for them A_p equal to 0.44 m² 0.39 m².

Finally, from the checks made on the structural pounding for each time history, it is possible to know when compressive failure (i.e. overcoming of the f_m) occurs because of that phenomenon. In that case, an increase by one grade of the in-plane DL for the interested pier was conventionally assigned. Note that a parametric analyses on the effect of this conventional method has been also performed by supposing an increase of two or more grades of DL due to pounding. Results of these preliminary analyses have shown an almost negligible effect on the number of grades assumed for such an increment. That was merely due to the DL assignment criterion adopted in this study, based on the “minimum DL” concept that consider the damage state of all the pier at a certain level (see §3.1) and not only a single peak of damage.

4 Derivation of fragility curves

4.1 Adopted methodology

Among several procedures available in the current literature for characterizing the relationship between engineering demand parameter (EDP) and intensity measure (IM), in the present study, the Cloud Method (e.g. Jalayer 2017) was adopted—so that at each record represents a single IM value and corresponds to a single EDP response. As introduced in §2.2, natural unscaled ground motions (i.e. 370 and 320 for rocky soil and free-field models, respectively), selected to be representative of a fairly large range of IMs, were adopted to model the record-to-record variability. Hence, fragility curves were computed by estimating the probability of exceeding (P_DLi) of different i-th DL given a level of ground shaking quantified through the IM. As usual in risk analyses (Baraschino et al. 2019), a lognormal cumulative distribution function was assumed for the fragility function, as following:

$${\mathrm{P}}_{\mathrm{DLi}}\left(\mathrm{DL}>{\mathrm{DL}}_{\mathrm{i}}|\mathrm{IM}\right)=\Phi \left(\frac{\mathrm{log}\left(\upmu {\left.\right|}_{PGA} \right)}{\upsigma {\left.\right|}_{PGA }}\right)$$

(2)

where P(DL > DL_i|IM) is the probability that a ground motion with a certain intensity measure IM will cause the collapse, Φ is the standard normal cumulative distribution function (CDF), µ is the mean of the fragility function and σ is the lognormal standard deviation. The IM adopted in this work is the peak ground acceleration (PGA). representing also a quite common and robust choice for URM buildings. This choice is also related to the fact that previous works already testified that results tend to be less or equally dispersed by considering, as IM, the PGA rather than, for example, Sa(T₁) (see Kita et al 2020; Brunelli et al. 2021b). Note that, for each k-th analyses, the geometrical mean of the PGA associated with the k-th accelerations in the X and Y directions was used. This choice may be inconsistent in the case of fragility curves derived for OOP mechanisms, for which the failure is mainly due to the PGA of a specific direction of the seismic acceleration (Y direction for 1FMs and 2FMS; X direction for TMs). However, aiming to compare and combine those curves (see §4.5), the authors reputed reasonable to assume for OOP mechanisms the same IM assumed also for the IP response. Furthermore, note that the not-amplified PGA values were considered for the computation of the fragility curves regarding the freefield model (i.e. the PGA values of the freefield condition coincide with the rocky-soil ones).

A description of the derivation of fragility curves, of each structural unit, combined between both IP behaviour and local mechanisms (i.e. OOP and pounding), defined in §4.5, is described in the following. Once IP fragility curves were evaluated directly on the DLs that occurred for the NDAs, due to the difficulty associated with the definition of different DL thresholds to derive opportune fragility curves specifically for structural pounding, the latter was taken into account by negatively affecting the IP response (see §3.3). That condition is considered as IP*. Then, to combine the IP* and OOP fragility curves, for each structural unit, in unique curves considering for both the behaviours, the most punitive condition between IP* and OOP is considered for each time-history. For example, for a specific time history, for which a certain PGA is associated, the worse among the OOP mechanisms of U1 led to DL4, whereas IP* led to DL2. Hence, for the combined fragility curves of U1, the reference PGA is treated to compute the mean and dispersion values of the fragility curve of DL4.

4.2 Bedrock associated with the global in plane response

Figure 13a-c groups the 370 time-histories as a function of the attained DL; each record is associated to its respective PGA. As expected, the DL tend to be higher for increasing PGA, especially from DL2 to DL3. A detail of the number of cases for which a certain DL that occurred during the NDAs is illustrated in Fig. 13d, showing that U1_A is characterized by the higher vulnerability.

Fig. 13

IP response of U1_A, U2_A and U3_A under the rocky soil assumption: a-c DL that occurred for the 370 time histories as a function of their respective PGA geometrical mean (between the PGAs associated with the X and Y directions); d number of time histories for which a specific DL occurred

Indeed, DL4 and DL5 occurred more frequently for U1_A with respect to U2_A and U3_A; moreover, DL0 occurred in a very low number of cases for U1_A. Anyhow, those considerations are merely qualitative, and results are better interpreted in terms of fragility curves in Fig. 14a where they are plotted for each structural unit in-aggregate (U1_A, U2_A and U3_A) for the different DLs (from 1 to 5). Table 9 summarizes the results of the fragility curves in terms of µ and ln(σ) values. In particular, one can see the increasing in the µ values of the curves associated with increasing DL values; furthermore, similar σ values can be observed for all the curves.

Fig. 14

a-c Fragility curves of the IP behaviour (rocky soil assumption) in terms of the five DL for the three structural units

Table 9 Results of the IP fragility curves for the five DLs in terms of µ/ln(σ) values, under the rocky soil case

Aiming to better compare the fragility curves reported above as a function of specific DL, one can observe Fig. 15. Results show that U1_A is characterized by the higher IP vulnerability as well as that U2_A and U3_A have similar seismic fragility. The higher vulnerability of U1_A cannot be associated mainly with its structural features, as it presents a compact geometrical plan as well as the high RA (with respect to the other units). The justification for this result can be found in the dynamic response of the unit during seismic action. As also highlighted in Angiolilli et al. (2021), this trend confirms that pushover analyses describe in a quite rough way the actual seismic behaviour of buildings in aggregates. Indeed, the capacity curves of Fig. 7 illustrated that U1_A was not the most vulnerable unit for both the X and Y directions. On the other hand, the NDAs expressed in terms of fragility curves show a different behaviour for U1_A. Furthermore, in Fig. 15 one can observe the “aggregate-effect” for the only U3 cell by comparing the U3_A and U3_I curves (solid and dotted lines, respectively). In particular, it is clear the benefit offered by the confinement of the adjacent structural units to U3 especially for increasing DL values, as µ is decidedly lower for U3_I with respect to that of U3_A.

Fig. 15

a-e Comparison between fragility curves obtained for specific DL (from 1 to 5) and different structural units (U1_A, U2_A and U3_A) under the bedrock assumption. The dotted curves represt the response of U1_I and U3_I

4.3 Bedrock accounting for the local mechanisms

Figure 16 depicts the results in terms of maximum OOP displacement (d^*_max) that occurred during the NDAs for the four investigated structural units by only considering the 1FM; for the sake of brevity, the results considering 2FM and TM are discussed in the following directly in terms of fragility curves. Results of Fig. 16 show that d^*_max tends to increase for increasing PGA values, up to the attainment of the limit value d₀ (for which the total overturning of the panel occurs). Furthermore, the results highlight the unstable OOP response, showing a consistent number of analyses (d^*_max,k—PGA_k, points obtained for all the k time history) with d^*_max values lower than the A threshold or directly higher than CF threshold. Focusing only on the CF condition among the various units one can see that CF occurred more frequently for the façade of U1 (i.e. 79 times) although that case was characterized by a good OOP constitutive-law (it is worse only with respect to that associated with U3). This result is mainly due to the higher amplification in the floor accelerations that occurred for that façade because of the higher structural height for which d* was evaluated (i.e. at base of the 3^rd level for U3 and U1—whereas for U2 and U4 it was evaluated at the base of the 2nd floor level) as well as the lower constrain level because of a free-side of the U1 building. Moreover, although U3 has the same structural height of U1, the best OOP constitutive-law and the lower floor accelerations that occurred for U3 led to a lower number of certain failures (i.e. 26) with respect to that of U1. Finally, the consistent number of certain failures for U2 and U4 can be merely associated with their respective poor OOP constitutive laws since the amplification of the floor accelerations was lower for them (storey accelerations taken at the 2nd level).

Fig. 16

In that figure is also reported, for each structural unit, the number of time histories for which the various OOP limit states occurred

Aiming to justify the consideration provided above related to the amplification of the floor accelerations, Fig. 17a shows the comparison between the PFA (evaluated at the upper level of U1_A) and PGA values for all the 370 time histories, highlighting that PFA values are higher than the PGA ones, as usually observed in the dynamic response of structures under seismic actions. The PFA-PGA ratio (evaluated at the upper building levels) for all the structural units in aggregate are illustrated in Fig. 17b. In particular, U1_A and U3_A (characterized by 4 stories) suffered higher floor amplification than U2_A and U4_A (characterized by 3 stories) confirming that filtering effect tends to be higher for increasing building levels (e.g. Degli Abbati et al. 2018). Note that the U1_A and U3_A are characterized by 4 stories, whereas U2_A by 3 stories. Note also that U3_A, being placed in the middle of the aggregate and, therefore, more confined in the seismic movement, is characterized by a slightly lower PFA-PGA ratio than U1_A, which has a free-side. It is important to observe how, in Fig. 17b, the major amplification occurs for initial time histories (characterized by lower PGA values).

Fig. 17

a PFA-PGA relations for U1A under bedrock condition; b PFA -PGA ratio for the 370 time histories at bedrock

In general, results highlighted that OOP mechanisms were affected by the combination of PFA amplifications and constitutive law associated with that mechanism (based on the geometric-mechanical features and structural details of the wall subject to overturning).

Referring to fragility curves associated with OOP, due to the issue discussed above about the definition of DL thresholds, in Fig. 18 a sensitivity analysis performed on this issue is reported. The Figure focuses only to U1_A under 1FM but similar effect of the sensitivity analysis was provided also for U2_A, U3_A and U4_A, as well as for 2FM and TM mechanisms. In particular, results of Fig. 18a-d regards the effect of different OOP thresholds (varied one by one with respect to those reported in Table 7): in Fig. 18a the lower bound of A varied from 0.05d₀ to 0.1 d₀; in Fig. 18b the upper bound of A (and lower bound of AS) varied from 0.2d₀ to 0.3d₀; in Fig. 18c the upper bound of AS (and lower bound of AU) varied from 0.4d₀ to 0.5 d₀; in Fig. 18d the upper bound of AU (and lower bound of CF) varied from 0.95d₀ to 0.85d₀. In general, the results show a moderate sensitivity of the fragility curves to the thresholds, especially to the upper bound of AS (or the lower bound of AU).

Fig. 18

Sensitivity of the OOP fragility curves for the U1_A on the different OOP thresholds a lower bound of A; b upper bound of A (and lower bound of AS); c upper bound of AS (and lower bound of AU); d upper bound of AU (and lower bound of CF)

The OOP fragility curves of the four units are reported in Fig. 19, by considering the three individual possible mechanisms (1FM, 2FM, TM). One can see that the most vulnerable condition for both A and AS regards the U1_A under the 1FM assumption, especially for high PGA value. For low PGA values, U1_A under 2FM assumption and U3_A under TM assumption appear slightly more punitive. On the other hand, the most vulnerable condition for both AU and CF involves the U4_A under the 2FM assumption. In general, one cannot see a clear trend among the different mechanisms, highlighting the importance of considering several mechanisms in the analyses of the OOP response. Only for U4, one can see that 2FM is more severe than 1FM for all the four performance states. This is mainly because, in absence of interlocking, the 2FM is always characterized by a more severe constitutive law (see Fig. 9) with respect to 1FM, due to disadvantageous geometrical conditions. Therefore, even if the storey accelerations taken into account for the 1FM (i.e. at the 3rd floor) tend to be higher (because of the amplification effect) to those considered for the 2FM (evaluated at the 2^nd floor), the constitutive law governs the overall OOP behaviour. Obviously, this statement is not always true for OOP mechanisms regarding walls characterized by good interlocking with the orthogonal walls, such as the U2 and U3 cases. Indeed, one can see that 1FM is always the prevailing governing mechanism for U2, whereas 1FM is more punitive than 2FM for U3 (except for the CF limit state). Furthermore, for U3, TM is the prevailing governing mechanism (also because 1FM and 2FM of U3 are characterized by a very good constitutive law). Table 10 lists the parameters characterizing the OOP-DLs fragility curves of the four units.

Fig. 19

Fragility curves of individual OOP mechanisms at different performance states

Table 10 Results of the OOP-DLs fragility curves for the four units in terms of µ/ln(σ) values, under the rocky soil case

Aiming to statistically investigate the most severe OOP mechanism (1FM, 2FM or TM) that occurred for the four structural units, Fig. 20 shows their percentage of occurrence at the different performance states. This figure highlights that, as also commented above, it should be a good practice defining various possible mechanisms for each structure due to the difficulty in defining the prevailing mechanisms at priori when the record-to-record variability is explicitly accounted for. This is fundamental to derive fragility curves in a robust way, by taking into account the interaction between the various mechanisms. Indeed, the higher the percentage of occurrence for a specific mechanism (i.e. for U4 mainly governed by 2FM) the lower the effect in terms of fragility curves of combined mechanisms. The lower the prevalence of occurrence of a specific mechanism (i.e. for U1) the higher the effect in terms of fragility curves of combined mechanisms. This effect can be observed in Fig. 21, where the fragility curves of combined OOP mechanisms obtained through the criteria defined in Table 11 are illustrated.

Fig. 20

a-c Statistic investigation on the most severe OOP mechanism (1FM,2FM or TM) occurred for the four structural units at the differend DL. (* at least two mechanissms for which CF occurred)

Fig. 21

a-e Comparison between fragility curves of combined OOP mechanisms obtained for specific DL (from 1 to 5) and different structural units (U1_A, U2_A, U3_A and U4_A) under the rocky soil assumption

Table 11 Results of the fragility curves of combined OOP mechanisms for the five DLs in terms of µ/ln(σ) values, under the rocky soil case

Finally, regarding the structural pounding, Fig. 22a shows the pounding failure that occurred between the adjacent structural units at the different building levels. In particular, between U2 and U1, pounding led to a consistent frequency of failure (about 32% of the 370 NDAs) only at the third level (i.e. L3) because of the very small masses acting at the first two levels (see Table 8). On the other hand, between U2 and U3, failure occurred for only about 10% of the NDAs, albeit with a failure diffusion among the three building levels. The effect of the pounding in terms of fragility curves can be observed in Fig. 22b-d, where it is possible to see that the IP curves are negatively affected (up to about 6% for U3_A) at the medium–high DL (i.e. DL3, DL4, DL5). Note that, the entity of negative effect could be more evident if a different method would have been adopted to define the building DL (i.e. not based on the minimum DL but on peak principles).

Fig. 22

a Pounding failures occurred between U2-U1 and U2-U3 at the various building levels (L1, L2, L3), under rocky soil condition. (b-d) Effect of the consideration of the structural pounding on U1_A and U3_A (bedrock) (note that the percentage of variation are computed with respect to the µ value of the IP response)

4.4 Site amplification effects on both global and local behaviour

The site amplification effects on the vulnerability of the buildings in aggregate are here discussed. Regarding the IP response, that effect can be observed in Fig. 23a in terms of fragility curves. In particular, it is possible to observe the strong reduction in the µ value in the case of freefield condition, as compared to those referred to bedrock condition. Moreover, for freefield and contrary to bedrock, the vulnerability of the different structural units is pretty similar to each other; U1_A is not so much vulnerable as the other units as observed for bedrock condition (§4.2). The µ and σ values of the fragility curves are reported in Table 12. From Fig. 23a one can see the response associated with individual buildings (dotted lines for U1_I and U3_I) noting that the aggregate-effect positively influenced the nonlinear dynamic response of the buildings leading especially for U3_I and medium–high DL. However, it is worth noting that the aggregate-effect is much more evident for bedrock than freefield.

Fig. 23

a, b Site effect (bedrock Vs freefield condition) on the IP (a) and OOP (b) fragility curves of the four structural units. (* not evaluated for OOP)

Table 12 Results of the IP fragility curves for the five DLs in terms of µ/ln(σ) values, under the freefield case

Regarding the OOP response, first note that a not strong variation in the most severe OOP mechanisms (1FM, 2FM or TM) that occurred for the four structural units at the four performance states, with respect to bedrock condition (see Fig. 20). Hence, the site effect in terms of fragility curves is represented in Fig. 23b. In particular, the curves representative of the freefield condition are more punitive with respect to the bedrock ones keeping almost the same trend observed for the bedrock condition.

Regarding structural pounding, a higher effect of the site-amplification can be observed in Fig. 24 with respect to the bedrock condition. In particular, pounding led up to 40% of failures (note that, for freefield, this value is computed on a small number of ground motions). Moreover, IP curves are negatively affected in a more diffused way (up to 5% for U1_A) at the different DL, as compared to the bedrock condition. Tables 13, 14 and 15 list the parameters characterizing the fragility curves for combined OOP mechanisms, IP-OOP combined mechanisms and IP*-OOP mechanisms, respectively. 

Fig. 24

Effect of the structural pounding on U1_A, U2_A and U3_A (freefield). The percentage of variation is computed with respect to the µ value of the IP- freefield response

Table 13 Results of the fragility curves of combined OOP mechanisms for the five DLs in terms of µ/ln(σ) values, under the freefield case

Table 14 Results of the fragility curves of the combined IP-OOP mechanisms for the five DLs in terms of µ/ln(σ) values, under the freefield case (*only characterized by OOP behaviour)

Table 15 Results of the fragility curves of the combined IP*&OOP mechanisms for the five DLs in terms of µ/ln(σ) values, under bedrock and freefield conditions (IP* = in plane affected by pounding; *only characterized by OOP behaviour)

4.5 Integration of the in-plane response with the local analysis

To derive fragility curves associated with combined global and local analysis, for each time history, the highest DL produced by them was considered (see also §4.1). Hence, giving a specific DL, if a prevailing failure mode is observed, the combined curve almost coincides with the most severe one. On the other hand, if one cannot observe a prevailing failure mode between IP or local mechanisms, the combined curve is much more severe than those associated with individual analyses.

Figure 25 shows the comparison between fragility curves of the four structural units under bedrock and freefield conditions, for each DL. Those curves are representative of individual mechanisms (IP* or OOP) as well as of combined analyses. Since pounding effect was already discussed in the previous section, here only IP* is reported for the sake of clarity. Note also that in the case of the filling structural unit U4_A, the combined curve coincides with the OOP one. The results show that DL1 is governed by the IP* response and, therefore, the combined fragility curve coincide exactly with it. Also for DL2, IP* prevails on OOP but, especially for U1_A and U3_A, the fragility curves of combined mechanisms are slightly more severe than the IP* ones. This means that for some time histories, OOP mechanisms led to higher DL as compared to IP*. The effect of the combined analyses could be better observed for the DL3 curves, especially for U1_A and U3_A under bedrock conditions, for which OOP prevails on the IP* response for low PGA values (up to about 0.4 g). For freefield, the effect of the combined analyses is almost negligible as the IP* behaviour is much more severe than OOP. For DL4, one can observe similar trends commented for DL3 although less interaction between mechanisms can be observed. Finally, for DL5, one can observe that the IP* response tends to become as severe as (or even much more severe) the OOP one because a damage concentration usually occurs mainly on the elements located at the bottom building level, with a consequent strong reduction of the seismic amplification at the upper floor (where the OOP is evaluated). This result confirms the outcomes reported in (Angiolilli et al. 2021; Lagomarsino et al. 2022) at the collapse performance state. In particular, for DL5, OOP prevails for U1_A whereas IP* prevails for U2_A and U3_A.

Fig. 25

a-d Fragility curves related to IP* and OOP mechanisms as well as the combined ones (IP* represents the curve with pounding effect) for all the structural units

The same results of Fig. 25 are illustrated in Fig. 26a (focusing only to IP* + OOP mechanisms) by comparing the fragility curves of the structural units given a specific DL. This plot is important to understand which is the most vulnerable unit for each DL. In general, U1_A tends to be the most vulnerable structural unit for all the DL and both soil conditions, although the extreme vulnerability of U4_A prevails for DL4 (bedrock), due to its scarce OOP behaviour. Note that passing from bedrock to freefield, the high vulnerability of U4_A is strongly reduced (at severe DL), as OOP is no longer the prevailing mechanism.

Fig. 26

a Units by units comparison for each DL in terms of combined mechanisms (IP* and OOP) at both bedrock and freefield conditions; b DL probability density function of the four units under the two soil conditions; c μ_D of the four units under the two soil conditions, also in the case of freefield combined with soil-structure interaction (SFS interaction) (*estimated from Brunelli et al. (2022b))

Finally, from the results of Fig. 26a it is possible to define the damage probability of each unit and each DL, as depicted in Fig. 26b for both bedrock and free field conditions. Therefore, it is possible to compute the mean damage μ_D=$\sum_{i=1}^{5}{DL}_{i}{P}_{D{L}_{i},\widehat{PGA}}$ (expressed as continuous values and depicted in Fig. 26c) for each unit under both bedrock and free field, where ${P}_{D{L}_{i},\widehat{PGA}}$ is the probability associated with the $\widehat{PGA}$ (equal to 0.2604 g) measured during the E2 seismic event and evaluated in Brunelli et al. (2021a) through an opportune deconvolutional study. It is worth noting that soil-foundation-structure (SFS) interaction was neglected in this study, while in other works (e.g. Brunelli et al. 2022b) it was highlighted that SFS interaction combined with site-effect can also have a potential beneficial effect with respect to the only site-effect in terms of fragility curve. Therefore, only for greater completeness, it is reported in Fig. 26c also the μ_D value in the case in which freefield is combined with SFS interaction by applying the corrective coefficients provided in Brunelli et al. (2022b) to the fragility curves obtained by fixed-base models. In general, results show a good consistency with the field evidence although a general overestimation of the DL with respect to the observed one can be noted, especially for U3, which represents the unit with the higher number of possible local mechanisms (thus strongly impacting the results obtained in this study). However, it is worth noting that the procedure proposed in this paper was not addressed to the simulation of the actual response of the aggregate to a specific event but instead to develop fragility curves.

5 Conclusions

This paper presents an integrated evaluation of both the in-plane (IP) behaviour and local mechanisms (out-of-plane, OOP, and structural pounding) within a procedure for deriving seismic fragility curves of mutually interacting existing URM buildings aggregated in a row layout. The procedure has been exemplified on an aggregate located in Visso (Italy) and struck by the Central Italy 2016/2017 earthquakes.

The first important outcome of this study regards the inefficacy of capturing the actual seismic behaviour of masonry buildings in aggregate through nonlinear static analyses, at least with common load patterns proposed for ordinary isolated buildings. This outlines an important goal that future research efforts aim to be addressed especially to develop practice-oriented seismic assessment procedures.

Therefore, the seismic behaviour of the aggregate was investigated performing nonlinear dynamic analyses (NDAs), according to the Cloud Method approach, on the global 3D equivalent frame model of the aggregate accounting for the interaction effects among adjacent structural units, thus estimating more accurately their IP damage state. Then, storey accelerations derived from the 3D model—explicitly accounting for the filtering effect provided by the nonlinear response of the structure -provided more realistic seismic inputs to be used in the local mechanism assessment, which is very sensitive to the record-to-record variability. Note that several plausible OOP mechanisms, such as the overturning of the façades (the so-called cantilever mechanism) and the tympanum mechanism were investigated through the adoption of SDOF analytical models. Additionally, the structural pounding between adjacent structures was evaluated through a new simplified procedure, also based on the storey accelerations derived from the 3D model. According to that, the evaluation of the corresponding pounding force eventually may lead to additional IP damage level to the structural elements for which that phenomenon appeared.

The combination of IP and local mechanisms was then investigated also considering site effects. The results highlighted that site-amplification may increase the failure probability associated with IP damage even if buildings, under the bedrock motion, appear vulnerable to local mechanisms. This result is obviously related to the investigated buildings, which are characterized by an inherent high IP vulnerability due to the low ratio between cross-section areas of masonry walls and openings. Note that the prevalence of the IP response for the investigated buildings is consistent with the field evidence.

On the other hand, under the bedrock condition, the results showed that, especially for medium damage levels (i.e. DL3), the overall seismic response of the buildings in aggregate was significantly affected by OOP behaviour. For low damage level (i.e. DL1 and DL5), the overall seismic response of the buildings in aggregate was instead mainly governed by IP behaviour. In particular, for DL1, the IP behaviour prevails on the OOP because of the effectiveness of the sporadic seismic strengthening system, preventing the OOP of the façades. For DL5, the IP response tends to become as severe as the OOP one because of the damage concentration that occurred mainly on the elements located at the bottom level, with a consequent strong reduction of the seismic amplification at the upper floor (where the OOP is evaluated).

Especially at the bedrock condition, the combined fragility curve, considering the highest DL produced by the IP or OOP mechanisms, is much more punitive than those associated with individual mechanisms. Therefore, even if evaluated in a separate way, local and IP responses should be combined to obtain the actual response of the buildings under seismic action.

The study also highlights that it is fundamental to consider various OOP mechanisms to derive robust fragility curves. Indeed, although some geometric/mechanical configurations may suggest the prevalence of a specific mechanism rather than others, it is not recommended to consider only the most probable one because, within nonlinear dynamic analyses performed by using a large set of time histories, for some of them, it is possible that a less probable mechanism leads to the most severe response, thus negatively affecting the fragility curves.

Regarding the structural pounding, the simple engineering practice-oriented procedure introduced in this paper was a first attempt to consider this phenomenon in relation to seismic fragility curves, and obviously, further research into this methodology should be provided in future works. However, the proposed rocedure could be easily introduced when explicit dynamic contact is not possible to introduce in the numerical model (as in the case of most of the current FEM software/framework available nowadays). The results showed that structural pounding could have a not negligible effect, especially for high-very high DL (i.e. DL3, DL4, DL5). Therefore, its evaluation should be further investigated  in the seismic assessment of mutually interacting URM buildings in aggregate.

Finally, although some outcomes on the relationship between the IP and OOP response and its possible sensitivity to rocky/soft soil conditions may depend on the specific architectural/structural configuration of the examined aggregate, the procedure turned out quite effective in quantitively assessing such effects and could be conveniently replicated on other cases study. Indeed, the fragility curves developed in this study – enriched by others developed on further aggregate’s archetypes and further investigations on the soil-structure-foundation interaction effects—have been already applied also with the aim of developing damage scenario at urban scale for the whole historical centre of Visso (see Brunelli et al. 2022c). Results have proven a quite good agreement between actual and simulated damage levels of structural units and, thus, have confirmed the potential effectiveness and relevance of the proposed numerical approach to discriminate the response of aggregates characterized by different configurations, masonry typologies and structural details. This outcome further encourages a wider application of the numerical strategy tested in the paper to other case studies.