1 Introduction

The concept of business continuity, which aims to ensure continuity of business activities in the event of a disaster, has become popular since the 1970’s (Maruya et al. 2006, 2008). In response to earthquakes, typhoons, floods, terrorism, and other disasters, national standards for business continuity (AS/NZS 2004; BSI 2003, 2006, 2007; Central Disaster Management Council 2005) have been established in many countries since the 2000’s, and ISO standards (ISO 2012, 2013) have also been published. This has increased interest in the ability of structures to endure disasters. Moreover, it has increased interest in determining the state of usability immediately after a disaster and the ability to quickly recover if the structure is damaged.

In fact, even in past earthquakes, structural damage has had a great impact on the society and the economy. In the 1995 Hyogo-ken Nanbu (Kobe) Earthquake, the damage to buildings and equipment of companies and factories disrupted the supply chain, and local economies such as the steel, automobile, liquor brewing, and chemical shoe industries suffered great damage (Maruya 2008). Moreover, following this earthquake, the number of seismically isolated buildings has increased rapidly (Melkumyan 2013), reflecting the increasing attention to continuing daily life and business and using buildings even in the event of a large earthquake.

In the subsequent 1999 Chi-Chi earthquake in Taiwan, damage to the electronic component industry caused a global crisis in computer production (Lee et al. 2019). Even in the case of the 2011 Great East Japan Earthquake, the effect on corporate operations extended not only to the earthquake-damaged areas but also to Japan as a whole, and the importance of a business continuity plan and business continuity management was reaffirmed (Maruya 2013). After the 2016 Kumamoto earthquakes, it was confirmed that many buildings were damaged by two consecutive strong earthquakes, and some gymnasiums could not be used as evacuation centers because of the structural damage (Iyama 2018).

To reduce such economic damage, the safety of buildings and infrastructure after an earthquake must be immediately confirmed. In addition, if the structure is damaged, the degree and location of the damage must be identified, and the type of repair that should be performed must be quickly determined. Structural health monitoring technologies are a promising method to achieve this and have been the focus of several studies in recent years. Numerous seismographs have been installed on the ground and on structures since the 1970’s, and real-time analysis after earthquakes and operational modal analysis have been applied to many structures, such as stadiums (Jones et al. 2011; Magalhães et al. 2008; Peeters et al. 2007) and tall buildings (Brownjohn 2005), to understand the vibration behavior and damage status. For civil infrastructure, many attempts to apply accelerometers to bridges (Ali et al. 2019; Brownjohn et al. 2010; Castellanos-Toro et al. 2018; Deraemaeker et al. 2008; Diaz et al. 2012; Magalhães et al. 2012; Peeters et al. 2003; Reynders et al. 2010; Ubertini et al. 2013; Whelan et al. 2009; Xu et al. 2019) or arch dams (Darbre et al. 2000; Prior et al. 2018) for the detection of vibration properties have been made. Additionally, several monitoring systems for building structures have become commercially available (Sivasuriyan et al. 2021). Most of them estimate the overall behavior of the structure by measuring the acceleration response, such as the natural period, damping ratio, and inter-story drift, to determine the structural performance and integrity (Brownjohn 2003; Nayeri et al. 2007; Todorovska et al. 2007; Yousefianmoghadam et al. 2018).

However, the change in the response behavior of a building structure due to structural damage is usually very slight, which makes detection difficult even when the structural damage was severe. Kubota et al. (Kubota et al. 2017, 2018) conducted a large-scale shaking table test using an 18-story steel moment frame specimen and found that even when many of the beam ends in the structure yielded, the dominant frequency of the system did not change as long as the individual structural elements did not fracture. In contrast, according to the measurements acquired from actual buildings, the dominant frequency and damping ratio may change even if the building suffers little or no structural damage (Iiba et al. 2012). Extensive efforts to develop advanced techniques for identifying damaged members and their locations by analyzing the acceleration response to microtremors have been made. Hann et al. (2009) proposed a mathematical method based on only the acceleration response of steel frames. Bernal (2002) proposed using vectors for damage localization in truss structures; however, since these are mainly based on analytical study or small experimental models, the applicability to actual buildings or civil structures was yet to be confirmed.

Strain can be mentioned as a measurement index instead of acceleration. Since strain is strongly related to the behavior of individual structural members, it is considered to be more appropriate as a damage evaluation index than acceleration. Many attempts have been made to detect fractures in civil infrastructure using strain gauges and optical fiber sensors to measure traffic load and changes in stress distribution (Brownjohn et al. 2007; Catbas et al. 2002; Kobayashi et al. 2004; Li et al. 2006; Liu et al. 2009; Miura et al. 1994; Pines et al. 2002; Reynders et al. 2007; Sousa et al. 2013; Toyota et al. 2008). For building structures, Kurata et al. (2013) and Matarazzo et al. (2018) proposed the use of piezoelectric sensors to measure the strain at the lower flange of beam ends and compared the strain amplitudes before and after seismic loading to detect the reduction in cross-sectional area due to crack propagation or fracture. Iyama et al. (2017, 2019) proposed a shaking table test method and defined the “local stiffness” using the strain response measured by the strain gauges attached to the beam flanges and the displacement measured by the displacement transducer; the results confirmed that this method is effective for fracture localization. However, methods for detecting the buckling damage rather than fracture have not been established.

In recent years, large-span steel structures have been widely adopted for stadiums, airports, and train stations owing to the advantage of realizing a large space for multi-functional use, such as temporary shelters for evacuated people after a devastating earthquake. One of the most shocking damages caused by the 2016 Kumamoto earthquake was the fracture of space truss elements in a gymnasium, where the truss member fractured, fell down and stabbed into the floor of the gymnasium (Iyama et al. 2018). Fortunately, this structural damage did not lead to casualties, but the stadium could no longer be used as a shelter for people whose houses were damaged during earthquakes. The analysis clarified that the fracture of truss structures was triggered by buckling deformation (Terazawa et al. 2018). For early detection of this fracture damage, signs of destruction must be detected as early as possible. Therefore, if such damage is to be detected in advance, it is considered necessary to detect slight buckling before fractures occur. However, although some studies have been done relating to damage detection of large space structures (Magalphaes, Jones, Peeters), still it is difficult to detect small buckling damage prior to fracture and it is necessary to establish a new methodology.

As mentioned earlier, strain measurement is considered more effective than acceleration measurement for buckling detection of individual members. At the laboratory level, it is common practice to attach strain gauges to both sides of a component and detect the occurrence of buckling when the values deviate from each other. In such experiments, strain measurement for buckling detection is performed while the load is applied and the damage progresses; however, even after the occurrence of an earthquake and termination of the damage process, if residual deformation due to buckling remains, it is expected that the strain vibration properties will change under subsequent minor earthquakes and microtremors, which can be used for buckling detection.

Aiming to establish a technology to detect such signs of damage in truss structures, which are often used in large-span structures, the abovementioned changes in the predominant frequency, mode shape and strain vibration properties due to buckling of truss members are analyzed in this study through static loading test, shaking table test, and finite element analysis (FEA). Especially in the strain measurement and analysis, the mathematical relationship between the difference in strain amplitude on both sides of the member and the residual deformation due to buckling is introduced and compared with the experimental results to show the possibility of quantitative evaluation of buckling damage by strain measurement.

2 Experiment

2.1 Methodology

A cantilever beam was extracted from a three-dimensional truss and used as the specimen. It was statically loaded or excited by a shaking table to cause damage. Microtremor measurements were performed before and after loading and excitation, and changes in the predominant frequency, damping ratio, natural mode, and strain distribution were investigated.

The test procedures are listed in Table 1. Two types of tests—static loading and shaking-table tests—were performed. The former consisted of static loading, impulse response measurements, and microtremor measurements. In the static loading step, displacement was applied statically to the tip of the specimen to cause structural damage. The acceleration and strain were measured during the impulse response or a microtremor to investigate the change in the vibration characteristics owing to the structural damage. The shaking table test involved earthquake wave excitation, random wave excitation, and microtremor measurements. The former was applied to cause structural damage; subsequently, the other two were performed to capture the effect of the damage.

Table 1 Test procedures
Full size table

2.2 Specimen

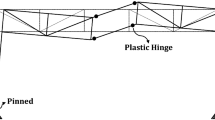
A reduced-scale model of a part of the three-dimensional truss structure supporting a large space was used as the test structure. Figures 1 and 2 show the photograph and schematic, respectively, of the test specimen. The test was conducted at the shaking table facility in Institute of Technology of Tokyu Construction, Kanagawa, Japan. A cantilever beam was selected as the specimen that would cause buckling upon excitation within the limitations of the size and capacity of the shaking table. It was assumed that the two lower chord members marked as BE (bottom east) and BW (bottom west) in the figure would lose their strength and stiffness owing to buckling in the final state. An aluminum pipe (30 mm outer diameter, 3 mm wall thickness, JIS A6063) was used as the upper and lower chord material, whereas angle steel L-75 × 75 × 9 (JIS SS400 material) was used as the diagonal and horizontal material. The yield stresses for A6063 and SS400 are 121 MPa and 245 MPa, respectively. Each element was connected via a joint block using a slip-critical joint with high-strength bolts. Mass was added to the free end by means of two steel plates (1270 mm × 600 mm × 22 mm, approx. 131. kg each); loading and excitation were applied so that the tip of the three-dimensional truss would swing in the vertical direction. Two specimens were fabricated, one for the static test and the other for the shaking table test, as described in the following sections.

Fig. 1
figure 1

Photograph of the test specimen

Full size image
Fig. 2
figure 2

Specimen, measurement, and loading method (Unit: mm)

Full size image

This specimen was designed so that the buckling would occur at the aluminum chord members, which may have a different relationship between frequency and strain response from that of steel truss structures. However, the effect of buckling damage to the frequency and strain responses mainly depends on the geometric nonlinearity and the sensitivity does not depend on the Young’s modulus of the material. For this reason, it is considered that the difference of Young’s modulus would not have a significant effect on the subsequent analysis from a viewpoint of whether buckling damage can be detected or not by small vibration response measurement, and that the obtained conclusions are to be applicable to steel truss structures.

2.3 Static loading test

Vertical loading was statically applied at the tip of the test specimen at two points, as shown in Fig. 2. The wire connected to the specimen via load cell was loaded with a lever block connected to the reaction floor, as shown in Fig. 3. The test was conducted from Phase 1 to 5, as shown in Table 2. In each phase, the axial strain of the BE/BW lower chord member was used as the control value, and loading was performed up to the loading target strain, followed by unloading. In Phase 4, it was observed that the load reached a maximum; at this point, loading was stopped, and the specimen was unloaded. After the loading process in each phase, the free vibration was measured by applying an impulse manually. In Phase 5, the material of BE and BW underwent significant buckling, and the specimen came into contact with the collapse prevention structure; therefore, the experiment was terminated. Fig. 4 shows a photograph of the final condition after the test.

Fig. 3
figure 3

Loading method in static loading test

Full size image
Table 2 Static loading test procedure
Full size table
Fig. 4
figure 4

Photograph of final condition in static loading test

Full size image

The load–displacement curves obtained in the static loading test are shown in Fig. 5. The results of each test can be distinguished based on the line color and plot shape. The displacement was calculated as the average value measured at the two loading points of the test specimen. From the load–deformation relationship, it can be confirmed that the nonlinearity progressed in each test, and the residual displacement increased after unloading. Figure 6 depicts the buckling observed in the lower chords after the static loading test. After experiencing a maximum strength of approximately 1.9 kN in Phase 5, the buckling of the lower chord material progressed and the stiffness entered a negative state, as shown in the Fig. 5 Force was applied until the displacement reached approximately 58 mm; then, the load was removed and the experiment was terminated.

Fig. 5
figure 5

Load–displacement curve from static loading test

Full size image
Fig. 6
figure 6

Buckling observed in the lower chords after static loading test

Full size image

2.4 Shaking table test

As explained in Section 2.1, in the shaking table test, steps (1) through (3) in Table 1 were cyclically applied; the acceleration magnification factor of the earthquake wave was gradually increased until the structure collapsed owing to buckling of the chord members. JMA Kobe wave (NS and UD directions) recorded during Kobe earthquake was used for earthquake wave excitation. Table 3 lists the test number and test name representing the input magnification factor. In the random wave excitation step after the earthquake wave excitation, white noise with a maximum acceleration of 0.2 m/s2 was applied to obtain the acceleration and strain response and estimate the buckling deformation of the chord element.

Table 3 Shaking table test procedure
Full size table

Before the “115%-1” test, no noticeable damage was observed. The “115%-1” test caused out-of-plane deformation of the lower chord elements of BE and BW, which was visually confirmed. The “115%-2” test caused the lower chord members BE and BW to completely buckle, and the specimen touched the collapse prevention frame. Figure 7 shows the photograph after the tests.

Fig. 7
figure 7

Photograph of final condition after shaking table test

Full size image

2.5 Measurement

2.5.1 Acceleration measurement

In the microtremor measurement step, the acceleration was measured with a high-precision servo-type speedometer to capture very slight changes in the vibration characteristics. The speedometer positions are indicated with circular dots in Fig. 2. They were placed at the main nodes of the specimen to determine the response mode shape.

Impulse response measurement and random wave excitation were conducted to verify the applicability of damage detection methods. In these steps, the MEMS accelerometer was used because although it is less precise and accurate than servo-type accelerometers, it is considered more suitable for actual applications because of its affordability. Although it cannot capture small vibrations during microtremors, it can measure the response during a small earthquake, such as an aftershock, with sufficient accuracy. The MEMS sensor layout is represented as a square in Fig. 2.

2.5.2 Strain measurement

The strain measurements were performed for two purposes. Measurements during static loading and seismic wave excitation were performed to understand the damage level of the members as a reference for determining the next excitation acceleration level. In addition, strain measurements were performed during impulse response and random wave excitation for damage detection.

The strain measurement position and naming convention of the strain gauges on a chord member are shown in Fig. 8. Fourteen strain gauges were attached to seven cross sections for each of the three chord members, i.e., BE, TC (top center), and BW.

Fig. 8
figure 8

Strain measurement positions (Unit: mm)

Full size image

The strain was measured using dynamic strain amplifier units developed independently using an inexpensive A/D converter chip. Although each unit synchronizes its internal clock with a network time protocol (NTP), the measurement was performed according to its own clock; hence, it was not completely time-synchronized. In addition, time synchronization based on the NTP may have a discrepancy of several tens of milliseconds.

Figure 9 shows a sample time history and its spectrum of strain and acceleration measured using the inexpensive dynamic strain amplifier unit with strain gauges, BE_s4U, BE_s4L, BW_s4U, BW_s4L, and MEMS accelerometers, b01 and b02, during random wave excitation. The lower graphs show an enlarged view of the upper graphs. The measured time history and spectrum of the two MEMS accelerometers and four strain gauges display almost the same shape, indicating successful measurement. From Fig. 9a, a slight phase shift is observed between strain and acceleration. This is because the accelerometer and strain gauge operate independently and are not completely time- synchronized in this measurement system. Therefore, the following analysis only focuses on the Fourier amplitude, ignoring the phase.

Fig. 9
figure 9

Recorded time history and spectrum

Full size image

2.5.3 Motion capture system

In the static loading test, a motion capture system was used to measure the deformation of the lower chord member. Ten targets were attached to the BW element, as shown in Fig. 10, and the change in the deformation was measured in the test.

Fig. 10
figure 10

Measurement target locations for motion capture system placed on BW element in static loading test (Unit: mm)

Full size image

In the shaking table test, to capture the deformation of the entire specimen, the target was attached to the main nodes of the specimen, and measurement was performed after every earthquake wave excitation. The locations of the targets are marked with triangles in Fig. 2.

3 Measurement results

3.1 Change in predominant frequency and mode shape

This section discusses the predominant frequency and mode shape obtained by the microtremor measurements in the static loading and shaking table tests.

Figure 11a shows the change in predominant frequency obtained by curve fitting of the transfer function obtained from the microtremor measurement as well as the unloading stiffness measured from the load–displacement curve shown in Fig. 5. It can be seen that the results become smaller as the static loading test proceeds, implying the gradual development of buckling damage. To be precise, between phase 1 and phase 5 where a clear local buckling was observed, the change ratio of frequency was about − 16%, while the stiffness change read from the load–displacement curve is − 34%. These values are consistent, considering the frequency is proportional to the square root of the stiffness, given the mass is constant.

Fig. 11
figure 11

Predominant frequency and damping ratio

Full size image

Figure 11b shows the predominant frequency and damping ratio obtained from the shaking table test. The horizontal axis shows the vibration magnitude of the input wave. Two types of plots are included, calculated from the data collected during random wave excitation, and microtremor measurement. It can be observed that the predominant frequency becomes smaller as the shaking table test proceeds, but the changes are not so significant. By comparing the natural frequencies for the first “10%” test and the last “115%-1” test, the frequency changes in the microtremor measurement and random wave excitation were − 2.7% and − 3.2%, respectively. Comparing these values to the static loading test result shown in Fig. 11a, it is considered that the last “115%-1” (with − 2.7% changes in frequency) test corresponds to Phase 2 or 3 (with frequency changes between − 1.5% and − 4.9%) and has not reached the maximum strength yet. Considering that the specimen has collapsed due to the next excitation of the same strength (115%-2), it is inferred that the change in the natural frequency that can be measured before the collapse is small and it may be difficult to detect it. The damping ratio shown in Fig. 11b fluctuated widely, and no clear relationship was observed with the progress of the tests.

Figure 12 shows the mode shape transition obtained from the acceleration measurement in the shaking table test. The horizontal axis shows the position of the acceleration measurement, and the symbols (e.g. “1” and “a”) in “X Dir” and “Y Dir” axes correspond to the axis names shown with parenthesis in Fig. 2. It can be seen that after the buckling of the BE elements after “115%-1” test, the mode shape was slightly changed. It can be seen that, in Fig. 12a, the participation vectors at the tip of the beam became slightly larger after “115%-1” test. It may be possible to detect the occurrence of buckling during this change in the mode shape but is difficult as the change is very slight.

Fig. 12
figure 12

Mode shape obtained through microtremor measurement in shaking table test

Full size image

3.2 Residual deformation of structure

Figure 13 shows the residual deformation measured by the motion capture system after each excitation in the shaking table test. The two-letter symbols (e.g., “a1”) shown on the horizontal axis in the figure. represent the measured location and each letter (e.g., “a” and “1”) corresponds to the axis name shown in Fig. 2. It can be seen that the residual deformation gradually increases, and the deformation curve tends to bend in the buckling vicinity (i.e., a3, c3, and e3). It may be possible to estimate the approximate buckling location from the residual deformation curves.

Fig. 13
figure 13

Residual deformation obtained with the motion capture system

Full size image

3.3 Local stiffness of axial force and bending moment

In this study, small strain vibrations in the truss members, caused by small aftershocks or microtremors, were considered. Theoretically, only the axial force is cyclically applied to the undamaged truss member; therefore, the stress amplitude is uniform inside a cross section. However, after buckling deformation occurs owing to excessive axial force, both axial force and a bending moment are generated in the member. If this bending moment can be measured quantitatively, buckling can be detected.

The local axial stiffness \(K_{\varepsilon ,a}\) and local bending stiffness \(K_{\varepsilon ,b}\) are indices representing the axial force and bending moment, respectively, and defined as shown in the following equations, where \(f_{peak}\) is the predominant frequency of response; \(\hat{\varepsilon }_{top} \left( {f_{peak} } \right)\) and \(\hat{\varepsilon }_{bot} \left( {f_{peak} } \right)\) are the Fourier amplitudes of the strain at the top and bottom, respectively, of a section at \(f_{peak}\); and \(\hat{d}\left( {f_{peak} } \right)\) is the Fourier amplitude of displacement at the tip of the beam.

$$K_{\varepsilon ,a} = \frac{{\hat{\varepsilon }_{top} \left( {f_{peak} } \right) + \hat{\varepsilon }_{bot} \left( {f_{peak} } \right)}}{{2\hat{d}\left( {f_{peak} } \right)}}$$
(1)
$$K_{\varepsilon ,b} = \frac{{\hat{\varepsilon }_{top} \left( {f_{peak} } \right) - \hat{\varepsilon }_{bot} \left( {f_{peak} } \right)}}{{2\hat{d}\left( {f_{peak} } \right)}}$$
(2)

\(\hat{d}\left( {f_{peak} } \right)\) is calculated from the acceleration recorded, \(\hat{a}\left( {f_{peak} } \right)\), by b01 and b02, as follows:

$$\hat{d}\left( {f_{peak} } \right) = \frac{{\hat{a}\left( {f_{peak} } \right)}}{{\omega_{peak}^{2} }},\quad {\text{where}}\,\,\,\omega_{peak} = 2\pi f_{peak}$$
(3)

It can be understood that \(K_{\varepsilon ,a}\) and \(K_{\varepsilon ,b}\) are the amplitudes of the axial and bending strain, respectively, under unit deformation amplitude. In a strict sense, these values do not have a unit of stiffness, but as long as the material is in the elastic range, they are proportional to the axial force and the bending moment, respectively, under unit deformation. In this sense, this can have similar physical meaning to "stiffness" but reflects the local characteristics so they are called "local stiffness" in this paper.

Figures 14, 15, and 16 show the \(K_{\varepsilon ,a}\) and \(K_{\varepsilon ,b}\) of the BE, BW, and TC elements, respectively. In (a1) and (b1) graphs in each figure, which depict \(K_{\varepsilon ,a}\), the horizontal dashed line shows the theoretical value calculated from the static frame analysis, which is 33.3 με/mm. It can be observed that \(K_{\varepsilon ,a}\) remains almost unchanged and is close to the theoretical value.

Fig. 14
figure 14

Transition of local stiffness distribution of BE element

Full size image
Fig. 15
figure 15

Transition of local stiffness distribution of BW element

Full size image
Fig. 16
figure 16

Transition of local stiffness distribution of TC element

Full size image

Meanwhile, the (a2) and (b2) graphs in each figure show \(K_{\varepsilon ,b}\), demonstrating that \(K_{\varepsilon ,b}\) significantly changes after damage, especially at the center of the truss element. The \(K_{\varepsilon ,b}\) values are proportional to the bending moment caused by microtremor or small random vibration and the positive value indicates that the top strain is larger than the bottom strain, which corresponds that the measuring position is concave upward. This correspondence can be confirmed comparing (a2) and (b2) graphs and (a3) and (b3) photos.

In addition, the values at the two ends were estimated by extrapolating from the two nearest sections. For example, the values at the left connection were calculated from Sects. 1 to 2. The values of \(K_{\varepsilon ,b}\) at the two ends are not zero after buckling, implying that the ends are not under completely pinned condition and bears some bending moment.

3.4 Eccentric distance estimated from strain amplitude

Since \(K_{\varepsilon ,a}\) and \(K_{\varepsilon ,b}\) are the amplitudes of the axial and bending strain, the axial force amplitude \(\hat{N}\) and bending moment amplitude \(\hat{M}\) at \(f_{peak}\) can be represented as follows:

$$\hat{N} = K_{\varepsilon ,a} \times E \times {\text{A}}$$
(4)
$$\hat{M} = K_{\varepsilon ,b} \times E \times Z$$
(5)

here E represents the Young’s modulus; A represents the section area; Z represents the plastic modulus. The eccentricity e can be estimated as follows:

$$e = \frac{{\hat{M}}}{{\hat{N}}} = \frac{{K_{\varepsilon ,b} }}{{K_{\varepsilon ,a} }} \times \frac{Z}{A} = \frac{{\left| {\hat{\varepsilon }_{top} - \hat{\varepsilon }_{bot} } \right|}}{{\left| {\hat{\varepsilon }_{top} + \hat{\varepsilon }_{bot} } \right|}} \times \frac{Z}{A}$$
(6)

Figure 17 compares the eccentricity e, defined in Eq. (6) and calculated from \(K_{\varepsilon ,a}\) and \(K_{\varepsilon ,b}\), and the out-of-plane deformation at the center of the element for the BE and BW elements during the shaking table test. The latter was determined by visually measuring the displacement between the center of the member and the position of the thread stretched between the ends of the member. The horizontal axis corresponds to the test numbers presented in Table 2. Although the measured value has a large dispersion because of the difficulty in measurement, the trends of the two values almost agree with each other. In particular, in the case of the BW element in the static loading test, the two values show good agreement. It should be noted that in the shaking table test, e gradually increased in the earlier stages of the test, where no other apparent sign of buckling was observed. This result implies the possibility to capture small signs of buckling, such as small out-of-plane deformations of 1 or 2 mm, using this method.

Fig. 17
figure 17

Eccentric distance estimated from the strain amplitude

Full size image

Figure 18 shows the out-of-plane deformation measured by the motion capture system after each static loading test. It can be seen that the deformation becomes larger as the test proceeds. The deformations calculated using the strain measured data at the center of the member (Section 4) and Eq. (6) are also plotted. The plots agree well with those measured with the motion capture system. This result indicates that by applying the strain gauges, the degree of buckling deformation of individual truss elements can be estimated under micro-tremor through strain measurement.

Fig. 18
figure 18

Deformation of lower chord member BW during static test

Full size image

4 Numerical investigation

4.1 Predominant frequency and mode shape

An attempt was made to reproduce the changes in the predominant frequency and mode shape obtained in the experiment through analysis. The numerical model is shown in Fig. 19. The test structure was modeled using 3D wire elements in the structural analysis software, midas iGen. The decrease in stiffness due to buckling of the BE and BW elements was reproduced by adjusting the Young's modulus of the member used in the analysis.

Fig. 19
figure 19

Eigen value analysis model

Full size image

As shown in Fig. 11, changes of − 16% and − 2.7% in predominant frequency was observed in the static loading test and the shaking table test, respectively. According to the test results, equivalent values of the Young's modulus of the BE and BW elements was obtained through trial and error to reproduce such decrease in the predominant frequency. The results are listed in Table 4. “Case A” is the model of the undamaged state, where the Young’s modulus is equal to 100% of the nominal value of the material. “Case B” and “Case C” are the models for reproducing the change observed in the shaking table test and static loading test, respectively. The results imply that the axial stiffness can decrease up to approximately 35% owing to buckling damage. Figure 20 shows the participation function representing the mode shape obtained in the three cases. It can be seen that the natural mode shape hardly changes even when the predominant frequency decreases. This result is consistent with the experimental result that the mode shape hardly changes. The analysis confirmed that it was difficult to detect buckling damage caused by capturing the change in mode shape.

Table 4 Eigen value analysis results
Full size table
Fig. 20
figure 20

Eigen mode shape

Full size image

4.2 Change in strain distribution owing to buckling deformation

In Section 3.4, the out-of-plane deformation estimated from the strain response showed good agreement with that measured by visual inspection and the motion capture system. In this section, one of the chord elements was extracted and analyzed using the FEA software ABAQUS (SIMULIA 2011) to confirm the experimental results. The model shape and loading protocol are illustrated in Fig. 21. This model is a reproduction of the chord element (BE or BW), and has the same shape as that used in the experiment. The material properties are shown in Fig. 21a, where E is the Young's modulus, Et is the post-yield stiffness, and Fy is the yield point. The stress–strain relation of aluminum is assumed to be bilinear, as shown in Fig. 21b, where the post-yield stiffness Et is 5% of the initial stiffness.

Fig. 21
figure 21

Finite element analysis model

Full size image

In the experiment, the end of the chord was connected to the joint unit by bolting; although they are usually designed as pinned joints, there may be some rotational stiffness at the ends. Because it is difficult to estimate the rotational stiffness quantitatively, in this analysis, two types of analysis were performed as two extreme conditions: one with pinned ends and the other with fixed ends.

Axial deformation was repeatedly applied to this model, as shown in Fig. 21c, to cause buckling damage and obtain the out-of-plane deformation and strain distribution after buckling.

Figure 22 shows the results of the FEA, including the buckling shape, stress distribution, and relationship between axial load and displacement. Here, positive values indicate compression load or displacement.

Fig. 22
figure 22

Result of the finite element analysis

Full size image

In Sect. 3.4, the estimated out-of-plane deformation e was calculated using Eq. (6) from the micro-strain amplitude after unloading under a small vibration. In this section, e is estimated from FEA. However, \(\varepsilon_{top}\) and \(\varepsilon_{bot}\), used in Eq. (6), are the strain amplitudes under small vibrations and cannot be determined through static FEA. Therefore, the strain amplitude in Eq. (6) is replaced with the strain difference between the calculated values in FEA. In other words, Eq. (6) can be rewritten as follows:

$$e = \frac{{\Delta \varepsilon_{top} - \Delta \varepsilon_{bot} }}{{\Delta \varepsilon_{top} + \Delta \varepsilon_{bot} }} \times \frac{Z}{A}$$
(7)

here \(\Delta \varepsilon\) represents the change in strain when the load is near 0; top and bot denote the measuring positions of the strain at the top and bottom of the section, respectively. The specific calculation method is shown in Fig. 23. Specifically, two steps (e.g., A and B) located before and after the sign of the load is reversed are selected. The difference in strain between these steps is defined as \(\Delta \varepsilon\), as shown in Fig. 23b.

Fig. 23
figure 23

Calculation of strain difference ∆ε at zero load from finite element analysis

Full size image

In addition, in FEA, a deformed shape can be obtained, which means that the out-of-plane deformation can also be directly obtained. Here, the value obtained by directly reading the amount of out-of-plane deformation at the center of the truss element from the FEA result is expressed as \(e^{*}\).

Figure 24 shows the relationship between e, estimated from Eq. (7), and \(e^{*}\), measured directly. The solid black line shows the result of the fixed model, whereas the dashed one shows that of the pinned model. The results of the pinned model almost match the straight line of \(e = e^{*}\), indicating that Eq. (7) has good accuracy. However, for the fixed model, \(e^{*}\) is larger than e by approximately 1.4 times. The reason for this is shown in Fig. 25. The value of e is calculated using Eqs. (6) and (7), which theoretically correspond to the amount of out-of-plane deformation from the point of zero moment (inflection point), as shown in Fig. 25a. Therefore, in this case, the observed out-of-plane deformation agrees with the estimated value e. In contrast, in the case of fixed support at both ends, \(e^{*}\) can theoretically be up to twice as large as e, as shown in Fig. 25b. However, in this fixed model, the end of the pipe is not directly fixed but joined via a plate. Because the bending stiffness of the plate is not large, it was presumed that \(e^{*}\) would not become twice as large as e.

Fig. 24
figure 24

Comparison between calculated and measured eccentric distances

Full size image
Fig. 25
figure 25

Illustration of the relation between e and e* under pinned and fixed end conditions

Full size image

Furthermore, in the case of the experimental results displayed in the shapes of △, ○, and ◇ in Fig. 24, e indicates the estimated value according to Eq. (6), and e* indicates the value measured via visual inspection or motion capture. The BE plot of the experimental results roughly matches the straight line of the fixed model, and the BW plot roughly matches the dashed line of the pinned model. One possible reason is that although BE and BW were designed with the same end conditions in the experiment, the buckling deformation shapes of BE and BW differed because of a slight difference in the actual installation and loading conditions. The estimated out-of-plane deformation obtained using Eqs. (6) and (7) approximately agrees with the experimental results, although they may be slightly underestimated depending on the degree of restraint at the ends.

5 Conclusion

In the health monitoring of building structures, acceleration response is often measured, and frequency characteristics such as natural frequency and mode shape are analyzed from it, which would be effective to capture the characteristics of the entire building. On the other hand, the measurement of strain response behavior is presumed to be effective for damage detection of individual structural members. In this study, with the goal of detecting damage to three-dimensional truss structural members used in large-span structures, static loading tests and shaking table tests were conducted with a test structure reproducing a part of the truss structure. In this series of tests, the changes in the vibration characteristics of acceleration and strain response of the truss members are discussed and compared with the observed buckling damage and buckling shape.

First, the possibility of detecting the damage was examined by identifying the vibration characteristics, such as the predominant frequency, damping ratio, and mode shape of the test specimen from the acceleration measurement data before and after damage. A decrease in the predominant frequency was observed as the damage progressed; in the static loading test where the loading was performed gradually and carefully, a frequency drop of about 16% was observed at maximum before the complete collapse owing to buckling, therefore, it can be used as an indicator of damage. However, the frequency drop observed in the shaking table test before the collapse was only 3% and the change of the predominant mode shape was also slight; therefore, precise measurement is required to detect this small change. The change in the damping ratio was also investigated, but no clear correspondence was observed with the progress of buckling damage. It can be said that in this structural system, using these physical indicators as indicators of damage is difficult. In addition, it is difficult to determine whether the change in acceleration response is due to damage or other factors; hence, it is essential to use these physical indicators in combination with a judgment method not based on acceleration.

In contrast, a clear tendency was observed in the strain measurement data before and after damage. The experimental and analysis results confirmed that it was possible to calculate the amount of out-of-plane deformation from the strain measured on both sides of the buckling part, and even small out-of-plane deformations of 2 or 3 mm could be detected. Numerical investigations simulating the experiments also showed that the results of the FEA and static loading test were consistent with the theoretical values. However, the end condition of the truss member may affect the accuracy of the out-of-plane deformation estimated using the strain measurements.

In this study, a very inexpensive strain amplifier developed by the authors was used for the micro-strain measurement; although the accuracy is relatively low when compared with commercial measuring devices, measurement was possible with sufficient accuracy. Therefore, the application of the device to buildings is expected to be feasible owing to its low cost and sufficient accuracy. However, considering that the information provided by the strain measurement is very local and that measurement requires a large amount of strain gauges which makes it difficult to apply in an actual building when compared with acceleration measurement, it is necessary to establish optimization and minimization techniques of the measurement points to improve the practicality and applicability.