Nonlinear modeling of the ten-story RC building at E-Defense (2015): assessment with different modeling assumptions

Abstract

Two models of the 10-story reinforced concrete building tested at E-Defense laboratory in 2015 are built: the F model, in which nonlinear behavior is distributed over the element length, and the H model, in which nonlinear behavior is lumped in plastic hinges with a moment-chord rotation response assigned based on empirical formulations proposed in the literature. Nonlinear time–history analyses are performed to reproduce the experimental shaking-table tests performed at increasing seismic intensity level. The incremental experimental test has been performed twice: the first time (BS test), the structure base was free to slip on a concrete base fixed to the shaking table. After the BS test, a second test was performed on the same structure with the foundation fixed to the concrete base (BF test). Both tests are simulated for both models. When simulating both the BS and BF tests, the seismic input adopted for the numerical analyses is the displacement time-history registered at the base of the specimen’s columns, in order to implicitly account for base slip through the input signal without explicitly modeling the slipping devices. It is observed that the significant damage experienced by the specimen during the runs of BF tests at medium–high seismic intensity is probably triggered by softening and damage of beam-column joints: this is reproduced also by H numerical model and highlights the influence of beam-column joints on the overall seismic response of the structure. In general, it is observed that both numerical models, which were constructed, based on experimental data, only by adopting available and well-established tools proposed in the literature, can reproduce the overall response of the case-study structure, especially in terms of maximum top displacement demand and maximum damage state for structural members, provided that beam-column joints’ contribution is adequately considered.

1 Introduction

Past and recent earthquakes showed that the death toll due to severe seismic events is still unacceptably high; in addition, the direct and indirect economic losses following earthquakes put a significant strain on community resilience and challenges its recovery capacity. Therefore, current research in earthquake engineering is focused on both (i) reduction of seismic risk through seismic retrofit of existing buildings/safe design of new buildings and (ii) definition of fast and non-invasive interventions immediately applicable upon earthquake events to restore buildings’ safety.

Focusing on safe design of new buildings, the main challenge is identifying, designing, and validating construction techniques able to assure the protection of building users from collapse and the protection of equipment, assets, and services from damage. There is consensus in the scientific community on the fact that the first goal can be achieved via design tools directly or indirectly accounting for the nonlinear displacement/deformation capacity of ductile structural members, thus allowing widespread but limited and repairable damage to them: this concept has been implemented in structural codes mainly by means of capacity design rules. On the other hand, displacement- and acceleration-sensitive nonstructural components can be effectively protected from damage under the worst earthquake scenarios by limiting the acceleration and displacement demand transferred from the ground to the structure: to this aim, base isolation systems may be considered for new buildings and for the retrofit of existing ones. In fact, through base isolation, it is possible to significantly reduce the global acceleration/force demand acting on buildings struck by earthquakes, as well as the local displacement demand acting on structural and nonstructural members (for example, the interstorey drift ratio demand).

Typically, base isolation systems are realized through steel or rubber sliding devices: however, cutting-edge research is also focused on the assessment of the performance of more simple, less expensive base isolation techniques. To this aim, experimental programs performed on real-scale specimens are a valuable tool to validate the efficiency of these novel techniques, as well as to evaluate the main deficiencies and opportunities related to the response of existing and modern buildings (Pinto et al. 2002, Magenes et al. 2014, Senaldi et al. 2020 Lourenço et al. 2016, Yeow et al. 2020, Kajiwara et al. 2021, Schoettler et al. 2009, Xiao et al. 2015, Zhang et al. 2019).

The ten-storey Reinforced Concrete (RC) building shaking table testing program at E-Defense (2015) is aimed at the assessment of the seismic response of a tall RC bare (i.e., without infill walls) structure (shown in Fig. 1a) with a novel base isolation system simply realized by putting in contact, without any connection, the foundation system of the building, equipped with cast iron plates fixed to the foundation (as shown in Fig. 1b), to the ground, represented by a raft concrete base anchored to the shaking table. This system, which will be described more in detail in Sect. 2, allows base-slipping and rocking of the building under earthquake loading, thus working as a base isolation system. The results of the experimental tests are presented in Kajiwara et al. (2021). In summary, this kind of base-slip system allowed a significant limitation of seismic demand and damage on the case-study structure, as furtherly highlighted by the following test performed on the very same structure after fixing it to the ground. In fact, the base-fixed structure subjected to the same records exhibited significantly higher damage with respect to the base-slipping structure.

Fig. 1

Adopted from Kajiwara et al. (2021)

View of the case-study structure (a) and of the cast iron plates to be embedded in the bottom side of the RC foundation for the realization of the base-slipping system (b).

This study presents the numerical simulation of both the base-slip and base-fix tests and the obtained results in comparison with the experimental ones.

The study is mainly dedicated to the assessment of the efficiency of two different numerical models of the case-study structure in predicting its response during the base-slip and the base-fix tests. Regardless of the actual/experimentally-observed efficiency of a newly-proposed construction practice, its application can be proposed at large scale, only if accurate (but not too much complex for the average expert practitioner) numerical models are actually able to reproduce the experimental response and, by extension, to reliably predict the potential response of a new building constructed by applying the same newly-proposed construction technique. Also, the validation of numerical models can be the base for deriving reliable general-purpose design recommendations for this kind of structures.

So, in this work, two numerical models of the case-study structure are built: first, a fiber-based (“F”) model in which structural members nonlinearity is accounted for by means of a distributed fiber formulation approach that allows the spreading of plasticity along the element length by integrating the element response at given integration points; second, a hinge-based (“H”) model in which structural members nonlinearity is accounted for by means of the definition of plastic hinges at their ends whose response is pre-defined based on a phenomenological/empirical approach. The numerical outcomes are compared in order to show and explain limits and advantages of the two modeling approaches and how they influence the quality of the experimental/observed-vs-numerical/predicted response comparison. It should be noted that the modeling assumptions adopted in this work are not “calibrated” based on the experimental response. In addition, no novel modeling strategy is proposed and applied in this paper. In fact, the objective of this work is showing the performance (in terms of experimental-vs.-predicted response comparison) of well-established modeling approaches proposed in the literature. As already mentioned, both the base-slip and the base-fix tests are simulated in this work. When simulating both tests, the seismic input adopted for the numerical analyses is the displacement time-history registered at the base of the specimen’s columns, in order to implicitly account for base slip within the input signal without explicitly modeling the slipping devices, as described more in detail in Section 2.

Apart for the aims and purposes already mentioned, the institution of reliable numerical models also allows the analysis of the effect of specific design choices on the expected response of a structure. More specifically, also based on the outcomes of this paper, the paper by Del Vecchio et al. (2023), also published in this Special Issue, investigates the effect of beam-column joints design procedure on the expected response of the case-study structure (and so, by extension, of potentially similar structures).

The paper is organized as it follows: Sect. 2 proposes a basic description of the case-study structure and of the testing procedure adopted. Based on this preliminary information, also including modal properties of the case-study structure, the general assumptions adopted for the construction of both the F and H models are presented and discussed. Sections 3 and 4 present and discuss the specific features of F and H models of the case-study structure, respectively, also focusing on the critical aspects faced during their institution. Section 5 describes the procedure adopted to perform nonlinear time–history analyses of the numerical models, thus reproducing the experimental shaking-table tests performed at E-Defense. Section 6 is dedicated to the discussion of the results of the experimental-vs-numerical response comparison. Finally, some conclusions are drawn in Sect. 7.

2 General description of the case-study structure

2.1 Description and initial modal properties of the case-study building

In 2015 a three-dimensional shaking table test was performed on a full-scale 10 story Reinforced Concrete (RC) building specimen at the E-Defense laboratory. The lateral resisting system of the building primarily consists of Moment-Resisting Frames (MRFs) in the longitudinal direction and dual wall-frame systems (WFs) with multi-story shear walls from 1st to 7th story, in the transverse direction. The horizontal system consists of RC floor slabs.

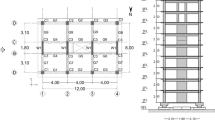
The overall height of the specimen, including foundations, is 27.45 m. The floor heights range from 2.80 m for the 1st story to 2.50 for the 10th story. The building is rectangular and symmetric in plan, with total dimensions for the superstructure equal to 13.5 m in the longitudinal and 9.5 m in the transverse direction. The in-plan and elevation views in frame and wall directions are reported in Fig. 2a–c, respectively, while Fig. 2d shows a prospect view of the 3D model.

Fig. 2

In plan (a), elevation (b, c) and 3D (d) schematized view of the RC building specimen tested at the E-Defense laboratory. Dimensions are reported in meters

The size and details of columns and beams along with shear walls are compliant with current Japanese seismic design standards (MLIT 2007; AIJ 2010). All the columns have rectangular cross-section equal to 55 × 55 cm² from 1st to 3rd story and 50 × 50 cm² from 4 to 10th story, except for the columns substituting shear walls from the eighth to the tenth storey, that have 23 × 45 cm² rectangular cross-section. The dimension for beams cross-section varies between 35 × 55 and 23 × 42 cm² in elevation, depending on the position and orientation, while dimension of beams cross-section at the foundation level varies between 90 × 115 and 35 × 60 cm². The thickness of shear walls is constant along the height and equal to 23 cm except for the 7th story in which it is equal to 15 cm. Nominal concrete compressive strength decreases along the height and is equal to 42 N/mm² from the foundation beams to the 3rd floor slab, 33 N/mm² for the 3rd level columns to the 5th floor slab and 27 N/mm² for the 6th story column to the top of the building. Different steel grades were adopted for longitudinal and transverse reinforcement bars. For RC beams and columns SD345-grade steel bars with diameter ranging between 19 and 22 mm were used for longitudinal reinforcement, while 10 mm or 13 mm bars with steel grades KSS785, S10, or SD295A were used to realize two- or four-leg welded stirrups. For RC walls web and for slabs, a double reinforcement layer is adopted with 10–13 mm bars realized with SD295A steel. Finally, for RC joints two-leg 150 mm-spaced stirrups with 10 mm rebars were used.

In this study, RC member behavior is characterized by adopting different material properties at the different storeys; based on the experimental tests performed on the materials, average values for concrete cylinder compressive strength (f_c) and steel yielding (f_y), reported in Tables 1 and 2, were adopted.

Table 1 Mean values for concrete cylinder compressive strength f_c and Young’s modulus E_cm

Table 2 Mean values for steel parameters

Total loads and masses are extracted from available documentation in order to account for design and added loads acting on the structure during the shaking-table tests. Further details about the geometry of the RC members, material properties and loads can be found in Kajiwara et al. (2015a,b).

The RC building was subjected to increasing values of earthquake shaking. In particular, the experimental test consisted of two different phases characterized by different constraint conditions: a base-slip (BS) test, to examine the efficacy of the base-slip construction method, and fixed-base (FB) test to simulate common construction practice. For both the phases, a raft concrete base (CB) was anchored to the shaking table and the 10-story building specimen was placed above. However, during the BS test, the building specimen was merely placed on the top of the CB, and the contact between the CB and the foundation beam takes place via cast iron bearings, while during the BF test, the specimen foundation beams were anchored to the CB (already fixed to the shaking table itself) by fixing it with prestressed steel bars passing through suitably prepared holes.

The ground motion record of Kobe 1995 earthquake, recorded at the Southern Hyogo Prefecture (JMA 2022), was adopted as seismic input for the experimental tests. The seismic input excitation was simultaneously applied along the three directions. The NS component is applied along the frame direction, the EW component along the wall-frame direction, and the UD component along the vertical direction. The specific record adopted for tests is characterized by Peak Ground Acceleration (PGA) equal to 0.61 g in frame direction, 0.84 g in wall direction; 0.82 g in the vertical direction. During both the BS and BF tests, the intensity of the ground motion was gradually scaled considering four increasing scaling factors, namely 10%, 25%, 50% and 100%. However, as shown in Kajiwara et al. (2021), measured accelerations at the shaking table level (i.e., those actually applied by the shaking table to the structure) are close, but not identical to those of the input signal. This can be noted, for example in terms of measured PGA during BS, at 100% run, where the measured PGA is roughly equal to 1 g in wall direction and in the vertical direction instead of 0.84 and 0.82 g, respectively, as shown in Fig. 6 in the paper by Kajiwara et al. (2021). The difference between target and measured PGA is less significant during 10%, 25%, and 50% runs. The not-perfect consistency between the target input signal and the signal actually reproduced by the shaking table is typical during dynamic tests, especially if performed on big and heavy real-scale structures, as in this case, due to the complex control of shaking tables and of their movements.

2.2 Common modeling assumptions

Three-dimensional models are developed using a Finite Element software to simulate the response of the structure under the sequence of ground motions. The OpenSees (2020) software was chosen in the study to simulate elements and buildings since it offers advanced capabilities for modeling and analyzing structures subjected to static and dynamic loads in linear and non-linear stages. Two different finite element modeling strategies were adopted to simulate the behavior of the structure, namely a Fiber-based (F) model (see Sect. 3) and a plastic Hinge (H) model (see Sect. 4). Both modeling strategies are characterized by some common assumptions reported in the following.

The RC foundation beams are modeled as elastic beam-column elements with cross-sectional characteristics and elastic properties derived from design documents. The presence of openings in the floor slab is not accounted for in the modeling of the slab. Due to transport constraints, the specimen was fabricated in two separate parts and joined using cast iron plates during the assembly phase. In the numerical model, the two parts of the specimen were considered perfectly joined and no additional deformability is accounted for.

Since the seismic design of the building prototype has been carried out by applying a modern code (i.e., accounting for capacity design rules), it has been assumed that beams and columns of the building are ductile, i.e., shear and/or bar slip are considered only for their contribution to the overall deformation of members, not as potential failure modes. The nonlinear response of beams and columns is modeled adopting a fiber-based distributed plasticity approach for the F model and in terms of lumped bending moment-chord rotation response approach for the H model.

Several macroscopic modeling approaches were proposed to reproduce the behavior of RC walls, and the choice of the more reliable modeling strategy still represents an open debate (Kolozvari et al 2018). One of the most common approaches is to simulate the uncoupled flexural and shear behavior modeling wall flexural behavior by means of force-displacement material models (e.g., force-based nonlinear fiber-section beam-column element) to account for the axial-flexural behavior and using a horizontal spring to model the shear behavior (Vàsquez et al. 2016). To realistically simulate the complicated axial-bending-shear behavior of wall piers, improved beam elements such as the Multiple-Vertical-Line element (MVLEM) with or without shear-flexure interaction were also proposed (e.g., Orakcal et al. 2004; Kolozvari et al. 2015, 2021; Isakovic et al. 2019). Finally, the behavior of shear walls can be simulated via 2D membrane or 3D shell elements (Lu et al. 2015, 2018). In both the F and H models, the presence of RC walls is simulated by adopting a distributed plasticity approach via the Force-Based Beam-Column Element with five integration points and the Gauss–Lobatto integration scheme. Fiber sections are defined to simulate the nonlinear cross-section behavior of concrete and steel rebars. In particular, the concrete part is discretized into 10 × 30 fibers for the core, and 3 × 9 fibers for the cover. The confining effect of transverse reinforcement on the concrete is considered for the characterization of constitutive relationships for concrete core fibers of the confined part of the wall cross-section, while it has been neglected elsewhere. The presence of steel rebars embedded in the concrete cross section is modeled by means of straight layers of equivalent thickness. The uniaxial material characterization adopted to model the behavior of concrete core and cover and steel is the same as discussed in Sect. 3.1 for the F model columns and beams.

In both numerical models, the foundation system of the structure is modeled as simply supported, with supports placed in correspondence to the intersection points between the columns/shear walls and the foundation beams. The consistency of this choice with the simulation of the base-slip test will be discussed in Sect. 5. The cross-sections geometries and the steel reinforcement areas of the frame and wall members were derived from design tables and documents. The values for concrete compressive strength and steel yielding are taken from Tables 1 and 2, respectively. The finite length of structural members is properly accounted for by introducing rigid offsets at the intersections between different structural members.

The behavior of beam-column joints is modeled using the “scissor model” approach proposed by Alath and Kunnath (1995) with different constitutive models depending on the modeling strategy (see Sects. 3 and 4).

Table 3 anticipates the elements and materials adopted in OpenSees for both the F model (Sect. 3) and the H model (Sect. 4), evidencing common assumptions and main differences between the two modeling strategies.

Table 3 Modeling assumptions for the F and H models and OpenSees objects adopted to implement them

3 Fiber (F) model

3.1 General description of the model

In the first model (hereinafter referred to as “F” model, in Fig. 3) beams, columns, and shear walls are modeled using a three-dimensional beam-column element adopting a Force-Based Element formulation (Spacone et al 1996). Force-based elements have been employed since they satisfy the equilibrium conditions in a strong form. The advantages of the force-based over the displacement-based elements were already highlighted by Neuenhofer and Filippou (1997). Five Gauss–Lobatto integration points are adopted for columns and walls and three integration points for beam elements. The use of a reduced number of integration points for beams is justified by the needing to reduce the global computational effort required for the model. In fact, each beam is divided into multiple segments in order to constrain displacements of the RC slab and beams in nodes at which beam elements intersect the slab. However, it is expected that the use of only three integration points introduces a limited error in element response when adopting the force-based formulation with Gauss–Lobatto integration scheme, as evidenced by Maranhão et al. 2021. A corotational transformation is adopted to account for P-Delta effects both in columns and shear walls.

Fig. 3

Schematic representation of the F model

Fiber cross sections for nonlinear RC members are defined considering both the concrete and the steel rebars. The parameters for the numerical materials model were set based on the measured mechanical properties for the concrete (Table 1) and the reinforcement (Table 2). For RC columns and beams the section is discretized into 10 × 10 fibers for the core and 5 × 5 fibers for the cover. The confining effect of transverse reinforcement is accounted for during the characterization of constitutive relationships for the concrete core fibers for both columns and beams. The presence of steel rebars embedded in the concrete cross section is modeled by means of straight layers of equivalent thickness. The material models Concrete04 and Steel02 are adopted to model the concrete and reinforcement of the beams, column, and walls, respectively. The modeling strategy adopted for the the confined part of the wall cross-section and web have been already described in Sect. 2.2. The Concrete04 uniaxial material model is based on the Popovics (1973) concrete envelope with degraded linear unloading/reloading stiffness according to the work of Karsan-Jirsa (1969) and tensile strength with exponential decay. The parameters values adopted for the Concrete04 model parameters are differentiated depending on the concrete strength class and for concrete core and cover fibers in order to account for confinement effect provided by longitudinal and transverse reinforcement bars. The Concrete04 requires the definition of the concrete compressive strength (f_c0), the concrete strain at maximum strength (ε_c0), the concrete strain at crushing strength (ε_cu), the initial stiffness (E_c), the maximum tensile strength (f_ct) and the maximum tensile strain (ε_tu) for concrete, along with a parameter defining the residual stress at ε_tu (set equal to 0.1). The values adopted for Concrete04 are resumed in Table 3. In particular, f_c0 and E_c were set equal to mean values of the measured mechanical properties for concrete (Table 1), the value of ε_cu are derived from the specifications of the JSCE (2007) and f_ct and ε_tu are defined according to Chang and Mander (1994). The confined concrete behavior is modeled assuming the confinement parameters by Mander et al. (1988) depending on the arragement of longitudinal and transverse reinforcement. The Steel02 model is an elastic–plastic material with isotropic strain hardening based on the Giuffrè–Menegotto–Pinto formulation (Giuffrè and Pinto 1970, Menegotto et al. 1973). The values adopted for Steel02 model are the same in every structural element and depend on the steel class. The steel model parameters are presented in Table 4, the parameter bst represents the ratio between the post-yield tangent and the initial elastic tangent, and R₀, R₁ and R₂, which control the transition from elastic to plastic branches, reported in Table 2 are set according to (Filippou et al. 1983; Lu and Panagiotou 2014).

Table 4 Parameters for Concrete04 material model for unconfined concrete

The RC slab is divided into meshes with a maximum dimension equal to 50 × 50 cm² and the beam elements intersecting slab nodes are separated into multiple segments in order to constraint displacements of RC slab and beams in those nodes. To model the RC slab, the nonlinear multi-layer shell element ShellMITC4 (Lu et al. 2014, 2015), employing a four-node iso-parametric formulation, is adopted. The ShellMITC4 element (Dvorkin et al. 1995) allows the simulation of both in-plane and out-of-plane states of stress by combining membrane and plate behavior. The concrete in the RC slab is divided into three layers of nonlinear multi-linear shell elements, two for outer covers and one for the inner concrete layer, and the longitudinal and transverse rebars are smeared into four layers to represent the two reinforcement grids. The concrete layers for the RC slab are modeled via the multi-dimensional concrete material model based on the damage mechanism and smeared crack model PlaneStressUserMaterial proposed by Lu et al. (2015, 2018). The latter is a nDmaterial which employs planar concrete constitutive model where cracks are assumed to occur once the principle tensile stress exceeds the concrete tensile strength. After cracking in the concrete occurs, the concrete is treated as an orthotropic material. The effect of aggregate interlock on the shear stiffness is incorporated into the model through the use of a shear retention factor, set equal to 0.05 (Mitra and Lowes 2008), which reduces the shear modulus depending on the total cumulative plastic strain Lu et al. (2015). This material is coupled with the PlateFromPlaneStress material to account for the out-of-plane behavior of the slab via the definition of the shear modulus for the concrete. The remaining parameters adopted for the PlaneStressUserMaterial are the same as for Concrete04 (Table 4).

The nonlinear behavior of the steel reinforcement is incorporated through the uniaxial material Steel02 (Tables 2 and 5). This is transformed into an nDmaterial assigned to the section layer using the PlateRebar command, which requires the orientation of the steel layer being defined (0° for the longitudinal steel reinforcement and 90° for the transverse steel reinforcement). No rigid diaphragm is considered applied to constraint slab nodes since the multi-layer shell element adopted is able to reproduce the actual in-plane stiffness in a realistic way.

Table 5 Parameters for Steel02 material model

The presence of beam-column joints is modeled by adopting the scissor model approach. However, the joint equivalent spring is modeled as an elastic element characterized by cracked stiffness while the actual nonlinear behavior was neglected (see Sect. 3.2).

Zero-length section elements are incorporated at the end of columns and beams to simulate the effects of the bar-slippage associated with the strain penetration effects and bond-slip mechanism. Uniaxial Elastic Material is assigned to zero-length section with properties derived according to (Sezen and Mohele 2003; Sezen and Setzler 2008) to simulate the additional flexibility produced by the bond-slip phenomenon.

To simulate the presence of rigid offsets, rigid elements are modeled via elastic beam-column elements whose stiffness was set equal to 1000 times the corresponding original value. The value of this stiffness modifier was calibrated by the authors performing a sensitivity analysis in order to avoid numerical convergency problems or an ill-conditioned model.

Fiber elements, section and materials adopted for the F model are resumed in Fig. 4.

Fig. 4

Fiber elements, section and materials adopted in the H model

Loads and masses are applied to mesh nodes as concentrated nodal loads and lumped masses under the hypothesis of uniform distribution.

3.2 Discussion of modeling aspects

Fiber-based models of RC members are widely used since they can inherently account for both geometrical and mechanical nonlinearities without the need of proper calibration of plastic hinges mechanisms typical of lumped plasticity models, which requires the assumption of plastic hinge location and characterization in terms of backbone and hysteretic rules. In Fiber-based models the member is represented by one element with distributed plasticity along its axis that describe the formation and spreading of plasticity in a realistic way. The element is divided in several control sections that are discretized into a given number of fibers. To each fiber a uniaxial hysteretic stress–strain relationship is assigned according to the type of material (i.e., concrete, steel). The global element behavior is then extracted by integrating the behavior of all control sections. In this way the plasticity can form and spread into the element in a more realistic way. Further, these modeling strategies allows to account for the real cross-section geometry and describes material behavior by assuming for each fiber constitutive relationships that are more realistic than pre-assumed moment–curvature relationships since capturing axial-flexure interaction. However, fiber-based elements generally do not account for shear deformations or local phenomena such as bar-buckling, concrete spalling, lap-splicing. While shear deformations could be included by introducing additional spring elements at the members ends (Feng and Xu 2018) or by adopting modified force-based elements employing force-shear distortion laws at the section level to account for shear failure formulation for the element response (Marini and Spacone 2006), local phenomena could be simulated by adopting suitably calibrated constitutive laws for concrete and steel fibers. Since from experimental results these local phenomena were not highlighted, these effects are not included in the present model.

Under large cyclic load reversals, bond-slip phenomena may occur at the interface between concrete and reinforcement bars thus leading to substantial increase in lateral deflections (e.g., Lehman and Mohele 2000; Sezen and Mohele 2006). However, since no bond failure was expected to occur according to experimental evidence, only the additional flexibility produced the bond-slip phenomenon is included in the model.

Another critical aspect in modeling adopting FMs is the correct choice of uniaxial constitutive laws for each fiber in which the section is discretized. The adoption of different uniaxial constitutive laws may affect the final results. Several concrete and steel uniaxial material models available in OpenSees have been analyzed and the ones leading to the best prediction in terms of global numerical response were adopted.

Finally, from the measurements performed during the whole experimental test sequence, joint panels experienced distortions of up to 2%. Despite that the presence of degrading beam-column joints can significantly affect the response of RC frame buildings, this effect has been neglected in this model, considering the joints as elastic. This choice is due to both theoretical and practical reasons. From the theoretical point of view, F model is characterized by reproducing the nonlinear behavior of structural members based on their response to normal stresses due to flexure, a response calculated based on equilibrium, compatibility, and uniaxial constitutive laws of materials. The nonlinear response of beam-column joints is based on complex strut-and-tie mechanisms, which are hardly reproduced by means of fiber models. Thus, a phenomenological approach fits better with the aim of reproducing the nonlinear response of beam-column joints. However, phenomenological response models, as those adopted—also for beam-column joints—for the H model, are derived from experimental test results which are typically performed with loading protocols and experimental setups implying unvarying axial load on columns and shear length of members. Hence, also phenomenological response models for beam-column joints implicitly include these assumptions, which are typical of H models and unfit for F models. Also, as a matter of fact, trial analyses revealed that coupling fiber-based (for columns, beams, and slabs) with lumped-plasticity elements (for beam-column joints) led to worst results when compared to experimental results with respect to those obtained by using a simply elastic spring to model joint behavior. For these reasons, the nonlinear behavior of beam-column joints was neglected in the F model. However, as will be shown in Sect. 4, it is considered for the H model by means of a phenomenological approach. It will be shown, as also in the paper by Del Vecchio et al. (2023), that the nonlinearity of beam-column joints has affected the response of the specimen under strong earthquake.

4 Hinge (H) model

4.1 General description of the model

In the second model (hereinafter called “H” model) beams and columns are modeled adopting a lumped-plasticity approach, while the contribution of the walls is modeled adopting the same distributed-plasticity approach as for the F model (Sect. 3). More specifically, as shown in Fig. 5, beams and columns are modelled adopting Elastic Beam-Column elements while the nonlinear response is simulated via suitably-calibrated nonlinear rotational springs at both the element ends. The nonlinear behavior of these springs is reproduced via a Parallel Material assigned to Zero-Length elements.

Fig. 5

Schematic representation of the H model

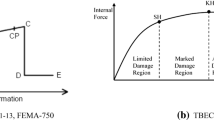
The Parallel Material is employed to merge the ModIMKPeakOriented Material with the uniaxialMaterial Hysteretic. In particular, the ModIMKPeakOriented Material is adopted to simulate the backbone and the hysteretic behavior of beams and columns according to formulations proposed in Haselton et al. (2008), while the Hysteretic Material is placed in parallel in order to allow introducing the cracking point in the multilinear backbone assigned to members (see Fig. 6). The introduction of cracking point increases the complexity of the model, but it has been deemed necessary to observe a satisfactory match between the observed and the numerical results also at low seismic intensities (e.g., Kobe 10%).

Fig. 6

Moment-chord rotation envelope (black line) according to Haselton et al. (2008) with addition of the cracking point and example of the associated cyclic response (blue line) with degradation of strength and stiffness

The nonlinear response of RC members is modeled by adopting a phenomenological approach (i.e., empirical response models also based on experimental data). The empirical moment-chord rotation envelopes proposed by Haselton et al. (2008) are adopted. As shown in Fig. 6, this model backbone is defined via three characteristic points: yielding point (corresponding to the yielding moment predicted with a fiber-based analysis of the end cross-sections of the members); capping point (corresponding to the maximum moment capacity of the end cross-sections of the members), collapse point (corresponding to a moment equal to zero). Chord rotations corresponding to these points are calculated, according to Haselton et al. (2008), by applying empirical formulations derived from the analysis of a large experimental database collecting the response of ductile rectangular RC columns with deformed reinforcement bars provided with seismic detailing, which is consistent with the features of the analyzed structure. These formulations implicitly account for the bond-slip effect and shear deformation of beams and columns. Note that, among the other predictive parameters, the formulation requires the definition of the shear span of members which is set equal to one-half the length of the member for both beams and columns. Haselton et al. (2008) response model also provides hysteretic rules aimed at reproducing the cyclic degradation as a function of the normalized energy-dissipation capacity, calculated as a function of the axial load acting on members and the stirrups spacing-to-effective depth ratio.

The studied building is provided with a 130 mm-thick RC slab at each floor. Given the thickness of the slab, it can be assumed that it imposes an in-plane diaphragm restraint between slab nodes both in the frame and in the wall direction. Therefore a rigidDiaphragm restraint is assigned to slab nodes to reproduce the in-plane effect of the presence of the concrete slab. However, it is expected that the concrete slab, which is monolithically cast-in-place together with beams, may significantly influence the flexural deformability of beams (i.e., providing an additional out-of-plane stiffness) and their nonlinear response. The out-of-plane contribution of the slabs is implicitly included in the model by deriving the nonlinear response envelopes for beams for an equivalent beam section, composed by the RC beam cross-section and the contribution of the rectangular flange on the top edge (with a thickness equal to the slab thickness and width equal to an “effective width” as defined in Sect. 4.2).

The potential nonlinear response of beam-column joints is explicitly modeled via the “scissors model” approach, by adopting rotational springs acting in both main directions that connect rigid offsets of beams and columns in the node corresponding to the intersection of beams and columns. The joint nonlinear shear stress–strain relationship is calculated according to the proposal by Kim and LaFave (2012), derived from the analysis of an experimental database of beam-column joints provided with core reinforcement (i.e., stirrups). The model backbone (see Fig. 7) is defined by four significant points (i.e., cracking point, pre-peak point, peak point, and the ultimate point corresponding to the 15% of peak strength degradation). Joint shear stress and strain at cracking, pre-peak and ultimate points are calculated by multiplying the shear stress–strain at peak point times reducing/amplifying factors experimentally calibrated. The joint shear stress and strain at peak point are instead calculated by means of empirical formulations depending on the number of members converging in the joint (i.e., on the position in the frame of the joint), the amount of joint transverse reinforcement and longitudinal beam reinforcement, the beam-column joint panel dimensions and the concrete compressive strength. Moreover, the value of the peak shear stress resulting from the application of the Kim and LaFave (2012) model has been reduced by 30% to account for the effects of biaxial bending, according to the observations by Han and Lee (2020). The equivalent moment-chord rotation response is obtained starting from the adopted joint shear stress–strain envelope by assuming that the shear length for the members is equal to one-half their length as shown, among others, in De Risi et al. (2017). More specifically, the chord rotation is set equal to the shear strain, while the moment is set equal to the joint shear times a factor depending on the geometry of the beam-column joint sub-assembly (i.e., the beam-column dimensions, the shear length of converging members, and the position of the joint in the frame). Note that the value of the peak load moment determined starting from the relationship by Kim and LaFave (2012) is further limited depending on the flexural strength of adjacent beam/column members according to Celik and Ellingwood (2008).

Fig. 7

Moment-chord rotation envelope (black line) according to Kim and Lafave (2012) and example of the associated cyclic response (blue line) with degradation of stiffness and pinching according to Jeon (2013)

The beam-column response envelope has been modeled in OpenSees via the Pinching4 Material model, which also allows reproducing the potential hysteretic degradation in the response due to cyclic loading. The hysteretic parameters for the Pinching4 are derived from Jeon (2013), which proposes different sets of parameters for exterior and interior joints.

4.2 Discussion of modeling aspects

In the H model, both beams and columns are modeled by adopting a lumped plasticity approach. This modeling approach allows reproducing the expected response of structural members up to “real” collapse (i.e., loss of lateral strength capacity) based upon experimental evidence.

Despite some recent research is increasingly focused on resolving this issue (e.g., Ghannoum et al. 2021), one of the major drawbacks of lumped plasticity approaches relies in the assignation to members of pre-determined force–displacement generalized response envelopes, which may unavoidably affect the analyses results and the quality of the observed-vs-numerical comparison. In particular, the moment-rotation response of members is determined based on fixed values of acting axial loads (i.e., the effect of axial load variations on element response is neglected) and fixed values of members shear length.

It is worth noting that predictive equations suggested in Haselton et al. (2008) were derived for members with symmetrical reinforcement and, in most cases, subjected to axial loads, which is not the case for RC beams. However, macro-modeling approaches specifically calibrated for beams are missing. For this reason, and according to other studies (e.g., Ricci et al. 2018; De Risi et al. 2022), the application of the response model by Haselton et al. has been extended to reproducing the nonlinear response also for the beams.

Moreover, with reference to the considered analyzed building, some structural parts of a reinforced concrete building are ill-suited to lumped plasticity modeling tools. For example, RC structural walls are involved in significant axial load variations influencing the flexural response. When adopting a lumped plasticity approach, the modeling of RC walls becomes a complicated issue due to the absence, in the literature, of consolidated phenomenological models describing the force–displacement response of such elements. Further, the lateral response of RC walls is significantly influenced by axial load variation, which can significantly vary during the analysis due to non-negligible vertical components of the earthquake signal. Therefore, the variation of axial loads cannot be neglected without the loss of the predictive capacity of the model. For these reasons, RC walls were modeled by adopting a distributed plasticity fiber-based approach also in the H model, as already described in Sect. 3, in order to account for the variation of axial loads during the time-history analysis.

In general, lumped plasticity modeling adopting nonlinear end hinges does not acceptably fit the response of two-dimensional members. This applies to RC slabs as to RC walls. In OpenSees, the out-of-plane stiffness of the slab and its influence on beams behavior could be explicitly considered by modeling the slab with 2D nonlinear finite elements appropriately “connected” to the beams, as for the F model. Alternatively, as adopted in this study, it is common practice in lumped-plasticity modeling to account for the out-of-plane stiffness of the slab by modeling beams as if they had a T- or L-shaped section, i.e., as if they had a rectangular flange on the top edge, with thickness equal to the slab thickness and width equal to an “effective width” (greater than the beam width at the bottom edge), as shown in Fig. 8. Different code-based proposals for the assessment of the effective width have been preliminary considered, namely the proposals by Eurocode 8 (2004), ASCE/SEI 41-17 (2017) and NZSEE (2017). Among these, the proposal by Eurocode 8 (2004) has been adopted basically because it assured a better matching between the numerical and the observed initial period of the structure.

Fig. 8

Effective width of the structure beams according to different codes

In fact, as shown in Fig. 8, other proposals generally result in greater effective widths with respect to Eurocode, thus resulting in stiffer and stronger beams (the higher the effective width, the higher the number of reinforcing bars of the slab considered when calculating the resisting moment of beam cross-section). As will be shown in Sect. 6, the numerical results obtained from time-history analyses of the H model may apparently benefit, in some cases, from the increase of members strength (delaying the occurrence of the post-yielding hardening and post-peak softening nonlinear response). However, some preliminary analyses (here omitted for brevity reasons) revealed that the influence of the effective width is higher in terms of initial stiffness/period of the building model than in terms of local/global nonlinear response. Hence, the final model adopts in calculations an effective width defined according to Eurocode 8 (2004), since this value assures a satisfactory accordance between the observed and numerical initial vibration period of the studied structure, while no significant benefit was observed by adopting higher values of effective width in terms of numerical lateral response during time-history analyses, also for increasing level of nonlinear demand.

5 Analysis procedure

5.1 Input for time-history analyses

As already mentioned, the case-study building has been tested by applying at its base the three components (two horizontal components plus the vertical one) of the record of Kobe earthquake. More specifically, two tests were performed: the first one was a base-slip test (BS) in which the case-study building was simply placed on a concrete basement anchored to the shaking table. Hereinafter, the raft concrete basement ensemble will be briefly referred as “basement”. During this test, the building foundation, which is provided with some embedded cast iron plates on the bottom side of the foundation beams, can slip on the basement, since no anchorage is set between the foundation and the basement. The second test was performed on the same specimen after BS. In this case, i.e., during the base-fix test (BF), the building foundation was anchored to the basement system, hence no relative displacement is allowed between the building foundation and the basement. Both tests were performed by applying Kobe earthquake record scaled by 10%, then by 25%, then by 50% and, finally, by 100%. In other words, a total of 8 runs were performed, 4 runs for the BS and 4 runs for the BF (the white noise tests performed between one run and another to investigate the evolution of modal properties of the building are not considered here). This means that Kobe earthquake records were applied through the shaking table below the base-slip interface between the foundation of the building and the basement; the input signal is transformed by the base-slip interface and transferred to the building foundation during the BS test, while it is transferred unaltered to the building foundation during BF. This can be confirmed by comparing the response spectrum calculated for the input signal applied by the shaking table, with the response spectrum calculated for the acceleration history registered at the building foundation level: these response spectra are technically the same for the BF test, while they are significantly different for the BS test due to the filtering effect of the slipping base.

Based on the above discussion, 8 time-history analyses were performed on the F model and on the H model of the case-study structure. The analyses were performed in sequence, in order to simulate the real tests and the damage cumulation to the structure (as far as the adopted modeling approaches allow it).

To simulate the passage from the BS specimen to the BF specimen, a first straightforward approach is possible: first, modeling the hysteretic response of the concrete-steel interface between the building foundation and the basement during the BS test simulation; after that, applying appropriate constraints at the base of the building model when passing from the fourth run of the BS test (100% of Kobe earthquake) to the first run of the BF test (10% of Kobe earthquake). Although information was available regarding the behavior of the slipping interface, it was deemed not sufficiently detailed to allow the reliable choice of a base-slip model available in the literature, nor the robust calibration of a new one. Hence, the approach based on explicitly modeling the slip device response was ruled out in this study.

To overcome the issue related to modeling the hysteretic response of the slip interface, it was decided to adopt an alternative approach. In particular, the input registered at the foundation level, that can be assumed as the earthquake records already “filtered” by the effect of the slipping interface, were applied at the base of the numerical model, in correspondence of the simple supports adopted for the model. This procedure should give equivalent results as modeling the base-slip interface and applying Kobe earthquake records below it.

Since both acceleration and displacement histories of the building foundation level are available from experimental results, both could be used as input for time-history analyses.

To define the potential input in terms of displacement time-history, the absolute displacements to be applied to the foundation can be obtained through filtering and suitable composition of the displacements recorded by available instrumentations, including extensometers and laser devices, as descried below (see also Fig. 9a, b).

Fig. 9

Derivation of the displacement time-history input at the base of the columns/walls based on the displacement time-history of the shaking table and of the relative displacement of the foundation: a Displacement components considered for derivation of absolute displacements of foundation beam; b Absolute displacements obtained along x axis for column with coordinates (0,0) for the BS phase

It is assumed that the relative shifts between the concrete basement and the shaking table are negligible, a hypothesis confirmed by experimental results. Then, it is possible to obtain the displacements to be applied to the base of the foundation as the sum of the absolute displacements of the shaking table, and the relative displacements (slipping) between the foundation and the concrete basement or the shaking table. During the composition it is assumed that both the shaking table and the foundation are infinitely rigid both in-plane and out-of-plane, obtaining horizontal and vertical displacement histories at the centerline of each column and wall. The composition also allows taking into account the rocking effect produced during the base-slip phase.

The displacement time-history at the foundation level has been preferred as input signal for different reasons. The experimental results considered for the observed-vs-numerical response comparison are registered by displacement transducers. Then, observed displacement demands are compared with numerically predicted displacement demands. For this reason, with the aim of assuring a given consistency between input and output, the time-history analyses were performed by adopting the displacement time-history of the building foundation as input for both the BS and BF tests simulations. Also, it should be noted that using an input signal expressed in terms of displacement history allows a quite reliable reproduction of the rocking of the building base during the BS test. For the sake of brevity, the results of some preliminary time-history analyses performed for comparison purposes with acceleration time-history as input are not reported in this study. However, a better outcome of the observed-vs-numerical response comparison is found when the displacement time-history input is adopted. This seems to confirm the effectiveness of the choice adopted.

The displacement time-history input is applied in OpenSees by using a MultipleSupport pattern in which a different time-history is assigned at the base of each vertical member of the first storey. Each displacement time-history assigned is determined by combining the absolute displacements of each point of the shaking table, determined under the hypothesis that it moves as a rigid body both in its plane and out of its plane, with the relative displacement of each point of the building foundation, determined under the hypothesis that the foundation system moves as a rigid body in its plane: this component is technically equal to zero during the BF test, as expected.

For both the F and H models, a mass-and-tangent-stiffness-proportional Rayleigh damping with damping ratio equal to 5% assigned to the first and the second modes is adopted. Damping forces are activated only for the elastic elements in the H model, to prevent the arising of spurious damping forces (Chopra and McKenna 2016) in yielding plastic hinges. In F model and, in general, in elements with fiber sections (which are present also in the H model for modeling shear walls), it is not possible to relate damping only to elastic parts of elements. For this reason, tangent-stiffness proportional Rayleigh damping was adopted to limit spurious damping forces in this case, despite the potential drawbacks associated with tangent-stiffness proportional damping mentioned by Chopra and McKenna (2016). As already mentioned, first vibration mode (i.e., the first vibration mode in frame direction) and second vibration mode (i.e., the first vibration mode in wall direction) are adopted as control modes for both models. As will be shown in the next section, F and H model have different vibration periods in frame and wall directions, so this choice implies different damping ratios applied to higher vibration modes for the two models: this may affect the result of the comparison between the response exhibited by the two models of such a tall structure as the tested specimen. This kind of discrepancy is unavoidable when applying Rayleigh Damping model: so, it was preferred to assure that at least the damping ratio assigned to the two fundamental modes in the two horizontal directions are the same for the two models.

5.2 Modal analyses

During the experimental campaign, modal identification analyses were carried out before performing each run of BS and BF tests. This allows the assessment of the evolution of modal properties of the specimen, namely the elongation of the vibration period due to damage.

As shown in Table 6, the modal identification test performed before the BS test revealed that the vibration period of the specimen is 0.57 s in frame direction and 0.57 s in wall direction. It is quite hard to establish if the fact that the building foundation is not fixed to the ground influenced the results of this test, i.e., the vibration periods of the specimen. This should not occur if the static friction between the foundation and the concrete base, together with the self-weight of the specimen, prevents whichever relative translation and rotation of the specimen with respect to the ground under the white-noise signal.

Table 6 Vibration periods of the case-study building

Under this assumption, modal analysis can be performed on the numerical models of the specimen, even if they are fixed at their base, and their results can be reasonably compared with the abovementioned experimental outcomes to check the reliability of F and H model at least in terms of expected elastic response (i.e., to verify the accuracy of geometry, masses, material properties reproduction, etc.). Eigen analysis of F and H models provided a vibration period in frame direction equal to 0.58 s and 0.60 s, respectively. On the contrary, in wall direction, F model is characterized by vibration period equal to 0.45 s, while the H model is characterized by vibration period equal to 0.51 s.

First, it should be noted that the H model is systematically more deformable than the F model: most likely, this is due to the fact that beams of the H model are provided with a given effective width reproducing the out-of-plane stiffness of slabs, while in F model the slab is explicitly modelled with more realistic out-of-plane stiffness.

Second, the fact that in the frame direction the vibration periods of both models are very similar seems to assure that the effective width assigned to beams according to Eurocode is able to equivalently reproduce the elastic out-of-plane stiffness of the slab. The fact that both periods are very similar to the experimental one seems to testify the accuracy of the elastic model of the framed resisting system and to corroborate the assumption that the base slip system has no influence on the free vibration of the specimen. The better performance of the F model is justified, most likely, by the fact that the out-of-plane stiffness of the slab is explicitly modelled.

However, the good matching in the frame direction is not observed in the wall direction. Since the F model, at least from the elastic point of view, is the more accurate one, a first comparison can be performed between this model and the experimental outcome. First, it is possible that the error of the numerical model is due to the influence of base slip. However, it seems from the results in the frame direction that base slip does not influence the modal response of the specimen and there is no clear reason why it should influence modal properties of the structure in a direction (wall direction) rather than in the other (frame direction). Also, it is possible that the specimen includes some sources of further deformability in the wall direction that has not been identified. It is interesting to note that according to Gomez (2020), a specimen tested in 2018 and identical in terms of geometric characteristic to the one tested in 2015, which is the object of this work, has initial vibration period in the frame direction equal to 0.58 s and in the wall direction equal to 0.45 s. In addition, as will be shown in the next section, during the first run of the BS test, in which the 10% of Kobe earthquake is applied as input, the specimen is expected to behave elastically, hence its maximum displacement demand should be strictly dependent on its modal properties. As will be shown in the next section, the F model subjected to 10% of Kobe earthquake during the BS test provides a top displacement demand technically equal to the experimental one.

Regarding modal properties of the H model in wall direction, it has a higher vibration period than the F model, most likely due to the fact that the out-of-plane stiffness of the slab is not explicitly modelled as in the F model. Actually, in the frame direction it seems that the out-of-plane stiffness of the slab is correctly reproduced by the effective width assigned to beams. It is possible that a greater effective width of the flange should be assigned to beams framing into shear walls. In fact, it should be considered that Eurocode formulation for the assessment of the effective flange width is indifferently applied for framed system and for wall systems. However, as it can be presumed from the geometry shown in Fig. 10, the behavior of a beam in a framed system could be different with respect to the behavior of a beam framing into a wall system: this may yield to a different width of the portion of the slab collaborating with the beam itself. Unfortunately, this topic is not investigated in detail in the literature: further study should be undertaken to clarify this issue. However, the above-discussed numerical results seem to testify that, actually, the effective flange width of a beam framing into a wall system should be different, and greater, than the effective flange width assigned to an identical beam belonging to a frame system.

Fig. 10

Boundary conditions potentially influencing beams effective width in frame and wall directions

In summary, both models well predict the vibration period in frame direction, while they provide different results (F vs H but also numerical vs experimental) in the wall direction. Since the only difference between F and H in wall direction is the model approach for slabs in wall direction, it seems that this choice affects significantly the initial elastic properties of the modelled structure; however, current literature provisions for slab modeling do not allow the achievement of a better experimental versus numerical matching in wall direction, thus suggesting the importance of future studies focused on this issue, especially in wall or mixed wall-frame structures.

6 Nonlinear analysis results

The results of the numerical analyses are presented in this section and compared with the experimental outcomes. During the experimental tests, interstorey drift ratios (IDRs) were registered by means of dedicated laser displacement transducers. Hence, the main comparison between numerical and experimental results is herein performed by comparing the numerically predicted with the experimentally observed envelope of (non-contemporary) maximum interstorey drift ratios per each storey and per each run of the BS and of the BF tests. Each run will be identified with a percentage related to the scaling applied to the Kobe earthquake record to perform the shaking table test. Also, experimental and numerical results are discussed in terms of maximum roof displacement demand and beam-column joint shear strain demand (where available).

6.1 Interstorey drift ratios and roof displacement demands during BS tests

Starting from the BS test, at Kobe 10% run, also considering the slipping effect, it is expected that the building experiences limited deformation demand, thus behaving as an elastic structure. This is confirmed by the experimental envelopes of the IDR demand. In fact, the maximum IDR demand registered in the frame direction is slightly higher than 0.1%; the maximum IDR demand registered in the wall direction is roughly equal to 0.05%. In other words, the response in the wall direction is elastic; in the frame direction, some columns may have attained a first cracking condition, with no or very limited nonlinearity. In the frame direction, the maximum IDR demand is observed between the second and the fourth storey, most likely due to the influence of higher vibration modes, as expected in such a tall structure; in the wall direction, the IDR demand envelope is quite uniform along the building height, as expected for a structure which, in the elastic field, has a cantilever-like response. The numerical models are able to capture in a quite satisfying way the response of the specimen, as shown in Fig. 11, during this run, in terms of both values and shape of IDRs envelope. Of course, this does not testify the reliability of the nonlinear models but just the fact that their initial elastic features (geometry of sections and members, materials elastic properties, masses) have been modelled as correctly as possible given the modeling approaches applied and the modeling assumptions adopted. In other words, this is a further confirmation of the results obtained from the initial modal analysis of the structure. However, it is interesting to note that, although minimal, some differences can be already observed between the results of the F and of the H models: this is a direct consequence of some different basic modeling assumption (also testified from the slightly different results of modal analyses), such as the initial stiffness of beam-column joints (especially in the frame direction) and the presence of the 2D model of the RC slab in the F model, while it is reproduced by means of T- and L-shaped beams with “equivalent” effective width in the H model (especially in the wall direction). In general, the results of the experimental-vs-numerical comparison are quite good in the frame direction, while in the wall direction the H model tends to underestimate both the IDR demand envelope and the top displacement. Note that this occurs despite the initial vibration period of the numerical model in the wall direction is higher for the H model with respect to the F model. This occurs because the input signal has a non-smoothed response spectrum with peaks and valleys.

Fig. 11

Maximum IDR demand per storey during BS tests (up to Kobe 50%) and during the corresponding numerical simulations

At Kobe 25%, during the BS test, the experimental maximum IDR demand is roughly equal to 0.3% in the frame direction, while it is roughly equal to 0.1% in the wall direction. So, also in this case, no significant level of nonlinear demand is expected in both directions. In fact, the response of the two models is very similar in the frame direction and is consistent with the experimentally observed outcome up to the fourth/fifth storey; however, both models underestimate the maximum IDR demand at upper storeys. Note that this result can be also observed for Kobe 10% run, even if less significant. In other words, it seems that in the frame direction there is a source of deformability in the specimen, “lumped” at the sixth/seventh storey, which is not modelled in both numerical models. Clearly, the cold-joint realized at the sixth storey to connect the two parts in which the specimen was realized may be the source of the not-modelled additional deformability; however, this is quite hard to demonstrate, also considering that this phenomenon does not occur in the wall direction. Maybe for this reason, both models slightly underestimate the top displacement demand at Kobe 25% run in the frame direction. In the wall direction, the F model provides a better prediction of the lateral response; however, both models overestimate the maximum IDR demand at upper storeys and, in general, the top displacement demand.

At Kobe 50% run of the BS test, the IDR demands are still limited, with maximum values around 0.4% in the frame direction and around 0.15% in the wall direction. In the frame direction, a very good predictive performance is provided by the H model, which appears to be able to capture the experimentally observed response of the specimens in terms of both maximum IDR envelope—IDR values and shape—and top displacement demand, with a slight overestimation at the building mid-height; on the other hand, the F model underestimates the building deformation demand, especially at top storeys. In the wall direction, instead, the experimentally observed behavior of the building appears to be “intermediate” between those predicted by H and F models. More specifically, the H model well predicts the building response at bottom storeys; F model well predicts the building response at mid-height and top storeys; in general, however, the F underestimates the top displacement demand, while the H model overestimates it.

At Kobe 100% run of the BS test the maximum IDR demand is roughly equal to 0.6% in the frame direction and to 0.3% in the wall direction. Maximum IDR demands are registered at the fourth and at the eighth storey. As shown in Fig. 12, both models completely fail the prediction of the IDR demand envelope shape in the IDR demand, especially the H model, which, above all, significantly overestimates the top displacement demand; in the wall direction, the H model behaves quite good, with an underestimation of drift demands at lower storeys and an overestimation at top storeys: this yields to a quite good prediction of the top displacement demand. On the other hand, the F model underestimated both IDR demands and top displacement demand.

Fig. 12

Maximum IDR demand per storey during BS tests (up to Kobe 100%) and during the corresponding numerical simulations

The results of BS tests are summarized in Table 7.

Table 7 Results of BS test (Exp) and of its numerical simulations (F model and H model) in terms of maximum IDR demand (IDR_max), storey at which it is registered (Storey) and maximum top displacement demand (Δ_TOP)

Some basic considerations can be drawn at the end of the BS test. Some discrepancies between the results of the two numerical models are visible for low intensity of the seismic input. This occurs above all in wall direction in which, most likely, there is a significant effect of the different approaches adopted for slab modeling. However, the elastic models of the case-study structure result quite satisfactorily instituted; both models, in fact, provide good estimates of the order of magnitude experimental results up to a limited nonlinearity level. The more the nonlinear demand (even in terms of post-cracking deformation demand), the more the bias between the numerical prediction and the experimental evidence, at least at local level, also because of some higher order effects which are missed by both numerical models. However, despite the increasing error at increasing seismic intensity (as shown, in terms of top displacement demand, in Fig. 13) at least the order of magnitude of the maximum deformation demand at local level is quite always well predicted.

Fig. 13

Maximum top displacement demand during BS tests and during the corresponding numerical simulations at increasing intensity of the seismic input

In summary, at Kobe 100% run of the BS test, the maximum IDR demand is roughly equal, in frame direction, to 0.6% (i.e., the most deformed columns have cracked but they have not yielded) according to the experimental results; according to both the H and F models, such a deformation demand is no more than 0.9%, corresponding to the onset of yielding: despite the error in percentage is roughly equal to 50%, members’ state is predicted with a quite good approximation. Similar considerations apply also in wall direction.

There is a final issue that should be adequately highlighted: the prediction error at local level passes from underestimation to overestimation from the bottom to the top of the building, from the frame to the wall direction, from the F to the H model, from Kobe 10% run to Kobe 100%, apparently with no systematic trend. Of course, despite the previous comment regarding the capability of the models to catch the general state of vertical members, this casts a shadow of the reliability of the numerical simulations carried out. This will be discussed at the end of the next subsection, dedicated to BF tests simulation.

6.2 Interstorey drift ratios and roof displacement demands during BF tests

Again, at Kobe 10% run of BF test, it is expected that the structure behaves in the elastic range, even if with degraded stiffness due to the previous BS test. It is interesting to observe that the H model well predicts the experimental response in terms of IDR envelope and maximum top displacement demand in frame direction, while a better performance in wall direction is exhibited by the F model. The effect of the absence of slipping and of the degradation due to the previous BS tests is visible in the increase of the local deformation demand with respect to those registered during the corresponding run of the BS test. The fact that the numerical models are still able to reproduce quite well the experimental results seems to corroborate the reliability of the numerical models despite the shortcomings exhibited during the BS test simulations. In other words, it seems that despite the error committed in the prediction of the maximum IDR demand distribution is quite high in percentage, the fact that at least the range in which the structural members behaves during the numerical simulation is consistent with experimental evidences allows a generally correct reproduction of the residual damage of the building at the end of the BS test and of its initial state (in terms of stiffness distribution along the building height) at the beginning of the BF test.

In the case of BF test, the discussion of the general trends exhibited by the specimen and by the numerical models at increasing input intensity is quite simpler, since they show some repetitions. In fact, as shown in Fig. 14, the IDR demand envelope is generally underestimated at bottom storeys and overestimated at top storeys by the H model, in both the frame and the wall direction, for both Kobe 25% and Kobe 50% runs of BF test. The same occurs for the F model, but only in wall direction, while a systematic underestimation of deformation demand is registered in frame direction, maybe due to damping overestimation. In average terms, in frame direction the H model scores a slightly better performance than the F model, as shown by the comparison between experimental and predicted values of the top displacement demand; the contrary occurs in the wall direction. It should be noted that the overestimation of IDR_max values at top storeys in frame direction by the H model anticipates the shape of IDR_max that is exhibited also during Kobe 100% run by both the numerical model and the specimen, as if the experimental IDR_max envelope shape for Kobe 100% is determined by phenomena which are trigged in the numerical model already during Kobe 50% simulation.

Fig. 14

Maximum IDR demand per storey during BF tests (up to Kobe 50%) and during the corresponding numerical simulations

Regarding the Kobe 100% run of the BF test, both models completely fail the prediction of the IDR demand at bottom storeys in the wall direction with a significant underestimation, thus testifying the occurrence of deformability phenomena in shear walls which are not adequately modelled (such as shear deformability of walls or effect of potential rocking and bar slip) or a damping overestimation. However, both models exhibit a quite good predictive capacity in the frame direction. Note that the H model appears able to predict (even if with some error) the shape of the IDR demand envelope characterized by a sort of double convexity: as will be shown in the next subsection, this is due to a concentration of shear strain demand in the beam-column joints at mid-height of the building, which cannot be caught by the F model, whose beam-column joints are indefinitely elastic (Fig. 15).

Fig. 15

Maximum IDR demand per storey during BF tests (up to Kobe 100%) and during the corresponding numerical simulations

The results of BF tests are summarized in Table 8. The evolution of the top displacement demand as a function of the seismic intensity during BF tests is reported in Fig. 16. As previously mentioned, despite significant discrepancies in the reproduction of peak local displacement demand, the top displacement demand is predicted quite well by both models, also at high seismic intensity of the base input.

Table 8 Results of BF tests (Exp) and of its numerical simulations (F model and H model) in terms of maximum IDR demand (IDR_max), storey at which it is registered (Storey) and maximum top displacement demand (Δ_TOP)

Fig. 16

Maximum top displacement demand during BF tests and during the corresponding numerical simulations at increasing intensity of the seismic input

In summary, as shown in Figs. 17 and 18, the predictive capacity of both models appears quite satisfying in terms of (i) absolute maximum IDR for the entire building height; (ii) top displacement prediction, especially for the BF test, for which less uncertainty affects the definition of the base input; and (iii) at least for the BS test, prediction of the storey at which the maximum IDR demand is registered. It should be noted that, apart for the case of very low seismic intensity, both models’ performance is quite poor when dealing with the assessment of the distribution of maximum IDR demand per storey along the building height. Generally speaking, while the H model appears more able to capture the top displacement demand and the maximum IDR demand, the F model appears more able to capture the localization of maximum IDR demand at low excitation intensity (i.e., up to Kobe 25–50%). Most likely, this occurs because the response of the members of the F model is characterized by a tangent stiffness that changes continuously during the time-history, differently from the members in the H model, whose tangent stiffness abruptly changes when passing from the elastic to the post-cracking to the post-yielding range of response. In other words, in the F model, the evolution of the relative stiffness of one storey with respect to another one may be captured more accurately than in the H model: since the distribution of IDR demand at relatively low seismic intensity mainly depends on the relative stiffness of different storeys, the F model is more able to capture it than the H model.

Fig. 17

Maximum IDR demand and storey at which it is registered during tests and during numerical simulations

Fig. 18

Maximum top displacement demand during tests and during numerical simulations

It can be concluded that the developed numerical models are characterized by a quite satisfying reliability, also considering that they derive from the simple data-driven choice and application of well-known and well-established modeling approaches proposed in consolidated literature and codes, with no calibration or “adjustments” of geometric and mechanical properties of the modelled structures, and also considering that the base-slipping interface has not been modelled. However, as already mentioned, despite the observed discrepancies, the simulation of the BS test by assuming as input the displacement history registered at the foundation level allowed a quite good assessment of the specimen general state at the end of the BS test, thus laying the groundwork to a satisfying simulation of the results of BF tests.

6.3 Beam-column joints

The instrumentation layout adopted during the experimental tests included couples of Linear Variable Displacement Transducers (LVDTs) placed corresponding to the panels of five exterior beam-column joints in the frame direction. This allows the reconstruction of the variation, during shaking table tests, of the shear strain in these beam-column joints at first, second, third, fourth and sixth storey (see Del Vecchio et al. 2023 for more details on formulation adopted to evaluate the strains starting from LVDT measures).

As mentioned in Sect. 4, the H model included the nonlinear response of beam-column joints determined according to Kim and Lafave (2012) model. Hence, the maximum shear strain registered during the time-history analyses of this model is compared in Fig. 19 with the experimental value of the maximum shear strain.

Fig. 19

Experimental and numerical values of the maximum shear strain demand in monitored beam-column joints along frame direction

Regarding the BS test, it is shown that, as expected, both experimental and numerical values of the shear strain increase at increasing intensity of the seismic input. The maximum shear strain is registered at the fourth storey according to both the experimental data and the numerical model. The minimum shar strain is generally registered at the second storey for the specimen, at the first storey for the numerical model. However, as discussed in Sect. 6.1, the simulation of base slip test is not expected to provide exact estimates of deformation demands, given the uncertainty related to the definition of the seismic input for time-history analyses, but a good estimate of their order of magnitude in strict relation with their damage state. In this regard, it should be noted that ranging from Kobe 10 to Kobe 100% runs of BS tests, the experimental shear strain demand ranges from technically zero to around 0.35%. The numerical analyses indicate that the expected maximum shear strain demand ranges from technically zero to around 0.30%, with this maximum value registered for Kobe 100% run at the sixth storey, as also shown by experimental tests. Note that, according to the Kim and Lafave modeling approach, this value of the shear strain is compatible with the cracking of the beam-column joint panel and roughly corresponds to the yielding of reinforcement.

Regarding BF tests, Fig. 19 shows that the maximum shear strain in beam-column joints is significantly increased with respect to BS tests. This also occurred in terms of IDR and top displacement demand, thus certifying the effectiveness of the base-slip technique in controlling the deformation demand (and, so, the damage) in such a kind of tall structure. The increase of shear strain demand in beam-column joints is also shown by the H model. Namely, according to the model the shear strain demand in beam-column joints is similar for the monitored beam-column joints up to Kobe 50% and ranges from around 0.05% (Kobe 10% run) to 0.30% (Kobe 50% run). The model slightly underestimated the maximum shear strain registered during the experimental test for the third and fourth storey which attains and overcomes 0.50% during Kobe 50% run. This underestimation is observed also for the Kobe 100% run. However, the maximum experimental shear strain demand jumps to around 2% at sixth storey for this last run; this jump is also reproduced by the H model, in which the shear strain demand in the exterior beam-column joint at the sixth storey jumps to around 1.4%. According to Kim and Lafave model, this is compatible with the softening in the response of beam-column joints and, hence, to their significant damage, which has been actually observed at the end of BF tests. The numerical model is able to reproduce this damage increase quite well.

In the paper by Del Vecchio et al. (2023), it is shown that beam-column joint subassemblages at intermediate storeys of 2015 specimen (the one which is the object of this study) are characterized, due to their design and due to the potential effect of biaxial bending, which is accounted in the adopted modeling approach, by the attainment of the maximum shear stress and consequent softening and damage before yielding of the converging beams and columns. Also, it will be shown that this may significantly influence the overall lateral response of the building in terms of maximum IDR demand values. In other words, the softening of beam-column joints in the specimen seems to have triggered the heavier damage of the structure during Kobe 50% and Kobe 100% runs of BF tests. This effect is caught by the H model: in fact, as shown in Figs. 15 and 19, the order of magnitude of the maximum deformation demand in both columns and beam-column joints is quite well predicted.

7 Conclusions

In this paper, two different models of the 10-story RC building tested at E-Defense laboratory in 2015 are built: the F model, in which, basically, beams, columns, and walls are modelled by adopting a lumped plasticity approach with fiber sections at ends of members; the H model, in which, differently from the F model, beams and columns are modelled by adopting a lumped plasticity approach with plastic hinges at ends. In this case, the moment-chord rotation response assigned to plastic hinges is determined based on empirical formulations proposed in the literature.

Nonlinear time–history analyses are performed on both models to reproduce the experimental shaking-table tests performed at E-Defense laboratory. More specifically, the real structure has been tested with the consecutive application of the tri-directional record of Kobe earthquake (1995) scaled at 10%, 25%, 50% and 100% of its intensity. The incremental test has been performed two time: the first time (BS test), the horizontal and vertical displacement of the structure foundation with respect to a concrete base fixed to the shaking table were not prevented: in other words, the structure base was free to slip on the concrete base. After the BS test, a second test was performed on the same structure with the foundation fixed to the concrete base (BF test).

From the experimental tests it was observed that the construction with slipping base is extremely useful to reduce local displacement demands in the structure, above all in terms of maximum IDR demand and maximum shear strain demand for beam-column joints. In other words, the application of this construction technique could be a turning point for the general reduction of seismic vulnerability of buildings without the use of more expensive or complex techniques involving base isolation with rubber/steel devices or even more complex solutions such as mass dampers.

However, the main aim of this study is the assessment of the capability of numerical models to catch the response of the case-study structure. To this aim, note that the Authors decided, also based on the experimental results, to apply the models proposed in the literature with no calibration or adjustment of geometric and mechanical properties of the modelled structures. As above mentioned, both the BS and BF tests were reproduced, but the hysteretic response of the slipping interface was not explicitly modelled. In fact, both the F and the H numerical models of the case-study structure were simply-supported at their base: to account for base-slipping, the base input for numerical analyses was not the Kobe earthquake record (adopted for the BF test simulation) but the displacement history at the structure base (i.e., above base-slipping interface) registered during the BS experimental test: this kind of input should already account for the “filtering” effect of the base-slipping interface. From the modal and the time-history analyses performed, the following conclusions can be drawn:

• The static friction between the foundation and the concrete base during the BS test is not overcome during random identification tests. Hence, a simple modal analysis on the simply-supported elastic model is able to provide reliable information about the initial modal properties of the building, at least in the frame direction;

• During the BS test at low intensity, the structure behaves elastically. The numerical models are able to catch this;

• Despite the significant uncertainties related to modeling of the input, the chosen approach for simulating the BS test is able to provide a quite good prediction of the structural response in terms of maximum IDR demand in the entire building height, which is related to the damage state of the structural members at the end of each run of the BS test. This also allows to start the simulation of the BF test with a quite satisfying reproduction of the stiffness/damage state of the structure at the beginning of the BF test after the BS test;

• The simulation of the BF test is able to provide quite good prediction of the structural response in terms of top displacement demand, shear strain demand in beam-column joints, maximum IDR demand registered along the building height and, so, maximum damage state for structural members (including beam-column joints) at the end of each run of the BF test;

• The H model appears more able to capture the top displacement demand and the maximum IDR demand, the F model appears more able to capture the localization of maximum IDR at low excitation intensity (i.e., up to Kobe 25–50%);

• The significant damage experienced by the specimen during Kobe 50% and 100% runs of BF tests is probably triggered by softening and damage of beam-column joints: this is reproduced also by the H numerical model and highlight the influence of beam-column joints design and response on the overall seismic response of the base-fixed structure. This topic is deeply investigated in the paper by Del Vecchio et al. (2023). In fact, this paper validates a numerical model which is adopted to extrapolate some considerations regarding good practice to be applied when designing beam-column joints in Del Vecchio et al. (2023). The study presented in this paper also shows that if the potential nonlinear response of beam-column joints is neglected when modeling (this involves also modeling and response analysis of existing buildings), the severity of structural damage (not only of beam-columng joints themselves, but also of converging beams and columns) may be significantly underestimated.

In summary, selected numerical modeling approaches available in the literature, without any significant calibration, are able to correctly reproduce the overall response of the case-study structure, especially if the comparison is performed in terms of predicted maximum damage state for structural members, provided that beam-column joints contribution is adequately considered. However, to benefit from this reliability level for the potential assessment of structures different from the one tested at E-Defense in 2015, but with slipping base, one should know how the base input is filtered and modified by the base-slipping interface. Future studies may be dedicated to the definition of simplified and user-oriented tools for the assessment of the “filtered” input that a practitioner could adopt for the design, analysis and safety assessment of a new construction built by applying this innovative solution for earthquake protection.