1 Introduction

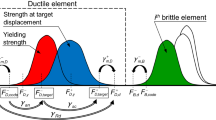
Timber structures generally lack efficiency when designed in capacity (see e.g. (European Committee for Standardization (CEN) 2004; Piazza et al. 2011; prEN 2019; Follesa et al. 2018; Jorissen and Fragiacomo 2011)). Until now, ductile zones have been mainly based on laterally loaded dowel-type fasteners that usually provide modest ductility combined with high overstrength, which lead to two unfavourable effects. Firstly, a low ductility does not allow to reach a high behaviour factor q. Secondly, these high overstrength values (Jorissen and Fragiacomo 2011; Ottenhaus et al. 2017; Izzi et al. 2018) correspondingly imply high overstrength factorsγRd. The gain brought by the behaviour factor q is partially or even completely lost by considering the over-strength factors γRd to apply for the dimensioning of non-dissipative zones. If not capacity designed, CLT walls can be damaged due to brittle failures of the timber parts or in connections such as angle brackets and hold-downs.

The ductility potential of optimized timber connections based on laterally loaded dowel type fasteners has recently been investigated and already published concerning steel to timber doweled connections (Geiser et al. 2021). The proposed full confinement combined with notch effect and constriction restraining measures and a suitable steel quality have probably allowed to approach the limits of the plastic deformation capacity of such connections (Geiser et al. 2022). To further increase ductility, a change of paradigm, from laterally to axially loaded elements, is probably needed.

2 Background research and state of the art

2.1 New approaches for seismic design of tall buildings

Following the modern philosophy of the Damage Avoidance Design (DAD) (Mander and Cheng 1997; Bradley et al. 2008), “a structure should be designed not only to survive a high intensity earthquake ground motion, but also to minimize the structural and non-structural damage” (Sancin et al. 2014). Need for densified cities and new regulations are pushing engineers to design tall wooden buildings, but this requires adapted seismic design. Follesa M. (Follesa et al. 2018) states: “Hold-down connectors commonly available for the construction of timber buildings have a maximum characteristic strength of 100 kN. However, it is not unusual to calculate uplift forces up to 500–700 kN even in low seismicity areas for medium-rise buildings (6–7 storeys).” An excessive number of connectors locally can lead to risk of brittle failure (e.g. splitting) within the timber member. New approaches are developed for the seismic design of tall buildings. For instance innovative low-damage structural systems such as pre-stressed re-centring walls (Buchanan et al. 2008), new types of dissipative steel connections (Cesare et al. 2019a, 2019b) or innovative energy dissipators (Wrzesniak et al. 2013) and tuned mass dampers (Poh’sie GH et al.. 2016; Hervé Poh'Sié et al. 2016) have been developed. Deformable floor diaphragms or multi-storey segmental rocking walls should be further investigated (Pei et al. 2014). Innovations offer numerous solutions for seismic design, but costs remain one of the principal factors of decision. In particular, this influences the use of advanced materials such as superelastic shape memory alloys (Lindt and Potts 2008) or passive base isolation systems for timber buildings (Sancin et al. 2014).

2.1.1 Pre-stressed re-centring walls

During the 1990s, various experimentations of the U.S. PRESSS (PREcast Seismic Structural System) program investigated the properties of precast concrete moment-resisting frames or interconnected shear walls (Priestley 1996; Priestley et al. 1999). It has resulted in a new precast concrete technology that has since been implemented in wood engineering (Buchanan et al. 2008; Palermo et al. 2005, 2006a, b).

When using jointed ductile connections, timber frame and wall systems “can undergo inelastic displacements […], while limiting the structural damage and assuring full re-centering capability after the seismic event (no residual/permanent deformations)” (Buchanan et al. 2008). This can be achieved by a hybrid system in beam-column connection where “an adequate combination of self-centring capacity (unbonded tendons plus axial load) and energy dissipation (mild steel or other dissipation devices) leads to a controlled rocking motion, which consists of a peculiar “flag-shaped” (dissipative-recentering) hysteresis loop (Buchanan et al. 2008). Epoxied threaded bars can be used as dissipaters internally or externally if encased in a steel tube to prevent buckling.

This type of connection allows rocking motion and is shown in Fig. 1 from Palermo et al. (2005). It can be adapted to post-tension timber walls with either threaded bars or strands like in Fig. 2 from Pei and Lindt (2009). In addition, internal or external dissipaters can also be used (Figs. 3 and 4 from Sarti et al. (2012)) with flexural U-shaped steel plated positioned between two adjacent walls (Iqbal et al. 2007) and (Smith et al. 2007).

Fig. 1
figure 1

Basic concept of hybrid jointed ductile connections for LVL timber frame systems and flag-shape hysteresis behaviour (Palermo et al. 2005)

Full size image
Fig. 2
figure 2

A typical example of rod hold-down system (Pei and Lindt 2009)

Full size image
Fig. 3
figure 3

Hybrid concept for wall systems, with external dissipaters or U-shaped Flexural Plates (UFP) devices modified (Sarti et al. 2012)

Full size image
Fig. 4
figure 4

Mild steel dissipation devices: a internal bar; b replaceable fused bar; c replaceable internal bar (Sarti et al. 2012)

Full size image

The mechanical principle of these systems restrains the damage in the dissipators. In contrast with conventional connectors (e.g. steel dowels, nails, bolts), their “improved post-earthquake reparability leads to significant reductions in repair costs and business downtime” (Buchanan et al. 2008).

Bonding requires a more fastidious quality assurance procedure compared with mechanical connectors. Nevertheless, the replaceability of mild steel dissipation devices can improve the life span of the structure.

2.1.2 Dissipative steel angles at beam-column or column-foundation connections

Based on the PRESS system (Poh’sie GH et al.. 2016), pre-stressed laminated (Pres-Lam) timber structures use high strength unbounded steel cables or bars to connect beams and columns (Fig. 5 from Cesare et al. (2017)), or columns and foundations (Cesare et al. 2019a, 2019b). The post-tensioning avoids loss of strength and potential brittle failure modes that can occur under loading in traditional timber connections (Buchanan et al. 2008). Furthermore, recent applications also added hysteretic dampers or dissipative viscous dampers (Polocoșer et al. 2018) to enhance the strength and energy dissipation capability. Thus, it creates a damage-avoiding structural system (Pu et al. 2018) by creating a rocking motion, that soften the structural response elastically through gap opening mechanisms (Chopra and Yim 1985; Palermo et al. 2012). A passive dissipation system can consist of yielding steel angle devices (Fig. 6 from Cesare et al. (2017)). The dissipative-rocking impacts on the seismic demand and the capacity of the structure by reducing maximum drift and increasing the system secant stiffness and the total equivalent viscous damping (Cesare et al. 2019b; Ponzo et al. 2015, 2017; Smith et al. 2013).

Fig. 5
figure 5

Details of beam-column connection of post-tensioned timber frame building with passive energy dissipation systems (Cesare et al. 2017)

Full size image
Fig. 6
figure 6

Definition of steel angle characteristics and steel angles device for beam-column joints (Cesare et al. 2017)

Full size image

These properties, interesting in a design seismic level, seem to be limited to a beam-column structure.

2.1.3 High force to volume (HF2V) viscous dampers

As described earlier, a possible solution to dissipate energy and avoid excessive displacement response lies in the use of mild steel dampers with pre-stressed tendon to a rocking wall (Ponzo et al. 2017; Marriott et al. 2008) or flexural U-shaped steel plates attached between two adjacent walls (Sarti et al. 2012). It has also been studied in a retrofitting situation analysis (Bahmani et al. 2014, 2017). However, “major drawbacks of these damping systems are the dissipation of energy through irreversible yielding of the steel parts. Yielding means these elements must be replaced after an earthquake, which may be difficult due to their position within the structure and can reduce the energy dissipation delivered on subsequent cycles after initial yielding.” (Wrzesniak et al. 2013). That is the reason why a new type of damping device has been developed: high force to volume HF2V viscous dampers. It can dissipate energy by a “reversible plastic extrusion of lead” and exhibit “no change in strength or stiffness under cyclic load” (Wrzesniak et al. 2013). For concrete and steel constructions, the viability of using HF2V devices in precast, post tensioned rocking wall or rigid structural steel beam-to-column connections was investigated (Marriott et al. 2008; Rodgers et al. 2012; Mander et al. 2009). Consequently, HF2V shows high, repeatable and stable energy dissipation without damage. Nevertheless, the system is not self-centring and needs a restoring force by tendons or mass by added vertical load to return to its neutral position after an earthquake (Wrzesniak et al. 2013). Further experimentations were carried out on glulam timber walls (Wrzesniak et al. 2013) (Figs. 7, 8 and 9). In contrast, wood is an anisotropic and light weighted material. This difference in properties in contrast with steel and concrete may cause a problem linked with “development of concentrated point loads from rocking reactions and damping/energy dissipation elements to avoid crushing or localised damage in the timber walls.” (Wrzesniak et al. 2013) When connectors between wall and energy dissipation are carefully designed, load transfer and dissipation can be maximised. Finally, HF2V viscous damping devices in timber structures show “a structurally feasible and cost-effective solution for rocking timber structures” in the range of US$500–1000 per device (Wrzesniak et al. 2013).

Fig. 7
figure 7

Damping device used for experimental tests (Wrzesniak et al. 2013)

Full size image
Fig. 8
figure 8

Test set-up: glulam wall with damping elements (dimension in mm) (Wrzesniak et al. 2013)

Full size image
Fig. 9
figure 9

Test specimen: glulam wall with damping elements (Wrzesniak et al. 2013)

Full size image

The dissipator itself has yet to be fixed to the structure, which requires careful consideration of possible brittle failures in timber. Although the properties of the dissipator remain constant under cyclic loads, it seems to be more suitable for special buildings due to its cost.

2.1.4 Superelastic shape memory alloy

Superelastic shape memory alloy (SMA) can be applied in many ways. It can provide self-centring properties to post tensioned steel beam-column (Fig. 10 from Chowdhury (2013)) and to seismic isolators (Attanasi et al. 2008).

Fig. 10
figure 10

Gap opening behaviour of SMA based end plate connection (Chowdhury 2013)

Full size image

As dowelled timber connections, it offers a larger ductility and a superior self-centring behaviour than the conventional and shows a lower residual deformation with a better ductility (Attanasi et al. 2008). Adapted in tuneable mass damper, it reduces excessive in-service vibration (Huang et al. 2020). Based on an earthquake shake table test (Lindt and Potts 2008) SMA device can significantly lower the displacement of a shear wall, and thereby effectively reduce its damage.

This technology seems to be promising in view of its recent developments. Its success probably depends on the cost at which it can be implemented.

2.2 Buckling restrained brace (BRB) principle

The use of Buckling Restrained Braces (BRB) has been gaining popularity since the late 1980s in countries with high seismic activities. The mechanical principle of these bracing devices is that a steel core is free to deform plastically by tensile and compressive forces but is prevented from buckling by an unbonded casing (Fig. 11 from Star Seismic Europe 2012). Thus, the BRB has a certain deformability for successive and alternating forces in its longitudinal axis. Figure 12 from Kersting et al. 2015 shows a typical BRB. The strut core—here a flat steel—takes up the normal tensile and compressive forces and fulfils its function of the structure's bracing. In addition, a lateral support by means of a hollow profile filled with concrete ensures it against buckling. This steel core has a constant cross-section to provide a flow area along the entire length that is impeded from buckling. Then its oversized ends guarantee structural safety to the connection.

Fig. 11
figure 11

BRB concept (STAR SEISMIC EUROPE, 2012 p. 4) (Star Seismic Europe 2012)

Full size image
Fig. 12
figure 12

Structure of a BRB (Kersting et al. 2015, p. 2) (Kersting et al. 2015)

Full size image

3 A new, highly ductile base hold-down

Directly inspired by the BRB principle, the new base hold-down offers energy dissipation through a high elongation of its core, a ductile reinforcing bar. Commonly used in ductile reinforced concrete construction (Bachmann 2003; SIA 262. Swiss code for concrete structures. Published by Swiss Society of Engineers and Architects 2013), the type of bar is crimped by a threaded coupler at each end. An intermediate steel element serves as buckling sheath, indispensable during core recompression and to compensate for the difference in diameter between the bar and its couplers. Then, a steel mantle welded to the bar couplers increases stiffness and allows to be lowered in due course. Figure 13 shows the buckling restrained hold-down’s principle. Precise cutting provides tongues which must be calibrated to fail at a force level between the characteristic value and the ultimate resistance of the core. It provides the system with increased initial stiffness for wind actions. During a strong earthquake, the forces exceed the mantle’s strength, breaking the tongues and making the ductile bar the only working element. Thus, it allows the system to deform and gives an enhanced flexibility to the structure. Using the Simplex bolt’s principle, the new hold-down is fixed at the base of a CLT wall. Moreover, the adaptive stiffness allows to lengthen the fundamental period T1 of the structure which also contributes to a reduction of the earthquake forces to be considered. In addition, as the hold-down becomes flexible, its contribution to the deformation of the structure is high, which should lead to a high ductility of the structure.

Fig. 13
figure 13

Buckling restrained hold-down’s principle

Full size image

After an earthquake, it is relatively easy to observe the condition of the tongues through an opening in the wall to see if the bar has started to plasticize. Thus, a replacement of the hold-down in case of tongue failure can easily be decided, which facilitates the renovation of the structure.

The idea, the preliminary tests and the Bachelor’s Thesis of Maître (Maître 2021 (in French)), were conducted as part of a project co-financed by Ancotech AG and the Swiss Innovation Agency (Innosuisse). There is a patent pending for the studied system and it has been registered under the trademark “Duktiplex”. Based on Maître’s Bachelor’s Thesis (Maître 2021 (in French)), the following chapters investigate stiffness, resistance and ductility of single hold-down and of CLT shear walls using two of these hold-downs.

4 Hold-down stiffness, strength, and ductility

4.1 Specimens, test and evaluation methods

4.1.1 Specimens

Single reinforcement bars and complete hold-downs with a length of 700 mm were tested following monotonic and cyclic tests methods. The hold-down core is a B500C (Maître 2021 (in French)) ductile reinforcing bar with a 12 mm diameter with a design tensile strength of TRd = 49.2 kN. At each end, it is crimped by a "BARON®-C type w" reinforcement coupler manufactured by Ancotech AG. It can be connected to the testing machine via the metric threads of the sleeves. Counter plates and RRW profiles allow for efficient mounting using 8.8 M16 bolts. The intermediate element is a steel tube with an inner diameter of 16 mm and an outer diameter of 22 mm. The mantle is a precision steel tube with an inner diameter of 23 mm and an outer diameter of 29 mm. Its rounded tongues are 50 mm long and 6.4 mm wide (Fig. 14). Figure 15 shows a specimen before and after the rupture.

Fig. 14
figure 14

Schemes of hold-down’s components and mantle geometry

Full size image
Fig. 15
figure 15

Intact and broken hold-down specimens with timber casing

Full size image

4.1.2 Test method and evaluation

The tests use a universal testing machine (RM 250, Schenck, Switzerland), which can withstand tensile and compression forces of up to 250 kN and is equipped with computer software (testXpert II V 12.0, Zwick, Switzerland). The hold-down displacement is recorded directly by the machine and not by independent sensors which lead to a slight imprecision. Since the new hold-down is primarily examined for its behaviour, and the tests focus on the ultimate displacement vu, this imprecision is negligible for high values of ultimate displacement vu.

4.1.2.1 Monotonic tests

Three single reinforcing bars and three complete hold-downs (Fig. 16) were subjected to monotonic tension tests according to the test standard EN 12512:2001 (European Committee for Standardization (CEN) 2001) to determine their yield displacement vy, ultimate displacement vu, and ductility D, slip modulus Kser, ultimate peak load PL (respectively PL,B (B = Bar) and PL,A (A = Anchor = hold-down)). The yield displacement vy is required to carry out the planned cyclic test and determined according to the same standard. The ductility from the monotonic tests was determined as follows:

$$D_{m} = \frac{{V_{u,m} }}{{V_{y,m} }}$$
(1)
Fig. 16
figure 16

Schemes and photos of bar and hold-down monotonic tests

Full size image

Based on previous tests on similar hold-downs, the ultimate tensile force \(F_{est}\) was estimated at about 70 kN. The loading speed amounts to 0.12 mm/s.

4.1.2.2 Cyclic tests

For cyclic tests, a timber casing is added to prevent buckling when the system is "recompressed". This consists of a CLT panel grooved to a diameter of 30 mm. Finally, full threaded 5.3 × 80 screws are given to prevent splitting of the CLT-element due to buckling restraining forces during recompression (Fig. 17). To allow the specimen to stretch in tension and then shorten in compression to its original length, the timber casing has a length of 697 mm. This means that the normal force exerted by the test machine is taken up exclusively by the hold-down and not by the timber casing.

Fig. 17
figure 17

Schemes of hold-down cyclic tests

Full size image

The mantle around the ductile bar stiffens the connection in the elastic domain and reduce the yield displacement vy. In plastic domain only the ductile bar, which has a greater yield displacement vy, takes the loads. Cyclic tests are based on the mean yield displacement vy,m,mean (= 2.85 mm) of single bars obtained by monotonic test. The complete procedure proposed by the test standard EN 12512:2001 (European Committee for Standardization (CEN) 2001) is followed. It assesses the same properties as the monotonic one, but under alternated and cyclic displacements. Table 1 gives the related diagram and chosen criteria to define the ultimate displacement of the cyclic test vu,c. The loading speed amounts to 0.12 mm/s. To test this hold-down, the procedure follows a cyclic loading in tension only, i.e. the elongation of the system remains positive. This accepted practice is already used in Brown and Li (2020) for example. The cycles are defined as a function of the target cyclic ductility and of the yield displacement vy,m.

Table 1 Loading procedure with chosen criteria
Full size table
4.1.2.3 Tests overview

Table 2 gives the details about the specimens used in monotonic and cyclic tests for single bars and complete hold-downs.

Table 2 Single bar and complete hold-down tests setup
Full size table

4.2 Results and discussion

4.2.1 Monotonic tests

Table 3 gives an overview of the results from the monotonic tests. It shows a mean yield displacement vy,m,mean of 2.85 mm for ductile bars. The assembly of the hold-down does not reduce the plastic and ductile properties of the bar, as the ultimate displacement and ductility remain in the same order of value and the break occurs in the bar as assured by the manufacturer. Figure 18 compares force–displacement curves between a single ductile bar (B_EN_m_1) and a complete hold-down (A_EN_m_1) and shows the achieved additional gain in stiffness. The hold-down’s peak load PL,A should have been slightly lower to ensure failure of the mantle without initiating yielding in ductile bar. However, this connector demonstrates its adaptative stiffness and the hold-down’s peak loads PL,A do not exceed excessively those of the ductile bar PL,B.

Table 3 Results of the monotonic test in terms of yield displacement, ultimate displacement, ductility, stiffness, and peak load
Full size table
Fig. 18
figure 18

Comparison of the force–displacement curves of a complete hold-down and a single bar

Full size image

4.2.2 Cyclic tests

Figure 19 shows the evaluation of a cyclic test. In all cases, the ultimate displacement vu,c was capped by the failure. Table 4 gives an overview of the results from the cyclic tests. Based on the same type of hold-down and mean yield displacement vy,m,mean of 2.85 mm, a cyclic ductility Dc of 12 and a ultimate cyclic displacement vu,c of 34.2 mm are achieved. The achieved gain in stiffness is also shown here by the hold-down’s slip modulus Kser,A.. However, measured stiffness are 18% lower compared to that of the preliminary monotonic tests. Quantifying stiffness is a sensitive matter, which might be influenced by different test set-ups. In addition, the cyclic procedure recompresses the system, which may lead to slight differences. Figure 20 shows the components of the hold-down specimen A_EN_cc_1 after its cyclic test. The failure always occurs in the bar as assured by the manufacturer.

Fig. 19
figure 19

Evaluations from a complete hold-down under cyclic loading according to the EN 12512 complete procedure

Full size image
Table 4 Results of the cyclic test in terms of ultimate displacement, ductility, stiffness, and peak load
Full size table
Fig. 20
figure 20

Visual assessment of a cyclic test (A_EN_cc_1)

Full size image

4.2.3 Intermediate conclusion

The complete hold-down can achieve a very high ultimate displacement vu of up to 64 mm in monotonic tests and 34 mm in cyclic tests. It reaches also a high cyclic ductility Dc of 12. The addition of the welded mantle provides an 88% increase in stiffness (Fig. 18). The failure always occurs in the bar at a level around 70 kN for both monotonic and cyclic tests. With a value just under 1.5, the actual overstrength is limited. The limits of the system depend on the calculated monotonic horizontal yield displacement vy,m. The compared results reflect the oligocyclic fatigue of the load alternations which decreases the final strength of the hold-down.

5 CLT shear wall using the new hold-down—stiffness, strength, and ductility

5.1 Specimens, test and evaluation methods

5.1.1 Specimens

5.1.1.1 Cross laminated timber shear walls

Wood shear walls are tested following two different tests methods. The specimens were made of Cross Laminated Timber (CLT–GFP DD by Schilliger Holz AG) panels of 140 mm and made of 5 layers (40–20-20–20-40) with laterally glued joints. The ratio of width to height is 1:2, that means an effective length between the vertical hold-downs of 1′260 mm and a height of 2′620 mm.

As with the single specimens, full threaded screws 8 × 120 mm reinforce the CLT against cracking perpendicular to the grain due to the buckling restraining function to the timber member. Regular pre-drilling facilitates this installation. Figure 21 shows the whole system used to hold-down the CLT shear walls.

Fig. 21
figure 21

Schemes and photo of vertical and shear hold-downs fastening

Full size image
5.1.1.2 Vertical load bearing

On both sides, the same highly ductile hold-down is inserted through a 30 mm diameter drill hole and fixed to the platform of the testing frame. The fixing principle is based on an M16 threaded rod of quality 8.8 screwed at each coupler of the hold-down (Fig. 22). The two openings in the panel at the top of the hold-downs are used for fastening by contact. At this location, a first steel plate is inserted onto the M16 threaded rod, which can hold the wall up when it is pulled vertically. Then it is followed by a counter-plate which, when the wall descends on this side, ensures that the vertical compressive forces are transmitted back into the ductile bar, compressing it and re-plasticising it back to its original state. The plates are held in place by two pairs of M16 nuts and washers. The base of the hold-down lies on two thick steel plates, that can allow the fastening by a M16 threaded rod tightened with M16 nut and washer. It is also fixed to the testing frame by four M24 bolts. In that way, the two hold-downs only experience tensile deformations and take up the vertical tensile forces, as the CLT panel prevents shortening beyond their initial length due to compression. Vertical compressive force can re-plasticize the hold-down back to its original state and are directly transmitted to the platform by the contact with the CLT.

Fig. 22
figure 22

Photos of complete hold-down with fastening system

Full size image
5.1.1.3 Base shear fixing

The new hold-down’s system does not allow the use of conventional angle brackets that are rigidly fixed to foundations and walls. Indeed, its ductility is based on a high elongation. According to preliminary tests on simple specimens, it varies between 60 and 70 mm. A shear connector placed in the middle of the wall must therefore lift by approximately 35 mm while remaining connected to the foundation to transmit the forces. A single, large, trapezoidal central steel shoe is fabricated by welding six plates together. The long horizontal plate underneath, fixed by four M24 bolts, allows the plasticisation and the expected vertical deformation (Fig. 23). The shoe is held in the groove of the CLT wall, by a M16 threaded rod screwed in its centre. It is fixed vertically in an opening in the wall using a steel plate, M16 washer and nut.

Fig. 23
figure 23

Photos of the steel shoe for base shear fixing of the CLT shear walls

Full size image
5.1.1.4 Capacity design—hierarchy of the strength

According to the capacity design method all brittle parts of the bracing walls must be designed with sufficient overstrength. To avoid brittle failures, non-ductile elements are oversized based on the actual strength of the hold-down. Thus, the dimensions of the different oversize factors γRd ductile bar and depending on the force in question ensures a hierarchy of strengths. As the steel bar is the one used for ductile reinforced concrete walls, the overstrength factors are based on the SIA 262 standard (Sarti et al. 2012): 1.4 for moment and 1.7 for shear force (Geiser 2018).

5.1.2 Test method and evaluation

The tests require a testing frame controlled by the testing software DION 7 from Walter + Bai. A horizontal testing frame was used. The deformation of the system is captured by four different lasers: two for the vertical displacement at each foot of the wall and two for the horizontal displacement at the base and the top (Fig. 24).

Fig. 24
figure 24

Position of the lasers—1: Horizontal at the top of the wall—2 and 3: Vertical and horizontal laser at the bottom of the wall—4: Vertical at the bottom of the wall

Full size image
5.1.2.1 Vertical load and lateral stability

As the hold-downs are vertically elongated, they are directly dependent on the vertical load of the structure. For this reason, a constant vertical load of 100 kN applied to the top of the wall is added for half of the specimens. A fixed rail accommodates several ball-bearing sledges which can allow steel profiles with channel sections to be slid to ensure a centred vertical force by the vertical cylinder (Fig. 25). Furthermore, plastic rollers attached to an additional steel beam stabilise the system laterally on each side (Fig. 26).

Fig. 25
figure 25

Vertical constant loading system

Full size image
Fig. 26
figure 26

Lateral stabilisation by plastic rollers

Full size image
5.1.2.2 Monotonic tests

Three CLT shear walls were subjected to monotonic tension tests according to the test standard EN 12512:2001 (European Committee for Standardization (CEN) 2001) to determine yield displacement vy, ultimate displacement vu, and ductility D, slip modulus Kser, ultimate peak load PL. The first two walls are fixed respectively by two complete hold-downs or two simple ductile bars. Then the last one is fixed by two simple ductile bars and supports the additional vertical load of 100 kN. The yield displacement vy is required to carry out the planned cyclic test and determined according to the same standard. The ductility from the monotonic tests was determined as follows:

$$D_{m} = \frac{{V_{u,m} }}{{V_{y,m} }}$$
(2)

Based on ultimate tensile force of simple hold-downs (72 kN) and wall’s geometry ratio (1:2), the ultimate horizontal force \(F_{est}\) was estimated at about 36 kN. To get the same loading speed (0.12 mm/s) in the hold-down as before, the horizontal loading speed amounts to 0.24 mm/s.

5.1.2.3 Cyclic tests

As the mantle around the ductile bar stiffens the connection in the elastic domain, the cyclic tests are based on the horizontal yield displacement vy,m of 1 shear wall using single ductile bars obtained by monotonic test. Without and with the additional vertical force, this value equals 11.37 mm or 13.29 mm.

An international standard ISO 21581 (International Organization for Standardization Timber structures—Static and cyclic lateral load test methods for shear walls ISO s2010) exists to evaluate walls. However, in order to facilitate the interpretation of the results, the same loading procedure is followed as for single hold-downs. Despite EN12512 (European Committee for Standardization (CEN) 2001) being intended for assemblies, it is also used for walls. The protocol, already detailed in chapter 0 Test method and evaluation, loads the walls in positive and negative displacements. It assesses the same properties as the monotonic one, but under alternated and cyclic displacements. The horizontal loading speed amounts to 1 mm/s.

5.1.2.4 Tests overview

Table 5 and gives the details about the specimens used in monotonic and cyclic tests for CLT shear walls.

Table 5 Overview of CLT shear wall test program
Full size table

5.2 Results and discussion

5.2.1 Monotonic tests

Table 6 gives an overview of the results from the monotonic tests. The horizontal yield displacement vy,m is obtained by the tests of shear walls using two ductile bars. Two values are found: without the additional vertical force (11.37 mm) or with (13.29 mm).

Table 6 Results of the monotonic tests according to EN 12512 on CLT shear wall in terms of yield displacement, ultimate displacement, ductility, horizontal stiffness, and peak load
Full size table

The implementation of the new hold-down in the CLT wall does not reduce the ductility of the bar, since its ultimate displacement remains in the same range. Moreover, the failure always occurs in the bar as assured by the manufacturer. Figure 27 compares force–displacement curves between shear wall with complete hold-downs W(A)_EN_m_1, with ductile bars W(B)_EN_m_1 and with vertical load W(B)_EN_m_VL_1. It shows a 41% increase in stiffness. The horizontal peak loads PL are higher than the estimated ultimate force \(F_{est}\) (= 36 kN), because of the shear shoe’s underneath plate partially hinders the CLT wall uplift especially for large displacements. Furthermore, to overturn the vertical force and start lifting the wall, a horizontal force of 30 kN is required.

Fig. 27
figure 27

Comparison of the force–displacement curves of the three monotonic tests of shear walls

Full size image

5.2.2 Cyclic tests

Figure 28 shows the evaluation of cyclic tests. In all cases, the ultimate displacement vu,c was capped by the failure. Table 7 gives an overview of the results from the cyclic tests. Based on the same type of hold-down but with different vertical loading, yield displacement vy,m (= 11.37 mm respectively 13.29 mm) and horizontal ultimate cyclic displacement vu,c (between 90 and 112 mm), the same cyclic ductility Dc of 8 is always obtained. Compared to the monotonic test W_EN_m_1, the average hold-down’s stiffness Kser,A is 8% higher. This increase may be due to a higher stiffness of the wood used or the shear connector.

Fig. 28
figure 28

Example of the evaluation from walls under cyclic loading according to EN 12512 complete procedure

Full size image
Table 7 Results of the cyclic tests according to EN 12512 (assuming vy,m = 11,37 or 13,29 mm) of shear walls in terms of ultimate displacement, ductility, horizontal stiffness, and peak load
Full size table

Figure 29 compares force–displacement curves and area under curve between cyclic tests of shear wall W_EN_c_VL_1 and W_EN_cc_1. Their horizontal ultimate cyclic displacement vu,c is different, respectively 91 and 106 mm. As their monotonic yield displacement vy,m also varies, their cyclic ductility is finally the same. However, one shear wall without (W_EN_cc_1) and with vertical load (W_EN_c_VL_1) can dissipate respectively 23,107 Joules (69%) and 33,583 Joules (100%).

Fig. 29
figure 29

Comparison of the force–displacement diagrams and area between curves between cyclic tests of shear walls with and without vertical loads

Full size image

5.2.3 Comparison with a timber frame wall sheathed with OSB panel

Compared to a timber frame wall sheathed with OSB panels (Fig. 30 from), which was tested in 2019 at the BFH (Geiser et al. 2009), the CLT walls examined show better ductility properties. Evaluated according to the same full cyclic procedure from the test standard EN 12512:2001 (Mander et al. 2009), the timber frame shear wall has a monotonic yield displacement vy,m of 6.51 mm, an ultimate cyclic displacement vu,c of 28.4 mm and a cyclic ductility Dc of 4.36. Figure 31 superimposes this cyclic test on a cyclic test of CLT shear wall. The vertical axis corresponds to the horizontal force as a percentage of the horizontal cyclic peak loads PL,c. Thus, the new base hold-down allows a large increase (83%) in cyclic ductility Dc without peak load PL reduction and a very low pinching.

Fig. 30
figure 30

Plan and details of timber frame wall sheathed with OSB (Geiser et al. 2009)

Full size image
Fig. 31
figure 31

Comparison of cyclic tests: CLT wall (W_EN_cc_01) / timber frame wall sheathed with OSB

Full size image

5.2.4 Intermediate conclusion

CLT shear walls using the new hold-down demonstrate very high ultimate displacement and ductile properties. The addition of the mantle provides a significant increase in stiffness. The limits of the system depend on the additional vertical load. Without and with vertical force, the monotonic horizontal yield displacement vy,m amounts respectively 11.37 mm and 13.29 and the ultimate cyclic displacement vc,u 90.96 mm and 106.32 mm. Nevertheless, it achieves in each case a cyclic ductility Dc of 8. Compared to a timber frame wall sheathed with OSB, the new base hold-down allows a CLT shear wall to have greater ductility (83%) without peak load PL reduction and a very low pinching.

6 Practical implementation of the new hold-down

6.1 Provided implementation in a 4-storeys apartment building

A 12 m high and four-storeys apartment building in a medium seismicity zone and an unfavorable ground class is planned in Monthey (Switzerland). In the main direction X, the structure is braced by a series of short CLT walls arranged regularly along the ground plan. These shear walls have a length of 2.80 m, run in one piece over the entire height of the structure. Based on a non-dissipative pre-design (q = 1.5), an uplift force of more than 2 MN appears, implying a wall thickness of more than 400 mm. In this case, the practical feasibility of a timber solution would be questionable. However, following a careful pre-design with a behaviour factor of q = 4, the uplift force of TEd = 551 kN can be taken up by four hold-downs, produced with 20 mm diameter ductile bar, arranged in parallel (Fig. 32). The preliminary tests presented in this publication deal with 12 mm diameter bars. In situations, where large forces occur, diameters larger than 12 mm are required. Additional tests were conducted to verify the properties with a diameter of 16 mm and 20 mm. A parallel arrangement of these base hold-downs allows a wide range of forces up to 500–700 kN.

Fig. 32
figure 32

Schemes of vertical and shear hold-downs fastening for a four-storeys residential building (Ancotech AG)

Full size image

7 Conclusion

The results obtained, both on single hold-downs and on CLT shear walls including them, show a very high ductility, a limited overstrength and a low pinching. Hold-downs and walls respectively achieve an ultimate monotonic displacement vu,m of over 60 mm or 115 mm, an ultimate cyclic displacement vu,c of over 34 mm or 90 mm and finally a cyclic ductility Dc of 12 or 8. Compared to a timber frame wall sheathed with OSB, the new base hold-down allows a CLT shear wall to have greater ductility (83%) without peak load PL reduction and a very low pinching. This significant improvement is due to a paradigm shift: the ductile steel bar is no longer laterally loaded, but axially. In addition, the principle of adaptive stiffness works with increase of stiffness up to 88%. A trademark "Duktiplex" has been registered (UM18440743, CH768383) by Ancotech AG and a patent (EP 4 071 314 A1) is pending. By arranging several hold-downs in parallel, high forces can be connected, which is essential for modern timber structures. This new product should contribute to improve the attractiveness of timber structures.