1 Introduction

The behavior of individual buildings during earthquakes has been investigated by a great number of researchers (Haselton et al. 2011; Hadianfard and Gadami 2012; Inel et al. 2013; Rigi et al. 2021). Nonetheless, the earthquake-induced pounding between adjacent buildings must be examined independently. Pounding of buildings takes place as a result of impacts that structures inflict on each other at the time of an earthquake. The phenomenon was observed in a great number of earthquakes. In some cases, the effects of the phenomenon can be advantageous, e.g. when it comes to inter-story drifts; however, in many cases, the phenomenon can be very devastative. For instance, about 15% of buildings were greatly damaged, and the pounding phenomenon had a meaningful effect on 20–30 percent of the reported failures in Mexico’s earthquake (1985) (Rosenblueth and Meli 1986). In the Loma Prieta earthquake, 500 different structures were examined, and in 200 cases, the impact phenomenon was observed (Kasai and Maison 1997). Also the phenomenon of pounding between buildings in many recent earthquakes, including the Lorca earthquake (2001), the Christchurch earthquake (2011) and the Simav earthquake (2013), was observed. Moreover, after surveying these cities in which significant earthquakes took place, the impact phenomenon was determined as one of the main hazard for building failures (Romão et al. 2013; Cole et al. 2010, 2012; Inel et al. 2013).

In the case of a significant difference between the dynamic properties of the colliding structures (mass, period, the height of buildings, etc.), the impact phenomenon may lead to very critical situations (Anagnostopoulos and Spiliopoulos 1992; Jankowski 2008). The structural response is resonated in the direction of pounding, and this resonance is deeply dependent on the dynamic structural characteristics (Kazemi et al. 2021; Hosseini et al. 2021). In addition, the peak impact forces at the time of collision are substantially dependent on the parameters, such as gap size, and impact velocity (Naderpour et al. 2016). Since the phenomenon of earthquake-induced structural pounding is complex and unpredictable, the detailed studies considering the behavior of colliding buildings in series with different arrangements are necessary (see, Raheem et al. 2018; Elwardany et al. 2021, for example). Also, the research on impacts between adjacent buildings should take into account different numerical simulation strategies in order to understand the characteristics of structures (Bamer et al. 2018, Shi et al. 2018; 2019). The 3D analysis of collisions between adjacent 8- and 10-story buildings showed that shorter structures generally exhibited an amplified response, and the structural response was more dependent on the input parameters of the ground motion rather than on the seismic separation distance of structures (Pant et al. 2010). In the case of collisions between two buildings with equal heights but different dynamic characteristics, the results indicate that the collision affects the most flexible and the lightest buildings significantly, while the stiffest and the heaviest structures are only slightly affected (Jankowski 2008). For the ground motions with low frequencies range, the responses of flexible structures are exacerbated, while the same responses are magnified for stiff structures at high-frequency ground motions (Dimitrakopoulos et al. 2009). Given the substantial effect of infill on the structural behavior during earthquakes, and therefore on pounding, the infilled frames feature a greater stiffness, as compared to the bare frames (frames with no infill), and as a result, pounding is less prominent in infilled frames (Elwardany et al. 2017, 2019). In comparison with far-field ground motions, the near-field ground motions cause higher increases of the response of colliding structures (Chitte et al. 2014). Generally, the response of stiff-flexible buildings under pounding differs when the two colliding buildings are of different or the same heights, and it is impossible to present a universal conclusion about decreasing or increasing the structural responses because it is significantly dependent on the neighboring flexible (or stiff) structures and the ground motion characteristics (Sołtysik et al. 2017; Fujii and Sakai 2018). Also, some studies have been conducted to investigate the impact phenomenon between fixed-base and base-isolated structures, and it was finally concluded that the buildings with fixed-base are subjected to larger damages, as compared to the base-isolated ones (Barros et al. 2013). The results of investigations of pounding between isolated structures, either featuring a moat wall or against neighboring structures, indicate that provision of a sufficient gap cannot guarantee the prevention of a building from collisions with adjacent structures (Polycarpou and Komodromos 2010). The study of the impact spring stiffness and the effect of coefficient of restitution on impact forces indicates that as the stiffness of the impact spring increases, the impact force is uniformly increased; however, as the coefficient of restitution rises, the impact force is reduced uniformly (Naderpour et al. 2016). The pounding phenomenon effect will be more intense when buildings have different periods because this will increase the likelihood of collisions, and these collisions will be chaotic and irregular (Kharazian and López-Almansa 2019). The peak impact force value during the time of an earthquake is not really dependent on the PGA value of ground motion but it is dependent on the pounding scenario and the frequency content of excitation. Therefore, considering the design earthquake, it is advisable to individually determine the peak impact force of the building exposed to the impact of the structure during the ground movement for a particular configuration of structures. (Khatami et al. 2020). So far, in order to calculate the necessary seismic separation distance between neighboring buildings, much research has been conducted, each of which has presented a new formula, and in some of them, the effect of the period of colliding structures has been considered (Naderpour et al. 2017). Pounding between adjacent structures arranged in series causes them to inflict multiple blows on each other, and as a result, the phenomenon may result in damages ranging from partial non-structural local damages to very serious general structural damages and even complete failure of buildings. A parametric investigation on collisions of several neighboring SDOF buildings arranged in series showed that the peripheral buildings located at the end of the row were much more greatly destructed, as compared to the inner structures, while the inner buildings often behaved differently. Since a structure may have a higher or lower period than its neighboring structures, the response of interior buildings may be increased or decreased. In this case, stiffer structures generally exhibit an amplified response. On the other hand, flexible structures usually experience a response decrease. In accordance with numerical simulation of three buildings, Anagnostopoulos (1988) concluded that occasional pounding led to higher amplification of responses of peripheral buildings than internal buildings. By contrast, different evaluations of the damages inflicted by the Christchurch 2011 earthquake indicate different situations, in which interior structures are more damaged than peripheral ones (Cole et al. 2011). It should be added that pounding phenomenon may cause inelastic deformation or cracks at the contact point, which can considerably influence the structural behavior under earthquake excitation. For this reason, a number of studies in the field of pounding were focused on new computational strategies that allow us to model the effects of local damage on the global response behavior of the colliding structures (Bamer 2018; Bamer and Markert, 2018; Bamer et al. 2019).

This investigation concentrates on the effects of seismic pounding on the neighboring structures arranged in series with different heights to present a better evaluation of the structural behavior at the time of the pounding phenomenon. To formulate pounding among neighboring structures arranged in series, a nonlinear finite element modeling is developed. In order to create three different alignment configurations of three structures with series arrangement, three 4-, 8-, and 12-story Reinforced Concrete Special Moment Resisting Frames (RC SMRF) are considered. These structures are affected by 20 near-field ground motions. In addition, a contact element with a linear viscoelastic nature is chosen in order to model the pounding phenomenon. By using the Incremental Dynamic Analysis (IDA) (Vamvatsikos and Cornell 2002), the potential pounding between adjacent structures in series is evaluated under earthquake hazards. The collision effect is investigated for various separation distances, three alignment configurations and 20 different ground motions, including non-pulse and pulse-like records subsets presented by FEMA-P695, which is then compared to the model with no pounding. For the same purpose, in order to evaluate the seismic limit state capacity of buildings via OpenSees, nonlinear IDA is employed.

2 Research significance

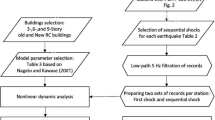
According to the literature, numerous studies have been conducted on the pounding phenomenon; however, there are still no integrated and comprehensive results for the concerned phenomenon, and a number of contradictions are encountered in some cases. This study examined the behavior of adjacent buildings with series arrangement located next to each other using nonlinear dynamic analysis. Also, the effect of adjacent buildings arrangement on the structures’ behavior under earthquake was scrutinized. Figure 1 presents the research flowchart.

Fig. 1
figure 1

Flowchart of various stages of this study

Full size image

The research innovations are as follows:

  1. 1.

    Three buildings are placed next to each other in series with various seismic distances and configurations. Then, their nonlinear behavior, incorporating earthquake-induced structural pounding, was studied.

  2. 2.

    Nonlinear analysis technique of IDA has been applied so as to provide IDA and fragility curves and to evaluate different performance levels of adjacent structures.

  3. 3.

    The effect of two-sided and one-sided pounding on neighboring buildings has been examined.

  4. 4.

    Twenty different near-field records, including non-pulse and pulsed records, have been considered (near-field earthquakes include critical energy pulses—see Hudson and Housner 1958).

3 Structural analysis

3.1 Ground motion characterization

The assumed structures are considered to be located on soil class D in California. The seismic design parameters are: SD1 = 0.9 g, SDS = 1.0 g (g stands for the ground acceleration), and the average shear wave velocity of Vs-30 = 285 m/s. The ground motions employed for nonlinear dynamic analyses were large-magnitude (i.e., 6.5–7.9) earthquakes. Twenty records of near-field ground motion, including non-pulsed and pulsed records, were chosen from FEMA P-695 (2009). The characteristics of these records are set out in Table 1.

Table 1 Selected near field records based on FEMA P-695 (2009)
Full size table

3.2 Modeling of adjacent RC buildings

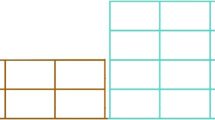
This research concentrates on the effects of seismic pounding on the Reinforced Concrete Special Moment Resisting Frames (RC SMRFs) adjacent buildings arranged in series with different heights. This study employed Haselton’s structural models (2D three-bay frames) with three different heights (4-, 8- and 12 stories) and a bay width of 20 ft (6.1 m). The 8- and 12-story buildings had a 120 × 120 ft2 (36.6 × 36.6 m2) square plan, while the 4-story building had a plan area of 120 × 180 ft2 (36.6 × 54.98 m2). Each prototype was designed in accordance with the provisions specified by ASCE 7–02, ACI 318, and International Building Code, including the requirements for stiffness, strength, detailing, and capacity design (Haselton et al. 2010, Haselton and Deierlein 2006). The buildings featured an 8-in. flat slab floor system. The ASCE/SEI 7–10 (2010) was used in order to calculate structural separation distance. A value of Rayleigh damping corresponding to 5% of the critical damping was applied. The structural specifications of analyzed buildings are presented in Table 2. Figure 2 depicts the plan of the chosen buildings. For all buildings, P-Delta effects were included by applying a combined form of gravity loads on the lateral resisting frames and gravity loads on the leaning column elements, which was modeled as pinned at the base and linked to the frame at floor levels via axially rigid connections. In Fig. 3, a schematic of the structural analysis model of the reinforced concrete frame has been presented. The lumped plasticity model was applied for the whole columns and beams, and joints were modeled considering the panel zone.

Table 2 Structural specifications of 4-, 8- and 12-story buildings (Haselton et al. 2010)
Full size table
Fig. 2
figure 2

The selected frame of prototype buildings (Haselton et al. 2010)

Full size image
Fig. 3
figure 3

Schematic of structural analysis model of a reinforced concrete frame (Haselton et al. 2011)

Full size image

As Fig. 4 shows, the nonlinear IDA has been conducted for three different alignment configurations of neighboring structures arranged in series.

Fig. 4
figure 4

Buildings system alignment configurations. a Configuration I (4–8–12), b Configuration II (8–12–4), c Configuration III (12–4–8)

Full size image

The beam-column elements were modeled through a nonlinear hinge model with stiffness and strength degradation. A trilinear backbone curve shown in Fig. 5 was employed to model plastic hinges. The Ibarra model capturing cyclic and monotonic deterioration modes was considered and imported into OpenSees software (see Ibarra et al. 2005). The model is defined by the following parameters: the post capping rotation capacity (θpc), the plastic rotation capacity (θcap, pl), an energy-based degradation parameter (λ), and the ratio of the maximum moment to yielding moment (Mc/My). According to calibration to the test data for reinforced concrete beams and columns with ductile detailing and low-moderate axial loads, the common values of the major parameters are as follows: θpc is equal to 0.10 rad, θcap, pl ranges within 0.035–0.085 rad (depending on the axial load level in the beam-column elements), λ ranges between 85 and 130, and Mc/My ranges between 1.17 and 1.21 (Haselton et al. 2007, 2008b). These values were used in the present study.

Fig. 5
figure 5

Illustration of spring model, monotonic backbone curve (Ibarra et al. 2005)

Full size image

3.3 Structural impact model

An impact element is essential in order to develop the pounding phenomenon model, which is placed between neighboring structures and simulates the impact force (Anagnostopoulos 1988; Rezaei et al. 2020; Miari and Jankowski 2021). A large number of different models presented for the impact element neglect the energy dissipation and plastic behavior during collisions; however, some models are more complicated.

In order to estimate the impact stiffness coefficient (k), a new technique was developed that considered the nonlinear stiffness of the spring on the basis of the impact forces of the first and the second structures instantly (Khatami et al. 2014). The linear viscoelastic model (called the Kelvin-Voigt model) was used in the study (Anagnostopoulos 1988). The model can include the energy dissipation in the course of the collision, and in particular, it does not have complicated modeling. It incorporates a damper (dashpot), in parallel with a spring, to reflect the dissipation of energy (Fig. 6).

Fig. 6
figure 6

Viscoelastic impact model

Full size image

The model is described via Eqs. (1), (2), and (3). The impact force represented by F(t) in the model is presented as (Anagnostopoulos 1988):

$$F\left(t\right)=\left\{\begin{aligned}k\delta \left(t\right)+&c\dot{\updelta }\left(t\right) \qquad \delta \left(t\right)>0\\ 0& \qquad \qquad~ \delta\,\left(t\right)\le 0\end{aligned}\right.$$
(1)
$$c=2\upzeta \sqrt{k\frac{{m}_{1}{m}_{2}}{{m}_{1}+{m}_{2}}}$$
(2)
$$\upzeta =-\frac{lne}{\sqrt{{\pi}^{2}+{(lne)}^{2}}}$$
(3)

where \(\dot{\updelta }\) and δ stand for the velocity and relative displacement between the colliding structural elements, respectively, and c and k represent the damping and stiffness of the impact model, respectively. Also, m1 and m2 are the masses of colliding structural elements, e stands for the coefficient of restitution, and \({\varvec{\upzeta}}\) represents the impact damping ratio.

According to ASCE/SEI 7–10 (2010) calculations, in order to calculate the necessary separation distance between structures, the linear displacement of the building in the height level is initially determined. In taller buildings, this value is equal to the roof displacement in the shorter building. When calculating the mentioned value from the pushover curve of the building, the displacement in the base shear of the building is regarded as the maximum roof displacement. Subsequently, the calculated value is multiplied by the Cd (deflection amplification factor) determined in accordance with the structural system from the code. The obtained value is then divided by the importance factor of the structure, I. Subsequently, this value is determined for both structures, and then the minimum value of the allowable distance is calculated according to Eq. 4. For all models designed in the collision, the necessary structural separation distance D is calculated by Eq. 4 (ASCE/SEI 7–10 2010).

$$D=\sqrt{{\left(\frac{Cd.\delta M}{I}\right)}_{1}^{2}+{\left(\frac{Cd.\delta M}{I}\right)}_{2}^{2}}$$
(4)

where Cd stands for the deflection amplification factor, I represents the importance factor, and δM stands for the largest inelastic response displacement.

4 Results and discussion

4.1 IDA curves

In the performance-based design methods, the performance of the structure due to the applied earthquake is the basis of structural design. Uncertainties in estimating demand and capacity lead to the discussion on probabilities in the field of earthquake engineering and the invention of probability-based design methods.

The IDA method (Vamvatsikos and Cornell 2002) is a technique of seismic structural analysis in accordance with their performance that describes the structural behavior within a wide range of various earthquake Intensity Measures (IMs). Given the nonlinear and dynamic nature of this technique, the method results are certainly closer to the real-world structural behavior when compared to alternative analyses, such as linear static analysis (Miari and Jankowski 2021). It is evident that the response of time history analyses features a high dependency on records and their dynamic properties. Thus, in general, time history analyses and definitely IDAs are performed with more than one record (Rigi et al. 2021). The IM (for this research, chosen as Sa (T1)) is increased up to the total collapse of the structures. In this paper, collapse is defined as the last point on the curve where the tangent slope is equal to 20% of the elastic slope.

It should be added that, in the nonlinear IDA time history analysis, the earthquake acceleration is gradually increased allowing us to conduct the analysis for the records with different accelerations which are equivalent to different levels of intensity. On the other hand, in the case of the nonlinear time history analysis, the investigation is conducted only once for the record scaled to a specific acceleration level. IDA involves a large number of nonlinear dynamic analyzes under the influence of earthquake accelerations which are scaled in such a way that they can cover the range of linear behavior, nonlinear behavior and finally the collapse behavior of the structure. By using IDA, the following information can be obtained (Vamvatsikos and Cornell 2002):

  • a clear picture of the response of the structure for different ranges of earthquake intensity,

  • the amount of damage for each intensity level of the earthquake,

  • understanding the structural behavior in the face of severe earthquakes,

  • understanding the response of the structure to a gradual increase in the intensity of earthquakes (for example, changing the pattern of deformation with height, the beginning of stiffness and strength degradation),

  • estimation of the behavior of the structure from the elastic state to the flow and instability of the structure under the dynamic load of the earthquake.

Twenty earthquakes that include near-field pulse-like and no-pulse record subsets presented by FEMA-P695 (2009) were employed in the present study. Three 4-, 8-, and 12-story RC SMRF buildings with various separation distances and heights are incorporated to create three diverse alignment configurations of three neighboring structures in series arrangement in OpenSees. Additionally, three separation distances, equal to 0.0, 0.75D, and 1.0D, were considered for the estimation of the seismic collapse capacity of the colliding buildings. In Figs. 7, 8, and 9, the IDA curves of the 4- 8- and 12-story RC SMRFs colliding structures are depicted with various separation distances and alignment configurations.

Fig. 7
figure 7

IDA curves of the 4-, 8-, and 12-story RC colliding buildings for various separation distances (configuration I)

Full size image
Fig. 8
figure 8

IDA curves of the 4-, 8-, and 12-story RC colliding buildings for various separation distances (configuration II)

Full size image
Fig. 9
figure 9

IDA curves of the 4-, 8-, and 12-story RC colliding buildings for various separation distances (configuration III)

Full size image

In Fig. 10, the median IDA curves of the 4-story RC SMRF pounding with 8-story and 12-story RC SMRFs colliding structures have been presented for configuration I (4–8–12) with various separation distances and also compared to no-pounding cases. Considering a separation distance of 0.0 for configuration I, the median IDA curve of the 4-story RC SMRF is reduced by 33.33% (from 1.8 to 1.2) as a result of the pounding effect; however, the median IDA curves of the 12-story and 8-story RC SMRF are increased by 118.18% (from 0.55 to 1.2) and by 84.6% (from 0.65 to 1.2), respectively. We may observe no changes in the median IDA curves of the 4-story, 8-story, and 12-story RC SMRFs when considering a separation distance of 0.75D instead of 0.0 for the same configuration, and when the separation distance is increased to 1.0D, the median IDA curve of the 4-story RC SMRF is reduced by 22.22% (from 1.8 to 1.4) but the median IDA curves of the 12-story and 8-story RC SMRF increase by 136.3% (from 0.55 to 1.3) and by 115.3% (from 0.65 to 1.4), respectively.

Fig. 10
figure 10

Comparison of the median IDA curves of the 4-, 8-, and 12-story RC colliding buildings for various separation distances (configuration I)

Full size image

Figure 11 depicts the median IDA curves of the 4-story RC SMRF pounding with 8-story and 12-story RC SMRFs colliding buildings for configuration II (8–12–4) with various separation distances and in comparison with no-pounding cases. By considering a separation distance of 0.0 for configuration II, the median IDA curves of the 12-story, 8-story, and 4-story RC SMRF decline by 9.09% (from 0.55 to 0.5), 23.07% (from 0.65 to 0.5), and 72.22% (from 1.8 to 0.5) as a result of the collision effect, respectively. As before, no change occurs in the median IDA curves of the 4-story, 8-story, and 12-story RC SMRFs by considering a separation distance of 0.75D instead of 0.0 for the same configuration. From another viewpoint, for a separation distance of 1.0D, the median IDA curves of the 8-story and 4-story RC SMRFs decline by 7.7% (from 0.65 to 0.6) and by 69.44% (from 1.8 to 0.55), respectively, but there was no change for the median IDA curve of 12-story RC SMRF structure for the configuration I with a separation distance of 1.0D, as compared to the no-pounding case.

Fig. 11
figure 11

Comparison of the median IDA curves of the 4-, 8-, and 12-story RC colliding buildings for various separation distances (configuration II)

Full size image

Figure 12 shows the median IDA curves of the 4-story RC SMRF pounding with 12-story and 8-story RC SMRFs colliding buildings for configuration III (12–4–8) with various separation distances and in comparison with no pounding cases. We can observe a decrease in the median IDA curves of all RC SMRFs structures with no distances between them. However, the median IDA curves of the 12-story, 8-story, and 4-story RC SMRFs are reduced by 18.18% (from 0.55 to 0.45), 30.76% (from 0.65 to 0.45), and 75% (from 1.8 to 0.45) as a result of the collision effect, respectively. Like the previous modes, no change was observed for the median IDA curves of the 12-story, 8- story, and 4- story RC SMRFs when considering a separation distance of 1.0D and 0.75D in comparison with 0.0 for the same configuration.

Fig. 12
figure 12

Comparison of the median IDA curves of the 4-, 8-, and 12-story RC colliding buildings for various separation distances (configuration III)

Full size image

Thus, the least median Sa (T1) value for all structures with any separation distance among the considered configurations is that of configuration III, and configuration I has the maximum value of median Sa (T1) in comparison with the other cases. As a result, the buildings in configuration III collapse before the other configurations due to its lower median value of Sa (T1) and the fact that in this configuration, structures are in a more critical condition than the alternative cases. If the separation distance is increased from 0.0 to 1.0D, the median Sa (T1) values increase for configurations II and I; however, no change is observed in this value for configuration III, even with the allowed separation distance of the code. Only in configuration I and for the three values of the separation distance considered in this study, the median Sa (T1) value for 8-story and 12-story structures increased significantly in the case when the structures were collided, as compared to the case with no collision between the buildings. But if the impact phenomenon occurs, this value is dramatically decreased for a 4-story structure. This means that 12-story and 8-story structures in this configuration collapse at higher Sa (T1) values, as compared to that in the non-collision case; however, the opposite applies for a 4-story structure. For configurations III and II, the median Sa (T1) values for all structures with any separation distance were reduced in the pounding case so that the structures did not collide.

4.2 Seismic fragility curves

To estimate the structural performance levels, considering a damage index is necessary. Since the maximum inter-story drift ratio is regarded as a damage indicator in this study, various performance levels are evaluated and described on the basis of the drift values. This study employed the performance levels described in the Hazus-MH guidelines (FEMA 2012, see Table 3). Four performance levels are considered for reinforced concrete structures with a moment frame system with a high and medium number of floors on the basis of the maximum inter-story drift ratio. These performance levels are respectively considered as slight, medium, extensive and complete.

Table 3 Average Inter Story Drift Ratio (ISDR) for structural damage state thresholds in accordance with Hazus-MH
Full size table

After modeling the neighboring structures, the chosen earthquake records were applied to these models, and after conducting IDA for all models under each of the records, the maximum drift was determined, and a comparison was made between the obtained values and the structural damage state thresholds described through Hazus-MH guidelines. The occurrence probability of each structural performance level in any Sa (T1) values was determined, and the fragility curves were plotted for whole models. Eventually, for the fragility curve of each structure, a comparison was made between the state that has not yet collided and the state in which the pounding phenomenon took place. A favorable criterion for comparison of the results of colliding structures is the probability curve. One can use the resulting IDA curves to extract seismic fragility curves for various performance levels indicated by Sa (T1).

In Table 4, the limit state capacities of RC MRFs buildings (the median Sa (T1) corresponds to the probability of 50%) are presented for the case in which the structures are individually subject to an earthquake with no structure located in its vicinity. In Table 5, the median Sa (T1) corresponds to the probability of 50% for RC MRFs buildings are presented for the case in which the structures collided with each other under various separation distances and configurations. The fragility curves for all structures under configuration I, II and III are shown in Figs. 13, 14, 15, respectively.

Table 4 Limit state capacities of the RC MRFs with no adjacent buildings (no pounding mode)
Full size table
Table 5 Limit state capacities of the RC MRFs with neighboring structures (pounding mode)
Full size table
Fig. 13
figure 13

Comparing the seismic fragility curves of 4-, 8-, and 12-story RC colliding buildings for various separation distances (configuration I)

Full size image
Fig. 14
figure 14

Comparing the seismic fragility curves of 4-, 8-, and 12-story RC colliding buildings for various separation distances (configuration II)

Full size image
Fig. 15
figure 15

Comparing the seismic fragility curves of 4-, 8-, and 12-story RC colliding buildings for various separation distances (configuration II)

Full size image

In Table 6, the percentage change in each performance level is shown in the pounding mode vs. the no-pounding mode of 4-, 8-, and 12-story RC colliding structures with various separation distances for the configuration I (4–8–12).

Table 6 Percentage change in limit state capacities of the RC MRFs for all buildings configuration versus the no pounding mode (%)
Full size table

According to the above table, which shows the results for 4-, 8-, and 12-story RC MRFs in configuration I, the median Sa (T1) has been increased in correspondence with the probability of 50% obtained in the case of the seismic fragility curves for different performance levels of all three structures and any of the three distances considered in this study. This means that the impact phenomenon enhances the structures’ condition compared to the state in which the impact did not place, and here, the pounding phenomenon is advantageous. Except for the 4-story building with a separation distance of 1.0D, as compared to the results acquired for no pounding case, the median Sa (T1) of the building has been decreased for the complete and extensive performance levels by 4.9% and 2.1%, respectively.

In configuration II, the median Sa (T1) has been decreased correspondently with the probability of 50% obtained in the case of the seismic fragility curve for different performance levels of 4-story and 8-story RC SMRF structures for the whole considered distances. On the other hand, the median Sa (T1) has been decreased for the 12-story RC SMRF building for the moderate and slight performance levels, but for the complete and extensive performance levels, it has been increased by the percentages shown in Table 5 for the whole distances. According to the Table 5 results, for 4-, 8-, and 12-story RC MRFs in configuration III, the median Sa (T1) decreased for different performance levels of all buildings and for all considered distances.

5 Conclusion

This study is concentrated on the seismic pounding effects of the neighboring buildings with series arrangement, non-equal story heights, and various configurations by considering three separation distances of 0.0, 1.0D and 0.75D. After conducting the IDA analysis for these models, the IDA curves were plotted. The various structural performance levels were investigated for the same neighboring structures in accordance with the Hazus-MH criteria subjected to various conditions. A comparison was made between the obtained results and those obtained for the analysis of a single building with no pounding (with no buildings in the vicinity). The results of the study are summarized as follows:

  • In accordance with the IDA curves, the median Sa (T1) increases for configurations I and II for all three structures when the distance increases from 0.0 to 1.0D, while for configuration III, increasing the distance has no effect on the median Sa (T1).

  • By changing the structures’ arrangement, the median Sa (T1) also attains different values, such as the maximum median Sa (T1) value that occurs for configuration I, and its lowest value occurring for configuration III. Thus, it can be concluded that the series arrangement of adjacent structures has a great effect on the collapse capacity of each structure. As a matter of fact, the lower the median Sa (T1) is, the sooner the buildings will collapse.

  • In the case of placing the shorter building between two taller ones, as a result of the impact phenomenon, the median Sa (T1) is decreased more than in the case in which the taller structure is located in the middle.

  • The configuration in which the structures are placed next to each other in ascending height order has the maximum median Sa (T1) value. The median Sa (T1) in this configuration is even greater than in the case with no collision phenomenon, and the structures collapse at higher accelerations.

  • By the analysis of the fragility curves for configuration I, in which the structures are placed next to each other in ascending height order, for all buildings with any separation distance except for two cases, the performance levels are improved, as compared to the case, in which the impact phenomenon does not occur. Thus, it can be concluded that the impact phenomenon has enhanced the structures’ performance significantly and has been advantageous.

  • For configuration III, in which the shorter structure is located in the middle of the two taller structures, for all buildings and the whole distances investigated in this research, performance levels are reduced. Generally, when the shorter structure is located between the two taller buildings, a decreased performance level is observed for the all three adjacent structures, while both increase and decrease can be observed for the other configurations.

  • In some cases, even when the allowable separation distance is considered between the structures, no improvement is observed in Sa (T1), and the performance levels of adjacent buildings or the amount of this enhancement are insignificant. Thus, arranging the structures next to each other has a greater effect, as compared to the case in which even the allowable separation distance is considered between the structures.