Multi-objective optimal design and seismic assessment of an inerter-based hybrid control system for storage tanks

Abstract

In this paper, a hybrid control system (HCS) endowing a base isolation system (BIS) with a Tuned Mass Damper Inerter (TMDI) is proposed for the protection of steel storage tanks from severe structural damages induced by seismic events. Among all the components of industrial plants, cylindrical steel storage tanks are widely spread and play a primary role when subjected to seismic hazard, since they suffer of many critical issues related to their dynamic response such as high convective wave height and base shear force. The adopted base isolation system is realized with spring and damper elements, whereas the TMDI is realized with a tuned mass damper connected to the ground by the inerter. The developed mechanical model consists of a MDOF system, which considers the impulsive and convective modes as well as the TMDI dynamics. An optimal design problem is tackled, making use of a multi-objective approach, with the scope to mitigate simultaneously the convective and impulsive response of the storage tank. A zero mean white noise excitation is assumed as input in the optimal design procedure. Once the HCS is optimally designed, a systematic investigation of its seismic effectiveness is reached through parametric analysis. Modal parameters and frequency response functions are discussed. A literature case study comparing the effectiveness of the proposed optimally designed HCS with traditional base isolation is illustrated and performances are assessed through stochastic excitation and natural earthquakes.

1 Introduction

The condition of industrial plants is very complex in relation to earthquakes. The extremely severe consequences related to such kind of natural events are particularly evident, especially in plants in the petrochemical sector or in the treatment of flammable substances, e.g. in chemical and oil processing industries (Hatayama 2008; Suzuki 2006).

Besides, the large number of components and connections makes them very complex systems, the environmental consequences of a component collapse, such as the release into the atmosphere of toxic or dangerous substances due to fires or explosions, render this topic a key emerging issue and explains the growth of interest in the engineering field towards the study of their seismic response. Related to the extremely severe consequences that accidents involving such structures can cause, it is worth to explore the applicability of the passive control techniques, such as energy dissipation, base isolation and Tuned Mass Damper (TMD) in the mitigation of their dynamic behaviour. The issue is extremely topical, as proved by recent accidents, among which one of the most impacting can be considered the damages related to either Izmit or Tokachi-Oki earthquake (Korkmaz et al. 2011).

Among all the components, cylindrical steel storage tanks play a primary role, due to their wide spread and by virtue of the extent of the critical issues that concern them, when subjected to seismic hazard. Thus, their dynamic behaviour has been extensively studied by authors in the past decades, both experimentally and analytically (Haroun and Housner 1981, Haroun 1983, Haroun and Ellaithy 1985, Housner 1957, Housner 1963, Kim and Lee 1995). Three components can be identified within the liquid stored mass: the first one which moves rigidly with the tank walls, named impulsive; the second one which represents the interaction between the liquid stored in the tank and the walls; the last one which experiences the convective motion, represented by some long period components. Therefore, such structures involve in their dynamic motion contemporaneously large and short period components. The types of damages in which a base excited tank can typically incur can be traced either to the impulsive dynamics that provokes high base shear force - e.g. elephant foot buckling, diamond buckling, wall-bottom plate joint failure, uplifting - or to the convective dynamics that provokes a high convective wave - e.g. overtopping, release of the storage (Merino et al. 2020), sinking of the floating roof, wall-roof gasket detachment. Moreover, it has been observed that damage due to convective dynamics increases when the storage tank becomes broader.

An overview of the main passive control techniques applicable in the mitigation of plants seismic response has been proposed in Paolacci et al. (2013). Thus, yielding-based devices are involved in preserving columns or reactors, by dissipative coupling to adjacent apparatus, having different dynamical properties; non-conventional TMDs are utilized to protect steel support frames. The employment of conventional base isolation is considered suitable for cylindrical liquid storage tanks to reduce the impulsive component of motion; it has been typically proposed in order to suppress the impulsive damage, as a result of the cut in base shear and overturning moment of the tank. Its principle of operation, based on the decoupling between the structural displacement and the shaking ground, through the insertion of a deformable layer of isolators, implies the location of most of the deformation between the basement and the ground, with lengthening of the fundamental period of the structure and reduction in the earthquake-induced forces transferred to it. In De Angelis et al. (2010) the effectiveness of base isolation in reducing the dynamic response of steel storage tanks has been studied both numerically and experimentally, firstly developing simplified numerical models, considering the impulsive motion and the convective modes, and then validating the results by means of a reduced scale physical model. However, two main drawbacks related to base isolation employment have been highlighted in that study: the onset of large displacements at the isolation layer and the ineffectiveness in reducing the convective response. Such drawbacks become particularly evident for ground motions rich in high period content, near fault and pulse-like earthquakes, with the danger of resonances.

In order to protect the safety and integrity of base isolated systems, Yang et al. (1991) proposed the employment of TMD, either active or passive, defining a novel mixed control system. Their effectiveness in mitigating the lateral seismic demands under strong earthquakes is shown referring to tall buildings. Tsai (1995) highlighted the strong link between seismic excitation frequency and control system effectiveness and evaluated TMD capability to reduce the deformation of the isolation layer through numerical analyses. Palazzo et al. (1997) equipped a base isolated 2DOF linear system with a TMD, assessing the seismic performance of the system, assuming stationary Gaussian excitation. Further confirmation of the above discussed mixed system effectiveness came from the experimental campaign conducted by Petti et al. (2010). Taniguchi et al. (2008) coped with an optimal design problem, assuming as optimal parameters of the TMD those which minimize the demand on the base-isolated structure, highlighting that the TMD capability in reducing the response is particularly stressed for low damped isolation systems and for TMD employing large mass.

In the last years, a great interest is grown for the use of the inerter, a two-terminal device able to produce a force proportional to the relative acceleration between its terminals and a constant, named inertance, which has dimension of a mass (Smith 2002).

Due to its mass amplification effect (Kawamata 1973; Saito et al. 2002), the inertial mass results even two orders of magnitude greater than the gravitational mass and this property makes it attractive in structural control applications (Lazar et al. 2014; Deastra et al. 2022). Combining an inerter device, which possesses large inertial mass in the face of a small gravitational mass, with a conventional TMD (Soong and Dargush 1997), which has a small auxiliary mass, a Tuned Mass Damper Inerter (TMDI) is defined (Garrido et al. 2013, Marian and Giaralis 2017). The resulting control system is characterized by the lightness typical of a conventional TMD, due to a small auxiliary gravitational mass, and by the high efficacy and robustness of a non-conventional TMD, due to a high inertial mass ratio (De Angelis et al. 2012; Reggio and De Angelis 2015). This circumstance has given rise to a flourishing literature on this theme (De Domenico et al. 2018, De Domenico and Ricciardi 2018a, De Domenico and Ricciardi 2018b, Di Matteo et al. 2019, Petrini et al. 2020, Wang et al. 2020, Pietrosanti et al. 2017, Marian and Giaralis 2014).

Thus, the idea of considering base-isolated structures equipped with a TMDI rather than a large mass TMD is born. De Domenico and Ricciardi (2018) studied the effectiveness of optimal designed TMDI systems in reducing the response of multi-story buildings, against earthquake excitations, achieving meaningful vibration reductions, in terms of both the isolation layer displacement and response of the isolated superstructure. The employment of a grounded inerter in the vibration control of seismically excited base-isolated systems is studied in De Angelis et al. (2019). An optimal energy based TMDI design procedure is proposed and the effectiveness of the control system is assessed taking into account both stochastic and recorded strong ground motion excitations. A wide study in this direction, assuming ground motions with different features has been conducted in Masnata et al. (2020).

Concerning the introduction of inerter-based control systems in base isolated storage tanks subject to earthquakes, Luo et al. (2016) proposed a new hybrid control method: a viscous mass damper (VMD) to be used with linear isolators to reduce liquid sloshing. In the study the assumption of tank as rigid wall was made and only convective modes were considered. Zhang et al. (2018) proposed to place in parallel with a linear visco-elastic isolation system an inerter and a viscous damper, considering two possible arrangements in series and parallel. They proposed a demand-oriented optimal design method, sought for the achievement of predefined target performance levels. Jiang et al. (2020) developed an optimal design method based on analytical formulae, derived by minimizing the height of the convective wave, mainly focusing on slender tanks. Zahedin et al. (2020) faced a preliminary multi-objective optimization problem (Reggio et al. 2020)-(Greco and Marano 2016) for an Inerter Base Isolation System (IBIS).

It is practice from the past literature, that the most suitable passive control system to mitigate the dynamic response of steel storage tanks should aim at minimizing the base shear force and convective wave height. Therefore, the complete uncoupling between the ground and the structure, making use of a properly designed isolation system, may seem the most appropriate choice to pursue. Nevertheless, it has been demonstrated, (De Angelis et al. 2010), that this strategy causes the arising of large displacement at the isolation layer, named displacement of the isolation layer, which conflicts with the two other criticalities, and should be considered for design purposes as well. In fact, it plays a key role as well since large displacements cause severe damage to connections. To the authors knowledge, there are no research studies that consider simultaneously in the design problem an objective function that considers together these three response quantities, critical for the safety of storage tanks. In light of the above, in this work it is proposed a Hybrid Control System (HCS) with the aim to mitigate simultaneously the convective and impulsive response of steel storage tanks induced by earthquakes. The HCS is pursued by a base isolation system (BIS) and a grounded TMDI. The adopted mechanical model consists of a multi-degrees-of freedom (MDOF) system, made up of a certain number of convective modes, one degree-of-freedom (DOF) representing the impulsive dynamics, and one the TMDI, according to the model with lumped mass and stiffness proposed by Housner and developed by other authors. Stochastic white noise excitation is firstly adopted. The employed optimal design methodology is based on a multi-objective approach, to explicitly consider in the objective function the conflict among more quantities involved. Once the HCS is optimally designed, a systematic investigation of its seismic effectiveness is reached through parametric analysis, considering variations of the TMDI mass, inertance and damping coefficient of the isolation system. Modal parameters and frequency response functions are presented and commented. The paper closes with the illustration of the utilization of the designed HCS to a literature case study comparing the effectiveness with traditional base isolation. Performances are assessed utilizing stochastic excitation and natural earthquakes.

The paper is organized as follows. In Sect. 2 the key steps for the solution of a free surface convective problem are briefly summarized; subsequently, the mechanical model is illustrated and the equations of motion are stated. A multi-objective optimization problem is stated in Sect. 3. The results obtained through numerical investigations are presented in Sect. 4. Considerations on the seismic performance base isolation when applied to storage tanks, with a comparison between the results obtained in this work and those reported in De Angelis et al. (2010), constitute the subject of Sect. 5.

2 Mechanical model and equations of motion

2.1 Fixed base tank

Consider a tank of cylindrical shape and vertical axis, with radius R, filled with liquid until a level H, as sketched in Fig. 1.

Fig. 1

Tank outline

According to the literature model originally proposed by Housner and further studied by other authors afterwards, three mass components can be identified within the liquid stored in the tank (Haroun and Housner 1981)-(Kim and Lee 1995). The first one moves rigidly with the tank walls and is named impulsive; the second one represents the interaction between the liquid stored in the tank and the walls; the last one experiences the convective motion.

Within this framework, the mass associated with the j-th convective mode, $m_{cj}$, can be expressed as

$$\begin{aligned} m_{cj} = m \frac{2}{s \lambda _j ( \lambda _j^2 - 1 )} tanh( s \lambda _j ) \end{aligned}$$

(1)

where m, calculated as $m = \pi \rho _L H R^2$, is the total liquid mass stored in the tank, $s = \frac{H}{R}$ is the aspect ratio, defined as the ratio between the fill level and the radius of the tank and $\lambda _j$ is the j-th zero of the first derivative of the Bessel function of the first kind.

Since broad tanks ($s < 1.0$) are considered in this work, the natural periods of the convective modes are typically much longer than the natural vibration periods of the shell modes and thus the tank wall has been assumed rigid. Therefore the component related to the liquid-walls interaction has been neglected.

Thus, the impulsive liquid mass $m_I$ can be derived as

$$\begin{aligned} m_I = m - \sum _{ j = 1}^{\infty } m_{cj} \end{aligned}$$

(2)

according to the number of convective modes considered.

Let $k_{cj}$ and $c_{cj}$ be, respectively, the stiffness and damping coefficient relative to the j-th convective mode. The resulting mechanical model is shown in Fig. 2. The equation of motion of the j-th mode, in the case of presence of damping, takes the form

$$\begin{aligned} \ddot{u}_j (t) + 2 \xi _j \omega _j \dot{u}_j (t) + \omega _j^2 u_j (t) = - \ddot{u}_g (t) \end{aligned}$$

(3)

where $u_j$ (t) is the j-th convective displacement and $\ddot{u}_g$ is the applied base acceleration. The overdot signifies differentiation with respect to time t. Moreover, $\xi _j$ stands for the damping ratio of the j-th mode, being

$$\begin{aligned} \omega _j = \sqrt{\frac{\lambda _j \ g \ tanh ( s \lambda _j )}{R}} \end{aligned}$$

(4)

the natural circular frequency of the j-th mode and g the acceleration of gravity.

Rename as $m_C$, $k_C$ and $c_C$ the first convective mode mass, stiffness and damping, respectively.

The uncoupled frequency ratios $\delta _j$ are defined as

$$\begin{aligned} \delta _j = \frac{\omega _j}{\omega _C} \quad j = 1,..., N \end{aligned}$$

(5)

where the circular frequency of the first convective mode has been renamed $\omega _C = \sqrt{\frac{k_C}{m_C}}$. Let ${\textbf {u}}_C$ be the vector which collects the convective displacements $u_j$.

The dimensionless equations of motion can be expressed in the matrix form as

$$\begin{aligned} \mathbf {{M}}_C \ddot{\varvec{q}}_{C}(t) + \mathbf {{L}}_C {\dot{\varvec{q}}}_C (t) + \mathbf {{K}}_C \varvec{q}_C (t) = - \mathbf {{M}}_C \varvec{\tau }_C \ddot{q}_g (t) \end{aligned}$$

(6)

where ${\textbf {M}}_C$ = diag ( $\mu _j$) , ${\textbf {K}}_C$ = diag ( $\mu _j \delta _j^2$), ${\textbf {L}}_C$ = diag ( $2 \mu _j \ \xi _j \ \delta _j$ ), thus standing for convective mass, stiffness and damping matrices, respectively and $\varvec{\tau }_C$ is the influence vector, represented in this case by an identity vector, and with $\mu _j = \frac{m_{cj}}{m_C}$. Moreover, $\varvec{q}_{C} (t) = \frac{\varvec{u}_{C} (t)}{\frac{g}{\omega _{C}^{2}}}, {\dot{\varvec{q}}}_{C} (t) = \frac{{\dot{\varvec{u}}}_{C} (t)}{\frac{g}{\omega _{C}}}, {\ddot{\varvec{q}}}_{C} (t) = \frac{{\ddot{\varvec{u}}}_{C} (t)}{g}, \ddot{q_{g}} (t) = \frac{\ddot{u_{g}} (t)}{g}$.

Fig. 2

Mechanical model of the fixed base tank

2.2 Tank equipped with HCS

In this work, a HCS is proposed to control the dynamics of the system. The mechanical model of the tank with HCS is reported in Fig. 3.

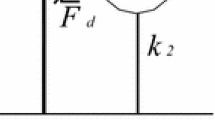
The control is achieved by means of an isolation layer together with a linear TMDI. The isolation layer is represented by $k_I$ and $c_I$, namely linear isolation system stiffness and damping. The TMDI consists of a linear TMD, connected to the ground by means of a linear inerter. $m_T$, $k_T$, $c_T$ and b are the mass, stiffness, damping and inertance of the grounded TMDI, respectively. The hypothesis of inerter linear behaviour is born in light of recent studies Pietrosanti et al. (2020), Pietrosanti et al. (2020).

Let $\omega _I = \sqrt{\frac{k_I}{m_I}}$ and $\omega _T = \sqrt{\frac{k_T}{m_T + b}}$ be the natural frequency of the isolation system and of the TMDI, respectively. The dimensionless Equations of motion which govern the dynamics of the system with HCS are written as

$$\begin{aligned} \mathbf {{M}} \varvec{\ddot{q}}(t) + \mathbf {{L}} \varvec{\dot{q}} (t) + \mathbf {{K}} \varvec{q} (t) = - \mathbf {{M}} \varvec{\tau } \ddot{q}_g (t) \end{aligned}$$

(7)

where M, L and K represent mass, damping and stiffness matrix, respectively, defined as follows

$$\begin{aligned} {\mathbf {M}}&= \begin{pmatrix} \mathbf {M}_C &{} \mathbf {M}_C \varvec{\tau }_C &{} \mathbf {O} \\ \varvec{\tau }_C^T \mathbf {M}_C &{} 1 + \sum _{ j = 1}^{N} \mu _j&{} 0 \\ \mathbf {O}^T &{} 0 &{} \mu _T + \beta \\ \end{pmatrix} \end{aligned}$$

(8)

$$\begin{aligned} {\mathbf {L}}&= \begin{pmatrix} \mathbf {L}_C &{} \mathbf {O} &{} \mathbf {O} \\ \mathbf {O}^T&{} 2 \xi _I \delta _I + 2 \xi _T \mu _T \delta _T &{} - 2 \xi _T \mu _T \delta _T \\ \mathbf {O}^T &{} - 2 \xi _T \mu _T \delta _T &{} 2 \xi _T \mu _T \delta _T \\ \end{pmatrix} \end{aligned}$$

(9)

$$\begin{aligned} {\mathbf {K}}&= \begin{pmatrix} \mathbf {K}_C &{} \mathbf {O} &{} \mathbf {O} \\ \mathbf {O}^T&{} \delta _I^2 + \mu _T \delta ^2_T &{} - \mu _T \delta ^2_T \\ \mathbf {O}^T &{} - \mu _T \delta ^2_T &{} \mu _T \delta ^2_T \\ \end{pmatrix} \end{aligned}$$

(10)

$\varvec{\tau }$ is the influence vector

$$\begin{aligned} \mathbf {M} \varvec{\tau } = \begin{pmatrix} \mathbf {M}_C \varvec{\tau }_C \\ 1 + \sum _{ j = 1}^{N} \mu _j \\ \mu _T \\ \end{pmatrix} \end{aligned}$$

(11)

where ${\textbf {q}} = [ {\textbf {q}}_C^T (t) \quad q_I (t) \quad q_T (t)]^T$. The uncoupled isolation frequency $\delta _I$, the uncoupled TMDI frequency ratio $\delta _T$, the convective damping ratio $\xi _C$, the isolation damping ratio $\xi _I$, the TMDI damping ratio $\xi _T$, the TMDI mass ratio $\mu _T$, the dimensionless inertance $\beta$, are defined as

$$\begin{aligned} \delta _I&= \frac{\omega _I}{\omega _C} \quad \delta _T = \frac{\omega _T}{\omega _C} \end{aligned}$$

(12)

$$\begin{aligned} \xi _C&= \frac{c_C}{2 \omega _C m_C} \quad \xi _I = \frac{c_I}{2 \omega _I m_I} \quad \xi _T = \frac{c_T}{2\omega _T (m_T+b)} \end{aligned}$$

(13)

$$\begin{aligned} \mu _T&= \frac{m_T}{m_I} \quad \beta = \frac{b}{m_I} \end{aligned}$$

(14)

The number of convective modes of interest can be selected on the basis of their significance for the purposes of the analysis.

Fig. 3

Mechanical model of the tank with HCS

2.3 Reduced order model

In this study, only the first convective mode has been taken into account, since the contributions related to the higher convective modes have been considered negligible (Haroun and Ellaithy 1985). However, their masses have been included within the impulsive mass.

To this end, a three degree of freedom (3-DOF) dynamical system is defined, including the first convective oscillator equipped with a HCS.

Therefore the matrices M, L and K can be rewritten as

$$\begin{aligned} {\hat{\varvec{M}}}&= \begin{pmatrix} \mu _C &{} \mu _C &{} 0 \\ \mu _C &{} 1 + \mu _C &{} 0 \\ 0 &{} 0 &{} \mu _T + \beta \\ \end{pmatrix} \end{aligned}$$

(15)

$$\begin{aligned} {\hat{\varvec{L}}}&= \begin{pmatrix} 2 \xi _C \mu _C &{} 0 &{} 0 \\ 0&{} 2 \xi _I \delta _I + 2 \xi _T \mu _T \delta _T &{} - 2 \xi _T \mu _T \delta _T \\ 0 &{} - 2 \xi _T \mu _T \delta _T &{} 2 \xi _T \mu _T \delta _T \\ \end{pmatrix} \end{aligned}$$

(16)

$$\begin{aligned} {\hat{\varvec{K}}}&= \begin{pmatrix} \mu _C &{} 0 &{} 0 \\ 0&{} \delta _I^2 + \mu _T \delta ^2_T &{} - \mu _T \delta ^2_T \\ 0 &{} - \mu _T \delta ^2_T &{} \mu _T \delta ^2_T \\ \end{pmatrix} \end{aligned}$$

(17)

and the influence vector $\varvec{\tau }$ becomes $\varvec{\hat{\tau }}$ such that

$$\begin{aligned} {\hat{\varvec{M}}} \varvec{\hat{\tau }} = \begin{pmatrix} \mu _C \\ 1 + \mu _c \\ \mu _T \\ \end{pmatrix} \end{aligned}$$

(18)

where $\mu _C = \frac{m_C}{m_I}$. It can be noticed that the system sketched in Fig. 3 includes the limiting cases below. If $\mu _T$ is set equal to zero ( $\mu _T$ = 0) the HCS falls back into a BIS equipped with a TID. If $\beta$ = 0, it represents a BIS with a TMD. When both the secondary mass and the inertance are equal to zero ($\mu _T$ = 0, $\beta$ = 0), the tank is controlled by means of a BIS.

2.4 State space formulation

Taking into account the probabilistic nature of the earthquake excitation, neglecting the dependence on the excitation frequency, the ground acceleration $\ddot{u_g}(t)$ is firstly modeled as a Gaussian zero mean white noise random process with power spectral density $S_{\ddot{u_g}}$ = $S_0$. Let ${\textbf {u}} (t)$ and ${\dot{\varvec{u}}} (t)$ be the displacement and velocity vectors, respectively. Rewriting the governing equations of motion in the first-order state space form

$$\begin{aligned} \dot{z} (t) = \mathbf {A} \mathbf {z}(t) + \mathbf {B} a (t) \ \qquad y (t) = \mathbf {C} \mathbf {z}(t) + \mathbf {D} a (t) \end{aligned}$$

(19)

where

$$\begin{aligned} {\mathbf {z}} (t) = \left[ \begin{array}{c} \mathbf {u} (t) \quad {\dot{\varvec{u}}}(t) \end{array} \right] ^{\text {T}} \end{aligned}$$

(20)

is the 6-by-1 state vector, a(t) is 1-by-1 the applied input process, the 6-by-6 A matrix and 6-by-1 B vector

$$\begin{aligned} {\mathbf {A}} = \begin{pmatrix} \mathbf {O} &{} \mathbf {I}\\ {\hat{\varvec{M}}}^{-1} {\hat{\varvec{K}}} &{} {\hat{\varvec{M}}}^{-1} {\hat{\varvec{L}}} \\ \end{pmatrix} \qquad {\mathbf {B}} = \begin{pmatrix} \mathbf {O} \\ \varvec{\hat{\tau }} \\ \end{pmatrix} \end{aligned}$$

(21)

are the state matrix and the input-to-state matrix, respectively. Aiming at extracting the convective displacement and the displacement of the isolation layer, the 2-by-6 state-to-output matrix C and the 2-by-1 direct feedthrough matrix D are expressed as

$$\begin{aligned} {\mathbf {C}} = \begin{pmatrix} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 \end{pmatrix} \qquad {\mathbf {D}} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} \end{aligned}$$

(22)

2.5 System response to white stochastic excitation

Since the stationary input process has zero mean and the initial conditions are zero, the response is fully represented by the covariance matrix G$_{zz}$ = ${\textbf {E}} \ [ \ {\textbf {z}}(t) \ {\textbf {z}}(t)^T \ ]$, that satisfies, by virtue of the stationarity of ${\textbf {z}}(t)$, the Lyapunov Equation

$$\begin{aligned} \mathbf {A} \mathbf {G}_{zz} + \mathbf {G}_{zz} \mathbf {A}^T + 2 \pi S_0 \mathbf {B} \mathbf {B}^T = \mathbf {O} \end{aligned}$$

(23)

${\textbf {E}} \ [ * ]$ represents the expected value operator. Eq. (23) can be solved numerically for $\mathbf {G}_{zz}$; the variance of j-th output variable, $\sigma ^2_j$ is expressed by

$$\begin{aligned} \sigma _j^2 = \mathbf {n}_j \mathbf {C} \mathbf {G}_{zz} \mathbf {C}^T \mathbf {n}_j^T \end{aligned}$$

(24)

where $\mathbf {n}_j$ is a 1 by 3 vector of zeros, except for the j-th component, equal to one.

Thus, concerning the controlled case, the following quantities of interest can be defined:

• $\sigma _{C}^2$, the variance of the convective displacement;

• $\sigma _{I}^2$, the variance of the displacement of the isolation layer;

• $\sigma _{\tau }^2$, the variance of the base shear force.

The corresponding quantities pertinent to the fixed base (FB) case are identified by the subscript 0. Thus:

• $\sigma _{C0}^2$ represents the variance of the convective displacement in the FB case;

• $\sigma _{\tau 0}^2$ is the variance of the base shear force in the FB case.

3 Multi-objective optimal design

An optimal HCS design problem is herein stated following a multi-objective (MO) approach, aiming at minimizing objective function vectors $\mathbf {F}_j$, j = 1,2, for pre-specified aspect ratio s, convective damping ratio $\xi _C$ and convective to impulsive mass ratio $\mu _C$. The mass ratio $\mu _C$ is known once the geometry is defined. Thus, a first dimensionless parameters vector, collecting the parameters s, $\xi _C$ and $\mu _C$, $\mathbf {x}_0 = [ s \quad \mu _C \quad \xi _C]^T$ is defined.

Six independent parameters are involved in the optimal design problem, grouped into two vectors. The first one, $\mathbf {x}_1 = [ \xi _I \quad \mu _T \quad \beta ] ^T$, which collects the isolation damping, the TMDI mass and inertance ratios. The second one, $\mathbf {x}_2 = [ \delta _I \quad \delta _T \quad \xi _T]^T$, which lists the isolation frequency, TMDI frequency and TMDI damping ratio. The optimization problem consists in finding the optimal design parameters $\mathbf {x}_2$, bounded within a predetermined searching range [$\mathbf {x}_2^{min}$$\mathbf {x}_2^{max}$], for several given values of the parameters listed in $\mathbf {x}_1$. Therefore this can be mathematically stated in the form:

$$\begin{aligned} \text {find}_{\mathbf {x}_2} min \ [ \mathbf {F}_j ( \mathbf {x}_2 \mid \mathbf {x}_1 ) ]\,\, \text {subjected} \,\text {to}\, \mathbf {x}_2^{min} \le \mathbf {x}_2 \le \mathbf {x}_2^{max} \end{aligned}$$

(25)

The system has been subjected to a white noise ground excitation. Three objective functions have been defined, to control convective displacement, isolation displacement and base shear force. To this end, the convective performance index $d_C$, the performance index $d_I$ related to the displacement of the isolation layer and the base shear force performance index $\tau _I$, which are expressed as

$$\begin{aligned} d_{C} = \sqrt{\frac{\sigma _{C}^2}{\sigma _{C0}^2}} \quad \quad d_{I} = \sqrt{\frac{\sigma _{I}^2}{\sigma _{C0}^2}} \quad \quad {\tau }_{I} = \sqrt{\frac{\sigma _{\tau }^2}{\sigma _{\tau 0}^2}} \quad \end{aligned}$$

(26)

have been introduced.

The first design criterion assumes $d_C$, $d_I$ and $\tau _I$ as objective functions, thus $F_1 = [ d_C \quad d_I \quad \tau _I ]^T$. The second design criterion assumes $d_C$ and $d_I$ as objective functions, thus $F_2 = [ d_C \quad d_I ]^T$.

Once the multi-objective optimization problem is stated, a standard and straightforward method for building the Pareto optimal set, based on the combination of the objective functions into a single objective function, making use of weighting coefficients, has been employed (Cohon 1978; Papadrakakis et al. 2002).

Denoting by $w_k$ and $f_k$, with $k =$ 1, 2, ..., n, the employed weighting coefficients and the single objective function, respectively, the multi-objective minimization problem represented by Eq. (25) can be rewritten as

$$\begin{aligned} \text {find} \ min\,\, \ [ \sum _{k = 1}^{n} w_k f_k ( \mathbf {x} ) ]\,\,\ \text {subjected} \ \text {to} \ \mathbf {x}^{min} \le \mathbf {x} \le \mathbf {x}^{max} \end{aligned}$$

(27)

The normalization of the weighting coefficients $w_k$ which has been used is such that their sum is equal to one, that is

$$\begin{aligned} \sum _{k = 1}^{n} w_k = 1 \end{aligned}$$

(28)

The set of the Pareto optimal solutions for the problem stated has thus been figured out by varying the weighting coefficients.

4 Numerical investigations

4.1 Optimal design

The employed optimal design procedure is exemplified in this section with reference to specific sets of dimensionless parameters $\mathbf {x}_0$ and $\mathbf {x}_1$.

Concerning the parameters collected in vector $\mathbf {x}_0$, it has been assumed: a value of the aspect ratio s = 0.5 in order to catch the behavior of broad tanks in which the convective effect is more marked, a damping ratio $\xi _C$ = 0.005, representing the low dissipative capacities of the fluid and the mass ratio $\mu _C$ = 1.94, estimated on the basis of the assigned geometry. Therefore $\mathbf {x}_0$ has been set equal to $\mathbf {x}_0 = [ 0.5 \quad 1.94 \quad 0.005]^T$. Concerning the parameters collected in vector $\mathbf {x}_1$ it has been assumed: $\xi _I$ = 0.15, which refers to commonly employed medium damped systems, $\mu _T$ = 0.01, which is typically adopted for conventional TMDs, and $\beta$ = 1.00, which is suitable for light inertance systems. These values are even placed at the center of the range subject to the parametric investigation shown below. It follows that $\mathbf {x}_1$ has been set equal to $\mathbf {x}_1= [ 0.15 \quad 0.01 \quad 1.00]^T$.

In numerically solving Eq.25 the bounds of $\mathbf {x}_2$ have been taken as $\mathbf {x}_2^{min} = [ 0.10 \quad 0.10 \quad 0.01]^T$ and $\mathbf {x}_2^{max} = [ 10.0 \quad 10.0 \quad 1.00 ]^T$, respectively.

The optimal HCS is found and its performance is investigated with respect to specific choices of the vectors $\mathbf {x}_1$ and $\mathbf {x}_0$. In the case under analysis, the domain described in the space $d_C$-$d_I$-$\tau _I$ is shown in Fig. 4a, while Fig. 4b represents the same domain on the plan $d_C$-$d_I$. The latter plan can be regarded as the plane projection of the three-dimensional domain. It plays a key role, since it shows clearly the conflict between $d_C$ and $d_I$. In the light of the above, the most suitable plot of the outcomes can be obtained on a plan whose axes are represented by $d_C$ and $d_I$, on the axis of the abscissas and of the ordinates, respectively. Results take the form of multi-objective performance maps. Each point belonging to the above-mentioned domain is associated with a specific performance of the control system, which can be read, in terms of $d_C$ and $d_I$. On this plan, based on the definition of $d_C$ and $d_I$, the vertex of coordinates (1,1) represents the fixed base case. Thus, the more the performance point is closer to the origin of the axes, the better the reduction of the response is.

The black curve illustrated in Fig. 4b represents a Pareto front. This curve clearly marks the boundary between a close area covered by points and a region, in the neighbourhood of the origin of the axes, where the access is denied. Each of these points represents an allowable state. A triplet of design parameters $\mathbf {x}_2$ can be associated to each of them.

The point of optimality, identified by the minimum distance from the origin of the axes on the plan ($d_C$, $d_I$) is marked in red in Fig. 4b. It is placed in the neighbourhood of the bisector of the plan, consistently with the need of reducing both the impulsive and the convective dynamics. It emerges from Fig. 4a and b that $\tau _I$ and $d_C$ share the same trend. The optimal designed parameters with the corresponding values of the performance indices associated are listed in Table 1. The first row of the Table represents the optimal parameters obtained minimizing ${\textbf {F}}_1$, i.e. $d_C$, $d_I$ and $\tau _I$, the second one is gained by minimizing ${\textbf {F}}_2$, i.e. $d_C$ and $d_I$. It is observed that all the three optimized parameters fall within the investigated range, none of which bumping towards the bounds. Concerning $\delta _I^{OPT}$, it draws values in the range (1-2); $\delta _T^{OPT}$ has values lower than one; $\xi _T^{OPT}$ values around 0.36. Regarding the performance indices, all of them assume values lower than 0.20, testifying a reduction of about the 80% with respect to the uncontrolled case. It is worth noticing that the two adopted objective function vectors ${\textbf {F}}_1$ and ${\textbf {F}}_2$ lead to comparable optimal parameters and performance indices. Therefore it makes sense to assume in the following only the latter, ${\textbf {F}}_2$, involving $d_C$ and $d_I$, as optimization methodology. Thus, the results will be illustrated making mainly use of the ($d_C$, $d_I$) performance plan. Moreover, for each explored case, the fielded domain is omitted, in favor of the Pareto front.

Fig. 4

Performance maps of: a $\mathbf {F_1}$, $d_C$-$d_I$-$\tau _I$ space; b $\mathbf {F_2}$, $d_C$-$d_I$ plan.HCS: $\xi _I$ = 0.15, $\mu _T$ = 0.01, $\beta$ = 1.00. The red mark represents the point of optimality

Turning the attention to the design parameters subject to optimization, contour plots of $\delta _I$ are shown in Fig. 5a. Their arrangement resembles a fan of lines. $\delta _I$ can be therefore traced back to the slope of the generic straight line of the pencil, in the sense that the more the line is pending, the less $\delta _I$ grows. Thus, the plan under examination can be divided in more subregions depending on $\delta _I$ values: the northern area is occupied by points identified by low $\delta _I$; whereas the southeastern part contains points associated with higher $\delta _I$.

Table 1 Optimal parameters and performance indices for several optimization criteria. HCS: $\mu _T$ = 0.01 – $\beta$ = 1.00 – $\xi _I$ = 0.15

Fig. 5

Contour plots of: a $\delta _I$; b $\delta _T$; c $\xi _T$.HCS: $\mu _T$ = 0.01 – $\beta$ = 1.00 – $\xi _I$ = 0.15. In each subplot, the red mark represents the point of optimality

A few more comments on $\delta _I$ can be made, since it plays a double role. On one side, when $\delta _I$ grows, it emerges clearly its beneficial effect on the isolation displacement reduction, which is a point of remarkable interest: the need to avoid the onset of a crisis due to static actions. It follows that low $\delta _I$ values would be rejected. On the other hand, $\delta _I$ increases imply a lower effectiveness against the convective component. In other words, it emerges that as the isolation stiffness increases the performance moves towards the southern region of the plan, at the limit approaching the $d_C$ axis. In the light of the above, a sort of compromise between the two conflicting instances is fulfilled in the neighbourhood of the bisector of the plan.

Contour plots of $\delta _T$ are illustrated in Fig. 5b, which shows that in the neighbourhood of the point of optimality it draws values around 1.0 or less.

Contour plots of $\xi _T$ are illustrated in Fig. 5c. It can be noticed that, the more $\xi _T$ increases, the more the HCS gets efficient. This trend is particularly evident for lower $\xi _T$ values. Moreover, it is noticed that values close to one are placed in the northwestern area of the depicted domain and are associated with convective displacement reductions of the order of 80% and more. Lower values are instead more widespread in the plane, especially in the southeastern part of the plan.

The following parametric studies are conducted employing the design criterion based on ${\textbf {F}}_2$.

4.2 Parametric studies

Fig. 6

Pareto fronts. First row: $\mu _T$ = 0 — second row: $\mu _T$ = 0.001 — third row $\mu _T$ = 0.01 — fourth row: $\mu _T$ = 0.10. First column: $\xi _I$ = 0.05 -—second column: $\xi _I$ = 0.15 — third column: $\xi _I$ = 0.35

A wide parametric analysis has been conducted with the aim to investigate the role of the parameters collected in vector $\mathbf {x_1}$ on the HCS performance. Specifically, the objective was to investigate how inertial and damping changes, through $\mu _T$, $\beta$ and $\xi _I$ respectively, affect the optimal design and the control effectiveness. For the parametric analysis, concerning the isolation damping ratio $\xi _I$, three values have been considered, $\xi _I$ = 0.05, 0.15, 0.35. The choice of these three values is due to the need of investigating low, medium and high damped systems. Concerning the TMDI physical mass, it has been assumed $\mu _T$ = 0, 0.001, 0.01, 0.10, in order to include null, very light, light and heavy mass. Concerning the inertance ratio, $\beta$, it has been considered equal to $\beta$ = 0.10, 1.00, 5.00, to include very light, light and heavy inertance.

Let notice that when the mass or the inertance terms are assumed null, three limit cases correspond:

• 1. HCS with TMD when $\beta$ = 0

• 2. HCS with TID when $\mu _T$ = 0

• 3. BIS when $\mu _T$ = 0 and $\beta$ = 0.

The main outcomes in terms of performance maps $d_C$-$d_I$ are illustrated in Fig. 6. Within the table of figures, each column is associated with a specific $\xi _I$ value, increasing from left to right, while figures within the same row are obtained for the same $\mu _T$. The case of null mass is provided in the first row, while the greatest one is illustrated in the last row. Thus, each subplot is identified by means of a couple ($\xi _I$, $\mu _T$) and shows four fronts obtained for increasing $\beta$ values. In the subfigures with $\mu _T$ = 0 (first row), the curves referred to a BIS ($\beta$ = 0) are reported in blue to highlight this limit control case.

The following comments can be made.

• Focusing on a subplot, it can be noticed that the fronts move towards the origin of the axes when $\beta$ increases. In fact the TMD curve ($\beta$ = 0) is the farthest from the origin. This effect is more evident for light $\beta$ values. The average distance between the curve associated with $\beta$ = 0.1 and the TMD curve is greater than the distance between the curve $\beta$ = 1.0 and $\beta$ = 5.0, which sometimes even overlap.

• By comparing plots on the same column it can be evinced that increasing $\mu _T$ leads to improvement in the performance. In fact curves tend to move towards the origin of the axes. Moreover, as $\mu _T$ increases the effect of $\beta$ gets less marked. In fact, the area of the spindle enclosed between the fronts associated with the TMD and $\beta$ = 0.10 decreases by increasing $\mu _T$. To further investigate the role of $\mu _T$, it can be worth focusing on TMD fronts, comparing them with the corresponding BIS front. It can be noticed that the TMD front obtained for $\mu _T$ = 0.001 almost overlaps the BIS front. Instead, fronts associated with $\mu _T$ = 0.01 and 0.10 are more distant than the previous one from the BIS front. The area enclosed between each pair of curves represents the increase in performance related to the introduction of $\mu _T$. Starting from the curve relative to the TMD it can be seen how the $\beta$ effect consists in the further approach of the curves to the origin of the axes. This effect saturates with $\beta$ starting from values around 1-2 and is particularly evident for low $\xi _I$ values.

• Taking into account plots belonging to the same row, it can be noticed that fronts get closer to the origin of the axes and tend to become symmetrical with respect to the bisector of the plan when $\xi _I$ increases. Thus it affects the dynamic behaviour by improving the performance. However the rate of increase of performance with $\xi _I$ saturates around the value $\xi _I$ = 0.35. Thus, on one side, the benefits of introducing inerter based systems are particularly evident for low damped isolation systems. On the hand, the influence of both $\mu _T$ and $\beta$ gets less marked when $\xi _I$ draws higher values.

• Fronts associated with HCS always outperform the front related to a BIS with the same damping ratio $\xi _I$. The gap is relevant for low damping values, while it is less marked for higher damping values.

The results in terms of HCS optimal parameters and relative performance indices for each case illustrated in Fig. 6 are shown in Table 2. The following remarks can be made.

• $\delta _I^{OPT}$ draws values belonging to the range 1.40-2.05. It is noted that the $\delta _I^{OPT}$ value associated with $\beta$ = 0 is in general higher than the value associated with high $\beta$ ($\beta$ = 5.0). As $\xi _I$ increases, it makes $\delta _I^{OPT}$ to decrease, leading it to values around 1.50 for $\xi _I$ = 0.35. Instead $\mu _T$ changes weakly affect $\delta _I^{OPT}$.

• $\delta _T^{OPT}$ is always lower than one. It is noted that $\delta _T^{OPT}$ monotonically decreases with $\beta$, regardless the values assumed by $\mu _T$ and $\xi _I$, that do not affect it.

• $\xi _T^{OPT}$ is more scattered than the other parameters. It considerably grows with $\beta$ and this trend occurs for each couple of $\mu _T$ and $\xi _I$.

Table 2 HCS optimal parameters and relative performance indices associated with fronts shown in Fig. 6

4.3 Modal properties and frequency response functions

In this section, the dynamic properties of a selection of optimally designed systems are investigated in terms of frequency response functions and modal parameters, i.e. natural frequencies and damping factors. The knowledge of frequency response functions and modal properties can help to understand better the system dynamics and its damping capabilities. Furthermore it allows to have an immediate estimate of the system response to generic input actions and brings out aspects which were hidden in the performance maps.

Fig. 7

Frequency response functions of convective displacement (first column), isolation displacement (second column) and shear force (third column). First row: $\mu _T$ = 0.001 - second row: $\mu _T$ = 0.10; $\xi _I$ = 0.15

Frequency response functions of the convective and impulsive displacements and of the shear force exerted at the base are illustrated in Fig. 7a, b, c, respectively, for the case $\mu _T$ = 0.001. In Fig. 7d, e, f, the same frequency response functions are reported for $\mu _T$ = 0.10. In each plot, the cases of BIS, BIS with TMD (HCS with $\beta$ = 0), BIS with TMDI (HCS with $\beta$ = 5.00) are compared. The curves are normalized as follows: $D_C$ represents the convective displacement normalized with respect to the maximum convective displacement in the fixed base case, $D_I$ represents the impulsive displacement normalized with respect to the maximum convective displacement in the fixed base case, $S_I$ represents the base shear force normalized with respect to the maximum value of the shear force in the fixed base case. Moreover, r stands for the circular frequency divided by the uncontrolled convective circular frequency. As a reference, in plots referring to the convective displacement (see Fig. 7a and d ) the uncontrolled convective displacement curve (FB) is illustrated as well. In Fig. 7b and e the reference line is the axis $D_I$ = 1.0. Similarly, in Fig. 7c and f the reference line is the axis $S_I$ = 1.0. Logarithmic scale has been adopted in all cases.

First it can be noticed that, for all the cases illustrated in Fig. 7, the curves related to BIS and to HCS with $\beta$ = 0 are substantially overlapping, while those obtained for the HCS with $\beta$ = 5.00 are strongly different. Moreover, it is noted that:

• Focusing on plot of $D_C$, the uncontrolled convective displacement is characterized by a single peak. It is identified by the coordinates (1,1), according to the adopted normalization of the axes. The introduction of a BIS or a HCS with TMD (HCS with $\beta$ = 0) leads to the doubling of the convective resonance, giving rise to two peaks, located one to the right and one to the left of the uncontrolled resonance. Besides, these two peaks are lower than the uncontrolled one. The effect of the employment of a HCS with an inerter (HCS with $\beta$ = 5.00) can be evinced on both these two peaks, which are reduced in amplitude. The first peak is strongly reduced, while the second one disappears. The effect played by the inerter consists in smoothing the curves and cutting the drawn peak value and gets particularly evident for greater $\mu _T$ values (Fig. 7d). In fact, comparing Fig. 7a and Fig. 7d it emerges that $\mu _T$ plays a well identifiable role in the reduction of the response, even for high $\beta$ values. It can be concluded, therefore, that frequency response functions better highlight the improvement in performance attributable to the introduction of the HCS of higher $\mu _T$ when compared to a traditional isolation system. This aspect was often hidden in the performance maps.

• Focusing on plots related to $D_I$, it can be noticed that for $\mu _T = 0.001$ (see Fig. 7b) the curves related to BIS (blue curve) and to HCS with $\beta = 0$ overlap in most of the range of frequencies and are characterized by evident peaks. Instead, the curve associated with HCS with $\beta = 5.00$ is on average placed below the two others and shows more damped peaks. The maximum amplitude is reduced of almost an order of magnitude with respect to the previous cases. Moreover, the area placed under this curve is smaller than the area under the others. Concerning curves obtained for $\mu _T$ = 0.10 (see Fig. 7e), it can be noticed that curves associated with BIS and HCS ($\beta$ = 0) do not overlap around the first peak value. The first peak of the BIS curve is clearly doubled in two peaks even for $\beta$ = 0. These two peaks are near to each other and are located below the BIS peak value. The curve related to HCS with $\beta$ = 5.00 is characterized by a first evident peak, placed on the left of the BIS one and reaching a value comparable to those obtained for $\beta$ = 0 and by two other more damped peaks. Comparing the curves illustrated in Figs. 7b and 7e, the effect played by $\mu _T$ is still evident, in particular in the neighbourhood of the peaks of the curves associated with $\mu _T$ = 0.001.

• Focusing on plots related to $S_I$ (see Fig. 7c), it is noted that curves associated with BIS and HCS ($\beta$ = 0) overlap and are characterized by two evident peaks. The curve associated with HCS ($\beta$ = 5.00) is placed below the others in the whole frequency range, except for the last branch. Peak values testify a reduction of the base shear force of two orders of magnitude with respect to the fixed base case, for $\beta = 5.00$. Curves in Fig. 7f are obtained involving $\mu _T$ = 0.10. Comparing the curves shown in Figs. 7c and 7f, a marked cut of response associated with the case HCS with $\mu _T$ = 0.10 and $\beta = 5.00$ is visible. It can be noticed that the effect of $\mu _T$ is more evident for lower $\beta$ values in terms of drawn peak values and area located under the frequency response curve.

Modal parameters are listed in Table 3, in terms of circular frequency ratios r and damping factors $\eta$. Circular frequencies are normalized with respect to the circular frequency of the first convective mode. Focusing first on r, it emerges how the insertion of a base isolation system doubles the convective period, giving rise to $r_{1}$ < 1 and $r_{2}$ > 1. Moreover, the TMDI addition leads to the birth of $r_{11}$ < $r_{1}$ and $r_{12}$ > $r_{1}$. $r_{12}$ seems to be almost independent of $\beta$ for $\mu _T$ = 0.001, while it increases with $\beta$ for $\mu _T$ = 0.10. For both $\mu _T$ = 0.001 and $\mu _T$ = 0.10, $r_{11}$ and $r_{12}$ move away as $\beta$ increases widening the operating range. The last frequency is weakly affected for $\beta$ = 0, while it changes slightly more for $\beta$ = 5.0. Concerning $\eta$, subscripts are assigned consistently with frequency ratios. They increase with $\beta$.

Thus, it can be concluded that equipping a fixed base tank with HCS constitutes an exploitable way to mitigate both the convective and the impulsive damage. Moreover, the use of either very high damping values or large auxiliary masses is unnecessary in order to render effective the control system.

Table 3 Frequency and damping ratios. $\xi _I$ = 0.15

5 A case study

In this section, a literature case study of a storage tank (De Angelis et al. 2010) is utilized to apply the multi-objective design approach for the HCS. The performances are first assessed through stochastic excitation, making use of performance maps. Then, frequency response functions are discussed. In the end, the results of the analyses performed in the time domain with a set of nine natural earthquakes are shown. Performances of such control schemes are compared with those obtained in the literature example that considered a BIS designed with the procedure reported in De Angelis et al. (2010).

Base isolation, if designed using standard criteria widely established in the literature, has been considered ineffective in the control of the convective response, as clearly explained in De Angelis et al. (2010). Instead, as shown above, whether designed involving a multi-objective optimization procedure, even BIS allows to achieve the control of both the impulsive and the convective response.

Moreover, results achieved involving a HCS, designed according to the proposed multi-objective optimization procedure, are shown, in order to highlight its role in further preserving the system.

The comparison is conducted assuming the same cylindrical tank which has been studied in De Angelis et al. (2010).

Results in terms of optimal design and the response in both frequency and time domain are shown in this section.

Concerning the optimization procedure, the Pareto front obtained assuming $\xi _I$ = 0.10 is illustrated in Fig.  8. Within the front, two points have been highlighted: the red one represents the performance of a BIS obtained adopting the design criterion of De Angelis et al. (2010); the blue one represents the performance of a BIS designed according to the multi-objective design ( BIS MO) proposed in this paper. It can be noticed that the red mark is placed in the southeast part of the performance map, testifying the achievement of strong reductions in the response of the isolation displacement, in the face of a weak control of the convective response. This findings are consistent with the results of De Angelis et al. (2010). On the other hand, the point of optimality gained employing the multi-objective procedure, i.e. the blue one, is placed in the neighbourhood of the bisector of the performance plan, thus proving the reduction in both impulsive and convective dynamics.

Moreover, two fronts obtained for HCS are illustrated, for $\xi _I$ = 0.10, $\mu _T$ = 0.10 and assuming $\beta$ = 0, 5.00. Both of them are located to the left of the former. The performance improves as $\beta$ increases.

The optimal parameters associated with each optimal case reported in Fig. 8 are listed in Table 4.

Fig. 8

Pareto fronts, obtained through the multi-objective procedure, assuming $\xi _I$ = 0.10. The red mark refers to the adoption of the criterion in De Angelis et al. (2010); the blue mark represents the point of optimality obtained involving the multi-objective procedure. HCS: $\mu _T$ = 0.10

Table 4 Optimal parameters corresponding to the cases reported in Fig. 8. $\xi _I$ = 0.10; HCS: $\mu _T$ = 0.10

Frequency response curves are displayed in Fig. 9, regarding the convective displacement (Fig. 9a), the isolation displacement (Fig. 9b) and the base shear force (Fig. 9c). Solid orange lines are related to BIS designed as in De Angelis et al. (2010); solid blue lines refer to the BIS designed according to the multi-objective approach ( BIS MO); the green dashed curve represents the uncontrolled convective response. Red curves refer to HCS with different $\beta$.

Concerning the convective wave height (see Fig. 9a), it is noticed that the green dashed curve is characterized by a single amplification and reaches in maximum value the highest value. The solid orange curve, which corresponds to BIS, shows two dynamic amplifications. Both the peaks are located under the peak value of the uncontrolled curve. Nevertheless, the trend does not show significant results in terms of control of the convective response. The curve associated with a BIS MO (blue curve) testifies a better control of the response, both in terms of peak values and of area under the curve. The first peak of the blue curve is lower than the corresponding peak of the orange one. Moreover, the area under the blue curve is smaller than the area under the orange curve. The first peak of the blue curve is doubled in two peaks involving a HCS. The curve obtained for HCS with $\beta$ = 0 is characterized by three dynamic amplifications. It overlaps with the blue curve, except for the neighbourhood of the first peak of the blue curve, in which two peaks arise. The curve associated with HCS ( $\beta$ = 5.00) is placed on average below the others and shows blunter and lower peaks. It emerges that increasing $\beta$, the performance of the control system is enhanced and HCS operating range is broadened.

The improvement in the control of the convective response obtained by designing the BIS through a MO approach has as a counterweight a worsening in the control of the impulsive response- see Fig. 9b-which, although penalized, remains well controlled. In fact, both the orange and the blue curves testify an effective response control, even if the blue curve is placed above the orange one. With reference to curves related to HCS, it is interesting to observe that increasing $\beta$ the performance of the control system is improved. Thus, recurring to higher $\beta$ values allows to reach greater effectiveness and robustness in controlling the isolation displacement. The peak value of the first dynamic amplification reaches a value inferior to 0.1 for HCS with $\beta$ = 5.0.

Concerning the shear force curves (see Fig. 9c) both the orange and the blue curves, corresponding to BIS and BIS MO respectively, are characterized by a peak value lower than 0.1. The HCS curves are located, on average, below the others and their peaks are much more damped, especially for $\beta$ = 5.0. The curve associated with $\beta$ = 5.0 is smoother and more damped than the others.

Fig. 9

Frequency transfer functions of a convective displacement ; b isolation displacement; c base shear force

These results are further confirmed by the analyses performed in time domain. In fact, in order to evaluate and assess the seismic effectiveness of the designed control system, numerical simulations have been carried out, assuming four different base motion histories, natural accelerograms, recorded during historically occurring seismic events. The earthquakes considered are: ChiChi, Duzce, El Centro and Gezbe.

In Fig. 10 the group of subfigures reported in each row refers to a same earthquake, whereas the group of subfigures reported in the left column depicts the convective displacement, in the middle column the impulsive displacement and in the right column the base shear force. In each subplot the responses reported are: FB, BIS (De Angelis et al. 2010), BIS MO, HCS. Three quantities have been monitored with the aim to evaluate the seismic response under natural earthquakes, i.e. the convective displacement $q_C$ and the isolation displacement $q_I$ both relative to the ground and the base shear force $\tau _I$. Displacement values are normalized with respect to the peak value of the convective displacement in the fixed base configuration, while the shear force is normalized by the peak value of the shear force in the same fixed base case. With the normalization introduced, a value smaller than one of each response means an effective reduction of the response quantities, whereas a value greater than one implies an amplification of the response with respect to the reference configuration.

Fig. 10

Time histories of normalized convective displacement ( left subplots), impulsive displacement (mid subplots) and base shear force (right subplots). Ground motions: a–c: Chi-Chi; d–f Duzce; g–i El Centro ; j–l Gezbe. HCS: $\xi _I$ = 0.10 - $\mu _T$ = 0.10 - $\beta$ = 5.00

In each subplot, the responses obtained for a system equipped with a BIS designed as De Angelis et al. (2010) (orange curve), for a system fitted with a MO designed BIS (blue curve) and for a system equipped with a MO designed (red curve), are shown. Both the forced trait and the free oscillation time lapse are considered. These two parts are divided by a dashed vertical blue line in plots in time domain.

Concerning the convective displacement (see the left column in Fig. 10), from the analysis of the results in time domain, the effectiveness of the three control systems in controlling the response can be evinced, in both the forced vibration in which the system is subject to the ground motion, and the free vibration. It is worth noticing that the average wave amplitude is always reduced with respect to the FB case. Comparing the three proposed control strategies, it emerges that the worst performance is gained by means of a BIS designed as De Angelis et al. (2010), in terms of both maximum amplitude and duration of the oscillations. Both amplitude and duration are reduced introducing a BIS MO (blue curve). Nevertheless, the HCS outperforms the two others. The difference is marked in the free oscillation time lapse, in which HCS curves reach zero quickly: because of the additional damping, the overall duration of the oscillation is much shorter.

Regarding the isolation displacement (see the mid column in Fig. 10), it draws reasonable values, consistent with the safety of connections and of the isolation system itself. It emerges that the BIS MO is less effective than the others in controlling the isolation displacement in terms of drawn peak value. The curve related to BIS designed as De Angelis et al. (2010) proves, on average, an intermediate performance between the BIS MO and the HCS. The latter shows a high effectiveness in controlling the isolation displacement, with oscillations of low amplitude, in both the forced and the free parts. In the free oscillation part, the system response reduction is very marked.

Concerning the base shear force (see the right column in Fig. 10), the reduction of the response is achieved by means of all the three systems, in both the forced and the free vibration phases. However, once again, the HCS shows the most effective performance in reducing the amplitude of the oscillations.

Table 5 $\hat{q}^T_C$,$\hat{q}^1_C$,$\hat{q}^2_C$, $\hat{q}^T_I$, $\hat{q}^1_I$, $\hat{q}^2_I$, $\hat{\tau }^T_I$, $\hat{\tau }^1_I$, $\hat{\tau }^2_I$, assuming $\xi _I$ = 0.10. HCS: $\mu _T$ = 0.10, $\beta$ = 5.00

Further confirmation of the above presented results is found in Table 5, where the outcomes of a broader analysis, assuming nine natural earthquakes are shown. Three indices have been assumed as indicators of the achievement of the mitigation of the response, i.e. the maximum values of the three response quantities: ${\hat{q}_C}$, ${\hat{q}_I}$, $\hat{\tau }_I$, as shown in Table 5. They represent the dimensionless maximum convective displacement, isolation displacement and base shear force respectively. Consistently, the hat stands for maximum. Three different time lapses have been considered. Each of them takes an apex: T making reference to the entire monitored time interval, 1 and 2 referring to the forced and free vibration phases, respectively. For each earthquake, the defined performance indices are reported for a BIS designed as in De Angelis et al. (2010), for a BIS MO and for a HCS, with $\mu _T$ = 0.10 and $\beta$ = 5.00. Regarding the peaks of the convective displacement, it is evinced that the HCS outperforms the others in most cases. The average cut of the response obtained with a HCS is around the 50 % in the forced part, while reaches peaks of 90 % in the free oscillation section. It can be noticed the strong improvement in performance related to the HCS introduction even with respect to a BIS designed as in De Angelis et al. (2010). The HCS proves to be effective even referring to natural earthquakes as Cape, Hachinohe, Irpinia, for which a BIS designed as De Angelis et al. (2010) is not able to control the convective displacement. Concerning the peaks of the isolation displacement, it is noted that the HCS outperforms the others, almost halving the values obtained for BIS MO. The peak of the shear force is strongly reduced. The HCS gains values around 0.10 on average.

6 Concluding remarks

A hybrid control system (HCS), involving a BIS and a grounded TMDI for vibration suppression of steel storage tanks subjected to seismic input has been proposed in this paper. The main objective of the control was to reduce, at the same time, both the impulsive and convective components of the dynamic response observed for storage tanks fulfilled with fluid.

Up to now in fact, in the literature, the available control strategies were targeted to mitigate either damage connected to the former or to the latter component, nor considering both objectives. Specifically, seismic base isolation has been currently applied with the purpose to control the impulsive dynamics only, often incurring in negative effects on the convective component, which was sometimes even amplified.

The adopted mechanical model for the tank equipped with the HCS was a 3-DOF system accounting for both the convective and impulsive components of motion of the system.

A multi-objective criterion was proposed to design the HCS by choosing objective function vectors that assume the convective and impulsive displacement as well as the base shear force as quantities to minimize. A white noise stochastic process has been chosen as input. Both the fixed base and the traditional base isolated tank have been assumed as terms of comparison, in order to evaluate the seismic performance of the HCS.

It has been demonstrated that the objective function vector that assumes the convective and impulsive displacement only was able to control the base shear force as well, even if not considered explicitly in the design problem.

It was demonstrated with Pareto fronts represented on the multi-performance plan that equipping a fixed base tank with the proposed HCS, optimally designed, is able to reduce the convective and impulsive displacement, as well as the base shear force, with reductions of more than the 80% with respect to the case of no control. Moreover, it was evinced that a HCS system outperforms always a BIS. The TMDI contribution is particularly evident in case of lightly damped isolation systems. Nevertheless, it was observed that, if designed through a multi-objective approach, even a BIS is quite effective in the mitigation of the response.

Results from parametric analysis, investigating how inertial and damping changes of the HCS, affected the optimal design and the control performance, showed that an increase of the inertance is beneficial to improve the performance, instead there is no need to utilize high damping in the isolation system to further improve the HCS effectiveness.

Frequency response curves testified the system capability in reducing the response, in both peak values and on average with varying frequencies. The essential role exercised by the TMDI mass, in widening the operating range, increasing effectiveness and robustness, even for sustained inertance values, clearly emerged from them.

A literature case study of a storage tank has been utilized to apply the multi-objective design approach for the HCS and a BIS. Performances of such control schemes were compared with those obtained in the literature example that considered a BIS designed with the procedure reported in De Angelis et al. (2010). The analyses, performed in the time domain with a set of nine natural earthquakes, demonstrated that even a BIS is able to effectively control both the impulsive and the convective components of the dynamic response of the tank, if the multi-objective optimization approach proposed in this paper is adopted. Moreover, the adoption of an optimally designed HCS outperforms also the BIS designed with the multi-objective approach. The performance is evident observing the responses in time domain, from which a marked cut is evinced, in both the forced and the free oscillation time lapse. The oscillations are reduced in both amplitude and in total time duration, compared to BIS and fixed base tank. This outcome is particularly meaningful for the convective displacement, which is typically characterized, in the uncontrolled case, by long time duration, due to the low damping.

The results obtained in this work can be extended to any MDOF base isolated systems characterized by a flexible superstructure. Further studies will first provide comparisons with other literature methodologies adopted to optimal design the HCS; then, the influence of a floating roof on the dynamic response will be explored.