Efficient non-ergodic ground-motion prediction for large datasets

Abstract

An efficient numerical method for non-ergodic ground-motion inference and prediction is proposed that alleviates the large computational and memory requirements associated with the traditional approach based on Gaussian Processes described in Landwehr et al. (Bull Seismol Soc Am, https://doi.org/10.1785/0120160118, 2016). The method uses the latest developments in Gaussian Processes and Machine Learning from Wilson and Nickisch (in: International Conference on Machine Learning, pp 1775–1784, 2015) (SKI) and Gardner et al. (in: International Conference on Artificial Intelligence and Statistics, pp. 1407–1416, 2018) (SKIP) and uses sparse approximations combined with efficient matrix decompositions to accurately approximate the large covariance matrices involved in the calculations. This efficient method can be used for both inference of hyperparameters of the non-ergodic ground-motion models and for forward predictions of non-ergodic median ground-motion. The application to predictions are presented. For large datasets of 100,000 to 1,000,000 ground motion values, the proposed method increases the computation speed by factors of 100 to 1000, reducing run times from days to minutes. In addition, the memory requirements are reduced from hundreds of GB to a few GB only, which makes the development of non-ergodic ground-motion models practical using traditional desktop computers.

1 Introduction

As ground-motion data sets have grown over the past decade, ground-motion models (GMMs) have been transitioning from ergodic GMMs, which assume that the GMM is applicable to all sites and sources in a broad region, to non-ergodic GMMs, which allow the GMM to vary based on the location of the earthquake and the location of the source. The first non-ergodic modifications to GMMs addressed the site amplification term. Using ground-motion data from multiple earthquakes at individual sites to estimate the standard deviation of the ground motion, Atkinson (2006) showed that the standard deviation of the ground motion at a single site (called single-station sigma) was smaller than the standard deviation from multiple sites used in traditional GMMs. Using global data sets with multiple recordings at each station, (Rodriguez-Marek et al. 2013) developed a single-station sigma model using data from multiple regions. Similarly, (Geopentech et al. 2015) developed a suite of single-station sigma models for the NGA-W2 data set. These two studies found that the single-station sigma is about 80–85% of the ergodic sigma.

Al-Atik et al. (2010) developed in initial framework for the notation for non-ergodic GMMs that expanded the non-ergodic approach to including non-ergodic source and path terms in addition to the non-ergodic site terms. Using this type of framework, Morikawa et al. (2008), Lin et al. (2011), and Anderson and Uchiyama (2011) used data with recordings from multiple earthquakes in a small region at a given site to estimate the standard deviation for a specific source/site pair. Including the non-ergodic source, path, and site effects, the standard deviation (called single-path sigma) is about 60% of the ergodic sigma.

With the large increase in ground-motion data sets, we now know that the standard deviation of the systematic location-specific effects on the median ground motion is large compared to the remaining aleatory variability. As a result, the ground motions at a specific site from a specific earthquake will have a narrow distribution as shown by the non-ergodic models, but the median will, in general, be different from the global, ergodic model median. The issue for seismic hazard applications is the estimation of the change in the median ground motion for a specific site/source pair compared to a reference ergodic GMM.

A partially non-ergodic approach only addresses the non-ergodic site terms (single-station sigma). The change in the median can be estimated from recordings at the site or using analytical modeling of the site response. A partial non-ergodic model has been used in seismic hazard studies for nuclear power plants and dams over the past six years (e.g. Bommer et al. 2015; Tromans et al. 2018; Renault et al. 2010; Geopentech et al. 2015; Hydro 2012; Coppersmith et al. 2014). Using this method does not require a modification of the reference GMM. The hazard is computed for a reference rock condition using the ergodic median and the single-station sigma for the aleatory variability. The site-specific site amplification and its epistemic uncertainty are then computed using traditional site response methods. Combining the reference rock hazard based in single-station sigma with the site amplification, including the epistemic uncertainty in the site amplification, leads to partially nonergodic hazard curves (e.g. Rodriguez-Marek et al. 2014).

A fully non-ergodic approach includes the source, path, and site terms. The first fully non-ergodic empirical GMM for California was developed by Landwehr et al. (2016), using the varying-coefficient models (VCM) approach. In this approach, the coefficients of the GMM vary as a function of the earthquake and site coordinates. In the (Landwehr et al. 2016) GMM, there are four coefficients that are varying spatially. If California is broken into 0.05 deg × 0.05 deg cells, this would lead to over 80,000 coefficients. To avoid estimating all of these terms in a standard regression, the VCM approach is used which first estimates only the spatial correlation length and variance (called hyperparameters) of each of the four coefficients (inference step). This leads to a total of 8 terms being estimated rather than over 80,000 terms, making the method practical. To be able to apply the non-ergodic GMM in seismic hazard, the change in the median ground motion and its epistemic uncertainty are needed for each source/site pair. These terms are estimated by combining the observed data with the hyperparameters (prediction step). In this paper, we address computational issues for the prediction step when the number of ground motions in the data set becomes very large.

2 Computational issues for large data sets

The VCM approach uses the residuals from the available dataset of recorded ground motions to identify systematic source, site, and path effects that are specific to each combination of earthquake location and site location. To have enough local data to constrain the path-specific and site-specific effects, ground-motion data from small magnitude events are included in the data set. These non-ergodic source, path, and site effects are estimated using the residuals from an applicable ergodic GMM. An applicable GMM needs to scale appropriately to smaller magnitudes than traditionally considered in GMM for seismic hazard applications. The traditional ground-motion data sets used to develop GMMs are being expanded to include ground-motion data from more frequent small-magnitude events: for example, the NGA-W2 data set included earthquakes with magnitudes as low as M3. This allows the GMMs to be used for computing residuals for small-magnitude events, which can then be used as input to the VCM models.

Another option for expanding the data set for constraining path-specific and site-specific effects is to use ground motions from analytical modeling using finite-fault simulation methods. For use in non-ergodic GMMs, the numerical simulations need to be based on 3-D crustal models rather than 1-D crustal models to model the path effects. For example, in Southern California, Cybershake has been used to compute the non-ergodic ground motions (Graves et al. 2011). Numerical simulations have the advantage that they can model path effects from large magnitude events, but there needs to be adequate validation of the 3-D crustal model before they are incorporated seismic hazard applications.

Because small-magnitude earthquakes are much more frequent than large-magnitude earthquakes, the empirical data sets that include small magnitudes can become very large: for example, new ground-motion data sets being compiled for California will have 100,000s recordings. If numerical simulations are used for the non-ergodic GMM, the size of the data set depends on the spatial sampling of the simulations and the number of realizations that can be generated. For example, with 1 km spacing for the San Francisco Bay Area, there will be on the order of 10,000 sites for each realization, and with 100 realizations, there would be on the order of 1,000,000 seismograms. For application with VCM methods, the size of the covariance matrix used in VCM becomes large (n × n), resulting in computational issues that need to be addressed.

The methodology for developing non-ergodic GMM is described in Lavrentiadis et al. (2021). The VCM models are developed using Gaussian Processes methods. There are two main steps for developing VCMs. The first step, inference, involves estimating of the variances and correlation lengths of the model terms, called hyperparameters, from the data. The second step, prediction, is the application of the model to predict the mean and epistemic uncertainty of the ground motion given the hyperparameters and the data.

The main equations for inference and predictions have a scale with $\mathcal {O}(N^3)$ in computational time and $\mathcal {O}(N^2)$ in memory requirements. Such computational requirements limit the use of these equations to a few thousand earthquake scenarios for typical desk-top computers. For example, a data set with 10,000 observations using double precision, the covariance matrix requires about 1 GB of memory, which is manageable on typical desktop computers, but for data sets with 100,000 observations, the memory requirements grow to 100 GB. The computational time for inverting a matrix of this size for inference and predictions requires high-performance computing facilities. To make the non-ergodic methodology practical for use on desktop computers, more efficient numerical methods are required for both inference and forward predictions.

In the past decade, multiple numerical methods have been developed with the attempt to make inferences and predictions of Gaussian Processes scalable for big amounts of data. In particular, the FITC approximation (Snelson and Ghahramani 2006) is the first attempt to approximate covariance matrices using a set of inducing points. With FITC, the covariance function is parameterized by the locations of the inducing points, which are learned by a gradient based optimization. FITC leads to a sparse regression method which has a lower training cost and prediction cost than from the direct approach, and it also allows to find hyperparameters of the covariance function in a joint optimization. However, with FITC, one is constrained to choose the number of inducing points to be significantly smaller than the size of the data, which often leads to a severe deterioration in predictive performance, and an inability to perform inference.

Later on, the development of sparse variational Gaussian processes (SGPR, Titsias (2009)) introduced a variational formulation for sparse approximations. SPGR jointly infers the inducing inputs and the kernel hyperparameters, by maximizing a lower bound of the true log marginal likelihood. More recently, an alternative to SGPR, which is also an efficient numerical method that deals with large data sets, was developed by (Wilson and Nickisch 2015) and called Scalable Kernel Interpolation (SKI). SKI performs sparse and accurate approximations of a covariance matrix via kernel interpolation from some inducing points. Additionally, SKI allows the use of fast numerical methods for matrix-vector multiplications that take advantage of the properties of the covariance functions such as stationary kernels and grid-based input data points. Combining sparse approximations and fast matrix-vector multiplication algorithms makes SKI a numerically efficient tool for fast hyper-parameter estimation and forward prediction with much smaller memory requirements than the direct method; however, both SGPR and SKI perform well only for covariance matrices of low dimensions: for example, using the covariance between the data along latitude or longitude only. When several dimensions are considered (latitude, longitude, depth, magnitude, distance, ...), SGPR and SKI do not perform well because each dimension requires a set of inducing points, leading to a total number of inducing points growing exponentially with the number of dimensions.

Some of the non-ergodic GMMs developed in this special issue use the integrated nested laplace approximation (INLA) approach (Rue et al. 2009, 2017) to reduce calculation time and memory requirements. INLA uses triangles as a mesh to place the inducing points for the approximation of the covariance matrices, while SKI (and SKIP) uses a grid mesh. The triangle meshing allows to discretize any domain with arbitrary geometry over which the user wants to perform prediction/inference. However, the fact that the inducing points are placed over triangles does not lead to any mathematical property that can be exploited for faster calculations, unlike the grid meshing from SKI (and SKIP). The grid meshing allows for much faster matrix-vector multiplications (MVMs) between grid-based covariance matrices and any vector, exploiting their Toeplitz structure. A requirement for Toeplitz structure is that the covariance functions must be stationary, but that is the case in this paper and for non-ergodic ground-motion models so far. Therefore, MVMs with SKI are performed several orders of magnitudes faster than with INLA, which makes SKI more efficient than INLA.

We therefore use an extension of SKI, called structured kernel interpolation for products (SKIP), developed by Gardner et al. (2018), that alleviates the exponential complexity of SKI (and SGPR) with increasing numbers of dimensions. SKIP approximates covariance matrices along each dimension separately using SKI and then combines them by exploiting mathematical properties of kernel products. SKIP results in linear, rather than exponential, scaling in complexity with dimension compared to SKI and leads to low-rank decompositions of the covariance matrices involved.

While a Python implementation of SKIP by the authors of Gardner et al. (2018) is available on GPyTorch, we present in this paper the application of the SKIP methodology to non-ergodic ground-motion models, and we also provide a Matlab implementation of SKIP that we believe is more efficient for non-ergodic ground-motion applications. The main difference between the proposed Matlab implementation and GPyTorch is the use of the algorithm from Halko et al. (2011), which we combine with an efficient matrix-vector multiplication implementation of Eq. (8). The main difference between the algorithms from Halko and Lancsoz, which is used in GPyTorch, is that, in the GPyTorch implementation, the first k singular values are obtained one by one using a for loop via the Lancsoz algorithm, whereas for the Halko algorithm, the first k singular values are obtained in one shot using vectorized operations. While both algorithms give similar results, the Halko algorithm is faster than the Lancsoz algorithm, but it requires more RAM. The proposed Matlab implementation is more efficient for traditional earthquake ground-motion recordings and simulation datasets, which typically do not exceed 1,000,000 datapoints, and it runs within minutes on a regular laptop.

In the next two sections, we introduce SKI and SKIP. We further describe their application to non-ergodic ground-motion prediction in the final sections.

3 Scalable Kernel interpolation (SKI)

Scalable Kernel interpolation obtains a sparse and accurate approximation of a large covariance matrix by interpolation from the values of a smaller covariance matrix of some fixed reference points, also called inducing points.

Consider a one-dimensional kernel function $k(x, x')$ over the domain x of the form:

$$\begin{aligned} k(x, x') = \theta \ e^{\dfrac{-||x - x'||^2}{2\rho ^2}} \end{aligned}$$

(1)

in which $\theta$ and $\rho$ are fixed hyperparameters. The kernel function $k(x, x')$ gives the covariance between the data-points x and $x'$. Next, consider two large vectors of data-points X and $X'$ of size n, from which we would like to approximate the $n \times n$ covariance matrix $K_{XX'} = K(X, X')$ of the data-points X and $X'$ with kernel k using SKI. To do so, we first place a set of fixed inducing points $U = \{u_1, ...u_m\}$, usually equally spaced, over the one-dimensional domain x. The number of inducing points m required for the approximation is typically much lower than the size of the large dataset n $(m<< n)$, with a few points per correlation length only.

The idea behind SKI is that the values from the large covariance matrix $K_{XX'}$ should be close enough to the values of the small covariance matrix of the inducing points $K_{UU} = K(U, U)$, so that we can accurately approximate the values of $K_{XX'}$ by interpolation of the values of $K_{UU}$. We therefore only need to compute the small covariance matrix $K_{UU}$ and the interpolation weights to obtain a sparse approximation of $K_{XX'}$ using SKI, which requires fewer computations and less memory. Mathematically, this sparse approximation is given by:

$$\begin{aligned} K_{XX'} = K_{SKI} = W_X \ K_{UU} \ W_{X'}^T \end{aligned}$$

(2)

In Eq. (2), $W_X$ and $W_{X'}$ are the matrices of interpolation weights of the data X and $X'$ with the inducing points U respectively. $W_X$ and $W_{X'}$ are sparse matrices and contain $n \times (d+1)$ non-zero entries only, where d is the degree of the interpolation. Typically, cubic interpolation is used, which leads to $W_X$ and $W_{X'}$ having only $n \times 4$ non-zero entries.

Scalable Kernel interpolation gives an accurate and sparse approximation of large covariance matrices for one-dimensional kernel functions; however, it does not remain efficient for multi-dimensional kernels. This is because the number of inducing points, m, required for multiple dimensions grows exponentially with the number of dimensions. For example, if $m_1 = 100$ inducing points were placed over a first dimension $x_1$, and $m_2 = 100$ inducing points were placed over a second dimension $x_2$, that would lead to $m_1 \times m_2 = 10^4$ inducing points required for the approximation using SKI. In this case, the $K_{UU}$ matrix is $10^4 \times 10^4$, which does not stay efficient in terms of computational and memory requirements. To reduce this computational demand from exponential to linear scaling with increasing number of dimensions, we use SKIP which is described in the next section.

4 Structured Kernel interpolation for products (SKIP)

Multidimensional kernels, like the ones involved in Eq. (13), are typically made of products of unidimensional kernels. Consequently, the covariance matrix from a multidimensional kernel is made of the element-wise product of the covariance matrices from the corresponding unidimensional kernels.

Unlike SKI, SKIP does not directly give a sparse representation of large covariance matrices from multidimensional kernels; however, SKIP takes advantage of this element-wise product structure of unidimensional covariance matrices to efficiently perform matrix-vector multiplications (MVMs) of the multidimensional covariance matrix with some vector. Efficient MVMs are then used to obtain low-rank decomposition of the multidimensional covariance matrices.

The low-rank decompositions are obtained without computing the covariance matrices involved and without directly performing the decomposition, which would be too heavy in terms of computational and memory requirements. Instead, probabilistic algorithms such as given by Halko et al. (2011) are used. The key idea behind these algorithms is that if we want to access the first k eigenvalues of a large $n \times n$ matrix C, we do not need to compute all of the n eigenvalues as it is done in the direct approach. Instead, we can find the first $k<< n$ eigenvalues by sampling a $n \times m$ Gaussian matrix and multiplying it with the target matrix C. This will lead to k linearly independent vectors spanning the range of the target matrix C from which the first k eigenvalues and eigenvectors can be efficiently reconstructed following the algorithms from Halko et al. (2011). This algorithm is described in Appendix.

The application of the SKIP method has three main steps. First, the unidimensional covariance matrices are approximated using SKI. This can be done accurately in one dimension using a large number of inducing points. SKI allows for fast MVMs of the unidimensional covariance matrices with some vectors, as explained below. Next, these fast MVMs from SKI are used to efficiently obtain the low-rank decompositions of the unidimensional covariance matrices using the Halko et al. (2011) algorithm. Finally, SKIP uses an algorithm that allows efficient MVM for the element-wise product of matrices using their low-rank decomposition as obtained in the previous step. This leads to the low-rank decomposition of the multidimensional covariance matrix by again using the Halko et al. (2011) algorithm.

4.1 Mathematical derivation

In this section, we describe the algorithm from Gardner et al. (2018) that provides efficient MVMs of large covariance matrices from multidimensional kernels.

A multidimensional kernel function of dimension d, that is separable over its dimensions, takes the following form:

$$\begin{aligned} k(x, x') = \prod _{i = 1}^d k^{(i)}(x^{(i)}, x'^{(i)}) \end{aligned}$$

(3)

where the $k^{(i)}$s are unidimensional kernel functions, and $x = \{x^{(1)}, ..., x^{(d)} \}$ and $x' = \{x'^{(1)}, ..., x'^{(d)} \}$ are two multidimensional vectors.

Let us now consider a large dataset X of size n and dimension d, $X = \{X^{(1)}, ..., X^{(d)} \}$ where each vector $X^{(i)} = \{x_1^{(i)}, ..., x_n^{(i)}\}$ of size n and has only one dimension. We want to perform efficient matrix-vector multiplications from the large multidimensional covariance matrix $K_{X, X}$ of the data X using SKIP. To do so, we first express $K_{X, X}$ as the element-wise product of its unidimensional covariance matrices $K_{X, X}^{(i)}$:

$$\begin{aligned} K_{X, X} = K_{X, X}^{(1)} \ \circ \ K_{X, X}^{(2)} \ \circ \ ... \ \circ \ K_{X, X}^{(d)} \end{aligned}$$

(4)

where $K_{X, X}^{(i)}$ is the covariance matrix of $X^{(i)}$ using the kernel function $k^{(i)}$ over dimension i, and where $\circ$ represents the element-wise product operation. For large datasets, the matrices $K_{X, X}^{(i)}$ are too large to be stored in the memory, and we therefore approximate them using SKI. That is, we use the following approximation:

$$\begin{aligned} K_{X, X}^{(i)} = W^{(i)} \ K_{UU}^{(i)} \ W^{(i) T} \end{aligned}$$

(5)

where $K_{UU}^{(i)}$ is a small covariance matrix obtained with kernel $k^{(i)}$ from m inducing points $U^{(i)} = \{u_1^{(i)}, ..., u_m^{(i)}\}$ placed over dimension i, and $W^{(i)}$ is the matrix of interpolation weights between $X^{(i)}$ and the inducing points $U^{(i)}$.

The sparse approximation from SKI in Eq. (5) allows for efficient MVMs of $K_{X, X}^{(i)}$ with some target vector if the multiplications are performed in the right order. The product $W^{(i)} \ K_{UU}^{(i)} \ W^{(i) T}$ is never explicitly computed, because it would result in a $n \times n$ matrix which would be not fit in the memory for large datasets. Instead, a $n \times 1$ vector x is multiplied from right to left in Eq. (5). We first multiply x with $W^{(i) T}$, which leads to another $m \times 1$ vector that is further multiplied with $K_{UU}^{(i)}$, which leads to another $m \times 1$ vector which is finally multiplied by $W^{(i)}$ to finally lead to the $n \times 1$ target vector.

We further use this efficient MVM from $K_{X, X}^{(i)}$ in the algorithm from Halko et al. (2011) to efficiently obtain a singular-value decomposition of $K_{X, X}^{(i)}$. This algorithm allows us to efficiently obtain the first k singular values and vectors of a matrix by only multiplying it with k vectors drawn independently from a Gaussian distribution and by performing the singular-value decomposition on the smaller matrix resulting from this product. We use this algorithm to efficiently obtain the k singular values $D^{(i)}$ and singular vectors $U^{(i)}$ and $V^{(i)}$ such that:

$$\begin{aligned} K_{X, X}^{(i)} = U^{(i)} \ D^{(i)} \ V^{(i) T} \end{aligned}$$

(6)

Once each unidimensional covariance matrix $K_{X, X}^{(i)}$ is approximated by its singular value decomposition, the multidimensional covariance matrix $K_{X, X}$ is given by:

$$\begin{aligned} K_{X, X} = K_{X, X}^{(1)} \ \circ ... \ \circ \ K_{X, X}^{(d)} \end{aligned}$$

(7)

It can be reconstructed in the following manner. Given two unidimensional covariance matrices $K_{X, X}^{(1)}$ and $K_{X, X}^{(2)}$ and their low-rank decomposition as given in Eq. (6), efficient MVMs of the two-dimensional covariance matrix $K_{X, X}^{(12)} = K_{X, X}^{(1)} \ \circ K_{X, X}^{(2)}$ with some vector v can be obtained by:

$$\begin{aligned} K_{X, X}^{(12)} \times v&= (K_{X, X}^{(1)} \ \circ K_{X, X}^{(2)}) \times v \nonumber \\&= \varDelta (K_{X, X}^{(1)} \ D_v \ K_{X, X}^{(2)}) \nonumber \\&= \varDelta ( U^{(1)} \ D^{(1)} \ V^{(1) T} \ D_v \ U^{(2)} \ D^{(2)} \ V^{(2) T}) \end{aligned}$$

(8)

In Eq. (8), $D_v$ is a diagonal matrix whose entries are the vector v, and the operator $\varDelta (.)$ simply takes the diagonal of a matrix. The order of the operations for efficient MVMs from Eq. (8) is illustrated in Fig. 1.

Fig. 1

Illustration of efficient matrix-vector multiplication using SKIP, as originally found in (Gardner et al. 2018)

Fig. 2

Illustration of efficient algebraic operations for the computation of epistemic uncertainty using SKIP

Fig. 3

Computational times measured from SKIP and the direct approach and their extrapolation to larger datasets (200 singular values retained)

Fig. 4

Memory requirements measured from the direct approach and SKIP and their extrapolation to larger datasets (200 singular values retained with SKIP)

MVMs of the matrix $K_{X, X}^{(12)} = K_{X, X}^{(1)} \ \circ K_{X, X}^{(2)}$ with some vector v as described in Eq. (8) turn out to be very efficient and can further be used to obtain a singular value decomposition of $K_{X, X}^{(12)}$ with the algorithm from Halko et al. (2011) shown below:

$$\begin{aligned} K_{X, X}^{(12)} = K_{X, X}^{(1)} \ \circ K_{X, X}^{(2)} = U^{(12)} \ D^{(12)} \ V^{(12) T} \end{aligned}$$

(9)

We have now replaced the element-wise product of two covariance matrices by its singular value decomposition and thus have reduced the dimension of the total covariance matrix by 1. We can repeat this procedure in a divide and conquer manner to obtain the low-rank decomposition of $K_{X, X}^{(3)}$ by replacing $K_{X, X}^{(1)}$ and $K_{X, X}^{(2)}$ in (9) by $K_{X, X}^{(12)}$ and $K_{X, X}^{(3)}$:

$$\begin{aligned} K_{X, X}^{(123)}&= K_{X, X}^{(1)} \ \circ K_{X, X}^{(2)} \ \circ K_{X, X}^{(3)} \nonumber \\&= (K_{X, X}^{(1)} \ \circ K_{X, X}^{(2)}) \ \circ K_{X, X}^{(3)} \nonumber \\&= (U^{(12)} \ D^{(12)} \ V^{(12) T}) \ \circ K_{X, X}^{(3)} \nonumber \\&= U^{(123)} \ D^{(123)} \ V^{(123) T} \end{aligned}$$

(10)

and again reduce the dimension of the total covariance matrix by 1. In a general way, by repeating this procedure $d-1$ times, we can efficiently obtain a low-rank decomposition of the d-dimensional covariance matrix $K_{X, X} = K_{X, X}^{(1)} \ \circ ... \ \circ \ K_{X, X}^{(d)}$:

$$\begin{aligned} K_{X, X} = U \ D \ V^T \end{aligned}$$

(11)

The low-rank decompositions of large multidimensional covariance matrices, such as in Eq. (11), can then be used in the operations presented in the next section to efficiently perform prediction of non-ergodic ground-motion models using large datasets.

5 Efficient non-ergodic ground motion prediction using SKIP

5.1 Non-ergodic ground motion model

An example of the functional form for a non-ergodic ground-motion model (GMM) is given by Landwehr et al. (2016):

$$\begin{aligned} y =&\beta _{-1}(\mathbf {t_e}) + \beta _{0}(\mathbf {t_s}) + \beta _1 M + \beta _2 M^2 \nonumber \\&+ (\beta _3(\mathbf {t_e}) + \beta _4 M) \ln \sqrt{(R_{JB}^2 + h^2)} + \beta _{5}(\mathbf {t_e})R_{JB} + \beta _6(\mathbf {t_s}) \ln VS_{30} \nonumber \\&+ \sigma _n \ \epsilon \end{aligned}$$

(12)

In the last equation, $\mathbf {t_e}$ and $\mathbf {t_s}$ are the latitude-longitude coordinate vectors of the earthquake source and the site, $\sigma _n$ is a noise term, and the $\beta _i$ are assumed to be independent Gaussian processes with mean zero and spatial covariance functions given by:

$$\begin{aligned} k_{\beta _i}(t, t') = {\left\{ \begin{array}{ll} \theta _i \ i = 1, 2, 4, 7, 8\\ \theta _i e^{-||t_e - t_e'||^2/2 \rho ^2} + \pi _i, i = -1, 3, 5 \\ \theta _i e^{-||t_s - t_s'||^2/2 \rho ^2} + \pi _i, i = 0, 6 \end{array}\right. } \end{aligned}$$

(13)

The form of the spatial correlation for the kernel functions given in Eq. 13 was modified from $e^{-||t_s - t_s'||/ \rho }$used by Landwehr et al. (2016) to $e^{-||t_s - t_s'||^2/2 \rho ^2}$ so that the terms are separable.

The coefficients $\theta _i, \rho _i$ and $\pi _i$ in Eq. 13 are called hyperparameters and control the variance and the correlation length of each of the Gaussian processes $\beta _i$. The parameters $t_e, t_s, M, R_{JB}, ln VS_{30}, F_R, F_{NM}$ are called features and give the parameters of the earthquake scenarios for a given source and site location.

Given some earthquake data with features $X = [x_1, ..., x_N]$ at locations $t = [t_1, ..., t_N]$, the ground-motion equations for predictions and inference involve the large covariance matrix $K_{X, X}$. In this section, we describe how to efficiently obtain a low-rank decomposition of $K_{X, X}$ using SKIP. In the later sections, we describe how to use this low-rank decomposition for efficient ground-motion prediction. Similar methods can also be used for inference.

Fig. 5

Maximum relative error in median prediction and epistemic uncertainty between SKIP and direct approach with number of singular values retained ($n = 2000$)

5.2 Efficient low-rank decomposition of large covariance matrices from the non-ergodic ground-motion model

Because the terms $\beta _i$ in Eq. (12) are assumed to be independent, the total covariance matrix $K_{X, X}$ between the data X from the non-ergodic ground-motion model Eq. (12) is the sum of the covariance matrices $K_{({X, X}), i}$ coming from each term in Eq. (12), so that:

$$\begin{aligned} K_{X, X} = \sum _{i = -1}^8 K_{({X, X}), i} + \sigma _n^2 I_d \end{aligned}$$

(14)

The covariance matrices $K_{({X, X}), i}$ are multidimensional and separable over their dimensions. For example, $K_{({X, X}), -1}$ has two dimensions, earthquake latitude $t_{e, lat}$ and longitude $t_{e, lon}$, and is given by the kernel function:

$$\begin{aligned} k_{-1}(t_{e}, t_{e'})&= \theta _{-1} e^{-||t_e - t_e'||^2/2 \rho ^2_{-1}} + \pi _{-1} \nonumber \\&= \theta _{-1} e^{-(t_{e, lat} - t_{e', lat})^2/2 \rho _{-1}^2} \times e^{-(t_{e, lon} - t_{e', lon})^2/2 \rho _{-1}^2} + \pi _{-1} \end{aligned}$$

(15)

As another example, $K_{({X, X}), 5}$ has three dimensions, latitude, longitude and $V_{S30}$:

$$\begin{aligned} k_{5}(t_{s}, t_{s'}, V_{S30}, V_{S30}')&= (\theta _{5} e^{-||t_s - t_s'||^2/2 \rho ^2_{5}} + \pi _{5} )V_{S30} V_{S30}' \nonumber \\&= \theta _{5} e^{-(t_{s, lat} - t_{s', lat})^2/2 \rho _{5}^2} \times e^{-(t_{s, lon} - t_{s', lon})^2/2 \rho _{5}^2} \ \times V_{S30} V_{S30}' \nonumber \\&\ \ \ \ +\pi _{5} V_{S30} V_{S30}' \end{aligned}$$

(16)

Because the covariance matrices $K_{({X, X}), i}$ are separable over their dimensions, their low-rank decomposition can be obtained using SKIP, such that;

$$\begin{aligned} K_{({X, X}), i} = U_i \ D_i \ V_i^T \end{aligned}$$

(17)

Substituting Eq. (17) into Eq. (14), we can obtain an approximation of the total covariance matrix as a sum of low-rank decompositions of the covariance matrices of each term:

$$\begin{aligned} K_{{X, X}} = \sum _{i = -1}^8 U_i \ D_i \ V_i^T \end{aligned}$$

(18)

We can further use the algorithm from Halko et al. (2011) to efficiently obtain the low-rank decomposition of the sum in Eq. (18), such that:

$$\begin{aligned} \sum _{i = -1}^8 U_i \ D_i \ V_i^T = U \ D \ V^T \end{aligned}$$

(19)

We finally obtain a low-rank decomposition of the total covariance matrix, such as:

$$\begin{aligned} K_{{X, X}} = U \ D \ V^T \end{aligned}$$

(20)

Having a low-rank decomposition of the total covariance matrix $K_{{X, X}}$ shown in Eq. (20) will allow efficient ground-motion prediction for large data sets, as explained in the next section.

5.3 Efficient non-ergodic prediction of median ground motion and its epistemic uncertainty

The ground motion at a new location $t^*$, with features $X^*$, given the observed data set $y = [y_1, ..., y_N]$ and features $X = [x_1, ..., x_N]$ at locations $t = [t_1, ..., t_N]$, follows a normal distribution with mean, $\mu$, and epistemic uncertainty, $\psi$, given by:

$$\begin{aligned}&\mu = K_{X^*, X} (K_{X, X} + \sigma _n^2 I_d)^{-1} y_{obs} \end{aligned}$$

(21)

$$\begin{aligned}&\psi = diag(K_{X^*, X^*} - K_{X^*, X} (K_{X, X} + \sigma _n^2 I_d)^{-1} K_{X, X^*}) \end{aligned}$$

(22)

In Eqs. (21 and 22), the matrices $K_{X, X}$ and $K_{X, X^*}$ represent the covariance matrix between the available data X itself and the covariance matrix between the data and the target scenarios $X^*$ for which we seek the ground-motion prediction.

We can use SKIP to obtain low-rank decompositions of $K_{X, X}$ and $K_{X, X^*}$, as described in Eq. (20):

$$\begin{aligned}&K_{X, X} = U_{X, X} \ D_{XX} \ V_{XX}^T \end{aligned}$$

(23)

$$\begin{aligned}&K_{X, X^*} = U_{XX^*} \ D_{XX^*} \ V_{XX^*}^T \end{aligned}$$

(24)

The low-rank decomposition of $K_{X, X}$ in Eq. (23) leads to fast MVM of $K_{(X, X)}$ with some vectors. We can take advantage of these fast MVMs to solve for the linear system of equations:

$$\begin{aligned} \alpha = (K_{X, X}+ \sigma _n^2 I_d)^{-1} y_{obs} \end{aligned}$$

(25)

This system of equations appears in Eq. (21), and we notice that it only involves the covariance matrix of the available data $K_{X, X}$. Therefore, the solution vector $\alpha$ in Eq. (25) only needs to be solved once for each available dataset, and it can be stored and called when computing forward median predictions as in Eq. (21).

The vector $\alpha$ in Eq. (25) can be efficiently solved for using a solver that only involves MVMs, such as in the Conjugate Gradient method. The Conjugate Gradient method can be thought of as a trial and error method that starts with an initial guess, $\alpha _0$, and which converges towards the solution, $\alpha$, by using MVMs in an iterative manner. The solution from the Conjugate Gradient method is not the exact solution but rather a numerical solution that can be obtained within a prescribed tolerance and using only a few iterations, typically many less iterations than the size n of the system of equations.

Once we solve for $\alpha$, median predictions $\mu$, given in Eq. (21) can be approximated by simply multiplying $\alpha$ with the low-rank decomposition of $K_{X, X^*}$:

$$\begin{aligned} \mu = U_{X, X^*} \ D_{X, X^*} \ V_{X, X^*}^T \alpha \end{aligned}$$

(26)

The accuracy of the approximation will depend on the order of the truncation in the low-rank decomposition, and a desired accuracy can be reached if enough singular values and vectors are used.

To efficiently compute $\mu$, the matrix-matrix product $U_{X, X^*} \ D_{X, X^*} \ V_{X, X^*}^T$ should not be compute directly, but instead, the matrix-vector multiplications should be computed only from right to left. Proceeding in this order of computations does not require the storage of the large matrix $U_{X, X^*} \ D_{X, X^*} \ V_{X, X^*}$, and reduces the amount of computations.

To obtain the epistemic uncertainty $\psi$ of predictions $\mu$, we approximate $K_{X, X^*}$ by its low-rank decomposition in Eq. (24) and approximate $K_{X, X}^{-1}$ by its pseudo-inverse $K_{X, X}^{\dagger } = U \ D^{-1} \ V^T$ using Eq. (23). Substituting back in Eq. (22):

$$\begin{aligned} \psi&= diag\{K_{X^*, X^*}\} \ - diag\{ (V_{X, X^*} \ D_{X, X^*} \ U_{X, X^*}^T) \nonumber \\&( U_{X, X} \ D_{X, X}^{-1} \ V_{X, X}^T + \sigma _n^{-2} I_d) (U_{X, X^*} \ D_{X, X^*} \ V_{X, X^*}^T)\} \end{aligned}$$

(27)

By again proceeding in the right order of computations and only taking the diagonal elements, Eq. (27) leads to a computationally efficient approximation of the epistemic uncertainty in the median ground-motion prediction.

The diagonal in $K_{X^*, X^*}$ from Eq. (27) can easily be computed analytically. Then, the diagonal in the second term of Eq. (27) is computed in the following manner. First, compute the matrices $VD_{X, X*}$ and $VD_{X, X}$:

$$\begin{aligned}&VD_{X, X*} = V_{X, X^*} \ D_{X, X^*} \end{aligned}$$

(28)

$$\begin{aligned}&VD_{X, X} = V_{X, X} \ (D_{X, X}^{-1} + \sigma _n^{-2} I_d) \end{aligned}$$

(29)

These matrices are easily computed because $D_{X, X}$ and $D_{X, X^*}$ are diagonal. Next, the matrix A is computed in the following manner:

$$\begin{aligned} A = VD_{X, X*} \ ((U_{X, X^*}^T) \ ( U_{X, X}) \ (VD_{X, X}) \ (U_{X, X^*})) \end{aligned}$$

(30)

The order in which these matrix products are computed is important and is given by the parentheses. Using this order of products will lead to small matrices of the size of the number of eigenvalues retained for $K_{X^*, X^*}$ and for $K_{X, X^*}$.

If we define the matrix B to be:

$$\begin{aligned} B = V_{X, X^*} \end{aligned}$$

(31)

then the epistemic uncertainty from Eq. (27) is then given by:

$$\begin{aligned} \psi = diag\{K_{X^*, X^*}\} \ - \sum _{i = 1}^{n} \sum _{j = 1}^{n*} A_{i, j} B_{i, j} \end{aligned}$$

(32)

where n and $n*$ are the size of datasets X and $X*$ respectively.

The order of the computations and the sizes of the different matrices involved are shown in Fig. 2. The accuracy of the approximation will again depend on the order of the truncation in the low-rank decomposition, and a desired accuracy can be reached if enough singular values and vectors are used.

An alternative to compute the epistemic uncertainty from Eq. (27) is to simply use the efficient matrix-vector multiplication for element-wise products from SKIP, from Eq. (8), and not compute the singular value decomposition of all the terms $K_{X, X*}^{(d)}$ and the total covariance matrix $K_{X, X*}$. This alternative will use more RAM, but can require less computations when the eigenvalues of $K_{X, X*}^{(d)}$ and $K_{X, X*}$ decay slowly due to short correlation lengths involved in the main Eq. (12).

6 Illustrative example

To illustrate the advantages of the proposed method compared with the direct approach, we perform the computations with SKIP and the direct approach from Eqs. (17–20 and 25) using synthetic datasets. For this comparison, the prediction is made for the same scenarios as contained in the observed data set. We compare the accuracy and the computational time and memory requirements between the two approaches with datasets of increasing size, from $n = 2000$, 4000, ... to $n = 10000$.

6.1 Computational comparison

Wilson and Nickisch (2015) show that for the direct approach, the computational time scales with $\mathcal {O}(n^3)$ and the memory requirements with $\mathcal {O}(n^2)$. We can therefore fit cubic and quadratic polynomials respectively to the time and memory requirements obtained from the synthetic data sets and extrapolate the results to larger data sets. The proposed method scales with $\mathcal {O}(n)$, and we can therefore proceed in a similar manner but with a linear polynomial fitting to extrapolate the computational time and memory requirements to estimate the requirements for larger data sets.

The computational time requirements from the two approaches and their extrapolation to larger data sets is shown in Fig. 3 and the memory requirements are shown in Fig. 4. For small data sets, the direct approach is faster, because there is an computational overhead to implement the SKIP method that is not efficient for small datasets but which becomes much more efficient as the size of the datasets grows.

SKIP is more efficient than the direct approach for data sets with more than a few thousand data points, because for these larger data sets, it becomes slower to compute and invert the large covariance matrix compared to obtaining its singular value decomposition with SKIP and using the conjugate gradient method to solve for $\alpha$ in Eq. (25). For data sets of size $n = 100,000$, the computations using SKIP scale to the order of a few minutes only, while the direct approach scales to several hours. The computational time required from SKIP will also depend on the number of singular values retained in the approximation and on the number of inducing points used for the initial sparse approximations in Eq. (5). In this example, 200 singular values and $m = 1000$ inducing points over latitude and longitude were used (1,000,000 total inducing points). Generally, there will be a trade-off between the number of singular values and inducing points used for accuracy and the corresponding computational time and memory required, but the scaling of SKIP with the size of the data sets will remain the same as in the illustrative example.

In terms of memory requirements, SKIP is much more advantageous than the direct approach, because it uses sparse matrices and efficient singular value decompositions to approximate the large covariance matrices involved in Eqs. (17–20). For datasets of size $n = 100,000$, SKIP would only require about 2 GB or memory, while the direct approach would require 320 GB. Similarly to the computational time requirements, the memory requirements from SKIP will also depend on the number of singular values and inducing points retained in the approximation (200 and 1000 here respectively), but will also scale linearly with increasing size of datasets.

6.2 Accuracy

The accuracy of solution using SKIP for this example is shown in Fig. 5. The maximum relative error in the median prediction and its epistemic uncertainty is shown as a function of the number of eigenvalues retained in SKIP. These predictions are computed following Eqs. (26–32) at the same scenarios from the available dataset. To obtain reasonable results, 150 eigenvalues are enough to reach an error of $10^{-4}$ in this example. The decay of the error with the number of singular values is directly related to the correlation lengths in the hyperparameters used in Eq. (12). The shortest correlation length controls the decay of the singular values. For shorter correlation lengths, a larger number of singular values would be required to reach the same level of accuracy (Wilson and Nickisch 2015). In general, it will not be possible to know in advance how many singular values are required to reach a certain accuracy using SKIP, since singular values depend on multiple factors such as the kernel, the correlation length and the dataset. It is therefore the role of the user to use SKIP with a given amount of singular values and to check if the smallest singular value is smaller than the desired accuracy, and if not to repeat the method with a larger amount of singular values.

In this example, the shortest correlation length is associated with the term $\beta _3$ and is equal to $\rho _3 = 20$km. The other correlation lengths were taken to be $\rho _{-1} = 80$ km, $\rho _{0} = 70$ km, $\rho _{5} = 60$ km and $\rho _{6} = 40$ km.

Figure 6 shows the decay of the maximum error in median prediction for different values of the shortest correlation lengths of 5, 10, and 20 km. This decay in the error stops decreasing after a certain number of singular values are retained because the error is then dominated by the sparse grid approximation in Eq. (5), and this error is controlled by the number of inducing points placed on the domain.

Fig. 6

Maximum relative error in median prediction between SKIP and direct approach with number of eigenvalues retained for different correlation lengths ($n = 2000$ data points, $m = 1000$ inducing points)

For shorter correlation lengths of 10 km and 5 km, a larger number of inducing points would also be required in the initial sparse approximation of the covariance matrices in Eq. (5) to maintain a similar level of accuracy in the approximation. Typically, a few inducing points per correlation length are required to obtain reasonably accurate results in the approximation from Eq. (5) (Wilson and Nickisch 2015).

For predictions that involve short correlation lengths over large domains, the number of inducing points required to obtain stable results in Eq. (5) can become very large. For the State of California and for a correlation length of 5 km, one should place about one inducing point at each km, which would involve 1000 inducing points over latitude and 1000 inducing points over longitude, leading to a total of 1,000,000 inducing points. For a large number of inducing points, SKI becomes much slower than SKIP.

This is the main advantage of using SKIP over SKI: there is no practical limitations to the number of inducing points using SKIP. As explained in Gardner et al. (2018), both SKI and SKIP scale linearly with the size of data n, but SKI scales exponentially with the number of inducing points m per dimension (here, per latitude and longitude), while SKIP scales linearly.

Using SKIP, the sparse approximation of covariance matrices using inducing points in Eq. (5) is first obtained by approximating the covariance matrices over latitude and longitude separately, which involves 1000 inducing points for latitude and 1000 inducing points for longitude. Then, these matrices are recombined using efficient numerical methods as described in the previous section. In contrast, SKI would require 1,000,000 inducing points to be used in the direct sparse approximation of the covariance matrices over latitude and longitude at the same time, which makes the computations of matrix-vector multiplications significantly slower.

To illustrate the advantage of SKIP over SKI, Fig. 7a–c show the computational time required to perform the previous calculations using SKI and SKIP for $m = 250$ and 1000 inducing points over latitude and longitude and with 200 and 600 singular values, for a dataset of size $n = 2000$. The 600 singular values were retained directly or by 3 groups of 200 to demonstrate the performance of the algorithm from Halko et al. (2011). While SKI is not limited in memory requirements (Wilson and Nickisch 2015), Fig. 7a and b show the burden in computational times from SKI after a few hundred inducing points over latitude and longitude only, which limits the use of the method for medium to large correlation lengths and over reasonably small domains. Additionally, SKI would become exponentially more expensive in computations if another dimension was to be added to Eq. (12), for example, correlation over depth; however, SKIP is barely affected by the number of inducing points per dimension, since each dimension in Eq. (5) is treated separately. There will be an increase in computational and memory requirements from SKIP as more singular values would be needed to maintain accuracy for shorter correlation lengths, and also for fixed correlation lengths but for data spread over larger domains (because more eigenfunctions are required to represent the zero correlation between data-points far from each other). However, these additional requirements are still more favorable than using SKI (Gardner et al. 2018). In terms of memory requirements, several hundreds of singular vectors can easily fit in a laptop’s memory even for very large datasets ($n = 1,000,000$). In terms of computations, additional singular values in SKIP could be either retained directly or could be obtained by groups in an iterative manner. These two approaches would also lead to an increase in computational time but it would still be faster to use SKIP (Gardner et al. 2018).

Figure 8a and b compare the memory requirements for SKI and SKIP, with 200 and 600 singular values retained with SKIP and 1000 inducing points per dimension. The memory requirements from SKIP are still manageable on a laptop for $n = 100,000$ data points, and the computational times from SKIP are still faster than SKI by one order of magnitude.

7 Conclusions

The numerical method described here can be used for the efficient prediction of non-ergodic median ground-motion and its epistemic uncertainty for large datasets. For covariance functions that involve large correlation lengths in the prediction Eq. (12), both SKI and SKIP are equivalent in terms of computational time and memory requirements. As the correlation lengths get smaller, more inducing points are needed to maintain accuracy in the sparse approximation in the two methods. In that case, SKI still requires little memory but performs significantly slower because SKI scales exponentially in computations with increasing numbers of inducing points (Gardner et al. 2018). In contrast, SKIP scales linearly in computations with increasing inducing points, but would require more singular values for a given accuracy because of the slower decay in the singular values for shorter correlation lengths of hyperparameters. Computing more singular values with SKIP does require more computations, but is still faster than using SKI. The memory requirements involved with larger amounts of singular vectors from SKIP still fits in a laptop for datasets of size $n = 100,000$.

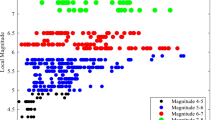
We recommend the use of SKIP over SKI for efficient predictions for short correlation lengths over large domains and large datasets. The main limitation from SKIP is requirement that the kernel functions are separable over the dimensions (latitude and longitude). The square-exponential kernel function satisfies this requirement, but SKIP cannot be used with non-separable kernels such as the exponential kernel. We consider this not to be a key limitation given the overall uncertainties in ground-motion models that should exceed the differences between square-exponential and exponential kernel functions. As an example, Fig. 9 compares the semivariograms for the exponential and Gaussian forms for the spatial correlation with the semivariograms of the within-event residuals from the Abrahamson et al. (2014) ground-motion model for response spectral values at T = 0.2 s for magnitude bins of 3–4, 4–5, 5–6, and 6–8. The range of the semivariograms for these different subsets of the data is larger than the difference between the exponential and Gaussian forms.

Fig. 7

Computational time requirements between direct approach, SKI and SKIP with 250 inducing points per latitude/longitude (200 singular values retained with SKIP). Computational time requirements between direct approach, SKI and SKIP with 1000 inducing points per latitude/longitude (200 singular values retained with SKIP). Computational time requirements between direct approach, SKI and SKIP with 1000 inducing points per latitude/longitude (600 singular values retained with SKIP)

Fig. 8

Memory requirements between direct approach, SKI and SKIP with 1000 inducing points per latitude/longitude (200 singular values retained with SKIP). Memory requirements between direct approach, SKI and SKIP with 1000 inducing points per latitude/longitude (600 singular values retained with SKIP)

Fig. 9

Comparison of the exponential and Gaussian forms for the spatial correlation with the semivariograms for different magnitude ranges from the within-event residuals for the ASK14 ground-motion model for T = 0.2 s.)

For datasets of size $n = 100,000$, the presented method reduces the computational times from hours to minutes, and it also reduces the memory requirements from several hundreds of GB to only a few GB. The proposed approach therefore makes non-ergodic ground-motion predictions practical to users and can be run on a laptop computer.

Appendix

1.1 Efficient eigenvalue decomposition of large scale matrices using randomized algorithms

We present here an overview of the method from Halko et al. (2011) for efficient singular value decomposition of large scale matrices.

Matrices can be approximated using their singular value decomposition. If all singular values and singular vectors are retained, the decomposition is numerically exact; however, in practice, not all singular values and vectors are retained in the singular value decomposition, because performing the total decomposition becomes computationally very expensive for matrices of size greater than a few thousands.

For large scale matrices, it is therefore of great interest to perform partial singular value decomposition and to approximate these matrices by only retaining a subset of the most significant singular values and vectors in the decomposition. An approximation with partial singular value decomposition is accurate to the magnitude of the lowest singular value retained in the decomposition. Such partial singular value decompositions are numerically much faster to obtain, and they provide a reasonable approximation of the large target matrix.

Additionally, matrices of size greater than a few thousand might not fit in the memory of most computers. Therefore, performing partial singular value decomposition also allows to approximate large scale matrices with a few singular values and vectors that fit in the memory, while the large target matrices might not.

This is the main idea behind the algorithm from Halko et al. (2011): obtain only a subset of the most significant singular values and vectors of large scale matrices. To do so, it is only necessary to obtain a subset of vectors that span the range of the large target matrices. These vectors can be obtained using probabilistic sampling techniques, as shown below.

Therefore the algorithm from Halko et al. (2011) does not require the computation and storage of large scale matrices but only requires the result of the product between the large matrices with some vectors (which is allowed by SKI in this paper).

Mathematically, the algorithm from Halko et al. (2011) is performed in a few steps that are summarized below.

Let us consider a large matrix A of size $n \times n$. To obtain the first $k<< n$ singular values and vectors of A, we first need a set of k vectors that span the range of A. We can obtain these vectors by sampling a Gaussian matrix $\varOmega$ of size $n \times k$, with k independent vectors of size n each, and then multiply A with $\varOmega$, such as:

$$\begin{aligned} Y = A \times \varOmega \end{aligned}$$

(33)

where Y is a matrix of k linearly independent vectors of length n each that span the range of the target matrix A.

From Y, an orthonormal basis B can be constructed efficiently using traditional algorithms such as the QR factorization. This orthonormalization is efficient because it only involves a few vectors k, where $k<<n$ is typically of the order of tens or hundreds. Using the QR factorization, we obtain:

$$\begin{aligned} Y = Q \times R \end{aligned}$$

(34)

where Q is a matrix whose columns form an orthonormal basis for the range of Y. Finally, the reduced singular value decomposition of A can also be performed efficiently over the k rows of the $k \times n$ matrix $B = Q^T \times A$, such that:

$$\begin{aligned} B = Q^T \times A = \tilde{U}\ D \ V^T \end{aligned}$$

(35)

In the last equation, D is the $k \times k$ diagonal matrix of the first k singular values, V is the $n \times k$ matrix of the first k right singular vectors, and the first k left singular vectors of A are obtained by an additional multiplication:

$$\begin{aligned} U = Q \times \tilde{U} \end{aligned}$$

(36)

Finally, the large matrix A can be approximated by:

$$\begin{aligned} A = U \ D \ V^T \end{aligned}$$

(37)

We note here that in all the steps involved in the previous algorithm, the computation and storage of the large matrix A was never involved, and only the result of the product of A with vectors was needed to obtain the first k singular values and vectors of A.