1 Introduction

Static redundancy, ductility and positive stiffness are among the most advantageous structural characteristics according to modern earthquake engineering. Yet, articulated structures with negative stiffness that are allowed to uplift have shown remarkable seismic performance in the past (Housner 1963; Makris 2014) and have motivated the creation of a new family of earthquake resilient post-tensioned systems (see for example Granello et al. 2020 and Kibriya et al. 2020). This unconventional response, which can be generally described as rocking, is representative of the dynamic behaviour of a wide range of structures, from small museum exhibits to articulated modern buildings and bridges (Calio and Marletta 2003; Giouvanidis and Dimitrakopoulos 2017; Makris and Vassiliou 2012, 2015).

While the dynamics of rocking bodies are complex, the simple theory initially outlined by Kirkpatrick (1927) and further developed by Housner (1963) has been shown able to reproduce well the main statistics of the seismic response of rocking structures (Bachmann et al. 2018). In this theory, the uplift condition is attained if the overturning moment exceeds the restoring moment, which in free rocking structures is mainly due to self-weight, hence when:

$$\begin{aligned} \ddot{u}_g \ge g \tan \alpha \end{aligned}$$
(1)

where \(\ddot{u}_g\) is the acceleration of the ground, g is the acceleration of gravity and \(\alpha\) is the slenderness of the rocking body as presented in Fig. 1.

Fig. 1
figure 1

Rocking block under horizontal ground motion

Full size image

By assuming that no sliding or bouncing occurs during impact and establishing dynamic moment equilibrium, Housner (1963) derived the following expression for the planar rocking motion of such a body:

$$\begin{aligned} \ddot{\theta }+p^2 \sin \left( \alpha - \theta \right) = \left[ - p^2 \dfrac{\ddot{u}_g}{g} \cos (\alpha - \theta ) \right] \end{aligned}$$
(2)

with an energy reduction factor, that relates the pre- and post-impact angular velocities, equal to:

$$\begin{aligned} r = \left( 1 - \dfrac{3}{2} \sin ^2 \alpha \right) ^2 \end{aligned}$$
(3)

where p is a frequency parameter that characterizes the dynamic response of the block dangling from its pivot point, which, for a rectangular block is:

$$\begin{aligned} p = \sqrt{\dfrac{3g}{4R}} \end{aligned}$$
(4)

with R being the size of the rocking body (Fig. 1).

Although Housner’s classic rigid rocking body idealization is reasonable in a variety of cases, (e.g. stone-based historical structures, stocky building content and equipment), there is another family of structures (slender buildings, wind turbine support towers, etc.) that exhibit important structural flexibility on top of their rocking response. The effects of this elastic flexibility on the rocking response was first investigated by Chopra and Yim (1985) who examined the response of a flexible single-degree-of-freedom (SDOF) system on an uplifting rigid base. They derived equations to describe the motion of flexible rocking structures and demonstrated that foundation uplift can reduce shears and moments at the base. Their model was later extended to deal with large deformations (Oliveto et al. 2003) and large rotations (Acikgoz and DeJong 2012). These analyses demonstrated that flexible structures are generally more stable than rigid ones but can be prone to significant deformations.

The proneness of rocking structures to large deformations and rotations together with the increased accelerations caused by impact and uplifted resonance have motivated researchers to look for suitable seismic vibration control strategies. While some have attempted to reduce the seismic vulnerability of rocking structures by preventing uplift (Makris and Zhang 2001), others have proposed a range of passive and semi-active control strategies (Ceravolo et al. 2016; Dimitrakopoulos and DeJong 2012; deLeo et al. 2016; Vassiliou and Makris 2012; Pan and Málaga-Chuquitaype 2020)

A promising seismic control strategy, recently investigated by Thiers-Moggia and Málaga-Chuquitaype (2019, 2020a), consists in the use of inerters. These devices, initially studied in Japan by Arakaki et al. (1999) and popularized in the West by Smith (2002), are two-node mechanical devices that develop resisting forces proportional to the relative acceleration between their terminals. Since the dynamic stability of rocking systems springs directly from the difficulty of mobilizing their rotational inertia (see Eq. 2), supplemental inertia devices like inerters constitute a perfect fit for the seismic response control of rocking structures. This was demonstrated by Thiers-Moggia and Málaga-Chuquitaype (2019) who showed that the addition of inerters to rocking bodies has an effect equivalent to reducing the frequency parameter of the block, effectively replacing p, in Eq. 2, by:

$$\begin{aligned} p_{\sigma } = \sqrt{\dfrac{3g}{R \left( 4 + 3 \sigma \cos ^2 (\alpha \text {sign}(\theta ) - \theta ) \right) }} \end{aligned}$$
(5)

where \(\sigma\) is the apparent mass ratio or the ratio between the inerter apparent mass (\(m_r\)) and the rocking block mass (m). Therefore, the frequency parameter of an inerter-equipped structure (Eq. 5) is lower than that of a bare rocking block (Eq. 2). This reduction of the frequency parameter results in lower demands due to the size effect of rocking behaviour (Housner 1963) that dictates that among two blocks of the same slenderness the one with the lower frequency parameter is more stable.

An added advantage of inerters, is that they can be coupled with ball-screw or gear systems, hence allowing the dissociation between their gravitational mass (the actual mass of the device) and their inertial mass (the apparent mass of the inerter). Inertial forces several orders of magnitudes larger than those corresponding to their gravitational mass have been generated by means of such amplifying mechanisms (Smith 2002; Ikago et al. 2012).

While studying the response of fixed-base elastic systems with inerters, Makris and Kampas (2016) recognised that inerters store energy that can be transferred back to the structure when it is not convenient, and proposed the use of twin inerters equipped with clutches to ensure the inerter only opposes the structural motion without inducing it. With this purpose, they hypothesized an energy dissipation mechanism that would be able to fully decelerate the inerter during its disengaged state allowing it to be ready for an ulterior re-engagement whenever needed. Accordingly, they assumed an acceleration-based clutch with a sequential engagement law described by:

$$\begin{aligned} F_i(t) = \left\{ \begin{matrix} m_r \ddot{u} &{} \text {, } &{}\left[ \dfrac{\ddot{u}}{\dot{u}}\right] >0\\ \\ 0 &{} \text {, } &{} \left[ \dfrac{\ddot{u}}{\dot{u}}\right] <0 \end{matrix} \right. \end{aligned}$$
(6)

where \(F_i\) is the force transferred from the inerter to the structure and u is the local translational degree of freedom. Although this sequential model has been widely used in studies with clutched inerters (Thiers-Moggia and Málaga-Chuquitaype 2019, 2020b; Wang and Sun 2018; Liang et al. 2021), it suffers from several drawbacks. First, the engagement/disengagement response is instantaneous, it depends on the direction of motion only and is therefore far from real systems where a more incremental state change depending on the stiffness of the clutch and the relative displacement increments is expected (Solfrank and Kelm 1999; Zhu and Parker 2003). Second, the mechanism by which the kinetic energy is dissipated in the inerter during its idle motion state is not explicitly modeled and does not reflect a mechanically feasible energy transfer. Moreover, as it stands, the sequential law of Eq. 6 does not allow for the examination of the clutch motion or the effects of its mechanical characteristics on the response of the structural system (Málaga-Chuquitaype et al. 2019).

In this paper, we adopt a more mechanistic idealization of the clutching system and use it to examine the influence of clutch stiffness, gears play, viscous damping and dry friction on the overall inerto-rocking system. The paper starts with an original account of the changes required in Housner’s restitution coefficient in order to incorporate the effects of the inerter during impact. These changes are more important for stockier rocking structures and larger inerter apparent masses. Subsequently, we evaluate the effects of impact on the acceleration demands and demonstrate that Housner’s model can be used to assess the acceleration response of rocking blocks under the assumption that impact forces are sufficiently distributed over time. The mechanistic model used to incorporate the clutch’s discontinuous stiffness non-linearity into the response of inerto-rocking systems is presented next. A hyperbolic tangent function is adopted and a set of analytical expressions are derived for rigid and flexible rocking structures equipped with a pair of clutched inerters. The newly proposed models are used to examine the evolution of the energy dissipation in the device and the influence of key parameters like the clutch stiffness, gears play, viscous damping and dry friction. Finally, the response of rocking structures with inerters is evaluated under a suite of real accelerograms.

2 Transition upon impact

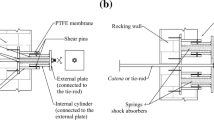
Housner’s restitution coefficient needs to be modified in order to account for the effect of the inerter during impact. Figure 2 depicts the rigid rocking block studied in the previous section at the instant of impact. This figure shows a horizontal inerter supported by a stiff chevron frame and connected to the centre of mass of a rocking structure (Thiers-Moggia and Málaga-Chuquitaype 2019). Similar configurations have been used to study the response of rigid and flexible rocking structures including museum artifacts as well as bridge piers and building walled structures (Thiers-Moggia and Málaga-Chuquitaype 2020b, 2021a).

Fig. 2
figure 2

Rigid rocking block connected to an inerter at the instant of impact

Full size image

Just before impact, the momentum of a mass element dm located at a distance \(l=\sqrt{x^2+y^2}\) from the pivot point O is:

$$\begin{aligned} dJ_m = l\,{\dot{\theta }}_1 dm \end{aligned}$$
(7)

and the momentum of the inerter’s apparent mass:

$$\begin{aligned} J_{m_r} = m_r \, {\dot{\theta }}_1 R \cos \alpha \end{aligned}$$
(8)

where \({\dot{\theta }}_1\) is the angular velocity before impact. The corresponding moment of momentum about the opposite corner, \(O'\), can be obtained as:

$$\begin{aligned} d\varLambda _m = dJ \delta = \rho \, l\, {\dot{\theta }}_1 \delta \, dx dy \end{aligned}$$
(9)

and

$$\begin{aligned} \varLambda _{m_r} = J_{m_r}R \cos \alpha = m_r R^2\, {\dot{\theta }}_1 \cos ^2 \alpha \end{aligned}$$
(10)

where \(\rho\) is the constant density of the block, and \(\delta = l -2Bx/l\) is the lever arm of the element momentum vector dJ about point \(O'\). The total moment of momentum of the rocking structure about point \(O'\) is then given by:

$$\begin{aligned} \varLambda _1 = \rho \, {\dot{\theta }}_1 \Bigg (\int _{A} (x^2+y^2) dx dy -2B \int _{A} x dx dy \Bigg ) + m_r \, {\dot{\theta }}_1 R^2 \cos ^2 \alpha \end{aligned}$$
(11)

where A is the total area of the block. Integration yields:

$$\begin{aligned} \varLambda _1 = I_0 {\dot{\theta }}_1 - 2 m {\dot{\theta }}_1 R^2 \sin ^2 \alpha + m_r \, {\dot{\theta }}_1 R^2 \cos ^2 \alpha \end{aligned}$$
(12)

On the other hand, the moment of momentum about point \(O'\) after impact is:

$$\begin{aligned} \varLambda _2 = I_0 {\dot{\theta }}_2 + m_r R^2\, {\dot{\theta }}_2 \cos ^2 \alpha \end{aligned}$$
(13)

Then, conservation of moment of momentum before and after impact gives:

$$\begin{aligned} I_0 {\dot{\theta }}_1 - 2 M {\dot{\theta }}_1 R^2 \sin ^2 \alpha + m_r R^2\, {\dot{\theta }}_1 \cos ^2 \alpha = I_0 {\dot{\theta }}_2 + m_r R^2\, {\dot{\theta }}_2 \cos ^2 \alpha \end{aligned}$$
(14)

On the other hand, the ratio of kinetic energy before and after impact is:

$$\begin{aligned} r_{\sigma } = \frac{{\dot{\theta }}_2^2}{{\dot{\theta }}_1^2}<1 \end{aligned}$$
(15)

Combination of Eqs. 14 and 15 yields:

$$\begin{aligned} r_{\sigma } = \Bigg ( \frac{1-\frac{3}{2} \sin ^2 \alpha + \frac{3}{4} \sigma \cos ^2 \alpha }{1 + \frac{3}{4} \sigma \cos ^2 \alpha } \Bigg )^2 \end{aligned}$$
(16)

Equation 16 defines the coefficient of restitution of a rigid rocking block connected to an inerter of apparent mass ratio \(\sigma\). When \(\sigma =0\) (no inerter case), this expression becomes identical to the one obtained by Housner (Eq. 3). Figure 3 shows the effect of increasing levels of inertance on the coefficient of restitution of blocks of different slenderness. The plot shows that as the apparent mass of the inerter increases, the coefficient \(r_{\sigma }\) becomes larger, indicating a lower amount of energy dissipation during impact. Importantly, this effect is much more significant for stocky structures.

Fig. 3
figure 3

Effect of the inerter on the restitution coefficient

Full size image

3 Impact and the acceleration response

The formulation presented in the previous section considered a classical impact framework, where vertical forces are assumed to be instantaneous and concentrated at the pivot corners. Although this model provides a good estimation of the amount of energy dissipated during impact (Bachmann et al. 2018), Eq. 15 predicts an instantaneous change of velocity and, therefore, an unrealistic infinite acceleration at the transition instant. A more detailed assessment of the acceleration response can be performed if Dirac-Delta functions are considered in order to distribute the impact forces over time, as suggested by Prieto et al. (2004) and Acikgoz and DeJong (2016). In this formulation, a vertical force is considered to act on the impending pivot point as the structure approaches \(\theta =0\), applying a moment that counteracts the rocking motion and decelerates the rotating structure. After the phase transition at \(\theta =0\), the force is terminated as any forcing from the pivot point will no longer influence the moment equilibrium. This process is schematically illustrated in Fig. 4a.

Fig. 4
figure 4

Impact forces in the Dirac-Delta model

Full size image

The impact force, \(F_i\), is approximated by a Gaussian function of the rocking angle, defined by a zero mean and a standard deviation of \(n/\sqrt{2}\), where n represents a width parameter that influences the sharpness of the impact force. The effect of changing the value of n on the form of the function is illustrated in Fig. 4b. Regardless of the value of n, the energy dissipated during a single impact cycle is given by:

$$\begin{aligned} E_{loss} = 2B\,\int _{-\infty }^{0} \frac{1}{n \sqrt{\pi }}\, e^{-\theta ^2/n^2}d\theta = B \end{aligned}$$
(17)

Using this property, the Gaussian function can then be scaled to obtain any desired energy loss, \(E_{ini}(1-r)\):

$$\begin{aligned} F_i = \frac{E_{ini}(1-r)}{B\, n\, \sqrt{\pi }}\, e^{-\theta ^2/n^2} \end{aligned}$$
(18)

In order to ensure that the specified amount of energy is dissipated during impact, the force-activation rotation is defined as \(\theta _i = 2.576(n/\sqrt{2})\), corresponding to the 99.5% confidence interval of the Gaussian function (Acikgoz and DeJong 2016). On the other hand, n is assumed to be an independent parameter of the system.

Figure 5 compares the response of the same rigid block analysed in the previous section, considering a classical impact framework (Housner) and the Dirac-Delta model for different values of n. The magnitude of the impact forces is defined based on Housner’s coefficient of restitution, r, according to Eq. 18. Accordingly, the three models compared in Fig. 5 have equivalent energy dissipation ratios during impact.

Fig. 5
figure 5

Response of a rigid block of \(\alpha =10^{\circ }\) and \(\sigma =0\), to a sine pulse ground acceleration of \(a_g/g \alpha = 1.5\) and \(\omega _g/p = 4\) for different impact models

Full size image

Figure 4b showed that impact forces become sharper as n decreases, tending to instantaneous impact as n approaches zero. This is evident in Fig. 5a, where the rotation responses obtained with Housner’s formulation and the Dirac-Delta model converge when \(n=0.0001\). Moreover, the acceleration spikes predicted by the classical formulation are clearly observed in Fig. 5b. As the impact forces become more distributed over time (\(n=0.005\)), these spikes disappear and the acceleration history approaches the in-between-impacts response obtained with Housner’s model. Likewise, very similar rotation amplitudes are obtained with the three models under consideration, even though changes in the duration of impact cause shifts in the phase of the response.

The results presented in Fig. 5 demonstrate that as soon as one deviates from the ideally instantaneous impact assumption (or what is the same, as soon as one deviates from the assumption that the change in velocities happens in a time interval of precisely 0 s), the infinite accelerations associated with this instantaneous change in velocities are mitigated dramatically. Therefore, in the context of classical dynamics, Housner’s model can be used to assess the acceleration response of rocking blocks provided those impact forces are sufficiently distributed overtime as to cause continuous velocity transitions, but sharp enough not to appreciably affect the rotational response of the block. On this note, Acikgoz and DeJong (2016) found that the smaller acceleration magnitudes predicted by the Dirac-Delta model are in better agreement with experimental observations. Accordingly, the analyses presented in the following sections consider the classical impact framework developed in Sect. 2, ignoring the velocity discontinuity (i.e. infinite acceleration) when assessing peak acceleration demands.

4 Modelling of clutched inerter devices

The simplified sequential clutch engagement model introduced by Makris and Kampas (2016) (Eq. 6) is computationally convenient. But, as mentioned above, it also has its shortcomings, chief among them is the fact that by treating the clutched inerters as an abstract discontinuous inertial entity an examination of the device characteristics and their impact on the seismic response of rocking structures is prevented. Its implicit assumption of an instantaneous deceleration can also limit its application towards practical design work. Besides, the unspecified energy dissipation mechanism contributes towards the reduction of peak displacements, but its relative importance cannot be established.

A more rational approach to modelling clutched inerters was adopted by Málaga-Chuquitaype et al. (2019). In their model, the rotation of inerters is considered explicitly as an additional DOF and the interaction between inerter-clutch-structure is modelled via a non-linear spring with continuous stepwise stiffness (Zhu and Parker 2003). This improved model allowed Málaga-Chuquitaype et al. (2019) to explore the nonlinear dynamics of fixed-base SDOF systems. In this paper, we extend such model to rocking structures, both rigid and flexible, and examine the ensuing nonlinear effects.

Consider the inerto-rocking system depicted in Fig. 2 and assume that the inerter now incorporates a one-way clutch within it. This clutch will be able to transmit torque or remain disengaged depending on the direction of motion. In such a case, the torque transmitted between the inerter’s flywheel and the structure can be represented mathematically as:

$$\begin{aligned} T_i (\varDelta \theta _i) = \dfrac{1}{2} k_{\theta } \left[ 1 + \tanh (\epsilon \varDelta \theta _i) \right] \varDelta \theta _i \end{aligned}$$
(19)

where \(\epsilon\) is a factor that controls the transition between engagement and disengagement. As can be appreciated from Fig. 6, a higher value of \(\epsilon\) avoids the local distortion near negative zero. In this paper, unless specified otherwise, \(\epsilon\) is set to \(10^6\). On the other hand, the clutch rotational stiffness \(k_{\theta }\) controls the rigidity of the contact between inerter and structure, an aspect that will be discussed later in this paper. Besides, \(\varDelta \theta\) stands for the incremental relative rotation which physically represents the intrusion between inerter and structure along the contact surface during engagement. It follows that the interaction between structure and inerter without clutch can be explicitly modelled by a linear function of the type \(T_i (\varDelta \theta _i) = k_{\theta } \varDelta \theta _i\).

It should be noted that, since the above defined functions are strictly valid only for static contact, some instances of re-engagement may fail to be identified given that they may happen at any point on the gear and not necessarily at the starting local coordinate (\(\theta _i\)) being monitored. To resolve this, we note that the clutch can re-engage if the velocity of structure surpasses that of the inerter again along the global engagement direction. Therefore, the local coordinate is updated in real time by resetting its value to the structure’s local coordinate once a re-engagement event is detected. An alternative approach is to introduce the number of teeth of the ratchet gear as an additional variable so that that inerter rotation can be reset to zero after the passing of each tooth. This formulation, however, is only valid for a clutch of the ratchet and pawl type and it becomes numerically expensive as the number of teeth in the ratchet becomes large. In this paper, the former approach is adopted by means of the event functions implemented in Matlab (Higham and Higham 2016) to control the integration process and to recognise the occurrence of re-engagement. At which point the system is re-set. If this is not done, then the clutch will be prevented from re-engaging after the first engagement event.

Fig. 6
figure 6

Clutch torque, T, transmission for different stiffness, \(k_{\theta }\), values and an \(\epsilon =10^6\)

Full size image

Finally, it is important to note that a clutch will work only in one direction. Hence, the clutched inerter device described above will disengage when the structure tends to reverse after a local maximum rotation has been attained. For the inerter system to be effective in both directions, a parallel inerter is needed to oppose the motion in the alternative direction, while the first inerter rotates idly. This idle inerter rotation also needs to be modelled in order to get a more precise description of the engagement-disengagement response of the overall system. To this end, we will now turn to the evaluation of rigid blocks equipped with a pair of clutched inerters in the next section before extending the discussion to flexible rocking structures.

5 Rigid blocks equipped with clutched inerters

5.1 Equations of motion

The rigid rocking block depicted in Fig. 7 can be used to study the response of inerto-rocking systems in a generalizable way. The rigid rocking block is characterized by its size (R), slenderness (\(\alpha\)) and mass (m); while the inerters are defined by their moment of inertia (\(J_i\)) and radii (\(\rho _i\)). Only symmetric pairs of inerters are considered in this study, hence \(\rho _a = \rho _b = \rho\) and \(J_a = J_b = J\). Assuming that the friction is large enough to prevent block sliding, the motion of system is described by the block uplift angle (\(\theta\)) and the rotation of the inerters (\(\theta _a\) and \(\theta _b\)). From the discussion on the preceding section, it follows that the contact between inerters and block is described by the following equations:

$$\begin{aligned} T_a (\varDelta \theta ) = \dfrac{1}{2} k_{\theta } \left[ 1 + \tanh \left( \epsilon (x/\rho - \theta _a) \right) \right] (x/\rho - \theta _a) \end{aligned}$$
(20)
$$\begin{aligned} T_b (\varDelta \theta ) = \dfrac{1}{2} k_{\theta } \left[ 1 + \tanh \left( \epsilon (x/\rho - \theta _b) \right) \right] (x/\rho - \theta _b) \end{aligned}$$
(21)

where x is the horizontal displacement of the centre of the block:

$$\begin{aligned} x = R\left( \text {sign} (\theta ) \cdot \sin \alpha - \sin \left( \text {sign} (\theta ) \cdot \alpha - \theta \right) \right) \end{aligned}$$
(22)

which for Slender blocks can be simplified to:

$$\begin{aligned} x = R \theta \end{aligned}$$
(23)

Lagrange’s principles are used to derive the equations of motion using the generalized coordinates \(\theta\), \(\theta _a\) and \(\theta _b\). Accordingly, the kinetic energy of the system including the rotation of inerters about their bearings and that of the block about O or O’ is given by:

$$\begin{aligned} T = \dfrac{1}{2} J \left( {\dot{\theta }}_a^2 + {\dot{\theta }}_b^2 \right) + \dfrac{1}{2} I_0 {\dot{\theta }}^2 \end{aligned}$$
(24)

On the other hand, the total potential energy including the gravity energy of block and the elastic energy stored in the clutch is:

$$\begin{aligned} V = m g R \cos \left( \text {sign} (\theta ) \cdot \alpha + \theta \right) + \int _0^{\varDelta \theta _a} T_a \mathrm {d} \left( \varDelta \theta _a \right) + \int _0^{\varDelta \theta _b} T_b \mathrm {d} \left( \varDelta \theta _b \right) \end{aligned}$$
(25)

while the Lagrange function is defined as:

$$\begin{aligned} L = T-V \end{aligned}$$
(26)

Furthermore, we assume that only the inerters are subjected to viscous damping while the block can only dissipate energy through impact, therefore the corresponding dissipative term defined by the Rayleigh’s function is:

$$\begin{aligned} D = \dfrac{1}{2} c \left( {\dot{\theta }}_a^2 + {\dot{\theta }}_b^2\right) \end{aligned}$$
(27)

and the non-conservative generalized force term due to ground motion is:

$$\begin{aligned} Q_{\theta } = -m \ddot{u}_g \frac{\partial {x}}{\partial {\theta }} = -m \ddot{u}_g R \cos \left( \text {sign}(\theta ) \cdot \alpha - \theta \right) \end{aligned}$$
(28)

Substituting each generalized coordinate into Lagrange’s equation gives:

$$\begin{aligned} \frac{\text {d}}{\text {d}{t}} \left( \frac{\partial {L}}{\partial {\dot{q}_i}} \right) - \frac{\partial {L}}{\partial {q_i}}+ \frac{\partial {D}}{\partial {q_i}} = Q_i \end{aligned}$$
(29)

from where the governing equations of the 3-DOF system are obtained:

$$\begin{aligned} \ddot{\theta } = -p^2 \left[ \sin (\alpha - \theta ) + \left( \dfrac{\ddot{u}_g}{g} + \dfrac{RJ(I_a+I_b)}{I_0 \rho p^2} \right) \cos (\alpha - \theta ) \right] \end{aligned}$$
(30)
$$\begin{aligned} \ddot{\theta }_a + {\bar{c}} {\dot{\theta }}_a -I_a =0 \end{aligned}$$
(31)
$$\begin{aligned} \ddot{\theta }_b + {\bar{c}} {\dot{\theta }}_b -I_b =0 \end{aligned}$$
(32)

where p is the frequency parameter of the rocking block, \({\bar{c}}\) is the (inertial) mass-normalized damping coefficient defined as \({\bar{c}} = c/J\), and \(I_a\) and \(I_b\) are the mass-normalized rotational inertia of the flywheel in the inerters. In order to facilitate comparisons with previous studies, the moment of inertia of the inerters can be replaced by their suppression coefficients: \(\sigma _a = \sigma _b = \sigma = \frac{J}{m \rho ^2}\). If is worth noting that for slender blocks (small \(\alpha\)), Eq. 30 can be simplified to:

$$\begin{aligned} \ddot{\theta } = -p^2 \left[ \alpha - \theta + \dfrac{\ddot{u}_g}{g} + \dfrac{RJ (I_a + I_b)}{I_0 \rho p^2} \right] \end{aligned}$$
(33)
Fig. 7
figure 7

Rigid rocking block with twin clutched inerters

Full size image

5.2 Numerical solution and model comparison

The equations of motion derived above were solved by means of numerical integration with event screening in Matlab (Higham and Higham 2016). Figure 8 shows the displacement, velocity, and acceleration response histories of a slender (\(\alpha =10^{\circ }\)) rigid rocking block with and without inerters. Included in this figure are the results obtained with the sequential model implemented by Thiers-Moggia and Málaga-Chuquitaype (2019) as well as the predictions of the newly proposed model described above. The suppression coefficient of inerters and clutched inerters is taken as \(\sigma =0.5\). Besides, a damping of \({\bar{c}}=1\ s^{-1}\) is used for the production of the new clutch model curves. This value of damping was chosen so as to obtain comparable responses between alternative models. The structures are subjected to a sinusoidal pulse excitation at their base of \(a_g/g\alpha =1.5\) and \(\omega _g/p=4\).

Fig. 8
figure 8

Response of a rigid block of \(\alpha = 10 ^{\circ }\), with and without inerters subjected to a sine pulse of \(a_g/g \alpha = 1.5\) and \(\omega _n/p = 4\)

Full size image

It is clear from Fig. 8a that the inerter (\(\sigma = 0.5\)) can greatly stabilize the block during the initial stages of the response. However, the response is amplified at later stages, relative to the uncontrolled structure (\(\sigma = 0\)), which indicates a lower amount of energy dissipation during impact and/or energy being transferred back from the inerter to the structure. On the other hand, Fig. 8b proves that the inclusion of one-way clutches can eliminate this phenomenon and improve the effectiveness of inerters. In addition, it can be appreciated from Fig. 8b that the sequential clutch formulation leads to a faster amplitude decrease in comparison with the newly proposed model. This is down to the intrinsic differences in the modelling assumptions as can be further explained with reference to Fig. 9. Figure 9 evidences the effects of the underlying assumption of the sequential model related to the complete sudden loss of the energy in inerter after disengagement. This contrasts with the relatively decelerated response of the newly proposed model which is controlled by an explicit modelling of the viscous dissipation within the device. It is also clear from Fig. 9a that the model proposed in this paper struggles to attain a strong re-engagement with the structure after \(t=3s\). This is because at this stage in the response the inerter has limited time to decelerate while the frequency of the rocking motion continues to increase rapidly. The sequential model (Fig. 9b), on the other hand, re-engages irrespectively of the conditions of relative motion until the rocking block comes to rest.

Fig. 9
figure 9

Comparison of rotational velocity and transmitted force histories between the newly proposed model and the sequential model of the clutch

Full size image

It should be noted that the apparently solid areas depicted in Fig. 9a for the newly proposed model corresponds to regions of intensive engagement-disengagement activity. This is shown in detail in Fig. 10. As explained above, once an engagement event is detected (Point A in Fig. 10), the inerter rotation assumes a value compatible with the structure’s deformation. This rotation starts to accumulate in successive time steps leading to a sharp increase in the interaction forces and a subsequent increment in the inerter acceleration. When the velocity of the inerter and the local velocity in the structure coincide (Point B), a maximum displacement difference and peak transmission is achieved. Subsequently, the inerter starts to catch up with the structure’s deformation and the strength of the interaction starts to decrease accordingly, until detachment (Point C). During disengagement, the inerter slows down due to damping until the next contact (Point D). This process, which is not modelled in the sequential engagement idealization, is repeated until the global engagement process finishes and has been observed in real systems (Centea et al. 2001).

Fig. 10
figure 10

Detail of the inerter velocity and clutch force during global engagement. Newly proposed model

Full size image

5.3 Inerter and clutch relative contributions to the response

Although the benefits of clutched inerters over single inerters towards the seismic control of rocking structures have been widely demonstrated (Thiers-Moggia and Málaga-Chuquitaype 2019, 2020a, 2020b, 2021b). The question of how much does the clutch itself contributes towards these improvements becomes pertinent in light of the abilities of the improved clutching model. This question is explored herein with reference to Figs. 11 and 12 which depict the response of rigid blocks of comparable geometry with and without inerters and clutches to a ground acceleration of \(a_g/g\alpha =1.5\) and \(\omega _g/p=4\). The blocks have a slenderness of \(\alpha =10^{\circ }\). The suppression coefficient of inerters and clutched inerters is assumed as \(\sigma =0.5\).

Figure 11 shows that the newly adopted model and the previously proposed sequential model achieve comparable peak displacement responses. This happens despite the sequential model assumption of an instantaneous energy dissipation at disengagement. By comparison, rocking blocks equipped with a single inerter without clutch reach a slightly higher peak displacement, and transfer energy back and forth between the inerter and the structure leading to marked peaks and throughs in the structure’s energy levels and a suboptimal performance. It is worth noting at this point that the sequential model does not necessarily represent an upper bound of energy dissipation. This is because the dissipation process in the sequential acceleration-based law starts after disengagement and is assumed to finish at an unspecified time before the next engagement event and will therefore not affect the motion of the structure. In other words, the velocity drop in the inerter is not modelled but pre-determined. By contrast, the condition of re-engagement in our new mechanistic model accounts for this relative velocity and the processes of energy transfer from structure to inerter as well as the dissipation in the inerter happen simultaneously. These actions are taken by the structure through contact forces during engagement and thus, the dissipation of inerters will actually affect the structural motion and it is possible that the proposed model can achieve greater energy dissipation than the sequential idealization even though the engagement time is shorter.

Fig. 11
figure 11

Response histories of a series of rigid blocks of \(\alpha =10^{\circ }\) with and without inerters subjected to a sine pulse of \(a_g/g\alpha = 1.5\) and \(\omega _g/p = 4\)

Full size image

Figure 12 presents the displacement and acceleration response spectra of the blocks under consideration. In these plots, the condition of overturning is attained when frequency ratio is approximately \(\omega _g/p <3\) and the curves are discontinued after that. It is clear from 12 that when looked in terms of peak response values, both the detailed model presented in this paper and the previous sequential idealization produce largely comparable maximum displacement results. For low frequency ratios, the more faithful representation of the of clutch in the new model leads to displacement estimations marginally lower than the sequential model. These differences are further reduced as the frequency ratio increases. On the other hand, the effects of a more detailed simulation of the clutch engagement process leads to higher acceleration levels, due to the juddering effects described above, and produce peak values of acceleration markedly larger than the ideally sequential assumption. It appears that the most effective way to control peak responses in rigid rocking blocks is by increasing the suppression coefficient of the inerter.

Fig. 12
figure 12

Response spectra of a series of rigid blocks of \(\alpha =10^{\circ }\) with and without inerters subjected to a sine pulse of \(a_g/g\alpha = 1.5\) and \(\omega _g/p = 4\)

Full size image

6 Flexible rocking structures equipped with clutched inerters

6.1 Equations of motion

In this section, we investigate the dynamics of flexible rocking structures equipped with twin inerter-clutch devices. To this end, Fig. 13 presents the analytical model considered. In it, a lumped mass (m) is fixed on the top of a flexible column of height h, horizontal stiffness k and damping coefficient c. The column is fixed to a rigid pad with half-width of B resting on a rigid ground. In addition to the mass vibrating about its neutral position with a displacement u, the rigid base is able to uplift about points O or O’ with angle \(\theta\) as long as the overturning moment is large enough. We assume the friction is large enough to prevent sliding between the block and the ground. For convenience of expression, the motion of the mass can be defined by using the distance to the pivot point (R) and the angle between straight distance and ground (\(\beta\)) as generalized Lagrange coordinates. The two coordinates (u,\(\theta\) and R,\(\beta\)) can be related according to Eqs. 34 and 35:

$$\begin{aligned} \theta = \beta - \text {sign}(\beta ) \cdot \arcsin (H/R) \end{aligned}$$
(34)
$$\begin{aligned} u = \text {sign}(\beta ) \cdot \left( B - \sqrt{R^2-H^2}\right) \end{aligned}$$
(35)

As with the rigid rocking block, a pair of clutched inerters is connected horizontally connected to the mass intended to resist only the horizontal component of the system’s motion. The same clutch model described above is adopted herein to transmit the clutch torque (\(T_i(\varDelta \theta )\)). Accordingly, the horizontal displacement of the mass is given by:

$$\begin{aligned} x = \text {sign}(\beta ) \cdot \left( B - R \cos \beta \right) \end{aligned}$$
(36)
Fig. 13
figure 13

Sketch of the flexible rocking modelling and equation parameters

Full size image

6.1.1 Phase transition

The motion of a flexible rocking structure can be dissembled into a series of full contact phases and rocking phases. During a full contact phase, the base pad lies firmly on the ground and only the mass oscillates about its horizontal position. Once the overturning condition is reached, the structure would enter into a rocking phase in which the base uplifts and keeps rocking while the mass oscillates simultaneously. The criteria of transition from full contact phase to rocking can be derived by equating overturning moment and restoring moment:

$$\begin{aligned} \mp \left( F_a + F_b + m \ddot{u}_g + m \ddot{u} \right) H > mg \left( B \mp u \right) \end{aligned}$$
(37)

leading to the definition of a critical displacement for uplift (Oliveto et al. 2003; Thiers-Moggia and Málaga-Chuquitaype 2020a):

$$\begin{aligned} u_{cr} = \pm \dfrac{gB \mp 2 \xi \omega _n H \dot{u}}{g + \omega _n^2H} \end{aligned}$$
(38)

The transition from rocking phase to full contact phase defined by Chopra and Yim (1985) Vertical Velocity Energy Loss (VVEL) model is used here. In it impact is assumed to be a perfect inelastic collision process in which the full vertical velocity of the mass is dissipated while the horizontal energy is conservative. As a result, after each impact, the mass would move completely horizontally, thus transiting into a full contact phase. The relation between pre-impact velocity \(\dot{u}_2\),\({\dot{\theta }}_2\) and post-impact velocity \(\dot{u}_1\),\({\dot{\theta }}_1\) of the structure is given by:

$$\begin{aligned} \dot{u}_2 = H {\dot{\theta }} + \dot{u}_1 \end{aligned}$$
(39)
$$\begin{aligned} {\dot{\theta }}_2 = 0 \end{aligned}$$
(40)

6.1.2 Governing equations for full contact phase

During the full contact phase, the mass oscillates about neutral position subjected to resistance of inerter and the ground acceleration. The mass motion is exactly the same as a fix-based SDOF structure equipped with twin inerters whose governing equations were given by Málaga-Chuquitaype et al. (2019):

$$\begin{aligned} \ddot{u} + 2 \xi \omega _n \dot{u} + \omega _n^2 u + \sigma \rho (I_a + I_b) = - \ddot{u}_g \end{aligned}$$
(41)
$$\begin{aligned} \ddot{\theta }_a + {\bar{c}} {\dot{\theta }}_a -I_a (\varDelta \theta )=0 \end{aligned}$$
(42)
$$\begin{aligned} \ddot{\theta }_b + {\bar{c}} {\dot{\theta }}_b -I_b(\varDelta \theta ) =0 \end{aligned}$$
(43)

where \(\xi\) and \(\omega _n\) are the damping ratio and natural frequency of the column-mass oscillator, \({\bar{c}}= c/J\) and \(I_i = T_i/J\) are the normalized damping coefficient and force transmitted between the interter and the mass, and \(\sigma = \dfrac{J}{m \rho ^2}\) is the suppression coefficient.

6.1.3 Governing equations for rocking phase

The governing equations of a flexible rocking structure undergoing rocking phase are derived using Lagrange’s equation. The generalized coordinates R, \(\beta\), \(\theta _a\) and \(\theta _b\) introduced above are employed with this purpose. The kinetic energy of the system is expressed as:

$$\begin{aligned} T = \dfrac{1}{2} m \left( \dot{R}^2 + R^2 {\dot{\beta }}^2 \right) + \dfrac{1}{2} J \left( {\dot{\theta }}_a^2 + {\dot{\theta }}_b^2\right) \end{aligned}$$
(44)

while the potential energy is:

$$\begin{aligned} V = \text {sign} (\beta ) \cdot m g R \sin \beta + \dfrac{1}{2}k u^2 + \int T_a (\varDelta \theta ) \mathrm {d} (\varDelta \theta ) + \int T_b (\varDelta \theta ) \mathrm {d} (\varDelta \theta ) \end{aligned}$$
(45)

which can be substituted into the Lagrangian:

$$\begin{aligned} L = T - V \end{aligned}$$
(46)

Besides, the corresponding dissipative term for the viscous damping of the inerter and mass-column oscillator is defined by Rayleigh’s function as:

$$\begin{aligned} D = \dfrac{1}{2}c_s \dot{u}^2 + \dfrac{1}{2}c \left( {\dot{\theta }}_a^2 + {\dot{\theta }}_b^2 \right) = \dfrac{1}{2}c_s \dfrac{R^2\dot{R}^2}{R^2 - H^2} + \dfrac{1}{2} c {\dot{\theta }}_a^2 + \dfrac{1}{2} c {\dot{\theta }}_b^2 \end{aligned}$$
(47)

while the non-conservative force term due to ground motion is:

$$\begin{aligned} Q_R = - m \ddot{u}_g \frac{\partial {x}}{\partial {R}} = \text {sign}(\beta ) \cdot m \ddot{u}_g \cos \beta \end{aligned}$$
(48)
$$\begin{aligned} Q_{\beta } = - m \ddot{u}_g \frac{\partial {x}}{\partial {\beta }} = - \text {sign}(\beta ) \cdot m \ddot{u}_g R \sin \beta \end{aligned}$$
(49)

Applying Lagrange’s equation to each generalized coordinate:

$$\begin{aligned} \frac{\text {d}}{\text {d}{t}}\left( \frac{\partial {L}}{\partial {\dot{q}_i}}\right) - \frac{\partial {L}}{\partial {q_i}} + \frac{\partial {D}}{\partial {q_i}} = Q_i \end{aligned}$$
(50)

leads to the following governing equations of the 4-DOF system:

$$\begin{aligned} \begin{aligned} {\ddot{R}} - R {\dot{\beta }}^2 + \text {sign}(\beta ) \cdot g \sin \beta + \dfrac{2 \xi \omega _n R^2 \dot{R}}{R^2-H^2} + \omega _n^2 \left( 1 - \dfrac{B}{\sqrt{R^2-H^2}} \right) R\\ = \text {sign} (\beta ) \cdot \left[ \ddot{u}_g + \dfrac{1}{2} \sigma \rho (I_a + I_b)\right] \cos \beta \end{aligned} \end{aligned}$$
(51)
$$\begin{aligned} \ddot{\beta } + \dfrac{2 \dot{R} {\dot{\beta }}}{R} + \text {sign}(\beta ) \cdot \dfrac{g}{R} \cos \beta + \text {sign} (\beta ) \cdot \left[ \dfrac{\sigma \rho }{2R}(I_a + I_b) + \dfrac{\ddot{u}_g}{R} \right] \sin \beta = 0 \end{aligned}$$
(52)
$$\begin{aligned} \ddot{\theta }_a + {\bar{c}} {\dot{\theta }}_a -I_a =0 \end{aligned}$$
(53)
$$\begin{aligned} \ddot{\theta }_b + {\bar{c}} {\dot{\theta }}_b -I_b =0 \end{aligned}$$
(54)

6.2 Numerical solution and model comparison

Figure 14 shows the histories of response of a flexible rocking column with a frequency \(\omega _n/p=8\), a size of \(R_0=10\ m\), slenderness of \(\alpha =0.2\), and damping ratio of \(\xi =0.02\). Where the frequency parameter p for flexible structures is taken as \(p=\sqrt{mgR_0/I_0}\) with \(I_0\) being the moment of inertia of the mass with respect to the pivot point. The responses of an uncontrolled structure (\(\sigma = 0\)) as well as structures connected to single inerters or clutched twin inerters are presented. When controlled, the suppression coefficient of inerters and clutched inerters is taken as \(\sigma = 0.5\). In the case of a single inerter with dissipation and the clutched inerter modelled with the proposed model an additional viscous dissipation in the device itself is assumed with \({\bar{c}}=1\ s^{-1}\). The structures are subjected to single sine pulses of \(a_g/gtan\alpha =1.5\) and \(\omega _g/p=8\).

Fig. 14
figure 14

Response of flexible rocking structure of \(\omega _n/p=8\), \(\alpha =0.2\), \(R_0=10\ m\) and \(\xi =0.02\), subjected to a single sine pulse of \(a_g/g/tan\alpha =1.5\) and \(\omega _g/p=8\)

Full size image

Figure 14 demonstrates that the introduction of a single inerter without clutch can significantly reduce the peak base uplift rotation but has negligible effects on the elastic deformations of the column. The horizontal acceleration levels are also benefited by the additional inertia provided by the single inerter. The addition of clutches can further reduce the peak uplift rotation and horizontal drift, but only a small improvement in the structure’s deformation is observed. However, the structure equipped with clutched inerter has far more efficient energy dissipation than single inerter, which makes the structure quickly reach rest from peak response. Although clutched inerters can improve displacement response, they appear less effective in controlling peak horizontal accelerations under single pulses and larger acceleration values than with the single inerter configuration are observed.

6.3 Inerter and clutch relative contributions to the response

Figure 15 shows the evolution of energy and its dissipation for the different flexible rocking configurations under investigation. It can be seen in this figure that, for a structure with single inerters, part of the inerter’s energy transferred back to the structure during the rocking motion as shown in Fig. 15c and d. In addition, Fig. 15e shows the energy evolution of the structure predicted by the classic sequential model, where the energy of inerter is fully lost after each disengagement event. This contrasts with the response depicted in Fig. 15f which maintains the conservation of energy throughout the motion of inerter. It is worth mentioning that the damping inside the inerter can also improve the energy dissipation and Fig. 15e and f prove that the clutch can fully prevent the energy stored in inerter from being transferred back to structure. It should also be noted that the proposed inerter model with a normalized damping ratio of \(\xi _{\theta }=0.02\) has similar dissipating capacity than the sequential model used by Thiers-Moggia and Málaga-Chuquitaype (2020a). This becomes apparent in the relationships presented in Fig. 15b.

Fig. 15
figure 15

Evolution of the energy dissipation in alternative models

Full size image

The dynamic response for ground motions of different frequencies is examined in Fig. 16 which presents the response spectra of structures with \(\alpha =0.2\), \(R_0=10\) m, \(\omega _n/p=8\) and \(\xi =0.02\) for different inerter configurations. This figure confirms the observations made above where structures with natural frequency of \(\omega _n/p=8\) show a behaviour that is dominated by rocking motion instead of elastic deformations. Therefore, the horizontal drift is controlled mainly by uplift peak rotation, which explains partly why different models have similar peak response predictions. The limited effects of clutched inerters on peak elastic deformations are also evident from Fig. 16. Moreover, the increased accelerations predicted by our mechanistic clutch model are also confirmed for most of the frequency ratios.

Fig. 16
figure 16

Response spectra of flexible rocking structures. \(m=1\) kg, \(\alpha =0.2\), \(R_0=10\ m\), \(\xi =0.02\), subjected to a single sine pulse of \(a_g/g\tan \alpha =1.5\)

Full size image

7 Influence of clutch characteristics

7.1 Clutch stiffness

As mentioned in Sect. 4, the clutch rotational stiffness \(k_{\theta }\) controls the rate of torque transmission between the inerter and the structure. In order to examine the influence of different realistic values of clutch stiffness (Brzeski and Perlikowski 2017; Zhu and Parker 2005) on the dynamic response of inerter-equipped rocking structures the velocity, displacement and rotation responses of these structures are presented in Figs. 17 and 18. Figure 17 presents a close-up view into the velocity history during the engagement process. A mild juddering associated with the engagement-disengagement cycles described above is noticeable for a low value of \(k_{\theta }\) (Fig. 17a). Higher clutch stiffnesses result in a smoother engagement process at the macro scale while softer clutches may cause a small delay in the disengagement at the very local level. However, for all practical purposes, the influence of the clutch stiffness is not determinant. This is demonstrated in Fig. 18 which presents the response spectra for flexible inerto-rocking structures with different clutch stiffness values. The structure under consideration in this figure has the dynamic properties of \(\alpha =0.2\), \(R_0=10\) m, \(\xi =0.02\), and \(\omega _n/p=8\) while a ground motion of amplitude \(a_g/g\tan \alpha =1.5\) is employed.

Fig. 17
figure 17

Inerter and structure velocities for different clutch stiffness values

Full size image
Fig. 18
figure 18

Response spectra for flexible inerto-rocking system with \(\alpha =0.2\), \(R_0=10\ m\), \(\xi =0.02\), \(\omega _n/p=8\), connected to pair of clutched inerters with different levels of clutch stiffness

Full size image

7.2 Viscous damping

As discussed previously, one of the most effective means of improving the dynamic response of rocking structures with inerters is by increasing the viscous damping in the device. This can be achieved by immersing the inerter, or a part of it, into a viscous fluid as proposed by Hwang et al. (2007) or Ikago et al. (2012), for example. To analyse this, two different levels of damping are explored in Fig. 19: (i) a local inerter viscous damping corresponding to \(\xi _{\theta } = 2\%\) of the critical value, which represents typical operational conditions of a standard inerter device, and (ii) a damping of \(\xi _{\theta } = 20\%\) which represents supplemental damping values provided by external means. The results for an undamped inerter are also presented in Fig. 19 for comparison purposes. In all these cases, the inerter’s damping ratio \(\xi _{\theta }\) is defined as \(\xi _{\theta }=c I_i/(2 \sqrt{k_{\theta } J_i})\). The lower values of damping are selected considering the values usually employed to model the energy dissipation present in the real systems due to imperfections, dry friction, internal damping, etc. (Horton et al. 2008) without additional viscous dampers. While the larger value of damping was used to represent how the response of the system changes when we drastically increase the viscous damping coefficient usually with the aid of supplemental damping (Brzeski et al. 2014; Brzeski and Perlikowski 2017).

Fig. 19
figure 19

Response spectra for flexible inerto-rocking systems with \(\alpha =0.2\), \(R_0=10\ m\), \(\xi =0.02\), \(\omega _n/p=8\), connected to pair of clutched inerters with different level of damping under pulse excitation of amplitude \(a_g/g\tan \alpha =1.5\)

Full size image

It can be observed from Fig. 19 that operational levels of damping (i.e. \(\xi = 2\%\)) are practically immaterial to the peak displacement or rotational response of flexible inerto-rocking structures. However, supplemental damping (i.e. \(\xi = 20\%\)) is able to reduce significantly the base rotations (more than halving it for low frequency ratios in the order of \(\omega _g/p \approx 5\) and reduce the overturning for stiffer structures. Similarly, reductions in peak elastic displacement demands are also observed for inerters with important damping levels, although the reductions are less dramatic than in the rotations. These observations are valid for the full range of frequency ratios investigated.

7.3 Dry friction

The energy dissipation in the inerter system can also be modelled as dry friction, which can be more realistic for bare inerters without supplemental damping. To introduce dry friction into the model without introducing hard discontinuities, a continuous step function is adopted Málaga-Chuquitaype et al. (2019):

$$\begin{aligned} F_{\mu i} = \dfrac{2 f_{mu}}{\pi } \arctan (\eta {\dot{\theta }}_i) \end{aligned}$$
(55)

Where \(f_\mu\) controls the magnitude of friction and \(\eta\) controls the transition of the frictional force as shown in Fig. 20. By replacing the damping terms by dry frictions terms in Eqs. 53 and 54 a new set of equations governing the motion of the inerters can be found:

$$\begin{aligned}&\ddot{\theta }_a - I_a + \dfrac{F_{\mu a} \rho }{J} = 0 \end{aligned}$$
(56)
$$\begin{aligned}&\ddot{\theta }_b - I_b + \dfrac{F_{\mu b} \rho }{J} = 0 \end{aligned}$$
(57)
Fig. 20
figure 20

Dry friction force for different values of transition coefficient

Full size image

To evaluate the effect of dry friction, Fig. 21 presents the response curves of structures equipped with clutched inerters with different levels of frictional forces (i.e. \(f_{\mu }=0\),\(f_{\mu }=0.1m_rg\) and \(f_{\mu }= 0.2m_rg\)). These values of friction coefficients, ranging from 0 to 0.2, are adopted to explore the effects of dry friction on the response of the system with ideally frictionless response and a strong friction that can be caused by imperfections or targeted friction devices like friction pads (Brzeski et al. 2014; Brzeski and Perlikowski 2017). In the latter case, however, attention should be placed to the forces transferred to the system and the threshold of activation of the device.

In general, the effects of dissipating energy through friction are similar to those observed for viscous damping, with operational levels of dissipation resulting in negligible changes in the peak displacement and rotation responses. Higher magnitude of dry friction can significantly reduce peak response for both elastic deformation and uplift rotation and can completely eliminate the rocking phase for high frequency excitations.

Fig. 21
figure 21

Response spectra for flexible inerto-rocking systems with \(\alpha =0.2\), \(R_0=10\ m\), \(\xi =0.02\), \(\omega _n/p=8\), connected to pair of clutched inerters with different dry friction levels under pulse excitation of amplitude \(a_g/g\tan \alpha =1.5\)

Full size image

7.4 Influence of gear play

In reality, gears are not perfectly aligned and there are inevitable gaps between their teeth. This is known as ‘gear play’ and can be incorporated into the newly proposed model by assuming that all the plays present in the inerter can be transferred to the interface between the pinion and the rack. Hence, Eqs. 20 and 21 can be modified to introduce a total play distance \(u_p\):

$$\begin{aligned} T_a (\varDelta \theta )= & {} \dfrac{1}{2} k_{\theta } \left[ 1 + \tanh \left( \epsilon (x/\rho - \theta _a - u_p) \right) \right] (x/\rho - \theta _a - u_p) \end{aligned}$$
(58)
$$\begin{aligned} T_b (\varDelta \theta )= & {} \dfrac{1}{2} k_{\theta } \left[ 1 + \tanh \left( \epsilon (x/\rho - \theta _b + u_p) \right) \right] (x/\rho - \theta _b + u_p) \end{aligned}$$
(59)

The consideration of gear play effectively introduces a series of collisions whenever the clutch engages. This is exemplified in Fig. 22 where the inerter velocity and its corresponding acceleration histories are presented. It can be noticed that upon first engagement, a strong discontinuity is introduced in the inerter’s velocity leading to a large peak in the acceleration response.

Fig. 22
figure 22

Collision caused by gear play resulting in non-smooth behaviour and acceleration peaks

Full size image

The effects of different levels of gear play are evaluated with reference to Fig. 23 that summarizes the response of flexible rocking structures with inerters for gear plays varying from 0 to 1 cm. This latter value of gear play is very large and was adopted to represent faulty devices or gears with broken teeth. It can be concluded from Fig. 23 that even these large values of gear play have an almost unnoticeable effect on peak deformations (displacements or rotations).

Fig. 23
figure 23

Response spectra of flexible rocking structures. \(\alpha =0.2\), \(R_0=10\ m\), \(\xi =0.02\), subjected to a single sine pulse of \(a_g/g\tan \alpha =1.5\), for different levels of gear play

Full size image

8 Response under real pulse-like ground motions

Previous sections of this paper have concerned themselves with the assessment of different modelling strategies that make manifest the different nonlinearties encountered in clutched inerto-rocking systems from a fundamental perspective by using coherent harmonic pulses. Real records, however, are non-coherent and as such they have a rich frequency content that can sometimes amplify the demands on rocking structures, especially larger ones (Makris and Roussos 2000). In this section we examine the response of relatively large structures subjected to real ground motion records. The family of structures selected has dimensions of \(R_0=10\ m\) with \(\alpha =0.2\) and \(\xi = \xi _{\theta }=0.02\) and can be representative of a wall building system or a tall pier. They comprise bare uncontrolled flexible rocking systems as well as controlled ones for which a twin pair of clutched inerters are employed following both the sequential and the alternative modelling approach proposed in this study.

A representative set of 5 earthquake accelerograms is used to construct deformation, rotation and acceleration response spectra. The ground motions considered are summarized in Table 1. They have been selected from the pulse-like database identified by Baker (2007) and comprise series with peak ground velocities of up to 1.67 (m/s) and pulse periods ranging from 1.2 to 5.1 (s). The listed records were selected in light of their strong coherent and non-coherent components in order to impose appreciable demands in the rocking structures being examined.

Table 1 Pulse-like ground motion records used.
Full size table

Figure 24 presents the response spectra generated for structures of different flexibility levels (\(\omega _n\)). Results are presented for peak base rotation, maximum elastic deformation, peak drift and absolute horizontal acceleration. Values of elastic deformation, drift and absolute acceleration are not reported in those cases where the structure overturns (\(\theta \rightarrow \infty\)) as they are not deemed relevant under such condition. Overall, Fig. 24 demonstrates the important reductions in the number of such overturning cases when the clutched inerter system is incorporated as discussed in detail by Thiers-Moggia and Málaga-Chuquitaype (2020a). Similarly, the noticeable reduction in the dispersion associated with clutched systems identified in previous studies is also evident.

Figure 24 shows the same trends observed in our previous analyses. The clutched inerter system leads to important reductions in base rotation but only mild elastic deformation mitigation. Interestingly, however, both the rotation and elastic displacement estimations of the clutch model advanced in this study are slightly lower (by around 8%) than the predictions made on the basis of the sequential engagement law adopted in previous studies. This is attributed to the more faithful representation of the engagement process leading to a relatively larger number of inerter engagement events over the response history of the structure. This level of reductions is fairly constant throughout the frequency range under consideration.

Although past research has proved that a single inerter implementation can reduce peak accelerations in rocking structures to acceptable levels Thiers-Moggia and Málaga-Chuquitaype (2020a), the same authors identified the difficulties in controlling accelerations through clutching inerter devices. These difficulties are also evidenced in Fig. 24, especially within the range of \(12<\omega _n<18\). Moreover, the mechanistic clutch model of the present study estimates higher acceleration levels than the sequential model of previous studies. This is in line with the discussion presented in previous sections of this paper. In some cases, notably for the El Centro record, these peak accelerations may be even higher than those experienced in bare structures.

Fig. 24
figure 24

Rocking spectra for a structure of \(\alpha =0.2\), \(R_0=10\ m\), \(\xi =0.02\), subjected to a set of real ground motions (Table 1)

Full size image

9 Conclusions

In this paper, we have extended previously proposed models of clutched inerto-rocking structures by considering an improved mechanistic representation of the clutching system. This new formulation enables a more detailed assessment of the inerter’s influence on the rocking behaviour, as it explicitly models the flywheel’s rotational response and takes into account key clutch parameters like stiffness, gears play, viscous damping and dry friction.

Firstly, the effect of the inerter on the rotation transition was evaluated using an extension of Housner’s impact formulation. This analysis showed that, in general, the inclusion of the inerter results in higher coefficients of restitution, indicating lower energy dissipation during impact. Importantly, this effect was found not to be significant in slender blocks, although it can affect the efficiency of the proposed strategy when high apparent mass ratios or nonslender structures are considered.

The suitability of this classical impact framework to assess acceleration demands in rocking structures was examined next. Although Housner’s approach has been shown to provide a good estimation of the amount of energy dissipated during impact, its underlying assumptions imply an instantaneous change of velocity and, therefore, an unrealistic infinite acceleration at the transition instant. Using an alternative formulation based on Dirac-Delta forces, it was demonstrated that the infinite acceleration spikes predicted by Housner’s model can be ignored under the assumption that impact forces are sufficiently distributed over time as to cause continuous velocity transitions, but sharp enough not to appreciably affect the rotation response.

The clutch modelling strategy presented in this paper was first compared with the sequential approach proposed previously in the scientific literature. The results of response history analyses conducted on rigid rocking blocks equipped with clutched inerters showed that the sequential clutch formulation leads to a faster amplitude decrease in comparison with the newly proposed mechanistic model. This difference is explained by the underlying assumption of the sequential formulation, by which energy stored in the inerter is dissipated instantly after disengagement. This contrasts with the relatively decelerated response of the newly proposed model which is controlled by an explicit modelling of the viscous dissipation within the device. Moreover, the new mechanistic model was able to predict periods of intensive engagement-disengagement activity, a behaviour that has been observed experimentally and that can have significant consequences on the acceleration demands.

In order to assess the relative importance of the clutch and inerters’ viscous damping on the response improvements observed in the previous analyses, the behaviour of rocking blocks equipped with single and twin inerters with identical levels of internal energy dissipation was examined. The results of the analyses showed that the blocks equipped with clutched inerters experienced lower rotation demands in comparison with their single-inerter counterparts, thus confirming the advantages of incorporating a clutch. Moreover, evaluation of the temporal evolution of the system’s energy showed that the clutch can prevent the energy stored in the inerter from being transferred back to the structure. In terms of accelerations, however, the intensive engagement-disengagement behaviour mentioned above had a detrimental effect, resulting in larger demands for the structures equipped with clutched inerters. Nevertheless, it should be noted that in all cases the inerter-equipped structures experienced smaller rotation and accelerations demands than unprotected ones.

The effects of different clutch parameters on the rocking response of a more general flexible oscillator, including stiffness, viscous damping, dry friction and gear play, were evaluated considering the newly proposed mechanistic model. Analyses conducted for a wide range of ground motion frequencies demonstrated that, for all practical purposes, the influence of the clutch stiffness is not determinant. Viscous damping and dry friction, on the other hand, were shown to have a more significant impact on the rotation and elastic deformation responses. Although small values of viscous damping and dry friction forces had a negligible effect on the response, values representative of highly damped systems (such as viscous mass dampers or clutches with frictional pads) considerably reduced the rocking and deformation demands. Contrastingly, the gear play did not have an appreciable effect on the base ration and elastic deformation response, but it significantly increased the acceleration demands. This effect is related to the delay in the activation of the inerter and subsequent impact between the moving structure and the idle flywheel. It should be noted, however, that an adequate quantification of this effect requires a more detailed modelling of the impact phenomenon.

Finally, the observations presented above were extended to real ground motions by considering the response of a case of study structure to a set of real pulse-like acceleration records. In general, the results of these analyses are in agreement with the conclusions obtained in the previous sections. Importantly, the mechanistic clutch model proposed in this paper predicts slightly lower rocking demands than the sequential model used in previous studies, while both formulations suggest that the incorporation of a clutch can increase the acceleration demands in flexible uplifting structures.