An improved capacity design procedure incorporating the effect of gap-opening on higher mode responses in rocking wall structures

Abstract

Rocking wall structures present a resilient alternative to conventional structures. Although the displacement responses of these structures have been discussed in past works, the force-based responses especially in the context of nonlinearity due to gap-opening behavior need to be explored in detail. In the current research, the effect of gap-opening behavior at predetermined locations in the rocking walls on the seismic force responses has been discussed. For this purpose, five rocking walls of varying heights and against two levels of seismic intensity are designed and analyzed using time history analysis procedure. A modal decomposition technique is used to separate the complex responses to their modal responses to better understand the different factors in play. It is found that the modal properties based on initial stiffness properties are unable to predict the inelastic seismic demands and a new capacity design procedure, based on modified modal properties incorporating the effect of gap-opening, has been proposed. The issues associated with the use of modified modal properties are discussed in detail and a simple, yet effective solution is shown to provide a much better prediction of inelastic seismic responses of these structures.

Appendices

Appendix A: DDBD procedure

Starting point of DDBD procedure is to convert a MDOF structure to an equivalent SDOF structure. Properties of this substitute structure and the overall design procedure is as follows: (Pennucci et al. 2009; Qureshi and Warnitchai 2017).

Design displacement of equivalent structure (${\Delta }_{d}$)

$${\Delta }_{d}=\sum_{k=1}^{n}\left({m}_{k}{\Delta }_{k}^{2}\right)/\sum_{k=1}^{n}\left({m}_{k}{\Delta }_{k}\right)$$

(1)

where ${m}_{k}$ is mass at Kth story, n is the number of total stories and ${\Delta }_{k}$ is design displacement at any Kth story equals to a product of design drift (${\theta }_{c}$) and height (${h}_{k}$) of that story. In this study, a design drift of 2% is selected for the case study structure.

Effective height of equivalent structure (${H}_{e}$)

$${H}_{e}=\sum_{k=1}^{n}\left({m}_{k}{\Delta }_{k}{H}_{k}\right)/\sum_{k=1}^{n}\left({m}_{k}{\Delta }_{k}\right)$$

(2)

Effective mass of equivalent structure (${M}_{e}$)

$${m}_{e}=\sum_{k=1}^{n}\left({m}_{k}{\Delta }_{k}\right)/{\Delta }_{d}$$

(3)

Effective Time period of equivalent structure (${T}_{eff}$)

To find out effective period of the equivalent structure, displacement spectra, design displacement, displacement ductility ratio and equivalent viscous damping (EVD) are required. Displacement ductility ($\mu$) can be calculated by dividing the design displacement (${\Delta }_{d}$) with the yield displacement (${\Delta }_{yk}$) value. Priestley et al. (2007) described the yield curvature (${\upphi }_{y}$) of the wall to be independent of its sectional strength and hence it can be calculated by using the yield strain of longitudinal reinforcement (${\varepsilon }_{y}$) and length of the wall (${L}_{w}$) using the relationship $2{\varepsilon }_{y}/{L}_{w}$. As the rocking wall is designed to remain elastic against the seismic actions, the design curvature (${\upphi }_{b}$) is assumed to be two times the yield curvature. The yield/gap-opening displacement of a rocking wall is composed of two parts: the flexural component (${\Delta }_{yk\_flex})$ and the rocking component (${\Delta }_{yk\_rock})$ (rigid body motion) and can be calculated by using the relationships proposed by Pennucci et al. (2008) as shown in Eqs. 4, 5 and 6.

$${\Delta }_{yk}={\Delta }_{yk\_flex}+{\Delta }_{yk\_rock}$$

(4)

$${\Delta }_{yk\_flex}=0.5{\phi }_{b}.\left[{H}_{k}^{2}-\frac{{H}_{k}^{3}}{2.{H}_{r}}+\frac{{H}_{k}^{5}}{20.{H}_{r}^{3}}\right]$$

(5)

$${\Delta }_{yk\_rock}=\frac{{\varepsilon }_{y}.\left({l}_{ub}+2.{\Delta }_{sp}\right)}{\left({L}_{w}-a-{d}_{ED}\right)}.{H}_{k}$$

(6)

where ${l}_{ub}, {\Delta }_{sp}, a$ and ${d}_{ED}$ are the unbonded length of mild steel bars, strain penetration in ED bars during yielding, neutral axis depth and distance from the center of the ED bars to the tension face, respectively.

Next step is to calculate the EVD using the displacement ductility and the hysteresis behavior. Rocking walls with external energy dissipation mechanism (ED bars) have been found to exhibit flag-shaped hysteresis behavior. The case study rocking wall in the current study is designed such that the ratio of the moment capacity contributed by PT steel plus the gravity load carried by the wall and the moment capacity provided by energy dissipation bars ($\lambda$) is 1.25. The relationship for calculating the EVD for a rocking wall with flag-shaped hysteresis (${\xi }_{FS})$ and with $\lambda$ equal to 1.25 is given in Eq. 7 (Pennucci et al., 2008).

$${\xi }_{FS}=5\%+0.524.\frac{\mu -1}{\mu .\pi }$$

(7)

Using the values of different parameters discussed above, ${T}_{eff}$ can be calculated from response spectrum.

Effective stiffness of equivalent structure (${K}_{e}$)

$${k}_{e}=\frac{4\pi .{M}_{e}}{{T}_{e}^{2}}$$

(8)

Base shear (${V}_{b}$) and floor forces

$${V}_{b}={K}_{e}.{\Delta }_{d}$$

(9)

$${{F}_{k}={V}_{b}.m}_{k}{\Delta }_{k}/\sum_{k=1}^{n}{m}_{k}{\Delta }_{k}$$

(10)

Once the design forces are known, design of structural members is conducted. The final step is to provide capacity protection to the designed structure.

Appendix B: Capacity design procedures

First capacity design procedure used in this study is modified modal superposition (MMS) procedure which is based on combining the individual modal responses to total response. It is based on the understanding that against increasing seismic intensity, only the first mode goes into nonlinear range causing a saturation of seismic demands while the higher modes remain in linear elastic range. The shear profile can be determined by combining the intensity-independent first mode shear with intensity-dependent elastic shear demand of higher modes by using square root sum of squares (SRSS) approach. Moment profile is calculated same as shear except that the moment values are multiplied by an overstrength factor (${\varnothing }^{o}$) of 1.1 and the moment profile is then created by joining the mid-height demand and the base design demand with a straight line while the values in the upper half are directly taken from the SRSS results (Priestley et al., 2007). Following are the relationships to determine shear and moment profiles.

$${V}_{MMS,k}=\sqrt{\left({V}_{1D,k}^{2}+{V}_{2E,k}^{2}+{V}_{3E,k}^{2}+...\right)}$$

(11)

where ${V}_{MMS,k}$ and ${M}_{MMS,k}$ are the shear and moment at level $k$, ${\varnothing }^{o}$ is the overstrength factor, ${V}_{1D,k}$ and ${M}_{1D,k}$ are the shear and design moment at level $k$. ${V}_{2E,k}$, ${V}_{3E,k}$, ${M}_{2E,k}$ and ${M}_{3E,k}$ are the 2nd and 3rd mode elastic response values of shear and bending moment at story level $k$.

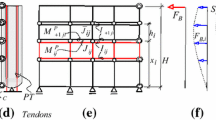
The working and different parameters of the simplified capacity design procedure are explained in Fig. 16. It is important to note that the simplified capacity design procedure is intensity dependent, and the values of ductility and effective time period are calculated separately for the DBE and MCE level seismic hazards resulting in slightly different capacity design values for both cases.

Fig. 16

Simplified capacity design procedure (Qureshi and Warnitchai, 2017)