Abstract
This paper focuses on the optimum design of the e-CLT technology. The e-CLT technology consists in adding cross laminated timber (CLT) walls to an existing reinforced concrete (RC) infilled frame via asymmetric friction connection (AFC). The authors carried out quasi-static and nonlinear dynamic analyses. The RC frame is modeled in OpenSees by fiber-section-based elements with force-based formulation. The contribution of the infill is simulated using a degrading data-driven Bouc–Wen model with a slip-lock element while the AFC is modelled with a modified Coulomb model. Different types of infill, aspect ratio, scaling, and member size are considered. The benefits of using e-CLT technology are discussed and the ranges of optimum performance of the AFC are estimated. A comparison of the performance of traditional infills with the e-CLT system is presented. The authors provide optimum intervals of the ratio between slip force and in-plane stiffness of the CLT panel, following energy and displacement-based criteria. The seismic displacement demand under various seismic scenario is investigated. Correlations between the RC characteristics and the optimum design ratios bestow possible criteria for the design of the AFC.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In seismic-prone areas, many structures lack proper seismic details since they have been designed without proper seismic provisions or before implementing seismic codes and guidelines (Perrone et al. 2019). Demolition of damaged buildings is considered a costly option from economic and environmental points of view (Power 2008). Therefore, the retrofit of existing structures is a widely accepted solution (Asadi et al. 2014). In some instances, an external retrofit can be a preferable option because it does not interfere with the function of the structure. Within external retrofit systems, Bolis et al. (2017), Di Trapani et al. (2020), Takeuchi et al. (2010) introduced the concept of “Integrated Façade” to improve the seismic performance of buildings using seismic energy dissipation devices appended from outside of the building. In this field, there are multiple pieces of research about the use of external structures connected to the main one using dissipating devices, like friction dampers (Jaisee et al. 2021).
This paper examines the design of a novel seismic retrofitting system, named e-CLT, based on an integrated facade concept. The e-CLT technology has been developed within the ongoing Horizon 2020 research project e-SAFE (Margani et al. 2020). Essentially, a RC building is retrofitted by cladding its outer shell with Cross-Laminated Timber Panels (CLT). Each CLT panel, comprised between each bay of the RC frame, has a twofold objective: enhancing the thermal insulation of the building and reducing the seismic demand of the building. The reduction of the seismic demand derives from the connection between the CLT panel and the RC frame. The CLT panels are rigidly connected along the lower side and equipped with an asymmetric friction connection (AFC) on the upper side. Accordingly, the CLT panels are rigidly connected to the frame under low seismic excitation thus providing additional stiffness to the structure. Under higher excitations, the AFC activates and starts dissipating energy, thus enhancing the dissipative capacity of the structure. The combined use of timber and friction connections is a non-secondary aspect of the originality of this retrofitting system.
The popularity of friction dampers is growing in the last years due to their simplicity, reliability, and maximum energy dissipation as a result of the generation of rectangular hysteretic loops (Jaisee et al. 2021). Additionally, their performance is not significantly influenced by the loading amplitude, frequency, and the number of cycles.
The use of friction connections has become extensive in timber engineering since the successful attempts by Filiatrault and Cherry (1990). Furthermore, friction connection is a new frontier in timber engineering since it enhances the resilience of mass timber buildings, severely affected by the pinching phenomena of screwed or nailed connections. The first studies about friction dampers were directed with experimental tests on friction-based devices with hysteresis loop’s rectangular shape (Cho and Kwon 2004), as the Slotted Bolted Connection (Fitzgerald et al. 1989; Popov et al. 1995; Grigorian et al. 1993). Recently, several researchers proposed alternative friction dampers featured by non-rectangular hysteresis curves. In the last decade, several scholars attempted to use friction connections in timber structures. Loo et al. (2014) applied symmetric slip friction connections to replace the traditional nail plate hold-downs for timber Laminated-Veer-Lumber (LVL) walls. Hashemi et al. (2018) extended the study by Loo et al. (2014) to Cross-Laminated Timber (CLT) coupled walls and hybrid timber-steel core walls. Recently, Hashemi et al. (2020) developed an innovative, resilient slip friction joint (RSFJ) characterized by a non-rectangular hysteresis shape.
The e-CLT technology is based on the use of AFC, initially developed by Clifton et al. (2007). The AFC is an arrangement of five plates, three steel plates and two thinner plates named shims, assembled by high strength bolts. The role of the shim material is crucial to achieving a stable hysteresis curve. The use of steel-to-steel friction dampers is not practical, determining erratic hysteresis curves with limited dissipation capacity. The shim material can be either harder or softer than steel. Primary attempts employed brass shims (Grigorian et al. 1993), harder than steel, for slotted bolted connections. Supervening studies by Mackinven et al. (2006) extended the SHJ concept to mild steel and aluminium shims, with lower hardness than steel.
a Components of the e-CLT restoration system: the AFC devices are used to connect CLT panels to the bays without windows of an existing RC frame building; b e-CLT panel subjected to seismic action: the AFC devices present an elongated hole and are clamped together by pre-stressed bolts. When the seismic forces reach a designed threshold the AFC devices starts to slide and dissipates energy via friction and c details of the AFC device. Modified from (Boggian et al. 2022; Tardo et al. 2020)
In the proposed e-CLT system, the authors tested AFC with aluminium shims, which exhibited significant stability compared to other shim materials, like brass.
Figure 1 illustrates the e-CLT system. The RC building is partially cladded with CLT panels connected to the RC beams by steel profiles. The bottom profile has slotted holes and is connected to the upper one by pre-tensioned high strength bolts. Standard timber screws connect both the upper and bottom profile to the CLT panels.
The studies about the e-CLT systems are still embryonal, and no author focused on the practical application of this solution to an existing RC building. This paper focuses on the preliminary design of the elementary unit of the e-CLT, i.e. a single bay RC frame equipped with the AFC and the CLT panel. Specifically, the paper investigates the optimum design of the e-CLT by proposing the mathematical description of this system and determining the optimal slip force in the AFC, which guarantees the best enhancement of the seismic performance.
The theme of slip force optimization is peculiar of structural systems with friction dampers and derives from the following elementary observation. For a very high value of slip load, the stick phase will be the dominant phase without slipping, and there will be zero energy dissipation due to friction. On the other hand, for a very low value of slip load, the amount of energy dissipated will be negligible. Therefore, a friction damper must be tuned between those two boundaries to maintain the optimum slip load for maximum energy dissipation.
The optimum slip load depends on the characteristics (amplitude and frequency) of the ground motion (Filiatrault and Cherry 1990; Miguel et al. 2016; Nabid et al. 2021) and the characteristics of the structures where the friction damper is installed (Taiyari et al. 2019). As remarked by Jaisee et al. (2021), this evidence conflicts with other studies in which observations were based on a limited number of numerical studies (Pall 1986, 1987). According to the recent state-of-art review (Jaisee et al. 2021), there are 14 research papers about friction damper optimization from 1989 to 2021. None of them addresses parametric analyses of RC frames equipped with friction dampers by modelling different structural geometries and including the role of the infill or the aspect ratio (Nabid et al. 2020). Additionally, the mentioned research adopted simplified constitutive models for concrete, and using an elementary Coulomb-like friction model, often inadequate in modelling the cyclic response of actual AFCs, as extensively discussed in the following sections (Golondrino et al. 2012). Non-secondarily, the researches on friction dampers optimize the slip force in friction devices in case of retrofitting systems different from the e-CLT, i.e. there is no contribution of the CLT panel. The limits of these studies and the originality of the e-CLT system support the investigation of the effect of RC frame characteristics on the optimization of the slip force in the e-CLT system.
The authors modelled the RC frame in OpenSees using fiber-section elements with distributed plasticity, while a degrading Bouc–Wen term with a slip-lock element, calibrated on several experimental data sets published in the past years (Basha and Kaushik 2016; Cavaleri and Di Trapani 2014a; Colangelo 2005; Kakaletsis and Karayannis 2008; Mansouri et al. 2014; Mehrabi et al. 1996; Morandi et al. 2018), reproduces the cyclic response of the infill. Furthermore, the AFC is modelled by a modified Coulomb model calibrated on the experimental cyclic responses of the AFCs tested by the authors in the Norwegian University of Life Sciences laboratories (Boggian et al. 2022). The seismic performance of the e-CLT system has not been investigated so far. Therefore, the paper focuses on the structural performance of a structural archetype, a single bay single-story frame, to thoroughly understand the design aspects of the e-CLT system. The main novelties of this research are:
-
Proposal of a mathematical model of the e-CLT system and optimization of the AFC slip force in RC structural archetypes distinguished by different geometrical, constructive and mechanical features.
-
Comparison between structural optimization from quasi-static and nonlinear dynamic analyses, based on energy and drift optimization, respectively.
-
Correlation between the features of the RC structure and the results of optimization.
-
Estimation of the effects of the infill on the structural performance of the e-CLT.
The paper’s main objective is the proposal of a design procedure for the AFC, based on the RC frame typology and the stiffness of the CLT panel connections. In addition, the authors aim to assess the effect of the RC frame infill, often challenging to predict, on the proper design of the slip force.
The paper has the following organization. Section 2 presents the mathematical modelling of the e-CLT system. Section 3 describes the experimental tests and modelling of the hysteresis of the AFC. Section 4 presents the hysteresis models for RC frame and infill panel, while in Sect. 5 the model for the CLT panel is described. Sections 6 and 7 deal with the results of the slip force optimization from quasi-static and nonlinear dynamic analyses, respectively. A parametric study is also presented in Sect. 7, where the optimization is carried out under different choices of the aspect ratio of the RC frame.
2 Mechanical response of the e-CLT system
Figure 2 illustrates the elementary unit of the e-CLT system. The CLT panel between the two stories is rigidly connected to the lower RC beam, while an AFC connects the CLT panel to the upper RC beam. During the stick phase, the AFC does not activate, and the total resisting force at the i-th story (\(f_t\)) is the summation of the resisting forces of the CLT panel (\(f_{\text {clt}}\)) and the RC frame (\(f_{\text {rc}}\)). If the reaction of the CLT panel exceeds the slip force (\(f_s\)), the AFC activates, and the total resisting force is the summation of the resisting force of the RC frame and the slip force of the AFC.
The e-CLT unit behaves like a parallel system, whose governing equations are:
The conditional statement on the exceedance of the slip force drives the transition between the two stick and slip phases of the response. This paper examines the quasi-static and dynamic response of the considered system by accurately modelling the response of the RC frame, the AFC and the CLT panel. Figure 3 illustrates the idea behind the optimization of the friction damper.
Qualitative explanation of the design problem: \(k_{clt}\) is the in-plane stiffness of the CLT wall, \(d_y\) and \(d_u\) are the yield and ultimate displacements of the RC frame, \(d_s\) is the slip displacement of the AFC, and \(\delta _f\) is the displacement interval corresponding to the AFC activation
The RC frame possesses its peculiar nonlinear response due to the plasticization of concrete and the local failure of the infill. The backbone curve exhibits a typical nonlinear trend, distinguished by a rigid-elastic phase and a softening phase with prominent plasticization. Conversely, the CLT panel equipped with the AFC behaves like an elasto-plastic oscillator. The overstrength of the rigid connections of the CLT panel to the slip force should guarantee an elastic behaviour up to the attainment of the slip force. If \(k_{\text {clt}}\) is the in-plane stiffness of the CLT panel, the AFC starts activating when the horizontal displacement of the upper beam equals \(d_s=f_s/k_{\text {clt}}\). Therefore, \(\delta _f=d_u-d_s\), where \(d_u\) is the ultimate displacement of the RC frame, identifies the slip phase of the e-CLT.
The target of the optimization problem is the optimization of the slip phase duration. As anticipated in the introduction, the design of the slip phase is an optimization problem. If the slip force is deficient, the energy dissipated by the AFC is also deficient. Conversely, if the slip force is very high, the extension of the slip phase can be limited, thus reducing the energy dissipation. Therefore, the optimum length of the slip phase stands between the two extremities. Furthermore, the lateral stiffness of the CLT panel also plays a crucial role. If \(k_{\text {clt}}\) is much higher than the lateral stiffness of the frame, the structural system will attain the ultimate resistance of the CLT panel without activating the AFC. Therefore, as later remarked, the lateral stiffness of the CLT panel must be comparable with that of the RC frame in order to satisfy the following inequality: \(f_{\text {clt}}<f_{\text {clt},u}\) where \(f_{\text {clt},u}\) is the ultimate resistance of the CLT panel.
3 Experimental tests and modelling of the AFC
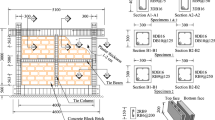
The authors tested the cyclic response of several configurations of the AFC, illustrated in Fig. 4. This research is based on the experimental data of the specimen characterized by the most stable performance, labeled as ALT.3. The full details of the experimental tests are discussed in Aloisio et al. (2022). Figure 4 shows the arrangement of the tested AFC devices. The steel plates are compressed by two M14 bolts with \(A_s\) equal to 115 \(\hbox {mm}^2\) and \(f_{u,b} = 1000\) MPa. The hysteresis loop does not display a pure rectangular shape, as visible in Fig. 5. There is a significant increment of the slip resistance in the first few cycles at lower displacements, while it stabilizes at higher displacement to an almost constant value equal to 30 kN. This effect is not negligible since there is an approximate 56% increment of the peak to the stable value at higher deformations.
Illustration and photo of the parts of a specimen in Boggian et al. (2022)
The modelling of this phenomenon is necessary to achieve a reliable prediction of structural performance.
This aspect is in full accordance with the experimental tests reported by Golondrino et al. (2012). The mutual sliding between the plates determines the reduction of the friction coefficients after multiple cycles.
where \(n_s\) is the number of sliding surfaces, \(n_b\) is the number of bolts, \(f_{s}\) is the slip force, \(f_{p}\) is the preload force.
Coulomb friction governs the cyclic response of the AFC. Therefore, the authors adopted the following definition of the slip force:
where \({\dot{x}}\) is the velocity of deformation, \(\epsilon\) is the dissipated hysteretic energy. The experimental data are used to calibrate the following energy dependent expression of the friction coefficient:
The parameters \(\mu _0\) and \(\xi\), estimated by minimizing the squared error between experimental and numerical data, are equal to 0.33 and 0.00005 respectively The authors chose to develop a physical, rather than empirical hysteresis model to possibly use the model with different preload forces or friction coefficients. A classical Bouc–Wen model does not explicitly depends on the slip force and it does not allow a straightforward extension to other design cases.
Comparison between the experimental data of ALT.3 test of (Boggian et al. 2022) and the Coulomb-like friction model: a Hysteresis loop; b Force-Time function; c Dissipated Energy-time function
Figure 5 shows the comparison between the experimental data of the tested specimen and the simulated ones using Eq. (4). The correspondence is quite accurate despite a minor overestimation of the dissipated energy due to the lacking of the chipping effect (Fitzgerald et al. 2020), i.e. the corner-cutting of the experimental hysteresis curves. However, the hysteresis curve is quite rectangular, and the use of hysteresis models more sophisticated than the proposed one might be unnecessary for engineering purposes. Future research efforts will aim at reproducing the chipping effect by developing a LuGre class friction model (De Wit et al. 1995).
The two estimated values \(\mu _0=0.33\) and \(\xi =0.00005\) are used to simulate the cyclic response of AFCs characterized by different preloads. The results of the parametric analyses are shown in terms of peak slip load:
where \(f_{s,0}\) is the peak slip force and \(\mu _0\) is the peak friction coefficient.
4 Hysteresis model for the infilled RC frame
Mechanics-based models for infilled RC frames were often used to assess their cyclic response (Di Trapani 2021; Preti et al. 2015). However, it was many times discovered that the uncertainties on the hypotheses regarding damage and failure mechanisms lead to erroneous results, that are not consistent with real experiments. For this reason, in the present work the infilled RC frame is modeled using the macro-modeling approach proposed in (Sirotti et al. 2021), which was calibrated and validated on the basis of a large set of experimental data.
The considered macro-model does not aim to provide a detailed mechanical representation of the system, instead to propose a phenomenological description. The model considers the bare frame and the infill as two springs connected in parallel, whose sum of contributions gives the resisting force of the infilled frame. The bare frame and infill experience the same displacement and, accordingly, behave like a parallel system. The fact that their contributions are decoupled does not affect the model’s accuracy because the contribution of the infill panel is calibrated based on actual tests. The hysteresis of the bare frame is obtained with the OpenSees FE simulation. The hysteresis of the infill panel is simulated with a smooth hysteresis equation that combines a degrading Bouc–Wen element with a slip-lock element for pinching effect.
The overall behavior of the infilled frame is obtained as sum of the two contributions (RC frame and infill panel). The advantage of this modeling approach is its simplicity and reliability, since no assumptions on failure of the infill are made and the calibration of the model parameters was based on experimental data.
Six infilled frames with different geometrical and mechanical features were considered (Table 1). Each RC frame and infill panel was modeled with the approaches mentioned above and described in detail in the following paragraphs.
4.1 OpenSees FE model for the RC frames
The single-bay single-storey RC frames were modelled on the OpenSees 2.5.0 software platform, following a classic approach for modelling nonlinear RC frames. A schematic representation of the model is given in Fig. 6. Both beam and columns were modelled using the forceBeamColumn element implemented in OpenSees, namely fiber-section-based nonlinear elements with a force-based formulation. The base of the columns was fixed. A Kent-Scott-Park-type model (Scott 1982) and a Giuffrè-Menegotto-Pinto model (Filippou et al. 1983) were chosen as constitutive laws for concrete and steel, respectively. They are implemented in OpenSees in the library materials Concrete02 and Steel02. Concrete02 material requires four parameters to regulate the behaviour of concrete in compression: peak strength (\(f_{pc}\)), peak strain (\(\epsilon _{c0}\)), ultimate strength (\(f_{pcu}\)) and ultimate strain (\(\epsilon _{u}\)). Confinement of concrete was considered by choosing specific parameters for the core fibers. The tensile concrete strength was neglected. As an example, the constitutive parameters chosen for specimen TA2 by Morandi et al. (2018) are listed in Tables 2 and 3. The vertical loads acting on the columns in the experimental tests were considered by applying two vertical forces at the upper nodes of the columns.
The OpenSees FE model described above was used to predict the contribution of the bare frame. In the following, the hysteresis model for the contribution of the infill is described. It should be noted that, for some of the works listed in Table 1, the experimental data of the cyclic response of the bare frame were available and allowed to validate the OpenSees FE model.
4.2 Bouc–Wen model for the infill panel
The hysteresis of the infill panel is simulated with a smooth hysteresis equation that combines a degrading Bouc–Wen element with a slip-lock element for pinching effect. The hysteresis displacement z(t) is given by the differential equation
where the damage functions are defined as
with damage index \(d_i(t) = \epsilon (t)/(k x_y^2/m) + |x_{max} (t) |/x_y\). The pinching functions of the slip-lock element are
The model parameters (\(\alpha , \beta _0, \eta _0, n, k, x_y, \delta _k, \delta _f, \psi , Z_s, A_s, \epsilon _p\)) were estimated (Sirotti et al. 2021) for each infill panel of the infilled frames listed in Table 1. Using such values for the parameters, the cyclic responses of the infilled panels are predicted. The sum of the infill panel response with the RC frame response gives the behavior of the entire infilled frame. Figure 7 shows the hysteresis curves of two of the specimens considered, compared with the corresponding experimental data available.
5 CLT panel model
In the e-CLT system, the CLT panel is constrained on two sides by AFCs and fixed connectors to the RC beam. The constraint arrangement does not allow the panel rotation and the consequent rocking motion typical of CLT shear walls. Therefore, the overall deformation is given by three possible contributions: the panel sliding, the elastic bending and shear deformation. The sliding motion depends on the timber-connection interaction. However, while the lateral stiffness of a shear-type panel with no sliding is straightforward to predict from elasticity theory, the sliding contribution depends on the arrangement, number and typology of the connections. In the e-CLT system, the CLT panel should not reach the plasticization of the connections. The panel should not experience extensive damage, and the dissipation should be localized in the AFC. Consequently, the authors modelled the CLT panel with an equivalent elastic spring:
where \(f_{\text {clt}}\) is the resisting force of the CLT panel, \(k_{\text {clt}}\) is the secant stiffness and x the horizontal displacement.
The following equation provides the lateral stiffness of a clamped-clamped beam with shear deformability:
where \(k_{\text {clt}}\) is the lateral stiffness, h the panel’s height, E the Young’s modulus, I the cross-section inertia, G the shear modulus and A the cross-section area. The analyses are valid up to the attainment of the ultimate force value of the CLT panel. If the total resisting force exceeds the CLT panel resistance, the e-CLT system does not exhibit proper functioning, and it is not worth of investigation.
In this paper, the authors derive general rules of design of the e-CLT and will not assume a specific connection arrangement. The elastic stiffness of a clamped-clamped CLT panel is approximately equal to 33 kN/mm, corresponding to a square panel, with a 8 cm thickness, characterized by the conventional parameters \(E=11600\) MPa and \(G=450\) MPa (Brandner et al. 2016). The above evidence led the authors to choose a wide range of variation of the CLT panel stiffness equal to 1–100 kN/mm to cover all variabilities in the Young’s modulus and possible effects of sliding deformations.
6 Energy-based optimization from quasi-static analyses
In this section, the authors analyze the quasi-static response of the six infilled frames coupled with an AFC and a CLT panel, as described in Eq. (1). First, the cyclic response of the bare RC frames is coupled with AFC and CLT. Subsequently, the effect of the infill on the cyclic response is introduced through the hysteresis model described in Sect. 4.2. Hence, firstly the term \(f_{\text {rc}}\) of Eq. (1) contains only the RC frame response simulated with OpenSees. Then, the effect of the infill is introduced and term \(f_{\text {rc}}\) becomes the summation of the contributions of both bare frame and infill panel.
6.1 Cyclic response of the bare frames with the e-CLT system
The considered RC structures are the bare frames of the infilled systems with geometrical and typological features reported in Table 1. The applied loading protocols are the ones reported by the authors in the corresponding reference works, listed in Table 1.
The optimization problem consists in the optimum design of the \(\delta _f\) displacement interval, i.e. the extension of the slip phase. The slip phase equals the difference between the ultimate displacement of the RC frame and the displacement value \(d_f=f_s/k_{\text {clt}}\) corresponding to the activation of the AFC. Therefore, \(f_s\) and \(k_{\text {clt}}\) are not considered as independent variables and the analyses are parametrized by the \(f_s/k_{\text {clt}}\) ratio.
Figure 8 illustrates the effect of the AFC and CLT panel on the RC frame of specimen TA2 from Morandi et al. (2018).
Effect of variations of the slip force \(f_{s0}\) on the response of the bare RC frame TA2 (Morandi et al. 2018) coupled with AFC and CLT: a hysteresis response; b energy dissipation and optimal condition
Figure 8a superposes the cyclic response of the e-CLT characterized by different preload values. The inspection of the hysteresis curve reveals that higher slip forces lead to higher resisting force since the total force of the e-CLT system is the summation of that of the RC frame and the AFC. However, Fig. 8b shows that higher slip loads do not always lead to higher dissipated energy. In fact, Fig. 8b shows the variation of the dissipated energy as a function of the \(f_s/k_{\text {clt}}\) ratio, obtained by considering four different stiffness values of the CLT panel: 5, 10, 20 and 40 kN/mm. If the slip force is zero, the dissipated energy corresponds to the one of the RC structure. Conversely, the choice of higher slip forces determines the increment of the shear resistance, the apparent pinching reduction and increment of the dissipated energy. However, if the slip force activates after the approximate yielding point of the RC frame, the dissipated energy reduces. Accordingly, the further increment of the slip force does not lead to the AFC activation, and the dissipated energy equals that of the RC frame without AFC.
The use of higher values of \(k_{\text {clt}}\) leads to higher energy dissipation. Remarkably, the maximum point is invariant to the \(f_s/k_{\text {clt}}\) ratio, which can be chosen as design parameter. The peak of the energy dissipation almost corresponds to the yielding displacement \(x_y\) of the frame
The yielding displacement of the frame is computed as follows:
with \(F_y\) the yielding force of the frame, h the columns height, \(E_c\) the concrete Young’s modulus, \(I_c\) the columns inertia, and c a coefficient established as function of the constraints conditions.
Table 4 shows the optimal values of ratio \(f_{s0}/k_{\text {clt}}\) for the six RC frames considered, along with the theoretical values of \(x_y\) computed with Eq. (13).
For each specimen, there is a good correspondence between the optimal \(f_{s0}/k_{\text {clt}}\) ratio and the yielding displacement \(x_y\). Therefore, the optimal design of the AFC can be done by selecting a ratio \(f_{s0}/k_{\text {clt}}\) as close as possible to the theoretical value of yielding displacement of the RC frame.
6.2 Effect of the presence of the infill
The influence of the infill panel is now investigated by adding its contribution to the cyclic response of the RC frame. The authors expect to observe some variations in the optimum slip load with respect to the proposed expression in Eq. (13). The optimal condition defined in the previous subsection is discussed and analyzed also for the case of RC infilled frames.
The cyclic response of the six RC infilled frames is simulated by summing the contribution of the infill panels to the cyclic response of the bare frames. The hysteresis of the bare frames is obtained with the OpenSees FE simulations, as done in the previous subsection. The hysteresis of the infill panels is simulated with the hysteresis model presented in Sect. 4.2. By summing up these two contributions, the behavior of the infilled frames is obtained.
The system is coupled with AFC and CLT by using Eq. (1), with \(f_{\text {rc}}\) given by the sum of bare frame and infill panel contributions. As in the previous subsection, the authors analyzed the trend of energy dissipation with variations of the \(f_{s0}/k_{\text {clt}}\) ratio. Again it is found that, for each specimen, there is an optimal condition where the energy dissipation is maximum.
Table 4 lists the optimum values of the \(f_{s0}/k_{\text {clt}}\) ratio for the considered six infilled frames. Interestingly, the infill has no manifest effect on the optimum energy dissipation. The percentage difference between the optimum values is always less than 8%. This difference is insignificant for engineering purposes and proves that these results do not contrast with the analyses on bare frames and that the expression for the optimum slip load estimation is also valid in the case of infilled RC frames.
Effect of variations of the slip force \(f_{s0}\) on the response of infilled frames S1A and S1C (Cavaleri and Di Trapani 2014) coupled with AFC and CLT: a hysteresis response, specimen S1A; bhysteresis response, specimen S1C; c energy dissipation, specimen S1A; denergy dissipation, specimen S1C
Essentially, the presence of the masonry infill has two main effects: increasing the lateral stiffness of the frame and, as a consequence, increasing the energy dissipation. However, the major part of the contribution of the infill panel is limited to small displacements, after which failure mechanisms activate. In fact, the hysteresis of infilled frames S1A and S1C (Fig. 9) shows a pronounced degradation after a certain displacement, due to failure of the infill. For the largest part of the typical infilled RC frames, if not all, failure mechanisms of the infill take place before the yielding of the frame. This means that the yielding point of an infilled frame corresponds more or less to the one of the sole RC frame. In light of this, since the optimal condition for energy dissipation of the e-CLT system is found to be close to the yielding displacement, the presence of the infill does not provide a significant change. It goes without saying that the infill produces an increasing in the magnitude of energy dissipation, but in terms of trend with variations of ratio \(f_{s0}/k_{\text {clt}}\) the influence is limited. This fact determines the substantial agreement between the optimal activation displacement of RC frame with and without infill.
The above results demonstrate that the optimal condition for energy dissipation, namely \(f_{s0}/k_{\text {clt}} = x_y\), is not affected by the presence of the infill. It is also interesting to explore the structure’s performance obtained using the e-CLT technology in a RC frame without masonry infill. To this aim, Fig. 10 shows a comparison of cyclic response and energy dissipation of the following three systems: RC frame without infill, infilled RC frame and RC frame with e-CLT but no infill panel (only CLT shear wall).
Comparison between performances of bare RC frame, infilled RC frame and RC frame with e-CLT technology. The specimens considered are S1A and S1C from Cavaleri and Di Trapani (2014): a hysteresis response, specimen S1A; b hysteresis response, specimen S1C; c energy dissipation, specimen S1A; d energy dissipation, specimen S1C
The specimens considered are S1A and S1C from Cavaleri and Di Trapani (2014). The stiffness of the CLT panel is assumed to be \(k_{\text {clt}} = 6\) kN/mm. The optimal slip force is computed as \(f_{s0} = k_{\text {clt}} x_y = 72\) kN.
It is observed that for both specimens, the use of the e-CLT in bare RC frames provides a higher energy dissipation than the masonry infill. Therefore, this system can also be used to substitute the masonry infill. The advantages of using the e-CLT without masonry infill are not limited to incrementing the dissipation performance due to the AFCs. The substitution of the masonry infill with the e-CLT reduces the structural mass and, possibly, the seismic force. However, the benefits in reducing the structural mass cannot be stated a priori and depend on the dynamic interaction between the earthquake and the building response.
In the next section, dynamic analyses will be carried out to observe if there is an optimal condition also in terms of minimization of the drift and, in case, if it corresponds to the optimal design in terms of maximum energy dissipation. Since the quasi-static simulations showed that the infill does not significantly affect the optimal design of the e-CLT system, the authors will carry out the nonlinear dynamic analyses on the sole RC frames.
7 Displacement-based optimization from nonlinear dynamic analysis
This section examines the results of nonlinear dynamic analyses of the considered six RC frames coupled with AFC and CLT panel. The dynamic analyses were entirely carried out in OpenSees. The e-CLT system was modelled by a zero-length element linked to the head of the frame. A perfect elasto-plastic relationship was chosen as constitutive law for the zero-length element. The stiffness of the elastic branch corresponds to the elastic stiffness of the CLT panel, whereas the yielding force corresponds to the peak slip force of the AFC connector. Due to the choice of this simple constitutive law, the cyclic degradation of the slip force was neglected during the dynamic analyses. However, as depicted in Fig. 5, degradation in the AFC system is not very pronounced and therefore this assumption gives a sufficiently accurate simulation of the dynamic response of the structure.
The model for the RC frame is the same as described in Sect. 4.1. The equilibrium equation under ground motion excitation is integrated with the Newmark method. The mass is concentrated at the upper nodes of the frame and it corresponds to the vertical loads applied at the top of the columns during the experimental tests. The dynamic analyses are carried out to assess the slip force which guarantees the lowest inter-storey drift. It must be remarked that any structure is a stand-alone case and deserves dedicated analyses. However, the investigation of this elementary model supports a mindful assessment of the optimum ranges to be expected in more complicated structures.
In contrast with the previous section, the displacement is unknown and must descend from the numerical integration of the equilibrium equation.
The authors selected seven earthquakes, listed in Table 5, representative of diverse seismic scenarios (Aloisio et al. 2021; Pagliaro et al. 2020). This section aims to compare the response of the e-CLT under quasi-static and nonlinear dynamic analyses. Therefore, the authors used a reduced number of earthquakes to comment the structural response under each of them.
Figure 11 shows the cyclic response of specimen TA2 to El Centro earthquake under variations of the peak slip force.
The parallel nature of the structural system determines a reduction of the displacement demand under increasing slip loads. Higher slip loads are associated with a reduction of the dissipated energy and an increment of the natural frequency. Asymptotically, if the slip loads tends to infinity, the AFC never activates and the system behaves like an RC frame infilled with a CLT panel.
The authors estimated the response of the considered six RC frames by varying the \(f_{s0}/k_{\text {clt}}\) ratio and the seismic excitation. Each of the seven earthquakes was scaled so that the maximum displacement reached by the RC frame has the same magnitude of the one reached in the quasi-static analysis. The authors made this choice for two reasons. Firstly, the OpenSees model of the RC frame was validated on quasi-static experimental tests. There is not evidence that the model is still accurate if the displacement increases further. Secondarily, the seismic excitation was scaled to observe enough damage and degradation associated with the attainment of the yielding point of frames.
Figure 12 summarizes the outcome of nonlinear dynamic analyses by plotting the maximum displacement attained by the seismic response of the six specimens under different earthquakes and \(f_{s0}/k_{\text {clt}}\) ratios.
Dynamic simulations with OpenSees showing the displacement demand (\(x_{\text {max}}\)) as a function of the slip ratio for a Spec. TA2, b Spec. S1A, c Spec. S1C, d Spec. 5, e Spec. 6, f Spec. S. The vertical dotted line indicates the optimal activation displacement from quasi-static tests (\(x_{\text {opt}}\)), while the continuous line marks the yielding displacement of the frame (\(x_{y}\))
The curves corresponding to each earthquake are pretty different and show that the optimum values obtained from an energy-based optimization do not match exactly with those from the displacement demand reduction.
In all considered scenarios, small increments of the slip load from 0 determine a significant reduction of the displacement demand. However, there are two opposing trends as the slip load further increases. In some instances (e.g., L’Aquila, Northridge, Kobe), the displacement demand remains constant. Under different earthquakes (e.g., El Centro, Parkfield), the displacement demand exhibits a zone of minima followed by constant values. Additionally, the presence of a more evident interval of minima does not feature all samples under the same earthquake.
As shown in Fig. 12, the minimum points, where present, are associated with \(f_{s0}/k_{\text {clt}}\) ratios lower than the ones obtained from the dissipated energy maximization (\(x_\text {opt}\)), indicated by vertical lines. In conclusion, the curves in Fig. 12 prove that:
-
The response of the e-CLT system is significantly affected by the seismic scenario. This result is in full accordance with the research papers by Kim and An (2017), Miguel et al. (2018), Taiyari et al. (2019) on friction damper optimization.
-
The optimum \(f_{s0}/k_{\text {clt}}\) ratio obtained from the maximization of the dissipated hysteretic energy is generally higher that the \(f_{s0}/k_{\text {clt}}\) ratios associated with a lower displacement demand. The optimum \(f_{s0}/k_{\text {clt}}\) ratio, dotted line in Fig. 12, obtained from quasi-static tests, approximately corresponds to the yielding displacement of the frame, solid line in Fig. 12. These values are generally beyond the ranges of minima observed in nonlinear dynamic analyses.
-
After reaching a minimum, the displacement demand never reduces as the \(f_{s0}/k_{\text {clt}}\) ratio grows. It is either stable or grows again slightly.
The second observation is justified by the different nature of the optimizations performed. The plastic range of the frame is the region where both large displacements and high energy dissipation occur. In the quasi-static tests, the goal is to maximize the dissipated energy. Therefore, the optimum value of \(f_{s0}/k_{\text {clt}}\) almost coincides with the yielding displacement of the frame to fully exploit the plastic branch and the dissipation capacity of the e-CLT system. Instead in the nonlinear dynamic analyses the purpose is to minimize the displacement demand. Thus, the damper activates before the yielding displacement of the frame to reduce the plastic excursion and the displacement demand. This is why in the dynamic analyses the minimum displacement demand is found for lower values of the \(f_{s0}/k_{\text {clt}}\) ratio.
As pointed out in the third observation, after a certain value of slip load further increments do not affect the displacement demand, or cause only a slight increase. Consequently, the designer has a large margin for the choice of the design slip load, and the simplified expression for the estimate of optimum slip load in Eq. (14) can be considered valid. Actually, by observing Fig. 12, one can notice that in most cases, the yielding displacement \(x_y\) is closer to the minimum displacement demand than the optimum displacement \(x_{opt}\) obtained from energy maximization. This evidence proves that, for dynamic excitations, the proposed design criterion based on the yielding displacement of the frame can be more beneficial than the value \(x_{opt}\), corresponding to the maximization of the dissipated energy in the quasi-static analyses. Finally, it is worth mentioning that the extensive range of minima for the displacement demand guarantees that inaccuracies in the preload application do not significantly affect the optimal performance of the AFC.
7.1 Parametric analysis of the aspect ratio of the frame
The above analyses refer to RC frames characterized by a specific geometry corresponding to the experimental tests. Theoretically, the range of the optimal design displacement, estimated from dynamic simulations, could be affected by the geometrical features of the frame, like the aspect ratio. Variations of the aspect ratio, calculated as the ratio between height and width of the structure, determine a different force distribution between beam and columns. Specifically, the columns height is kept constant, while the beam length is subjected to variations. A decrease in the value of the aspect ratio leads to a decrease of the frame’s lateral stiffness. This because, given the same columns height, a longer beam determines a reduction of the rotation constraint at the beam-column joints. On the other hand, a shorter column causes an increment of the stiffness of the frame. Given the above, it is expected that the displacement demand under earthquake excitation is influenced by variations of the aspect ratio. In particular, lower values of the aspect ratio should decrease the displacement demand, and vice versa.
The authors varied the aspect ratio in the range 1–0.5. In this range, typical of existing buildings, the failure mechanism of the frame does not change since it is mostly driven by the failure of the column base joints. Accordingly, the ductility of the frame is substantially invariant to the aspect ratio in the considered range.
Figure 13 shows the demand displacement of the frame TA2 shaped by different aspect ratios from 1 to 0.5 under the seven earthquakes from (a) to (e), respectively. The trend of the curves shape does not meaningfully depend on the aspect ratio. Higher aspect ratios only determine a curve shift upwards due to a reduction of the lateral stiffness.
As remarked in the previous paragraph, the aspect ratio does not significantly modify the inelastic response of the frame since the failure modes of the frame do not change. Therefore, the shape of the hysteresis curve does not change, and the aspect ratio variations do not contradict the design considerations discussed in the previous sections. Static-load tests reveal an activation displacement associated with the highest energy dissipation, almost corresponding to yielding displacement of the frame. However, the nonlinear dynamic analyses showed that there is not a specific, optimal activation displacement. Conversely, there is a broader region, in some instances centred by the yielding displacement, associated with the highest demand reduction, although significantly affected by the seismic excitation.
In conclusion, the yielding displacement of the frame can be considered as target parameter for the estimation of the design slip force, given the value of the lateral stiffness of the CLT panel. The results of the above analyses suggest the following expressions of the optimum peak slip load:
where \(f_{s0,\text {design}}\) is the design slip force, \(x_y\) is the yielding displacement of the RC frame, \(f_{\text {clt}}\) the resisting force of the CLT panel and \({f_{\text {clt},u}}\) its ultimate resistance, \(\gamma\) is a safety factor, and \(k_{\text {clt}}\) the lateral stiffness of the CLT panel. Eq. (14) summarizes the outcomes of the current analyses. The product between the lateral stiffness of the CLT panel and the yielding displacement of the RC frame must not exceed the ultimate resistance of the CLT panel. Otherwise, the proposed retrofitting system is ineffective. In that case, the optimum slip force can be set equal to the ultimate resistance of the CLT panel, reduced by an adequate safety factor. If the product \(k_{\text {clt}} x_y\) is below the ultimate resistance of the CLT panel, the yielding value of the RC frame can be used to estimate the optimum slip load.
8 Conclusions
The e-CLT technology aims at improving the seismic performance of existing RC structures using an external retrofitting system based on CLT panels and asymmetric friction connections (AFC). This paper discusses the practical application of the e-CLT system by simulating the quasi-static and dynamic response of RC frames equipped with the mentioned retrofitting system. The authors assessed the dependence of the optimum slip force, i.e. the slip force associated with the highest dissipation and displacement demand reduction, under variations of the RC frame characteristics. The AFC is simulated using an improved Coulomb-like model calibrated on experimental data. The CLT panel is modelled by an equivalent linear elastic spring. The model for the RC frame is developed in OpenSees and the masonry infill is modelled using the Bouc–Wen data-driven hysteresis model proposed in Sirotti et al. (2021). The results of the analyses showed that:
-
The hysteresis curve of the e-CLT archetype depends on the ratio between the slip force and the lateral stiffness of the CLT panel. However, the maximum of the dissipated energy is independent on the ratio between the slip force and the lateral stiffness of the CLT panel.
-
The optimal activation displacement estimated from quasi-static tests almost coincides with the yielding displacement of the frame.
-
The optimal slip force does not significantly depend on the presence of the infill of the RC frame.
-
The nonlinear dynamic analysis under earthquake excitation revealed a wide range, almost centered by the yielding displacement, associated with a reduced displacement demand with respect to the structure without e-CLT retrofitting.
-
The displacement demand is strongly affected by the nature of earthquake excitation, as proved by comparing the system response under seven selected earthquakes.
-
The results of nonlinear dynamic analyses are also confirmed by additional parametric analyses under variations of the aspect ratio of the frame. The optimal ranges of the slip force are not affected by the aspect ratio of the frame.
In conclusion, the yielding displacement of the frame can be considered as a target parameter for the estimation of the design slip force, given the value of the lateral stiffness of the CLT panel:
where \(f_{s0,\text {design}}\) is the design peak slip force, \(x_y\) the yielding displacement of the frame and \(k_{\text {clt}}\) the lateral stiffness of the CLT panel. Hence, the outcome of this research is a criterion for the optimal use of the e-CLT technology. This is useful in practical applications for estimating the design slip force, given the lateral stiffness of the CLT panel. The initial stiffness of the CLT panel depends on its height, width, and thickness, which can be selected based on the target thermal insulation. Therefore, the initial stiffness of the CLT panel can be considered a fixed parameter, while the slip force is the design one to be optimized following the proposed procedure.
The main advantages of the e-CLT system compared to traditional infills are higher seismic and thermal performances. The proposed system can dissipate more hysteretic energy than traditional masonry infills due to the presence of the AFCs. Further, the use of solid timber guarantees a satisfactory thermal performance without the need of additional insulating coatings. The possible drawback of this structural solution is the degradation of the AFCs, typical of all friction connections, and the higher care in the construction phase, especially in the bolts pre-loading. Additionally, the comparison between the cyclic response of a traditional infill and the cyclic response of the e-CLT system in terms of force-displacement and dissipated energy proves that the use of the e-CLT system is beneficial and provides a better performance in terms of dissipated energy, also in absence of the masonry infill.
The paper follows a component-based approach since there are no experimental tests of an RC frame equipped with CLT panel and AFC connectors. The experimental tests of the entire structural assembly will be carried out in the future within the framework of the Horizon 2020 research project e-SAFE.
Availability of data and material
All data, models, or code that support the findings of this study are available from the corresponding author upon reasonable request.
References
Aloisio A, Pelliciari M, Alaggio R, Nuti C, Fragiacomo M, Briseghella B (2021) Structural robustness of an rc pier under repeated earthquakes. Proceedings of the institution of civil engineers-bridge engineering (pp 1–20)
Aloisio A, Boggian F, Tomasi R (2022) Design of a novel seismic retrofitting system for rc structures based on asymmetric friction connections and clt panels. Engineering Structures 254:113807. https://doi.org/10.1016/j.engstruct.2021.113807
Asadi E, da Silva MG, Antunes CH, Dias L, Glicksman L (2014) Multi-objective optimization for building retrofit: a model using genetic algorithm and artificial neural network and an application. Energy Build 81:444–456
Basha SH, Kaushik HB (2016) Behavior and failure mechanisms of masonry-infilled rc frames (in low-rise buildings) subject to lateral loading. Eng Struct 111:233–245
Boggian F, Tardo C, Aloisio A, Marino EM, Tomasi R (2022) Experimental cyclic response of a novel friction connection for seismic retrofitting of RC buildings with CLT panels. J Struct Eng. https://doi.org/10.1061/(ASCE)ST.1943-541X.0003313
Bolis V, Stavridis A, Preti M (2017) Numerical investigation of the in-plane performance of masonry-infilled rc frames with sliding subpanels. J Struct Eng 143(2):04016168
Brandner R, Flatscher G, Ringhofer A, Schickhofer G, Thiel A (2016) Cross laminated timber (clt): overview and development. Eur J Wood Wood Prod 74(3):331–351
Cavaleri L, Di Trapani F (2014) Cyclic response of masonry infilled rc frames: experimental results and simplified modeling. Soil Dyn Earthq Eng 65:224–242
Cho CG, Kwon M (2004) Development and modeling of a frictional wall damper and its applications in reinforced concrete frame structures. Earthq Eng Struct Dyn 33(7):821–838
Clifton G, MacRae G, Mackinven H, Pampanin S, Butterworth J (2007) Sliding hinge joints and subassemblies for steel moment frames. Palmerston north, New Zealand: Proc of new zealand society for earthq eng conf
Colangelo F (2005) Pseudo-dynamic seismic response of reinforced concrete frames infilled with non-structural brick masonry. Earthq Eng Struct Dyn 34(10):1219–1241
De Wit CC, Olsson H, Astrom KJ, Lischinsky P (1995) A new model for control of systems with friction. IEEE Trans Autom Control 40(3):419–425
Di Trapani F (2021) A novel data-driven force-displacement macro-model for nonlinear analysis of infilled frames: development, validation and reliability comparison. Bull Earthq Eng 19(14):6157–6186
Di Trapani F, Bolis V, Basone F, Preti M (2020) Seismic reliability and loss assessment of rc frame structures with traditional and innovative masonry infills. Eng Struct 208:110306
Filiatrault A, Cherry S (1990) Seismic design spectra for friction-damped structures. J Struct Eng 116(5):1334–1355
Filippou FC, Popov EP, Bertero VV (1983) Effects of bond deterioration on hysteretic behavior of reinforced concrete joints. Report EERC 83–19
Fitzgerald D, Miller TH, Sinha A, Nairn JA (2020) Cross-laminated timber rocking walls with slip-friction connections. Eng Struct 220:110973
Fitzgerald T, Anagnos T, Goodson M, Zsutty T (1989) Slotted bolted connections in aseismic design for concentrically braced connections. Earthq Spectra 5(2):383–391
Golondrino JC, MacRae G, Clifton C (2012) Behaviour of asymmetrical friction connections using different shim materials. Proceedings of the New Zealand society for earthquake engineering conference
Grigorian CE, Yang TS, Popov EP (1993) Slotted bolted connection energy dissipators. Earthq Spectra 9(3):491–504
Hashemi A, Bagheri H, Yousef-Beik SMM, Darani FM, Valadbeigi A, Zarnani P, Quenneville P (2020) Enhanced seismic performance of timber structures using resilient connections: full-scale testing and design procedure. J Struct Eng 146(9):04020180
Hashemi A, Zarnani P, Masoudnia R, Quenneville P (2018) Experimental testing of rocking cross-laminated timber walls with resilient slip friction joints. J Struct Eng 144(1):04017180
Jaisee S, Yue F, Ooi YH (2021) A state-of-the-art review on passive friction dampers and their applications. Eng Struct 235:112022
Kakaletsis DJ, Karayannis CG (2008) Influence of masonry strength and openings on infilled r/c frames under cycling loading. J Earthquake Eng 12(2):197–221
Kim J, An S (2017) Optimal distribution of friction dampers for seismic retrofit of a reinforced concrete moment frame. Adv Struct Eng 20(10):1523–1539
Loo WY, Kun C, Quenneville P, Chouw N (2014) Experimental testing of a rocking timber shear wall with slip-friction connectors. Earthq Eng Struct Dyn 43(11):1621–1639
Mackinven H (2006) Sliding hinge joint for steel moment frames experimental testing. ENCI 493 Project Report. Department of Civil Engineering, University of Canterbury
Mansouri A, Marefat MS, Khanmohammadi M (2014) Experimental evaluation of seismic performance of low-shear strength masonry infills with openings in reinforced concrete frames with deficient seismic details. Struct Des Tall Spec Build 23(15):1190–1210
Margani G, Evola G, Tardo C, Marino EM (2020) Energy, seismic, and architectural renovation of rc framed buildings with prefabricated timber panels. Sustainability 12(12):4845
Mehrabi AB, Benson Shing P, Schuller MP, Noland JL (1996) Experimental evaluation of masonry-infilled rc frames. J Struct Eng 122(3):228–237
Miguel LFF, Miguel LFF, Lopez RH (2016) Failure probability minimization of buildings through passive friction dampers. Struct Design Tall Spec Build 25(17):869–885
Miguel LFF, Miguel LFF, Lopez RH (2018) Methodology for the simultaneous optimization of location and parameters of friction dampers in the frequency domain. Eng Optim 50(12):2108–2122
Morandi P, Hak S, Magenes G (2018) Performance-based interpretation of in-plane cyclic tests on rc frames with strong masonry infills. Eng Struct 156:503–521
Nabid N, Hajirasouliha I, Margarit DE, Petkovski M (2020) Optimum energy based seismic design of friction dampers in rc structures. Structures 27:2550–2562
Nabid N, Hajirasouliha I, Petkovski M (2021) Simplified method for optimal design of friction damper slip loads by considering near-field and far-field ground motions. J Earthq Eng 25(9):1851–1875
Pagliaro S, Aloisio A, Alaggio R, Di Egidio A (2020) Rigid block coupled with a 2 dof system: numerical and experimental investigation. Coupled Syst Mech 9(6):539–562
Pall A (1986) Energy dissipation devices for aseismic design of buildings. Proceedings of a seminar and workshop on base isolation and passive energy dissipation, pp 223–232
Pall A, Verganelakis V, Marsh C (1987) Friction dampers for seismic control of concordia university library building. Fifth Canadian conference on earthquake engineering, Ottawa, pp 191–200
Perrone D, Calvi P, Nascimbene R, Fischer E, Magliulo G (2019) Seismic performance of non-structural elements during the 2016 central Italy earthquake. Bull Earthq Eng 17(10):5655–5677
Popov EP, Grigorian CE, Yang TS (1995) Developments in seismic structural analysis and design. Eng Struct 17(3):187–197
Power A (2008) Does demolition or refurbishment of old and inefficient homes help to increase our environmental, social and economic viability? Energy Policy 36(12):4487–4501
Preti M, Migliorati L, Giuriani E (2015) Experimental testing of engineered masonry infill walls for post-earthquake structural damage control. Bull Earthq Eng 13(7):2029–2049
Scott BD, Park R, Priestley MJ (1982) Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rates. J Proc 79:13–27
Sirotti S, Pelliciari M, Di Trapani F, Briseghella B, Carlo Marano G, Nuti C, Tarantino AM (2021) Development and validation of new bouc-wen data-driven hysteresis model for masonry infilled rc frames. J Eng Mech 147(11):04021092
Taiyari F, Mazzolani FM, Bagheri S (2019) Damage-based optimal design of friction dampers in multistory chevron braced steel frames. Soil Dyn Earthq Eng 119:11–20
Takeuchi T, Yasuda K, Iwata M (2010) Seismic retrofitting using energy dissipation façades. In: ATC and SEI conference on improving the seismic performance of existing buildings and other structures in December 9–11, 2009 San Francisco, California, pp 1000–1009
Tardo C, Boggian F, Hatletveit M, Marino E, Margani G, Tomasi R (2020) Mechanical characterization of energy dissipation devices in retrofit solution of reinforced concrete frames coupled with solid wood panels. Proceedings of the 12th international conference on structural analysis of historical constructions
Funding
Open access funding provided by Norwegian University of Life Sciences. This paper was carried out in the framework of the “Energy and seismic affordable renovation solutions” (e-SAFE) project, which has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No.893135. Neither the Executive Agency for Small and Medium-sized Enterprises (EASME) nor the European Commission is in any way responsible for any use that may be made of the information it contains.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
No potential competing interest was reported by the authors.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Aloisio, A., Pelliciari, M., Sirotti, S. et al. Optimization of the structural coupling between RC frames, CLT shear walls and asymmetric friction connections. Bull Earthquake Eng 20, 3775–3800 (2022). https://doi.org/10.1007/s10518-022-01337-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10518-022-01337-8