1 Introduction

Incremental dynamic analysis (IDA) is a parametric analysis method used for seismic assessment of structures (Vamvatsikos and Cornell 2002). IDA involves a structural model being subjected to an ensemble of ground motion records, each scaled to multiple intensity levels, covering a wide range of structural behavior from elastic domain to global instability. The results of IDA are generally presented as curves of maximum responses parameterized versus the intensity measure.

Since IDA entails numerous nonlinear dynamic analyses (NDA), the computational burden involved is known to be the main disadvantage to this method, especially in tall buildings comprising a large number of nonlinear structural elements. Hence, approximate procedures have been proposed in the literature aiming at reducing the computational cost associated with IDA.

By exploring the relationship between the static pushover (SPO) and the IDA outcomes through parametric studies, Vamvatsikos and Cornell (2005) developed the SPO2IDA method to predict approximate 16th, 50th, and 84th percentile IDA curves. The procedure was recently employed to produce structure-specific fragility curves (Baltzopoulos et al. 2017). Designed for the first-mode dominated structures, SPO2IDA is not expected to maintain high levels of accuracy in high-rise or asymmetric buildings. Han and Chopra (2006) proposed an incremental version of the well-known modal pushover analysis (MPA) (Chopra and Goel 2002) to produce approximate IDA curves. This method has the advantage of considering the contribution of higher modes. However, the distortions occasionally encountered in capacity curves of higher modes often cause disruption in the process of MPA (FEMA 2005). This is especially the case when the building is subjected to ground motion records causing significant nonlinearity in higher modes. Dolšek and Fajfar (2004) introduced an incremental version of the N2 method (Fajfar 2000), called IN2, to predict approximate IDA curves, which showed reasonable accuracy in assessing in-filled concrete frames. Using a precedence list of ground motion records, Azarbakht and Dolšek (2007) developed a procedure to reduce the number of ground motion records required to predict median IDA; the procedure starts with the calculation of the IDA curve for the first ground motion record in the list then advances progressively through the list until an acceptable tolerance is achieved. The authors later extended the method to predict summarized IDA curves, i.e., the 16, 50, and 84th fractiles (Azarbakht and Dolšek 2011). Brozovič and Dolšek (2014) presented the envelope-based pushover analysis in which a pushover analysis is conducted for each mode, and the total demands are determined by enveloping the results obtained from all pushover analyses performed. A web-based methodology was also introduced by Peruš et al. (2013a, b). The method was tested on a 4-story RC building, achieving good estimates of the exact IDA curves.

A few studies in the literature have addressed asymmetric-plan buildings. Dolšek and Fajfar (2007) evaluated the IN2 method on a three-story asymmetric reinforced concrete structure and concluded that the method is viable in assessing plan-asymmetric buildings. Based on the 2DMPA method (Lin and Tsai 2007), Birzhandi and Halabian (2017) developed an approximate IDA procedure for plan-asymmetric structures, allowing for the hysteresis characteristics of structures such as pinching, strength loss, and stiffness deterioration. The authors later extended the method to take soil‑structure interactions into account (Birzhandi and Halabian 2018, 2020).

The only approximate IDA method to address biaxial seismic excitations in asymmetric-plan buildings was "bidirectional energy-based pushover" (BEP) (Soleimani et al. 2018). Biaxial IDA has demonstrated its value in assessment of 3D structures (Lagaros 2010; Kostinakis and Athanatopoulou 2016). While symmetric buildings could be assessed independently along x- and y-directions, it is essential for asymmetric-plan buildings to be evaluated under both components of ground motions simultaneously. This is because the two horizontal components could neutralize or amplify each other's effect when applied simultaneously. Conventional pushover procedures analyze the structures for x and y-components of ground motions separately, then combine the results using the SRSS combination rule (Reyes and Chopra 2011; Soleimani et al. 2017). The basic assumption behind SRSS is that there is no correlation between the two horizontal components and nor between their effects (Reyes-Salazar et al. 2012, 2016), which is unrealistic in asymmetric-plan buildings. Relevant studies on the accuracy of this method have reported inaccuracy of the results, especially for inelastic systems (Reyes-Salazar et al. 2004). The BEP formulation addresses this issue by allowing for both components of ground motions to be applied simultaneously, and SRSS is removed from the process.

The BEP method can be summarized in three steps. Firstly, modal capacity curves—i.e., the force–deformation relationships for modal single-degree-of-freedom (SDF) systems—are established from energy-based modal pushover analyses. Secondly, each SDF system is subjected to a combination of the two horizontal components of the ground motion, and the peak responses are extracted. Finally, the corresponding structural responses are combined using a modified CQC formula.

The energy-based pushover approach employed in the BEP is a technique to prevent the distortion of capacity curves. The conventional pushover methods use the roof displacement during pushover analysis as an index to derive the displacement of the corresponding SDF system. The same goal is achieved in the energy-based pushover using the absorbed energy rather than roof displacement throughout the pushover analysis. The method was first proposed by Hernandez-Montes et al. (2004) for two-dimensional structures and extended to asymmetric-plan buildings by Soleimani et al. (2017). The energy-based pushover also found application in the assessment of structures exposed to other load scenarios rather than earthquakes (Saedi Daryan et al. 2017; Saedi-Daryan et al. 2018).

The usefulness of BEP has been demonstrated in the previous research (Soleimani et al. 2018) through the assessment of a three-story asymmetric building. However, its suitability for taller buildings is still unknown. While the first triple modes are adequate to estimate the demands of low-rise buildings, the dynamic response of tall buildings is strongly influenced by higher modes, which poses a challenge to BEP. When the building plan is asymmetric, the torsional motions are also involved, adding to the complexity of the structural behavior.

This study aims to evaluate BEP for medium- and high-rise buildings. The influence of asymmetry on the accuracy of the results is also assessed. First, a detailed step-by-step procedure to perform BEP is presented. Then, the structural models and ground motions used in this evaluation are introduced. The structural models are defined in two groups of 9- and 20-story steel buildings, with each group comprising a symmetric, a one-way asymmetric, and a two-way asymmetric model. The models are chosen in this way so as to provide an insight into the effects of the building height and asymmetry on the accuracy of predicted IDA curves. Twenty-two far-field ground motion pairs are considered for this study. Finally, the results of BEP are presented in comparison with those of the exact IDA. The accuracy of the method in predicting the maximum demands over the plan of the asymmetric models is evaluated (i.e., 'flexible side,' mass center (CM), and 'stiff side'). The drift-ratio demands over the height of the buildings are also covered.

2 Step by step methodology

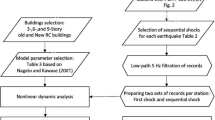
A step-by-step methodology to perform BEP is presented in this section. A flowchart is also represented in Fig. 1, illustrating the process of BEP. More information on the theoretical background can be found in Soleimani et al. (2018).

  1. 1.

    Create a nonlinear 3D model of the building under assessment.

  2. 2.

    Calculate the natural frequencies, \({\mathbf{\omega_{n}}}\), and the modes of natural vibration, \({\mathbf{\varphi_{n}}}\), for the initial state of the structure.

  3. 3.

    Apply gravity loads; then conduct the nth-mode pushover analysis using \({\mathbf{{\it m}}}\varphi_{n}\) as the lateral load pattern. The term \({\mathbf{{\it m}}}\) is the matrix of mass.

  4. 4.

    Extract the nth-mode capacity curve (i.e., \({\alpha }_{n} - y_{n}\) curve) from the corresponding pushover analysis carried out in step 3. To do so, first, determine \({\alpha }_{n}\) and \(y_{n}\), which are the resisting force and the displacement of the nth-mode SDF system throughout the pushover analysis; then combine the two parameters into a \({\alpha }_{n} - y_{n}\) curve. To determine \({\alpha }_{n}\) and \(y_{n}\), follow the subsequent sub-steps:

    1. 4(1)

      Depending on the available component of the base shear, choose one of the following formulas to calculate \({\alpha }_{n}\):

      $${\alpha }_{n} = \frac{{V_{nx} }}{{L_{nx} }}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\alpha }_{n} = \frac{{V_{ny} }}{{L_{ny} }}$$
      (1)

      in which \(V_{nx}\) and \(V_{ny}\) are the x- and y-components of the base shear throughout the nth-mode pushover analysis, and

      $$\begin{gathered} L_{{nx}} = \varphi _{n}^{T} {\mathbf{ml}}_{x} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,L_{{ny}} = \varphi _{n}^{T} {\mathbf{ml}}_{y} \hfill \\ {\mathbf{l}}_{x} = \left( {\user2{1,0,0}} \right)^{{\text{T}}} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\mathbf{l}}_{y} = \left( {\user2{0,1,0}} \right)^{{\text{T}}} \hfill \\ \end{gathered}$$
      (2)

      The terms 1 and 0 are \(1 \times N\) vectors with all elements equal to unity and zero, respectively, and N is the number of building floors. It should be mentioned that if the building is two-way asymmetric, any of the two formulas in Eq. (2) can be used to calculate \({\alpha }_{n}\) since all modes would normally include both x- and y-components. Otherwise, the formula needs to be chosen so that the associated component of the base shear is nonzero.

    2. 4(2)

      Calculate yn using the following formula:

      $$y_{n} = \int\limits_{0}^{T} {dy_{n} } = \int\limits_{0}^{T} {\frac{{dE_{n} }}{{{\alpha }_{n} M_{n} }}}$$
      (3)
Fig. 1
figure 1

Flowchart illustrating the process of BEP

Full size image

in which T is the final step of pushover analysis, and \(M_{n}\) represents the modal mass of the nth mode (\(M_{n} = \varphi _{{\mathbf{n}}}^{{\mathbf{T}}} {\mathbf{m}}\varphi _{n}\)). The term \(dE_{n}\) is the energy absorbed by structure at each step of pushover analysis. It is calculated by multiplying the pushover load, which involves the lateral forces and torques, by the structure's displacement at that step:

$$dE_{n} = \left( {{\mathbf{m}}\varphi _{n} } \right)^{{\text{T}}} d{\mathbf{u}}_{n}$$
(4)

where \({\mathbf{u}}\) is the displacement vector with the order of \(1 \times 3N\).

  1. 5.

    Establish the nth-mode hysteresis curve by idealizing the \({\alpha }_{n} - y_{n}\) curve as a multi-linear curve, then defining the unloading and reloading branches given the martial properties and the structural system. In this study, capacity curves are idealized by bilinear curves to be compatible with the definition of beam and column plastic hinges defined as bilinear. If complex behaviors are utilized for the structural sections, or in the case of reinforced concrete buildings, which exhibit stiffness and strength deteriorations in cyclic loads, the hysteresis functions of the SDF systems could be more accurately acquired by performing unloading and reloading pushover analyses (Bobadilla and Chopra 2008).

  2. 6.

    Repeat steps 3–5 for as many modes as needed to achieve sufficient accuracy and save the results for the subsequent steps.

  3. 7.

    Choose a pair of orthogonal ground-acceleration records.

  4. 8.

    Choose a scale factor for the first stage of the BEP analysis, and calculate the 'effective dynamic force' of the nth-mode SDF system for all the included modes using the following formula:

    $$q_{n} \left( t \right) = - SF({\Gamma }_{nx} \ddot{u}_{gx} + {\Gamma }_{ny} \ddot{u}_{gy} )$$
    (5)

In Eq. (5), SF stands for the scale factor. The terms \(\ddot{u}_{gx}\) and \(\ddot{u}_{gy}\) represent x- and y-components of the ground acceleration record, and

$${\Gamma }_{nx} = \frac{{L_{nx} }}{{M_{n} }}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\Gamma }_{ny} = \frac{{L_{ny} }}{{M_{n} }}$$
(6)
  1. 9.

    Having the hysteresis function and the 'effective dynamic force', solve the differential equation of motion for the nth-mode SDF system (Eq. (7)) using one of the existing time-stepping methods [chapter 5—(Chopra 2011)], and determine the peak response, \(y_{no}\).

    $$\ddot{y}_{n} \left( t \right) + 2\zeta_{n} {\omega }_{n} \dot{y}_{n} \left( t \right) + {\alpha }_{n} \left( t \right) = q_{n} \left( t \right)$$
    (7)

    The term \(\zeta_{n}\) is the damping ratio of the nth mode.

  2. 10.

    Extract the structural responses associated with \(y_{no}\) from the nth-mode pushover analysis database established in step 3.

  3. 11.

    For all the included modes, repeat the steps 9–10, and combine the results using the modified CQC formula:

    $$r_{o} = \left( {\sum\limits_{i = 1}^{X} {\sum\limits_{j = 1}^{X} {{\eta }_{ij} {\rho }_{ij} r_{io} r_{jo} } } } \right)$$
    (8)

In this equation, X stands for the number of modes involved. The terms \(r_{io}\) and \(r_{jo}\) are the peak structural responses associated with ith and jth modes. The term \({\rho }_{ij}\) is the correlation coefficient between the ith and jth modes in terms of modal characteristics, and it is obtained from the following equation [Chapter 13—(Chopra 2011)]:

$${\rho }_{ij} = \frac{{8\sqrt {{\zeta }_{i} {\zeta }_{j} } ({\beta }_{ij} {\zeta }_{i} + {\zeta }_{j} ){\beta }_{ij}^{3/2} }}{{(1 + {\beta }_{ij}^{2} )^{2} + 4{\xi }_{i} {\xi }_{j} {\beta }_{ij} (1 + {\beta }_{ij} )^{2} + 4({\zeta }_{i}^{2} + {\zeta }_{j}^{2} ){\beta }_{ij}^{2} }}$$
(9)

where \({\beta }_{ij} = {{{\omega }_{i} } \mathord{\left/ {\vphantom {{{\omega }_{i} } {{\omega }_{j} }}} \right. \kern-\nulldelimiterspace} {{\omega }_{j} }}\). The term \({\eta }_{ij}\), which has been added to the standard CQC formula for the BEP method, represents the correlation between two modes in terms of their 'effective dynamic forces,' and it is computed by the following formula:

$${\eta }_{ij} = \frac{{{\rm{cov}}(q_{i} (t),q_{j} (t))}}{{\sqrt {{\rm{var}} (q_{i} (t)){\rm{var}} (q_{j} (t)} }} = \frac{{\int\limits_{0}^{{\tau }} {q_{i} (t)q_{j} (t)dt} }}{{\sqrt {\int\limits_{0}^{{\tau }} {(q_{i} (t))^{2} \int\limits_{0}^{{\tau }} {(q_{j} (t))^{2} dt} } } }}$$
(10)

where \({\tau }\) is the final stage of the ground acceleration time history. It should be noted that the CQC is not used in its original form in BEP, because CQC is originally designed to combine modal structural responses when all modes are subjected to the same ground acceleration record, while in BEP, each mode is subjected to a combination of the x- and y-components of ground accelerations, varying from mode to mode. Therefore, the coefficient \({\eta }_{ij}\) is added to the standard CQC formula to account for the correlations between the 'effective dynamic forces' of different modes

  1. 12.

    Choose another SF and redo steps 8–11 until \(r_{o}\) exceeds the maximum capacity of the corresponding component in the structure.

  2. 13.

    Pick another pair of ground acceleration records and redo steps 7–12.

3 Mathematical models

3.1 Structural systems

Six steel structures were considered for this study in two sets of 9- and 20-story buildings. The first model in each set is the symmetric one, obtained from the SAC Steel Project (Gupta and Krawinkler 1999). Both buildings were designed according to UBC 1994 to be located in Los Angles, California, as standard office buildings. The second model is a variation of the first model with 15% eccentricity along the y-axis: the CM was moved from the geometric center as much as 15% of the plan dimension in the y-direction. The third model is another variation of the first model with 15% eccentricity along both x- and y-axes: CM was moved as much as15% of the plan dimension in each direction. Fifteen percent eccentricity was chosen to provide a good understanding of the influence of asymmetry on the accuracy of the results. These models are referred to in this paper with the letter M followed by the height of the building, followed by the model number: M91, M92, M93 for the 9-story buildings, and M201, M202, M203 for the 20-story buildings.

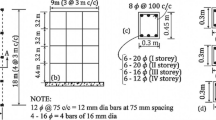
The floor heights, seismic mass, and moment of inertia are represented in Table 1 for the 9- and 20-story buildings. Figure 2 shows the plans of the 9- and 20-story buildings; the CMs of the three models in each set are specified in the plans. The solid and dashed lines indicate the moment-resisting frames (MRFs) and the gravity frames, respectively, with the columns being located at the intersection of the lines. The 9- and 20-story buildings are designed with a single-level and two-level basement, respectively. In the 9-story buildings, the columns at the corner of the building have moment-resisting connections to the beams of only one side so as to avoid biaxial bending. In the 20-story buildings, however, all the exterior connections are moment-resistant, with box columns at the corners to resist biaxial bending. The design details (loading information, member sections, etc.) can be found in Gupta and Krawinkler (1999).

Table 1 Mass, moment of inertia, and height of the 9- and 20-story building floors
Full size table
Fig. 2
figure 2

The plans of a 9-story and b 20-story structural models. The points indicated by CM1, CM2 and CM3 are the mass centers of different models in each category. Solid lines represent moment resisting frames

Full size image

3.2 Modeling

The mathematical models were created in PERFORM 3D (CSI 2011), by which the NDA and pushover analyses were carried out. The BEP analyses were performed using computer codes written in MATLAB in conjunction with PERFORM 3D. The P-delta effect was activated in both pushover and NDA analyses. All the gravity columns were included in the mathematical models (as linear elements) to ensure that the P-delta effect in torsion is accurately taken into account.

Beams and columns were modeled using FEMA Beam and FEMA Column elements in PERFORM 3D. The moment-rotation behaviors of the beam and column sections were defined by bilinear curves, with yield strength equal to FyZ, where Fy is the steel yield-strength and Z is the plastic section modulus, and a post-yield stiffness equal to 3% of the elastic flexural stiffness. The P-M-M interactions were defined according to (El-Tawil and Deierlein 2001), with \({\alpha }\) and \({\beta }\) equal to 2 and 1.1, respectively. The maximum plastic hinge rotation for beams and columns was presumed to be equal to \(11\Phi_{y}\) as per ASCE 41–13, with \(\Phi_{y}\) being the yield rotation; any component exceeding this threshold was equated with the collapse of the building. Damping of structures was defined by modal damping ratio equal to 2% for each mode. Modal damping was preferred to Rayleigh Damping because it makes it easier to make a fair comparison between BEP and NDA, as in BEP, we need to specify damping for each mode separately. The implied damping matrix is determined by PERFORM 3D using the following formula:

$${\mathbf C} = \sum\limits_{{n = 1}}^{{n = N}} {\frac{{4\pi }}{{T_{n} }}} {\mathbf \zeta _{n}} \frac{{\left( {\mathbf {m\phi _{n}} } \right)\left( {\mathbf {m\phi _{n}} } \right)^{T} }}{{M_{n} }}$$
(11)

where Tn is the period of the nth-mode, and N is the number of damped modes.

3.3 Modal properties

The roof motions corresponding to the first three natural modes of vibration are shown in Figs. 3 and 4 for the 9- and 20-story buildings, respectively.

Fig. 3
figure 3

First triple of periods and modes of vibration for M91, M92, and M93

Full size image
Fig. 4
figure 4

First triple of periods and modes of vibration for M201, M202, and M203

Full size image

In the symmetric models (M91 and M201), lateral displacements dominate the motion of the first two modes, while the third mode is purely rotational. Since the third modes of vibration in the symmetric models lack any lateral components, these modes are not triggered by any of the x- and y-components of ground accelerations. On the other hand, in asymmetric models, there is a weak coupling between the lateral and torsional components of motion in the third modes, which allows them to contribute to the overall response of the buildings.

As M92 and M202 are eccentric only along the x-axis, the first modes of vibration in these two models exhibit torsional rotation coupled with x-lateral motion, and the second modes are dominated by y-lateral motion. Stronger coupling between the lateral and torsional components of motion is observed in the first three modes of M93 and M203, as these models are eccentric along both x- and y-axes.

In all structural models, the natural vibration period for the dominantly torsional mode (i.e., mode #3) is shorter than that of the first two lateral modes. This indicates that the buildings are torsionally stiff, a quality of structures with lateral load-resisting systems located along their perimeters. In the 9-story buildings, as the plan dimensions and the design of MRFs are identical along the two orthogonal axes, the natural vibration periods of the first two modes are very close, leading to a high correlation factor between the first two modes (Eq. (9)). In the 20-story buildings, however, the dimensions differ along the x- and y-axes, so the natural vibration periods of the first two modes are not close.

4 Ground motion records

A benchmark set of ground motion records that creates the far-field ground motion dataset of FEMA (2009) is considered in this study. The set consists of 22 pair of ground motion records chosen from 14 different earthquake incidents with magnitudes of at least 6.5. The ground motions were recorded at sites of at least 10 km away from the fault rupture on soil types C or D. The peak ground acceleration and velocity of the records are greater than 0.2 g and 15 cm/s. The maximum useable frequencies for the 22 ground motions ranged between 0.05 and 0.25 Hz. The pseudo-acceleration spectra of all ground motion records with their 16th, 50th, and 84th percentile spectra are presented in Fig. 5. The component specified in the FEMA (2009) as component 1 was assigned to the x-axis and component 2 to the y-axis. For better consistency, each spectrum is normalized to the peak ground acceleration of the x-component.

Fig. 5
figure 5

Pseudo-acceleration spectra for the 22 pairs of ground motion records together with their 16th, 50th, and 84th percentile spectra

Full size image

5 Results and discussion

Next, the results of the exact IDA are compared with those of the BEP. First, the IDA and BEP curves are presented. Then, the accuracy of BEP in estimating the demands at the 'flexible side', CM, and the 'stiff side' is evaluated. The 'flexible side' is defined as the edge of the building closer to the CM, and the 'stiff side' is considered to be the opposite edge. Finally, the median drift ratios predicted by BEP over the elevations of the buildings are compared with those of the exact NDA for a wide range of ground motion intensity levels.

The curves for IDA and BEP were obtained from 12 NDAs on average, covering the structural behavior from the elastic domain to the point of collapse. The preferred choice for intensity measure (IM) is the 5%-damped pseudo-acceleration spectral ordinate at the first-mode period [\(S_{a} (T_{1} ,\zeta_{n} = 5\% )\)], where the pseudo-acceleration spectrum is considered to be the geometric mean of the pseudo-acceleration spectra associated with the x- and y-components of ground motions. The following formula is used to determine the geometric mean:

$$A\left( T \right) = \sqrt {\left( {A_{x} \left( T \right) \times A_{y} \left( T \right)} \right)}$$
(12)

where \(T\) stands for the period and \(A\left( T \right)\) represents the pseudo-acceleration quantity for each period. The terms \(A_{x} \left( T \right)\) and \(A_{y} \left( T \right)\) are pseudo-accelerations associated with the two components of ground-motions, shown in Fig. 5 for the set of ground motion records used in this study for the period range between zero and 4 s.

To calculate the error in the BEP results, the normalized area between the approximate and the exact IDA curves is taken as an index, which is determined using the following formula:

$$Error(\% ) = \frac{{\int_{0}^{{{\theta }_{\max } ({\rm{BEP}},{\rm{IDA}})}} {\left| {\Delta IM} \right|d{\theta }} }}{{\int_{0}^{{{\theta }_{\max } ({\rm{IDA}})}} {IM_{{{\rm{IDA}}}} d{\theta }} }} \times 100$$
(13)

In Eq. (13), \({\theta }\) is the maximum of the peak inter-story drift-ratios, extracted from the whole building or the part of the structure under assessment. The term \(IM_{IDA}\) is the ground acceleration intensity for the IDA curves, and \(\Delta IM\) represents the difference between the IMs of BEP and IDA for a given drift ratio. The term \({\theta }_{\max } \left( {{\rm{IDA}}} \right)\) is the maximum drift ratio of the IDA curve at which the curve flattens (as explained earlier, this drift ratio represents a point at which a component reaches its maximum plastic rotation, i.e., \(11\Phi_{y}\)), and \({\theta }_{\max } \left( {{\rm{BEP}},{\rm{IDA}}} \right)\) is the maximum drift ratio recorded considering both BEP and IDA curves.

The number of modes to achieve maximum accuracy was found to be 9 and 12 for the 9- and 20-story buildings, respectively. The discussions in this section are based on the results obtained from the 9- and 12-mode BEP (for 9- and 12-story models), unless otherwise stated. To examine the effect of higher modes on the overall response, the results derived from the first triple modes are also reported.

5.1 IDA curves

Shown in Figs. 6 and 7 are the 16, 50, and 84th percentile IDA curves together with the predicted BEP curves for the 9- and 20-story buildings, respectively.

Fig. 6
figure 6

Sixteenth, 50, and 84th percentile IDA curves together with the 3- and 9-mode BEP curves for M91, M92, and M93. The x- and y-axes represent the maximum drift ratio and IM, respectively

Full size image
Fig. 7
figure 7

Sixteenth, 50, and 84th percentile IDA curves together with the 3- and 12-mode BEP curves for M201, M202, and M203. The x- and y-axes represent the maximum drift ratio and IM, respectively

Full size image

The BEP procedure showed no limitation in the inclusion of higher modes. This is an advantage of BEP compared to the conventional displacement-based methods, which often encounter distortions in the pushover curves of higher modes (Hernandez-Montes et al. 2004; Soleimani et al. 2018). This feature of BEP provides the opportunity to include as many modes as necessary to achieve the highest accuracy.

The comparison of BEP and IDA curves for the 9-story buildings (Fig. 6) demonstrates that the first three modes were inadequate to achieve sufficient accuracy. This is in contrast to the previous research findings on low-rise buildings, for which the first triple modes were adequate to acquire reasonable accuracy (Soleimani et al. 2018). For the 9-story buildings, the average error of the estimated median IDA curves was 22.3% for the 3-mode BEP, compared to 9.6% and 8.3% for the 6- and 9-mode BEP. The inclusion of higher modes than nine didn't improve the accuracy of the results. Hence, 6 or 9 modes could be recommended to be involved for BEP analysis of 9-story buildings.

For 20-story models, the average error for the 3-mode BEP was equal to 39.3% (Fig. 7), which is significantly higher than that of the 9-story buildings. It should be noted that the maximum drift ratios determined by the 3-mode BEP are generally extracted from lower stories, while the maximum drift ratios in medium and high-rise buildings often occur at upper stories, mainly caused by higher modes (Figs. 10, 11, 12 and 13). So, for more realistic results in medium and high-rise buildings, the inclusion of higher modes is necessary. Adding the second triple modes to the assessment reduced the average error to 21.7%. But the best results were obtained by 9- and 12-mode BEP, with 15.8 and 14.7% average errors, respectively. The addition of modes above 12 showed minimal influence on the accuracy of the results. Therefore, 9 or 12 modes could be recommended for achieving better accuracy in 20-story buildings.

It is observed in Figs. 6 and 7 that BEP offers similar accuracies for both symmetric and asymmetric models. In the 9-story buildings, for example, BEP predicted the medium IDA curve of the symmetric model (M91) with 9% error, and the errors for M92 and M93 were 6% and 10%, respectively. Similarly, the median IDA curves for the 20-story buildings were predicted with roughly the same degree of accuracy (15%, 15%, and 14% error for M201, M202, and M203, respectively). It shows that the presence of asymmetry in structures did not deteriorate the accuracy of the method.

The results also demonstrate that BEP provides lower accuracy in the 20-story buildings than in 9-story buildings. Considering both symmetric and asymmetric models, the average error of the median IDA curves was 8.3% for the 9-story buildings and 16.7% for the 20-story buildings. This can be compared to the results of the previous study on a 3-story building under the same ensemble of ground motions, in which the error for the median BEP curves was lower than 4%. The observation allows for the conclusion that the accuracy of BEP decreases to some extent with the increase in the height of the structures.

As a general tendency in both 9- and 20-story buildings, the 16th percentile curves were estimated with the highest accuracy, followed by the 50th and 84th percentile curves, respectively. Taking all structural models into account, the mean error of BEP in predicting the 16th percentile curves was equal to 5.6%, compared to 11.5% and 15.7% for the 50th and 84th percentile curves, respectively. The only exception to this trend was M93, for which 10% error was reported for all three percentile BEP curves. The most significant error among all BEP curves was observed in the 84th percentile curve for M91, in which a surge of the IDA curve at around 3.5% drift ratio was not detected by BEP.

The BEP also shows reasonable accuracy in predicting the point of collapse. According to the median IDA curves shown in Figs. 6 and 7, the ultimate drift-ratios, indicated by the points the IDA curves are flattened, are roughly equal to 6% and 4% for 9- and 20-story buildings, respectively.

Regarding computational effort, BEP roughly takes 3% of the computer time required for the exact IDA. In our analyses, using a Core i7, 2.9 GHz processor, around 6 h were needed to perform IDAs for each 9-story building considering all the 22 ground motion records, and this time was about 9 h for the 20-story buildings. On the other hand, BEP took only 11 and 15 min to produce approximate IDA curves for the 9- and 20-story buildings, respectively. In case only the first three modes were included, the computing time for BEP was about 4 min for each building.

5.2 Stiff and flexible sides

The IDA curves presented in the previous section reflect the maximum of the peak drift-ratios throughout the whole structure. In asymmetric buildings, these maximum drift ratios often occur at the 'flexible side' of the buildings. To examine the accuracy of BEP in predicting the demands over the plan of the asymmetric models, the BEP and IDA curves for the 'flexible side,' CM, and the 'stiff side' are separately presented in this section. The 'flexible side' comprises the northern and eastern MRFs as they are the closest to the CM, and the 'stiff side' includes the southern and western MRFs. The drift ratios at CMs are also provided for the sake of comparison, which encompass the demands along both x- or y-directions.

The results for M93 and M203 are presented in Figs. 8 and 9, respectively. It is found that the accuracy of the method remains consistent over the plan of the asymmetric buildings, with no systematic bias observed. For M93 (Fig. 8), the average errors of the BEP curves at the 'flexible side', CM, and 'stiff side' were 10%, 8%, and 13%, respectively. The trend was similar in M203, with 12%, 13%, and 9% errors for the 'flexible side,' CM, and the 'stiff side,' respectively. The results of M92 and M202 are not reported for the sake of brevity, but the findings apply to those models as well.

Fig. 8
figure 8

Sixteenth, 50, and 84th percentile IDA curves together with the BEP curves at the 'flexible side', mass center, and 'stiff side' for M93

Full size image
Fig. 9
figure 9

Sixteenth, 50, and 84th percentile IDA curves together with the BEP curves at the 'flexible side', mass center, and 'stiff side' for M203

Full size image

5.3 Drift ratios over the elevations

To examine the accuracy of the demands over the height of the buildings, the BEP and NDA median drift-ratios over the elevations are compared in Figs. 10, 11, 12 and 13. The chosen MRFs for this comparison are those at the northern edge (oriented in the x-direction) and the eastern edge (oriented in the y-direction) because, being located at the 'flexible edge,' these frames are more likely to experience the maximum demands.

Fig. 10
figure 10

Median drift-ratios by NDA and BEP at the northern MRF of M91, M92, and M93 for the ground-motion intensities Sa(T1) = 0.1 g, 0.2 g, 0.35 g, and 0.5 g

Full size image
Fig. 11
figure 11

Median drift-ratios by NDA and BEP at the eastern MRF of M91, M92, and M93 for the ground-motion intensities Sa(T1) = 0.1 g, 0.2 g, 0.35 g, and 0.5 g

Full size image
Fig. 12
figure 12

Median drift-ratios by NDA and BEP at the northern MRF of M201, M202, and M203 for the ground-motion intensities Sa(T1) = 0.1 g, 0.2 g, 0.3 g, and 0.4 g

Full size image
Fig. 13
figure 13

Median drift-ratios by NDA and BEP at the eastern MRF of M201, M202, and M203 for the ground- motion intensities Sa(T1) = 0.1 g, 0.2 g, 0.3 g, and 0.4 g

Full size image

Figures 10 and 11 show the median drift-ratio demands of the northern and eastern MRFs, respectively, for the 9-story buildings. Four ground motion intensities are covered, ranging from \({\rm{S}}_{a} (T_{1} ) = 0.1g\) to \(0.5g\). Those of the 20-story buildings are also presented in Figs. 12 and 13, covering four ground motion intensities varying from \({\rm{S}}_{a} (T_{1} ) = 0.1g\) to \(0.4g\). For each diagram, the height-wise average error of the BEP drift-ratios is also reported. The following formula is used to calculate the errors:

$$Error(\% ) = \frac{{\sum\nolimits_{1}^{N} {\left| {{\theta }_{{{\rm{BEP}}}} - {\theta }_{{{\rm{NDA}}}} } \right|} }}{{\sum\nolimits_{1}^{N} {{\theta }_{{{\rm{NDA}}}} } }} \times 100$$
(14)

where \({\theta }_{{{\rm{BEP}}}}\) and \({\theta }_{{{\rm{NDA}}}}\) are the median drift-ratio demands for BEP and NDA, and N is the number of stories.

As is demonstrated in Figs. 10, 11, 12 and 13, when higher modes were included, the median drift-ratios predicted by BEP were reasonably consistent with the results of NDA. The range of errors lied between 4 and 20%. The average errors, considering all the diagrams, were equal to 9% and 12% for the 9- and 20-story buildings, respectively. The highest error among the 9-story buildings was 19%, observed in M93 at \({\rm{S}}_{a} (T_{1} ) = 0.35g\). For the 20-story buildings, the largest error was 20% in almost all models at \({\rm{S}}_{a} (T_{1} ) = 0.1g\).

A tendency is observed in the 20-story buildings for BEP to underestimate the drift-ratio demands in the elastic domain (i.e., \({\rm{S}}_{a} (T_{1} ) = 0.1g\)). This bias can also be seen in the IDA curves of all 20-story models (Fig. 7), as the estimated IDA curves lie marginally over the exact IDA curves throughout the linear range of the building behavior. This is interpreted to be due to an error in the combination of modal responses by the modified CQC formula, since this is the only approximation included in BEP when the structure is still elastic. As this trend is observed in both symmetric and asymmetric models, the error cannot be attributed to the modifications made to the CQC formula; note that the modified CQC will be equivalent to the original CQC in the symmetric buildings. Moreover, in the elastic phase of the symmetric models, the BEP procedure will be equivalent to the well-known response spectrum analysis (RSA), and the CQC method used in RSA is known to estimate the peak responses generally on the unconservative side, with errors up to 25% being reported in previous studies [Chapter 13—(Chopra 2011)]. This is in agreement with the results of this research. Nevertheless, these errors were only observed in the 20-story buildings, and the median drift-ratios over the elastic range of the 9-story buildings were predicted quite accurately. For the 20-story buildings at higher intensity levels (i.e., \(S_{a} (T_{1} ) = 0.2g,\,\,0.3g\) and \({0}{\rm{.4}}g\)), which drive the structures into the nonlinear range, BEP has provided more accurate estimates of the median peak responses compared to that observed in the linear range (Fig. 7).

Over the first five stories of the 9-story buildings (Figs. 10 and 11), little difference is observed between the drift-ratio demands of the 3- and 9-mode BEP, which implies that higher modes have a minimal share in the drift-ratio demands of the lower stories (the first five stories). On the other hand, higher modes are inferred to have a substantial contribution to the drift-ratio demands of the upper stories, as there are significant discrepancies between the results of the 3- and 9-mode BEP in the upper stories. In 20-story buildings, this trend changes only to a limited degree. Higher modes appear to have relatively more contribution to the drift-ratio demands of lower stories in the 20-story models (the first ten stories). But the upper story demands remain primarily linked to the higher modes (Figs. 12, 13).

No significant alteration in the BEP accuracy was detected throughout the nonlinear range of structural behavior (Figs. 10, 11, 12 and 13). Nevertheless, there is a tendency to underestimate the drift ratios at the upper stories unless in the most intense ground motion levels. For almost all of the buildings considered, the median drift ratios of the upper stories were underestimated in the intensities \({\rm{S}}_{a} (T_{1} ) = 0.1g\) and \(0.2g\), but they were more accurately estimated in the higher intensities, albeit with some exceptions among the 20-story models.

Comparing the median drift-ratios in the northern and eastern MRFs (Figs. 10 and 12 compared to Figs. 11 and 13) shows consistency in the accuracy of the results in the x- and y-directions. Considering all four intensity levels, the average drift-ratio error in the northern MRF of the 9-story buildings was equal to 10.2% (Fig. 10), compared to 8% for the eastern MRF (Fig. 11). For 20-story buildings, the average errors in both edges were similar at around 12% (Figs. 12 and 13).

6 Conclusion

BEP is evaluated for medium- and high-rise buildings. The accuracy of the method to predict two-component IDA curves is assessed as well as its utility to estimate median drift-ratios over the height of the structures. Six steel structures were considered for this evaluation in two groups of 9- and 20-story buildings. Each group consisted of one symmetric model, one asymmetric model about the y-axis, and one asymmetric model about both x- and y-axes. The assessment was carried out for an ensemble of 22 two-component far-field ground motion records, and the results led to the following conclusions:

  • BEP provides sufficiently accurate IDA curves for medium- and high-rise buildings under biaxial seismic excitations, while it takes only 3% of the computational time required for the exact IDA.

  • Having a significant share in the dynamic response of medium- and high-rise buildings, higher mode effects are well addressed in BEP.

  • The accuracy of the method is not affected by asymmetry in buildings, i.e., the method offers the same degree of accuracy in asymmetric buildings as it does in symmetric buildings.

  • The accuracy of BEP slightly decreases with the increase in the height of buildings. Previous research showed around 4% error in predicting the median IDA curves of low-rise buildings, while this figure increased to 8.3% and 16.7% for medium- and high-rise buildings, respectively, as this study revealed.

  • The 16th percentile IDA curves are predicted with the highest accuracy (5.6% average error), followed by 50th and 84th percentile curves, respectively (11.5% and 15.7% average error).

  • The drift ratios at the 'flexible side,' CM, and the 'stiff side' of asymmetric buildings are determined with roughly the same accuracy level.

  • BEP estimates the median inter-story drift-ratios reasonably accurate over the height of the medium and high-rise structures (about 9 and 12% error for 9 and 12 story buildings, respectively).