1 Introduction

To simulate the in-plane (IP) behaviour of unreinforced masonry (URM) structures under seismic loading, several different modelling methods are presently available in the literature, ranging from advanced micro-modelling to the more simplified macro-modelling approaches (Lourenço 2002; Roca et al. 2010; D’Altri et al. 2020). The selection of the modelling scale and refinement level is unavoidably related to the specific structure and mechanical phenomenon under investigation. A low degree of idealisation typically characterises micro-modelling approaches (D’Altri et al. 2020), according to which the actual masonry texture is explicitly reproduced, unit-by-unit.

In this framework, discrete models, initially conceived to analyse soil mechanics problems, proved to be particularly suitable for simulating IP-governed responses of URM components and building sub-systems (Malomo et al. 2019a, Pulatsu et al. 2020). Building on previous advancements (e.g. Kawai 1978; Meguro and Hakuno 1989; Casolo and Peña 2007), a recent effort to increase the computational efficiency of discrete methods was made by Meguro and Tagel-Din (2000), developing an innovative rigid body and spring modelling technique, the Applied Element Method (AEM). In the AEM, masonry members are represented as an assembly of rigid elements connected by nonlinear springs interfaces, where material properties are lumped and failure occurs. This efficient tool proved to be suitable to model the heterogeneous nature of URM structures, also enabling the possibility of representing their behaviour up to complete collapse (Karbassi and Nollet 2013; Keys and Clubley 2017; Malomo et al. 2020).

Nonetheless, and despite recent upgrades to these initial schemes (Malomo and DeJong 2021a), the high computational cost and number of material parameters entailed by the abovementioned approaches often make their application prohibitively expensive for professional aims and for e.g. numerically-based seismic risk studies, where a large suite of simulated responses is needed. To decrease computational burden, simplified methods, ranging from the application of limit analysis (Block et al. 2006; Milani et al. 2006) to story mechanism models (Braga and Dolce 1982, Tomazevic 1978) and equivalent single-degree-of-freedom systems (Graziotti et al. 2016; Snoj and Dolšek 2020), have been used over the years to study the structural behaviour of low-rise and regular masonry constructions subjected to either quasi-static or dynamic IP loading. Amongst others, Equivalent Frame Model (EFM)-based approaches demonstrated to represent an acceptable solution for simulating the IP nonlinear response of large-scale URM buildings. EFM are currently widely employed by both practitioners and researchers, and their use is endorsed by several codes (e.g. Italian code, NTC18 2018).

This simplified modelling strategy idealises masonry into an assembly of deformable elements (i.e. spandrels and piers), connected by rigid regions, building a frame of macroelements and nodes. Thanks to its simple approach, the EFM has a limited computational cost, allowing it to be employed for professional aims without losing accuracy. The EFM has proven to be a reliable tool to assess URM building governed by in-plane mechanisms (Magenes 2000; Belmouden and Lestuzzi 2009; Costa et al. 2011; Raka et al. 2015; Penna et al. 2016; Cattari et al. 2018, 2021; Kallioras et al. 2019; Peruch et al. 2019; Vanin et al. 2020a; Malomo and DeJong 2021b). Its application has been recently extended to include the out-of-plane response (Vanin et al. 2020b; Malomo and DeJong 2021a).

Although several codes allow the use of the EF approach, they do not provide clear indications on the discretisation criterion for the frame geometry definition. Discretisation criteria and other modelling choices can lead to a dispersion of results, especially when irregular opening distributions are present, being also a source of uncertainty (Parisi and Augenti 2013; Bracchi et al. 2015; Berti et al. 2017).

In the EFM, piers are the main loadbearing elements, carrying vertical loads and providing resistance towards horizontal actions. Spandrels couple the response of those vertical elements affecting their boundary conditions, lateral capacity and crack propagation. Based on these considerations, the first simplified frame approaches defined piers effective height, assuming two limit conditions on spandrels contribute, as suggested by FEMA 356 (ATC 2000). The first condition assumes strong spandrels and weak piers (SSWP) and represents the most logical choice for new buildings with rigid diaphragms. This hypothesis assumes that piers crack first, assuming infinitely rigid spandrels and perfect coupling between piers, which are in a fixed–fixed condition with any rotation allowed (storey-mechanism, POR method, Tomazevic 1978). The opposite hypothesis requires uncoupled piers in a cantilever condition, WSSP, weak spandrels and strong piers. In this case, the assumption is that spandrels crack first and represents a more realistic choice when flexible floors provide at the most coupled horizontal displacement for vertical elements (Lagomarsino et al. 2013). However, those upper and lower bounds often are not representative of the actual building’s response.

Based on the results of a full-scale test (Yi et al. 2006), Moon et al. (2006) proposed a method defining the effective height as the height over which a compression strut is likely to develop. According to this criterion, the compressive strut is defined assuming that cracks can propagate at 45° or horizontally, offering the minimum lateral resistance (with the steepest possible angle). A similar criterion was formulated by Augenti (2006), and it was based on post-earthquake observation. According to Augenti, the effective height of a pier should be the height of the opening following the pier in the direction of seismic load. These criteria lead to different discretisation depending on the direction of the applied load in the presence of irregular openings. Nonetheless, the use of the EF approach for dynamic analyses requires a unique model.

Dolce (1991) proposed a more complex criterion for the definition of the effective height of piers in a storey-mechanism approach, and it was based on FEM analyses on pier-spandrels sub-systems accounting for the pier stiffness, and the elastic rotational and translational restrains provided by spandrels. This criterion assumed the equivalent effective height of the pier equal to the distance of midpoints of the line connecting two consecutive opening corners further incremented by a contribution proportional to the difference between such distance and the inter-storey height. A limit of 30° was assumed for the inclination of the line connecting consecutive opening corners. The criterion was calibrated by Dolce, comparing the statistical evaluation of the equivalent stiffness obtained with FEM and the elastic stiffness of a pier calculated considering the classical relation for a Timoshenko’s beam. The criterion proposed by Lagomarsino (2013) and currently implemented in the TREMURI computer program is similar to the one of Dolce, without any limit on the inclination of cracks.

The problem of the reliability of EFM in the presence of irregular opening distribution (Siano et al. 2017; Quagliarini et al. 2017) and the definition of the discretisation criteria was discussed by several authors (Calderoni et al. 2017; Camilletti et al. 2018), but a commonly accepted criterion is still missing. The most employed rules come from empirical observation of earthquake damage (Augenti 2006), simplified numerical simulations (Dolce 1991) or assumptions on crack propagation. However, their employment choice is delegated to engineering judgment for the lack of general indication in the presence of irregularities.

Several authors investigated the problem of the reliability of the EFM in the presence of irregular openings considering a single discretisation criterion (Parisi and Augenti 2013; Pagani et al. 2017; Berti et al. 2017). On the other hand, many studies analysed the effect of different EFM discretisation criteria (Bracchi et al. 2015), in some cases using continuum FEM as a reference (Calderoni et al. 2017; Siano et al. 2017; Camilletti et al. 2018; Cattari et al. 2021) to compare EFM results.

Since the coupling effect provided by spandrels is also affected by the presence of lintels, adjoining walls, floor connection, and brick arrangement that influences crack propagation, the idealisation of masonry as a continuum is not suitable to account for such contributes. The comparison with a numerical approach that accounts for such features is needed to extend the validity of the EFM to URM buildings with irregular opening distributions providing a general discretisation criterion.

In this work, a discrete modelling approach was considered as a reference solution to evaluate the reliability of EFM, discretised adopting different criteria. Contrary to previous research, which commonly adopted a phenomenological description of masonry, the macroelement considered in this work has the main advantage of relating the structural behaviour to quantities measured experimentally, such as mechanical properties, using mechanically based relationships and applying strength criteria having a solid scientific basis. Moreover, both EF and discrete models were validated against experimental tests, thus providing reliable results for the comparison.

The problem of the EF discretisation criterion was scrutinised in this study. To this end, a set of irregular opening layouts were analysed to investigate whether different criteria lead to significantly different results. Then, the lateral response of a few selected irregular configurations, discretised with different criteria, was compared with micro-modelling predictions, used here as a benchmark to evaluate the accuracy of EF results. Finally, some critical situations were discussed.

2 Selected numerical modelling strategies

In this section, the employed modelling strategies are presented, and their idealisation approach to URM buildings is discussed.

2.1 Equivalent Frame Model (EFM)

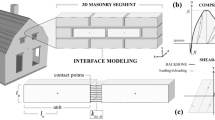
According to the EFM, masonry structures are ideally subdivided into rigid nodes and deformable elements (i.e. spandrels and piers), as depicted in Fig. 1a. This assumption is based on experimental outcomes and post-earthquake observations indicating that deformations are located in recurrent areas while others work as rigid parts. In this work, the research version of TREMURI software (Lagomarsino et al. 2013) was used, considering the macroelement model initially proposed by Penna et al. (2014) and then further improved by Bracchi et al. (2021).

Fig. 1
figure 1

a EFM idealisation (adapted from Lagomarsino et al. 2013), b selected criteria for the identification of the effective height of piers in EF wall discretisation

Full size image

A macroelement is a two-node element with eight degrees of freedom (DOFs), and it consists of three main parts: a central body where only shear deformations are allowed and where two internal DOFs are placed, and two zero-thickness spring interfaces governing the axial-flexural behaviour, where six DOFs are located. A no-tension model with the bilinear law in compression proposed by Bracchi et al. (2021) is assigned to the zero-thickness springs, whereas the shear damage model is based on the one proposed by Gambarotta and Lagomarsino (1997). Shear failure is predicted by multiple shear strength criteria implemented in the macroelement by Bracchi and Penna (2021).

In this work, the strength criterion was selected to be representative of the expected failure mode (i.e. diagonal shear failure). The selected strength criterion is the one proposed by Mann and Müller (1982), accounting for the brick tensile failure, fbt. Originally formulated as a local criterion, it was converted into a global strength criterion (1) by Magenes and Calvi (1997), introducing the correction to consider the influence of the shear span ratio.

$$V = \frac{{f_{bt} lt}}{{2.3\left( {1 + \alpha_{v} } \right)}}\sqrt {\frac{N}{{f_{bt} lt}} + 1}$$
(1)

where \({\alpha }_{v}\) is the shear span ratio, and it is equal to h0/l. h0 is the distance between the section with zero moment and the section with the maximum moment, and \(l\) is the wall length.

Mechanical properties considered in the macroelement model are: density ρ, Young modulus E, shear modulus G, compressive strength fm, brick tensile failure, fbt, cohesion c, friction coefficient μ. Two phenomenological parameters govern the nonlinear shear response: Gct, controlling macroelement inelastic shear deformability, and β, which influences the slope of the post-peak softening branch.

The identification of rigid nodes and deformable elements (i.e. spandrels and piers) is often a challenging process, especially when considering irregular opening distributions, a common feature of pre-code existing URM buildings. Moreover, the selection of effective height of deformable elements might be affected by several aspects, influencing e.g. the direction of crack propagation (as the presence of lintels or other irregularities which can lead to local weaknesses), and it might vary depending on the direction of the lateral load, leading to a different failure mode. In practice, in the presence of regular opening distribution, spandrels are identified as the elements between two aligned vertical openings, and piers are defined according to a discretisation criterion among the available in the literature. Rigid nodes are the portions delimited by these deformable elements. Several discretisation approaches define geometrical rules for piers effective height identification, mostly based on experimental (Yi et al. 2006) or post-earthquake observation (Augenti 2006) and on the assumption of the expected failure mode and the inclination of cracks, which delimits the deformable parts of the structure. Although some criteria (e.g. Augenti 2006, and Moon et al. 2006) lead to different discretisation depending on the direction of the applied load, the use of the EF approach for dynamic analyses requires a unique model (e.g. Lagomarsino et al. 2013).

In this work, three discretisation criteria were chosen according to the most common assumptions (Rota et al. 2014; Bracchi et al. 2015), generating a single EF discretisation for both loading directions. The first criterion (MIN) assumes piers effective height as the masonry wall's minimum clear height between two consecutive openings. The second approach (LIM) assumes the effective height of piers as the distance between midpoints of the segments connecting two corners of adjacent openings, with a limit of 30° for the inclination of that line. Where the hypothesis to limit to 30° the maximum cracks inclination is derived from the criterion proposed by Dolce (1991) for the definition of pier effective height in models based on storey mechanisms (POR). The third criterion (AVG) is equal to the second one without limiting the ideal corner connecting line’s maximum inclination. This last criterion, which was also adopted for spandrels element, is the criterion implemented in 3Muri, the commercial version of the TREMURI computer program (Lagomarsino et al. 2013). The three criteria are graphically represented in Fig. 1b: MIN, LIM and AVG from left to right.

2.2 Applied Element Method (AEM)

The AEM was selected in this work as a reference model to evaluate the EFM predictions. It can be classified as a rigid body and spring model. Its application to masonry structures modelling consists of the ideal representation of this material as an assembly of rigid elements connected by zero-thickness springs interfaces, where material properties are lumped. This discrete approach is naturally suitable for modelling heterogeneous material, and it explicitly represents the actual brick arrangement (Fig. 2a). The material model in compression is the one originally developed by El-Kashif and Maekawa (2004) with a tension cut-off without any softening branch. Sliding along mortar joints is represented by Coulomb’s friction model. Each spring interface is characterised by a normal and a shear stiffness evaluated through Eq. (2)–(5), where the nomenclature can be found in Fig. 2b. Springs placed between bricks units and representing mortar-brick interaction are here named brick–mortar springs. Their normal (kn,b-mo) and shear (ks,b-mo) stiffnesses are evaluated considering mortar and brick springs in series by Eqs. (2) and (3). In order to capture the possible cracking through brick, units are further divided into two elements connected by brick-brick springs interfaces, evaluating their stiffnesses (kn,b-b and ks,b-b) by Eq. (4) and (5). Where Eb, Gb, Emo and Gmo are the unit and mortar Young’s and shear moduli, respectively.

$$\frac{1}{{k_{n,b - mo} }} = \frac{{a - l_{mo} }}{{E_{b} dt}} + \frac{{l_{mo} }}{{E_{mo} dt}}$$
(2)
$$\frac{1}{{k_{s,b - mo} }} = \frac{{a - l_{mo} }}{{G_{b} dt}} + \frac{{l_{mo} }}{{G_{mo} dt}}$$
(3)
$$\frac{1}{{k_{n,b - b} }} = \frac{{a_{b} }}{{E_{b} dt}}$$
(4)
$$\frac{1}{{k_{s,b - b} }} = \frac{{a_{b} }}{{G_{b} dt}}$$
(5)
Fig. 2
figure 2

a Brick based arrangement, b masonry discretisation

Full size image

3 Model validation against experimental data

The models material properties employed in this work were calibrated by simulating the experimental shear-compression tests on two masonry panels tested at the Joint Research Centre (Ispra, Italy) by Anthoine et al. (1995). Both AEM and EFM were then validated on a full-scale in-plane cyclic test of a building façade tested at the University of Pavia (Italy) by Magenes et al. (1995). The first simulations are discussed in Sect. 3.1, whereas the latter, which allowed the EFM spandrel mechanical parameters refinement, is presented in Sect. 3.2.

3.1 Simulation of shear compression test on single components

Two solid bricks two-wythe walls with an English bond pattern arrangement were tested at the Joint Research Centre of Ispra under a compression level of 0.6 MPa and double-fixed boundary conditions. A horizontal displacement history was applied in a quasi-static test to the top beam performing two or three cycles at each amplitude. The two walls, named Highsta and Lowsta, were 0.25 m thick and 1 m in length, with different height/length ratios of 2 and 1.35. The squat wall (i.e. Lowsta) exhibited a shear failure with diagonal cracking and a peak shear force of 84 kN, which was reached at 2.8 mm of horizontal displacement, corresponding to a 0.2% drift, with a strength degradation from this point on. The slender wall (i.e. Highsta) was characterised by a flexural behaviour with horizontal cracks at the top and bottom due to the partialisation of the panel section, without any strength degradation. The peak shear force of 72 kN was reached at 0.6% of drift (12.7 mm). The EFM parameters, calibrated through the shear compression tests on these two walls, are presented in Table 1.

Table 1 Macroelement mechanical parameters (EFM)
Full size table

Compression strength, fm, and density, ρ, were obtained by characterisation test. Elastic and shear moduli, E and G, as well as the brick tensile strength, fbt, were initially derived by component tests and further refined through the comparison with the experimental shear-compression tests on piers. The shear model parameters (i.e. the shear deformation parameter ct and the softening parameter β) were calibrated through the presented numerical simulations. As discussed in Sect. 2, the macroelement here adopted for pier elements assumed an equivalent Mohr–Coulomb criterion, automatically evaluating the equivalent cohesion and friction coefficient for the selected shear strength criterion, as presented by Bracchi and Penna (2021). The macroelement proposed by Penna et al. (2014) was adopted for spandrel elements. A preliminary sensitivity analysis (whose results are not reported here for space constraints) was carried out to set optimal convergence parameters.

The AEM Young’s and shear moduli of brick–mortar springs were first estimated and further calibrated, comparing numerical and experimental results of the two shear-compression tests considered, as discussed in Sect. 2. The other material parameters were assumed according to the characterisation test results and further refined simulating the shear-compression tests on individual piers. In Table 2, material properties of the AEM model are presented, identified for brick-brick (subscript b) and mortar-brick (subscript b-mo) interfaces. A brick based discretisation was adopted, and, as the failure modes involved cracks passing through bricks, the units were further separated into two parts connected by brick-brick springs.

Table 2 Material properties of AEM model
Full size table

Eb, Gb, fbt, cb and µb are elastic and shear moduli, tensile strength, cohesion and friction coefficient of brick. Eb-mo, G b-mo, ft b-mo, c b-mo and µ b-mo, are the elastic and shear moduli, tensile strength, cohesion and friction coefficient of mortar-brick interfaces. Eb, fbt, ft b-mo and c b-mo were derived from characterisation tests (Binda et al. 1996a,b). The compression strength fm was assumed equal to the brick one for both brick-brick and mortar-brick interfaces to avoid premature failure, as already suggested by other researchers (Mayorca and Meguro 2003; Malomo et al. 2018). Gb and G b-mo were evaluated assuming G = 0.35E. cb was derived analytically assuming a Mohr–Coulomb criterion. µ b-mo and µb were refined in the calibration process.

The comparison in terms of hysteretic curves of the two numerical models and the experimental tests on both squat and slender walls is presented in Fig. 3.

Fig. 3
figure 3

Experimental (adapted from Anthoine et al. 1995) vs numerical force–displacement hysteresis of Highsta and Lowsta obtained with the EFM (in red) and AEM (in blue) models

Full size image

Both numerical models satisfactorily captured the Highsta wall behaviour. The EF macroelement showed flexural cracks at the top and bottom sections, showing a good agreement in peak base shear capacity and initial lateral stiffness (Fig. 3), with differences around 7% and 5%, respectively, while energy dissipation is slightly underestimated (Fig. 4). The AEM showed a flexural-rocking behaviour with cracks developed at the top and bottom sections and then propagated through the first courses. A good agreement was found in initial lateral stiffness and shear force (Fig. 3), with differences lower than 5%, while stiffness deterioration was underestimated.

Fig. 4
figure 4

Experimental (EXP) vs numerical (AEM, EFM) cumulative dissipated energy, normalised with respect to the total experimental value, of Highsta and Lowsta

Full size image

Regarding the squat wall, Lowsta, both models captured initial lateral stiffness (differences < 10%) and post-peak deterioration, predicting a diagonal shear failure mechanism. The EFM predicted almost the exact value of the peak base shear in the positive direction and a difference around 10% in the negative, with a good agreement in energy dissipated. The AEM showed few brick failures at the top and bottom corners and at the centre of the panel. The energy dissipated was slightly overestimated in the central cycles due to the brick failures, and it was underestimated in the last, while minor differences were found in peak base shear (< 5%), reached at 0.4% of drift (where the experimental peak was at 0.2% of drift ratio). These differences found in the AEM response of Lowsta model are consistent with what was already found by other researchers using discrete approaches and allowing only a single failure surface into brick elements (Miglietta et al. 2017; Malomo and DeJong 2021a). Despite these differences, the AEM predicts the strength deterioration with a good agreement, with differences around 20% with respect to the experimental decreasing, whereas a difference of 30% was found in EFM. The cumulative energy dissipated is reported in Fig. 4, normalised with respect to the total experimental energy dissipated.

As the cyclic behaviour obtained with the two modelling approaches was in good agreement with the experimental ones, in this work, the attention was focused on the effect of the irregularity on the monotonic response.

3.2 Simulation of a quasi-static cyclic test on a full-scale URM prototype

The prototype considered in this work is a two-storey URM masonry building consisting of four two-wythe walls of solid bricks arranged in an English bond pattern. The structure had a regular opening distribution, and flexible diaphragms consisted of a series of isolated steel beams where the vertical load of 10 kN/m2 was applied at both floor levels. One of the two longitudinal walls, named Door Wall, was disconnected from the transversal walls, and it was here referred to as a regular baseline for the following study. The full-scale prototype was tested at the University of Pavia in 1995 under a quasi-static cyclic test. Horizontal forces were applied in displacement control through actuators placed at each level of the longitudinal façades, keeping a constant ratio between the applied loads. Three EF models of the independent wall, Door Wall, were built assuming the three discretisation criteria considered. Material properties adopted in EFM are reported in Table 3, while the AEM ones are the same implemented in the component tests Table 2. In both AEM and EFM models, the steel trusses placed at each floor level and used to apply the horizontal loads were explicitly modelled considering the actual cross-section and providing axial and flexural stiffness. No additional restraints were necessary at the floor level. Regarding the AEM, units are placed in a brick-based arrangement (i.e. two-wythe), and forces were applied through a system of trusses and steel beams with the aim to obtain equal forces at each floor level.

Table 3 Material properties of EFM piers for MIN, AVG and LIM criteria
Full size table

Two in-plane monotonic static analyses (i.e. in both positive and negative directions) were performed with the four models (i.e. AEM and the three EFM), and results are compared in terms of damage, initial lateral stiffness and peak base shear. Out-of-plane displacements were restrained in the AEM model, whereas the EF 2D model allowed IP analyses.

First cracks developed through spandrels in the experimental cyclic test, with minor flexural damage at piers edges. Then, with the loss of the coupling effect of spandrels, the central ground-level pier developed a diagonal shear mechanism, and external ground-level piers failed in shear (Fig. 5a). Both AEM and EFM predicted an in-plane response mainly governed by ground-level piers, as experienced by the experimental prototype.

Fig. 5
figure 5

a Experimental (adapted from Magenes et al. 1995), b AEM and c EFM damage patterns

Full size image

In the AEM, first cracks developed through spandrels and piers edges due to flexural mechanisms, then the ground-level central pier showed diagonal cracks. The external ground-level pier on the compressed side exhibited diagonal cracks due to a shear mechanism at large displacements (corresponding to a drift of 0.4%), whereas only flexural cracks at top and bottom edges occurred for lower displacements (Fig. 5b). As monotonic static analyses were performed, the ground-level pier subjected to a lower compression (i.e. in the negative side for positive pushover and vice versa) showed only flexural cracks at both edges. Minor flexural damage was detected in piers at the first level, as shown in (Fig. 5b).

A good agreement was found between numerical and experimental results in terms of initial lateral stiffness, peak and residual base shear (Vb), with differences under 15% and 10%, respectively, compared to the experimental backbone (Fig. 6). Moreover, the AEM showed a slightly higher base shear than the experimental counterpart. This result was somehow expected, given that cyclic degradation experienced by the experimental specimen could not occur in a monotonic test. The EFM initially showed damage located at spandrels, more significant in the one at the more compressed side. Then, according to what exhibited by AEM and by the experimental specimen, a shear failure mechanism developed in the central pier and the external one at the compressed side. In Fig. 5c, the EFM damage pattern with the three criteria is presented. The shear damage parameter α > 1 represents the attainment of the maximum shear strength of the macroelement.

Fig. 6
figure 6

Experimental versus numerical IP monotonic pushover curves

Full size image

4 EFM vs AEM numerical outcomes

This work aims to evaluate the effect of different discretisation criteria on the predicted EFM response to formulate suggestions on the use of this modelling approach when the distribution of the openings is irregular. To this end, a set of façades (Fig. 7) characterised by various irregularities on the opening distribution, selected according to the classification proposed by Parisi and Augenti (2013), and including vertical and horizontal misalignments and different opening sizes, was chosen starting from the regular layout (i.e. Door Wall, configuration 1). Fourteen EF models were created applying the selected discretisation criteria, i.e. MIN, LIM and AVG.

Fig. 7
figure 7

Selected façade layouts

Full size image

Monotonic static analyses in displacement control were performed in both directions with EFM, and their results were compared for each configuration in terms of initial lateral stiffness (ILS) and peak base shear (Vbp), Fig. 8.

Fig. 8
figure 8

Results in terms of initial lateral stiffness (ILSn) and peak base shear (Vb,np), normalised with respect to the experimental value of the regular configuration (i.e. 1)

Full size image

As discussed in Sect. 3.1, in the EFM local drift limits, corresponding to a sudden drop of the lateral capacity, were not explicitly introduced as the post-peak deterioration was adequately predicted by the macroelement shear model. Monotonic static analyses were also performed with the AEM models, which were assumed as a benchmark. As constructing AEM models is time-consuming, only the relevant configurations were analysed using this modelling approach. The selection was based on the larger differences found between the three EFM results in terms of lateral strength and stiffness. Figure 8 compares the results obtained with the three EF discretisation criteria on the fourteen configurations in peak base shear (Vbp) and initial lateral stiffness (ILSn), normalised with respect to the experimental values of the regular configuration, whereas Figs. 9 and 10 present the damage pattern predicted by EFM and AEM models. The ILS was computed considering the inclination of the line connecting the points that correspond to the 15% and the 30% of the Vbp. The three criteria showed a good agreement in configurations 4,6,9,10,11,12, and 14, with almost equal values of Vbp and variability of ILS under 20%.

Fig. 9
figure 9

Deformed shape and damage of AEM and EFM of configurations 2, 5 and 6 at 25 mm of top displacement

Full size image
Fig. 10
figure 10

Deformed shape and damage of AEM and EFM of configurations 7, 8 and 13 at 25 mm of top displacement (15 mm for configuration 8 in positive direction)

Full size image

On the contrary, more significant differences were found in the other layouts. Among the considered set of irregular configurations, a selection of case study was analysed using the AEM approach, and it comprised configurations 1,2,5,6,7,8 and 13. The selection was driven by the need to analyse further the configurations where the EF geometrical identification is more challenging, leading to different discretisations and lateral responses. Among the considered layouts analysed with the AEM approach, more significant differences were found when a reduced or missing opening was considered, with differences up to 80% in terms of ILS and up to 30% in Vbp.

When loaded in the positive direction, all the considered configurations showed the initial cracking of first and second floor spandrels and the partialisation of piers at ground level due to flexural mechanisms. Then, increasing the horizontal applied load, piers and spandrels at ground level exhibited shear damage up to the attainment of their shear strength. AEM models first showed the extensive diagonal cracking of the central pier at ground level, followed by the downwind pier. In contrast, the external pier with the lower compression level (i.e. on the left side) exhibited flexural cracks. Consistently, EFM presented a shear mechanism on the elements at the compressed side, with the attainment of their maximum lateral strength, which corresponds to the peak base shear of the façade. Typically, MIN discretisation reached its lateral strength at lower displacement than LIM and AVG in both positive and negative loading directions. EF and AEM models predicted similar responses when façades were loaded in the negative direction, with the initial development of flexural cracks, followed by extensive shear damage on the elements at the compressed side. Generally, EFM resulted in a higher value of Vbp and ILS, even greater when the MIN criterion is considered.

Due to the presence of different irregularities or discretisations, some differences were found with respect to the above presented general response:

  • In the positive direction, the AEM models of configurations 2, 5, 7 and 8 experienced a sudden decrease of the global base shear after the opening of the diagonal crack on the central pier, then configurations 5,7 and 8 exhibited a brittle failure due to the stress concentration caused by the application of the horizontal load through the second floor trusses, accompanied by the diagonal cracking of central pier at first level in configuration 7 and 8. The analyses were interrupted when a brittle failure occurred at 15 mm of top displacement in configurations 5 and 8. EFM did not present this phenomenon.

  • EFM of configuration 5 predicted flexural damage in spandrels and piers, followed by light shear damage at ground level. This configuration showed a global cantilever behaviour of the whole façade without attaining the peak shear strength in any element. A similar response was detected when EFM of configuration 5 were loaded in the negative direction. On the contrary, the AEM model lateral response was governed by the diagonal shear mechanism on the squat pier when the load was applied in the positive direction. In contrast, the predicted failure mechanisms of the two modelling approaches were consistent in the negative direction.

  • In configuration 6, EFM showed almost the same damage pattern of configuration 1 at ground level, whereas the squat pier at first level was substantially undamaged, as well as, naturally, the large rigid nodes. On the contrary, the squat pier at the first level was interested by the development of diagonal cracks when the AEM model was pushed in the positive direction.

  • In the positive direction, the AEM model of configuration 8 predicted a lateral response governed by the diagonal cracking passing through the small window at ground level. EFM predicted slight shear damage on the downwind piers at the ground level, with a global response consistent with the one predicted by EFM in configuration 5.

5 Analysis and interpretation of results

The crack pattern predicted by AEM models, concentrated in recurring areas, suggests that it is still possible to idealise a structure as an assemble of deformable and rigid portions even when the distribution of the openings is irregular. On the other hand, some differences were found in the geometry of EFM deformable elements and the AEM regions interested by crack propagation. Moreover, generally, EFM tend to predict higher initial lateral stiffness (ILS) than the AEM models. This can be attributed to the larger rigid nodes, compared to the portions not affected by cracks in the AEM. The authors already noted this phenomenon, as in previous works discrete models predicted lower initial stiffness with respect to the EF approach (Malomo et al. 2019b). The MIN discretisation, which led to larger rigid portions, often predicted higher lateral stiffness than AEM and the other discretisation criteria.

In contrast, AVG and LIM seem to represent better the deformable regions identified by the cracks in the AEM models, and consequently, the lateral stiffness. Moreover, the MIN criterion led to a stiffer response despite the lower value of E and G compared to the other criteria, as the effective height of piers more influenced the lateral stiffness than the material properties. For this reason, in the configurations where discretisation criteria led to similar rigid portions (e.g. 4,6,14), MIN resulted in a lower ILS (see Fig. 8). In terms of peak base shear (Vb,p), good agreement was found between AEM and AVG and LIM models in configuration 2,6,7 and 13 (< 10%) in the positive direction, whereas higher differences were found in terms of ILS. The MIN criterion showed greater Vb,p and ILS differences in configurations with a reduced opening at the ground level (i.e. 2,5,7 and 8). This last aspect was further scrutinised in the following (Sect. 6).

In order to compare the influence of the selected discretisation criteria on the EFM reliability, the lateral response of the irregular configurations was further analysed comparing the equivalent bilinear curves obtained from the EFM and AEM force–displacement curves. Where the equivalent lateral stiffness was obtained considering the secant stiffness at the 70% of the maximum base shear (as proposed by several codes like NTC 2008) and the yielding force, Fy, was found by equating the areas below the curves between the origin and the ultimate displacement (which was limited to the maximum displacement of the experimental test on configuration 1). The comparison between the bilinear curves obtained from the EFM and the AEM pushover curves is reported in Fig. 11. Contrary to other discrete approaches, which proved to be a suitable reference for the identification of the ultimate displacement capacity (Malomo et al. 2019a), the AEM reliability has not been demonstrated. For this reason, the ultimate displacement of the considered façades was limited to the maximum displacement attained in the experimental test. No drift limits, needed to identify the ultimate capacity in the EFM, were imposed.

Fig. 11
figure 11

Comparison between the equivalent bilinear curves obtained from the EFM and AEM pushover curves

Full size image

Piers at ground level governed the IP response of the irregular façades, consistently with what experimentally found in the regular configuration. This led to the different response of the EFM defined with the three criteria when the irregularity was located at the ground level, as the discretisation approach affected the effective height of piers at ground level, which mostly influenced the lateral response. Consistently, the equivalent bilinear curves obtained with the EFM in configurations 4,9,10,11,12 and 14 were almost superimposable (see Fig. 11). These configurations were not further analysed with the AEM model, as the three adopted discretisation criteria led to equivalent results. Configuration 3 (C3) showed noticeable differences between the bilinear curves obtained with the three EFM. Nevertheless, as this layout was generated by introducing a horizontal misalignment on the ground level window of C2, and the EFM of C2 and C3 resulted in comparable responses, only C2 was modelled and analysed with the AEM.

Regarding the configurations analysed with the micro-modelling approach, i.e. 1,2,5,6,7,8 and 13, the comparison between the yielding force, Fy, obtained by the bilinearisation process is presented in Fig. 12, and it is expressed in terms of percent difference with respect to the AEM value. The MIN criterion generally led to significant differences with respect to the AEM model in both directions, whereas AVG and LIM resulted more consistent with the value of Fy obtained with the micro-models. When considering C5, no differences were found between the three EFM, which predicted significant differences compared to AEM. Two modified discretisation layouts were proposed for C5 to overcome this problem, and they are discussed in the following (Sect. 6).

Fig. 12
figure 12

Comparison between the equivalent yielding force obtained for EFM and AEM models

Full size image

The lateral stiffness of EFM was computed and compared for each configuration considering the secant line passing through the origin and the point corresponding to a different percentage of the peak base shear: 40%, 50%, 60% and 70%. This last, k,70, was considered in the bilinearisation process. The stiffness degradation predicted by EFM and AEM models was compared in Fig. 13. The more significant differences in lateral stiffness between AEM and EFM were found when the MIN criterion was adopted. Indeed, LIM and AVG predicted a higher initial lateral stiffness which converged to the AEM values when the secant stiffness, k,70, was considered. On the contrary, in C2 and C8, MIN predicted a stiffer response even considering the secant value of k,70. The results obtained by comparing configurations 1, 2, 5, 6, 7, 8, and 13 EFM responses with those of AEM models are summarised in Table 4. The qualitative assessment in terms of damage pattern and failure mechanism is reported as G, M and S, which mean good agreement, moderate differences, and significant differences. The comparison in terms of yielding force and lateral stiffness of the bilinear curve with respect to the AEM model is expressed in percentage form.

Fig. 13
figure 13

Degradation of the lateral stiffness with EFM and AEM model

Full size image
Table 4 Summary of numerical results
Full size table

Although a general tendency to overestimate the size of rigid nodes was found, interesting regions undamaged in the AEM counterpart, the EFM was still generally capable of representing the damage pattern and the failure mechanism, even in the presence of an irregular opening distribution. This tendency can be related to the need of a single model for both loading directions, leading to a compromise that overestimated the size of the nodes in the presence of small openings. AVG and LIM criteria generally predicted a good agreement in Fy and k,70 compared to the AEM model. Whereas MIN led to higher values of both k,70 and Fy, suggesting AVG and LIM criteria should be preferred. On the other hand, further investigation on C5 and C8 seems needed as the EFM predicted different damage patterns and, in C5, a different failure mechanism.

5.1 Influence of the opening size

Further considerations are discussed below to overcome the issues on EF discretisation of C5 and C8. Considering configurations 1, 2, 7, 8, and 5 in this order, we could compare the lateral response predicted by the models when reducing the size of one of the two openings at the ground level.

As shown in Fig. 14, ILS and V,bp of both AVG and LIM increased with reducing the irregular opening at the ground level. AEM predicted increasing V,bp and ILS when reducing the opening size, consistently with AVG and LIM. On the contrary, MIN predicted greater ILS and V,bp in configuration 8, even compared to C5, where one opening is missing.

Fig. 14
figure 14

Parametric analysis on opening size: comparison between configurations 1,2,5,7,8 in terms of initial stiffness (ILS) and peak base shear (V,bp)

Full size image

Figure 15 compares AEM and EFM pushover curves of C7 and C8 with C5, which should represent a higher limit for both ILS and V,bp. Both C5 and C8 exhibited a lower displacement capacity in the positive direction, compared to the other configurations considered. This was due to a brittle mechanism caused by the stress concentration on the second floor where the steel trusses applied the horizontal load. In the presence of small openings (e.g. C8), AEM cracks propagation (Fig. 10), and stress distribution (Fig. 16) suggested the activation of a single strut when stress propagation was not disturbed by the presence of the opening, as already noted by (Camilletti et al. 2018). On the contrary, in the EFM, two deformable portions surrounding the opening were considered, leading to different predictions of the façade response by the two modelling approaches. As shown in Fig. 16, for small displacement (< 5 mm) in the positive direction, C7 and C8 showed two compressed struts through the central squat pier and the slender one at the compressed side. Whereas C5 developed only a single strut crossing the squat pier. C8 had an intermediate stress distribution, disturbed by the presence of the small opening. Once diagonal cracks developed through the squat ground pier of C5, stress distribution became analogous to C8. The pushover curve of C5 experienced a drop, reaching a residual base shear closer to C8. Indeed, from this point on, the two façades showed the same response, with a brittle failure occurred at the same displacement, as shown in Fig. 15.

Fig. 15
figure 15

Comparison between configurations 5–8 (left) and 5–7 (right) pushover curves obtained with AEM and EFM

Full size image
Fig. 16
figure 16

Stress distribution of configurations 5, 7 and 8

Full size image

The three configurations (i.e. 5,7, and 8) developed the same stress distribution when loaded in the negative direction, with two main compressed struts through the slender and the squat piers at ground level. This observation is consistent with what found comparing the V,bp, as the three configurations had almost the same lateral resistance in the negative direction, whereas more significant differences were found in terms of stiffness.

The stress distribution reported in Fig. 16 suggests that the small opening can be neglected when the stress propagation is not disturbed by its presence. In this case, the small opening of both C7 and C8 can be neglected. Indeed, the C5 capacity curve (Fig. 15) is very close to the C7 and C8 in the negative direction. In the positive direction, the small opening of C7 should be considered, as it affected the location of the diagonal cracks on the central squat pier at ground level. Considering C8, the presence of the small opening allowed diagonal cracking at the same location of C5 at ground level. Crack propagation seems to be favoured by the presence of that small opening, but not modified, suggesting its presence can be neglected. Moreover, comparing stress distribution and crack propagation in the AEM model of C5 with EFM discretisations and damage patterns, a different elements geometry seems needed, as the two modelling approaches led to different damage location and global behaviour.

Once C5 was loaded in the positive direction, the diagonal shear cracks experienced by the AEM around 8 mm of top displacement caused the development of two compressed struts at ground level. The façade was still able to carry vertical and lateral loads, and the static analyses could continue with lower shear capacity due to the separation of the two struts. This effect cannot be reproduced by the EFM, as the squat pier was modelled as a single element. To account for this phenomenon, two solutions for the EF discretisation were proposed and discussed in Sect. 6.

6 Numerically-calibrated EFM layouts

To overcome the problem of the EF discretisation of C5, two different solutions were proposed. The first model, named C5M2, considered to reduce the shear strength of the squat pier at ground level, according to the actual portion interested by the stress distribution. The inclination of stress direction of propagation was assumed 45°; then, we considered the pier length equal to its height. It was possible to evaluate an equivalent value of fbt, reducing the shear strength accounting for the “effective” pier length, according to Eq. (1), without affecting the lateral stiffness. It is worth noting that this approach allowed maintaining the discretisation based on simple geometrical rules, modifying the local value of fbt. The same consideration can be adopted even if the criterion based on the shear failure due to the attainment of tensile strength of masonry is considered (Turnšek and Sheppard 1980).

As the crack propagation produced the separation of two struts in AEM, the second model, named C5M3, assumed to separate the squat pier into two elements. This assumption has to be carefully chosen as it causes the reduction of the lateral stiffness. This effect could be eventually balanced considering the minimum effective height of the new piers. Moreover, the different aspect ratios of the two piers might lead to a different mechanism. Deformed shape and pushover curves of the new discretisations C5M2 and C5M3 are shown in Fig. 17.

Fig. 17
figure 17

Configuration 5: pushover curves, deformed shape and damage of AEM and EFM (C5M2 and C5M3)

Full size image

In both models, the AVG mechanical parameters were assumed. Compared to the original discretisations, the new models better represented the lateral response of configuration 5 in terms of failure mechanism, V,bp and damage pattern. C5M3 predicted ILS closer to the AEM (+ 10%), whereas C5M2 was more consistent with the standard discretisations obtained with AVG and LIM (+ 40%). In the positive direction, C5M2 and C5M3 predicted with a good agreement the V,bp with respect to what was exhibited by the AEM, with differences around 10%, whereas the three models converged to the same residual lateral strength. In C5M2, the squat pier at the ground level attained its peak shear strength at 12 mm of top displacement, 4 mm later than the AEM. The shift of the maximum base shear is related to the parameter Gct, which was calibrated on the experimental test on the Door Wall. On the contrary, C5M3 predicted a significant stiffness degradation for intermediate displacement. The residual base shear and damage of C5M3 were consistent with those predicted by AEM and C5M2, with the attainment of the peak shear strength by the external pier at ground level. Both C5M2 and C5M3 predicted flexural mechanism with light shear damage and flexural partialisation at ground-level piers edges when loaded in the negative direction. In C5M3, the slender downwind pier attained its peak shear strength. C5M2 predicted higher V,bp (+ 10%) and ILS (+ 40%) with respect to the AEM. The two EF proposed models (C5M2 and C5M3) predicted a lateral response of configuration 5 more consistent with the AEM than the original discretisation (i.e. AVG, LIM and MIN), as also shown by Table 5, where damage pattern, failure mechanism, Fy and k,70 obtained with the different discretisations are compared with the AEM benchmark.

Table 5 Summary of the results obtained with different discretisations for configuration 5
Full size table

These preliminary results suggest that modifying the EF discretisation according to the development of compressed struts, assuming the inclination of stress propagation, might help to improve the EFM capacity to simulate the lateral response of irregular walls in the presence of small or absent openings and squat piers.

7 Conclusions

Equivalent Frame Models are widely employed in the seismic assessment of the in-plane governed behaviour of unreinforced masonry buildings, representing a good compromise between accuracy and computational burden when performing large-scale nonlinear analyses. However, the selection of the most appropriate discretisation criterion, i.e. the definition of frame topology and effective length/height of the structural members, is still challenging because of the irregular distribution of openings. An inaccurate definition of deformable and rigid elements may significantly affect the numerical predictions. In this work, three commonly employed discretisation criteria (i.e. minimum, MIN, limited, LIM and average, AVG, effective height criteria), based on simple geometrical rules, were selected. Their effectiveness was analysed in a study investigating the differences in terms of predicted in-plane behaviour of multiple opening configurations derived from a baseline model, i.e. an experimentally tested building façade. The EFM results were compared with the benchmark predictions by detailed micro-models developed using the Applied Element Method (AEM), where each brick is modelled separately.

First, AEM and EF models were calibrated against cyclic quasi-static tests on two individual URM piers and a full-scale regular URM building façade. Then pushover analyses were performed on a set of irregular configurations, obtained from the regular one combining horizontal and vertical misalignments and variations of the opening size. The lateral response of models was discussed and compared for the selected configurations. Although only minor differences were found between EFM and AEM in some cases, results were scattered in others, especially in terms of peak base shear and initial lateral stiffness, mostly when the irregularity consisted of an opening with a reduced size. Forcing the EF discretisation in case of very little openings multiple small-size deformable and non-deformable regions are created,even in regions affected by cracks in the AEM analyses, leading to a stiffer response and a higher base shear resistance prediction, especially when the MIN criterion was considered. The presence of small openings only marginally affected the lateral response predicted by the AEM models, suggesting that only openings with a minimum dimension should be accounted for in the EF discretisation, unless their presence significantly alter the stress distribution. Noticeable differences were also found where the absence of an opening (or the presence of a very small one) produced a pier with a small aspect ratio (height/length). In this case, the stress distribution obtained from the AEM models allowed identifying the development of a single diagonal strut affecting only a part of such a pier, hence producing an element with a reduced effective length. A correction of the shear strength of the resulting squat piers proportional to the ratio of effective and nominal lengths solved the inconsistent overprediction of lateral strength in the EF model.

Results also showed that EFM tends to overestimate the initial lateral stiffness with respect to AEM. However, this difference becomes generally minor when considering the secant stiffness adopted for the bilinear approximation of the pushover curves.

Despite the differences between EFM and AEM results discussed above, this research indicates that even in the presence of irregular opening distributions, it is still possible to identify recurring uncracked regions and portions of the structure where damage is concentrated. In general, it was observed that simple geometrical rules as AVG or LIM resulted in very similar predictions of lateral response compatible with those by detailed micro-models. Moreover, no significant differences were found between these two criteria, suggesting the two are equally valid even in the presence of the considered irregularities. Although this study was limited only to some of the many possible irregular opening layouts, it suggests that considering the actual stress distribution and the development of compressed struts based on simple geometrical rules can improve standard EFM discretisation strategies. When the application of such improved techniques is not feasible, the AVG or the LIM criteria should be adopted. The use of MIN criterion should be recommended, however, when the presence of strong lintels extended into the masonry well beyond the opening width would not allow the formation of inclined cracks starting from the opening corners, hence limiting the effective height of piers (e.g. Penna et al. 2016).