Abstract
One of the most effective approaches for seismic protection of structural systems is isolation. The majority of existing seismic protection systems are related to horizontal ground motion and only few focus on vertical seismic components, as this would require vertical flexibility, a feature conflicting with the need for sufficient support of the isolated structure. In order to overcome this difficulty, a novel vertical Stiff dynamic absorber (SDA) is proposed that combines a Quasi-Zero Stiffness design including negative stiffness elements, an enhanced Tuned Mass Damper, and Inerter elements. The present work deals with the optimization problem for the determination of the various design parameters of the proposed configuration, aiming at minimizing the vertical accelerations induced on the structure while keeping the displacement within reasonable limits. The values of the optimized design parameters depend only on the characteristics of the isolated structure irrespectively of the excitation input. This feature differentiates the proposed SDA from similar versions found in the literature and renders the design applicable for use across a wide range of vertical vibration control applications. The proposed configuration is designed to achieve great acceleration isolation without compromising the weight-bearing capacity of the structure. This is realized through the appropriate determination of the static and dynamic stiffnesses via a novel calculation approach that is based on the initial static equilibrium point. The role of various design factors is investigated based on time-history responses of a reference structure to artificial accelerograms matching EC8 criteria, and the effect of the optimized SDA is evaluated on real earthquake records, confirming its capacity to greatly reduce the response to structure accelerations. The selection of the design parameters is based on engineering criteria and an indicative implementation of the design elements is included, demonstrating the feasibility of the proposed configuration.










Similar content being viewed by others
Data availability
The data used to support the findings of this study are available from the corresponding author upon request.
Code availability
The data used to support the findings of this study are available from the corresponding author upon request.
References
Abaqus Non-Linear FEA Software - The Best Simulation Solver | Simuleon (2021). https://www.simuleon.com/simulia-abaqus/. Accessed 27 Sep 2021
Antoniadis IA, Kanarachos SA, Gryllias K, Sapountzakis IE (2018) KDamping: a stiffness based vibration absorption concept. Jvc/j Vib Control 24(3):588–606. https://doi.org/10.1177/1077546316646514
Attary N, Symans M, Nagarajaiah S (2017) Development of a rotation-based negative stiffness device for seismic protection of structures. J Vib Control 23(5):853–867. https://doi.org/10.1177/1077546315585435
Carrella A, Brennan MJ, Waters TP (2007) Static analysis of a passive vibration isolator with quasi-zero-stiffness characteristic. J Sound Vib 301(3–5):678–689. https://doi.org/10.1016/j.jsv.2006.10.011
Chen J-L, Georgakis CT (2015) Spherical tuned liquid damper for vibration control in wind turbines. J Vib Control 21(10):1875–1885. https://doi.org/10.1177/1077546313495911
Chen MZQ, Smith MC (2009) Restricted complexity network realizations for passive mechanical control. IEEE Trans Autom Control 54(10):2290–2301. https://doi.org/10.1109/TAC.2009.2028953
Compression Spring Calculator (Load Based Design) (2021). https://amesweb.info/MechanicalSprings/CompressionSpringForcedBasedDesign.aspx. Accessed 27 Sep 2021
DeSalvo R (2007) Passive, nonlinear, mechanical structures for seismic attenuation. J Comput Nonlinear Dyn 2(4):290. https://doi.org/10.1115/1.2754305
Debnath N, Deb SK, Dutta A (2016) Multi-modal vibration control of truss bridges with tuned mass dampers under general loading. Jvc/j Vib Control 22(20):4121–4140. https://doi.org/10.1177/1077546315571172
De Domenico D, Deastra P, Ricciardi G, Sims ND, Wagg DJ (2019) Novel fluid inerter based tuned mass dampers for optimised structural control of base-isolated buildings. J Franklin Inst 356(14):7626–7649. https://doi.org/10.1016/j.jfranklin.2018.11.012
De Domenico D, Impollonia N, Ricciardi G (2018) Soil-dependent optimum design of a new passive vibration control system combining seismic base isolation with tuned inerter damper. Soil Dyn Earthq Eng. https://doi.org/10.1016/j.soildyn.2017.11.023
De Domenico D, Ricciardi G (2018) An enhanced base isolation system equipped with optimal tuned mass damper inerter (TMDI). Earthq Eng Struct Dynam. https://doi.org/10.1002/eqe.3011
De Domenico D, Ricciardi G (2018) Optimal design and seismic performance of tuned mass damper inerter (TMDI) for structures with nonlinear base isolation systems. Earthq Eng Struct Dynam 47(12):2539–2560. https://doi.org/10.1002/eqe.3098
EN 1998–1 (2004) Eurocode 8: design of structures for earthquake resistance – part 1: general rules, seismic actions and rules for buildings
Fluid Viscous Dampers | Seismic Dampers | ITT Infrastructure | ITT Enidine (2020). https://www.itt-infrastructure.com/en-US/Products/Viscous-Dampers/. Accessed 22 Jan 2020
Gasparini D, Vanmarcke EH (1976) Simulated earthquake motions compatible with prescribed response spectra. M.I.T. Dep Civ Eng Res Rep
Giaralis A, Taflanidis AA (2018) Optimal tuned mass-damper-inerter (TMDI) design for seismically excited MDOF structures with model uncertainties based on reliability criteria. Struct Control Health Monit. https://doi.org/10.1002/stc.2082
Gong W, Xiong S (2016) Probabilistic seismic risk assessment of modified pseudo-negative stiffness control of a base-isolated building. Struct Infrastruct Eng 12(10):1295–1309. https://doi.org/10.1080/15732479.2015.1113301
Hashimoto T, Fujita K, Tsuji M, Takewaki I (2015) Innovative base-isolated building with large mass-ratio TMD at basement for greater earthquake resilience. Future Cities Environ. https://doi.org/10.1186/s40984-015-0007-6
Ibrahim RA (2008) Recent advances in nonlinear passive vibration isolators. J Sound Vib 314(3–5):371–452. https://doi.org/10.1016/j.jsv.2008.01.014
Iemura H, Pradono MH (2009) Advances in the development of pseudo-negative-stiffness dampers for seismic response control. Struct Control Health Monit 16(7–8):784–799. https://doi.org/10.1002/stc.345
Kapasakalis KA, Alvertos AE, Mantakas AG, Antoniadis IA, Sapountzakis EJ (2020c) Advanced negative stiffness vibration absorber coupled with soil-structure interaction for seismic protection of buildings. Proc Int Conf Struct Dyn EURODYN 2:4160–4176. https://doi.org/10.47964/1120.9340.19963
Kapasakalis KA, Antoniadis IA, Sapountzakis EJ (2020b) Optimal design of advanced negative stiffness absorbers. Proc Int Conf Struct Dyn EURODYN 2:4177–4188 https://doi.org/10.47964/1120.9341.20128
Kapasakalis KA, Antoniadis IA, Sapountzakis EJ (2020a) Performance assessment of the KDamper as a seismic absorption base. Struct Control Health Monit. https://doi.org/10.1002/stc.2482
Kapasakalis KA, Antoniadis IA, Sapountzakis EJ (2021a) Constrained optimal design of seismic base absorbers based on an extended KDamper concept. Eng Struct. https://doi.org/10.1016/j.engstruct.2020.111312
Kapasakalis KA, Antoniadis IA, Sapountzakis EJ (2021b) A soil-dependent approach for the design of novel negative stiffness seismic protection devices. Appl Sci 11(14):6295. https://doi.org/10.3390/APP11146295
Kapasakalis KA, Antoniadis IA, Sapountzakis EJ (2021c) Feasibility assessment of stiff seismic base absorbers. J Vib Eng Technol 2021:1–17. https://doi.org/10.1007/S42417-021-00362-2
Kapasakalis KA, Antoniadis IA, Sapountzakis EJ (2021d) STIFF vertical seismic absorbers. Jvc/j Vib Control. https://doi.org/10.1177/10775463211001624
Kapasakalis KA, Antoniadis IA, Sapountzakis E (2019) KDamper concept for base isolation and damping of high-rise building structures
Kelly JM (1999) The role of damping in seismic isolation. Earthq Eng Struct Dynam 28(1):3–20. https://doi.org/10.1002/(SICI)1096-9845(199901)28:1%3c3::AID-EQE801%3e3.0.CO;2-D
Lazar IF, Neild SA, Wagg DJ (2014) Using an inerter-based device for structural vibration suppression. Earthq Eng Struct Dynam. https://doi.org/10.1002/eqe.2390
Li H, Li Y, Li J (2020) Negative stiffness devices for vibration isolation applications: a review. Adv Struct Eng. https://doi.org/10.1177/1369433219900311
Lu LY, Chen PR, Pong KW (2016) Theory and experiment of an inertia-type vertical isolation system for seismic protection of equipment. J Sound Vib 366:44–61. https://doi.org/10.1016/j.jsv.2015.12.009
Luft RW (1979) Optimal tuned mass dampers for buildings. J Struct Div 105(12):2766–2772
MatWeb - The Online Materials Information Resource (2021). http://www.matweb.com/errorUser.aspx?msgid=2&ckck=nocheck. Accessed 27 Sep 2021
Molyneaux W (1957) Supports for vibration isolation. G. Britain: ARC/CP-322, Aer Res Council
Naeim F, Kelly JM (1999) Design of seismic isolated structures: from theory to practice. Wiley, New Jersey
Nagarajaiah S, Pasala DTR, Reinhorn A, Constantinou M, Sirilis AA, Taylor D (2013) Adaptive negative stiffness: a new structural modification approach for seismic protection. Adv Mater Res 639–640:54–66. https://doi.org/10.4028/www.scientific.net/amr.639-640.54
Newland DE (2005) An introduction to random vibrations, Spectral & wavelet analysis, 3rd edn. Dover Civil and Mechanical Engineering, p 512
Platus DL, Platus DL (1992) Negative-stiffness-mechanism vibration isolation systems. In Proc. of SPIE, vol 1619. pp 44–54
Qin L, Yan W, Li Y (2009) Design of frictional pendulum TMD and its wind control effectiveness. J Earthq Eng Eng Vib 29(5):153–157
Ramezani M, Bathaei A, Ghorbani-Tanha AK (2018) Application of artificial neural networks in optimal tuning of tuned mass dampers implemented in high-rise buildings subjected to wind load. Earthq Eng Eng Vib 17(4):903–915. https://doi.org/10.1007/s11803-018-0483-4
Saha A, Mishra SK (2019) Adaptive negative stiffness device based nonconventional tuned mass damper for seismic vibration control of tall buildings. Soil Dyn Earthq Eng 126:105767. https://doi.org/10.1016/j.soildyn.2019.105767
Saitoh M (2012) On the performance of gyro-mass devices for displacement mitigation in base isolation systems. Struct Control Health Monit 19(2):246–259. https://doi.org/10.1002/stc.419
Seismosoft (2018) SeismoArtif - A computer program for generating artificial earthquake accelerograms matched to a specific target response spectrum. http://www.seismosoft.com
Smith MC (2002) Synthesis of mechanical networks: the inerter. In: IEEE transactions on automatic control, vol 47. https://doi.org/10.1109/TAC.2002.803532
Taniguchi T, Der Kiureghian A, Melkumyan M (2008) Effect of tuned mass damper on displacement demand of base-isolated structures. Eng Struct 30(12):3478–3488. https://doi.org/10.1016/j.engstruct.2008.05.027
Weber B, Feltrin G (2010) Assessment of long-term behavior of tuned mass dampers by system identification. Eng Struct 32(11):3670–3682. https://doi.org/10.1016/j.engstruct.2010.08.011
Xiang P, Nishitani A (2014) Optimum design for more effective tuned mass damper system and its application to base-isolated buildings. Struct Control Health Monit 21(1):98–114. https://doi.org/10.1002/stc.1556
Acknowledgements
Marina Kalogerakou has been financed by the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant (grant agreement No INSPIRE-813424, “INSPIRE—Innovative Ground Interface Concepts for Structure Protection”). The authors are grateful to the reviewers for their observations and constructive comments.
Funding
Marina Kalogerakou has been financed by the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant (grant agreement No INSPIRE-813424, “INSPIRE—Innovative Ground Interface Concepts for Structure Protection”).
Author information
Authors and Affiliations
Contributions
Conceptualization: [MK, KK, IA], Methodology: [MK, KK, IA], Software: [MK], Formal analysis: [MK, IA], Investigation: [MK], Resources: [MK, KK], Data curation: [MK, KK], Writing—original draft: [MK], Visualization: [MK, KK, IA], Validation: [MK], Writing—review and editing: [MK, KK, IA], Project administration: [IA, ES], Funding acquisition: [IA, ES], Supervision: [IA. ES].
Corresponding author
Ethics declarations
Conflict of interest
The authors declare there are no conflicts of interest regarding the publication of this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1: Analysis of the proposed indicative implementation of the assembly
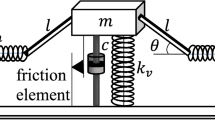
The potential energy of the assembly in Fig. 2 is:
where \({k}_{H}\) is the stiffness of the inclined spring, \({l}_{H}\) its length at position u and \({l}_{HI}\) its initial (uncompressed) length. The spring compression is denoted by V(u):
Equation (A.1) becomes:
The negative stiffness force of the assembly results as
and the negative stiffness \({\text{k}}_{\text{N}}\) is:
Moreover, the compression force Q on the spring kH is:
In view of Fig. 2 the following equations hold:
The combination of Eqs. (A.2) and (A.7) leads to:
As a result, Eqs. (A.4) and (A.5) become:
Introducing the notations
Equations (A.11) and (A.12) become:
Appendix 2: SDA under external force excitation
Considering an external force \(f(t) = \tilde{F}e^{j\omega t}\) acting on the structure of Fig. 1c (while XG = 0), the equations of motions of the two masses take the form:
The steady state responses of the system are
where \(\tilde{X}_{S} , \tilde{X}_{D}\), denote the response complex amplitudes. The above-mentioned equations of motion of the system hence become:
The complex amplitude \({{\tilde{\text{F}}}}\) of the acting force can be conveniently written in terms of the complex amplitude of the displacement \({{\tilde{\text{X}}}}_{{ST}}\) and total stiffness \({k}_{T}\):
The resulting transfer functions (TFs) of the displacement are
where \(\tilde{H}\) has been defined in (31) as
The resulting force \(f_{B }\) at the base is calculated as:
Hence the TF of the force at the base is:
In view of (B.6) the above reads
where
and \(D = \tilde{H}_{11} \tilde{H}_{22} - \tilde{H}_{12}^{2}\) is the determinant of the matrix \(\tilde{H}\). It follows that:
Turning to paragraph 2.3 and in view of Eq. (31.a), the transfer function of the structure acceleration as for a ground acceleration excitation of amplitude \({\text{A}}_{\text{G}}\) is calculated:
Rearranging the above
In view of the above and (B-13) it follows that:
The transfer function of the response structure acceleration for a base excitation is the same as the transfer function of the response force at the base in the case of a force excitation.
Appendix 3: Selection of ground motion acceleration excitation power spectrum
Expressions (34) and (35) call for a specific ground excitation profile. The relevant excitation power spectrum is selected following the same procedure used in Kapasakalis et al. (2021d). The vertical component of the ground motion is described in EN1998-1 (2004) by an elastic ground acceleration response spectrum. For each seismic zone the vertical acceleration is given by the ratio avg/ag, the recommended values of which are 0.9 for seismic action Type 1 (magnitude Mw > 5.5) and 0.45 for Type 2. The basic shape of the spectrum is similar to the recommended horizontal. However, the spectral amplification in the vertical case is 3.0 instead of 2.5. The vertical acceleration response spectrum with spectral acceleration ag = 0.36 g and Type 1 is can be found in Fig. 1b of Kapasakalis et al. (2021d).
A database of 50 artificial accelerograms was generated matching the aforementioned spectrum using the SeismoArtif Software (Seismosoft 2018). The method used for the generation of each accelerogram was the “Artificial Accelerogram Generation & Adjustment”, an iterative procedure based on the adaptation of a random process (Gasparini and Vanmarcke 1976) to a target spectrum, which in this case is that of EC8 described above. The process can be summarized as follows:
A random process is used for the generation of a large enough set of phase angles for a series of sinusoidal waves, the sum of which comprise a periodic function. To simulate the transient nature of the earthquakes, the steady state motions are multiplied by a relevant envelope shape (or intensity function), forming an initial artificial accelerogram. In each iteration, this is transferred to the frequency domain using the Fourier Transformation Method, and it is corrected to match the target spectrum. Subsequently, the Inverse Fourier Transform is utilized for the appropriate PGA and Baseline corrections in the time domain. The Fourier Transformation Method is again applied on the corrected accelerogram and the same process is repeated until convergence is achieved. An example of such generated accelerogram can be found in Fig. 1c of Kapasakalis et al. (2021d).
The mean acceleration response spectrum of the 50 artificial accelerograms of the database compared to the EC8 design vertical acceleration response spectrum has been shown in Fig. 1b of Kapasakalis et al. (2021d). An accurate match is observed with a percentage deviation under 10% in all the range of the natural periods.
Τhe mean power spectral density SAM of the 50 accelerograms is calculated (Fig.
11). Finally, the PSD of the ground motion acceleration, SA, which is used for the calculation of RAS in Eq. 35.c is calculated as the least-square fitting curve of the mean power spectral density SAM. SAM together with the PSD of a random artificial accelerogram are also shown in Fig. 11.
Appendix 4: Effect of key SDA design factors to real earthquakes records
4.1 Effect of objective function
Table 8 below presents the results of the SDA optimized with the two different objective functions, QAS and RAS, defined in Eqs. (33.c) and (35.c) respectively and discussed in paragraph 3.4. Peak response quantities (structure acceleration, aS, structure relative displacement, uS, oscillating mass relative displacement, uD) are shown for the SDA optimized under each method, and for the conventional damping system. The results verify the equivalency of the two methods in terms of the resulting response.
4.2 Effect of inerter between structure-base
Table
9 below presents the results of the system optimized (i) including the inerter bR placed between the structure and the base (SDA as shown in Fig. 1c), and (ii) without the inerter bR (SDA-NI). Peak response quantities (structure acceleration, aS, structure relative displacement, uS, oscillating mass relative displacement, uD) are shown for the SDA optimized under each method, and for the conventional damping system. The results verify the beneficial impact of the inerter for all response quantities in almost all the earthquake cases.
4.3 Effect of additional internal inerters
Table
10 below presents the results of the system optimized (i) including a single inerter bR (SDA as shown in Fig. 1c), and (ii) including two additional inerers, bN, bP, bR (SDA-II as shown in Fig. 1d). Peak response quantities (structure acceleration, aS, structure relative displacement, uS, oscillating mass relative displacement, uD) are shown for the SDA optimized under each method, and for the conventional damping system. The results confirm that the additional inerters do not add a significant advantage in the efficiency of the system.
4.4 Effect of static stiffness k S
Tables
11 and
12 below present the results of the SDA system optimized for different values of static displacement (XVSD = 1, 2, 3 cm), compared to the conventional damping system (CD) of corresponding static stiffness.). Peak response quantities (structure acceleration, aS, structure relative displacement, uS, oscillating mass relative displacement, uD) are shown for each earthquake. Structure acceleration, aS, and structure relative displacement, uS, are shown in comparison to those of the conventional damping system of corresponding static stiffness.
Appendix 5: Indicative implementation of key elements of the SDA configuration—negative stiffness element and inerter
5.1 Detailed design of conventional spring and stress analysis
An indicative example regarding the realization of the NS element having constant NS (cI = 0), with the proposed configuration presented in Fig. 2 and Appendix 1, is presented below. The value (constant) of the NS element is obtained from Table 2 which corresponds to the optimized SDA with an objective function that of QAS (kNS = − 86.45 kN/m). The fixed values for this set of optimized parameters are presented in Table 1.
In order for the generated NS to be constant, the dimensionless parameter cI (Eq. A.12.a) is set equal to zero. Thus, the length of the undeformed conventional stiffness element kH (lHI) is equal to the parameter b. In addition, in the static equilibrium position, when we consider cI = 0, the rod of length a is placed horizontally. As a consequence, the maximum absolute NS element stroke (uD) is equal to the rod length a.
In Appendix 4, the dynamic responses of the SDA are presented for all the considered real earthquake records. It is observed that the maximum (absolute) value of the additional mass relative displacement is below 8 cm, for all real and artificial seismic records. Having this value as an upper limit of the uD (and thus the NS stroke) the rod length is set equal to 8 cm.
The value of the two horizontal conventional stiffness elements (kH) is obtained from Eq. (A.14) (kH = 43.225 kN/m). In this example, the kH is realized as a conventional spiral spring. The design parameters for this spiral spring are presented in Table
13, and are selected with analytical expressions (Compression Spring Calculator (Load Based Design) 2021) in order for the spring to have a factor of safety against torsional yielding at its solid length greater than 1.3, and a factor of safety against buckling greater than 1.2. The material used is chrome-vanadium (ASTM A232 Alloy Steel Wire).
In addition, a stress analysis for the spiral spring is performed by employing the FE code ABAQUS (2021) in order to evaluate the maximum stresses that occur when the spring is fully deformed (8 cm). The mechanical properties used in order to model the spiral spring are obtained from MatWeb (2021). In Fig.
12, the deflections along the spring length, and the maximum von Mises stresses are presented when the spring with the characteristics presented above, is in its fully deformed state. It is observed that the stresses are retained 25% (safety factor 1.32) below the maximum allowable stress that this material allows.
5.2 Realization of inerter element
The inerter can be realized by an easy to construct mechanical device proposed in Smith (2002), which satisfies certain practical conditions. More specifically, a plunger sliding is inserted in a cylinder which drives a flywheel through a rack, pinion, and gears (see Fig. 3 of Smith 2002). This configuration does not have the limitation that one of the two terminals of the inerter needs to be grounded. To model the dynamics of this device, let r1 be the radius of the rack pinion, r2 the radius of the gear wheel, r3 the radius of the flywheel pinion, γ the radius of gyration of the flywheel, m the mass of the flywheel, and assume the mass of all other components is negligible. The equivalent inertance generated by this mechanical device is:
where m2 is the mass of the flywheel, α1 = γ/r3 and α2 = r2/r1. The required inertance ratio for the SDA device is μb = 43%, thus for a reference structure mass of 1000 kg, the generated inertance is 430 kg. For α1 = α1 = 5, and a radius of the flywheel R2 = 7.5 cm with a thickness of 1 cm, the mass of the flywheel (steel) is m2 = 1.376 kg, leading to a generated inertance of 430 kg.
Rights and permissions
About this article
Cite this article
Kalogerakou, M.E., Kapasakalis, K.A., Antoniadis, I.A. et al. Vertical seismic protection of structures with inerter-based negative stiffness absorbers. Bull Earthquake Eng 21, 1439–1480 (2023). https://doi.org/10.1007/s10518-021-01284-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10518-021-01284-w