1 Introduction

The seismic assessment and retrofitting of existing masonry buildings remains a challenging topic in structural engineering due to both the complexity and variability of unreinforced masonry structures and the several factors affecting their dynamic behaviour.

Among these factors, the in-plane flexibility of traditional timber floors and the lack of effective connections to load bearing walls are usually responsible for the development of local collapse mechanisms. Consequently, the seismic performance of a building can be improved by employing floors and roofs with a high in-plane stiffness, thereby allowing the seismic load to be effectively transferred to shear-resistant walls and reducing the out-of-plane overturning of perimeter walls.

Several in-plane strengthening techniques for timber floors have been experimentally studied in recent years, with a particular focus on the reversibility of the intervention and its compatibility with the existing parts of the buildings. These solutions may use steel elements, fibre-reinforced polymer strips, timber boards or timber-based panels (Gubana, 2015). Accordingly, the in-plane performance of flexible and strengthened timber floors have been the focus of many numerical studies and analytical models (Peralta et al. 2003; Whitney and Agrawal 2015; Rizzi et al. 2017, 2019a, b; Giongo et al. 2018; Metelli et al. 2019; Gubana and Melotto 2019b).

The influence of the mechanical properties of floors on the global seismic behaviour of masonry buildings has been addressed in different studies using linear dynamic numerical analysis (Tena-Colunga and Abrams 1996), push-over analysis (Giongo et al. 2012; Gattesco and Macorini 2014; Ortega et al. 2018; Jiménez-Pacheco et al. 2020) and non-linear dynamic analysis (Betti et al. 2014; Gubana and Melotto 2017, 2019a; Nakamura et al. 2017; Scotta et al. 2018; Trutalli et al. 2019). Moreover, previous investigations have evaluated the possibility of designing and calibrating the in-plane properties of the floor to cap the shear forces transferred to shear-resistant walls (Preti et al. 2017; Longarini et al. 2019).

In addition to the floor in-plane properties, the quality of the connections between the floors and vertical elements strongly influences the seismic response. Proper connections are needed to reduce the vulnerability to out-of-plane actions. However, in most existing masonry buildings, the link between timber beams and walls is mainly friction-based, and in many cases, these timber beams are inserted in pockets with no embedment on the perimeter walls. Hence, many solutions have been studied and implemented to connect joists to masonry walls by using steel elements anchored to the floor. A review of these different techniques can be found in Moreira et al. (2014).

This study investigates the influences of the floor in-plane hysteretic properties and the floor-to-wall connection properties on the seismic response of a typical heritage masonry building. The analysis is conducted by means of the Discrete Element Method (DEM), recently applied to masonry structures, as it allows to consider the complete separation of bodies and the formation of new contacts during the evolution of the seismic event. Stresses and deformations are transmitted by contact forces between blocks, and thus, collapse sequences can be followed in detail.

Therefore, this approach can be adopted to better understand the complex dynamic behaviour of masonry structures under seismic action (Lancioni et al. 2012; Lemos and Campos Costa 2017; Bui et al. 2017) and to simulate all the mechanisms (out-of-plane rocking and out-of-plane collapse of masonry piers) observed in masonry buildings without “box behaviour”. Moreover, recent studies (Baraldi et al., 2018, 2020; Bui et al., 2019; Pulatsu et al. 2020) confirm the efficiency and robustness of the DEM in simulating the in-plane behaviour of regular masonry wall panels. Gubana and Melotto (2019a) first investigated a simple masonry cell via DEM. The results of this work emphasized the capability of the DEM to capture the triggering of the out-of-plane mechanisms of masonry walls and the effectiveness of the considered strengthening interventions in preventing their failure.

In this paper, a more complex structure is addressed, and a heritage building is considered as a case study. The dynamic responses of the structure with unstrengthened and strengthened floors are compared, and the effect of the actual cyclic hysteretic response of the floor and its capability to dissipate energy are investigated by using a specially developed floor model combined with the DEM masonry model. The cyclic behaviour assigned to both unreinforced and reinforced floors is derived from previous tests (Gubana and Melotto 2018) and specially developed numerical models (Gubana and Melotto 2021). The experimental samples replicate traditional timber floors unreinforced or reinforced with timber-based panels connected to the original floor by means of nails or self-tapping screws. These techniques are reversible and minimally invasive and are characterised by a small mass and low thickness.

Five different earthquake records are applied for the analyses. Three of these records are scaled to be compatible with the local spectrum. The other two are the original records and are characterised by greater magnitudes. The results are compared, considering the out-of-plane displacements of the masonry walls, the base reaction of the structures, the dissipated energy and the collapse mechanisms.

In Sect. 2, the building selected for the case study is described. In Sect. 3, the modelling strategies for masonry walls and timber floors are reported. In Sect. 4, the numerical results for the five seismic records are reported.

2 Description of the case study

The building selected for the case study is a typical example of a noble villa in north-eastern Italy. The current appearance of this building, an ancient country residence of the Cattaneo family, is attributable to two important renovations. The first renovation began in 1718, and the second renovation began at the end of the eighteenth century. At that time, the two-storey palace was raised two floors with respect to the original building, and a new principal façade crowned by a triangular tympanum with a star decoration on the exterior was erected on the south side to replace the original façade on the east side. Due to this intervention, the internal wall layout on the new storeys does not match that on the lower storeys, as better explained in the following. In addition, the 4th storey covers only a small portion of the building.

The main façade of the villa (south) and the east façade are shown in Fig. 1.

Fig. 1
figure 1

Pictures of the Villa Cattaneo (San Quirino, PN, Italy), chosen for the case study

Full size image

The building has a compact rectangular shape approximately 16 m by 15 m in size.

Drawings of the floor plans, a cross-section through the building and a profile of the front façade are shown in Fig. 2. The internal layout of each storey is characterised by a central hall spanning the length of the building with rooms on either side. The internal walls are oriented mainly east–west, and the timber floor beams are oriented north–south. The walls are made of rubble stone masonry and range in thickness from 55 cm (ground floor) to 45 cm (upper storeys).

Fig. 2
figure 2

Drawings of the villa chosen for the case study (measurements in centimetres)

Full size image

Non-invasive surveys were carried out using micro cameras inside the walls and by means of thermographic imaging. Considering the texture and the quality of the masonry, the reference values suggested in the Italian building code were employed (CS.LL.PP. 2018). Additional visual inspections and ground penetrating radar investigations were further performed to acquire accurate knowledge of the timber structures (Riggio et al. 2018).

A north–south masonry wall was added to the ground and first floors in the years immediately following the 1976 Friuli earthquake. On the third floor, the main hall is oriented orthogonally to the main halls of the lower storeys, so the internal walls have large openings and are oriented only east–west. Unfortunately, this increases the vulnerability of the main façade to out-of-plane mechanisms and makes this building an interesting case study for evaluating the effect of the floor behaviour on the dynamic response of the building.

3 Description of the numerical model

The building described above is selected for the case study to investigate the effect of the timber floor behaviour and to evaluate the effectiveness of strengthening solutions. The geometry, wall thickness and applied loads in the numerical model comply with those of the actual building. However, the shape of the building is slightly simplified for ease of modelling. Moreover, the roof structure and the small 4th storey are not considered in the model, although their masses are applied to the 3rd floor.

The numerical simulations are carried out by using the DEM with the commercial general-purpose ABAQUS/Explicit software (Abaqus 2011). Figure 3 shows a view of the numerical model. The highlighted points are the control points used for the results in the following sections.

Fig. 3
figure 3

Numerical model of the building using the DEM

Full size image

3.1 Masonry walls modelling

The actual walls are characterised by rubble stone masonry, but regularly shaped stones are used at the corners. In the DEM, the discontinuities within the masonry are explicitly taken into account by considering masonry blocks that interact through contact points at the interfaces.

The masonry walls are divided into distinct blocks with approximate dimensions of 1.0 m × 0.5 m × 0.5 m. The block division is not intended to describe the wall texture. Due to computational limits, the possibility of considering individual stones is now reserved for isolated masonry walls or very simple structures. However, the chosen block size is considered to be sufficiently small with respect to the building size to study the collapse mechanisms.

The material assigned to the masonry blocks is isotropic, homogeneous and elastic. The density and elastic modulus are typical of the Italian rubble stone masonry employed in the considered building (Table 1).

Table 1 Properties assigned to the masonry blocks and interfaces
Full size table

The masonry non-linearity is considered at the interfaces between blocks. In the analyses, a frequently used approach is followed (Lemos and Campos Costa 2017; Bui et al. 2019), where the interaction in the normal direction is of rigid contact with infinite compressive strength. In the tangential direction, a Coulomb isotropic friction relationship and a cohesive model with a tensile-shear Rankine failure criterion are considered. Thus, masonry elements fully adhere at the beginning of the analysis; when the interface failure criterion is reached, the blocks separate, and large displacements can occur. The properties assigned to the blocks and to the interactions are reported in Table 1. The tensile and shear strengths and the friction coefficient are typical of the considered masonry type. The strength values are those reported in the Italian building code (CS.LL.PP. 2018). A viscous elastic damping coefficient of 0.05 is assigned to the masonry material, whereas no additional damping is assigned to the contact interfaces. The dissipation is described by plasticization and damage at the interfaces.

The ABAQUS General Contact method is used, and the significant contact pairs are automatically generated by a Python script and are applied as surface-to-surface contacts.

Due to the recognised importance of the density of contact points for correctly evaluating the stress distribution and hence the failure mechanism, a sensitivity analysis is performed to assess the reliability of the assigned contact model. The contact point density is progressively increased, and a mesh size of 10 cm is considered a reasonable compromise between accuracy and computational time (Gubana and Melotto 2019a) and for this reason is adopted in the present work.

3.2 Timber floor modelling

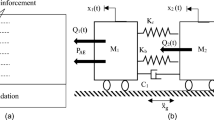
In the numerical DEM model, accurate modelling of the floor is implemented. The floor is composed of timber beams spaced 50 cm apart which are inserted in the pockets of the bearing walls. The floor global behaviour is modelled by using non-linear springs between adjacent joists, as shown in Fig. 4 (Gubana and Melotto 2019a). This global model of the floor is properly developed and checked on the basis of the experimental tests in Gubana and Melotto (2018). The spring hysteretic properties are calibrated to exactly reproduce the tested floor results (Gubana and Melotto 2019a). In particular, the assigned properties (stiffness, strength, hardening and damage) are the average properties extrapolated from the experimental results for each floor type.

Fig. 4
figure 4

Simplified modelling approach for the timber floor

Full size image

In those tests, traditional timber floors made by beams and boards are considered unreinforced specimens. The reinforced configurations use an overlay of Oriented Strand Boards (OSB) panels or Cross-Laminated Timber (CLT) panels to increase the in-plane stiffness and strength. Different fasteners (ring-type nails and self-tapping screws) are used. Cyclic tests are performed after loading the samples in the joist direction, and these experiments are replicated in the numerical models.

In the DEM model, the timber beams are set into wall pockets, and a Coulomb friction interaction is considered between the two materials. A friction coefficient μ = 0.4 is chosen by averaging literature data (e.g., Lin and LaFave 2012). The eventual contact between the joist heads and the masonry is taken into account.

The effect of the connection between the floor and the walls is also investigated, as the out-of-plane failure mechanisms in masonry buildings are often a direct result of poor connections between these two structural elements. In this research work, three basic assumptions are made: the absence of effective connections for the unreinforced floor case and either elastic connections (stiffness 15 kN/mm) or elastic–plastic connections (stiffness 15 kN/mm, strength 4.0 kN) for the reinforced and rigid floor cases. The properties are chosen considering a 16 mm diameter steel bar embedded in the masonry using the equations reported in Brignola et al. (2012).

3.3 Applied loads

The structure is loaded in two stages. In the first one, gravity is applied, and the equilibrium state is reached. The considered vertical loads are the self-weight of the masonry and of the floors. A floor live load of 3.0 kN/m2 is applied as a distributed mass, and the load combinations are those prescribed by the Eurocode (EN1990 2002). The load is chosen in the hypothesis of a public use of the listed building.

In the second stage, an acceleration history is applied to the rigid base in the north–south direction (Fig. 3).

Three seismic acceleration histories are chosen using the REXEL tool (Iervolino et al. 2009), which provides a group of scaled seismic records compatible with the site spectrum. The records used are the Gemona (Italy) seismic record of September 15th, 1976 (09:21 UTC), the Mirandola (Italy) seismic record of May 20th, 2012, and the San Felice sul Panaro (Italy) seismic record of May 29th, 2012. These three earthquakes are identified with the labels “GMN”, “MRN” and “SAN”, respectively. Figure 5a shows the spectra of the three scaled seismic histories and the Italian building code spectrum for the building site (475-year return period).

Fig. 5
figure 5

Response spectra of the three scaled seismic records and the two unscaled records

Full size image

Notably, the 1976 Friuli earthquake had limited effects on the building considered herein due to the strong attenuation of ground motions between the fault and the villa site (Bragato and Slejko 2005). In addition to the three scaled seismic records, which are compatible with the site spectrum, two real seismic acceleration histories are considered without scaling, both of which are from the 1976 Friuli earthquake, whose epicentre was just 50 km from the villa considered as the case study. The two records are the Gemona (Italy) seismic record of May 6th, 1976 (20:00 UTC) and the Gemona (Italy) seismic record of September 15th, 1976 (03:15 UTC), which are named “May76” and “Sep76”, respectively, in the following. Figure 5b shows the spectra of these two unscaled seismic histories.

4 Summary of the studied cases

A summary of the analysed numerical models is provided in Table 2. The label assigned to each model identifies the seismic acceleration history (using the strings defined above), namely, the floor type (UR for the unreinforced and unconnected floor; CLT for the floor reinforced by means of CLT panels; RIG for the ideal rigid case) and the floor-to-wall connection type (elastic, EL, or elastic–plastic, EP).

Table 2 Summary of the analysed models
Full size table

5 Numerical results

The results of the DEM analysis for the three scaled ground motions are plotted in Fig. 6, 7, 8. Several parameters are chosen for the comparison:

  1. (a)

    the out-of-plane displacements of the masonry walls loaded out of the plane (south façade, point P1.3 in Fig. 3);

  2. (b)

    the in-plane displacements of the lateral walls (point P4.3 in Fig. 3);

  3. (c)

    the base reaction force history;

  4. (d)

    the energy dissipated over time;

  5. (e)

    the load transferred from the floor to the lateral walls (elastic or elastic–plastic floor-to-wall connections).

Fig. 6
figure 6

Numerical results of the different DEM models for the GMN earthquake

Full size image
Fig. 7
figure 7

Numerical results of the different DEM models for the MRN earthquake

Full size image
Fig. 8
figure 8

Numerical results of the different DEM models for the SAN earthquake

Full size image

The reported energy values are the kinetic energy of the structure, the energy dissipated by the floor hysteretic behaviour and the energy dissipated by the masonry walls due to damage and friction effects.

All the results are summarised in Tables 3 and 4. For each seismic record and for each floor type, Table 3 reports the out-of-plane displacements of the face-loaded masonry walls and the corresponding inter-storey drift. Table 4 reports the in-plane displacements of the lateral walls and the minimum and maximum base reaction force values. The displacements are measured at each floor level, and the minimum and maximum values are reported.

Table 3 Summary of the results of the different numerical models (out-of-plane displacements and inter-storey drifts)
Full size table
Table 4 Summary of the results of the different numerical models (in-plane displacements and base reactions)
Full size table

The collapse mechanisms can be observed in Fig. 9 and in Fig. 10, where the displacements of the structures are shown for the UR floor and CLT-EL floor cases under the GMN earthquake and the SAN earthquake. The represented time step is the one when the maximum out-of-plane displacement of the south wall is reached.

Fig. 9
figure 9

Displacements of the building when the maximum out-of-plane value of the front façade is reached. The scaled seismic record is from the GMN earthquake

Full size image
Fig. 10
figure 10

Displacements of the building when the maximum out-of-plane value of the front façade is reached. The scaled seismic record is from the SAN earthquake

Full size image

In general, analyses of the models with an unreinforced floor clearly show the triggering of an out-of-plane mechanism of the north and south masonry walls. The masonry walls reach out-of-plane displacement values as high as 24 cm (Mirandola 2012 earthquake) or the complete collapse (SAN earthquake), as is evident in the out-of-plane displacement curves and the sudden increase in the kinetic energy.

When the CLT-reinforced floor elastically connected to the masonry walls is considered, the out-of-plane displacements of the masonry walls are overall smaller than those with an unreinforced floor. As an example, in Table 3, the out-of-plane displacement at point P1 on the third level of the building varies from 105 mm (drift 0.76%) in the case of an unreinforced floor to 24 mm (drift 0.29%) in the case of the floor reinforced by CLT under the GMN earthquake and varies from 239 mm (drift 3.73%) to 102 mm (1.74%) under the MRN earthquake. In contrast, out-of-plane collapse occurs with the unreinforced floor under the SAN earthquake, while this is prevented in the model with the CLT-reinforced floor. The floor transfers part of the seismic force to the in-plane loaded walls, where shear-sliding failure can be observed. The energy plots demonstrate that the CLT-reinforced floor is capable of dissipating a considerable amount of energy.

The use of elastic–plastic connections with the same floor type usually means slightly higher out-of-plane displacements and slightly lower base reaction force values. As shown in Figs. 6d, 7d and 8d, the energy dissipated by the floor system increases significantly with this connection type. Interestingly, this increase is compensated by a reduction in the energy dissipated by the walls, which means that the masonry is less damaged.

In almost all cases, the use of reinforced floors strongly increases the in-plane displacement of the lateral walls at all levels. This means that more cracks develop in the masonry, which is consistent with the increased transmission of forces to the sidewalls due to the stiffer floors. The use of elastic–plastic connections is associated with lower in-plane displacements than in the case of elastic floor-to-wall connectors. This confirms the reduced energy dissipation by the walls.

The displacements in the models with the ideal rigid floor are similar to those observed for the CLT-reinforced floor case. The out-of-plane displacements measured in the rigid floor case are due to the in-plane deformation of the lateral walls and to the deformation of the floor-to-masonry connectors. This comparison shows that the CLT-reinforced configuration is effective in creating a “box behaviour” of the masonry structure. It should be noted, however, that the peak base shear force is often higher when the ideal rigid floor is considered.

In the second series of analyses, the non-scaled accelerograms are used to test the structural responses under stronger earthquakes and, in particular, to study the effects of the floor-to-wall connections. The two seismic records from the 1976 Friuli earthquake are identified (as described above) with the labels “May76” and “Sep76”.

Only the CLT-EL (reinforced floor connected to the walls with elastic connections) and CLT-EP (reinforced floor connected to the walls with elastic–plastic connections) cases are considered with these two earthquake records.

The results of these DEM analyses are compared in Figs. 11 and 12. The load transferred from the floors to the lateral walls, the out-of-plane displacements of the face-loaded masonry walls (south and north façade, points P1 and P2 in Fig. 3), the in-plane displacements of the lateral walls (points P3 and P4 in Fig. 3), the base reaction force, and the energy dissipated over time are reported for both models. The reported energy values are the kinetic energy of the structure, the energy dissipated by the floor hysteretic behaviour and the energy dissipated by the masonry walls due to damage and friction effects.

Fig. 11
figure 11

Numerical results of the different DEM models for the May76 earthquake

Full size image
Fig. 12
figure 12

Numerical results of the different DEM models for the Sep76 earthquake

Full size image

The results are also summarised in Tables 5 and 6 considering the same parameters as before.

Table 5 Summary of the results of the different numerical models (May76 and Sep76 seismic records). Out-of-plane displacements and floor drifts
Full size table
Table 6 Summary of the results of the different numerical models (May76 and Sep76 seismic records). In-plane displacements and base reactions
Full size table

The collapse mechanisms can be observed in Fig. 13, where the displacements of the CLT-EL and CLT-EP structures are shown for the Sep76 earthquake. The represented time step is the one when the maximum out-of-plane displacement of the north wall is reached.

Fig. 13
figure 13

Displacements of the building when the maximum out-of-plane value of the rear façade is reached for the Sep76 earthquake

Full size image

The plasticization of the connectors in the CLT-EP case (Fig. 13b) can be observed as a displacement difference between the floor and the top of the lateral walls. These results confirm the possibility of properly designing and calibrating the strengthening intervention to cap the shear forces transferred to the shear-resistant walls and to dissipate energy, simultaneously reducing the out-of-plane displacements of the walls within their capacity.

The following final remarks can be deduced from the reported results:

  • The DEM allowed to obtain detailed information about the triggering of the out-of-plane behaviour of the structure;

  • Strengthened floors were shown to be able to counteract out-of-plane displacements;

  • The implemented model was able to estimate the energy dissipated by the floor hysteretic cycles and by the masonry damage;

  • Strengthened floors are able to dissipate a significant amount of seismic energy, thus reducing masonry damage.

6 Conclusions

Numerical simulations by means of the DEM were carried out to investigate the effectiveness of strengthening solutions for timber floors to enhance the seismic performance of a masonry building. The DEM approach can be used to analyse aspects of the masonry structure that cannot be captured by other numerical approaches, due to its ability to simulate the triggering and development of out-of-plane and in-plane collapse mechanisms.

Dynamic non-linear analyses were performed on a case study by considering the floor hysteretic behaviour and different seismic inputs. The building chosen as the case study is a noble villa representative of northeastern Italy that is characterised by the lack of internal walls in one direction.

The analyses were focused on the triggering of first-mode mechanisms, which were shown to be the governing mechanisms in all the analysed cases with unreinforced floors.

The application of CLT panels, dry connected to the existing floor, was experimentally demonstrated to increase the in-plane stiffness and strength of the floors. The comparison between the numerical results of the unreinforced and reinforced floor cases highlights the effectiveness of the proposed wood-based strengthening solution in reducing the out-of-plane displacements of the masonry walls to prevent overturning collapse mechanisms. The analyses also emphasised the ability of the reinforced floor to transfer the seismic forces to the shear-resistant walls by triggering in-plane shear collapse.

A comparison with an ideal rigid floor case confirms the good performance of the strengthening solution. The observed out-of-plane displacements are compatible with the masonry wall capacity, and energy is dissipated because of the reinforced floor hysteretic cycles.

The effects of different floor-to-wall connections are also assessed. Connections are needed to transfer the load to the bearing walls, but elastic–plastic connections can also be used to cap the load and to dissipate energy. This both reduces the out-of-plane displacement of the face-loaded walls and limits the in-plane damage to the seismic bearing walls.

In reality, floors that are too stiff could be detrimental to the seismic performance of masonry buildings, and in these cases, it is particularly important to cap the shear forces transferred to the shear-resistant walls. By using retrofitting solutions such as those considered in this work, the in-plane performance of the floor can be properly designed and calibrated to maximise the energy dissipation without exceeding the capacity of the existing masonry structure.

The combined approach of DEM modelling and timber floor cyclic modelling discussed here has proven to be a valid strategy to perform further investigations on the possibility of controlling the energy dissipation involved in the dynamic responses of masonry buildings with strengthened timber floors.